Engage NY Eureka Math 7th Grade Module 1 Lesson 8 Answer Key
Eureka Math Grade 7 Module 1 Lesson 8 Example Answer Key
Write an equation that will model the real-world situation
Example 1.
Do We Have Enough Gas to Make It to the Gas Station?
Answer:
Your mother has accelerated onto the interstate beginning a long road trip, and you notice that the low fuel light is on, indicating that there is a half a gallon left in the gas tank. The nearest gas station is 26 miles away. Your mother keeps a log where she records the mileage and the number of gallons purchased each time she fills up the tank. Use the information in the table below to determine whether you will make it to the gas station before the gas runs out. You know that if you can determine the amount of gas that her car consumes in a particular number of miles, then you can determine whether or not you can make it to the next gas station.
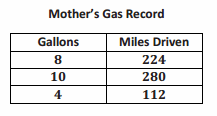
a. Find the constant of proportionality, and explain what it represents in this situation.
Answer:
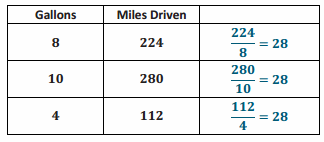
The constant of proportionality, k, is 28. The car travels 28 miles for every one gallon of gas.
b. Write equation(s) that will relate the miles driven to the number of gallons of gas.
Answer:
y = 28x or m = 28g
c. Knowing that there is a half gallon left in the gas tank when the light comes on, will she make it to the nearest gas station? Explain why or why not.
Answer:
No, she will not make it because she gets 28 miles to one gallon. Since she has \(\frac{1}{2}\) gallon remaining in the gas tank, she can travel 14 miles. Since the nearest gas station is 26 miles away, she will not have enough gas.
d. Using the equation found in part (b), determine how far your mother can travel on 18 gallons of gas. Solve the problem in two ways: once using the constant of proportionality and once using an equation.
Answer:
Using arithmetic: 28(18) = 504
Using an equation: m = 28g – Use substitution to replace the g (gallons of gas) with 18.
m = 28(18) – This is the same as multiplying by the constant of proportionality.
m = 504
Your mother can travel 504 miles on 18 gallons of gas.
e. Using the constant of proportionality, and then the equation found in part (b), determine how many gallons of gas would be needed to travel 750 miles.
Using arithmetic: \(\frac{750}{28}\) = 26.8
Using algebra:
m = 28g
750 = 28g
→ Use substitution to replace the m (miles driven) with 750.
→ This equation demonstrates dividing by the constant of proportionality or using the multiplicative inverse to solve the equation.
(\(\frac{1}{28}\))750 = (\(\frac{1}{28}\))28g
26.8 = 1g
26.8 (rounded to the nearest tenth) gallons would be needed to drive 750 miles.
Example 2:
Andrea’s Portraits
Andrea is a street artist in New Orleans. She draws caricatures (cartoon-like portraits) of tourists. People have their portrait drawn and then come back later to pick it up from her. The graph below shows the relationship between the number of portraits she draws and the amount of time in hours she needs to draw the portraits.
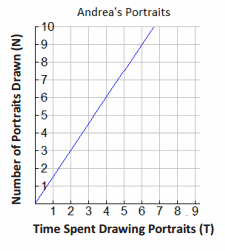
a. Write several ordered pairs from the graph, and explain what each ordered pair means in the context of this graph.
Answer:
(4,6) means that in 4 hours, she can draw 6 portraits.
(6,9) means that in 6 hours, she can draw 9 portraits.
(2,3) means that in 2 hours, she can draw 3 portraits.
(1,1\(\frac{1}{2}\)) means that in 1 hour, she can draw 1\(\frac{1}{2}\) portraits.
b. Write several equations that would relate the number of portraits drawn to the time spent drawing the portraits.
Answer:
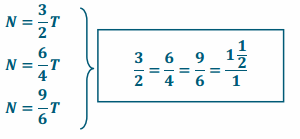
c. Determine the constant of proportionality, and explain what it means in this situation.
Answer:
The constant of proportionality is \(\frac{3}{2}\), which means that Andrea can draw 3 portraits in 2 hours or can complete 1 \(\frac{1}{2}\) portraits in 1 hour.
Tell students that these ordered pairs can be used to generate the constant of proportionality, and write the equation for this situation. Remember that = \(\frac{y}{x}\).
Eureka Math Grade 7 Module 1 Lesson 8 Problem Set Answer Key
Write an equation that will model the proportional relationship given in each real-world situation.
Question 1.
There are 3 cans that store 9 tennis balls. Consider the number of balls per can.
a. Find the constant of proportionality for this situation.
Answer:
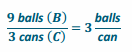
The constant of proportionality is 3.
b. Write an equation to represent the relationship.
Answer:
B = 3C
Question 2.
In 25 minutes, Li can run 10 laps around the track. Determine the number of laps she can run per minute.
a. Find the constant of proportionality in this situation.
Answer:
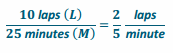
The constant of proportionality is \(\frac{2}{5}\).
b. Write an equation to represent the relationship.
Answer:
L = \(\frac{2}{5}\) M
Question 3.
Jennifer is shopping with her mother. They pay $2 per pound for tomatoes at the vegetable stand.
a. Find the constant of proportionality in this situation.
![]()
The constant of proportionality is 2.
b. Write an equation to represent the relationship.
Answer:
D = 2P
Question 4.
It costs $15 to send 3 packages through a certain shipping company. Consider the number of packages per dollar.
a. Find the constant of proportionality for this situation.
Answer:
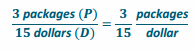
The constant of proportionality is \(\frac{1}{5}\).
b. Write an equation to represent the relationship.
Answer:
P = \(\frac{1}{5}\) D
Question 5.
On average, Susan downloads 60 songs per month. An online music vendor sells package prices for songs that can be downloaded onto personal digital devices. The graph below shows the package prices for the most popular promotions. Susan wants to know if she should buy her music from this company or pay a flat fee of $58.00 per month offered by another company. Which is the better buy?
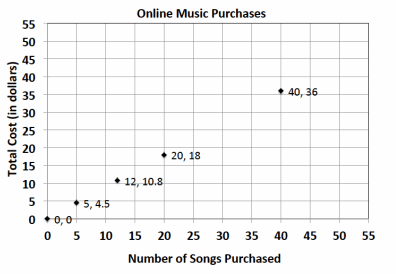
Answer:
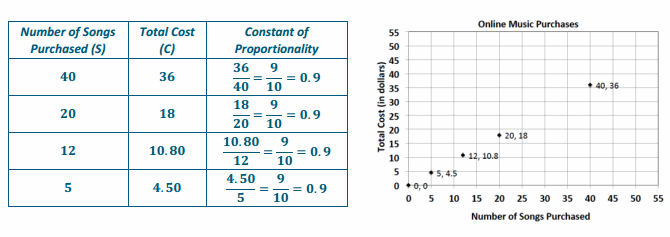
a. Find the constant of proportionality for this situation.
Answer:
The constant of proportionality, k, is 0.9.
b. Write an equation to represent the relationship.
Answer:
C = 0.9S
c. Use your equation to find the answer to Susan’s question above. Justify your answer with mathematical evidence and a written explanation.
Answer:
Compare the flat fee of $58 per month to $0.90 per song. If C = 0.9S and we substitute S with 60 (the number of songs), then the result is C = 0.9(60) = 54. She would spend $54 on songs if she bought 60 songs. If she maintains the same number of songs, the charge of $0.90 per song would be cheaper than the flat fee of $58 per month.
Question 6.
Allison’s middle school team has designed t-shirts containing their team name and color. Allison and her friend Nicole have volunteered to call local stores to get an estimate on the total cost of purchasing t-shirts. Print-o-Rama charges a set-up fee, as well as a fixed amount for each shirt ordered. The total cost is shown below for the given number of shirts. Value T’s and More charges $8 per shirt. Which company should they use?
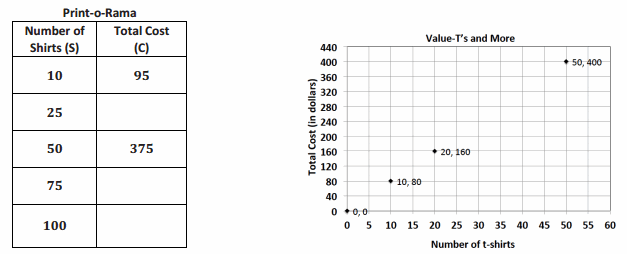
a. Does either pricing model represent a proportional relationship between the quantity of t-shirts and the total cost? Explain.
Answer:
The unit rate of \(\frac{y}{x}\) for Print-o-Rama is not constant. The graph for Value T’s and More is proportional since the ratios are equivalent (8) and the graph shows a line through the origin.
b. Write an equation relating cost and shirts for Value T’s and More.
Answer:
C = 8S for Value T’s and More
c. What is the constant of proportionality of Value T’s and More? What does it represent?
Answer:
8; the cost of one shirt is $8.
d. How much is Print-o-Rama’s set-up fee?
Answer:
The set-up fee is $25.
e. If you need to purchase 90 shirts, write a proposal to your teacher indicating which company the team should use. Be sure to support your choice. Determine the number of shirts that you need for your team.
Answer:
Since we plan on a purchase of 90 shirts, we should choose Print-o-Rama.
Print-o-Rama: C = 7S + 25; C = 7(90) + 25; C = 655
Value T’s and More: C = 8S; C = 8(90); C = 720
Eureka Math Grade 7 Module 1 Lesson 8 Exit Ticket Answer Key
John and Amber work at an ice cream shop. The hours worked and wages earned are given for each person.
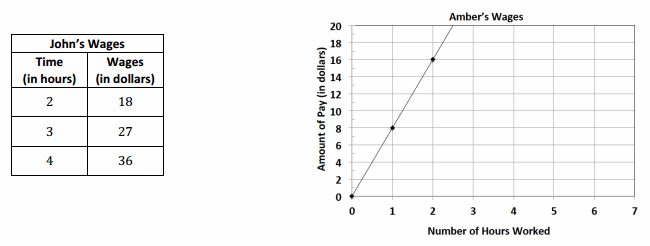
Answer:
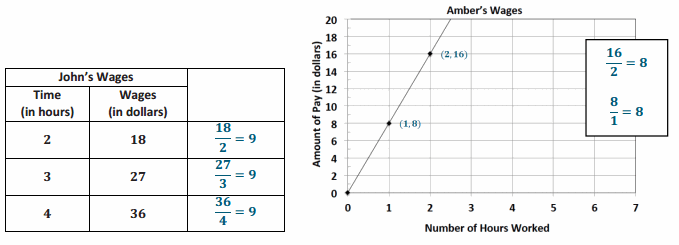
Question 1.
Determine if John’s wages are proportional to time. If they are, determine the unit rate of \(\frac{y}{x}\). If not, explain why they are not.
Answer:
Yes, the unit rate is 9. The collection of ratios is equivalent.
Question 2.
Determine if Amber’s wages are proportional to time. If they are, determine the unit rate of \(\frac{y}{x}\). If not, explain why they are not.
Answer:
Yes, the unit rate is 8. The collection of ratios is equivalent.
Question 3.
Write an equation for both John and Amber that models the relationship between their wage and the time they worked. Identify the constant of proportionality for each. Explain what it means in the context of the situation.
Answer:
John: w = 9h; the constant of proportionality is 9; John earns $9 for every hour he works.
Amber: w = 8h; the constant of proportionality is 8; Amber earns $8 for every hour she works.
Question 4.
How much would each worker make after working 10 hours? Who will earn more money?
After 10 hours, John will earn $90 because 10 hours is the value of the independent variable, which should be multiplied by k, the constant of proportionality. w = 9h; w = 9(10); w = 90. After 10 hours, Amber will earn $80 because her equation is w = 8h; w = 8(10); w = 80. John will earn more money than Amber in the same amount of time.
Question 5.
How long will it take each worker to earn $50?
Answer:
To determine how long it will take John to earn $50, the dependent value will be divided by 9, the constant of proportionality. Algebraically, this can be shown as a one-step equation: 50 = 9h; (\(\frac{1}{9}\))50 = (\(\frac{1}{9}\))9h;
\(\frac{50}{9}\) = 1 h; 5.56 = h (round to the nearest hundredth). It will take John nearly 6 hours to earn $50. To find how long it will take Amber to earn $50, divide by 8, the constant of proportionality. 50=8h;
(\(\frac{1}{8}\))50 = (\(\frac{1}{8}\))8h; \(\frac{50}{8}\) = 1h; 6.25 = h. It will take Amber 6.25 hours to earn $50.