Engage NY Eureka Math 7th Grade Module 2 Lesson 10 Answer Key
Eureka Math Grade 7 Module 2 Lesson 10 Example Answer Key
The numbers used throughout this example are a sample response. Students’ answers depend on the cards they pick.
Part A: Students pick four cards. Instruct students to record the values of their cards on the images in Part A. One of the four card images has a ★ beneath it. The ★ is used to indicate which of the four cards to copy (or multiply) in Part B.
Example 1.
Product of a Positive Integer and a Negative Integer

Part B: Instruct students to copy the value of the card with the ★ beneath it from Part A on each card with a ★ beneath it in Part B. The three remaining card values from Part A are entered in the three remaining card images in Part B. Students now have a total of six integer cards.

Use your cards from Part B to answer the questions below.
a. Write a product that describes the three matching cards.
Answer:
3 × (-5)
b. Write an expression that represents how each of the ★ cards changes your score.
Answer:
(-5) + (-5) + (-5)
c. Write an equation that relates these two expressions.
Answer:
3 × (-5) = (-5) + (-5) + (-5)
d. Write an integer that represents the total change to your score by the three ★ cards.
Answer:
-15
e. Write an equation that relates the product and how it affects your score.
Answer:
3 × (-5) = -15
Part C: Instruct students to pick three new cards and record the values of their cards on the images in Part C. The teacher chooses the fourth card and instructs the class to place a ★ beneath it to indicate which card will be cloned (multiplied) in Part D.
Part D: Instruct students to record the value of the card with the ★ beneath it from Part C on each image with a ★ beneath it in Part D. Also, rewrite the values of the three remaining cards on the other three images. Students now have a total of eight integer cards.

Use your cards from Part D to answer the questions below.
f. Write a product that describes the five matching cards.
Answer:
5 × 4
g. Write an expression that represents how each of the ★ cards changes your score.
Answer:
4 + 4 + 4 + 4 + 4
h. Write an equation that relates these two expressions.
Answer:
5 × 4 = 4 + 4 + 4 + 4 + 4
i. Write an integer that represents the total change to your score by the five ★ cards.
Answer:
20
j. Write an equation that relates the product and how it affects your score.
Answer:
5 × 4 = 20
Students write conclusions using their own words in the student materials.
k. Use the expression 5 × 4 to relate the multiplication of a positive valued card to addition.
Answer:
Multiplying a positive integer card is repeated addition of the positive integer card and increases your score.
5 × 4 = 4 + 4 + 4 + 4 + 4 = 20
i. Use the expression 3 × (-5) to relate the multiplication of a negative valued card to addition.
Answer:
Multiplying a negative integer card is repeated addition of the negative integer card and decreases your score.
3 × (-5) = (-5) + (-5) + (-5) = -15
Example 2.
Product of a Negative Integer and a Positive Integer
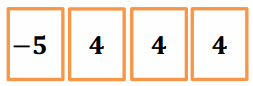
a. If all of the 4’s from the playing hand on the right are discarded, how will the score be affected? Model this using a product in an equation.
Answer:
The score decreases by 4 three consecutive times for a total decrease of 12 points. The equation is -3 × 4 = -12.
b. What three matching cards could be added to those pictured to get the same change in score? Model this using a product in an equation.
Answer:
To get the same change in score, you would add three (-4)’s. The equation is 3 × (-4) = -12.
c. Seeing how each play affects the score, relate the products that you used to model them. What do you conclude about multiplying integers with opposite signs?
Answer:
(-3) × 4 = 3 × (-4); adding a value multiple times has the same effect as removing the opposite value the same number of times.
Example 3.
Product of Two Negative Integers
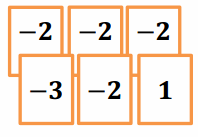
a. If the matching cards from the playing hand on the right are discarded, how will this hand’s score be affected? Model this using a product in an equation.
Answer:
Removing -2 from the set of cards will cause the score to increase by 2. Removing all four of the (-2)’s causes the score to increase by two, four consecutive times for a total increase of 8; -4 × (-2) = 8.
b. What four matching cards could be added to those pictured to get the same change in score? Model this using a product in an equation.
Answer:
An increase of 8 could come from adding four 2’s to the cards shown; 4 × 2 = 8.
c. Seeing how each play affects the score, relate the products that you used to model them. What do you conclude about multiplying integers with the same sign?
Answer:
-4 × (-2) = 4 × 2; adding a value multiple times has the same effect as removing the opposite value the same number of times.
d. Using the conclusions from Examples 2 and 3, what can we conclude about multiplying integers? Write a few examples.
Answer:
The product of two integers is equal to the product of their opposites; removing two (-4)’s is the same as adding two 4’s; adding three (-5)’s is the same as removing three 5’s.
Examples: (-4) × (-5) = 4 × 5; (-2) × 7 = 2 × (-7); 6 × (-4) = (-6) × 4
Removing two (-4)’s is the same as adding two 4’s; adding three (-5)’s is the same as removing three 5’s.
Eureka Math Grade 7 Module 2 Lesson 10 Problem Set Answer Key
Question 1.
Describe sets of two or more matching integer cards that satisfy the criteria in each part below:
a. Cards increase the score by eight points.
Answer:
Picking up: eight 1’s, four 2’s, or two 4’s
OR
Removing: eight (-1)’s, four (-2)’s, or two (-4)’s
b. Cards decrease the score by 9 points.
Answer:
Picking up: nine (-1)’s or three (-3)’s
OR
Removing: nine 1’s or three 3’s
c. Removing cards that increase the score by 10 points.
Answer:
Ten (-1)’s, five (-2)’s, or two (-5)’s
d. Positive cards that decrease the score by 18 points.
Answer:
Removing eighteen 1’s, nine 2’s, six 3’s, three 6’s, or two 9’s.
Question 2.
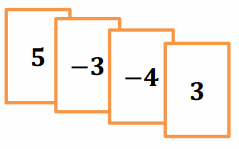
You have the integer cards shown at the right when your teacher tells you to choose a card to multiply four times. If your goal is to get your score as close to zero as possible, which card would you choose? Explain how your choice changes your score.
Answer:
The best choice to multiply is the -3. The cards currently have a score of one. The new score with the -3 multiplied by 4 is -8. The scores where the other cards are multiplied by 4 are 10, -11, and 16, which are all further from zero.
Question 3.
Sherry is playing the Integer Game and is given a chance to discard a set of matching cards. Sherry determines that if she discards one set of cards, her score will increase by 12. If she discards another set, then her score will decrease by eight. If her matching cards make up all six cards in her hand, what cards are in Sherry’s hand? Are there any other possibilities?
Answer:
There are two possibilities:
2, 2, 2, 2, -6, -6
OR
-3, -3, -3, -3, 4, 4
Eureka Math Grade 7 Module 2 Lesson 10 Exit Ticket Answer Key
Question 1.
Natalie is playing the Integer Game and only shows you the four cards shown below. She tells you that the rest of her cards have the same values on them and match one of these four cards.
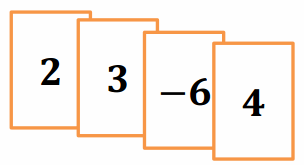
a. If all of the matching cards will increase her score by 18, what are the matching cards?
Answer:
If there were nine 2 cards, then 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2=18
9 × 2 = 18
If there were six 3 cards, then 3 + 3 + 3 + 3 + 3 + 3=18
6 × 3 = 18
b. If all of the matching cards will decrease her score by 12, what are the matching cards?
Answer:
If there were two -6 cards, then (-6) + (-6)=-12
2×(-6)=-12
Question 2.
A hand of six integer cards has one matching set of two or more cards. If the matching set of cards is removed from the hand, the score of the hand will increase by six. What are the possible values of these matching cards? Explain. Write an equation using multiplication showing how the matching cards yield an increase in score of six.
Answer:
If the matching cards are taken away from the playing hand and the score of the hand increases, then the matching cards must have negative values. The playing hand only has six cards, so the number of matching cards is limited to six. Taking away the following matching sets would increase the score by six:
Taking away one set of two -3 cards can be represented by -(-3)-(-3)
3 + 3 =6
3 × 2 = 6 or (-3) × (-2) = 6
Taking away one set of three -2 cards can be represented by -(-2) – (-2) – (-2)
2 + 2 + 2 =6
2 × 3 = 6 or (-2) × (-3) = 6
Taking away one set of six -1 cards can be represented by -(-1)-(-1)-(-1)-(-1)-(-1)-(-1)
1 + 1 + 1 + 1 + 1 + 1 = 6
1 × 6 = 6 or (-1) × (-6) = 6