Engage NY Eureka Math 7th Grade Module 2 Lesson 14 Answer Key
Eureka Math Grade 7 Module 2 Lesson 14 Example Answer Key
Example 1.
Can All Rational Numbers Be Written as Decimals?
a. Using the division button on your calculator, explore various quotients of integers 1 through 11. Record your fraction representations and their corresponding decimal representations in the space below.
Answer:
Fractions will vary. Examples:
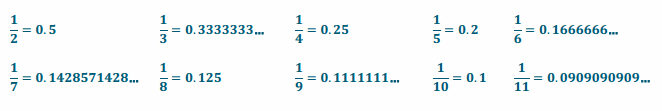
b. What two types of decimals do you see?
Answer:
Some of the decimals stop, and some fill up the calculator screen (or keep going).
→ Did you find any quotients of integers that do not have decimal representations?
→ No. Dividing by zero is not allowed. All quotients have decimal representations, but some do not terminate (end).
→ All rational numbers can be represented in the form of a decimal. We have seen already that fractions with powers of ten in their denominators (and their equivalent fractions) can be represented as terminating decimals. Therefore, other fractions must be represented by decimals that do not terminate.
Example 2.
Decimal Representations of Rational Numbers
In the chart below, organize the fractions and their corresponding decimal representation listed in Example 1 according to their type of decimal.
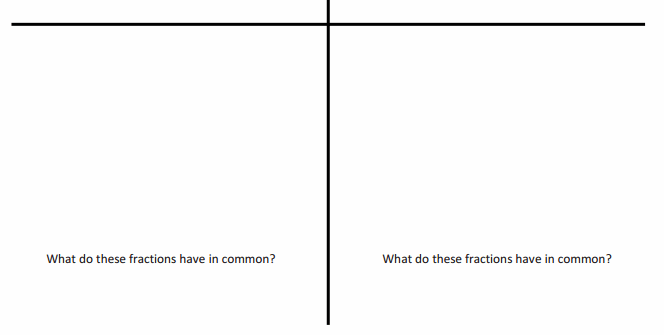
Answer:

Example 3.
Converting Rational Numbers to Decimals Using Long Division
Use the long division algorithm to find the decimal value of –\(\frac{3}{4}\).
Answer:
The fraction is a negative value, so its decimal representation will be as well.
–\(\frac{3}{4}\) = -0.75
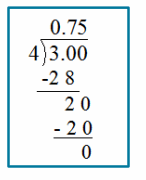
We know that -(-\(\frac{3}{4}\))= —\(\frac{3}{4}\) = \(\frac{3}{-4}\), so we use our rules for dividing integers. Dividing 3 by 4 gives us 0.75, but we know the value must be negative.
Answer: -0.75
Example 4.
Converting Rational Numbers to Decimals Using Long Division
Use long division to find the decimal representation of \(\frac{1}{3}\) .
Answer:
The remainders repeat, yielding the same dividend remainder in each step. This repeating remainder causes the numbers in the quotient to repeat as well. Because of this pattern, the decimal will go on forever, so we cannot write the exact quotient.
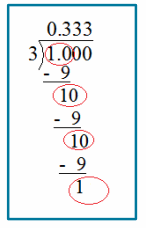
Example 5.
Fractions Represent Terminating or Repeating Decimals
How do we determine whether the decimal representation of a quotient of two integers, with the divisor not equal to zero, will terminate or repeat?
Answer:
In the division algorithm, if the remainder is zero, then the algorithm terminates, resulting in a terminating decimal.
If the value of the remainder is not zero, then it is limited to whole numbers 1, 2, 3, … , (d-1), where d is the divisor. This means that the value of the remainder must repeat within (d-1) steps. (For example, given a divisor of 9, the nonzero remainders are limited to whole numbers 1 through 8, so the remainder must repeat within 8 steps.) When the remainder repeats, the calculations that follow will also repeat in a cyclical pattern causing a repeating decimal.
Example 6.
Using Rational Number Conversions in Problem Solving
a. Eric and four of his friends are taking a trip across the New York State Thruway. They decide to split the cost of tolls equally. If the total cost of tolls is $8, how much will each person have to pay?
Answer:
There are five people taking the trip. The friends will each be responsible for $1.60 of the tolls due.

b. Just before leaving on the trip, two of Eric’s friends have a family emergency and cannot go. What is each person’s share of the $8 tolls now?
Answer:
There are now three people taking the trip. The resulting quotient is a repeating decimal because the remainders repeat
as 2s. The resulting quotient is \(\frac{8}{3}\) = 2.66666…= \(\text { 2. } \overline{6} \text { . }\) If each friend pays $2.66, they will be $0.02 shy of $8, so the amount must be rounded up to $2.67 per person.
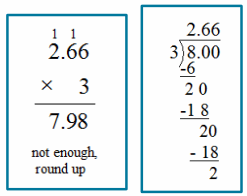
Eureka Math Grade 7 Module 2 Lesson 14 Exercise Answer Key
Exercise 1.
Convert each rational number to its decimal form using long division.
a. –\(\frac{7}{8}\) =
Answer:
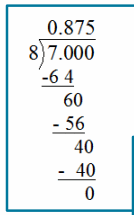
b. \(\frac{3}{16}\) =
Answer:
\(\frac{3}{16}\) = 0.1875
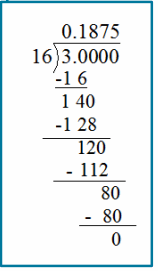
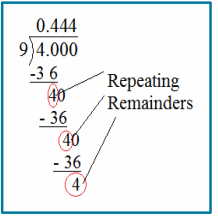
Students notice that since the remainders repeat, the quotient takes on a repeating pattern of 3s.
→ We cannot possibly write the exact value of the decimal because it has an infinite number of decimal places. Instead, we indicate that the decimal has a repeating pattern by placing a bar over the shortest sequence of repeating digits (called the repetend).
→ 0.333… = \(0 . \overline{3}\)
→ What part of your calculations causes the decimal to repeat?
→ When a remainder repeats, the calculations that follow must also repeat in a cyclical pattern, causing the digits in the quotient to also repeat in a cyclical pattern.
→ Circle the repeating remainders.
Refer to the graphic above.
Exercise 2.
Calculate the decimal values of the fraction below using long division. Express your answers using bars over the shortest sequence of repeating digits.
a. –\(\frac{4}{9}\)
Answer:
–\(\frac{4}{9}\) = -0.4444…= –\(0 . \overline{4}\)
b. –\(\frac{1}{11}\)
Answer:
–\(\frac{1}{11}\) = -0.090909…= –\(0 . \overline{09}\)

c. \(\frac{1}{7}\)
Answer:
\(\frac{1}{7}\) = 0.142857148…= \(0 . \overline{142857}\)
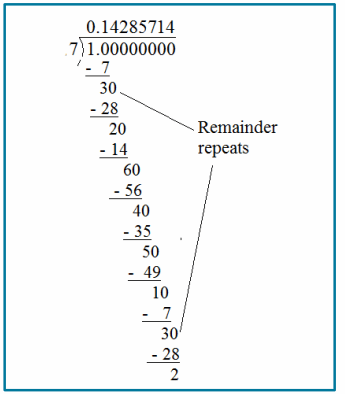
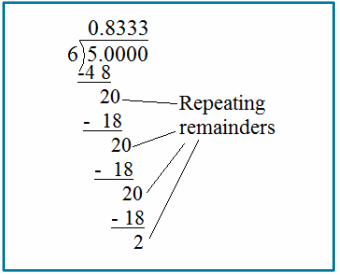
d. –\(\frac{5}{6}\)
Answer:
–\(\frac{5}{6}\) = -0.33333…= –\(0 . \overline{83}\)
Eureka Math Grade 7 Module 2 Lesson 14 Problem Set Answer Key
Question 1.
Convert each rational number into its decimal form.
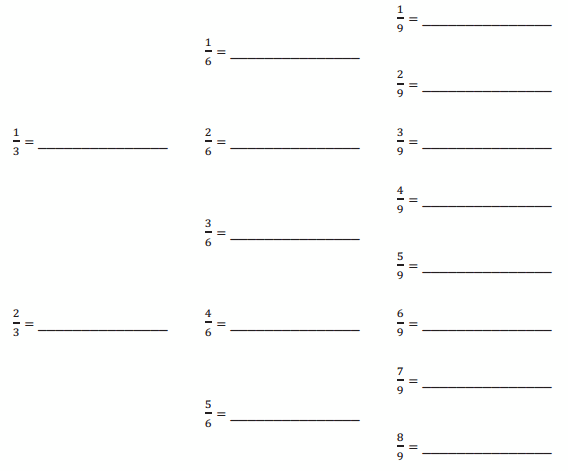
Answer:
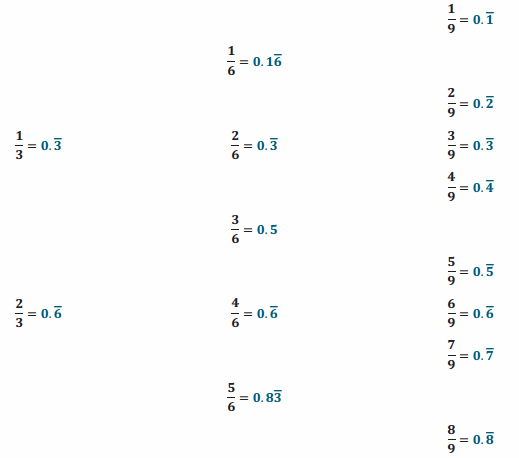
One of these decimal representations is not like the others. Why?
Answer:
\(\frac{3}{6}\) in its simplest form is \(\frac{1}{2}\) (the common factor of 3 divides out, leaving a denominator of 2, which in decimal form will terminate.
Enrichment:
Question 2.
Chandler tells Aubrey that the decimal value of –\(\frac{1}{17}\) is not a repeating decimal. Should Aubrey believe him? Explain.
No, Aubrey should not believe Chandler. The divisor 17 is a prime number containing no factors of 2 or 5, and therefore, cannot be written as a terminating decimal. By long division, –\(\frac{1}{17}\) = \(-0 . \overline{0588235294117647}\). The decimal appears as though it is not going to take on a repeating pattern because all 16 possible nonzero remainders appear before the remainder repeats. The seventeenth step produces a repeat remainder causing a cyclical decimal pattern.
Question 3.
Complete the quotients below without using a calculator, and answer the questions that follow.
a. Convert each rational number in the table to its decimal equivalent.
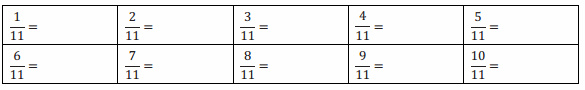
Answer:
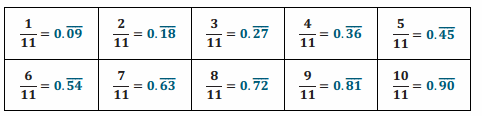
Do you see a pattern? Explain.
Answer:
The two digits that repeat in each case have a sum of nine. As the numerator increases by one, the first of the two digits increases by one as the second of the digits decreases by one.
b. Convert each rational number in the table to its decimal equivalent.
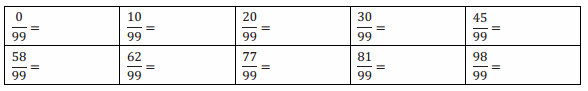
Answer:
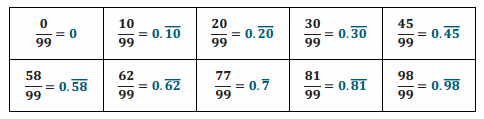
Do you see a pattern? Explain.
Answer:
The 2-digit numerator in each fraction is the repeating pattern in the decimal form.
c. Can you find other rational numbers that follow similar patterns?
Answer:
Answers will vary.
Eureka Math Grade 7 Module 2 Lesson 14 Exit Ticket Answer Key
Question 1.
What is the decimal value of \(\frac{4}{11}\) ?
Answer:
\(\frac{4}{11}\) = \(0 . \overline{36}\)
Question 2.
How do you know that \(\frac{4}{11}\) is a repeating decimal?
Answer:
The prime factor in the denominator is 11. Fractions that correspond with terminating decimals have only factors 2 and 5 in the denominator in simplest form.
Question 3.
What causes a repeating decimal in the long division algorithm?
Answer:
When a remainder repeats, the division algorithm takes on a cyclic pattern causing a repeating decimal.