Engage NY Eureka Math 7th Grade Module 2 Lesson 21 Answer Key
Eureka Math Grade 7 Module 2 Lesson 21 Exercise Answer Key
Question 1.
The table below shows two hands from the Integer Game and a series of changes that occurred to each hand. Part of the table is completed for you. Complete the remaining part of the table; then summarize the results.
Answer:
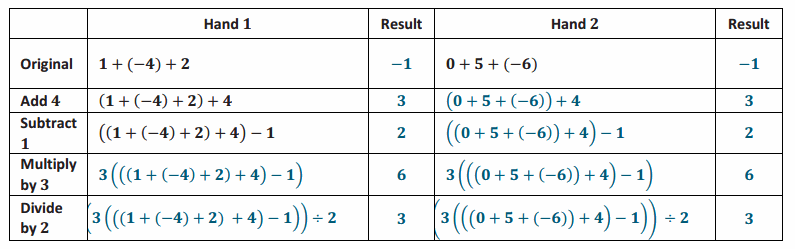
Since the sums of each original hand are the same, the same cards can be added, subtracted, multiplied, and divided, and the sums will remain equal to each other.
Question 2.
Complete the table below using the multiplication property of equality.

Answer:
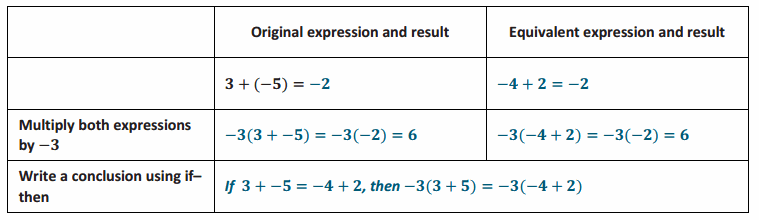
Eureka Math Grade 7 Module 2 Lesson 21 Exploratory Challenge Answer Key
Exploratory Challenge: Integer Game Revisited
Let’s investigate what happens if a card is added or removed from a hand of integers.
Event 1.

Answer:
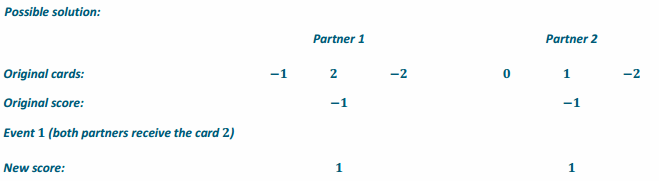
Repeat this process with one minor change; this time both students receive one integer card containing the same negative value. Have students record their new scores and, after comparing with their partners, write a conclusion using an if–then statement.
Event 1 (both partners receive the card – 1)
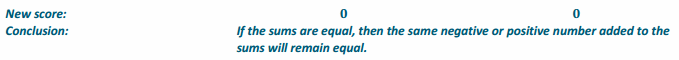
Series of questions leading to the conclusion:
→ Were your scores the same when we began?
→ Yes
→ Did you add the same values to your hand each time?
→ Yes
→ Did the value of your hand change each time you added a new card?
→ Yes
→ Was the value of your hand still the same as your partner’s after each card was added?
→ Yes
→ Why did the value of your hand remain the same after you added the new cards?
→ We started with the same sum; therefore, when we added a new card, we had equivalent expressions, which resulted in the same sum.
→ Since your original cards were different, but your original sum was the same, write a conclusion that was exemplified by this event.
→ If the original sums were equal, you can add a number, either positive or negative, and the sums will remain equal.
Event 2.

Answer:
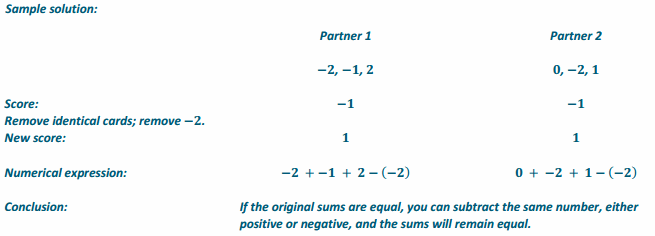
Event 3.
Answer:
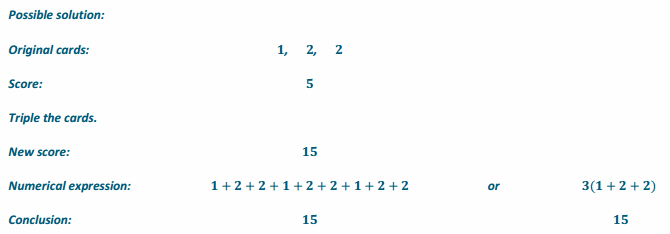
If the sums are the same, then the product of the sums will remain equal when both are multiplied by the same rational number.
Event 4.
Expression:
Conclusion:
Answer:

Eureka Math Grade 7 Module 2 Lesson 21 Problem Set Answer Key
Question 1.
Evaluate the following numerical expressions.
a. 2 + ( – 3) + 7=
Answer:
6
b. – 4 – 1=
Answer:
– 5
c. – \(\frac{5}{2}\) ×2=
Answer:
– 5
d. – 10÷2 + 3=
Answer:
– 2
e. (\(\frac{1}{2}\) )(8) + 2 =
Answer:
6
f. 3 + ( – 4) – 1=
Answer:
– 2
Question 2.
Which expressions from Exercise 1 are equal?
Answer:
Expressions (a) and (e) are equivalent.
Expressions (b) and (c) are equivalent.
Expressions (d) and (f) are equivalent.
Question 3.
If two of the equivalent expressions from Exercise 1 are divided by 3, write an if–then statement using the properties of equality.
Answer:
If 2 + ( – 3) + 7=(\(\frac{1}{2}\) )(8) + 2, then (2 + ( – 3) + 7)÷3=((\(\frac{1}{2}\) )(8) + 2)÷3.
Question 4.
Write an if–then statement if – 3 is multiplied by the following equation: – 1 – 3= – 4.
Answer:
If – 1 – 3 = – 4, then – 3( – 1 – 3) = – 3( – 4)
Question 5.
Simplify the expression.
5 + 6 – 5 + 4 + 7 – 3 + 6 – 3
Answer:
=17
Using the expression, write an equation.
Answer:
5 + 6 – 5 + 4 + 7 – 3 + 6 – 3=17
Rewrite the equation if 5 is added to both expressions.
Answer:
5 + 6 – 5 + 4 + 7 – 3 + 6 – 3 + 5=17 + 5
Write an if–then statement using the properties of equality.
Answer:
If 5 + 6 – 5 + 4 + 7 – 3 + 6 – 3 = 17, then 5 + 6 – 5 + 4 + 7 – 3 + 6 – 3 + 5
= 17 + 5
Eureka Math Grade 7 Module 2 Lesson 21 Exit Ticket Answer Key
Compare the two expressions.
Expression 1: 6 + 7 + – 5
Expression 2: – 5 + 10 + 3
Question 1.
Are the two expressions equivalent? How do you know?
Answer:
Yes, the expressions are equivalent because Expression 1 is equal to 8 and Expression 2 is equal to 8, as well. When two expressions evaluate to the same number, they are equivalent.
Question 2.
Subtract – 5 from each expression. Write the new numerical expression, and write a conclusion as an if–then statement.
Answer:
Expression 1:
6 + 7±5 – ( – 5)
13
Expression 2: – 5 + 10 + 3 – ( – 5)
13
If 6 + 7 + – 5= – 5 + 10 + 3, then 6 + 7 + – 5 – ( – 5)= – 5 + 10 + 3 – ( – 5).
If Expression 1= Expression 2, then (Expression 1 – ( – 5))=(Expression 2 – ( – 5)).
Question 3.
Add 4 to each expression. Write the new numerical expression, and write a conclusion as an if–then statement.
Answer:
Expression 1: 6 + 7±5 + 4
12
Expression 2: – 5 + 10 + 3 + 4
12
If 6 + 7 + – 5= – 5 + 10 + 3, then 6 + 7 + – 5 + 4= – 5 + 10 + 3 + 4.
If Expression 1 = Expression 2, then (Expression 1 + 4)=(Expression 2 + 4).
Question 4.
Divide each expression by – 2. Write the new numerical expression, and write a conclusion as an if–then statement.
Answer:
Expression 1: (6 + 7 + – 5)÷ – 2
8÷ – 2
– 4
Expression 2: ( – 5 + 10 + 3)÷ – 2
8÷ – 2
– 4
If 6 + 7 + – 5= – 5 + 10 + 3, then (6 + 7 + – 5)÷ – 2=( – 5 + 10 + 3)÷ – 2
If Expression 1= Expression 2, then (Expression 1 ÷ – 2)=(Expression 2 ÷ – 2).