Eureka Math Grade 7 Module 2 Lesson 9 Answer Key

Engage NY Eureka Math 7th Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 7 Module 2 Lesson 9 Example Answer Key

Represent each of the following expressions as one rational number. Show and explain your steps.

Example 1.
4\(\frac{4}{7}\) – (4\(\frac{4}{7}\) – 10)
= 4\(\frac{4}{7}\) – (4\(\frac{4}{7}\) + (- 10)) Subtracting a number is the same as adding its inverse.
= 4\(\frac{4}{7}\) + (- 4\(\frac{4}{7}\) + 10) The opposite of a sum is the sum of its opposites.
= (4\(\frac{4}{7}\) + (- 4\(\frac{4}{7}\))) + 10 The associative property of addition
= 0 + 10 A number plus its opposite equals zero.
= 10

Example 2.
5 + (- 4\(\frac{4}{7}\))
= 5 + (- (4 +\(\frac{4}{7}\))) The mixed number 4\(\frac{4}{7}\) is equivalent to 4 +\(\frac{4}{7}\).
= 5 + (- 4 + (-\(\frac{4}{7}\))) The opposite of a sum is the sum of its opposites.
= (5 + (- 4)) + (-\(\frac{4}{7}\)) Associative property of addition
= 1 + (-\(\frac{4}{7}\)) 5 + (- 4) = 1
=\(\frac{7}{7}\) + (-\(\frac{4}{7}\))\(\frac{7}{7}\) =1
=\(\frac{3}{7}\)

Eureka Math Grade 7 Module 2 Lesson 9 Exercise Answer Key

Exercise 1
Unscramble the cards, and show the steps in the correct order to arrive at the solution to 5\(\frac{2}{9}\) – (8.1 + 5\(\frac{2}{9}\)) .

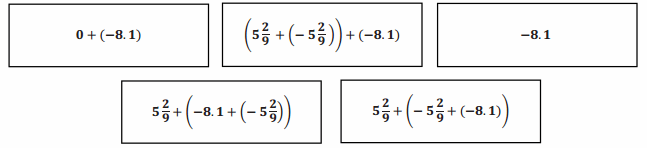
Answer:
5\(\frac{2}{9}\) + (- 8.1 + (- 5\(\frac{2}{9}\)) ) The opposite of a sum is the sum of its opposites.
5\(\frac{2}{9}\) + (- 5\(\frac{2}{9}\) + (- 8.1)) Apply the commutative property of addition.
(5\(\frac{2}{9}\) + (- 5\(\frac{2}{9}\)) ) + (- 8.1) Apply the associative property of addition.
0 + (- 8.1) A number plus its opposite equals zero.
– 8.1 Apply the additive identity property.

Exercise 2.
Team Work!
a. – 5.2 – (-3.1) + 5.2
Answer:
= – 5.2 + 3.1 + 5.2
= – 5.2 + 5.2 + 3.1
= 0 + 3.1
= 3.1

b. 32 + (- 12\(\frac{7}{8}\))
Answer:
= 32 + (- 12 + (-\(\frac{7}{8}\)) )
= (32 + (- 12)) + (-\(\frac{7}{8}\))
= 20 + (-\(\frac{7}{8}\))
= 19\(\frac{1}{8}\)

c. 3\(\frac{1}{6}\) + 20.3 – (- 5\(\frac{5}{6}\))
= 3\(\frac{1}{6}\) + 20.3 + 5\(\frac{5}{6}\)
= 3\(\frac{1}{6}\) + 5\(\frac{5}{6}\) + 20.3
= 8\(\frac{6}{6}\) + 20.3
= 9 + 20.3
= 29.3

d.\(\frac{16}{20}\) – (- 1.8) –\(\frac{4}{5}\)
=\(\frac{16}{20}\) + 1.8 –\(\frac{4}{5}\)
=\(\frac{16}{20}\) + 1.8 + (-\(\frac{4}{5}\))
=\(\frac{16}{20}\) + (-\(\frac{4}{5}\)) + 1.8
=\(\frac{16}{20}\) + (-\(\frac{16}{20}\)) + 1.8
= 0 + 1.8
= 1.8

Exercise 3.
Explain, step by step, how to arrive at a single rational number to represent the following expression. Show both a written explanation and the related math work for each step.
– 24 – (-\(\frac{1}{2}\)) – 12.5
Answer:
Subtracting (-\(\frac{1}{2}\)) is the same as adding its inverse\(\frac{1}{2}\): = – 24 +\(\frac{1}{2}\) + (- 12.5)
Next, I used the commutative property of addition to rewrite the expression: = – 24 + (- 12.5) +\(\frac{1}{2}\)
Next, I added both negative numbers: = – 36.5 +\(\frac{1}{2}\)
Next, I wrote\(\frac{1}{2}\) in its decimal form: = – 36.5 + 0.5
Lastly, I added – 36.5 + 0.5: = – 36

Eureka Math Grade 7 Module 2 Lesson 9 Problem Set Answer Key

Show all steps taken to rewrite each of the following as a single rational number.

Question 1.
80 + (- 22\(\frac{4}{15}\))
= 80 + (-22 + (-\(\frac{4}{15}\)))
= (80 + (-22)) + (-\(\frac{4}{15}\))
= 58 + (-\(\frac{4}{15}\))
= 57\(\frac{11}{15}\)

Question 2.
10 + (- 3\(\frac{3}{8}\))
Answer:
= 10 + (- 3 + (-\(\frac{3}{8}\)))
= (10 + (- 3)) + (-\(\frac{3}{8}\))
= 7 + (-\(\frac{3}{8}\))
= 6\(\frac{5}{8}\)

Question 3.
\(\frac{1}{5}\) + 20.3 – (-5\(\frac{3}{5}\))
= \(\frac{1}{5}\) + 20.3 + 5\(\frac{3}{5}\)
= \(\frac{1}{5}\) + 5\(\frac{3}{5}\) + 20.3
= 5\(\frac{4}{5}\) + 20.3
= 5\(\frac{4}{5}\) + 20\(\frac{3}{10}\)
= 5\(\frac{8}{10}\) + 20\(\frac{3}{10}\)
= 25\(\frac{11}{10}\)
= 26\(\frac{1}{10}\)

Question 4.
(\(\frac{11}{12}\)) – (- 10) – \(\frac{5}{6}\)
Answer:
= (\(\frac{11}{12}\)) + 10 + (-\(\frac{5}{6}\))
= (\(\frac{11}{12}\)) + (-\(\frac{5}{6}\)) + 10
= (\(\frac{11}{12}\)) + (- \(\frac{10}{12}\)) + 10
= (\(\frac{1}{12}\)) + 10
= 10 (\(\frac{1}{12}\))

Question 5.
Explain, step by step, how to arrive at a single rational number to represent the following expression. Show both a written explanation and the related math work for each step.
1 – \(\frac{3}{4}\) + (- 12\(\frac{1}{4}\))
Answer:
First, I rewrote the subtraction of \(\frac{3}{4}\) as the addition of its inverse – \(\frac{3}{4}\):
= 1 + (- \(\frac{3}{4}\)) + (- 12\(\frac{1}{4}\))
Next, I used the associative property of addition to regroup the addend:
= 1 + ((- \(\frac{3}{4}\)) + (- 12\(\frac{1}{4}\)))
Next, I separated – 12\(\frac{1}{4}\) into the sum of – 12 and –\(\frac{1}{4}\):
= 1 + ((-\(\frac{3}{4}\)) + (- 12) + (-\(\frac{1}{4}\)))
Next, I used the commutative property of addition:
= 1 + ((- \(\frac{3}{4}\)) + (-\(\frac{1}{4}\)) + (- 12))
Next, I found the sum of – \(\frac{3}{4}\) and –\(\frac{1}{4}\):
= 1 + ((- 1) + (- 12))
Next, I found the sum of – 1 and – 12:
= 1 + (- 13)
Lastly, since the absolute value of 13 is greater than the absolute value
of 1, and it is a negative 13, the answer will be a negative number.
The absolute value of 13 minus the absolute value of 1 equals 12,
so the answer is – 12.
= – 12

Eureka Math Grade 7 Module 2 Lesson 9 Integer Subtraction Round 1 Answer Key

Directions: Determine the difference of the integers, and write it in the column to the right.

Answer:

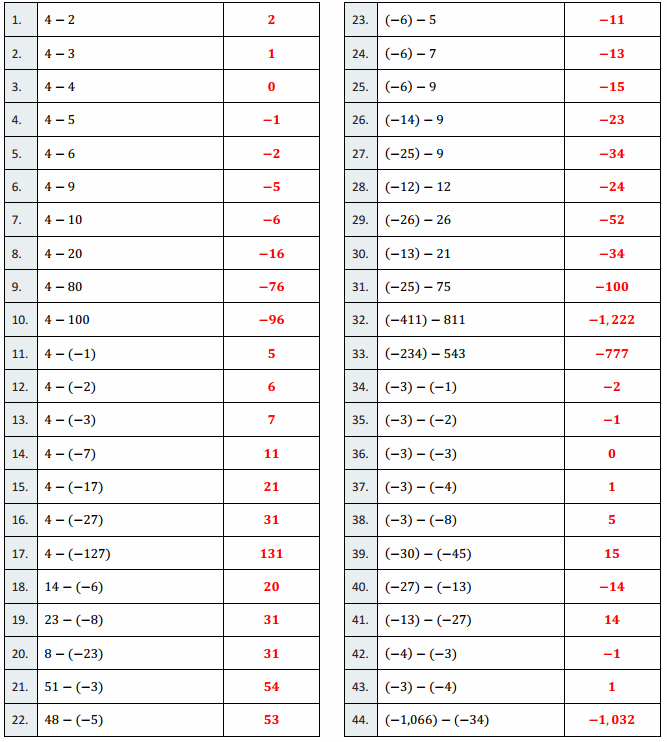
Question 1.
4 – 2
Answer:
2

Question 2.
4 – 3
Answer:
1

Question 3.
4 – 4
Answer:
0

Question 4.
4 – 5
– 1

Question 5.
4 – 6
Answer:
– 2

Question 6.
4 – 9
Answer:
– 5

Question 7.
4 – 10
Answer:
– 6

Question 8.
4 – 20
Answer:
– 16

Question 9.
4 – 80
Answer:
– 76

Question 10.
4 – 100
Answer:
– 96

Question 11.
4 – (- 1)
Answer:
5

Question 12.
4 – (- 2)
Answer:
6

Question 13.
4 – (- 3)
Answer:
7

Question 14.
4 – (- 7)
Answer:
11

Question 15.
4 – (- 17)
Answer:
21

Question 16.
4 – (- 27)
Answer:
31

Question 17.
4 – (- 127)
Answer:
131

Question 18.
14 – (- 6)
Answer:
20

Question 19.
23 – (- 8)
Answer:
31

Question 20.
8 – (- 23)
Answer:
31

Question 21.
51 – (- 3)
Answer:
54

Question 22.
48 – (- 5)
Answer:
53

Question 23.
(- 6) – 5
Answer:
– 11

Question 24.
(- 6) – 7
– 13

Question 25.
(- 6) – 9
Answer:
– 15

Question 26.
(- 14) – 9
Answer:
– 23

Question 27.
(- 25) – 9
Answer:
– 34

Question 28.
(- 12) – 12
Answer:
– 24

Question 29.
(- 26) – 26
Answer:
– 52

Question 30.
(- 13) – 21
Answer:
– 34

Question 31.
(- 25) – 75
Answer:
– 100

Question 32.
(- 411) – 811
Answer:
– 1,222

Question 33.
(- 234) – 543
Answer:
– 777

Question 34.
(- 3) – (- 1)
Answer:
– 2

Question 35.
(- 3) – (- 2)
Answer:
– 1

Question 36.
(- 3) – (- 3)
Answer:
0

Question 37.
(- 3) – (- 4)
Answer:
1

Question 38.
(- 3) – (- 8)
Answer:
5

Question 39.
(- 30) – (- 45)
Answer:
15

Question 40.
(- 27) – (- 13)
Answer:
– 14

Question 41.
(- 13) – (- 27)
Answer:
14

Question 42.
(- 4) – (- 3)
Answer:
– 1

Question 43.
(- 3) – (- 4)
Answer:
1

Question 44.
(- 1,066) – (- 34)
Answer:
– 1,032

Eureka Math Grade 7 Module 2 Lesson 9 Integer Subtraction Round 2 Answer Key

Directions: Determine the difference of the integers, and write it in the column to the right.

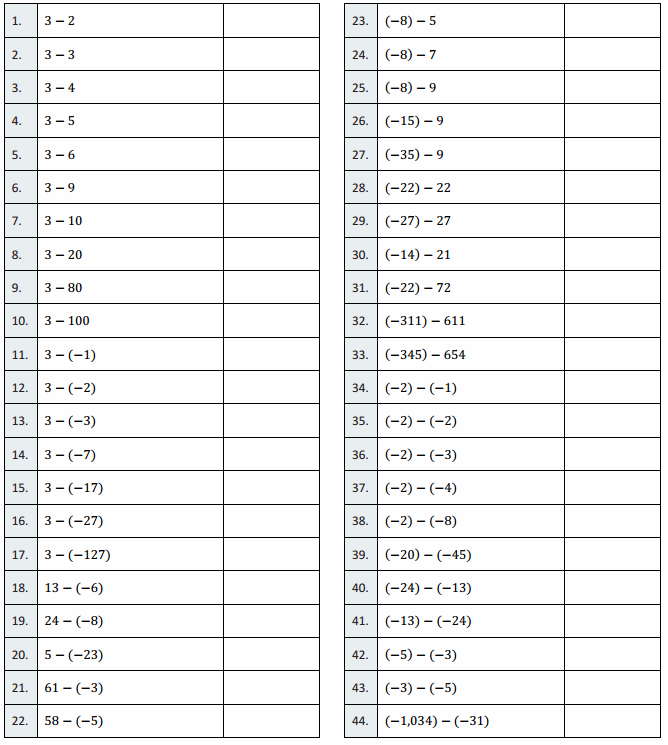
Answer:

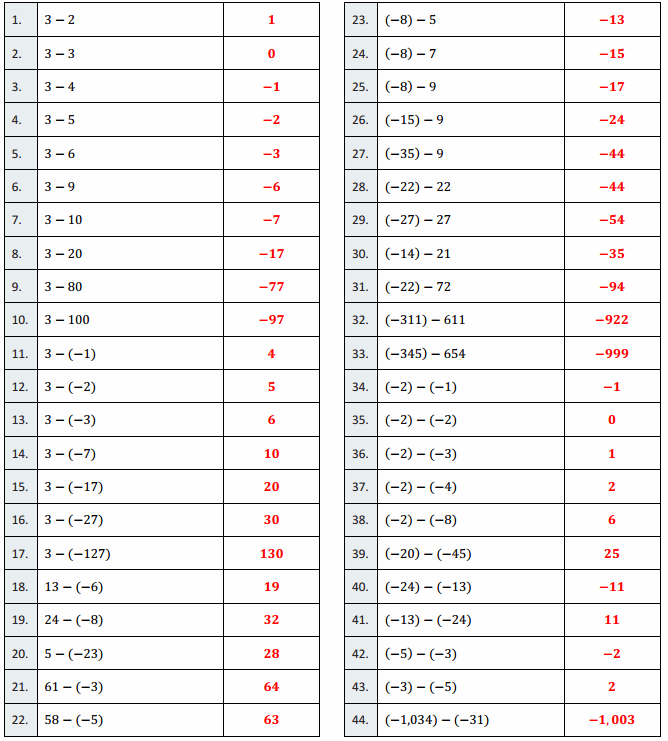
Question 1.
3 – 2
Answer:
1

Question 2.
3 – 3
Answer:
0

Question 3.
3 – 4
Answer:
– 1

Question 4.
3 – 5
Answer:
– 2

Question 5.
3 – 6
Answer:
– 3

Question 6.
3 – 9
Answer:
– 6

Question 7.
3 – 10
Answer:
– 7

Question 8.
3 – 20
Answer:
– 17

Question 9.
3 – 80
Answer:
– 77

Question 10.
3 – 100
Answer:
– 97

Question 11.
3 – (- 1)
Answer:
4

Question 12.
3 – (- 2)
Answer:
5

Question 13.
3 – (- 3)
Answer:
6

Question 14.
3 – (- 7)
Answer:
10

Question 15.
3 – (- 17)
Answer:
20

Question 16.
3 – (- 27)
Answer:
30

Question 17.
3 – (- 127)
Answer:
130

Question 18.
13 – (- 6)
Answer:
19

Question 19.
24 – (- 8)
Answer:
32

Question 20.
5 – (- 23)
Answer:
28

Question 31.
61 – (- 3)
Answer:
64

Question 32.
58 – (- 5)
Answer:
63

Question 33.
(- 8) – 5
Answer:
– 13

Question 34.
(- 8) – 7
Answer:
– 15

Question 35.
(- 8) – 9
Answer:
– 17

Question 36.
(- 15) – 9
Answer:
– 24

Question 37.
(- 35) – 9
Answer:
– 44

Question 38.
(- 22) – 22
Answer:
– 44

Question 39.
(- 27) – 27
Answer:
– 54

Question 40.
(- 14) – 21
Answer:
– 35

Question 41.
(- 22) – 72
Answer:
– 94

Question 42.
(- 311) – 611
Answer:
– 922

Question 43.
(- 345) – 654
Answer:
– 999

Question 44.
(- 2) – (- 1)
Answer:
– 1

Question 45.
(- 2) – (- 2)
Answer:
0

Question 46.
(- 2) – (- 3)
Answer:
1

Question 47.
(- 2) – (- 4)
Answer:
2

Question 48.
(- 2) – (- 8)
Answer:
6

Question 49.
(- 20) – (- 45)
Answer:
25

Question 41.
(- 24) – (- 13)
Answer:
– 11

Question 42.
(- 13) – (- 24)
Answer:
11

Question 43.
(- 5) – (- 3)
Answer:
– 2

Question 44.
(- 3) – (- 5)
Answer:
2

Question 45.
(- 1,034) – (- 31)
Answer:
– 1,003

Eureka Math Grade 7 Module 2 Lesson 9 Exit Ticket Answer Key

Question 1.
Jamie was working on his math homework with his friend, Kent. Jamie looked at the following problem.
-9.5 – (-8) – 6.5
He told Kent that he did not know how to subtract negative numbers. Kent said that he knew how to solve the problem using only addition. What did Kent mean by that? Explain. Then, show your work, and represent the answer as a single rational number.
Answer:
Kent meant that since any subtraction problem can be written as an addition problem by adding the opposite of the number you are subtracting, Jamie can solve the problem by using only addition.
Work Space:
-9.5 – (-8) – 6.5
= -9.5 + 8 + (-6.5)
= -9.5 + (-6.5) + 8
= -16 + 8
= -8
Answer:
-8

Question 2.
Use one rational number to represent the following expression. Show your work.
3 + (- 0.2) – 15\(\frac{1}{4}\)
Answer:
= 3 + (-0.2) + (-15 + (-\(\frac{1}{4}\)))
= 3 + (-0.2 + (-15) + (- 0.25))
= 3 + (-15.45)
= -12.45