Engage NY Eureka Math 7th Grade Module 3 Lesson 16 Answer Key
Eureka Math Grade 7 Module 3 Lesson 16 Example Answer Key
Example
a. The following circles are not drawn to scale. Find the circumference of each circle. (Use \(\frac{22}{7}\) as an approximation for π.)
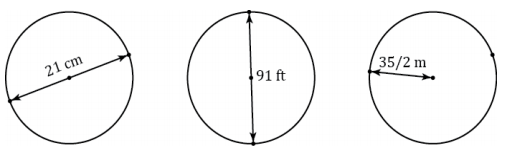
Answer:
66 cm; 286 ft.; 110 m; Ask students if these numbers are roughly three times the diameters.
b. The radius of a paper plate is 11.7 cm. Find the circumference to the nearest tenth. (Use 3.14 as an approximation for π.)
Answer:
Diameter: 23.4 cm; circumference: 73.5 cm
c. The radius of a paper plate is 11.7 cm. Find the circumference to the nearest hundredth. (Use the π button on your calculator as an approximation for π.)
Answer:
Circumference: 73.51 cm
d. A circle has a radius of r cm and a circumference of C cm. Write a formula that expresses the value of C in terms of r and π.
Answer:
C = π ∙ 2r, or C = 2πr.
e. The figure below is in the shape of a semicircle. A semicircle is an arc that is half of a circle. Find the perimeter of the shape. (Use 3.14 for π.)
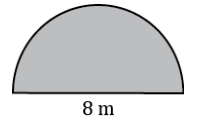
Answer:
8 m + \(\frac{8(3.14)}{2}\) m = 20.56 m
Eureka Math Grade 7 Module 3 Lesson 16 Exercise Answer Key
Opening Exercise
a. Using a compass, draw a circle like the picture to the right.
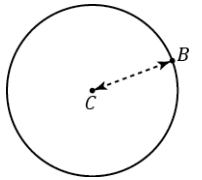
C is the center of the circle.
The distance between C and B is the radius of the circle.
b. Write your own definition for the term circle.
Answer:
Student responses will vary. Many might say, “It is round.” “It is curved.” “It has an infinite number of sides.” “The points are always the same distance from the center.” Analyze their definitions, showing how other figures such as ovals are also “round” or “curved.” Ask them what is special about the compass they used. (Answer: The distance between the spike and the pencil is fixed when drawing the circle.) Let them try defining a circle again with this new knowledge.
c. Extend segment CB to a segment AB, where A is also a point on the circle.
Answer:
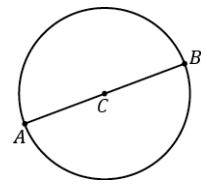
The length of the segment AB is called the diameter of the circle.
d. The diameter is ______________________ as long as the radius.
Answer:
The diameter is twice, or 2 times, as long as the radius.
e. Measure the radius and diameter of each circle. The center of each circle is labeled C.
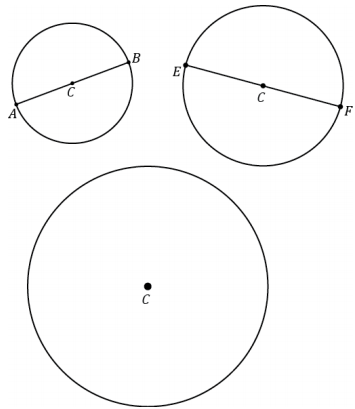
Answer:
CB = 1.5 cm, AB = 3 cm, CF = 2 cm, EF = 4 cm
The radius of the largest circle is 3 cm. The diameter is 6 cm.
f. Draw a circle of radius 6 cm.
Answer:
Part (f) may not be as easy as it seems. Let students grapple with how to measure 6 cm with a compass. One difficulty they might encounter is trying to measure 6 cm by putting the spike of the compass on the edge of the ruler (i.e., the
0 cm mark). Suggest either of the following: (1) Measure the compass from the 1 cm mark to the 7 cm mark, or (2) Mark two points 6 cm apart on the paper first; then, use one point as the center.
Eureka Math Grade 7 Module 3 Lesson 16 Problem Set Answer Key
Question 1.
Find the circumference.
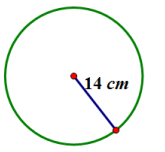
a. Give an exact answer in terms of π.
Answer:
C = 2πr
C = 2π ∙ 14 cm
C = 28π cm
b. Use π ≈ \(\frac{22}{7}\) , and express your answer as a fraction in lowest terms.
Answer:
C ≈ 2 ∙ \(\frac{22}{7}\) ∙ 14 cm
C ≈ 88 cm
c. Use the π button on your calculator, and express your answer to the nearest hundredth.
Answer:
C = 2 ∙ π ∙ 14 cm
C ≈ 87.96 cm
Question 2.
Find the circumference.
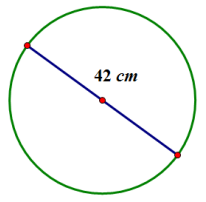
a. Give an exact answer in terms of π.
Answer:
d = 42 cm
C = πd
C = 42π cm
b. Use π ≈ \(\frac{22}{7}\) , and express your answer as a fraction in lowest terms.
Answer:
C ≈ 42 cm ∙ \(\frac{22}{7}\)
C ≈ 132 cm
Question 3.
The figure shows a circle within a square. Find the circumference of the circle. Let π ≈ 3.14.
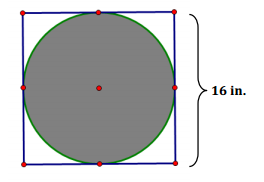
Answer:
The diameter of the circle is the same as the length of the side of the square.
C = πd
C = π ∙ 16 in.
C ≈ 3.14 ∙ 16 in.
C ≈ 50.24 in.
Question 4.
Consider the diagram of a semicircle shown.
a. Explain in words how to determine the perimeter of a semicircle.
Answer:
The perimeter is the sum of the length of the diameter and half of the circumference of a circle with the same diameter.
b. Using d to represent the diameter of the circle, write an algebraic equation that will result in the perimeter of a semicircle.
Answer:
P = d + \(\frac{1}{2}\) πd
c. Write another algebraic equation to represent the perimeter of a semicircle using r to represent the radius of a semicircle.
Answer:
P = 2r + \(\frac{1}{2}\) π ∙ 2r
P = 2r + πr
Question 5.
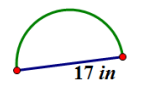
Find the perimeter of the semicircle. Let π ≈ 3.14.
Answer:
P = d + \(\frac{1}{2}\) πd
P ≈ 17 in. + \(\frac{1}{2}\) ∙ 3.14 ∙ 17 in.
P ≈ 17 in. + 26.69 in.
P ≈ 43.69 in.
Question 6.
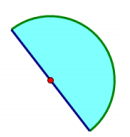
Ken’s landscape gardening business makes odd-shaped lawns that include semicircles. Find the length of the edging material needed to border the two lawn designs. Use 3.14 for π.
a. The radius of this flowerbed is 2.5 m.
Answer:
A semicircle has half of the circumference of a circle. If the circumference of the semicircle is C = \(\frac{1}{2}\)(π ∙ 2 ∙ 2.5 m), then the circumference approximates 7.85 m. The length of the edging material must include the circumference and the diameter; 7.85 m + 5 m = 12.85 m. Ken needs 12.85 meters of edging to complete his design.
b. The diameter of the semicircular section is 10 m, and the lengths of the two sides are 6 m.
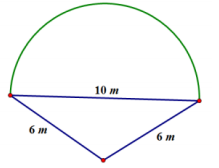
Answer:
The circumference of the semicircular part has half of the circumference of a circle. The circumference of the semicircle is C = \(\frac{1}{2}\) π ∙ 10 m, which is approximately 15.7 m. The length of the edging material must include the circumference of the semicircle and the perimeter of two sides of the triangle;
15.7 m + 6 m + 6 m = 27.7 m. Ken needs 27.7 meters of edging to complete his design.
Question 7.
Mary and Margaret are looking at a map of a running path in a local park. Which is the shorter path from E to F, along the two semicircles or along the larger semicircle? If one path is shorter, how much shorter is it? Let π ≈ 3.14.
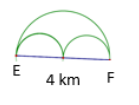
Answer:
A semicircle has half of the circumference of a circle. The circumference of the large semicircle is C = \(\frac{1}{2}\) π ∙ 4 km, or 6.28 km. The diameter of the two smaller semicircles is 2 km. The total circumference would be the same as the circumference for a whole circle with the same diameter. If C = π ∙ 2 km, then C = 6.28 km. The distance around the larger semicircle is the same as the distance around both of the semicircles. So, both paths are equal in distance.
Question 8.
Alex the electrician needs 34 yards of electrical wire to complete a job. He has a coil of wiring in his workshop. The coiled wire is 18 inches in diameter and is made up of 21 circles of wire. Will this coil be enough to complete the job? Let π ≈ 3.14.
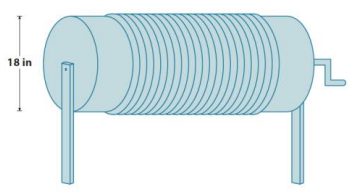
Answer:
The circumference of the coil of wire is C = π ∙ 18 in., or approximately 56.52 in. If there are 21 circles of wire, then the number of circles times the circumference will yield the total number of inches of wire in the coil. If 56.52 in. ∙ 21 ≈ 1186.92 in., then \(\frac{1186.92 \mathrm{in.}}{36 \mathrm{in.}}\) ≈ 32.97 yd. (1 yd. = 3 ft. = 36 in. When converting inches to yards, you must divide the total inches by the number of inches in a yard, which is 36 inches.) Alex will not have enough wire for his job in this coil of wire.
Eureka Math Grade 7 Module 3 Lesson 16 Exit Ticket Answer Key
Brianna’s parents built a swimming pool in the backyard. Brianna says that the distance around the pool is 120 feet.
Question 1.
Is she correct? Explain why or why not.
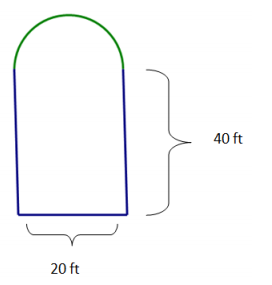
Answer:
Brianna is incorrect. The distance around the pool is 131.4 ft. She found the distance around the rectangle only and did not include the distance around the semicircular part of the pool.
Question 2.
Explain how Brianna would determine the distance around the pool so that her parents would know how many feet of stone to buy for the edging around the pool.
Answer:
In order to find the distance around the pool, Brianna must first find the circumference of the semicircle, which is C = \(\frac{1}{2}\) ∙ π ∙ 20 ft., or 10π ft., or about 31.4 ft. The sum of the three other sides is
20 ft. + 40 ft. + 40 ft. = 100 ft.; the perimeter is 100 ft. + 31.4 ft. = 131.4 ft.
Question 3.
Explain the relationship between the circumference of the semicircular part of the pool and the width of the pool.
Answer:
The relationship between the circumference of the semicircular part and the width of the pool is the same as half of π because this is half the circumference of the entire circle.