Engage NY Eureka Math 7th Grade Module 3 Lesson 19 Answer Key
Eureka Math Grade 7 Module 3 Lesson 19 Example Answer Key
Example: Area of a Parallelogram
The coordinate plane below contains figure P, parallelogram ABCD.
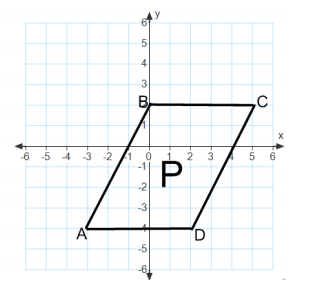
Answer:
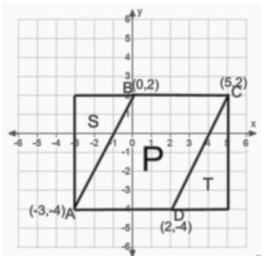
a. Write the ordered pairs of each of the vertices next to the vertex points.
Answer:
See figure.
b. Draw a rectangle surrounding figure P that has vertex points of A and C. Label the two triangles in the figure as S and T.
Answer:
See figure.
c. Find the area of the rectangle.
Answer:
Base = 8 units
Height = 6 units
Area = 8 units × 6 units = 48 sq. units
d. Find the area of each triangle.
Answer:
Figure S
Base = 3 units
Height = 6 units
Area = \(\frac{1}{2}\) × 3 units × 6 units
= 9 sq. units
Figure T
Base = 3 units
Height = 6 units
Area = \(\frac{1}{2}\) × 3 units × 6 units
= 9 sq. units
e. Use these areas to find the area of parallelogram ABCD.
Answer:
Area P = Area of rectangle – Area S – Area T
= 48 sq. units – 9 sq. units – 9 sq. units = 30 sq. units
The coordinate plane below contains figure R, a rectangle with the same base as the parallelogram above.
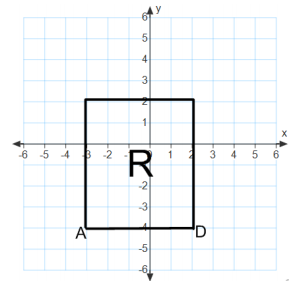
Answer:
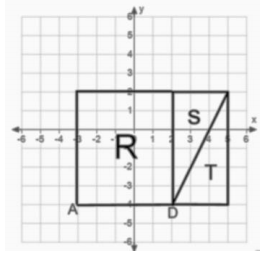
f. Draw triangles S and T and connect to figure R so that you create a rectangle that is the same size as the rectangle you created on the first coordinate plane.
Answer:
See figure.
g. Find the area of rectangle R.
Answer:
Base = 5 units
Height = 6 units
Area = 30 sq. units
h. What do figures R and P have in common?
Answer:
They have the same area. They share the same base and have the same height.
Eureka Math Grade 7 Module 3 Lesson 19 Exercise Answer Key
Exercise 1.
Find the area of triangle ABC.
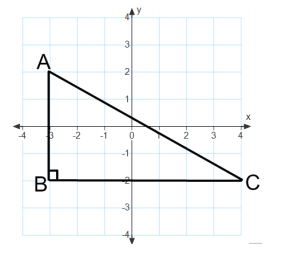
Answer:
A = \(\frac{1}{2}\) × 7 units × 4 units = 14 sq.units
Exercise 2.
Find the area of quadrilateral ABCD two different ways.
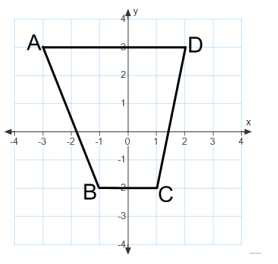
Answer:
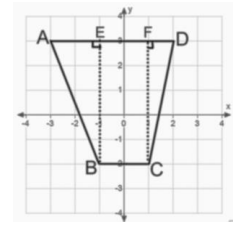
\(\frac{1}{2}\) × 2 × 5 + 2 × 5 + \(\frac{1}{2}\) × 1 × 5 = 5 + 10 + 2.5 = 17.5
The area is 17.5 sq.units.
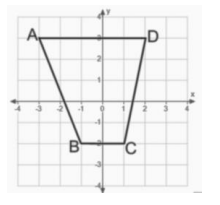
\(\frac{1}{2}\) × (5 + 2) × 5 = 17.5
The area is 17.5 sq.units.
Exercise 3.
The area of quadrilateral ABCD is 12 sq. units. Find x.
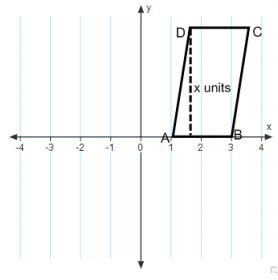
Answer:
Area = base×height
12 sq.units = 2x
6 units = x
Exercise 4.
The area of triangle ABC is 14 sq. units. Find the length of side \(\overline{B C}\).
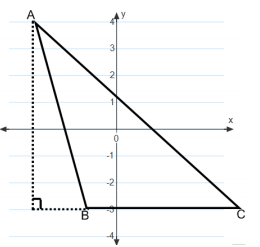
Answer:
Area = \(\frac{1}{2}\) × base×height
14 sq.units = \(\frac{1}{2}\) × BC × (7 units)
BC = 4 units
Exercise 5.
Find the area of triangle ABC.
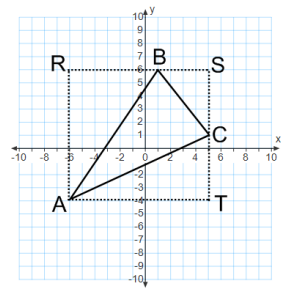
Answer:
Area of rectangle ARST = 11 units × 10 units = 110 sq.units
Area of triangle ARB = \(\frac{1}{2}\) × 7 units×10 units = 35 sq.units
Area of triangle BSC = \(\frac{1}{2}\) × 4 units×5 units = 10 sq.units
Area of triangle ATC = \(\frac{1}{2}\) × 11 units×5 units = 27.5 sq.units
Area of triangle ABC = Area of ARST – Area of ARB – Area of BSC – Area of ATC = 37.5 sq.units
Eureka Math Grade 7 Module 3 Lesson 19 Problem Set Answer Key
Find the area of each figure.
Question 1.
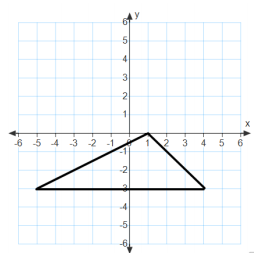
Answer:
Area = 13.5 sq. units
Question 2.
Answer:
Area = 4.5π sq. units ≈14.13 sq. units
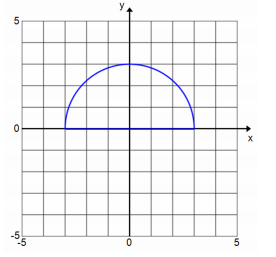
Question 3.
Answer:
Area = 48 sq. units
Question 4.
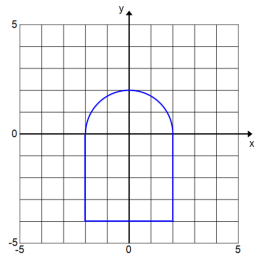
Answer:
Area = (2π + 16) sq. units ≈ 22.28 sq. units
Question 5.
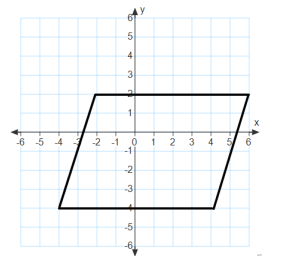
Answer:
Area = 68 sq. units
Question 6.
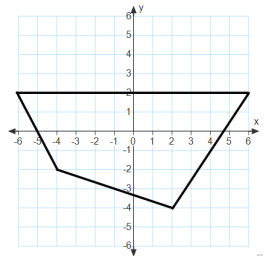
Answer:
Area = 46 sq. units
For Problems 7–9, draw a figure in the coordinate plane that matches each description.
Question 7.
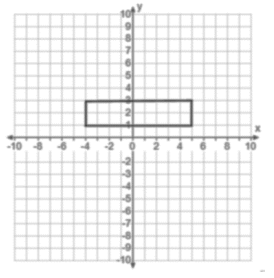
A rectangle with an area of 18 sq. units
Answer:
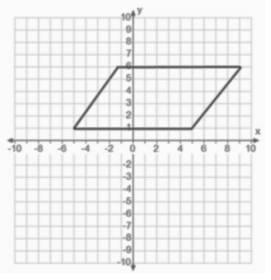
Question 8.
A parallelogram with an area of 50 sq. units
Answer:
Question 9.
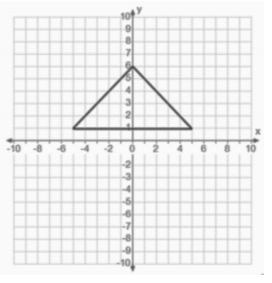
A triangle with an area of 25 sq. units
Answer:
Find the unknown value labeled as x on each figure.
Question 10.
The rectangle has an area of 80 sq. units.
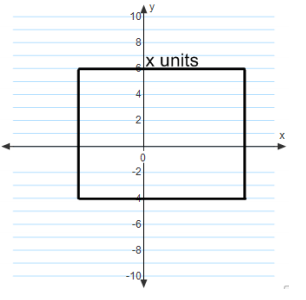
Answer:
x = 8
Question 11.
The trapezoid has an area of 115 sq. units.
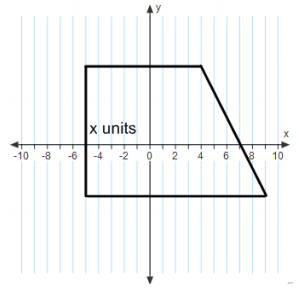
Answer:
x = 10
Question 12.
Find the area of triangle ABC.
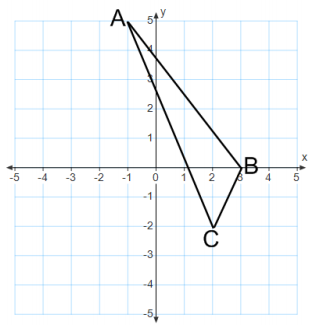
Answer:
Area = 6.5 sq. units
Question 13.
Find the area of the quadrilateral using two different methods. Describe the methods used, and explain why they result in the same area.
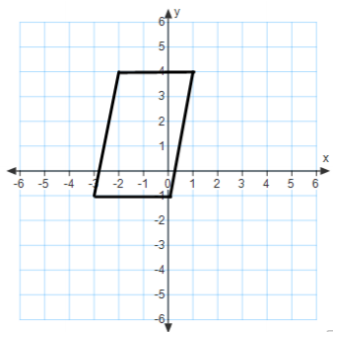
Answer:
Area = 15 sq. units
One method is by drawing a rectangle around the figure. The area of the parallelogram is equal to the area of the rectangle minus the area of the two triangles. A second method is to use the area formula for a parallelogram (Area = base × height).
Question 14.
Find the area of the quadrilateral using two different methods. What are the advantages or disadvantages of each method?
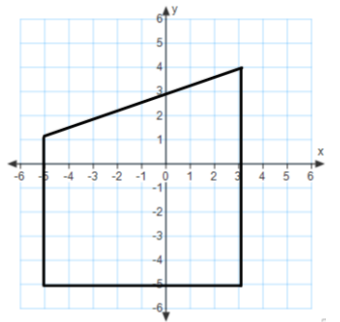
Answer:
Area = 60 sq. units
One method is to use the area formula for a trapezoid, A = \(\frac{1}{2}\) (base 1 + base 2)×height. The second method is to split the figure into a rectangle and a triangle. The second method requires more calculations. The first method requires first recognizing the figure as a trapezoid and recalling the formula for the area of a trapezoid.
Eureka Math Grade 7 Module 3 Lesson 19 Exit Ticket Answer Key
The figure ABCD is a rectangle. AB = 2 units, AD = 4 units, and AE = FC = 1 unit.
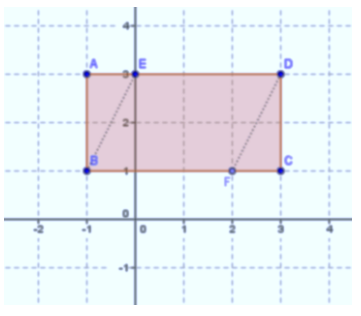
Question 1.
Find the area of rectangle ABCD.
Answer:
Area = 4 units × 2 units = 8 sq. units
Question 2.
Find the area of triangle ABE.
Answer:
Area = \(\frac{1}{2}\) × 1 unit × 2 units = 1 sq. unit
Question 3.
Find the area of triangle DCF.
Answer:
Area = \(\frac{1}{2}\) × 1 unit × 2 units = 1 sq. unit
Question 4.
Find the area of the parallelogram BEDF two different ways.
Answer:
Area = Area of ABCD – Area of ABE – Area of DCF
= (8 – 1 – 1) sq. units = 6 sq. units
Area = base × height
= 3 units × 2 units = 6 sq. units