Engage NY Eureka Math 7th Grade Module 3 Lesson 20 Answer Key
Eureka Math Grade 7 Module 3 Lesson 20 Example Answer Key
Example 1.
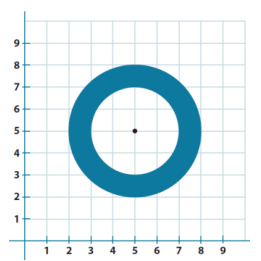
Find the composite area of the shaded region. Use 3.14 for π.
Answer:
Allow students to look at the problem and find the area independently before solving as a class.
→ What information can we take from the image?
Two circles are on the coordinate plane. The diameter of the larger circle is 6 units, and the diameter of the smaller circle is 4 units.
→ How do we know what the diameters of the circles are?
We can count the units along the diameter of the circles, or we can subtract the coordinate points to find the length of the diameter.
→ What information do we know about circles?
The area of a circle is equal to the radius squared times π. We can approximate π as 3.14 or \(\frac{22}{7}\).
→ After calculating the two areas, what is the next step, and how do you know?
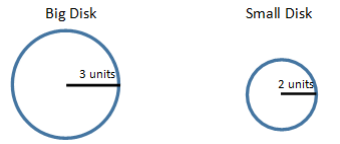
The non – overlapping regions add, meaning that the Area(small disk) + Area(ring) = Area(big disk). Rearranging this results in this: Area(ring) = Area(big disk) – Area(small disk). So, the next step is to take the difference of the disks.
→ What is the area of the figure?
9π – 4π = 5π; the area of the figure is approximately 15.7 square units.
Example 2.
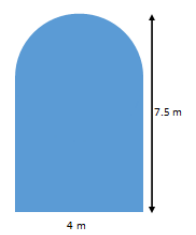
Find the area of the figure that consists of a rectangle with a semicircle on top. Use 3.14 for π.
Answer:
A = 28.28 m2
→ What do we know from reading the problem and looking at the picture?
There is a semicircle and a rectangle.
→ What information do we need to find the areas of the circle and the rectangle?
We need to know the base and height of the rectangle and the radius of the semicircle. For this problem, let the radius for the semicircle be r meters.
→ How do we know where to draw the diameter of the circle?
The diameter is parallel to the bottom base of the rectangle because we know that the figure includes a semicircle.
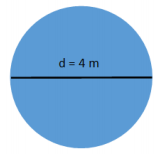
→ What is the diameter and radius of the circle?
The diameter of the circle is equal to the base of the rectangle, 4 m . The radius is half of 4 m, which is 2 m.
→ What would a circle with a diameter of 4 m look like relative to the figure?
→ What is the importance of labeling the known lengths of the figure?
This helps us keep track of the lengths when we need to use them to calculate different parts of the composite figure. It also helps us find unknown lengths because they may be the sum or the difference of known lengths.
→ How do we find the base and height of the rectangle?
The base is labeled 4 m, but the height of the rectangle is combined with the radius of the semicircle. The difference of the height of the figure, 7.5 m, and the radius of the semicircle equals the height of the rectangle. Thus, the height of the rectangle is (7.5 – 2) m, which equals 5.5 m.
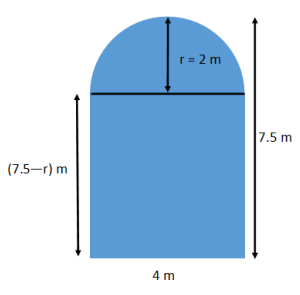
→ What is the area of the rectangle?
The area of the rectangle is 5.5 m times 4 m. The area is 22.0 m2.
→ What is the area of the semicircle?
The area of the semicircle is half the area of a circle with a radius of 2 m. The area is 4(3.14) m2 divided by 2, which equals 6.28 m2.
→ Do we subtract these areas as we did in Example 1?
No, we combine the two. The figure is the sum of the rectangle and the semicircle.
→ What is the area of the figure?
28.28 m2
Example 3.
Find the area of the shaded region.
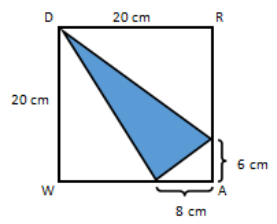
Redraw the figure separating the triangles; then, label the lengths discussing the calculations.
Answer:
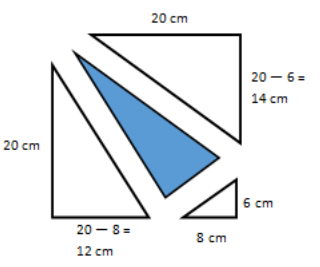
→ Do we know any of the lengths of the acute triangle?
No
→ Do we have information about the right triangles?
Yes, because of the given lengths, we can calculate unknown sides.
→ Is the sum or difference of these parts needed to find the area of the shaded region?
Both are needed. The difference of the square and the sum of the three right triangles is the area of the shaded triangle.
→ What is the area of the shaded region?
400 cm2 – ((\(\frac{1}{2}\) × 20 cm × 12 cm)+(\(\frac{1}{2}\) × 20 cm × 14 cm) + (\(\frac{1}{2}\) × 8 cm × 6 cm)) = 116 cm2
The area is 116 cm2.
Eureka Math Grade 7 Module 3 Lesson 20 Exercise Answer Key
Exercise 1.
A yard is shown with the shaded section indicating grassy areas and the unshaded sections indicating paved areas. Find the area of the space covered with grass in units2.
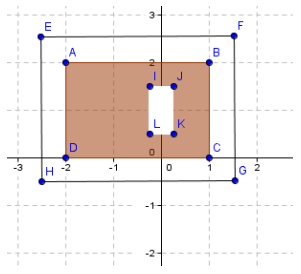
Answer:
Area of rectangle ABCD – area of rectangle IJKL = area of shaded region
(3 ∙ 2) – (\(\frac{1}{2}\) ∙ 1)
6 – \(\frac{1}{2}\)
5 \(\frac{1}{2}\)
The area of the space covered with grass is 5 \(\frac{1}{2}\) units2.
Exercise 2.
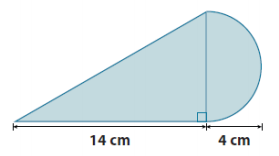
Find the area of the shaded region. Use 3.14 for π.
Answer:
Area of the triangle + area of the semicircle = area of the shaded region
\(\frac{1}{2}\) b × h) + \(\frac{1}{2}\) )(πr2 )
\(\frac{1}{2}\) ∙ 14 cm ∙ 8 cm) + \(\frac{1}{2}\) )(3.14 ∙ (4 cm)2 )
56 cm2 + 25.12 cm2
81.12 cm2
The area is approximately 81.12 cm2.
Exercise 3.
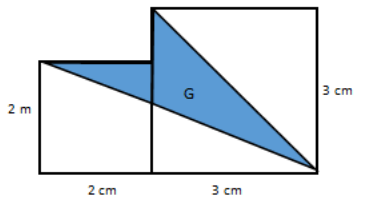
Find the area of the shaded region. The figure is not drawn to scale.
Answer:
Area of squares – (area of the bottom right triangle + area of the top right triangle)
((2 cm × 2 cm)+(3 cm × 3 cm)) – ((\(\frac{1}{2}\) × 5 cm × 2 cm)+(\(\frac{1}{2}\) × 3 cm × 3 cm))
13 cm2 – 9.5 cm2
3.5 cm2
The area is 3.5 cm2.
There are multiple solution paths for this problem. Explore them with students.
Eureka Math Grade 7 Module 3 Lesson 20 Problem Set Answer Key
Question 1.
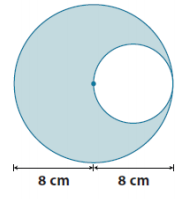
Find the area of the shaded region. Use 3.14 for π.
Answer:
Area of large circle– area of small circle
(π × (8 cm)2) – (π × (4 cm)2)
(3.14)(64 cm2) – (3.14)(16 cm2)
200.96 cm2 – 50.24 cm2
150.72 cm2
The area of the region is approximately 150.72 cm2.
Question 2.
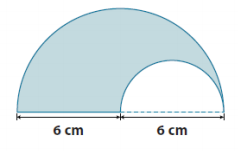
The figure shows two semicircles. Find the area of the shaded region. Use 3.14 for π.
Answer:
Area of large semicircle region – area of small semicircle region = area of the shaded region
(\(\frac{1}{2}\) )(π × (6 cm)2) – (\(\frac{1}{2}\) )(π × (3 cm)2)
(\(\frac{1}{2}\) )(3.14)(36 cm2) – (\(\frac{1}{2}\) )(3.14)(9 cm2)
56.52 cm2 – 14.13 cm2
42.39 cm2
The area is approximately 42.39 cm2.
Question 3.
The figure shows a semicircle and a square. Find the area of the shaded region. Use 3.14 for π.
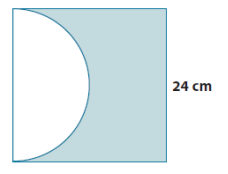
Answer:
Area of the square – area of the semicircle
(24 cm × 24 cm) – (\(\frac{1}{2}\) )( π × (12 cm)2)
576 cm2 – (\(\frac{1}{2}\) )(3.14 × 144 cm2)
576 cm2 – 226.08 cm2
349.92 cm2
The area is approximately 349.92 cm2.
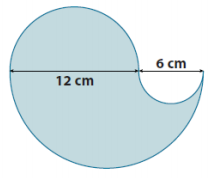
Question 4.
The figure shows two semicircles and a quarter of a circle. Find the area of the shaded region. Use 3.14 for π.
Answer:
Area of two semicircles + area of quarter of the larger circle
2(\(\frac{1}{2}\))(π × (5 cm)2 ) + (\(\frac{1}{4}\))(π × (10 cm)2)
(3.14)(25 cm2 )+(3.14)(25 cm2)
78.5 cm2 + 78.5 cm2
157 cm2
The area is approximately 157 cm2.
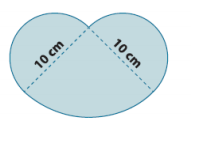
Question 5.
Jillian is making a paper flower motif for an art project. The flower she is making has four petals; each petal is formed by three semicircles as shown below. What is the area of the paper flower? Provide your answer in terms of π.
Answer:
Area of medium semicircle + (area of larger semicircle – area of small semicircle)
(\(\frac{1}{2}\) )(π × (6 cm)2 )+((\(\frac{1}{2}\) )(π × (9 cm)2 ) – (\(\frac{1}{2}\) )(π × (3 cm)2))
18π cm2+40.5π cm2 – 4.5π cm2 = 54π cm2
54π cm2 × 4
216πcm2
The area is 216π cm2.
Question 6.
The figure is formed by five rectangles. Find the area of the unshaded rectangular region.
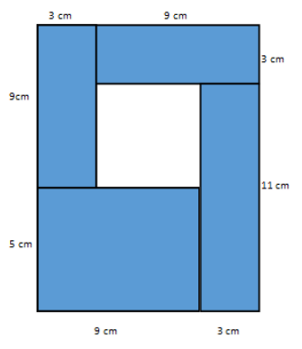
Answer:
Area of the whole rectangle – area of the sum of the shaded rectangles = area of the unshaded rectangular region
(12 cm × 14 cm) – (2(3 cm × 9 cm) + (11 cm × 3 cm) + (5 cm × 9 cm))
168 cm2 – (54 cm2 + 33 cm2 + 45 cm2 )
168 cm2 – 132 cm2
36 cm2
The area is 36 cm2.
Question 7.
The smaller squares in the shaded region each have side lengths of 1.5 m. Find the area of the shaded region.
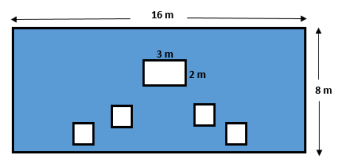
Answer:
Area of the 16 m by 8 m rectangle – the sum of the area of the smaller unshaded rectangles = area of the shaded region
(16 m × 8 m) – ((3 m × 2 m) + (4(1.5 m × 1.5 m)))
128 m2 – (6 m2 + 4(2.25 m2 ))
128 m2 – 15 m2
113 m2
The area is 113 m2.
Question 8.
Find the area of the shaded region.
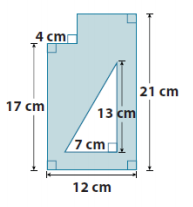
Answer:
Area of the sum of the rectangles – area of the right triangle = area of shaded region
((17 cm × 4 cm)+(21 cm × 8 cm)) – ((\(\frac{1}{2}\) )(13 cm × 7 cm))
(68 cm2+168 cm2 ) – (\(\frac{1}{2}\) )(91 cm2 )
236 cm2 – 45.5 cm2
190.5 cm2
The area is 190.5 cm2.
Question 9.
a. Find the area of the shaded region.
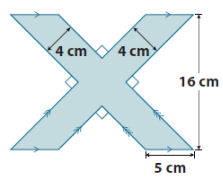
Answer:
Area of the two parallelograms – area of square in the center = area of the shaded region
2(5 cm × 16 cm) – (4 cm × 4 cm)
160 cm2 – 16 cm2
144 cm2
The area is 144 cm2.
b. Draw two ways the figure above can be divided in four equal parts.
Answer:
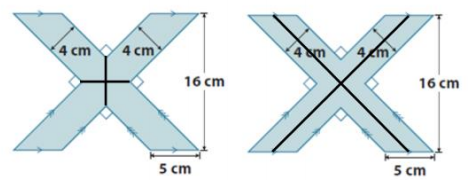
c. What is the area of one of the parts in (b)?
Answer:
144 cm2 ÷ 4 = 36 cm2
The area of one of the parts in (b) is 36 cm2.
Question 10.
The figure is a rectangle made out of triangles. Find the area of the shaded region.
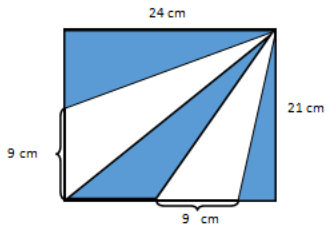
Answer:
Area of the rectangle – area of the unshaded triangles = area of the shaded region
(24 cm × 21 cm) – ((\(\frac{1}{2}\) )(9 cm × 21 cm)+(\(\frac{1}{2}\))(9 cm × 24 cm))
504 cm2 – (94.5 cm2 + 108 cm2 )
504 cm2 – 202.5 cm2
301.5 cm2
The area is 301.5 cm2.
Question 11.
The figure consists of a right triangle and an eighth of a circle. Find the area of the shaded region. Use \(\frac{22}{7}\) for π.
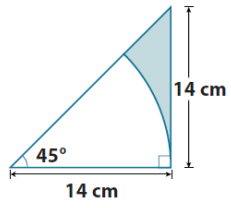
Answer:
Area of right triangle – area of eighth of the circle = area of shaded region
(\(\frac{1}{2}\))(14 cm × 14 cm) – (\(\frac{1}{8}\))(π × 14 cm × 14 cm)
(\(\frac{1}{2}\))(196 cm2) – (\(\frac{1}{8}\))(\(\frac{22}{7}\))(2 cm × 7 cm × 2 cm × 7 cm)
98 cm2 – 77 cm2
21 cm2
The area is approximately 21 cm2.
Eureka Math Grade 7 Module 3 Lesson 20 Exit Ticket Answer Key
Question 1.
The unshaded regions are quarter circles. Approximate the area of the shaded region. Use π ≈ 3.14.
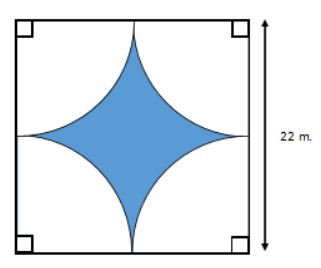
Answer:
Area of the square – area of the 4 quarter circles = area of the shaded region
(22 m ∙ 22 m) – ((11 m)2 ∙ 3.14)
484 m2 – 379.94 m2
104.06 m2
The area of the shaded region is approximately 104.06 m2.