Engage NY Eureka Math 7th Grade Module 3 Lesson 21 Answer Key
Eureka Math Grade 7 Module 3 Lesson 21 Example Answer Key
Example 1: Lateral Area of a Right Prism
A right triangular prism, a right rectangular prism, and a right pentagonal prism are pictured below, and all have equal heights of h.
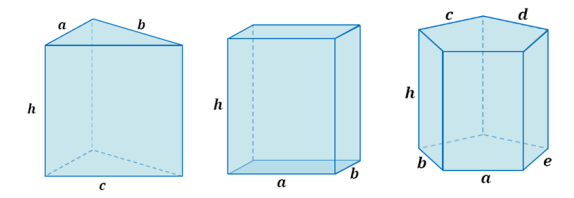
a. Write an expression that represents the lateral area of the right triangular prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + c ∙ h
b. Write an expression that represents the lateral area of the right rectangular prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + a ∙ h + b ∙ h
c. Write an expression that represents the lateral area of the right pentagonal prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + c ∙ h + d ∙ h + e ∙ h
d. What value appears often in each expression and why?
Answer:
h; Each prism has a height of h; therefore, each lateral face has a height of h.
e. Rewrite each expression in factored form using the distributive property and the height of each lateral face.
Answer:
h(a + b + c)
h(a + b + a + b)
h(a + b + c + d + e)
f. What do the parentheses in each case represent with respect to the right prisms?
Answer:
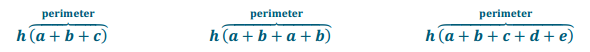
The perimeter of the base of the corresponding prism.
g. How can we generalize the lateral area of a right prism into a formula that applies to all right prisms?
Answer:
If LA represents the lateral area of a right prism, P represents the perimeter of the right prism’s base, and h represents the distance between the right prism’s bases, then:
LA = Pbase ∙ h.
Relevant Vocabulary
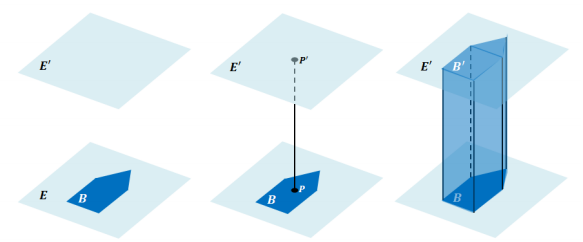
RIGHT PRISM: Let E and E’ be two parallel planes. Let B be a triangular or rectangular region or a region that is the union of such regions in the plane E. At each point P of B, consider the segment PP’ perpendicular to E, joining P to a point P’ of the plane E’. The union of all these segments is a solid called a right prism.
There is a region B’ in E’ that is an exact copy of the region B. The regions B and B’ are called the base faces (or just bases) of the prism. The rectangular regions between two corresponding sides of the bases are called lateral faces of the prism. In all, the boundary of a right rectangular prism has 6 faces: 2 base faces and 4 lateral faces. All adjacent faces intersect along segments called edges (base edges and lateral edges).
CUBE: A cube is a right rectangular prism all of whose edges are of equal length.
SURFACE: The surface of a prism is the union of all of its faces (the base faces and lateral faces).
NET: A net is a two-dimensional diagram of the surface of a prism.
1. Why are the lateral faces of right prisms always rectangular regions?
Answer:
Because along a base edge, the line segments PP’ are always perpendicular to the edge, forming a rectangular region.
2. What is the name of the right prism whose bases are rectangles?
Answer:
Right rectangular prism
3. How does this definition of right prism include the interior of the prism?
Answer:
The union of all the line segments fills out the interior.
Eureka Math Grade 7 Module 3 Lesson 21 Exercise Answer Key
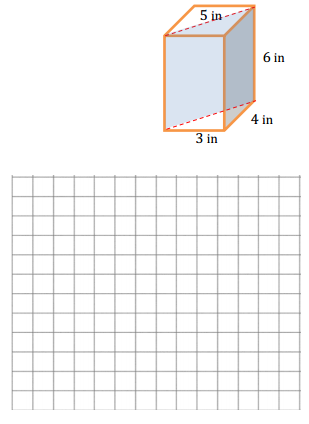
Opening Exercise: Surface Area of a Right Rectangular Prism
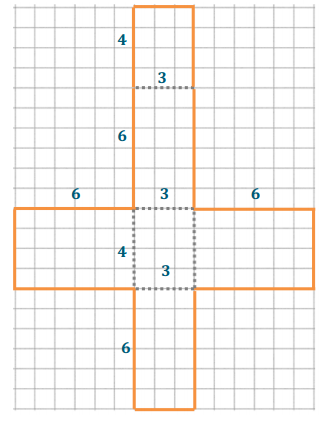
On the provided grid, draw a net representing the surfaces of the right rectangular prism (assume each grid line represents 1 inch). Then, find the surface area of the prism by finding the area of the net.

Answer:
There are six rectangular faces that make up the net.
The four rectangles in the center form one long rectangle that is 20 in. by 3 in.
Area = lw
Area = 3 in ∙ 20 in
Area = 60 in2
Two rectangles form the wings, both 6 in by 4 in.
Area = lw
Area = 6 in ∙ 4 in
Area = 24 in2
The area of both wings is 2(24 in2 ) = 48 in2.
The total area of the net is
A = 60 in2 + 48 in2 = 108 in2
The net represents all the surfaces of the rectangular prism, so its area is equal to the surface area of the prism. The surface area of
the right rectangular prism is 108 in2.
Exercise 1.
Marcus thinks that the surface area of the right triangular prism will be half that of the right rectangular prism and wants to use the modified formula SA = \(\frac{1}{2}\) (2lw + 2lh + 2wh). Do you agree or disagree with Marcus? Use nets of the prisms to support your argument.
Answer:
The surface area of the right rectangular prism is 108 in2, so Marcus believes the surface areas of each right triangular prism is 54 in2.
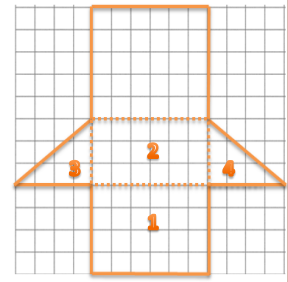
The net of the right triangular prism has one less face than the right rectangular prism. Two of the rectangular faces on the right triangular prism (rectangular regions 1 and 2 in the diagram) are the same faces from the right rectangular prism, so they are the same size. The areas of the triangular bases (triangular regions 3 and 4 in the diagram) are half the area of their corresponding rectangular faces of the right rectangular prism. These four faces of the right triangular prism make up half the surface area of the right rectangular prism before considering the fifth face; no, Marcus is incorrect.
The areas of rectangular faces 1 and 2, plus the areas of the triangular regions 3 and 4 is 54 in2. The last rectangular region has an area of 30 in2. The total area of the net is 54 in2 + 30 in2 or 84 in2, which is far more than half the surface area of the right rectangular prism.
Eureka Math Grade 7 Module 3 Lesson 21 Problem Set Answer Key
Question 1.
For each of the following nets, highlight the perimeter of the lateral area, draw the solid represented by the net, indicate the type of solid, and then find the solid’s surface area.
a. Right rectangular prism
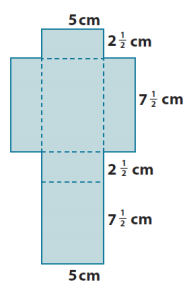
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (2 \(\frac{1}{2}\) cm + 7 \(\frac{1}{2}\) cm + 2 \(\frac{1}{2}\) cm + 7 \(\frac{1}{2}\) cm) ∙ 5 cm
LA = 20 cm ∙ 5 cm
LA = 100 cm2
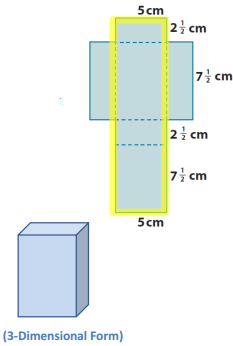
B = lw
B = 2 \(\frac{1}{2}\) cm ∙ 7 \(\frac{1}{2}\) cm
B = \(\frac{5}{2}\) cm ∙ \(\frac{15}{2}\) cm
B = \(\frac{75}{4}\) cm2
SA = 100 cm2 + 2(\(\frac{75}{4}\) cm2 )
SA = 100 cm2 + 37.5 cm2
SA = 137.5 cm2
The surface area of the right rectangular prism is 137.5 cm2
b. Right triangular prism
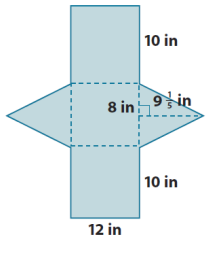
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (10 in. + 8 in. + 10 in.) ∙ 12 in.
LA = 28 in. ∙ 12 in.
LA = 336 in2
B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) (8 in.)(9 \(\frac{1}{5}\) in.)
B = 4 in.(9 \(\frac{1}{5}\) in.)
B = (36 + \(\frac{4}{5}\) )in2
B = 36 \(\frac{4}{5}\) in2
SA = 336 in2 + 2(36 \(\frac{4}{5}\) in2)
SA = 336 in2 + (72 + \(\frac{8}{5}\) )in2
SA = 408 in2 + 1 \(\frac{3}{5}\) in2
SA = 409 \(\frac{3}{5}\) in2
The surface area of the right triangular prism is 409 3/5 in22.
Question 2.
Given a cube with edges that are \(\frac{3}{4}\) inch long:
a. Find the surface area of the cube.
Answer:
SA = 6s22
SA = 6(\(\frac{3}{4}\) in.)2
SA = 6 (\(\frac{3}{4}\) in.) ∙ (\(\frac{3}{4}\) in.)
SA = 6(\(\frac{9}{16}\) in2)
SA = \(\frac{27}{8}\) in2 or 3 \(\frac{3}{8}\) in2
b. Joshua makes a scale drawing of the cube using a scale factor of 4. Find the surface area of the cube that Joshua drew.
Answer:
\(\frac{3}{4}\) in. ∙ 4 = 3 in.; The edge lengths of Joshua’s drawing would be 3 inches.
SA = 6(3 in.)2
SA = 6(9 in2)
SA = 54 in2
c. What is the ratio of the surface area of the scale drawing to the surface area of the actual cube, and how does the value of the ratio compare to the scale factor?
Answer:
54 ÷ 3 \(\frac{3}{8}\)
54 ÷ \(\frac{27}{8}\)
54 ∙ \(\frac{8}{27}\)
2 ∙ 8 = 16. The ratios of the surface area of the scale drawing to the surface area of the actual cube is 16:1. The value of the ratio is 16. The scale factor of the drawing is 4, and the value of the ratio of the surface area of the drawing to the surface area of the actual cube is 42 or 16.
Question 3.
Find the surface area of each of the following right prisms using the formula SA = LA + 2B.
a.
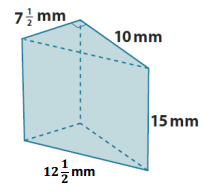
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (12 \(\frac{1}{2}\) mm + 10 mm + 7 \(\frac{1}{2}\) mm) ∙ 15 mm
LA = 30 mm ∙ 15 mm
LA = 450 mm2
B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ (7 \(\frac{1}{2}\) mm) ∙ (10 mm)
B = \(\frac{1}{2}\) ∙ (70 + 5) mm2
B = \(\frac{1}{2}\) ∙ 75 mm2
B = 75/2 mm2
SA = 450 mm2 + 2(\(\frac{75}{2}\) mm2)
SA = 450 mm2 + 75 mm2
SA = 525 mm2
The surface area of the prism is 525 mm2.
b.
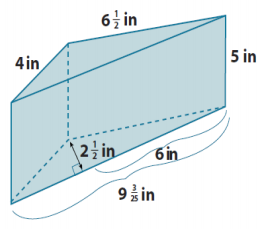
SA = LA + 2B
LA = P ∙ h
LA = (9 \(\frac{3}{25}\) in. + 6 \(\frac{1}{2}\) in. + 4 in.) ∙ 5 in in. ∙ 2 \(\frac{1}{2}\) in.
LA = (\(\frac{228}{25}\) in. + \(\frac{13}{2}\) in. + 4 in.) ∙ 5 in
LA = (\(\frac{456}{50}\) in. + \(\frac{325}{50}\) in. + \(\frac{200}{50}\) in.) ∙ 5 in.
LA = (\(\frac{981}{50}\) in.) ∙ 5 in.
LA = \(\frac{49,050}{50}\) in2
LA = 98 \(\frac{1}{10}\) in2
B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ 9 \(\frac{3}{25}\)
B = \(\frac{1}{2}\) ∙ \(\frac{228}{25}\) in. ∙ \(\frac{5}{2}\) in.
B = \(\frac{1,140}{100}\) in2
B = 11 \(\frac{2}{5}\) in2
2B = 2 ∙ 11 \(\frac{2}{5}\) in2
2B = 22 \(\frac{4}{5}\) in2
SA = LA + 2B
SA = 98 \(\frac{1}{10}\) in2 + 22 \(\frac{4}{5}\) in2
SA = 120 \(\frac{9}{10}\) in2
The surface area of the prism is 120 \(\frac{9}{10}\) in2.
c.
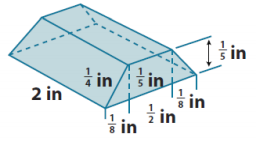
SA = LA + 2B
LA = P ∙ h
LA = (\(\frac{1}{8}\) in. + \(\frac{1}{2}\) in. + \(\frac{1}{8}\) in. + \(\frac{1}{4}\) in. + \(\frac{1}{2}\) in. + \(\frac{1}{4}\) in.) ∙ 2 in.
LA = (1 \(\frac{3}{4}\) in.) ∙ 2 in.
LA = 2 in2 + 1 \(\frac{1}{2}\) in2
LA = 3 \(\frac{1}{2}\) in2
B = Arectangle + 2Atriangle
B = (\(\frac{1}{2}\) in. ∙ \(\frac{1}{5}\) in.) + 2 ∙ \(\frac{1}{2}\) (\(\frac{1}{8}\) in. ∙ \(\frac{1}{5}\) in.)
B = (\(\frac{1}{10}\) in2 ) + (\(\frac{1}{40}\) in2 )
B = \(\frac{1}{10}\) in2 + \(\frac{1}{40}\)
B = \(\frac{4}{40}\) in2 + \(\frac{1}{40}\) in2
B = \(\frac{5}{40}\) in2
B = \(\frac{1}{8}\) in2
SA = 3 \(\frac{1}{2}\) in2 + 2(\(\frac{1}{8}\) in2) in2
SA = 3 \(\frac{1}{2}\) in2 + \(\frac{1}{4}\) in2
SA = 3 \(\frac{2}{4}\) in2 + \(\frac{1}{4}\) in2
SA = 3 \(\frac{3}{4}\) in2
The surface area of the prism is 3 \(\frac{3}{4}\) in2.
d.
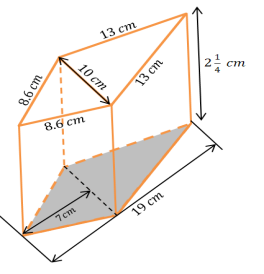
SA = LA + 2B
LA = P ∙ h
LA = (13 cm + 13 cm + 8.6 cm + 8.6 cm) ∙ 2 \(\frac{1}{4}\) cm
LA = (26 cm + 17.2 cm) ∙ 2 \(\frac{1}{4}\) cm
LA = (43.2)cm ∙ 2 \(\frac{1}{4}\) cm
LA = (86.4 cm2 + 10.8 cm2)
LA = 97.2 cm2
SA = LA + 2B
SA = 97.2 cm2 + 2(95 cm2)
SA = 97.2 cm2 + 190 cm2
SA = 287.2 cm2
B = \(\frac{1}{2}\) (10 cm ∙ 7 cm ) + \(\frac{1}{2}\) (12 cm ∙ 10 cm)
B = \(\frac{1}{2}\) (190 cm2)
B = \(\frac{1}{2}\) (70 cm2 + 120 cm2)
B = 95 cm2
The surface area of the prism is 287.2 cm2.
Question 4.
A cube has a volume of 64 m3. What is the cube’s surface area?
Answer:
A cube’s length, width, and height must be equal. 64 = 4 ∙ 4 ∙ 4 = 43, so the length, width, and height of the cube are all 4 m.
SA = 6s2
SA = 6(4 m)2
SA = 6(16 m2)
SA = 96 m2
Question 5.
The height of a right rectangular prism is 4 \(\frac{1}{2}\) ft. The length and width of the prism’s base are 2 ft. and 1 \(\frac{1}{2}\) ft. Use the formula SA = LA + 2B to find the surface area of the right rectangular prism.
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (2 ft. + 2 ft. + 1 \(\frac{1}{2}\) ft. + 1 \(\frac{1}{2}\) ft.) ∙ 4 \(\frac{1}{2}\) ft.
LA = (2 ft + 2 ft. + 3 ft.) ∙ 4 \(\frac{1}{2}\) ft.
LA = 7 ft. ∙ 4 \(\frac{1}{2}\) ft.
LA = 28 ft2 + 3 \(\frac{1}{2}\) ft2
LA = 31 \(\frac{1}{2}\) ft2
B = lw
B = 2 ft. ∙ 1 \(\frac{1}{2}\) ft.
B = 3 ft2
SA = LA + 2b
SA = 31 \(\frac{1}{2}\) ft2 + 2(3 ft2)
SA = 31 \(\frac{1}{2}\) ft2 + 6 ft2
SA = 37 \(\frac{1}{2}\) ft2
The surface area of the right rectangular prism is 37 \(\frac{1}{2}\) ft2.
Question 6.
The surface area of a right rectangular prism is 68 \(\frac{2}{3}\) in2. The dimensions of its base are 3 in and 7 in Use the formula SA = LA + 2B and LA = Ph to find the unknown height h of the prism.
Answer:
SA = LA + 2B
SA = P ∙ h + 2B
68 \(\frac{2}{3}\) in2 = 20 in. ∙ (h) + 2(21 in2)
68 \(\frac{2}{3}\) in2 = 20 in. ∙ (h) + 42 in2
68 \(\frac{2}{3}\) in2 – 42 in2 = 20 in. ∙ (h) + 42 in2 – 42 in2
26 \(\frac{2}{3}\) in2 = 20 in. ∙ (h) + 0 in2
26 \(\frac{2}{3}\) in2 ∙ \(\frac{1}{20 \mathrm{in.}}\) = 20 in ∙ \(\frac{1}{20 \mathrm{in.}}\) ∙ (h)
\(\frac{80}{3}\) in2 ∙ \(\frac{1}{20 \mathrm{in.}}\) = 1 ∙ h
\(\frac{4}{3}\) in. = h
h = \(\frac{4}{3}\) in. or 1 \(\frac{1}{3}\) in.
The height of the prism is 1 \(\frac{1}{3}\) in.
Question 7.
A given right triangular prism has an equilateral triangular base. The height of that equilateral triangle is approximately 7.1 cm. The distance between the bases is 9 cm. The surface area of the prism is 319 \(\frac{1}{2}\) cm2. Find the approximate lengths of the sides of the base.
Answer:
SA = LA + 2B
LA = P ∙ h
LA = 3(x cm) ∙ 9 cm
LA = 27x cm2
Let x represent the number of centimeters in each side of the equilateral triangle.
B = \(\frac{1}{2}\) lw
B = \(\frac{1}{2}\) ∙ (x cm) ∙ 7.1 cm
B = 3.55x cm2
319 \(\frac{1}{2}\) cm2 = LA + 2B
319 \(\frac{1}{2}\) cm2 = 27x cm2 + 2(3.55x cm2)
319 \(\frac{1}{2}\) cm2 = 27x cm2 + 7.1x cm2
319 \(\frac{1}{2}\) cm2 = 34.1x cm2
319 \(\frac{1}{2}\) cm2 = 34 \(\frac{1}{10}\) x cm2
\(\frac{639}{2}\) cm2 = \(\frac{341}{10}\) x cm2
\(\frac{639}{2}\) cm2 ∙ \(\frac{10}{341 \mathrm{~cm}}\) = \(\frac{341}{10}\) x cm2 ∙ \(\frac{10}{341 \mathrm{~cm}}\)
\(\frac{3195}{341}\) cm = x
x = \(\frac{3195}{341}\) cm
x ≈ 9.4 cm
The lengths of the sides of the equilateral triangles are approximately 9.4 cm each.
Eureka Math Grade 7 Module 3 Lesson 21 Exit Ticket Answer Key
Question 1.
Find the surface area of the right trapezoidal prism. Show all necessary work.
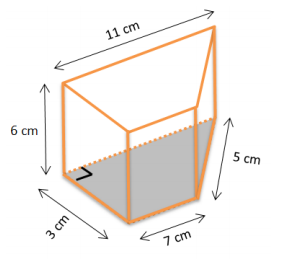
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (3 cm + 7 cm + 5 + 11 cm ) ∙ 6 cm
LA = 26 cm ∙ 6 cm
LA = 156 cm2
Each base consists of a 3 cm by 7 cm rectangle and right triangle with a base of 3 cm and a height of 4 cm. Therefore, the area of each base:
B = Ar + At
B = lw + \(\frac{1}{2}\) bh
B = (7 cm ∙ 3 cm) + (\(\frac{1}{2}\) ∙ 3 cm ∙ 4 cm)
B = 21 cm2 + 6 cm2
B = 27 cm2
SA = LA + 2B
SA = 156 cm2 + 2(27 cm2 )
SA = 156 cm2 + 54 cm2
SA = 210 cm2
The surface of the right trapezoidal prism is 210 cm2.