Eureka Math Grade 7 Module 3 Lesson 3 Answer Key

Engage NY Eureka Math 7th Grade Module 3 Lesson 3 Answer Key

Eureka Math Grade 7 Module 3 Lesson 3 Example Answer Key

Example 1.
Represent 3+2 using a tape diagram.
Answer:

→ Now, let’s represent another expression, x+2. Make sure the units are the same size when you are drawing the known 2 units.

Represent x+2 using a tape diagram.

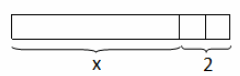
→ Note the size of the units that represent 2 in the expression x+2. Using the size of these units, can you predict what value x represents?
→ Approximately six units

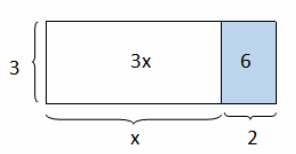
Draw a rectangular array for 3(3+2).

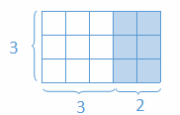
Then, have students draw a similar array for 3(x+2).

Draw an array for 3(x+2).
Answer:

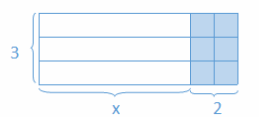
→ Determine the area of the shaded region.
→ 6
→ Determine the area of the unshaded region.
→ 3x
Record the areas of each region:

Example 2.
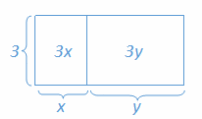
Draw a tape diagram to represent each expression.
a. (x+y)+(x+y)+(x+y)
Answer:

b. (x+x+x)+(y+y+y)
Answer:

c. 3x+3y
Answer:

d. 3(x+y)
Answer:

Ask students to explain to their neighbors why all of these expressions are equivalent.
Discuss how to rearrange the units representing x and y into each of the configurations on the previous page.
→ What can we conclude about all of these expressions?
→ They are all equivalent.
→ How does 3(x+y)=3x+3y?
→ Three groups of (x+y) is the same as multiplying 3 with the x and the y.
→ How do you know the three representations of the expressions are equivalent?
→ The arithmetic, algebraic, and graphic representations are equivalent. Problem (c) is the standard form of problems (b) and (d). Problem (a) is the equivalent of problems (b) and (c) before the distributive property is applied. Problem (b) is the expanded form before collecting like terms.
→ Under which conditions would each representation be most useful?
→ Either 3(x+y) or 3x+3y because it is clear to see that there are 3 groups of (x+y), which is the product of the sum of x and y, or that the second expression is the sum of 3x and 3y.
→ Which model best represents the distributive property?

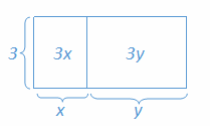
Summarize the distributive property.

Example 3.
Find an equivalent expression by modeling with a rectangular array and applying the distributive property to the expression 5(8x+3).

Answer:

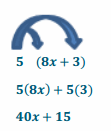
Substitute given numerical value to demonstrate equivalency. Let x=2
5(8x+3)=5 (8(2)+3)=5(16+3)=5(19)=95
40x+15=40(2)+15=80+15=95
Both equal 95, so the expressions are equal.

Example 4.
Rewrite the expression (6x+15)÷3 in standard form using the distributive property.
Answer:
(6x+15)×\(\frac{1}{3}\)
(6x) \(\frac{1}{3}\)+(15) \(\frac{1}{3}\)
2x+5

→ How can we rewrite the expression so that the distributive property can be used?
→ We can change from dividing by 3 to multiplying by \(\frac{1}{3}\).

Example 5.
Expand the expression 4(x+y+z).
Answer:

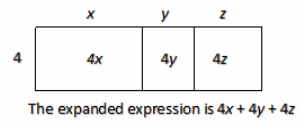
Example 6.
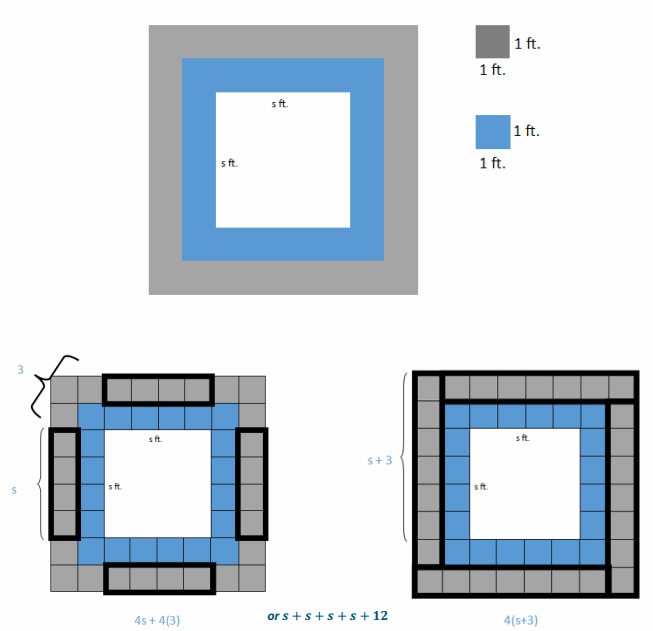
A square fountain area with side length s ft. is bordered by a single row of square tiles as shown. Express the total number of tiles needed in terms of s three different ways.

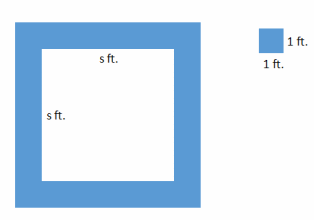
Answer:
→ What if s=4? How many tiles would you need to border the fountain?
→ I would need 20 tiles to border the fountain—four for each side and one for each corner.

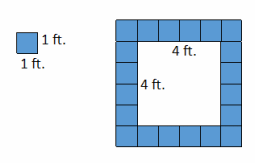
→ What if s=2? How many tiles would you need to border the fountain?
→ I would need 12 tiles to border the fountain—two for each side and one for each corner.
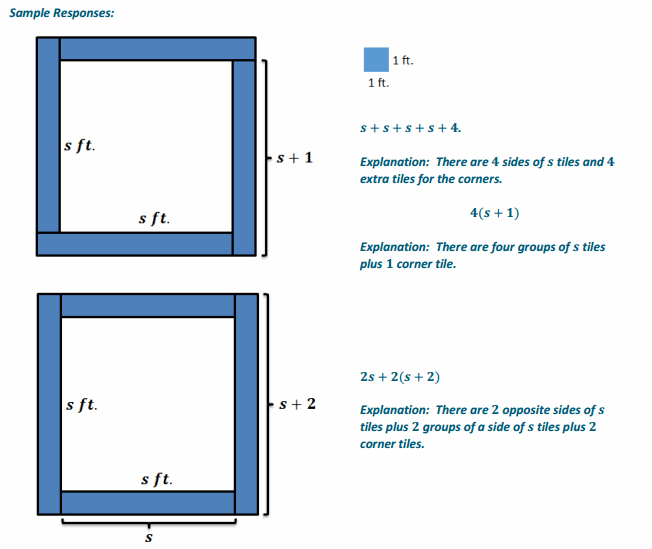
→ What pattern or generalization do you notice?
→ Answers may vary. Sample response: There is one tile for each corner and four times the number of tiles to fit one side length.
After using numerical values, allow students two minutes to create as many expressions as they can think of to find the total number of tiles in the border in terms of s. Reconvene by asking students to share their expressions with the class from their seat.
→ Which expressions would you use and why?
→ Although all the expressions are equivalent, 4(s+1), or 4s+4, is useful because it is the most simplified, concise form. It is in standard form with all like terms collected.

Eureka Math Grade 7 Module 3 Lesson 3 Opening Exercise Answer Key

Solve the problem using a tape diagram. A sum of money was shared between George and Benjamin in a ratio of 3∶4.
If the sum of money was $56.00, how much did George get?
Answer:
Have students label one unit as x in the diagram.

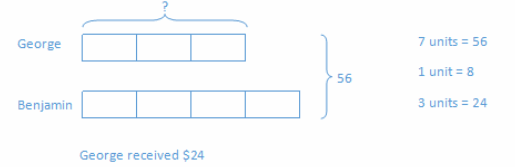
→ What does the rectangle labeled x represent?
→ $8.00

Eureka Math Grade 7 Module 3 Lesson 3 Exercise Answer Key

Exercise 1
Determine the area of each region using the distributive property.

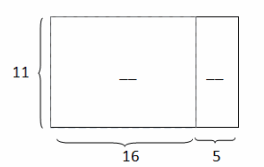
Answer:
176, 55

Draw in the units in the diagram for students.

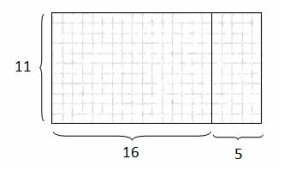
→ Is it easier to just imagine the 176 and 55 square units?
→ Yes

Exercise 2.
For parts (a) and (b), draw an array for each expression and apply the distributive property to expand each expression. Substitute the given numerical values to demonstrate equivalency.
a. 2(x+1), x=5
Answer:

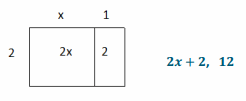
b. 10(2c+5), c=1
Answer:

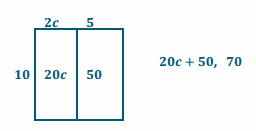
For parts (c) and (d), apply the distributive property. Substitute the given numerical values to demonstrate equivalency.

c. 3(4f-1), f=2
Answer:
12f-3, 21

d. 9(-3r-11), r=10
Answer:
-27r-99, -369

Exercise 3.
Rewrite the expressions in standard form.
a. (2b+12)÷2
Answer:
\(\frac{1}{2}\) (2b+12)
\(\frac{1}{2}\) (2b)+\(\frac{1}{2}\)(12)
b+6

b. (20r-8)÷4
\(\frac{1}{4}\) (20r-8)
\(\frac{1}{4}\) (20r)-\(\frac{1}{4}\)(8)
5r-2

c. (49g-7)÷7
\(\frac{1}{7}\) (49g-7)
\(\frac{1}{7}\) (49g)-\(\frac{1}{7}\)(7)
7g-1

Exercise 4.
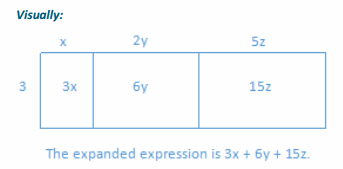
Expand the expression from a product to a sum by removing grouping symbols using an area model and the repeated use of the distributive property: 3(x+2y+5z).
Answer:
Repeated use of the distributive property: Visually:
3(x+2y+5z)
3∙x+3∙2y+3∙5z
3x+3∙2∙y+3∙5∙z
3x+6y+15z

Eureka Math Grade 7 Module 3 Lesson 3 Problem Set Answer Key

Question 1.
a. Write two equivalent expressions that represent the rectangular array below.

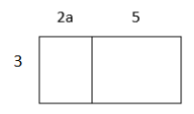
Answer:
3(2a+5) or 6a+15

b. Verify informally that the two expressions are equivalent using substitution.
Answer:
Let a=4.
3(2a+5)
3(2(4)+5)
3(8+5)
3(13)
39
6a+15
6(4)+15
24+15
39

Question 2.
You and your friend made up a basketball shooting game. Every shot made from the free throw line is worth 3 points, and every shot made from the half-court mark is worth 6 points. Write an equation that represents the total number of points, P, if f represents the number of shots made from the free throw line, and h represents the number of shots made from half-court. Explain the equation in words.
Answer:
P=3f+6h or P=3(f+2h)
The total number of points can be determined by multiplying each free throw shot by 3 and then adding that to the product of each half-court shot multiplied by 6.
The total number of points can also be determined by adding the number of free throw shots to twice the number of half-court shots and then multiplying the sum by three.

Question 3.
Use a rectangular array to write the products in standard form.
a. 2(x+10)
Answer:

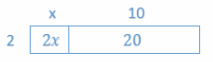
2x+20

b. 3(4b+12c+11)
Answer:

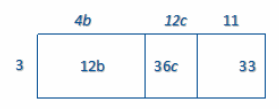
12b+36c+33

Question 4.
Use the distributive property to write the products in standard form.
a. 3(2x-1)
Answer:
6x-3

b. 10(b+4c)
Answer:
10b+40c

c. 9(g-5h)
Answer:
9g-45h

d. 7(4n-5m-2)
Answer:
28n-35m-14

e. a(b+c+1)
Answer:
ab+ac+a

f. (8j-3l+9)6
Answer:
48j-18l+54

g. (40s+100t)÷10
Answer:
4s+10t

h. (48p+24)÷6
Answer:
8p+4

i. (2b+12)÷2
Answer:
b+6

j. (20r-8)÷4
Answer:
5r-2

k. (49g-7)÷7
Answer:
7g-1

l. (14g+22h)÷\(\frac{1}{2}\)
Answer:
28g+44h

Question 5.
Write the expression in standard form by expanding and collecting like terms.
a. 4(8m-7n)+6(3n-4m)
Answer:
8m-10n

b. 9(r-s)+5(2r-2s)
Answer:
19r-19s

c. 12(1-3g)+8(g+f)
Answer:
-28g+8f+12

Eureka Math Grade 7 Module 3 Lesson 3 Exit Ticket Answer Key

A square fountain area with side length s ft. is bordered by two rows of square tiles along its perimeter as shown. Express the total number of grey tiles (the second border of tiles) needed in terms of s three different ways.
Answer: