Engage NY Eureka Math 7th Grade Module 3 Lesson 4 Answer Key
Eureka Math Grade 7 Module 3 Lesson 4 Example Answer Key
Example 1.

Answer:

→ What is happening when you factor and write equivalent expressions for parts (e), (f), (g), and (h)?
→ In the same way that dividing is the opposite or inverse operation of multiplying, factoring is the opposite of expanding.
→ What are the terms being divided by?
→ They are being divided by a common factor.
Have students write an expression that is equivalent to 8x+4.
→ Would it be incorrect to factor out a 2 instead of a 4?
Example 2
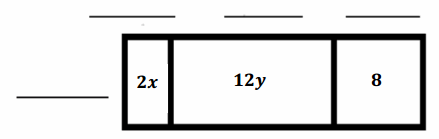
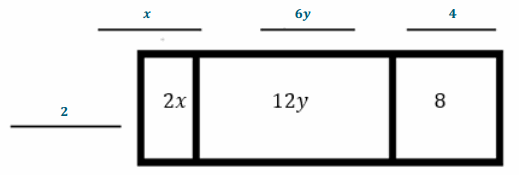
Let the variables x and y stand for positive integers, and let 2x, 12y, and 8 represent the area of three regions in the array. Determine the length and width of each rectangle if the width is the same for each rectangle.
Answer:
→ What does 2x represent in the first region of the array?
→ The region has an area of 2x or can be covered by 2x square units.
→ What does the entire array represent?
→ The entire array represents 2x+12y+8 square units.
→ What is the common factor of 2x, 12y, and 8?
→ The common factor of 2x, 12y, and 8 is 2.
→ What are the missing values, and how do you know?
→ The missing values are x, 6y, and 4. If the products are given in the area of the regions, divide the regions by 2 to determine the missing values.
Example 3.
A new miniature golf and arcade opened up in town. For convenient ordering, a play package is available to purchase. It includes two rounds of golf and 20 arcade tokens, plus $3.00 off the regular price. There is a group of six friends purchasing this package. Let g represent the cost of a round of golf, and let t represent the cost of a token. Write two different expressions that represent the total amount this group spent. Explain how each expression describes the situation in a different way.
Answer:
→ What two equivalent expressions could be used to represent the situation?
→ 6(2g+20t-3)
Each person will pay for two rounds of golf and 20 tokens and will be discounted $3.00. This expression is six times the quantity of each friend’s cost.
→ 12g+120t-18
The total cost is equal to 12 games of golf plus 120 tokens, minus $18.00 off the entire bill.
→ What does it mean to take the opposite of a number?
→ You can determine the additive inverse of a number or a multiplicative inverse.
→ What is the opposite of 2?
→ -2
→ What is (-1)(2)?
→ -2
→ What is (-1)(n)?
→ -n
→ What are two mathematical expressions that represent the opposite of (2a+3b)?
→ (-1)(2a+3b) or -(2a+3b)
→ Use the distributive property to write (-1)(2a+3b) as an equivalent expression.
→ -2a-3b or -2a+(-3b)
→ To go from -2a-3b to -(2a+3b), what process occurs?
→ The terms -2a and -3b are written as (-1)(2a) and (-1)(3b), and the -1 is factored out of their sum.
Example 4.
→ What does it mean to take the opposite of a number?
→ You can determine the additive inverse of a number or a multiplicative inverse.
→ What is the opposite of 2?
→ -2
→ What is (-1)(2)?
→ -2
→ What is (-1)(n)?
→ -n
→ What are two mathematical expressions that represent the opposite of (2a+3b)?
→ (-1)(2a+3b) or -(2a+3b)
→ Use the distributive property to write (-1)(2a+3b) as an equivalent expression.
→ -2a-3b or -2a+(-3b)
→ To go from -2a-3b to -(2a+3b), what process occurs?
→ The terms -2a and -3b are written as (-1)(2a) and (-1)(3b), and the -1 is factored out of their sum.
Example 5
Rewrite 5a-(a-3b) in standard form. Justify each step, applying the rules for subtracting and the distributive property.
Answer:
5a+(-(a+-3b)) Subtraction as adding the inverse
5a+(-1)(a+-3b) The opposite of a number is the same as multiplying by –1.
5a+(-1)(a)+(-1)(-3b) Distributive property
5a+-a+3b Multiplying by -1 is the same as the opposite of the number.
4a+3b Collect like terms
Eureka Math Grade 7 Module 3 Lesson 4 Exercise Answer Key
Exercise 1.
Rewrite the expressions as a product of two factors.
a. 72t+8
Answer:
8(9t+1)
b. 55a+11
Answer:
11(5a+1)
c. 36z+72
Answer:
36(z+2)
d. 144q-15
Answer:
3(48q-5)
e. 3r+3s
Answer:
3(r+s)
Exercise 2.
Write the product and sum of the expressions being represented in the rectangular array.
Answer:
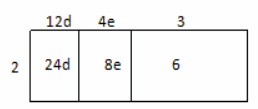
2(12d + 4e + 3); 24d + 8e + 6
b. Factor 48j+60k+24 by finding the greatest common factor of the terms.
Answer:
12(4j+5k+2)
Exercise 3.
For each expression, write each sum as a product of two factors. Emphasize the importance of the distributive property. Use various equivalent expressions to justify equivalency.
a. 2∙3+5∙3
Both have a common factor of 3, so the two factors would be 3(2+5). Demonstrate that 3(7) is equivalent to 6+15, or 21.
b. (2+5)+(2+5)+(2+5)
Answer:
This expression is 3 groups of (2+5) or 3(2)+3(5), which is 3(2+5).
c. 2∙2+(5+2)+(5∙2)
Answer:
Rewrite the expression as
2∙2+(5∙2)+(2+5), so 2(2+5)+(2+5), which equals 3(2+5).
d. x∙3+5∙3
Answer:
The greatest common factor is 3, so factor out the 3:
e. 3(x+5). (x+5)+(x+5)+(x+5)
Answer:
Similar to part (b), this is 3 groups of (x+5), so
f. 3(x+5). 2x+(5+x)+5∙2
Answer:
Combine like terms and then identify the common factor. 3x+15, where 3 is the common factor: 3(x+5). Or,
2x+2∙5+(x+5), so that 2(x+5)+(x+5)=3(x+5). Or, use the associative property and write:
2x+(5∙2)+(5+x)
2(x+5)+(5+x)
3(x+5).
g. x∙3+y∙3
Answer:
The greatest common factor is 3, so 3(x+y). (x+y)+(x+y)+(x+y)
There are 3 groups of
h. (x + y) + (x+ y) + (x+y)
Answer:
There are 3 groups of (x+y), so 3(x+y)
i. 2x + (y + x) + 2y
Answer:
Combine like terms and then identify the common factor. 3x+3y, where 3 is the common factor. 3(x+y). Or,
2x+2y+(x+y), so that 2(x+y)+(x+y) is equivalent to 3(x+y). Or, use the associative property, and write:
2x+2y+(y+x)
2(x+y)+(x+y)
3(x+y).
Exercise 4.
a. What is the opposite of (-6v+1)?
Answer:
-(-6v+1)
b. Using the distributive property, write an equivalent expression for part (a).
Answer:
6v-1
Exercise 5.
Expand each expression and collect like terms.
a. -3(2p-3q)
Answer:
-3(2p+(-3q)) Subtraction as adding the inverse
-3∙2p+(-3)∙(-3q) Distributive property
-6p+9q Apply integer rules
b. -a-(a-b)
Answer:
-a+(-(a+-b)) Subtraction as adding the inverse
-1a+(-1(a+-1b)) The opposite of a number is the same as multiplying by –1.
-1a+(-1a)+1b Distributive property
-2a+b Apply integer addition rules
Eureka Math Grade 7 Module 3 Lesson 4 Problem Set Answer Key
Question 1.
Write each expression as the product of two factors.
a. 1∙3+7∙3
Answer:
3(1+7)
b. (1+7)+(1+7)+(1+7)
Answer:
3(1+7)
c. 2∙1+(1+7)+(7∙2)
Answer:
3(1+7)
d. h∙3+6∙3
Answer:
3(h+6)
e. (h+6)+(h+6)+(h+6)
Answer:
3(h+6)
f. 2h+(6+h)+6∙2
Answer:
3(h+6)
g. j∙3+k∙3
Answer:
3(j+k)
h. (j+k)+(j+k)+(j+k)
Answer:
3(j+k)
i. 3(j+k) 2j+(k+j)+2k
Answer:
3(j+k)
Question 2.
Write each sum as a product of two factors.
a. 6∙7+3∙7
Answer:
7(6+3)
b. (8+9)+(8+9)+(8+9)
Answer:
3(8+9)
c. 4+(12+4)+(5∙4)
Answer:
4(1+4+5)
d. 2y∙3+4∙3
Answer:
3(2y+4)
e. (x+5)+(x+5)
Answer:
2(x+5)
f. 3x+(2+x)+5∙2
Answer:
4(x+3)
g. f∙6+g∙6
Answer:
6(f+g)
h. (c+d)+(c+d)+(c+d)+(c+d)
Answer:
4(c+d)
i. 2r+r+s+2s
Answer:
3(r+s)
Question 3.
Use the following rectangular array to answer the questions below.
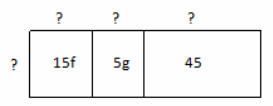
a. Fill in the missing information.
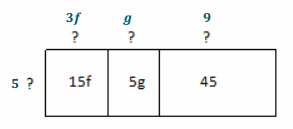
b. Write the sum represented in the rectangular array.
Answer:
15f + 5g + 45
c. Use the missing information from part (a) to write the sum from part (b) as a product of two factors.
Answer:
5(3f+g+9)
Question 4.
Write the sum as a product of two factors.
a. 81w+48
Answer:
3(27w+16)
b. 10-25t
Answer:
5(2-5t)
c. 12a+16b+8
Answer:
4(3a+4b+2)
Question 5.
Xander goes to the movies with his family. Each family member buys a ticket and two boxes of popcorn. If there are five members of his family, let t represent the cost of a ticket and p represent the cost of a box of popcorn. Write two different expressions that represent the total amount his family spent. Explain how each expression describes the situation in a different way.
Answer:
5(t+2p)
Five people each buy a ticket and two boxes of popcorn, so the cost is five times the quantity of a ticket and two boxes of popcorn.
5t+10p
There are five tickets and 10 boxes of popcorn total. The total cost will be five times the cost of the tickets, plus 10 times the cost of the popcorn.
Question 6.
Write each expression in standard form.
a. -3(1-8m-2n)
Answer:
-3(1+(-8m)+(-2n))
-3+24m+6n
b. 5-7(-4q+5)
Answer:
5+-7(-4q+5)
5+28q+(-35)
28q-35+5
28q-30
c. -(2h-9)-4h
Answer:
-(2h-9)-4h
-(2h+(-9))+(-4h)
-2h+9+(-4h)
-6h+9
d. 6(-5r-4)-2(r-7s-3)
Answer:
6(-5r-4)-2(r-7s-3)
6(-5r+-4)+-2(r-7s+-3)
-30r+-24+-2r+14s+6
-30r+-2r+14s+-24+6
-32r+14s-18
Question 7.
Combine like terms to write each expression in standard form.
a. (r-s)+(s-r)
Answer:
0
b. (-r+s)+(s-r)
Answer:
-2r+2s
c. (-r-s)-(-s-r)
Answer:
0
d. (r-s)+(s-t)+(t-r)
Answer:
0
e. (r-s)-(s-t)-(t-r)
Answer:
2r-2s
Eureka Math Grade 7 Module 3 Lesson 4 Exit Ticket Answer Key
Question 1.
Write the expression below in standard form.
3h-2(1+4h)
Answer:
3h-2(1+4h)
3h+(-2(1+4h)) Subtraction as adding the inverse
3h+(-2∙1)+(-2h∙4) Distributive property
3h+(-2)+(-8h) Apply integer rules
-5h-2 Collect like terms
Question 2.
Write the expression below as a product of two factors.
6m+8n+4
Answer:
The GCF for the terms is 2. Therefore, the factors are 2(3m+4n+2).