Engage NY Eureka Math 7th Grade Module 3 Lesson 9 Answer Key
Eureka Math Grade 7 Module 3 Lesson 9 Example Answer Key
Example 1.
Fred and Sam are a team in the local 138.2 mile bike-run-athon. Fred will compete in the bike race, and Sam will compete in the run. Fred bikes at an average speed of 8 miles per hour and Sam runs at an average speed of 4 miles per hour. The bike race begins at 6:00 a.m., followed by the run. Sam predicts he will finish the run at 2:33 a.m. the next morning.
a. How many hours will it take them to complete the entire bike-run-athon?
Answer:
From 6:00 a.m. to 2:00 a.m. the following day is 20 hours.
33 minutes in hours is \(\frac{33}{60}\)=\(\frac{11}{20}\)=0.55, or 0.55 hours.
Therefore, the total time it will take to complete the entire bike-run-athon is 20.55 hours.
b. If t is how long it takes Fred to complete the bike race, in hours, write an expression to find Fred’s total distance.
Answer:
d=rt
d=8t
The expression of Fred’s total distance is 8t.
c. Write an expression, in terms of t to express Sam’s time.
Answer:
Since t is Fred’s time and 20.55 is the total time, then Sam’s time would be the difference between the total time and Fred’s time. The expression would be 20.55-t.
d. Write an expression, in terms of t, that represents Sam’s total distance.
Answer:
d=rt
d=4(20.55-t)
The expressions 4(20.55-t) or 82.2-4t is Sam’s total distance.
e. Write and solve an equation using the total distance both Fred and Sam will travel.
Answer:
8t+4(20.55-t)=138.2
8t+82.2-4t=138.2
8t-4t+82.2=138.2
4t+82.2=138.2
4t+82.2-82.2=138.2-82.2
4t+0=56
(\(\frac{1}{4}\))(4t)=(\(\frac{1}{4}\))(56)
t=14
Fred’s time: 14 hours
Sam’s time: 20.55-t=20.55-14=6.55
6.55 hours
f. How far will Fred bike, and how much time will it take him to complete his leg of the race?
Answer:
8(14)=112
Fred will bike 112 miles and will complete the bike race in 14 hours.
g. How far will Sam run, and how much time will it take him to complete his leg of the race?
Answer:
4(20.55-t)
4(20.55-14)
4(6.55)
26.2
Sam will run 26.2 miles, and it will take him 6.55 hours.
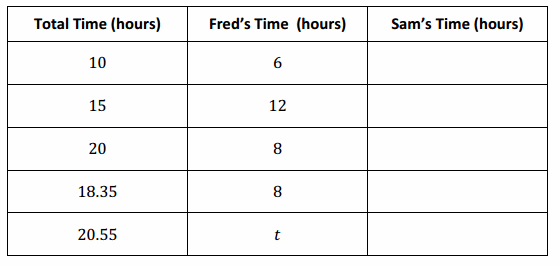
Answer:

→ How do you find the distance traveled?
→ Multiply the rate of speed by the amount of time.
→ Model how to organize the problem in a distance, rate, and time chart.

Answer:
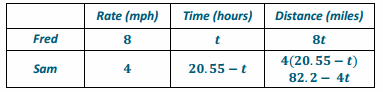
→ Explain how to write the equation to have only integers and no decimals. Write the equation.
→ Since the decimal terminates in the tenths place, if we multiply every term by 10, the equation would result with only integer coefficients. The equation would be 40t+822=1382.
Example 2.
Shelby is seven times as old as Bonnie. If in 5 years, the sum of Bonnie’s and Shelby’s ages is 98, find Bonnie’s present age. Use an algebraic approach.

Answer:
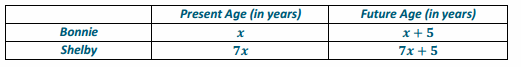
x+5+7x+5=98
8x+10=98
8x+10-10=98-10
8x=88
(\(\frac{1}{8}\))(8x)=(\(\frac{1}{8}\))(88)
x=11
Bonnie’s present age is 11 years old.
→ The first step we must take is to write expressions that represent the present ages of both Bonnie and Shelby. The second step is to write expressions for future time or past time, using the present age expressions. How would the expression change if the time were in the past and not in the future?
→ If the time were in the past, then the expression would be the difference between the present age and the amount of time in the past.
Eureka Math Grade 7 Module 3 Lesson 9 Opening Exercise Answer Key
Heather practices soccer and piano. Each day she practices piano for 2 hours. After 5 days, she practiced both piano and soccer for a total of 20 hours. Assuming that she practiced soccer the same amount of time each day, how many hours per day, h, did Heather practice soccer?
Answer:
h: hours per day that soccer was practiced
5(h+2)=20
5h+10=20
5h+10-10=20-10
5h=10
(\(\frac{1}{5}\))(5h)=(\(\frac{1}{5}\))(10)
h=2
Heather practiced soccer for 2 hours each day.
Over 5 days, Jake practices piano for a total of 2 hours. Jake practices soccer for the same amount of time each day. If he practiced piano and soccer for a total of 20 hours, how many hours, h, per day did Jake practice soccer?
Answer:
h: hours per day that soccer was practiced
5h+2=20
5h+2-2=20-2
5h=18
(\(\frac{1}{5}\))(5h)=(18)(\(\frac{1}{5}\))
h=3.6
Jake practiced soccer 3.6 hours each day.
Eureka Math Grade 7 Module 3 Lesson 9 Problem Set Answer Key
Question 1.
A company buys a digital scanner for $12,000. The value of the scanner is 12,000(1-\(\frac{n}{5}\)) after n years. The company has budgeted to replace the scanner when the trade-in value is $2,400. After how many years should the company plan to replace the machine in order to receive this trade-in value?
Answer:
12,000(1-\(\frac{n}{5}\))=2,400
12,000-2,400n=2,400
-2,400n+12,000-12,000=2,400-12,000
-2,400n=-9,600
n=4
They will replace the scanner after 4 years.
Question 2.
Michael is 17 years older than John. In 4 years, the sum of their ages will be 49. Find Michael’s present age.
Answer:
x represents Michael’s age now in years.

x+4+x-17+4=49
x+4+x-13=49
2x-9=49
2x-9+9=49+9
2x=58
(\(\frac{1}{2}\))(2x)=(\(\frac{1}{2}\))(58)
x=29
Michael’s present age is 29 years old.
Question 3.
Brady rode his bike 70 miles in 4 hours. He rode at an average speed of 17 mph for t hours and at an average rate of speed of 22 mph for the rest of the time. How long did Brady ride at the slower speed? Use the variable t to represent the time, in hours, Brady rode at 17 mph.
Answer:
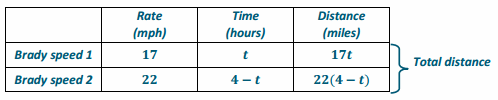
The total distance he rode: 17t+22(4-t)
The total distance equals 70 miles:
17t+22(4-t)=70
17t+88-22t=70
-5t+88=70
-5t+88-88=70-88
-5t=-18
t=3.6
Brady rode at 17 mph for 3.6 hours.
Question 4.
Caitlan went to the store to buy school clothes. She had a store credit from a previous return in the amount of $39.58. If she bought 4 of the same style shirt in different colors and spent a total of $52.22 after the store credit was taken off her total, what was the price of each shirt she bought? Write and solve an equation with integer coefficients.
Answer:
t: the price of one shirt
4t-39.58=52.22
4t-39.58+39.58=52.22+39.58
4t+0=91.80
(\(\frac{1}{4}\))(4t)=(\(\frac{1}{4}\))(91.80)
t=22.95
The price of one shirt was $22.95.
Question 5.
A young boy is growing at a rate of 3.5 cm per month. He is currently 90 cm tall. At that rate, in how many months will the boy grow to a height of 132 cm?
Answer:
Let m represent the number of months.
3.5m+90=132
3.5m+90-90=132-90
3.5m=42
(\(\frac{1}{3.5}\))(3.5m)=(\(\frac{1}{3.5}\))(42)
m=12
The boy will grow to be 132 cm tall 12 months from now.
Question 6.
The sum of a number, \(\frac{1}{6}\) of that number, 2 \(\frac{1}{2}\) of that number, and 7 is 12 \(\frac{1}{2}\). Find the number.
Answer:
Let n represent the given number.
n+\(\frac{1}{6}\) n+(2 \(\frac{1}{2}\))n+7=12 \(\frac{1}{2}\)
n(1+\(\frac{1}{6}\)+\(\frac{5}{2}\))+7=12 \(\frac{1}{2}\)
n(\(\frac{6}{6}\)+\(\frac{1}{6}\)+\(\frac{15}{6}\))+7=12 \(\frac{1}{2}\)
n(\(\frac{22}{6}\))+7=12 \(\frac{1}{2}\)
1\(\frac{1}{3}\) n+7-7=12 \(\frac{1}{2}\)-7
1\(\frac{1}{3}\) n+0=5 \(\frac{1}{2}\)
1\(\frac{1}{3}\) n=5 \(\frac{1}{2}\)
\(\frac{3}{11}\)∙1\(\frac{1}{3}\) n=\(\frac{3}{11}\)∙1\(\frac{1}{2}\)
1n=\(\frac{3}{2}\)
n=1 \(\frac{1}{2}\)
The number is 1 \(\frac{1}{2}\).
Question 7.
The sum of two numbers is 33 and their difference is 2. Find the numbers.
Answer:
Let x represent the first number, then 33-x represents the other number since their sum is 33.
x-(33-x)=2
x+(-(33-x))=2
x+(-33)+x=2
2x+(-33)=2
2x+(-33)+33=2+33
2x+0=35
2x=35
\(\frac{1}{2}\)∙2x=\(\frac{1}{2}\)∙35
1x=\(\frac{35}{2}\)
x=17 \(\frac{1}{2}\)
33-x=33-(17 \(\frac{1}{2}\))=15 \(\frac{1}{2}\)
{17 \(\frac{1}{2}\),15 \(\frac{1}{2}\)}
Question 8.
Aiden refills three token machines in an arcade. He puts twice the number of tokens in machine A as in machine B, and in machine C, he puts \(\frac{3}{4}\) of what he put in machine A. The three machines took a total of 18,324 tokens. How many did each machine take?
Answer:
Let A represent the number of tokens in machine A. Then \(\frac{1}{2}\) A represents the number of tokens in machine B, and \(\frac{3}{4}\) A represents the number of tokens in machine C.
A+\(\frac{1}{2}\) A+\(\frac{3}{4}\) A=18,324
\(\frac{9}{4}\) A=18,324
A=8,144
Machine A took 8,144 tokens, machine B took 4,072 tokens, and machine C took 6,108 tokens.
Question 9.
Paulie ordered 250 pens and 250 pencils to sell for a theatre club fundraiser. The pens cost 11 cents more than the pencils. If Paulie’s total order costs $42.50, find the cost of each pen and pencil.
Answer:
Let l represent the cost of a pencil in dollars. Then, the cost of a pen in dollars is l+0.11.
250(l+l+0.11)=42.5
250(2l+0.11)=42.5
500l+27.5=42.5
500l+27.5+(-27.5)=42.5+(-27.5)
500l+0=15
500l=15
\(\frac{500l}{500}\)=\(\frac{15}{500}\)
l=0.03
A pencil costs $0.03, and a pen costs $0.14.
Question 10.
A family left their house in two cars at the same time. One car traveled an average of 7 miles per hour faster than the other. When the first car arrived at the destination after 5 \(\frac{1}{2}\) hours of driving, both cars had driven a total of 599.5 miles. If the second car continues at the same average speed, how much time, to the nearest minute, will it take before the second car arrives?
Answer:
Let r represent the speed in miles per hour of the faster car, then r-7 represents the speed in miles per hour of the slower car.
5 \(\frac{1}{2}\) (r)+5 \(\frac{1}{2}\) (r-7)=599.5
5 \(\frac{1}{2}\) (r+r-7)=599.5
5 \(\frac{1}{2}\) (2r-7)=599.5
1\(\frac{1}{2}\) (2r-7)=599.5
\(\frac{2}{11}\)∙\(\frac{11}{2}\) (2r-7)=\(\frac{2}{11}\)∙599.5
1∙(2r-7)=\(\frac{1199}{11}\)
2r-7=109
2r-7+7=109+7
2r+0=116
2r=116
\(\frac{1}{2}\)∙2r=\(\frac{1}{2}\)∙116
1r=58
r=58
The average speed of the faster car is 58 miles per hour, so the average speed of the slower car is 51 miles per hour.
distance=rate∙time
d=51∙5 \(\frac{1}{2}\)
d=51∙\(\frac{11}{2}\)
d=280.5
The slower car traveled 280.5 miles in 5 \(\frac{1}{2}\) hours.
d=58∙5 \(\frac{1}{2}\)
d=58∙\(\frac{11}{2}\)
d=319
OR
599.5-280.5 = 319
The faster car traveled 319 miles in 5 \(\frac{1}{2}\) hours.
The slower car traveled 280.5 miles in 5 \(\frac{1}{2}\) hours. The remainder of their trip is 38.5 miles because
319-280.5=38.5.
distance=rate∙time
38.5=51 (t)
\(\frac{1}{51}\) (38.5)=\(\frac{1}{51}\) (51)(t)
\(\frac{38.5}{51}\)=1t
\(\frac{77}{102}\)=t
This time is in hours. To convert to minutes, multiply by 60 minutes per hour.
\(\frac{77}{102}\)∙60=\(\frac{77}{51}\)∙30=\(\frac{2310}{51}\)≈45
The slower car will arrive approximately 45 minutes after the first.
Question 11.
Emily counts the triangles and parallelograms in an art piece and determines that altogether, there are 42 triangles and parallelograms. If there are 150 total sides, how many triangles and parallelograms are there?
Answer:
If t represents the number of triangles that Emily counted, then 42-t represents the number of parallelograms that she counted.
3t+4(42-t)=150
3t+4(42+(-t))=150
3t+4(42)+4(-t)=150
3t+168+(-4t)=150
3t+(-4t)+168=150
-t+168=150
-t+168-168=150-168
-t+0=-18
-t=-18
-1∙(-t)=-1∙(-18)
1t=18
t=18
There are 18 triangles and 24 parallelograms.
Note to the Teacher: Problems 12 and 13 are more difficult and may not be suitable to assign to all students to solve independently.
Question 12.
Stefan is three years younger than his sister Katie. The sum of Stefan’s age 3 years ago and \(\frac{2}{3}\) of Katie’s age at that time is 12. How old is Katie now?
Answer:
If s represents Stefan’s age in years, then s+3 represents Katie’s current age, s-3 represents Stefan’s age 3 years ago, and s also represents Katie’s age 3 years ago.
(s-3)+(\(\frac{2}{3}\))s=12
s+(-3)+\(\frac{2}{3}\) s=12
s+\(\frac{2}{3}\) s+(-3)=12
\(\frac{3}{3}\) s+\(\frac{2}{3}\) s+(-3)=12
\(\frac{5}{3}\) s+(-3)=12
\(\frac{5}{3}\) s+(-3)+3=12+3
\(\frac{5}{3}\) s+0=15
\(\frac{5}{3}\) s=15
\(\frac{3}{5}\)∙\(\frac{5}{3}\) s=\(\frac{3}{5}\)∙15
1s=3∙3
s=9
Stefan’s current age is 9 years, so Katie is currently 12 years old.
Question 13.
Lucas bought a certain weight of oats for his horse at a unit price of $0.20 per pound. The total cost of the oats left him with $1. He wanted to buy the same weight of enriched oats instead, but at $0.30 per pound, he would have been $2 short of the total amount due. How much money did Lucas have to buy oats?
Answer:
The difference in the costs is $3.00 for the same weight in feed.
Let w represent the weight in pounds of feed.
0.3w-0.2w=3
0.1w=3
\(\frac{1}{10}\) w=3
10∙\(\frac{1}{10}\) w=10∙3
1w=30
w=30
Lucas bought 30 pounds of oats.
Cost=unit price×weight
Cost=($0.20 per pound)∙(30 pounds)
Cost=$6.00
Lucas paid $6 for 30 pounds of oats. Lucas had $1 left after his purchase, so he started with $7.
Eureka Math Grade 7 Module 3 Lesson 9 Exit Ticket Answer Key
Question 1.
Brand A scooter has a top speed that goes 2 miles per hour faster than Brand B. If after 3 hours, Brand A scooter traveled 24 miles at its top speed, at what rate did Brand B scooter travel at its top speed if it traveled the same distance? Write an equation to determine the solution. Identify the if-then moves used in your solution.
Answer:
x: speed, in mph, of Brand B scooter
x+2: speed, in mph, of Brand A scooter
d=rt
24=(x+2)(3)
24=3(x+2)
Possible solution 1:
24 = 3(x+2)
8=x+2
8-2=x+2-2
6=x
If-then Moves: Divide both sides by 3.
Subtract 2 from both sides.
Possible solution 2:
24=3(x+2)
24=3x+6
24-6=3x+6-6
18=3x+0
(\(\frac{1}{3}\))(18)=(\(\frac{1}{3}\))(3x)
6=x
If-then Moves: Subtract 6 from both sides.
Multiply both sides by \(\frac{1}{3}\).
Question 2.
At each scooter’s top speed, Brand A scooter goes 2 miles per hour faster than Brand B. If after traveling at its top speed for 3 hours, Brand A scooter traveled 40.2 miles, at what rate did Brand B scooter travel if it traveled the same distance as Brand A? Write an equation to determine the solution and then write an equivalent equation using only integers.
Answer:
x: speed, in mph, of Brand B scooter
x+2: speed, in mph, of Brand A scooter
d=rt
40.2=(x+2)(3)
40.2=3(x+2)
Possible solution 1:
40.2=3(x+2)
13.4=x+2
134=10x+20
134-20=10x+20-20
114=10x
(\(\frac{1}{10}\))(114)=(\(\frac{1}{10}\))(10x)
11.4=x
Possible solution 2:
40.2=3(x+2)
40.2=3x+6
402=30x+60
402-60=30x+60-60
342=30x
(\(\frac{1}{30}\))(342)=(\(\frac{1}{30}\))(30x)
11.4=x
Brand B’s scooter travels at 11.4 miles per hour.