Engage NY Eureka Math 7th Grade Module 4 Lesson 8 Answer Key
Eureka Math Grade 7 Module 4 Lesson 8 Example Answer Key
Example 1: How Far Off?
Find the absolute error for the following problems. Explain what the absolute error means in context.
a. Taylor’s Measurement 1
Answer:
|15 \(\frac{2}{8}\)in. – 15 in.| = |0.25 in| = 0.25 in.
Taylor’s Measurement 1 was 0.25 in. away from the actual value of 15 in.
b. Connor’s Measurement 1
Answer:
|15\(\frac{4}{8}\)in. – 15 in.| = |0.5 in.| = 0.5 in.
Connor’s Measurement 1 was 0.5 in. away from the actual value of 15 in.
c. Jordan’s Measurement 2
Answer:
|14\(\frac{6}{8}\) in. – 15 in.| = 0.25 in.
Jordan’s Measurement 2 was 0.25 in. away from the actual value of 15 in.
Example 2: How Right Is Wrong?
a. Find the percent error for Taylor’s Measurement 1. What does this mean?
Answer:
\(\frac{\left|15 \frac{2}{8} – 15\right|}{|15|}\) × 100%
\(\frac{|0.25|}{|15|}\) × 100%
\(\frac{1}{60}\) × 100%
1\(\frac{2}{3}\)%
This means that Taylor’s measurement of 15.25 in. has an error that is 1\(\frac{2}{3}\)% of the actual value.
b. From Example 1, part (b), find the percent error for Connor’s Measurement 1. What does this mean?
Answer:
\(\frac{0.5 \mathrm{in} .}{15 \mathrm{in} .}\) × 100% = 3\(\frac{1}{3}\)%
This means that Connor’s measurement of 15\(\frac{4}{8}\)in. has an error that is 3\(\frac{1}{3}\)% of the actual value.
c. From Example 1, part (c), find the percent error for Jordan’s Measurement 2. What does it mean?
Answer:
\(\frac{0.25 \mathrm{in} .}{15 \mathrm{in} .}\) × 100% = 1\(\frac{2}{3}\)%
This means that Jordan’s measurement of 14\(\frac{6}{8}\)in. has an error that is 1\(\frac{2}{3}\)% of the actual value.
d. What is the purpose of finding percent error?
Answer:
It tells you how big your error is compared to the true value. An error of 1 cm is very small when measuring the distance for a marathon, but an error of 1 cm is very large if you are a heart surgeon. In evaluating the seriousness of an error, we usually compare it to the exact value.
Example 3: Estimating Percent Error
The attendance at a musical event was counted several times. All counts were between 573 and 589. If the actual attendance number is between 573 and 589, inclusive, what is the most the percent error could be? Explain your answer.
Answer:
The most the absolute error could be is |589 – 573| = 16. The percent error will be largest when the exact value is smallest. Therefore, the most the percent error could be is \(\frac{16}{573}\) × 100%<2.8%. In this case, the percent error is less than 2.8%.
Eureka Math Grade 7 Module 4 Lesson 8 Exercise Answer Key
Calculate the percent error for Problems 1–3. Leave your final answer in fraction form, if necessary.
Exercise 1.
A real estate agent expected 18 people to show up for an open house, but 25 attended.
Answer:
\(\frac{|18 – 25|}{|25|}\) × 100% = 28%
Exercise 2.
In science class, Mrs. Moore’s students were directed to weigh a 300 – gram mass on the balance scale. Tina weighed the object and reported 328 grams.
Answer:
\(\frac{|328 – 300|}{|300|}\) × 100% = 9\(\frac{1}{3}\)%
Exercise 3.
Darwin’s coach recorded that he had bowled 250 points out of 300 in a bowling tournament. However, the official scoreboard showed that Darwin actually bowled 225 points out of 300.
Answer:
\(\frac{|250 – 225|}{|225|}\) × 100% = 11 \(\frac{1}{9}\)%
Eureka Math Grade 7 Module 4 Lesson 8 Problem Set Answer Key
Question 1.
The odometer in Mr. Washington’s car does not work correctly. The odometer recorded 13.2 miles for his last trip to the hardware store, but he knows the distance traveled is 15 miles. What is the percent error? Use a calculator and the percent error formula to help find the answer. Show your steps.
Answer:
15 is the exact value, and 13.2 is the approximate value. Using the percent error formula, \(\frac{|a – x|}{|x|}\) × 100%, the percent error is
\(\frac{|13.2 – 15|}{|15|}\) × 100% = 12%.
The percent error is equal to 12%.
Question 2.
The actual length of a soccer field is 500 feet. A measuring instrument shows the length to be 493 feet. The actual width of the field is 250 feet, but the recorded width is 246.5 feet. Answer the following questions based on this information. Round all decimals to the nearest tenth.
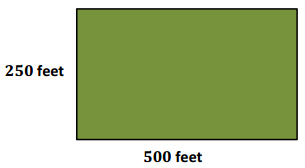
a. Find the percent error for the length of the soccer field.
Answer:
\(\frac{|493 – 500|}{|500|}\) × 100% = 1.4%
b. Find the percent error of the area of the soccer field.
Answer:
Actual area:
A = l × w
A = (500)(250) = 125,000
The actual area is 125,000 square feet.
Approximate area:
A = l × w
A = (493)(246.5)
The approximate area is 121,524.5 square feet.
Percent error of the area:
\(\frac{|121,524.5 – 125,000|}{|125,000|}\) × 100% = 2.8%
c. Explain why the values from parts (a) and (b) are different.
Answer:
In part (a), 1.4% is the percent error for the length, which is one dimension of area. Part (b) is the percent error for the area, which includes two dimensions―length and width. The percent error for the width of the soccer field should be the same as the percent error for the length if the same measuring tool is used. So, 2.8% = 1.4% × 2. However, this is not always the case. Percent error for the width is not always the same as the percent error for the length. It is possible to have an error for both the length and the width, yet the area has no error. For example: publicized length = 100 feet, publicized width = 90 feet,
actual length = 150 feet, and actual width = 60 feet.
Question 3.
Kayla’s class went on a field trip to an aquarium. One tank had 30 clown fish. She miscounted the total number of clown fish in the tank and recorded it as 24 fish. What is Kayla’s percent error?
Answer:
\(\frac{|24 – 30|}{|30|}\) × 100% = 20%
Question 4.
Sid used geometry software to draw a circle of radius 4 units on a grid. He estimated the area of the circle by counting the squares that were mostly inside the circle and got an answer of 52 square units.
a. Is his estimate too large or too small?
Answer:
A = πr2
A = 42 π = 16π
The exact area of the circle is 16π square units. 16π is approximately 50.3. His estimate is too large.
b. Find the percent error in Sid’s estimation to the nearest hundredth using the π key on your calculator.
\(\frac{|52 – 16 \pi|}{|16 \pi|}\) × 100% ≈ 3.45%
Question 5.
The exact value for the density of aluminum is 2.699 g/cm3. Working in the science lab at school, Joseph finds the density of a piece of aluminum to be 2.75 g/cm3. What is Joseph’s percent error? (Round to the nearest hundredth.)
Answer:
\(\frac{|2.75 – 2.699|}{|2.699|}\) × 100% ≈ 1.89%
Question 6.
The world’s largest marathon, The New York City Marathon, is held on the first Sunday in November each year. Between 2 million and 2.5 million spectators will line the streets to cheer on the marathon runners. At most, what is the percent error?
Answer:
\(\frac{|2.5 – 2|}{|2|}\) × 100% = 25%
Question 7.
A circle is inscribed inside a square, which has a side length of 12.6 cm. Jared estimates the area of the circle to be about 80% of the area of the square and comes up with an estimate of 127 cm2.
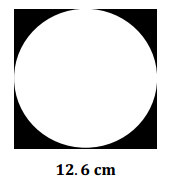
a. Find the absolute error from Jared’s estimate to two decimal places using the π key on your calculator.
|127 – π6.32|≈ 2.31
The absolute error is approximately 2.31 cm.
b. Find the percent error of Jared’s estimate to two decimal places using the π key on your calculator.
Answer:
\(\frac{\left|127 – \pi 6 \cdot 3^{2}\right|}{\left|\pi 6 \cdot 3^{2}\right|}\) × 100% ≈ 1.85%. The percent error is approximately 1.85%.
c. Do you think Jared’s estimate was reasonable?
Answer:
Yes. The percent error is less than 2%.
d. Would this method of computing the area of a circle always be too large?
Answer:
Yes. If the circle has radius r, then the area of the circle is πr2, and the area of the square is 4r2.
\(\frac{\pi r^{2}}{4 r^{2}}\) = \(\frac{\pi}{4}\). The area approximately equals 0.785 = 78.5%<80%.
Question 8.
In a school library, 52% of the books are paperback. If there are 2,658 books in the library, how many of them are not paperback to the nearest whole number?
Answer:
100% – 52% = 48%
Let n represent the number of books that are not paperback.
n = 0.48(2,658)
n = 1,275.84
About 1,276 books are not paperback.
Question 9.
Shaniqua has 25% less money than her older sister Jennifer. If Shaniqua has $180, how much money does Jennifer have?
Answer:
100% – 25% = 75%
Let j represent the amount of money that Jennifer has.
180 = \(\frac{3}{4}\)j
\(\frac{4}{3}\)(180) = (\(\frac{3}{4}\))(\(\frac{4}{3}\))j
240 = j
Jennifer has $240.
Question 10.
An item that was selling for $1,102 is reduced to $806. To the nearest whole, what is the percent decrease?
Answer:
Let p represent the percent decrease.
1,102 – 806 = 296
296 = p ∙ 1,102
\(\frac{296}{1,10.2}\) = p
0.2686 = p
The percent decrease is approximately 27%.
Question 11.
If 60 calories from fat is 75% of the total number of calories in a bag of chips, find the total number of calories in the bag of chips.
Answer:
Let t represent the total number of calories in a bag of chips.
60 = \(\frac{3}{4}\) t
\(\frac{4}{3}\) ∙ 60 = \(\frac{3}{4}\) ∙ \(\frac{4}{3}\) ∙ t
80 = t
The total number of calories in the bag of chips is 80 calories.
Eureka Math Grade 7 Module 4 Lesson 8 Exit Ticket Answer Key
Question 1.
The veterinarian weighed Oliver’s new puppy, Boaz, on a defective scale. He weighed 36 pounds. However, Boaz weighs exactly 34.5 pounds. What is the percent of error in measurement of the defective scale to the nearest tenth?
Answer:
\(\frac{|36 – 34.5|}{|34.5|}\) × 100% = 4 \(\frac{8}{23}\)%
≈ 4.3%
Question 2.
Use the π key on a scientific or graphing calculator to compute the percent of error of the approximation of pi, 3.14, to the value π. Show your steps, and round your answer to the nearest hundredth of a percent.
Answer:
\(\frac{|3 \cdot 14 – \pi|}{|\pi|}\) × 100% = 0.05%
Question 3.
Connor and Angie helped take attendance during their school’s practice fire drill. If the actual count was between 77 and 89, inclusive, what is the most the absolute error could be? What is the most the percent error could be? Round your answer to the nearest tenth of a percent.
Answer:
The most the absolute error could be is |89 – 77| = |12| = 12.
The percent error will be largest when the exact value is smallest. The most the percent error could be is
\(\frac{|12|}{|77|}\) × 100% < 15.6%. The percent error is less than 15.6%.