Engage NY Eureka Math 7th Grade Module 5 Lesson 1 Answer Key
Eureka Math Grade 7 Module 5 Lesson 1 Example Answer Key
Example 1: Spinner Game
Suppose you and your friend are about to play a game using the spinner shown here:
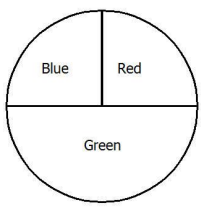
Rules of the game:
1. Decide who will go first.
2. Each person picks a color. Both players cannot pick the same color.
3. Each person takes a turn spinning the spinner and recording what color the spinner stops on. The winner is the person whose color is the first to happen 10 times.
Play the game, and remember to record the color the spinner stops on for each spin.
Answer:
Students try their spinners a few times before starting the game. Before students begin to play the game, discuss who should go first. Consider, for example, having the person born earliest in the year go first. If it is a tie, consider another option like tossing a coin. Discuss with students the following questions:
→ Will it make a difference who goes first?
The game is designed so that the spinner landing on green is more likely to occur. Therefore, if the first person selects green, this person has an advantage.
→ Who do you think will win the game?
The person selecting green has an advantage.
→ Do you think this game is fair?
No. The spinner is designed so that green will occur more often. As a result, the student who selects green will have an advantage.
→ Play the game, and remember to record the color the spinner stops on for each spin.
Example 2: What Is Probability?
Probability is a measure of how likely it is that an event will happen. A probability is indicated by a number between 0 and 1. Some events are certain to happen, while others are impossible. In most cases, the probability of an event happening is somewhere between certain and impossible.
For example, consider a bag that contains only red cubes. If you were to select one cube from the bag, you are certain to pick a red one. We say that an event that is certain to happen has a probability of 1. If we were to reach into the same bag of cubes, it is impossible to select a yellow cube. An impossible event has a probability of 0.
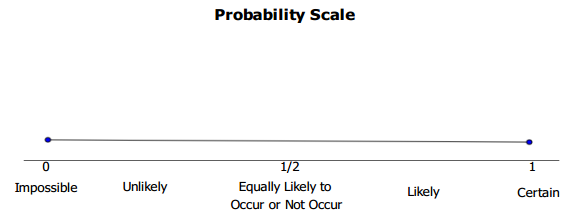
The figure below shows the probability scale.
Answer:
Eureka Math Grade 7 Module 5 Lesson 1 Exercise Answer Key
Exercise 1.
Which color was the first to occur 10 times?
Answer:
Answers will vary, but green is the most likely.
Exercise 2.
Do you think it makes a difference who goes first to pick a color?
Answer:
Yes. The person who goes first could pick green.
Exercise 3.
Which color would you pick to give you the best chance of winning the game? Why would you pick that color?
Answer:
Green would give the best chance of winning the game because it has the largest section on the spinner.
Exercise 4.
Below are three different spinners. On which spinner is the green likely to win, unlikely to win, and equally likely to win?
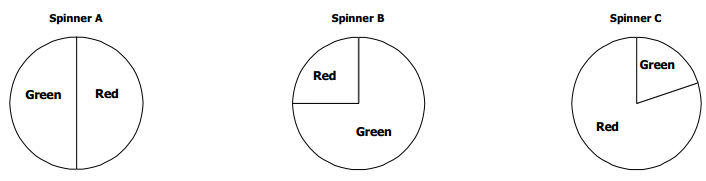
Answer:
Green is likely to win on Spinner B, unlikely to win on Spinner C, and equally likely to win on Spinner A.
Exercise 5.
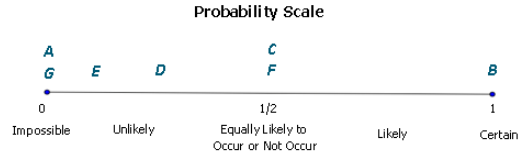
Decide where each event would be located on the scale above. Place the letter for each event in the appropriate place on the probability scale.
Event:
A. You will see a live dinosaur on the way home from school today.
B. A solid rock dropped in the water will sink.
C. A round disk with one side red and the other side yellow will land yellow side up when flipped.
D. A spinner with four equal parts numbered 1–4 will land on the 4 on the next spin.
E. Your full name will be drawn when a full name is selected randomly from a bag containing the full names of all of the students in your class.
F. A red cube will be drawn when a cube is selected from a bag that has five blue cubes and five red cubes.
G. Tomorrow the temperature outside will be -250 degrees.
Answer:
Answers are noted on the probability scale above.
Event:
A. Probability is 0, or impossible, as there are no live dinosaurs.
B. Probability is 1, or certain to occur, as rocks are typically more dense than the water they displace.
C. Probability is \(\frac{1}{2}\), as there are two sides that are equally likely to land up when the disk is flipped.
D. Probability of landing on the 4 would be \(\frac{1}{4}\), regardless of what spin was made. Based on the scale provided, this would indicate a probability halfway between impossible and equally likely, which can be classified as being unlikely to occur.
E. Probability is between impossible and equally likely to occur, assuming there are more than two students in the class. If there were two students, then the probability would be equally likely. If there were only one student in the class, then the probability would be certain to occur. If, however, there were more than two students, the probability would be between impossible and equally likely to occur.
F. Probability would be equally likely to occur as there are an equal number of blue and red cubes.
G. Probability is impossible, or 0, as there are no recorded temperatures at -250 degrees Fahrenheit or Celsius.
Exercise 6.
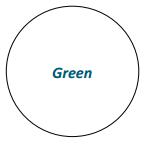
Design a spinner so that the probability of spinning a green is 1.
Answer:
The spinner is all green.
Exercise 7.
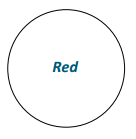
Design a spinner so that the probability of spinning a green is 0.
Answer:
The spinner can include any color but green.
Exercise 8.
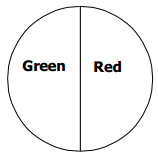
Design a spinner with two outcomes in which it is equally likely to land on the red and green parts.
Answer:
The red and green areas should be equal.
An event that is impossible has a probability of 0 and will never occur, no matter how many observations you make. This means that in a long sequence of observations, it will occur 0% of the time. An event that is certain has a probability of 1 and will always occur. This means that in a long sequence of observations, it will occur 100% of the time.
Exercise 9.
What do you think it means for an event to have a probability of \(\frac{1}{2}\)?
Answer:
In a long sequence of observations, it would occur about half the time.
Exercise 10.
What do you think it means for an event to have a probability of \(\frac{1}{4}\)?
Answer:
In a long sequence of observations, it would occur about 25% of the time.
Eureka Math Grade 7 Module 5 Lesson 1 Problem Set Answer Key
Question 1.
Match each spinner below with the words impossible, unlikely, equally likely to occur or not occur, likely, and certain to describe the chance of the spinner landing on black.
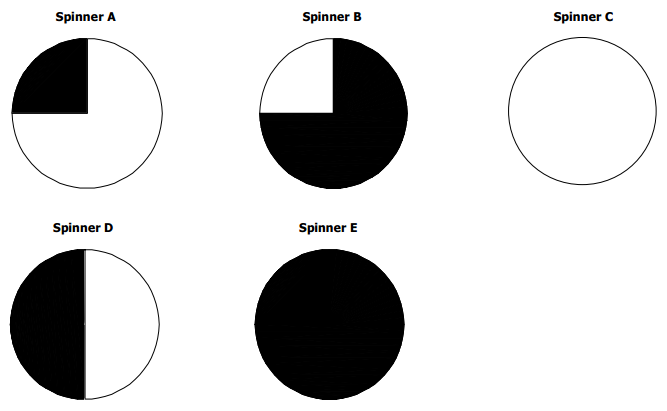
Answer:

Question 2.
Decide if each of the following events is impossible, unlikely, equally likely to occur or not occur, likely, or certain to occur.
a. A vowel will be picked when a letter is randomly selected from the word lieu.
b. A vowel will be picked when a letter is randomly selected from the word math.
c. A blue cube will be drawn from a bag containing only five blue and five black cubes.
d. A red cube will be drawn from a bag of 100 red cubes.
e. A red cube will be drawn from a bag of 10 red and 90 blue cubes.
Answer:
a. Likely; most of the letters of the word lieu are vowels.
b. Unlikely; most of the letters of the word math are not vowels.
c. Equally likely to occur or not occur; the number of blue and black cubes in the bag is the same.
d. Certain; the only cubes in the bag are red.
e. Unlikely; most of the cubes in the bag are blue.
Question 3.
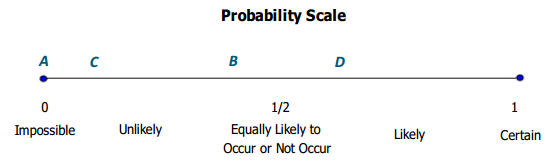
A shape will be randomly drawn from the box shown below. Decide where each event would be located on the probability scale. Then, place the letter for each event on the appropriate place on the probability scale.

Event:
A. A circle is drawn.
B. A square is drawn.
C. A star is drawn.
D. A shape that is not a square is drawn.
Probability Scale
Answer:
Question 4.
Color the squares below so that it would be equally likely to choose a blue or yellow square.
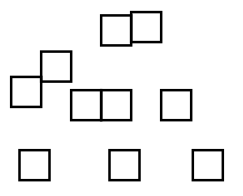
Answer:
Color five squares blue and five squares yellow.
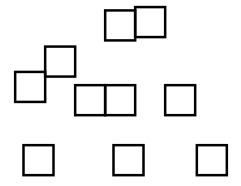
Question 5.
Color the squares below so that it would be likely but not certain to choose a blue square from the bag.
Answer:
Color 6, 7, 8, or 9 squares blue and the rest any other color.
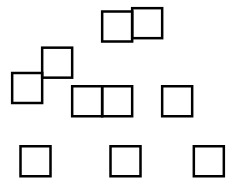
Question 6.
Color the squares below so that it would be unlikely but not impossible to choose a blue square from the bag.
Answer:
Color 1, 2, 3, or 4 squares blue and the others any other color.
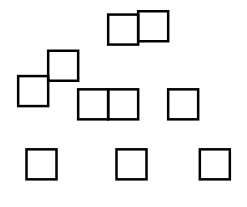
Question 7.
Color the squares below so that it would be impossible to choose a blue square from the bag.
Answer:
Color all squares any color but blue.
Eureka Math Grade 7 Module 5 Lesson 1 Exit Ticket Answer Key
Question 1.
Decide where each of the following events would be located on the scale below. Place the letter for each event on the appropriate place on the probability scale.

The numbers from 1 to 10 are written on small pieces of paper and placed in a bag. A piece of paper will be drawn from the bag.
A. A piece of paper with a 5 is drawn from the bag.
B. A piece of paper with an even number is drawn.
C. A piece of paper with a 12 is drawn.
D. A piece of paper with a number other than 1 is drawn.
E. A piece of paper with a number divisible by 5 is drawn.
Answer:
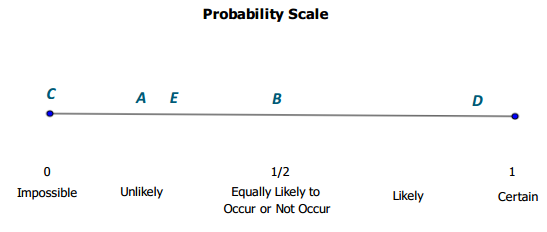
The numbers from 1 to 10 are written on small pieces of paper and placed in a bag. A piece of paper will be drawn from the bag.
A. A piece of paper with a 5 is drawn from the bag.
B. A piece of paper with an even number is drawn.
C. A piece of paper with a 12 is drawn.
D. A piece of paper with a number other than 1 is drawn.
E. A piece of paper with a number divisible by 5 is drawn.