Engage NY Eureka Math 7th Grade Module 5 Lesson 19 Answer Key
Eureka Math Grade 7 Module 5 Lesson 19 Example Answer Key
Example 1: Sample Proportion
Your teacher will give your group a bag that contains colored cubes, some of which are red. With your classmates, you are going to build a distribution of sample proportions.
a. Each person in your group should randomly select a sample of 10 cubes from the bag. Record the data for your sample in the table below.
Answer:
Students’ tables will vary based on their samples.
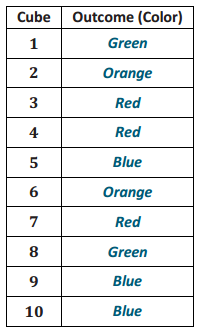
b. What is the proportion of red cubes in your sample of 10?
This value is called the sample proportion. The sample proportion is found by dividing the number of successes (in this example, the number of red cubes) by the total number of observations in the sample.
Answer:
Students’ results will be around 0.4. In this example, the sample proportion is 0.3.
c. Write your sample proportion on a sticky note, and place it on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion.
The graph of all students’ sample proportions is called a sampling distribution of the sample proportions.
Answer:
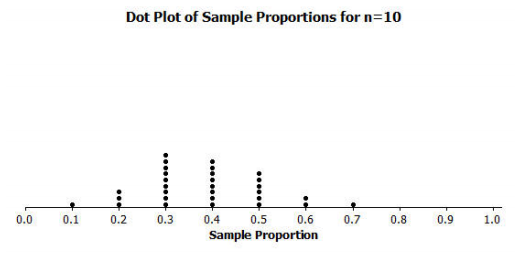
This is an example of a dot plot of the sampling distribution.
d. Describe the shape of the distribution.
Answer:
A nearly symmetrical distribution that is clustered around 0.4
e. Describe the variability in the sample proportions.
Answer:
The spread of the data is from 0.1 to 0.7. Much of the data cluster between 0.3 and 0.5.
Based on the distribution, answer the following:
f. What do you think is the population proportion?
Answer:
Based on the dot plot, an estimate of the population proportion is approximately 0.4.
g. How confident are you of your estimate?
Answer:
Because there is a lot of variability from sample to sample (0.1 to 0.7), I do not have a lot of confidence in my estimate.
Example 2: Sampling Variability
What do you think would happen to the sampling distribution if everyone in class took a random sample of 30 cubes from the bag? To help answer this question, you will repeat the random sampling you did in part (a) of Example 1, except now you will draw a random sample of 30 cubes instead of 10.
a. Take a random sample of 30 cubes from the bag. Carefully record the outcome of each draw.
Answer:
Answers will vary. An example follows:
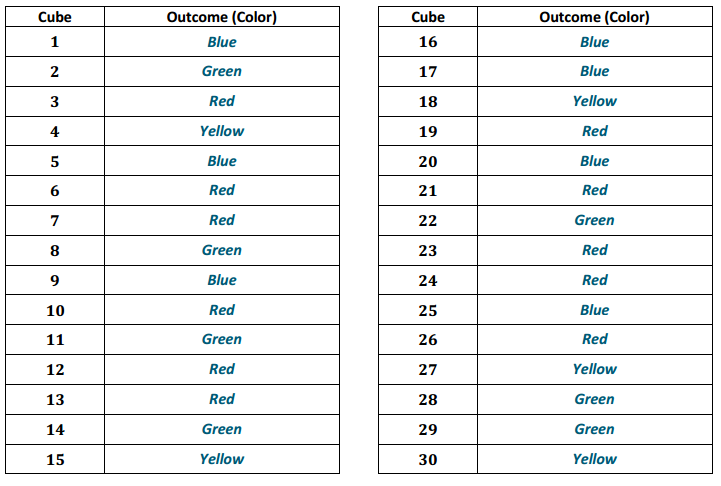
b. What is the proportion of red cubes in your sample of 30?
Answer:
Answers will vary. In this example, the sample proportion is \(\frac{11}{30}\), or approximately 0.367.
c. Write your sample proportion on a sticky note, and place the note on the number line that your teacher has drawn on the board. Place your note above the value on the number line that corresponds to your sample proportion.
Answer:
An example of a dot plot:
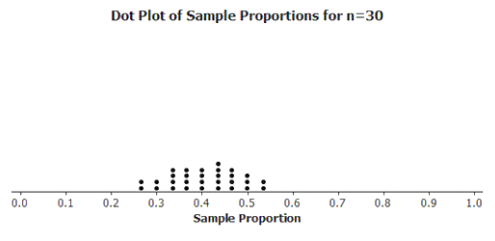
d. Describe the shape of the distribution.
Answer:
Mound shaped, centered around 0.4
Eureka Math Grade 7 Module 5 Lesson 19 Exercise Answer Key
Exercises 1–5
Exercise 1.
Describe the variability in the sample proportions.
Answer:
The spread of the data is from 0.25 to 0.55. Most of the data cluster between 0.35 and 0.5.
Exercise 2.
Based on the distribution, answer the following:
a. What do you think is the population proportion?
Answer:
Based on the dot plot, an estimate of the population proportion is approximately 0.4.
b. How confident are you of your estimate?
Answer:
Because there is less variability from sample to sample (0.35 to 0.5), I am more confident in my estimate.
c. If you were taking a random sample of 30 cubes and determined the proportion that was red, do you think your sample proportion will be within 0.05 of the population proportion? Explain.
Answer:
Answers depend on the dot plots prepared by students. If the dot plot in Example 2 part (c), is used as an example, note that only about half of the dots are between 0.35 and 0.45. There are several samples that had sample proportions that were farther away from the center than 0.05, so the sample proportion might not be within 0.05 of the population proportion.
Exercise 3.
Compare the sampling distribution based on samples of size 10 to the sampling distribution based on samples of size 30.
Answer:
Both distributions are mound shaped and center around 0.4. Variability is less in the sampling distribution of sample sizes of 30 versus sample sizes of 10.
Exercise 4.
As the sample size increased from 10 to 30, describe what happened to the sampling variability of the sample proportions.
Answer:
The sampling variability decreased as the sample size increased.
Exercise 5.
What do you think would happen to the sampling variability of the sample proportions if the sample size for each sample was 50 instead of 30? Explain.
Answer:
The sampling variability in the sampling distribution for samples of size 50 will be less than the sampling variability of the sampling distribution for samples of size 30.
Eureka Math Grade 7 Module 5 Lesson 19 Problem Set Answer Key
Question 1.
A class of seventh graders wanted to find the proportion of M&M’s® that are red. Each seventh grader took a random sample of 20 M&M’s® from a very large container of M&M’s®. The following is the proportion of red M&M’s each student found.

a. Construct a dot plot of the sample proportions.
Answer:
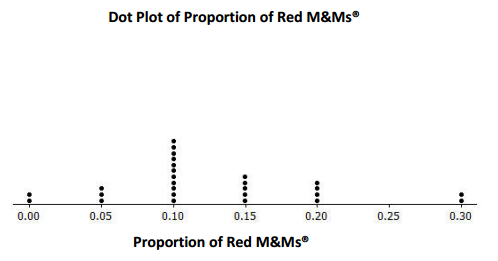
b. Describe the shape of the distribution.
Answer:
Somewhat mound shaped, slightly skewed to the right
c. Describe the variability of the distribution.
Answer:
The spread of the data is from 0.0 to 0.3. Most of the data cluster between 0.10 and 0.20.
d. Suppose the seventh-grade students had taken random samples of size 50. Describe how the sampling distribution would change from the one you constructed in part (a).
Answer:
The sampling variability would decrease.
Question 2.
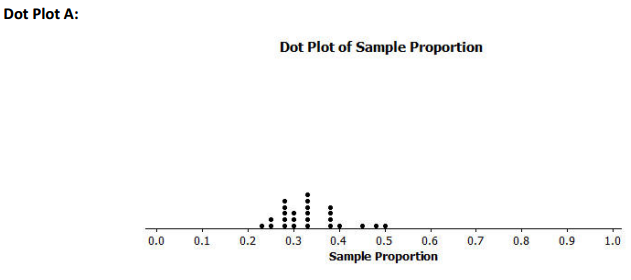
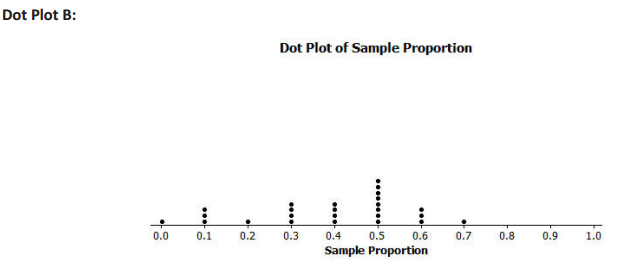
A group of seventh graders wanted to estimate the proportion of middle school students who suffer from allergies. The members of one group of seventh graders each took a random sample of 10 middle school students, and the members of another group of seventh graders each took a random sample of 40 middle school students. Below are two sampling distributions of the sample proportions of middle school students who said that they suffer from allergies. Which dot plot is based on random samples of size 40? How can you tell?
Answer:
Dot Plot A is based on random samples of size 40 rather than random samples of size 10 because the variability of the distribution is less than the variability in Dot Plot B.
Question 3.
The nurse in your school district would like to study the proportion of middle school students who usually get at least eight hours of sleep on school nights. Suppose each student in your class plans on taking a random sample of 20 middle school students from your district, and each calculates a sample proportion of students who said that they usually get at least eight hours of sleep on school nights.
a. Do you expect everyone in your class to get the same value for their sample proportions? Explain.
Answer:
No. We expect sample variability.
b. Suppose each student in class increased the sample size from 20 to 40. Describe how you could reduce the sampling variability.
Answer:
I could reduce the sampling variability by using the larger sample size.
Eureka Math Grade 7 Module 5 Lesson 19 Exit Ticket Answer Key
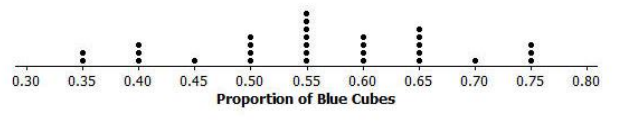
A group of seventh graders took repeated samples of size 20 from a bag of colored cubes. The dot plot below shows the sampling distribution of the sample proportion of blue cubes in the bag.
Question 1.
Describe the shape of the distribution.
Answer:
Mound shaped, centered around 0.55
Question 2.
Describe the variability of the distribution.
Answer:
The spread of the data is from 0.35 to 0.75, with much of the data between 0.50 and 0.65.
Question 3.
Predict how the dot plot would look differently if the sample sizes had been 40 instead of 20.
Answer:
The variability will decrease as the sample size increases. The dot plot will be centered in a similar place but will be less spread out.