Engage NY Eureka Math 7th Grade Module 5 Lesson 5 Answer Key
Eureka Math Grade 7 Module 5 Lesson 5 Example Answer Key
Example 1.
When Jenna goes to the farmers’ market, she usually buys bananas. The number of bananas she might buy and their probabilities are shown in the table below.

a. What is the probability that Jenna buys exactly 3 bananas?
b. What is the probability that Jenna does not buy any bananas?
c. What is the probability that Jenna buys more than 3 bananas?
d. What is the probability that Jenna buys at least 3 bananas?
e. What is the probability that Jenna does not buy exactly 3 bananas?
Notice that the sum of the probabilities in the table is one whole (0.1 + 0.1 + 0.1 + 0.2 + 0.2 + 0.3 = 1). This is always true; when we add up the probabilities of all the possible outcomes, the result is always 1. So, taking 1 and subtracting the probability of the event gives us the probability of something not occurring.
Answer:
a. You can see from the table that the probability that Jenna buys exactly 3 bananas is 0.2, or 20%.
b. The probability that Jenna buys 0 bananas is 0.1, or 10%.
c. The probability that Jenna buys 4 or 5 bananas is 0.2 + 0.3 = 0.5, or 50%.
d. The probability that Jenna buys 3, 4, or 5 bananas is 0.2 + 0.2 + 0.3 = 0.7, or 70%.
e. Remember that the probability that an event does not happen is
1-(the probability that the event does happen).
So, the probability that Jenna does not buy exactly 3 bananas is
1-(the probability that she does buy exactly 3 bananas)
1-0.2 = 0.8, or 80%.
Example 2.
Luis works in an office, and the phone rings occasionally. The possible number of phone calls he receives in an afternoon and their probabilities are given in the table below.
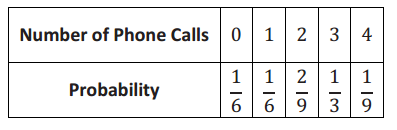
a. Find the probability that Luis receives 3 or 4 phone calls.
b. Find the probability that Luis receives fewer than 2 phone calls.
c. Find the probability that Luis receives 2 or fewer phone calls.
d. Find the probability that Luis does not receive 4 phone calls.
Answer:
a. The probability that Luis receives 3 or 4 phone calls is \(\frac{1}{3}\) + \(\frac{1}{9}\) = \(\frac{3}{9}\) + \(\frac{1}{9}\) = \(\frac{4}{9}\).
b. The probability that Luis receives fewer than 2 phone calls is \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\).
c. The probability that Luis receives 2 or fewer phone calls is \(\frac{2}{9}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{4}{18}\) + \(\frac{3}{18}\) + \(\frac{3}{18}\) = \(\frac{10}{18}\) = \(\frac{5}{9}\).
d. The probability that Luis does not receive 4 phone calls is 1-\(\frac{1}{9}\) = \(\frac{9}{9}\)–\(\frac{1}{9}\) = \(\frac{8}{9}\).
If there is time available, ask students:
How would you calculate the probability that Luis receives at least one call? What might be a quicker way of doing this?
→ I would add the probabilities for 1, 2, 3, and 4:
\(\frac{1}{6} + \frac{2}{9} + \frac{1}{3} + \frac{1}{9}\) = \(\frac{3}{18} + \frac{4}{18} + \frac{2}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)
→ The quicker way is to say that the probability he gets at least one call is the probability that he does not get zero calls, and so the required probability is 1-\(\frac{1}{6}\) = \(\frac{5}{6}\).
Eureka Math Grade 7 Module 5 Lesson 5 Exercise Answer Key
Exercises 1–2
Jenna’s husband, Rick, is concerned about his diet. On any given day, he eats 0, 1, 2, 3, or 4 servings of fruits and vegetables. The probabilities are given in the table below.

Exercise 1.
1. On a given day, find the probability that Rick eats
a. Two servings of fruits and vegetables
b. More than two servings of fruits and vegetables
c. At least two servings of fruits and vegetables
Answer:
a. 0.28
b. 0.39 + 0.12 = 0.51
c. 0.28 + 0.39 + 0.12 = 0.79
Exercise 2.
Find the probability that Rick does not eat exactly two servings of fruits and vegetables.
Answer:
1-0.28 = 0.72
Exercises 3–7
When Jenna goes to the farmers’ market, she also usually buys some broccoli. The possible number of heads of broccoli that she buys and the probabilities are given in the table below.
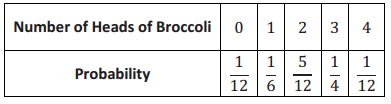
Exercise 3.
Find the probability that Jenna:
a. Buys exactly 3 heads of broccoli
b. Does not buy exactly 3 heads of broccoli
c. Buys more than 1 head of broccoli
d. Buys at least 3 heads of broccoli
Answer:
a. \(\frac{1}{4}\)
b. 1-\(\frac{1}{4}\) = \(\frac{3}{4}\)
c. \(\frac{5}{12}\) + \(\frac{1}{4}\) + \(\frac{1}{12}\) = \(\frac{3}{4}\)
d. \(\frac{1}{4}\) + \(\frac{1}{12}\) = \(\frac{1}{3}\)
The diagram below shows a spinner designed like the face of a clock. The sectors of the spinner are colored red (R), blue (B), green (G), and yellow (Y).
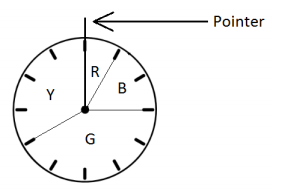
Exercise 4.
Writing your answers as fractions in lowest terms, find the probability that the pointer stops on the following colors.
a. Red:
b. Blue:
c. Green:
d. Yellow:
Answer:
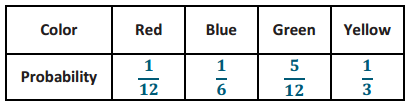
a. Red: \(\frac{1}{12}\)
b. Blue: \(\frac{2}{12}\) = \(\frac{1}{6}\)
c. Green: \(\frac{5}{12}\)
d. Yellow: \(\frac{4}{12}\) = \(\frac{1}{3}\)
Exercise 5.
Complete the table of probabilities below.
Answer:
Exercise 6.
Find the probability that the pointer stops in either the blue region or the green region.
Answer:
\(\frac{1}{6}\) + \(\frac{5}{12}\) = \(\frac{7}{12}\)
Exercise 7.
Find the probability that the pointer does not stop in the green region.
Answer:
1-\(\frac{5}{12}\) = \(\frac{7}{12}\)
Eureka Math Grade 7 Module 5 Lesson 5 Problem Set Answer Key
Question 1.
The Gator Girls is a soccer team. The possible number of goals the Gator Girls will score in a game and their probabilities are shown in the table below.

Find the probability that the Gator Girls:
a. Score more than two goals
b. Score at least two goals
c. Do not score exactly 3 goals
Answer:
a. 0.11 + 0.03 = 0.14
b. 0.33 + 0.11 + 0.03 = 0.47
c. 1-0.11 = 0.89
Question 2.
The diagram below shows a spinner. The pointer is spun, and the player is awarded a prize according to the color on which the pointer stops.
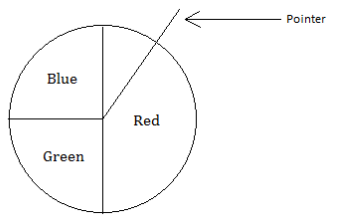
a. What is the probability that the pointer stops in the red region?
b. Complete the table below showing the probabilities of the three possible results.
c. Find the probability that the pointer stops on green or blue.
d. Find the probability that the pointer does not stop on green.
Answer:
a. \(\frac{1}{2}\)
b. 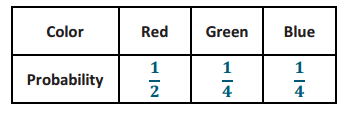
c. \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1}{2}\)
d. 1-\(\frac{1}{4}\) = \(\frac{3}{4}\)
Question 3.
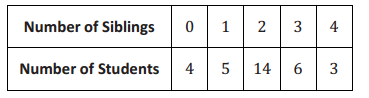
Wayne asked every student in his class how many siblings (brothers and sisters) they had. The survey results are shown in the table below. (Wayne included himself in the results.)

(Note: The table tells us that 4 students had no siblings, 5 students had one sibling, 14 students had two siblings, and so on.)
a. How many students are there in Wayne’s class, including Wayne?
b. What is the probability that a randomly selected student does not have any siblings? Write your answer as a fraction in lowest terms.
c. The table below shows the possible number of siblings and the probabilities of each number. Complete the table by writing the probabilities as fractions in lowest terms.
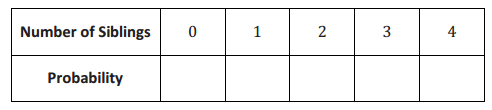
d. Writing your answers as fractions in lowest terms, find the probability that the student:
i. Has fewer than two siblings
ii. Has two or fewer siblings
iii. Does not have exactly one sibling
Answer:
a. 4 + 5 + 14 + 6 + 3 = 32
b. \(\frac{4}{32}\) = \(\frac{1}{8}\)
c. 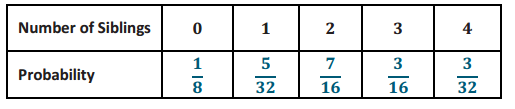
d. i) \(\frac{1}{8} + \frac{5}{32}\) = \(\frac{9}{32}\)
ii) \(\frac{1}{8} + \frac{5}{32} + \frac{7}{16}\) = \(\frac{23}{32}\)
iii) 1-\(\frac{5}{32}\) = \(\frac{27}{32}\)
Eureka Math Grade 7 Module 5 Lesson 5 Exit Ticket Answer Key
Carol is sitting on the bus on the way home from school and is thinking about the fact that she has three homework assignments to do tonight. The table below shows her estimated probabilities of completing 0, 1, 2, or all 3 of the assignments.

Question 1.
Writing your answers as fractions in lowest terms, find the probability that Carol completes
a. Exactly one assignment
b. More than one assignment
c. At least one assignment
Answer:
a. \(\frac{2}{9}\)
b. \(\frac{5}{18} + \frac{1}{3}\) = \(\frac{5}{18} + \frac{6}{18}\) = \(\frac{11}{18}\)
c. \(\frac{2}{9} + \frac{5}{18} + \frac{1}{3}\) = \(\frac{4}{18} + \frac{5}{18} + \frac{6}{18}\) = \(\frac{15}{18}\) = \(\frac{5}{6}\)
Question 2.
Find the probability that the number of homework assignments Carol completes is not exactly 2.
Answer:
1-\(\frac{5}{18}\) = \(\frac{13}{18}\)
Question 3.
Carol has a bag containing 3 red chips, 10 blue chips, and 7 green chips. Estimate the probability (as a fraction or decimal) of Carol reaching into her bag and pulling out a green chip.
Answer:
An estimate of the probability would be 7 out of 20, \(\frac{7}{20}\), or 0.35.