Engage NY Eureka Math 7th Grade Module 6 Lesson 2 Answer Key
Eureka Math Grade 7 Module 6 Lesson 2 Example Answer Key
Example 1.
Two lines meet at a point that is also the endpoint of a ray. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of p and r.
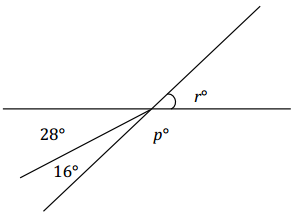
Answer:
The angle r° is vertically opposite from and equal to the sum of the angles with measurements 28° and 16°, or a sum of 44°. Angles r° and p° are angles on a line and sum to 180°.
r = 28 + 16
r = 44 Vert. ∠s
p + (44) = 180
p + 44 – 44 = 180 – 44
p = 136 ∠s on a line
Example 2.
Three lines meet at a point. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of z.
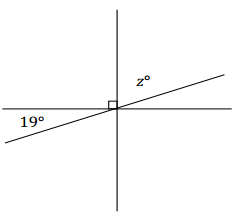
Answer:
Let y° be the angle vertically opposite and equal in measurement to 19°.
The angles z° and y° are complementary and sum to 90°.
z + y = 90
z + 19 = 90
z + 19 – 19 = 90 – 19
z = 71 Complementary ∠s
Example 3.
Two lines meet at a point that is also the endpoint of a ray. The ray is perpendicular to one of the lines as shown. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of t.
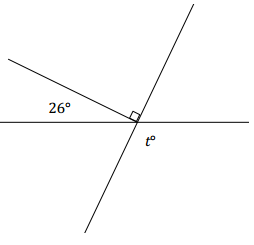
Answer:
The measurement of the angle formed by adjacent angles of 26° and 90° is the sum of the adjacent angles. This angle is vertically opposite and equal in measurement to the angle t°.
Let y° be the measure of the indicated angle.
y = 116 ∠s add
t = (y) Vert.∠s
t = 116
Example 4.
Three lines meet at a point. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Is your answer reasonable? Explain how you know.
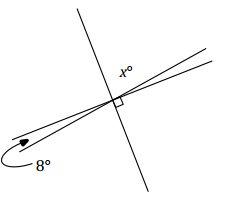
Answer:
The angle x° is vertically opposite from the angle formed by the right angle that contains and shares a common side with an 8° angle.
x = 90 – 8 ∠s add and vert.∠s
x = 82
The answer is reasonable because the angle marked by x° is close to appearing as a right angle.
Eureka Math Grade 7 Module 6 Lesson 2 Exercise Answer Key
Exercise 1.
Three lines meet at a point. In a complete sentence, describe the relevant angle relationship in the diagram. Set up and solve an equation to find the value of a.
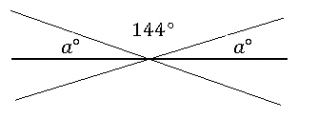
Answer:
The two a° angles and the angle 144° are angles on a line and sum to 180°.
2a + 144 = 180
2a + 144-144 = 180 – 144
2a = 36
a = 18 ∠s on a line
Exercise 2.
Three lines meet at a point; ∠AOF = 144°. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to determine the value of c.
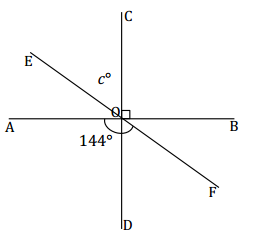
Answer:
∠EOB, formed by adjacent angles ∠EOC and ∠COB, is vertical to and equal in measurement to ∠AOF.
The measurement of ∠EOB is c° + 90° (∠s add).
c + 90 = 144
c + 90 – 90 = 144 – 90
c = 54 Vert. ∠s
Exercise 3.
Two lines meet at a point that is also the endpoint of a ray. The ray is perpendicular to one of the lines as shown. In a complete sentence, describe the relevant angle relationships in the diagram. You may add labels to the diagram to help with your description of the angle relationship. Set up and solve an equation to find the value of v.
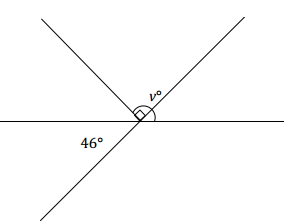
Answer:
One possible response: Let x° be the angle vertically opposite and equal in measurement to 46°. The angles x° and v° are adjacent angles, and the angle they form together is equal to the sum of their measurements.
x = 46 Vert.∠s
v = 90 + 46 ∠s add
v = 136
Exercise 4.
Two lines meet at a point that is also the endpoint of two rays. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurements of ∠AOB and ∠BOC.
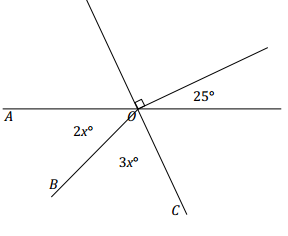
Answer:
∠AOC is vertically opposite from the angle formed by adjacent angles 90° and 25°.
2x + 3x = 90 + 25
5x = 115
x = 23 ∠s add and vert.∠s
∠AOC = 2(23)° = 46°
∠BOC = 3(23)° = 69°
Exercise 5.
a. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurements of ∠AOB and∠BOC.
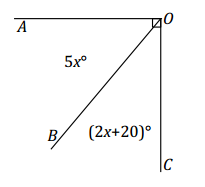
b. Katrina was solving the problem above and wrote the equation 7x + 20 = 90. Then, she rewrote this as 7x + 20 = 70 + 20. Why did she rewrite the equation in this way? How does this help her to find the value of x?
Answer:
a. ∠AOB and ∠BOC are complementary and sum to 90°.
5x + (2x + 20) = 90 complementary ∠s
7x + 20 = 90
7x + 20-20 = 90 – 20
7x = 70
x = 10
∠AOB = 5(10)° = 50°
∠BOC = 2(10)° + 20° = 40°
b. She grouped the quantity on the right-hand side of the equation similarly to that of the left-hand side. This way, it is clear that the quantity 7x on the left-hand side must be equal to the quantity 70 on the right-hand side.
Eureka Math Grade 7 Module 6 Lesson 2 Problem Set Answer Key
Question 1.
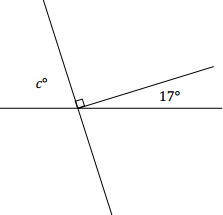
Two lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the value of c.
Answer:
c + 90 + 17 = 180 ∠s on a line
c + 107 = 180
c + 107 – 107 = 180 – 107
c = 73
Scaffolded solutions:
a. Use the equation above.
b. The angle marked c°, the right angle, and the angle with measurement 17° are angles on a line, and their measurements sum to 180°.
c. Use the solution above. The answer seems reasonable because it looks like it has a measurement a little less than a 90° angle.
Question 2.
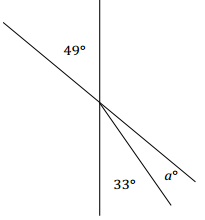
Two lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the value of a. Explain why your answer is reasonable.
Answer:
a + 33 = 49 ∠s add and vert.∠s
a + 33 – 33 = 49 – 33
a = 16
The answers seem reasonable because a rounded value of a as 20 and a rounded value of its adjacent angle 33 as 30 yields a sum of 50, which is close to the rounded value of the measurement of the vertical angle.
Question 3.
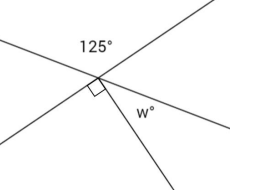
Two lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the value of w.
Answer:
w + 90 = 125 ∠s add and vert.∠s
w + 90-90 = 125 – 90
w = 35
Question 4.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of m.
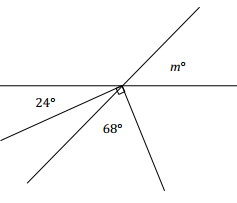
Answer:
(90 – 68) + 24 = m ∠s add and vert.∠s
m = 46
Question 5.
Three lines meet at a point. Set up and solve an equation to find the value of r.
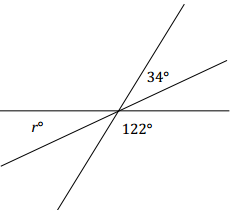
Answer:
r + 122 + 34 = 180 ∠s on a line and vert.∠s
r + 156 = 180
r + 156 – 156 = 180 – 156
r = 24
Question 6.
Three lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the value of each variable in the diagram.
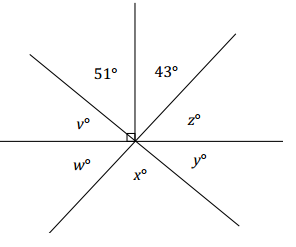
Answer:
v = 90-51 Complementary ∠s
v = 39
w + 39 + 51 + 43 = 180 ∠s on a line
w + 133 = 180
w + 133 – 133 = 180 – 133
w = 47
x = 51 + 43 Vert.∠s
x = 94
y = 39 Vert.∠s
z = 47 Vert.∠s
Question 7.
Set up and solve an equation to find the value of x. Find the measurement of ∠AOB and of ∠BOC.
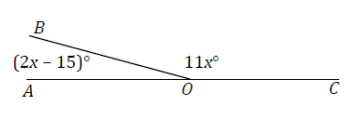
Answer:
(2x – 15) + 11x = 180 Supplementary ∠s
13x – 15 = 180
13x – 15 + 15 = 180 + 15
13x = 195
x = 15
The measurement of ∠AOB: 2(15)° – 15° = 15°
The measurement of ∠BOC: 11(15)° = 165°
Scaffolded solutions:
a. Use the equation above.
b. The marked angles are angles on a line, and their measurements sum to 180°.
c. Once 15 is substituted for x, then the measurement of ∠AOB is 15° and the measurement of ∠BOC is 165°. These answers seem reasonable since ∠AOB is acute and ∠BOC is obtuse.
Question 8.
Set up and solve an equation to find the value of x. Find the measurement of ∠AOB and of ∠BOC.
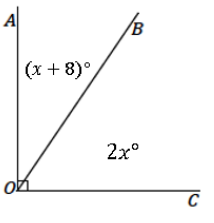
Answer:
x + 8 + 2x = 90 Complementary ∠s
3x + 8 = 90
3x + 8-8 = 90-8
3x = 82
x = 27\(\frac{1}{3}\)
The measurement of ∠AOB: (27\(\frac{1}{3}\))° + 8° = 35\(\frac{1}{3}\)°
The measurement of ∠BOC: 2(27\(\frac{1}{3}\))° = 54\(\frac{2}{3}\)°
Question 9.
Set up and solve an equation to find the value of x. Find the measurement of ∠AOB and of ∠BOC.
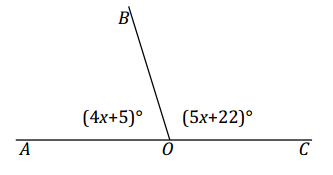
Answer:
4x + 5 + 5x + 22 = 180 ∠s on a line
9x + 27 = 180
9x + 27-27 = 180-27
9x = 153
x = 17
The measurement of ∠AOB: 4(17)° + 5° = 73°
The measurement of ∠BOC: 5(17)° + 22° = 107°
Question 10.
Write a verbal problem that models the following diagram. Then, solve for the two angles.
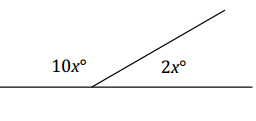
Answer:
One possible response: Two angles are supplementary. The measurement of one angle is five times the measurement of the other. Find the measurements of both angles.
10x + 2x = 180
12x = 180
x = 15 Supplementary ∠s
The measurement of Angle 1: 10(15)° = 150°
The measurement of Angle 2: 2(15)° = 30°
Eureka Math Grade 7 Module 6 Lesson 2 Exit Ticket Answer Key
Question 1.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of x. Explain why your answer is reasonable.
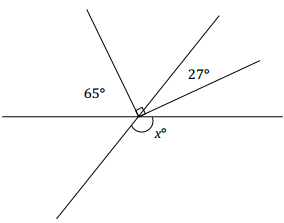
Answer:
65 + (90-27) = x
x = 128
OR
y + 27 = 90
y + 27 – 27 = 90 – 27
y = 63
65 + y = x
65 + (63) = x
x = 128
The answers seem reasonable because a rounded value of y as 60 and a rounded value of its adjacent angle 65 as 70 yields a sum of 130, which is close to the calculated answer.