Engage NY Eureka Math 7th Grade Module 6 Lesson 24 Answer Key
Eureka Math Grade 7 Module 6 Lesson 24 Example Answer Key
Example 1.
Determine the surface area of the image.
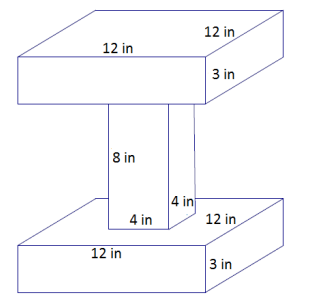
Answer:
Surface area of top or bottom prism:
Lateral sides = 4(12 in. × 3 in.) = 144 in2
Base face = 12 in. × 12 in. = 144 in2
Base face with hole = 12 in. × 12 in. – 4 in. × 4 in.
= 128 in2
There are two of these, making up 832 in2.
Surface area of middle prism:
Lateral sides: = 4(4 in. × 8 in.) = 128 in2
Surface area: 832 in2 + 128 in2 = 960 in2
→ Describe the method you used to determine the surface area.
Answers will vary. I determined the surface area of each prism separately and added them together. Then, I subtracted the area of the sections that were covered by another prism.
→ If all three prisms were separate, would the sum of their surface areas be the same as the surface area you determined in this example?
No, if the prisms were separate, there would be more surfaces shown. The three separate prisms would have a greater surface area than this example. The area would be greater by the area of four 4 in. × 4 in. squares (64 in2).
Example 2.
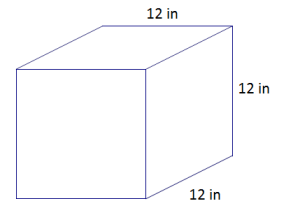
a. Determine the surface area of the cube.
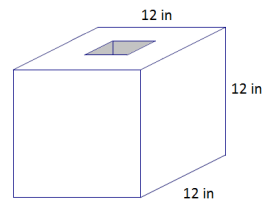
b. A square hole with a side length of 4 inches is cut through the cube. Determine the new surface area.
Answer:
a. Surface area = 6s2
SA = 6(12 in.)2
SA = 6(144 in2)
SA = 864 in2
→ Explain how 6(12 in.)2 represents the surface area of the cube.
The area of one face, one square with a side length of 12 in., is (12 in.)2, and so a total area of all six faces is 6(12 in.)2.
b. Area of interior lateral sides
= 4(12 in. × 4 in.)
= 192 in2
Surface area of cube with holes
= 6 (12 in.)2 – 2(4 in. × 4 in.) + 4(12 in. × 4 in.)
= 864 in2 – 32 in2 + 192 in2
= 1,024 in2
→ How does cutting a hole in the cube change the surface area?
We have to subtract the area of the square at the surface from each end.
We also have to add the area of each of the interior faces to the total surface area.
→ What happens to the surfaces that now show inside the cube?
These are now part of the surface area.
→ What is the shape of the piece that was removed from the cube?
A rectangular prism was cut out of the cube with the following dimensions: 4 in. × 4 in. × 12 in.
→ How can we use this to help us determine the new total surface area?
We can find the surface area of the cube and the surface area of the rectangular prism, but we will have to subtract the area of the square bases from the cube and also exclude these bases in the area of the rectangular prism.
→ Why is the surface area larger when holes have been cut into the cube?
There are more surfaces showing now. All of the surfaces need to be included in the surface area.
→ Explain how the expression 6(12 in.)2 – 2(4 in. × 4 in.) + 4(12 in. × 4 in.) represents the surface area of the cube with the hole.
From the total surface area of a whole (uncut) cube, 6(12 in.)2, the area of the bases (the cuts made to the surface of the cube) are subtracted: 6(12 in.)2 – 2(4 in. × 4 in.). To this expression we add the area of the four lateral faces of the cutout prism, 4(12 in. × 4 in.). The complete expression then is 6(12 in.)2 – 2(4 in. × 4 in.) + 4(12 in. × 4 in.)
Example 3.
A right rectangular pyramid has a square base with a side length of 10 inches. The surface area of the pyramid is 260 in2. Find the height of the four lateral triangular faces.
Answer:
Area of base = 10 in. × 10 in. = 100 in2
Area of the four faces = 260 in2 – 100 in2 = 160 in2
The total area of the four faces is 160 in2.
Therefore, the area of each triangular face is 40 in2.
Area of lateral side = \(\frac{1}{2}\)bh
40 in2 = \(\frac{1}{2}\)(10 in.)h
40 in2 = (5 in)h
h = 8 in.
The height of each lateral triangular face is 8 inches.
→ What strategies could you use to help you solve this problem?
I could draw a picture of the pyramid and label the sides so that I can visualize what the problem is asking me to do.
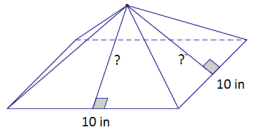
→ What information have we been given? How can we use the information?
We know the total surface area, and we know the length of the sides of the square.
We can use the length of the sides of the square to give us the area of the square base.
→ How does the area of the base help us determine the height of the lateral triangular face?
First, we can subtract the area of the base from the total surface area in order to determine what is left for the lateral sides.
Next, we can divide the remaining area by 4 to get the area of just one triangular face.
Finally, we can work backward. We have the area of the triangle, and we know the base is 10″ in.” , so we can solve for the height.
Eureka Math Grade 7 Module 6 Lesson 24 Exercise Answer Key
Determine the surface area of each figure. Assume all faces are rectangles unless it is indicated otherwise.
Exercise 1.
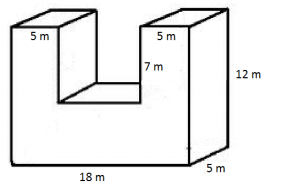
Answer:
Top and bottom = 2(18 m × 5 m) = 180 m2
Extra interior sides = 2(5 m × 7 m) = 70 m2
Left and right sides = 2(5 m × 12 m) = 120 m2
Front and back sides = 2((18 m × 12 m) – (8 m × 7 m))
= 2(216 m2 – 56 m2 )
= 2(160 m2 )
= 320 m2
Surface area = 180 m2 + 70 m2 + 120 m2 + 320 m2
= 690 m2
Exercise 2.
In addition to your calculation, explain how the surface area of the following figure was determined.
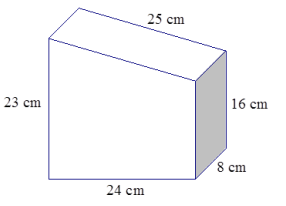
Answer:
The surface area of the prism is found by taking the sum of the areas of the trapezoidal front and back and the areas of the back of the four different – sized rectangles that make up the lateral faces.
Area top = 25 cm × 8 cm
= 200 cm2
Area bottom = 24 cm × 8 cm
= 192 cm2
Area sides = (23 cm × 8 cm) + (16 cm × 8 cm)
= 312 cm2
Area front and back = 2(\(\frac{1}{2}\)(16 cm + 23 cm)(24 cm))
= 2(468 cm2 )
= 936 cm2
Surface area = 200 cm2 + 192 cm2 + 312 cm2 + 936 cm2
= 1,640 cm2
Exercise 3.
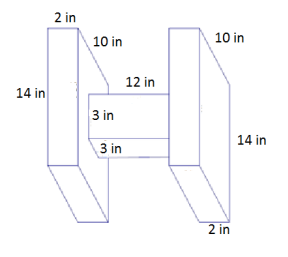
Answer:
Surface area of one of the prisms on the sides:
Area of front and back = 2(2 in. × 14 in.)
= 56 in2
Area of top and bottom = 2(2 in. × 10 in.)
= 40 in2
Area of side = 14 in. × 10 in. = 140 in2
Area of side with hole = 14 in. × 10 in. – 3 in. × 3 in.
= 131 in2
There are two such rectangular prisms, so the surface area of both is 734 in2.
Surface area of middle prism:
Area of front and back = 2(3 in. × 12in.) = 72 in2
Area of sides = 2(3 in. × 12 in.) = 72 in2
Surface area of middle prism = 72 in2 + 72 in2 = 144 in2
The total surface area of the figure is 734 in2 + 144 in2 = 878 in2.
Exercise 4.
In addition to your calculation, explain how the surface area was determined.
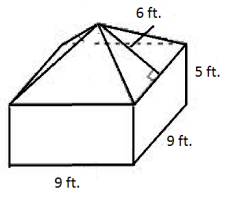
Answer:
The surface area of the prism is found by taking the area of the base of the rectangular prism and the area of its four lateral faces and adding it to the area of the four lateral faces of the pyramid.
Area of base = 9 ft. × 9 ft.
= 81 ft2
Area of rectangular sides = 4(9 ft. × 5 ft.)
= 180 ft2
Area of triangular sides = 4(\(\frac{1}{2}\)(9 ft.)(6 ft.))
= 108 ft2
Surface area = 81 ft2 + 180 ft2 + 108 ft2
= 369 ft2
Exercise 5.
A hexagonal prism has the following base and has a height of 8 units. Determine the surface area of the prism.
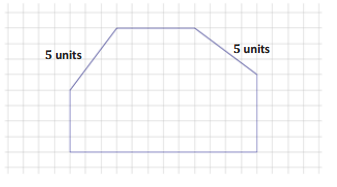
Answer:
Area of bases = 2(48 + 6 + 20 + 10) = 168
Area of 4 unit sides = 4(5 × 8)
= 160
Area of other sides = (4 × 8) + (12 × 8)
= 128
Surface area = 168 + 160 + 128
= 456
The surface area of the hexagonal prism is 456 units2.
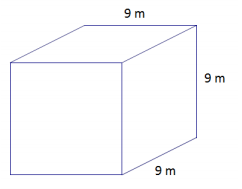
Exercise 6.
Determine the surface area of each figure.
a.
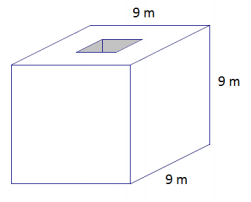
b. A cube with a square hole with 3 m side lengths has been cut through the cube.
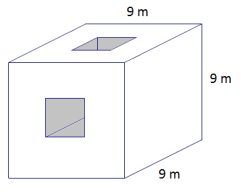
c. A second square hole with 3 m side lengths has been cut through the cube.
Answer:
a. SA = 6s2
= 6(9 m)2
= 6(81m2)
= 486 m2
b. Lateral sides of the hole = 4(9 m × 3 m) = 108 m2
Surface area of cube with holes = 486 m2 – 2(3 m × 3 m) + 108 m2
= 576 m2
c. Surface area = 576 m2 – 4(3 m × 3 m) + 2(4(3 m × 3 m))
= 612 m2
Exercise 7.
The figure below shows 28 cubes with an edge length of 1 unit. Determine the surface area.
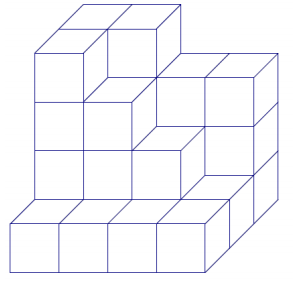
Answer:
Area top and bottom = 24 units2
Area sides = 18 units2
Area front and back = 28 units2
Surface area
= 24 units2 + 18 units 2 + 28 units2
= 70 units2
Exercise 8.
The base rectangle of a right rectangular prism is 4 ft. × 6 ft. The surface area is 288 ft2. Find the height. Let h be the height in feet.
Answer:
Area of one base: 4 ft. × 6 ft. = 24 ft2
Area of two bases: 2(24 ft2) = 48 ft2
Numeric area of four lateral faces: 288 ft2 – 48 ft2 = 240 ft2
Algebraic area of four lateral faces: 2(6h + 4h) ft2
Solve for h.
2(6h + 4h) = 240
10h = 120
h = 12
The height is 12 feet.
Eureka Math Grade 7 Module 6 Lesson 24 Problem Set Answer Key
Determine the surface area of each figure.
Question 1.
In addition to the calculation of the surface area, describe how you found the surface area.
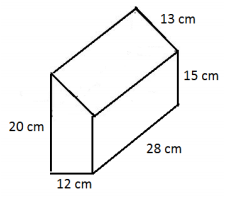
Answer:
Area of top = 28 cm × 13 cm
= 364 cm2
Area of bottom = 28 cm × 12 cm
= 336 cm2
Area of left and right sides = 28 cm × 20 cm + 15 cm × 28 cm
= 980 cm2
Area of front and back sides = 2(12 cm × 15 cm) + \(\frac{1}{2}\)(5 cm × 12 cm)
= 2(180 cm2 + 30 cm2 )
= 2(210 cm2 )
= 420 cm2
Surface area = 364 cm2 + 336 cm2 + 980 cm2 + 420 cm2
= 2,100 cm2
Split the area of the two trapezoidal bases into triangles and rectangles, take the sum of the areas, and then add the areas of the four different – sized rectangles that make up the lateral faces.
Question 2.
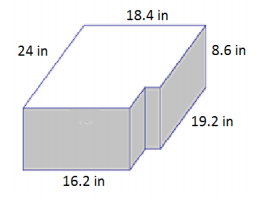
Answer:
Area of front and back = 2(18.4 in. × 8.6 in.) = 316.48 in2
Area of sides = 2(8.6 in. × 24 in.) = 412.8 in2
Area of top and bottom = 2(18.4 in. × 24 in.) – (4.8 in. × 2.2 in.)
= 2(441.6 in2 – 10.56 in2)
= 2(431.04 in2)
= 862.08 in2
Surface area = 316.48 in2 + 412.8 in2 + 862.08 in2
= 1,591.36 in2
Question 3.
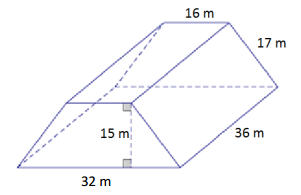
Answer:
Area of front and back = 2(\(\frac{1}{2}\)(32 m + 16 m)15 m)
= 720 m2
Area of top = 16 m × 36 m
= 576 m2
Area of left and right sides = 2(17 m × 36 m)
= 2(612 m2 )
= 1,224 m2
Area of bottom = 32 m × 36 m
= 1,152 m2
Surface area = 720 m2 + 1,152 m2 + 1,224 m2 + 576 m2
= 3,672 m2
Question 4.
Determine the surface area after two square holes with a side length of 2 m are cut through the solid figure composed of two rectangular prisms.
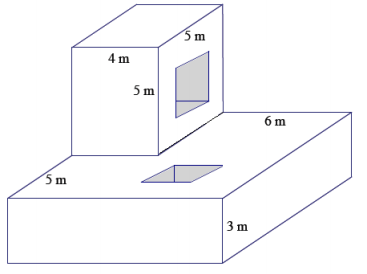
Answer:
Surface area of top prism before the hole is drilled:
Area of top = 4 m × 5 m
= 20 m2
Area of front and back = 2(4 m × 5 m)
= 40 m2
Area of sides = 2(5 m × 5 m)
= 50 m2
Surface area of bottom prism before the hole is drilled:
Area of top = 10 m × 10 m – 20 m2
= 80 m2
Area of bottom = 10 m × 10 m
= 100 m2
Area of front and back = 2(10 m × 3 m)
= 60 m2
Area of sides = 2(10 m × 3 m)
= 60 m2
Surface area of interiors:
Area of interiors = 4(2 m × 4 m) + 4(2 m × 3 m)
= 56 m2
Surface Area = 110 m2 + 300 m2 + 56 m2 – 16 m2
= 450 m2
Question 5.
The base of a right prism is shown below. Determine the surface area if the height of the prism is 10 cm. Explain how you determined the surface area.
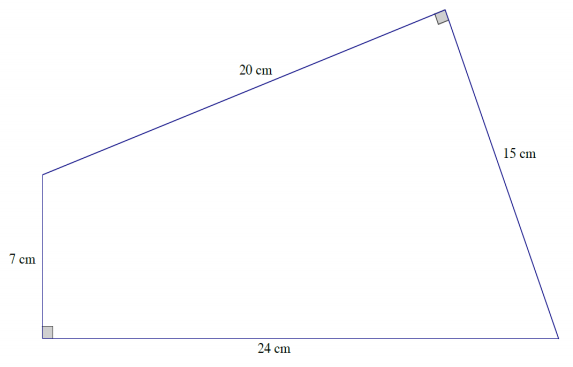
Answer:
Take the sum of the areas of the two bases made up of two right triangles, and add to it the sum of the areas of the lateral faces made up of rectangles of different sizes.
Area of sides = (20 cm × 10 cm) + (15 cm × 10 cm) + (24 cm × 10 cm) + (7 cm × 10 cm)
= 200 cm2 + 150 cm2 + 240 cm2 + 70 cm2
= 660 cm2
Area of bases = 2(\(\frac{1}{2}\)(7 cm × 24 cm) + 1/2 (20 cm × 15 cm))
= (7 cm × 24 cm) + (20 cm × 15 cm)
= 168 cm2 + 300 cm2
= 468 cm2
Surface area = 660 cm2 + 468 cm2
= 1,128 cm2
Eureka Math Grade 7 Module 6 Lesson 24 Exit Ticket Answer Key
Question 1.
Determine the surface area of the right rectangular prism after the two square holes have been cut. Explain how you determined the surface area.
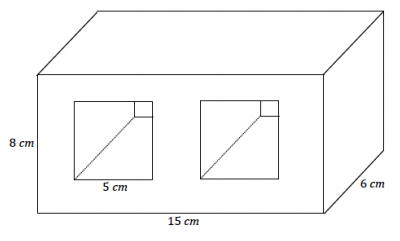
Answer:
Area of top and bottom = 2(15 cm × 6 cm)
= 180 cm2
Area of sides = 2(6 cm × 8 cm)
= 96 cm2
Area of front and back = 2(15 cm × 8 cm) – 4(5 cm × 5 cm)
= 140 cm2
Area inside = 8(5 cm × 6 cm)
= 240 cm2
Surface area = 180 cm2 + 96 cm2 + 140 cm2 + 240 cm2
= 656 cm2
Take the sum of the areas of the four lateral faces and the two bases of the main rectangular prism, and subtract the areas of the four square cuts from the area of the front and back of the main rectangular prism. Finally, add the lateral faces of the prisms that were cut out of the main prism.