Engage NY Eureka Math 7th Grade Module 6 Lesson 25 Answer Key
Eureka Math Grade 7 Module 6 Lesson 25 Example Answer Key
Example 1.
Calculate the volume of the following prism.
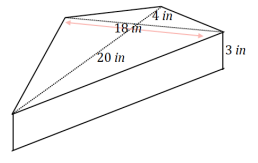
Answer:
→ What is the initial difficulty of determining the volume of this prism?
The base is not in the shape of a rectangle or triangle.
→ Do we have a way of finding the area of a kite in one step? If not, how can we find the area of a kite?
We do not have a way to find the area of a kite in one step. We can break the kite up into smaller shapes. One way would be to break it into two triangles, but it can also be broken into four triangles.
Once students understand that the base must be decomposed into triangles, allow them time to solve the problem.
→ Provide a numeric expression that determines the area of the kite – shaped base.
Area of the base: \(\frac{1}{2}\)(20 in.∙18 in.) + \(\frac{1}{2}\)(4 in.∙18 in.)
→ Find the volume of the prism.
Volume of the prism: (\(\frac{1}{2}\)(20 in.∙18 in.) + \(\frac{1}{2}\)(4 in.∙18 in.))(3 in.) = 648 in3
Example 2.
A container is shaped like a right pentagonal prism with an open top. When a cubic foot of water is dumped into the container, the depth of the water is 8 inches. Find the area of the pentagonal base.
Answer:
→ How can we use volume to solve this problem?
We know that the formula for the volume of a prism is V = Bh, where B represents the area of the pentagonal base and h is the height of the prism.
→ What information do we know from reading the problem?
The volume is 1 cubic foot, and the height of the water is 8 inches.
→ Knowing the volume formula, can we use this information to solve the problem?
We can use this information to solve the problem, but the information is given using two different dimensions.
→ How can we fix this problem?
We have to change inches into feet so that we have the same units.
→ How can we change inches into feet?
Because 12 inches make 1 foot, we have to divide the 8 inches by 12 to get the height in feet.
→ Convert 8 inches into feet.
\(\frac{8}{12}\) ft. = \(\frac{2}{3}\) ft.
→ Now that we know the volume of the water is 1 cubic foot and the height of the water is \(\frac{2}{3}\) feet, how can we determine the area of the pentagonal base?
Use the volume formula.
Use the information we know to find the area of the base.
1 ft3 = B(\(\frac{2}{3}\)ft.) Therefore, the area of the pentagonal base is \(\frac{3}{2}\) ft2, or 1\(\frac{1}{2}\) ft2.
Example 3.
Two containers are shaped like right triangular prisms, each with the same height. The base area of the larger container is 200% more than the base area of the smaller container. How many times must the smaller container be filled with water and poured into the larger container in order to fill the larger container?
Answer:
Solution by manipulating the equation of the volume of the smaller prism:
→ Let us call the area of the base of the smaller prism, B. Write an expression for the area of the larger base, and explain how it models the situation.
The base area of the larger prism is 3B because 200% more means that its area is 300% of B. Both prisms have the same height, h.
→ Compute the volume of the smaller prism.
The volume of the smaller prism is VS = Bh.
→ What is the volume of the larger prism?
The volume of the larger prism is VL = 3Bh.
→ How many times greater is the volume of the larger prism relative to the smaller prism?
\(\frac{3Bh}{Bh}\) = 3 The smaller container must be filled three times in order to fill the larger container.
Solution by substituting values for the smaller prism’s dimensions:
→ To solve this problem, create two right triangular prisms. What dimensions should we use for the smaller container?
Answers will vary, but for this example we will use a triangle that has a base of 10 inches and a height of 5 inches. The prism will have a height of 2 inches.
→ What is the area of the base for the smaller container? Explain.
The area of the base of the smaller container is 25 in2 because A = \(\frac{1}{2}\)(10 in.)(5 in.) = 25 in2.
→ What is the volume of the smaller container? Explain.
The volume of the smaller container is 50 in3 because V = 25 in2 × 2 in. = 50 in3.
→ What do we know about the larger container?
The area of the larger container’s base is 200% more than the area of the smaller container’s base.
The height of the larger container is the same as the height of the smaller container.
→ If the area of the larger container’s base is 200% more than the area of the smaller container’s base, what is the area of the larger container’s base?
The area of the larger container’s base would be 25 in2 + 2(25 in2) = 75 in2.
→ What is the volume of the larger container? Explain.
The volume of the larger container is 150 in3 because V = 75 in2 × 2 in. = 150 in3.
→ How many times must the smaller container be filled with water and poured into the larger container in order to fill the larger container? Explain.
The smaller container would have to be filled three times in order to fill the larger container. Each time you fill the smaller container, you will have 50 in3; therefore, you will need to fill the smaller container three times to get a volume of 150 in3.
→ Would your answer be different if we used different dimensions for the containers? Why or why not?
Our answer would not change if we used different dimensions. Because the area of the base of the larger container is triple the area of the base of the smaller container—and because the two heights are the same—the volume of the larger container is triple that of the smaller container.
Eureka Math Grade 7 Module 6 Lesson 25 Exercise Answer Key
Exercise 1.
a. Show that the following figures have equal volumes.
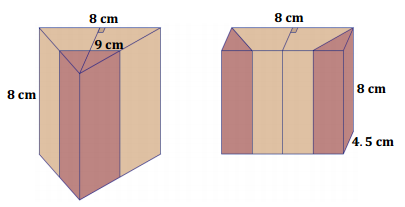
b. How can it be shown that the prisms will have equal volumes without completing the entire calculation?
Answer:
a. Volume of triangular prism:
\(\frac{1}{2}\)(8 cm × 9 cm) × 8 cm = 288 cm3
Volume of rectangular prism:
8 cm × 8 cm × 4.5 cm = 288 cm3
b. If one base can be cut up and rearranged to form the other base, then the bases have the same area. If the prisms have the same height, then the cutting and rearranging of the bases can show how to slice and rearrange one prism so that it looks like the other prism. Since slicing and rearranging does not change volume, the volumes are the same.
Exercise 2.
Two aquariums are shaped like right rectangular prisms. The ratio of the dimensions of the larger aquarium to the dimensions of the smaller aquarium is 3:2.
Addie says the larger aquarium holds 50% more water than the smaller aquarium.
Berry says that the larger aquarium holds 150% more water.
Cathy says that the larger aquarium holds over 200% more water.
Are any of the girls correct? Explain your reasoning.
Answer:
Cathy is correct. If the ratio of the dimensions of the larger aquarium to the dimensions of the smaller aquarium is 3:2, then the volume must be 1.53, or 3.375 times greater than the smaller aquarium. Therefore, the larger aquarium’s capacity is 337.5% times as much water, which is 237.5% more than the smaller aquarium. Cathy said that the larger aquarium holds over 200% more water than the smaller aquarium, so she is correct.
Eureka Math Grade 7 Module 6 Lesson 25 Problem Set Answer Key
Question 1.
The pieces in Figure 1 are rearranged and put together to form Figure 2.
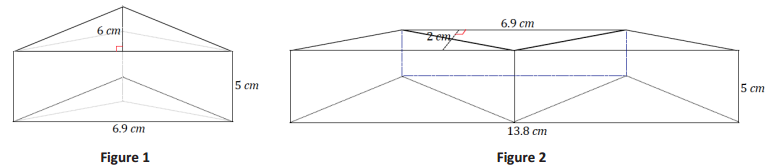
a. Use the information in Figure 1 to determine the volume of the prism.
b. Use the information in Figure 2 to determine the volume of the prism.
c. If we were not told that the pieces of Figure 1 were rearranged to create Figure 2, would it be possible to determine whether the volumes of the prisms were equal without completing the entire calculation for each?
Answer:
a. Volume: \(\frac{1}{2}\)(6.9 cm∙6 cm)(5 cm) = 103.5 cm3
b. Volume: (\(\frac{1}{2}\)(6.9 cm + 13.8 cm) ∙ 2 cm)(5 cm) = 103.5 cm3
c. Both prisms have the same height, so as long as it can be shown that both bases have the same area, both prisms must have equal volumes. We could calculate the area of the triangle base and the trapezoid base and find that they are equal in area and be sure that both volumes are equal.
Question 2.
Two right prism containers each hold 75 gallons of water. The height of the first container is 20 inches. The of the second container is 30 inches. If the area of the base in the first container is 6 ft2, find the area of the base in the second container. Explain your reasoning.
Answer:
We know that the volume of each of the two containers is 75 gallons; therefore, the volumes must be equal.
In order to find the volume of the first container, we could multiply the area of the base (6 ft2) by the height
(20 inches). To find the volume of the second container, we would also multiply the area of its base, which we will call A (area in square feet), and the height (30 inches). These two expressions must equal each other since both containers have the same volume.
6 × 20 = A × 30
120 = 30A
120 ÷ 30 = 30A ÷ 30
4 = A
Therefore, the area of the base in the second container is 4 ft2. Note: The units for the volume are 1 ft. × 1 ft. × 1 in. in this computation. Converting the inches to feet would make the computation in cubic feet, but it would not change the answer for A.
Question 3.
Two containers are shaped like right rectangular prisms. Each has the same height, but the base of the larger container is 50% more in each direction. If the smaller container holds 8 gallons when full, how many gallons does the larger container hold? Explain your reasoning.
Answer:
The larger container holds 18 gallons because each side length of the base is 1.5 times larger than the smaller container’s dimensions. Therefore, the area of the larger container’s base is 1.52, or 2.25 times larger than the smaller container. Because the height is the same in both containers, the volume of the larger container must be 2.25 times larger than the smaller container. 8 gal. × 2.25 = 18 gal.
Question 4.
A right prism container with the base area of 4 ft2 and height of 5 ft. is filled with water until it is 3 ft. deep. If a solid cube with edge length 1 ft. is dropped to the bottom of the container, how much will the water rise?
Answer:
The volume of the cube is 1 ft3. Let the number of feet the water will rise be x. Then, the volume of the water over the 3 ft. mark is 4 x ft3 because this represents the area of the base (4 ft2) times the height (x). Because the volume of the cube is 1 ft3, 4 x ft3 must equal 1 ft3.
4x = 1
4x ÷ 4 = 1 ÷ 4
x = \(\frac{1}{4}\)
Therefore, the water will rise \(\frac{1}{4}\) ft., or 3 inches.
Question 5.
A right prism container with a base area of 10 ft2 and height 9 ft. is filled with water until it is 6 ft. deep. A large boulder is dropped to the bottom of the container, and the water rises to the top, completely submerging the boulder without causing overflow. Find the volume of the boulder.
Answer:
The increase in volume is the same as the volume of the boulder. The height of the water increases 3 ft. Therefore, the increase in volume is 10 ft2 (area of the base) multiplied by 3 ft. (i.e., the change in height).
V = 10 ft2 × 3 ft. = 30 ft3
Because the increase in volume is 30 ft3, the volume of the boulder is 30 ft3.
Question 6.
A right prism container with a base area of 8 ft2 and height 6 ft. is filled with water until it is 5 ft. deep. A solid cube is dropped to the bottom of the container, and the water rises to the top. Find the length of the cube.
Answer:
When the cube is dropped into the container, the water rises 1 foot, which means the volume increases 8 cubic feet. Therefore, the volume of the cube must be 8 cubic feet. We know that the length, width, and height of a cube are equal, so the length of the cube is 2 feet because 2 ft. × 2 ft. × 2 ft. = 8 ft3, which is the volume of the cube.
Question 7.
A rectangular swimming pool is 30 feet wide and 50 feet long. The pool is 3 feet deep at one end, and 10 feet deep at the other.
a. Sketch the swimming pool as a right prism.
b. What kind of right prism is the swimming pool?
c. What is the volume of the swimming pool in cubic feet?
d. How many gallons will the swimming pool hold if each cubic feet of water is about 7.5 gallons?
Answer:
a.
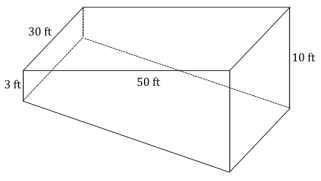
b. The swimming pool is a right trapezoidal prism.
c. Area of base = \(\frac{50 \mathrm{ft} \cdot(10 \mathrm{ft} + 3 \mathrm{ft})}{2}\) = 325 ft2
Volume of pool = 325 ft2 × 30 ft. = 9,750 ft3
d. (9,750 ft3 ) \(\frac{(7.5 \mathrm{gal})}{1 \mathrm{ft}^{3}}\) = 73,125 gal. The pool will hold 73,125 gal.
Question 8.
A milliliter (mL) has a volume of 1 cm3. A 250 mL measuring cup is filled to 200 mL. A small stone is placed in the measuring cup. The stone is completely submerged, and the water level rises to 250 mL.
a. What is the volume of the stone in cm3?
b. Describe a right rectangular prism that has the same volume as the stone.
Answer:
a. When the stone is dropped into the measuring cup, the increase in volume is 250 mL – 200 mL = 50 mL. We know that 1 mL has a volume of 1 cm3; therefore, the stone has a volume of 50 cm3.
b. Answers will vary. Possible answers are listed below.
1 cm × 1 cm × 50 cm
1 cm × 2 cm × 25 cm
1 cm × 5 cm × 10 cm
2 cm × 5 cm × 5 cm
Eureka Math Grade 7 Module 6 Lesson 25 Exit Ticket Answer Key
Question 1.
Determine the volume of the following prism. Explain how you found the volume.
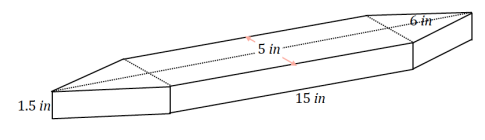
Answer:
To find the volume of the prism, the base must be decomposed into triangles and rectangles since there is no way to find the area of the base as is. The base can be decomposed into two triangles and a rectangle, and their areas must be summed to find the area of the base. Once the area of the base is determined, it should be multiplied by the height to find the volume of the entire prism.
Area of both triangles: 2(\(\frac{1}{2}\)(5 in. × 6 in.)) = 30 in2
Area of the rectangle: 15 in. × 5 in. = 75 in2
Total area of the base: (30 + 75) in2 = 105 in2
Volume of the prism: (105 in2)(1.5 in.) = 157.5 in3