Engage NY Eureka Math 7th Grade Module 6 Lesson 5 Answer Key
Eureka Math Grade 7 Module 6 Lesson 5 Example Answer Key
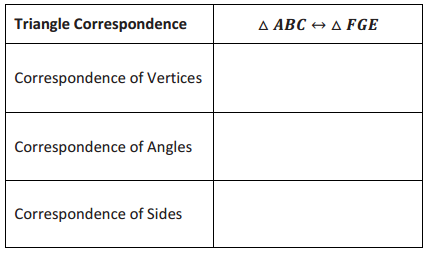
Example 1.
Given the following triangle correspondences, use double arrows to show the correspondence between vertices, angles, and sides.
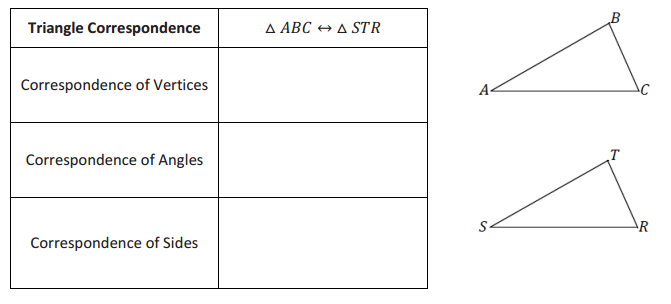
Answer:
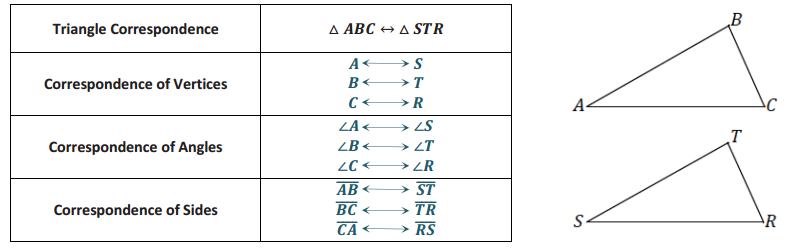
Example 2.
Two identical triangles are shown below. Give a triangle correspondence that matches equal sides and equal angles.
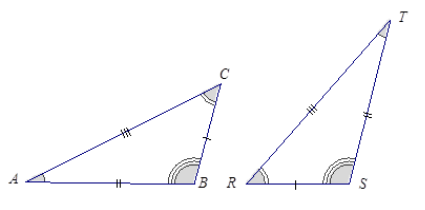
Answer:
△ABC ↔ △TSR
Eureka Math Grade 7 Module 6 Lesson 5 Exercise Answer Key
Exercises 1–7
Use the figure △ABC to fill in the following blanks.
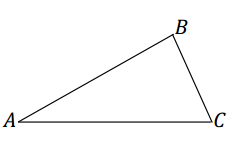
1. ∠A is ______________ sides \(\overline{A B}\) and \(\overline{A C}\).
2. ∠B is ______________ side \(\overline{A B}\) and to side \(\overline{B C}\).
3. Side \(\overline{A B}\) is ______________ ∠C.
4. Side ______________ is the included side of ∠B and ∠C.
5. ______________ is opposite to side \(\overline{A C}\).
6. Side \(\overline{A B}\) is between ______________ and ______________.
7. What is the included angle of sides\(\overline{A B}\) and \(\overline{B C}\)? ______________.
Answer:
1. between
2. adjacent to
3. opposite to
4. \(\overline{B C}\)
5. ∠ B
6. ∠A and ∠B
7. ∠B
Now that we know what to call the parts within a triangle, we consider how to discuss two triangles. We need to compare the parts of the triangles in a way that is easy to understand. To establish some alignment between the triangles, we pair up the vertices of the two triangles. We call this a correspondence. Specifically, a correspondence between two triangles is a pairing of each vertex of one triangle with one (and only one) vertex of the other triangle. A correspondence provides a systematic way to compare parts of two triangles.
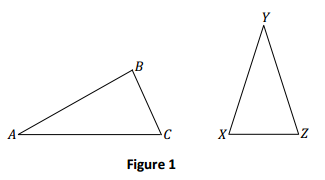
In Figure 1, we can choose to assign a correspondence so that A matches to X, B matches to Y, and C matches to Z. We notate this correspondence with double arrows: A ↔X, B ↔Y, and C ↔Z. This is just one of six possible correspondences between the two triangles. Four of the six correspondences are listed below; find the remaining two correspondences.
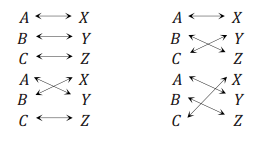
A simpler way to indicate the triangle correspondences is to let the order of the vertices define the correspondence (i.e., the first corresponds to the first, the second to the second, and the third to the third). The correspondences above can be written in this manner. Write the remaining two correspondences in this way.
△ABC ↔ △XYZ
△ABC ↔ △XZY
△ABC ↔ △ZYX
△ABC ↔ △YXZ
△ABC ↔ △YZX
△ABC ↔ △ZXY
Exercise 8.
Sketch two triangles that have a correspondence. Describe the correspondence in symbols or words. Have a partner check your work.
Answer:
Answers will vary. Encourage students to check for correct use of notation and correctly made correspondences.
Eureka Math Grade 7 Module 6 Lesson 5 Problem Set Answer Key
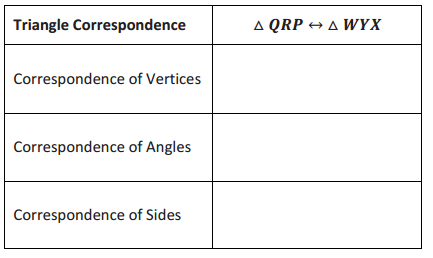
Given the following triangle correspondences, use double arrows to show the correspondence between vertices, angles, and sides.
Question 1.
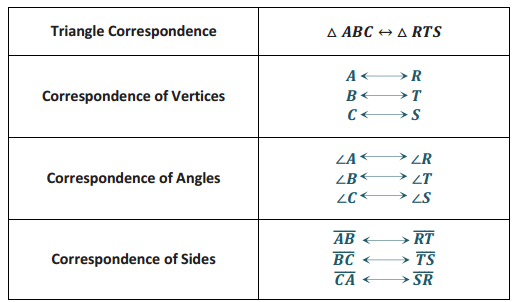
Answer:
Question 2.
Answer:
Question 3.
Answer:
Name the angle pairs and side pairs to find a triangle correspondence that matches sides of equal length and angles of equal measurement.
Question 4.
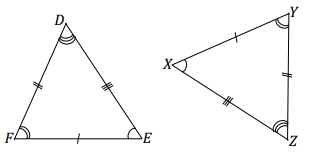
Answer:
DE = ZX
XY = EF
DF = ZY
∠E = ∠X
∠Z = ∠D
∠F = ∠Y
△DEF ↔ △ZXY
Question 5.
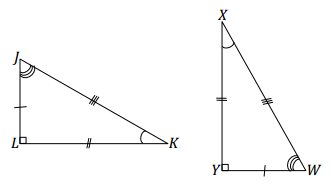
Answer:
JK = WX
YX = LK
LJ = YW
∠Y = ∠L
∠J = ∠W
∠K = ∠X
△JKL ↔ △WXY
Question 6.
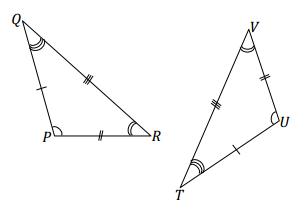
Answer:
PQ = UT
TV = QR
RP = VU
∠Q = ∠T
∠U = ∠P
∠R = ∠V
△PQR ↔ △UTV
Question 7.
7. Consider the following points in the coordinate plane.
a. How many different (non-identical) triangles can be drawn using any three of these six points as vertices?
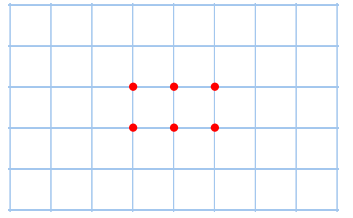
b. How can we be sure that there are no more possible triangles?
Answer:
a. There is a total of 18 triangles but only 4 different triangles. Each triangle is identical with one of these four:

b. Any other triangle will have a correspondence so that equal sides and angles of equal measurement can be lined up (i.e., one can be laid over another, and the two triangles will match).
Question 8.
Quadrilateral ABCD is identical with quadrilateral WXYZ with a correspondence A ↔W, B ↔X, C ↔Y, and D ↔Z.
a. In the figure above, label points W, X, Y, and Z on the second quadrilateral.
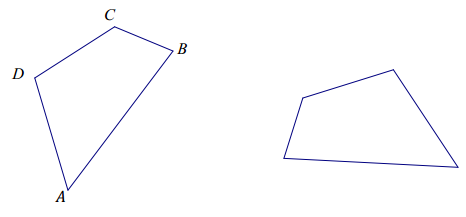
b. Set up a correspondence between the side lengths of the two quadrilaterals that matches sides of equal length.
c. Set up a correspondence between the angles of the two quadrilaterals that matches angles of equal measure.
Answer:
a. 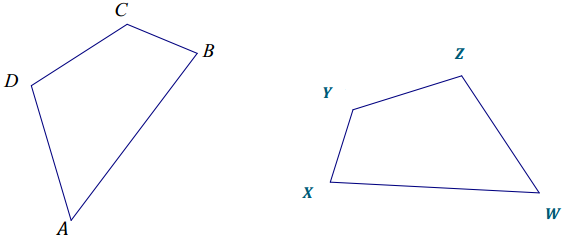
b. \(\overline{A B}\) ↔(\(\overline{W X}\), \(\overline{B C}\) ↔\(\overline{X Y}\), \(\overline{C D}\) ↔\(\overline{Y Z}\), and \(\overline{A D}\) ↔\(\overline{W Z}\)
c. ∠A ↔∠W, ∠B ↔∠X, ∠C ↔∠Y, and ∠D ↔∠Z
Eureka Math Grade 7 Module 6 Lesson 5 Exit Ticket Answer Key
Question 1.
The following triangles are identical and have the correspondence △ABC ↔ △YZX. Find the measurements for each of the following sides and angles. Figures are not drawn to scale.
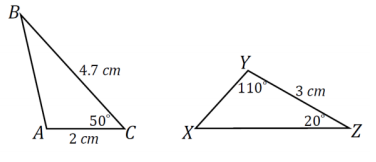
AB = ________
________ = ZX
________ = XY
∠A = ________
∠B = ________
________ = ∠X
Answer:
AB = 3 cm
4.7 cm = ZX
2 cm = XY
∠A = 110°
∠B = 20°
50° = ∠X
Question 2.
Explain why correspondences are useful.
Answer:
A correspondence offers a systematic way to compare parts of two triangles. We can make statements about similarities or differences between two triangles using a correspondence, whereas without one, we would not have a reference system to make such comparisons.