Engage NY Eureka Math 8th Grade Module 1 Lesson 13 Answer Key
Eureka Math Grade 8 Module 1 Lesson 13 Exercise Answer Key
Exercise 1.
The Fornax Dwarf galaxy is 4.6×105 light-years away from Earth, while Andromeda I is 2.430×106 light-years away from Earth. Which is closer to Earth?
Answer:
2.430×106=2.430×10×105=24.30×105
Because 4.6<24.30, then 4.6×105<24.30×105, and since 24.30×105=2.430×106, we know that 4.6×105<2.430×106. Therefore, Fornax Dwarf is closer to Earth.
Exercise 2.
The average lifetime of the tau lepton is 2.906×10-13 seconds, and the average lifetime of the neutral pion is 8.4×10-17 seconds. Explain which subatomic particle has a longer average lifetime.
Answer:
2.906×10-13=2.906×104×10-17=29,060×10-17
Since 8.4<29,060, then 8.4×10-17<29,060×10-17, and since 29,060×10-17=2.906×10-13, we know that 8.4×10-17< 2.906×10-13. Therefore, tau lepton has a longer average lifetime.
This problem, as well as others, can be solved using an alternate method. Our goal is to make the magnitude of the numbers we are comparing the same, which will allow us to reduce the comparison to that of whole numbers.
Here is an alternate solution:
8.4×10-17=8.4×10-4×10-13=0.000 84×10-13.
Since 0.00084<2.906, then 0.000 84×10-13<2.906×10-13, and since 0.000 84×10-13=8.4×10-17, we know that 8.4×10-17< 2.906×10-13. Therefore, tau lepton has a longer average lifetime.
Exploratory Challenge 1/Exercise 3.
THEOREM: Given two positive numbers in scientific notation, a×10m and b×10n, if m<n, then a×10m<b×10n.
Prove the theorem.
If m<n, then there is a positive integer k so that n=k+m.
By the first law of exponents (10) in Lesson 5, b×10n=b×10k×10m=(b×10k)×10m. Because we are comparing with a×10m, we know by (1) that we only need to prove a<(b×10k). By the definition of scientific notation, a<10 and also (b×10k)≥10 because k≥1 and b≥1, so that (b×10k)≥1×10=10. This proves a<(b×10k), and therefore, a×10m<b×10n.
Explain to students that we know that a<10 because of the statement given that a×10m is a number expressed in scientific notation. That is not enough information to convince students that a<b×10k; therefore, we need to say something about the right side of the inequality. We know that k≥1 because k is a positive integer so that n=k+m. We also know that b≥1 because of the definition of scientific notation. That means that the minimum possible value of b×10k is 10 because 1×101=10. Therefore, we can be certain that a<b×10k.
Therefore, by (1), a×10m<(b×10k)×10m. Since n=k+m, we can rewrite the right side of the inequality as
b×10n, and finally a×10m<b×10n.
Exercise 4.
Compare 9.3×1028 and 9.2879×1028.
Answer:
We only need to compare 9.3 and 9.2879. 9.3×104=93,000 and 9.2879×104=92,879, so we see that
93,000>92,879. Therefore, 9.3×1028>9.2879×1028.
Exercise 5.
Chris said that 5.3×1041<5.301×1041 because 5.3 has fewer digits than 5.301. Show that even though his answer is correct, his reasoning is flawed. Show him an example to illustrate that his reasoning would result in an incorrect answer. Explain.
Answer:
Chris is correct that 5.3×1041<5.301×1041, but that is because when we compare 5.3 and 5.301, we only need to compare 5.3×103 and 5.301×103 (by (1) above). But, 5.3×103<5.301×103 or rather 5,300<5,301, and this is the reason that 5.3×1041<5.301×1041. However, Chris’s reasoning would lead to an incorrect answer for a problem that compares 5.9×1041 and 5.199×1041. His reasoning would lead him to conclude that
5.9×1041<5.199×1041, but 5,900>5,199, which is equivalent to 5.9×103>5.199×103. By (1) again, 5.9>5.199, meaning that 5.9×1041>5.199×1041.
Exploratory Challenge 2/Exercise 6.
You have been asked to determine the exact number of Google searches that are made each year. The only information you are provided is that there are 35,939,938,877 searches performed each week. Assuming the exact same number of searches are performed each week for the 52 weeks in a year, how many total searches will have been performed in one year? Your calculator does not display enough digits to get the exact answer. Therefore, you must break down the problem into smaller parts. Remember, you cannot approximate an answer because you need to find an exact answer. Use the screen shots below to help you reach your answer.
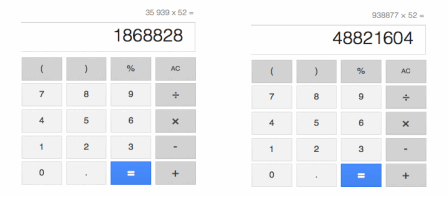
Answer:
First, I need to rewrite the number of searches for each week using numbers that can be computed using my calculator.
35 939 938 877=35 939 000 000+938 877
=35 939×106+938 877
Next, I need to multiply each term of the sum by 52, using the distributive law.
(35 939×106+938 877)×52=(35 939×106)×52+(938 877×52)
By repeated use of the commutative and associative properties, I can rewrite the problem as
(35 939×52)×106+(938 877×52).
According to the screen shots, I get
1 868 828×106+48 821 604=1 868 828 000 000+48 821 604
=1 868 876 821 604.
Therefore, 1,868,876,821,604 Google searches are performed each year.
Yahoo! is another popular search engine. Yahoo! receives requests for 1,792,671,335 searches each month. Assuming the same number of searches are performed each month, how many searches are performed on Yahoo! each year? Use the screen shots below to help determine the answer.
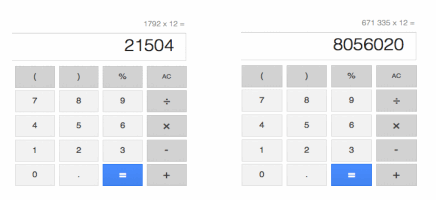
Answer:
First, I need to rewrite the number of searches for each month using numbers that can be computed using my calculator.
1 792 671 335=1 792 000 000+671 335
=1 792×106+671 335.
Next, I need to multiply each term of the sum by 12, using the distributive law.
(1 792×106+671 335)×12=(1 792×106)×12+(671 335×12).
By repeated use of the commutative and associative properties, I can rewrite the problem as
(1 792×12)×106+(671 335×12)
According to the screen shots, I get
21 504×106+8 056 020=21 504 000 000+8 056 020
=21 512 056 020
Therefore, 21,512,056,020 Yahoo! searches are performed each year.
Eureka Math Grade 8 Module 1 Lesson 13 Exit Ticket Answer Key
Question 1.
Compare 2.01×1015 and 2.8×1013. Which number is larger?
Answer:
2.01×1015=2.01×102×1013=201×1013
Since 201>2.8, we have 201×1013>2.8×1013, and since 201×1013=2.01×1015, we conclude 2.01×1015>2.8×1013.
Question 2.
The wavelength of the color red is about 6.5×10^-9 m. The wavelength of the color blue is about 4.75×10-9 m. Show that the wavelength of red is longer than the wavelength of blue.
Answer:
We only need to compare 6.5 and 4.75:
6.5×10-9=650×10-7 and 4.75×10-9=475×10-7, so we see that 650>475.
Therefore, 6.5×10-9>4.75×10-9.
Eureka Math Grade 8 Module 1 Lesson 13 Problem Set Answer Key
Question 1.
Write out a detailed proof of the fact that, given two numbers in scientific notation, a×10n and b×10n, a<b, if and only if a×10n<b×10n.
Answer:
Because 10n>0, we can use inequality (A) (i.e., (1) above) twice to draw the necessary conclusions. First, if a<b, then by inequality (A), a×10n<b×10n. Second, given a×10n<b×10n, we can use inequality (A) again to show an<b×10n by 10-n.
a. Let A and B be two positive numbers, with no restrictions on their size. Is it true that A×10-5<B×105?
Answer:
No, it is not true that A×10-5<B×105. Using inequality (A), we can write
A×10-5×105<B×105×105, which is the same as A<B×1010. To disprove the statement, all we would need to do is find a value of A that exceeds B×1010.
b. Now, if A×10-5 and B×105 are written in scientific notation, is it true that A×10-5<B×105? Explain.
Answer:
Yes, since the numbers are written in scientific notation, we know that the restrictions for A and B are
1≤A<10 and 1≤B<10. The maximum value for A, when multiplied by 10-5, will still be less than 1. The minimum value of B will produce a number at least 105 in size.
Question 2.
The mass of a neutron is approximately 1.674927×10-27 kg. Recall that the mass of a proton is
1.672622×10-27 kg. Explain which is heavier.
Answer:
Since both numbers have a factor of 10-27, we only need to look at 1.674927 and 1.672622. When we multiply each number by 106, we get
1.674927×106 and 1.672622×106,
which is the same as
1,674,927 and 1,672,622.
Now that we are looking at whole numbers, we can see that 1,674,927>1,672,622 (by (2b) above), which means that 1.674927×10-27>1.672622×10-27. Therefore, the mass of a neutron is heavier.
Question 3.
The average lifetime of the Z boson is approximately 3×10-25 seconds, and the average lifetime of a neutral rho meson is approximately 4.5×10-24 seconds.
a. Without using the theorem from today’s lesson, explain why the neutral rho meson has a longer average lifetime.
Answer:
Since 3×10-25=3×10-1×10-24, we can compare 3×10-1×10-24 and 4.5×10-24. Based on Example 3 or by use of (1) above, we only need to compare 3×10-1 and 4.5, which is the same as 0.3 and 4.5. If we multiply each number by 10, we get whole numbers 3 and 45. Since 3<45, then
3×10-25<4.5×10-24. Therefore, the neutral rho meson has a longer average lifetime.
b. Approximately how much longer is the lifetime of a neutral rho meson than a Z boson?
Answer:
45:3 or 15 times longer
Rapid White Board Exchange: Operations with Numbers Expressed in Scientific Notation
Question 1.
(5×104)2=
Answer:
2.5×109
Question 2.
(2×109)4=
Answer:
1.6×1037
Question 3.
\(\frac{\left(1.2 \times 10^{4}\right)+\left(2 \times 10^{4}\right)+\left(2.8 \times 10^{4}\right)}{3}\)=
Answer:
2×104
Question 4.
\(\frac{7 \times 10^{15}}{14 \times 10^{9}}\) =
Answer:
5×105
Question 5.
\(\frac{4 \times 10^{2}}{2 \times 10^{8}}\)=
Answer:
2×10-6
Question 6.
\(\frac{\left(7 \times 10^{9}\right)+\left(6 \times 10^{9}\right)}{2}\)=
Answer:
6.5×109
Question 7.
(9×10-4)2=
Answer:
8.1×10-7
Question 8.
(9.3×1010)-(9×1010)=
Answer:
3×109