Engage NY Eureka Math 8th Grade Module 1 Lesson 9 Answer Key
Eureka Math Grade 8 Module 1 Lesson 9 Exercise Answer Key
Are the following numbers written in scientific notation? If not, state the reason.
Exercise 1.
1.908×1017
Ans:
yes
Exercise 2.
0.325×10-2
Answer:
no, d<1
Exercise 3.
7.99×1032
Answer:
yes
Exercise 4.
4.0701 + 107
Answer:
no, it must be a product
Exercise 5.
18.432×58
Answer:
no, d>10 and it is ×5 instead of ×10
Exercise 6.
8×10-11
Answer:
yes
Exercises 7–9 (10 minutes)
Have students complete Exercises 7–9 independently.
Use the table below to complete Exercises 7 and 8.
The table below shows the debt of the three most populous states and the three least populous states.
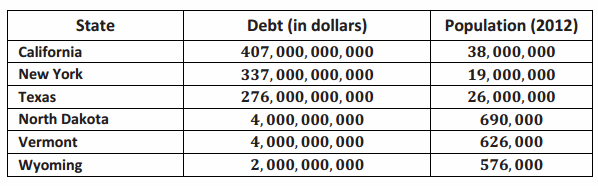
Exercise 7.
a. What is the sum of the debts for the three most populous states? Express your answer in scientific notation.
Answer:
(4.07×(10)11)+(3.37×1011)+(2.76×1011)=(4.07+3.37+2.76)×1011
=10.2×1011
=(1.02×10)×1011
=1.02×1012
b. What is the sum of the debt for the three least populous states? Express your answer in scientific notation.
Ans:
(4×109)+(4×109)+(2×109)=(4+4+2)×109
=10×109
=(1×10)×109
=1×1010
c. How much larger is the combined debt of the three most populous states than that of the three least populous states? Express your answer in scientific notation.
Answer:
(1.02×1012)-(1×1010)=(1.02×102×1010)-(1×1010)
=(102×1010)-(1×1010)
=(102-1)×1010
=101×1010
=(1.01×102)×1010
=1.01×1012
Exercise 8.
a. What is the sum of the population of the three most populous states? Express your answer in scientific notation.
Answer:
(3.8×107)+(1.9×107)+(2.6×107)=(3.8+1.9+2.6)×107
=8.3×107
b. What is the sum of the population of the three least populous states? Express your answer in scientific notation.
Answer:
(6.9×105)+(6.26×105)+(5.76×105)=(6.9+6.26+5.76)×105
=18.92×105
=(1.892×10)×105
=1.892×106
c. Approximately how many times greater is the total population of California, New York, and Texas compared to the total population of North Dakota, Vermont, and Wyoming?
Answer:
\(\frac{8.3 \times 10^{7}}{1.892 \times 10^{6}}\) = \(\frac{8.3}{1.892}\) × \(\frac{10^{7}}{10^{6}}\)
≈4.39×10
=43.9
The combined population of California, New York, and Texas is about 43.9 times greater than the combined population of North Dakota, Vermont, and Wyoming.
Exercise 9.
All planets revolve around the sun in elliptical orbits. Uranus’s furthest distance from the sun is approximately 3.004×109 km, and its closest distance is approximately 2.749×109 km. Using this information, what is the average distance of Uranus from the sun?
Answer:
average distance = \(\frac{\left(3.004 \times 10^{9}\right)+\left(2.749 \times 10^{9}\right)}{2}\)
= \(\frac{(3.004+2.749) \times 10^{9}}{2}\)
= \(\frac{5.753 \times 10^{9}}{2}\)
=2.8765×109
On average, Uranus is 2.8765×109 km from the sun.
Eureka Math Grade 8 Module 1 Lesson 9 Problem Set Answer Key
Students practice working with numbers written in scientific notation.
Question 1.
Write the number 68,127,000,000,000,000 in scientific notation. Which of the two representations of this number do you prefer? Explain.
Answer:
68 127 000 000 000 000=6.8127×1016
Most likely, students will say that they like the scientific notation better because it allows them to write less. However, they should also take note of the fact that counting the number of zeros in 68,127,000,000,000,000 is a nightmare. A strong reason for using scientific notation is to circumvent this difficulty: right away, the exponent 16 shows that this is a 17-digit number.
Question 2.
Here are the masses of the so-called inner planets of the solar system.

What is the average mass of all four inner planets? Write your answer in scientific notation.
Answer:

The average mass of the inner planets is 2.9531925×1024 kg.
Eureka Math Grade 8 Module 1 Lesson 9 Exit Ticket Answer Key
Question 1.
The approximate total surface area of Earth is 5.1×108 km2. All the salt water on Earth has an approximate surface area of 352,000,000 km2, and all the fresh water on Earth has an approximate surface area of 9×106 km2. How much of Earth’s surface is covered by water, including both salt and fresh water? Write your answer in scientific notation.
Answer:
(3.52×108)+(9×106)=(3.52×102×106)+(9×106)
=(352×106)+(9×106)
=(352+9)×106
=361×106
=3.61×108
The Earth’s surface is covered by 3.61×108 km2 of water.
Question 2.
How much of Earth’s surface is covered by land? Write your answer in scientific notation.
Answer:
(5.1×108)-(3.61×108)=(5.1-3.61)×108
=1.49×108
The Earth’s surface is covered by 1.49×108 km2 of land.
Question 3.
Approximately how many times greater is the amount of Earth’s surface that is covered by water compared to the amount of Earth’s surface that is covered by land?
Answer:
\(\frac{3.61 \times 10^{8}}{1.49 \times 10^{8}}\)≈2.4
About 2.4 times more of the Earth’s surface is covered by water than by land.