Engage NY Eureka Math 8th Grade Module 2 Lesson 3 Answer Key
Eureka Math Grade 8 Module 2 Lesson 3 Exercise Answer Key
Exercise 1.
Draw a line passing through point P that is parallel to line L. Draw a second line passing through point P that is parallel to line L and that is distinct (i.e., different) from the first one. What do you notice?
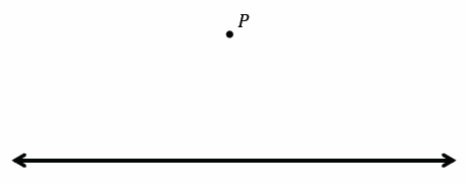
Answer:
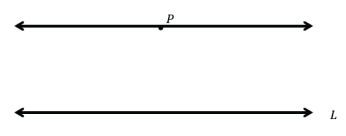
Students should realize that they can only draw one line through point P that is parallel to L.
Exercises 2–4 (9 minutes)
Students complete Exercises 2–4 independently in preparation for the discussion that follows.
Exercise 2.
Translate line L along the vector \(\overrightarrow{A B}\). What do you notice about L and its image, L’?

Answer:

L and L’ coincide. L=L’.
Exercise 3.
Line L is parallel to vector \(\overrightarrow{A B}\). Translate line L along vector (AB) ⃗. What do you notice about L and its image, L’?

Answer:
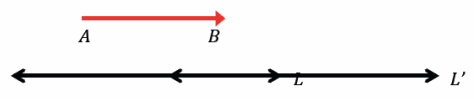
L and L’ coincide, again. L=L’.
Exercise 4.
Translate line L along the vector \(\overrightarrow{A B}\). What do you notice about L and its image, L’?
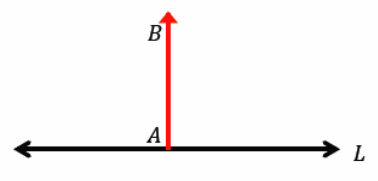
Answer:
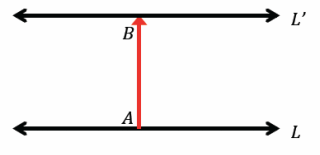
L || L’
Exercises 5–6 (5 minutes)
Students complete Exercises 5 and 6 in pairs or small groups.
Exercise 5.
Line L has been translated along vector \(\overrightarrow{A B}\), resulting in L’. What do you know about lines L and L’?
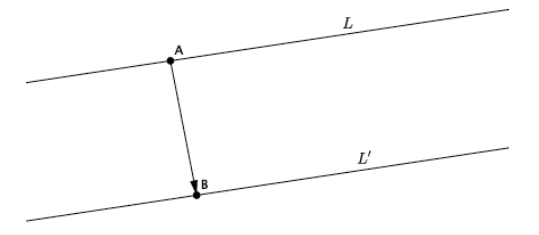
Answer:
L || T(L)
Question 6.
Translate L1 and L2 along vector \(\overrightarrow{D E}\). Label the images of the lines. If lines L1 and L2 are parallel, what do you know about their translated images?
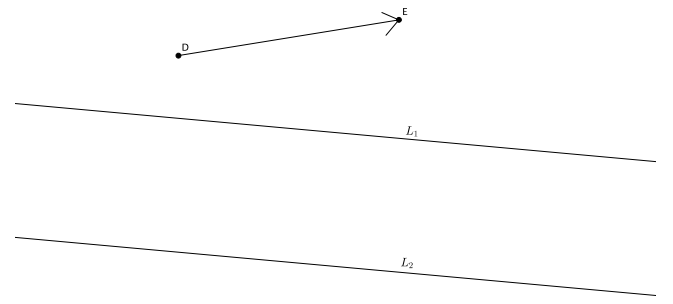
Answer:
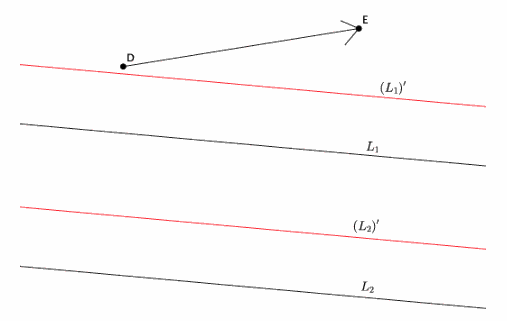
Since L1 || L1, then (L1)’ || (L2)’.
Eureka Math Grade 8 Module 2 Lesson 3 Exit Ticket Answer Key
Question 1.
Translate point Z along vector \(\overrightarrow{A B}\). What do you know about the line containing vector \(\overrightarrow{A B}\) and the line formed when you connect Z to its image Z’?
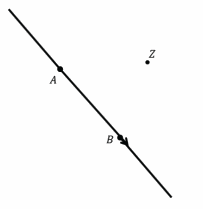
Answer:
The line containing vector \(\overrightarrow{A B}\) and ZZ’ is parallel.
Question 2.
Using the above diagram, what do you know about the lengths of segment ZZ’ and segment AB?
Answer:
The lengths are equal: |ZZ’|=|AB|.
Question 3.
Let points A and B be on line L and the vector \(\overrightarrow{A C}\) be given, as shown below. Translate line L along vector \(\overrightarrow{A C}\). What do you know about line L and its image, L’? How many other lines can you draw through point C that have the same relationship as L and L’? How do you know?
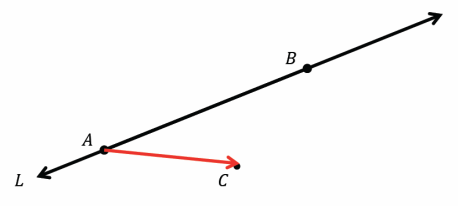
Answer:
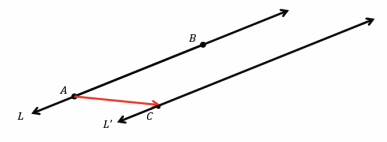
L and L’ are parallel. There is only one line parallel to line L that goes through point C. The fact that there is only one line through a point parallel to a given line guarantees it.
Eureka Math Grade 8 Module 2 Lesson 3 Problem Set Answer Key
Question 1.
Translate ∠XYZ, point A, point B, and rectangle HIJK along vector \(\overrightarrow{E F}\). Sketch the images, and label all points using prime notation.
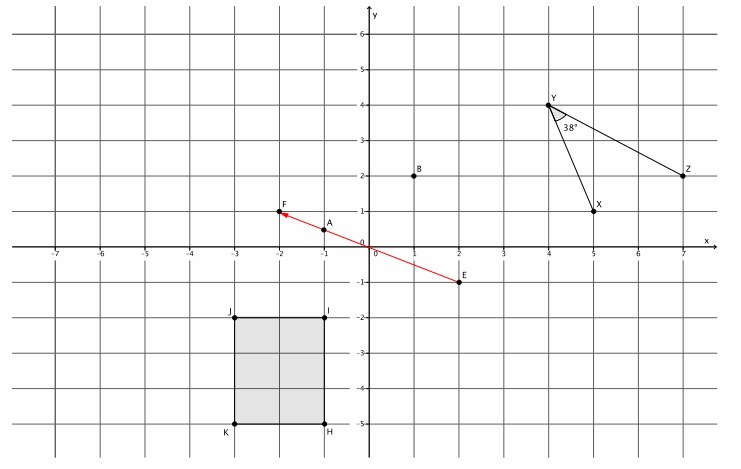
Answer:
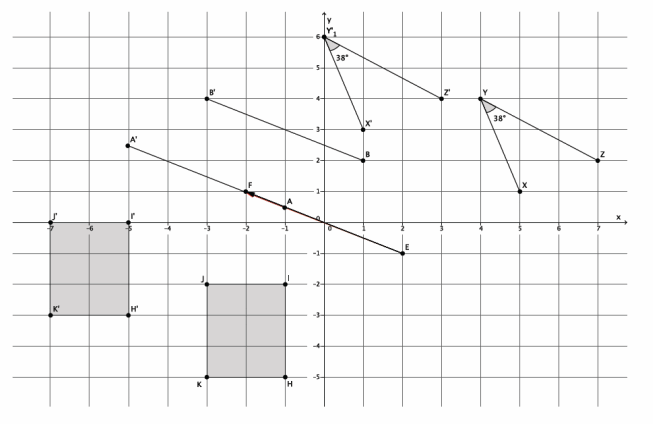
Question 2.
What is the measure of the translated image of ∠XYZ? How do you know?
Answer:
The measure is 38°. Translations preserve angle measure.
Question 3.
Connect B to B’. What do you know about the line that contains the segment formed by BB’ and the line containing the vector \(\overrightarrow{E F}\)?
Answer:
\(\overleftrightarrow{\boldsymbol{B B}^{\prime}} \| \overleftrightarrow{\boldsymbol{E F}}\)
Question 4.
Connect A to A’. What do you know about the line that contains the segment formed by AA’ and the line containing the vector \(\overrightarrow{\boldsymbol{E F}}\)?
Answer:
\(\overleftrightarrow{A A^{\prime}}\) and \(\overleftrightarrow{\boldsymbol{E F}}\) coincide.
Question 5.
Given that figure HIJK is a rectangle, what do you know about lines that contain segments HI and JK and their translated images? Explain.
Answer:
Since HIJK is a rectangle, I know that \(\overleftrightarrow{\boldsymbol{H} \boldsymbol{I}}\) || \(\overleftrightarrow{\boldsymbol{J K}}\). Since translations map parallel lines to parallel lines, then \(\overleftrightarrow{\boldsymbol{H}^{\prime} \boldsymbol{I}^{\prime}}\)||\(\overleftrightarrow{\boldsymbol{J}^{\prime} \boldsymbol{K}^{\prime}}\).