Engage NY Eureka Math 8th Grade Module 3 Lesson 8 Answer Key
Eureka Math Grade 8 Module 3 Lesson 8 Example Answer Key
Example 1.
In the picture below, we have triangle ABC that has been dilated from center O by a scale factor of r=\(\frac{1}{2}\). It is noted by A’B’C’. We also have triangle A”B”C”, which is congruent to triangle A’B’C’ (i.e., △A’B’C’≅△A”B”C”).
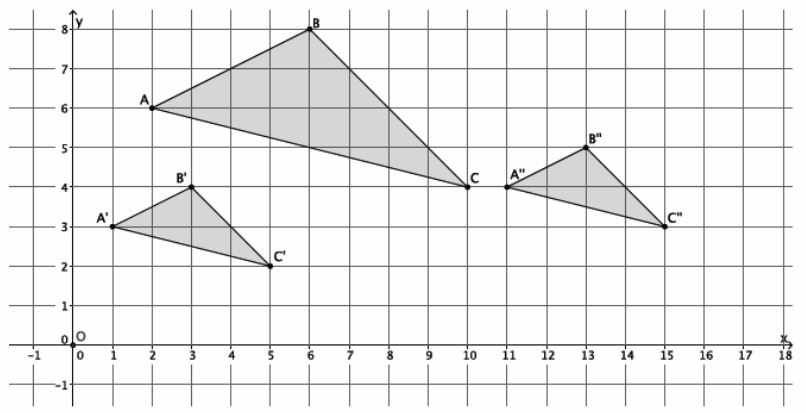
Describe the sequence that would map triangle A”B”C” onto triangle ABC.
→ Based on the definition of similarity, how could we show that triangle A”B”C” is similar to triangle ABC?
→ To show that △A” B” C”~△ABC, we need to describe a dilation followed by a congruence.
→ We want to describe a sequence that would map triangle A”B”C” onto triangle ABC. There is no clear way to do this, so let’s begin with something simpler: How can we map triangle A’B’C’ onto triangle ABC? That is, what is the precise dilation that would make triangle A’B’C’ the same size as triangle ABC?
→ A dilation from center O with scale factor r=2
→ Remember, our goal was to describe how to map triangle A”B”C” onto triangle ABC. What precise dilation would make triangle A”B”C” the same size as triangle ABC?
→ A dilation from center O with scale factor r=2 would make triangle A”B”C” the same size as triangle ABC.
→ (Show the picture below with the dilated triangle A”B”C” noted by A”’B”’C”’.) Now that we know how to make triangle A”B”C” the same size as triangle ABC, what rigid motion(s) should we use to actually map triangle A”B”C” onto triangle ABC? Have we done anything like this before?
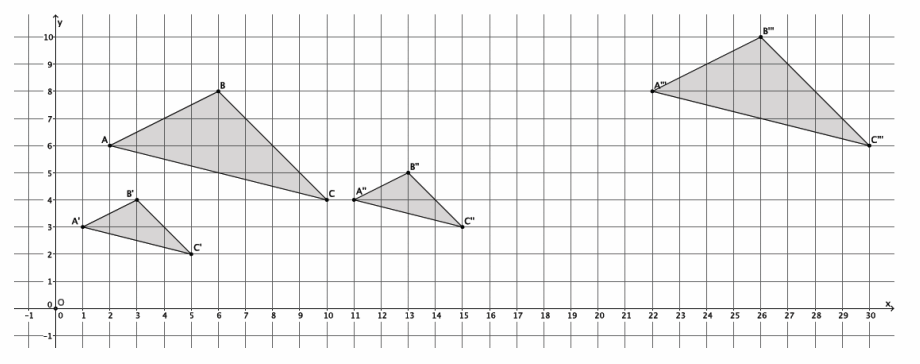
→ Problem 2 of the Problem Set from Lesson 2 was like this. That is, we had two figures dilated by the same scale factor in different locations on the plane. To get one to map to the other, we just translated along a vector.
→ Now that we have an idea of what needs to be done, let’s describe the translation in terms of coordinates. How many units and in which direction do we need to translate so that triangle A”’B”’C”’ maps to triangle ABC?
→ We need to translate triangle A”’B”’C”’ 20 units to the left and 2 units down.
→ Let’s use precise language to describe how to map triangle A”B”C” onto triangle ABC. We need information about the dilation and the translation.
→ The sequence that would map triangle A”B”C” onto triangle ABC is as follows: Dilate triangle A”B”C” from center O by scale factor r=2. Then, translate the dilated triangle 20 units to the left and 2 units down.
→ Since we were able to map triangle A”B”C” onto triangle ABC with a dilation followed by a congruence, we can write that triangle A”B”C” is similar to triangle ABC, in notation, △A” B” C”~△ABC.
Example 2.
In the picture below, we have triangle DEF that has been dilated from center O, by scale factor r=3. It is noted by D’ E’ F’. We also have triangle D” E” F”, which is congruent to triangle D’ E’ F’ (i.e., △D’ E’ F’≅
△D”E”F”).
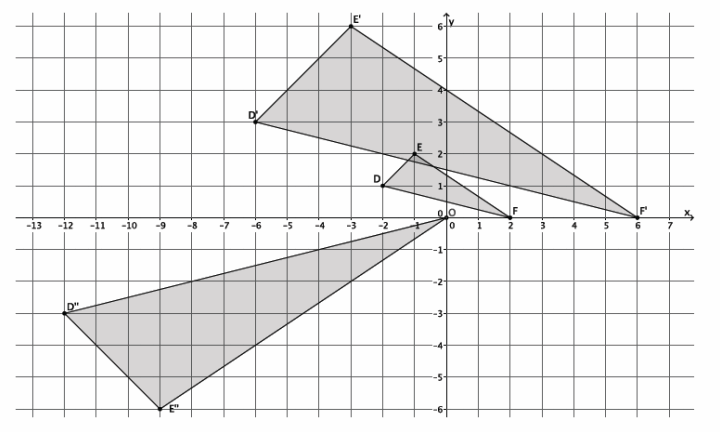
→ We want to describe a sequence that would map triangle D”E”F” onto triangle DEF. This is similar to what we did in the last example. Can someone summarize the work we did in the last example?
→ First, we figured out what scale factor r would make the triangles the same size. Then, we used a sequence of translations to map the magnified figure onto the original triangle.
→ What is the difference between this problem and the last?
→ This time, the scale factor is greater than one, so we need to shrink triangle D”E”F” to the size of triangle DEF. Also, it appears as if a translation alone does not map one triangle onto another.
→ Now, since we want to dilate triangle D”E”F” to the size of triangle DEF, we need to know what scale factor r to use. Since triangle D”E”F” is congruent to D’E’F’, then we can use those triangles to determine the scale factor needed. We need a scale factor so that |OF|=r|OF’|. What scale factor do you think we should use, and why?
→ We need a scale factor r=\(\frac{1}{3}\) because we want |OF|=r|OF’|.
→ What precise dilation would make triangle D”E”F” the same size as triangle DEF?
→ A dilation from center O with scale factor r=\(\frac{1}{3}\) would make triangle D”E”F” the same size as triangle DEF.
→ (Show the picture below with the dilated triangle D”E”F” noted by D”’E”’F”’.) Now we should use what we know about rigid motions to map the dilated version of triangle D”E”F” onto triangle DEF. What should we do first?
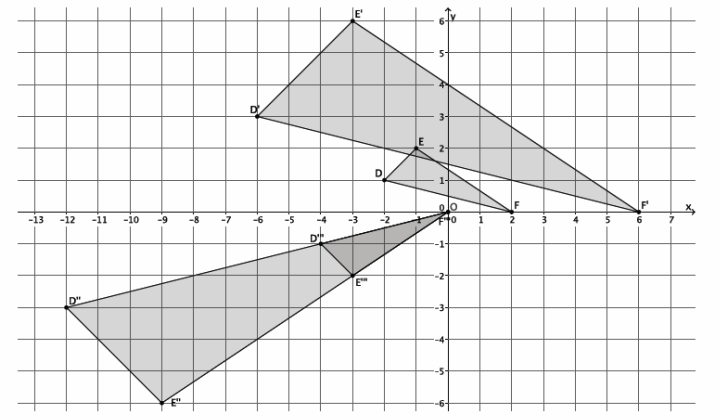
→ We should translate triangle D”’E”’F”’ 2 units to the right.
→ (Show the picture below, the translated triangle noted in red.) What should we do next (refer to the translated triangle as the red triangle)?
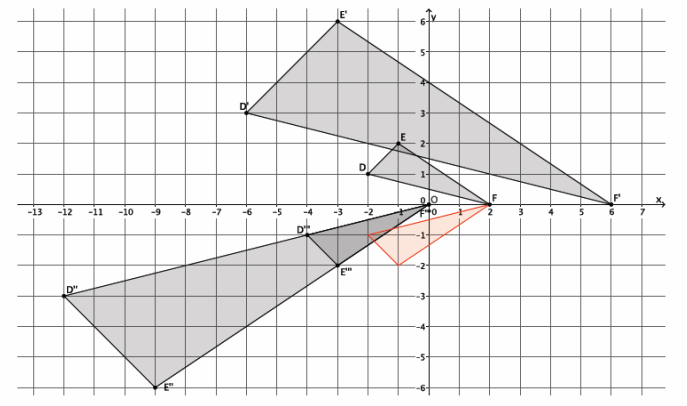
→ Next, we should reflect the red triangle across the x-axis to map the red triangle onto triangle DEF.
→ Use precise language to describe how to map triangle D”E”F” onto triangle DEF.
→ The sequence that would map triangle D”E”F” onto triangle DEF is as follows: Dilate triangle D”E”F” from center O by scale factor r=\(\frac{1}{3}\) . Then, translate the dilated image of triangle D”E”F”, noted by D”’ E”’ F”’, two units to the right. Finally, reflect across the x-axis to map the red triangle onto triangle DEF.
→ Since we were able to map triangle D”E”F” onto triangle DEF with a dilation followed by a congruence, we can write that triangle D”E”F” is similar to triangle DEF. (In notation: △D”E”F”~△DEF)
Example 3.
In the diagram below, △ABC ~△A’B’C’. Describe a sequence of a dilation followed by a congruence that would prove these figures to be similar.
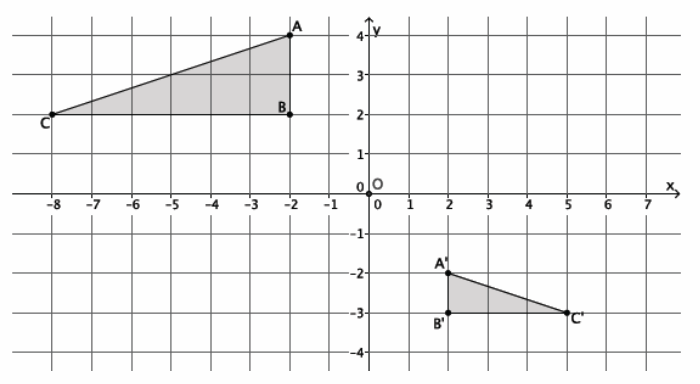
→ Let’s begin with the scale factor. We know that r|AB|=|A’B’|. What scale factor r makes △ABC the same size as △A’B’C’?
→ We know that r⋅2=1; therefore, r=\(\frac{1}{2}\) makes △ABC the same size as △A’ B’ C’.
→ If we apply a dilation from the origin of scale factor r=\(\frac{1}{2}\), then the triangles are the same size (as shown and noted by triangle A”B”C”). What sequence of rigid motions would map the dilated image of △ABC onto △A’B’C’?
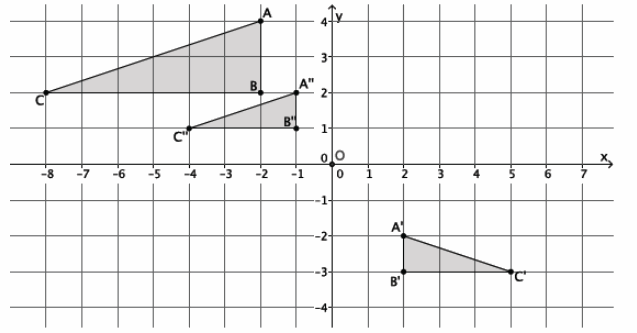
→ We could translate the dilated image of △ABC, △A”B”C”, 3 units to the right and 4 units down and then reflect the triangle across line A’B’.
→ The sequence that would map △ABC onto △A’B’C’ to prove the figures similar is a dilation from the origin by scale factor r=\(\frac{1}{2}\), followed by the translation of the dilated version of △ABC 3 units to the right and 4 units down, followed by the reflection across line A’B’.
Example 4.
In the diagram below, we have two similar figures. Using the notation, we have △ABC ~△DEF. We want to describe a sequence of the dilation followed by a congruence that would prove these figures to be similar.
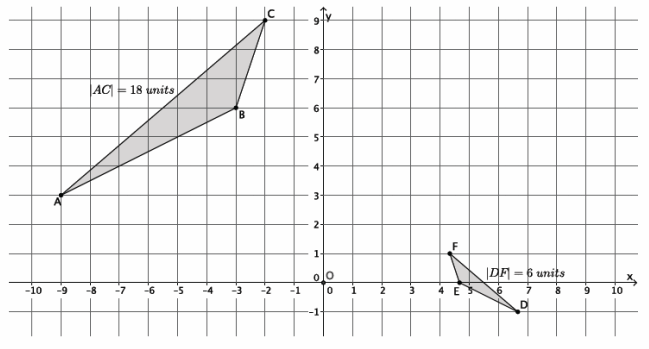
→ First, we need to describe the dilation that would make the triangles the same size. What information do we have to help us describe the dilation?
→ Since we know the length of side \(\overline{A C}\) and side \(\overline{D F}\), we can determine the scale factor.
→ Can we use any two sides to calculate the scale factor? Assume, for instance, that we know that side \(\overline{A C}\) is
18 units in length and side \(\overline{E F}\) is 2 units in length. Could we find the scale factor using those two sides, \(\overline{A C}\) and \(\overline{E F}\)? Why or why not?
→ No, we need more information about corresponding sides. Sides \(\overline{A C}\) and \(\overline{D F}\) are the longest sides of each triangle (they are also opposite the obtuse angle in the triangle). Side \(\overline{A C}\) does not correspond to side \(\overline{E F}\). If we knew the length of side \(\overline{B C}\), we could use sides \(\overline{B C}\) and \(\overline{E F}\).
→ Now that we know that we can find the scale factor if we have information about corresponding sides, how would we calculate the scale factor if we were mapping △ABC onto △DEF?
→ |DF|=r|AC|, so 6=r⋅18, and r=\(\frac{1}{3}\).
→ If we were mapping △DEF onto △ABC, what would the scale factor be?
→ |AC|=r|DF|, so 18=r∙6, and r=3.
→ What is the precise dilation that would map △ABC onto △DEF?
→ Dilate △ABC from center O, by scale factor r=\(\frac{1}{3}\).
→ (Show the picture below with the dilated triangle noted as △A’B’C’.) Now we have to describe the congruence. Work with a partner to determine the sequence of rigid motions that would map △ABC onto △DEF.
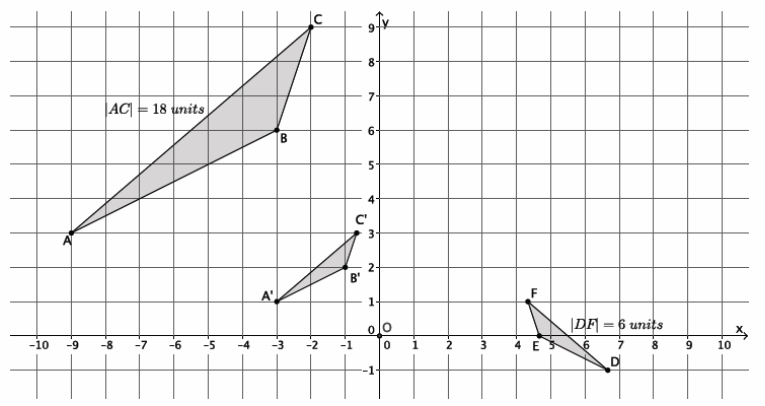
→ Translate the dilated version of △ABC 7 units to the right and 2 units down. Then, rotate d degrees around point E so that segment B’C’ maps onto segment EF. Finally, reflect across line EF.
Note that “d degrees” refers to a rotation by an appropriate number of degrees to exhibit similarity. Students may choose to describe this number of degrees in other ways.
→ The sequence of a dilation followed by a congruence that proves △ABC ~△DEF is as follows: Dilate △ABC from center O by scale factor r=\(\frac{1}{3}\). Translate the dilated version of △ABC 7 units to the right and 2 units down. Next, rotate around point E by d degrees so that segment B’C’ maps onto segment EF, and then reflect the triangle across line EF.
Example 5.
→ Knowing that a sequence of a dilation followed by a congruence defines similarity also helps determine if two figures are in fact similar. For example, would a dilation map triangle ABC onto triangle DEF (i.e., is △ABC ~△DEF)?
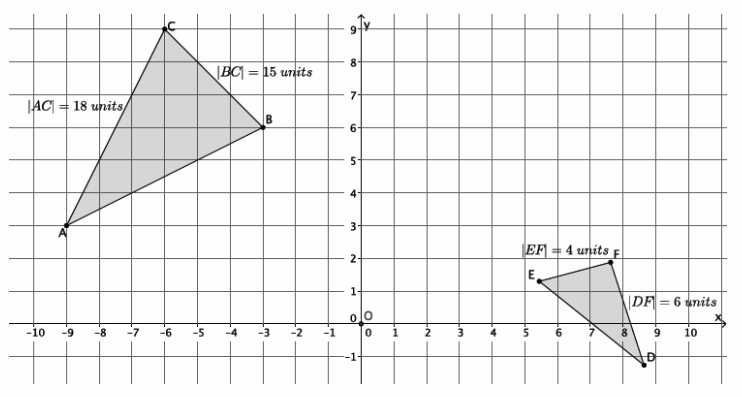
→ No. By FTS, we expect the corresponding side lengths to be in proportion and equal to the scale factor. When we compare side \(\overline{A C}\) to side \(\overline{D F}\) and \(\overline{B C}\) to \(\overline{E F}\), we get \(\frac{18}{6}\)≠\(\frac{15}{4}\).
→ Therefore, the triangles are not similar because a dilation does not map one to the other.
Example 6.
→ Again, knowing that a dilation followed by a congruence defines similarity also helps determine if two figures are in fact similar. For example, would a dilation map Figure A onto Figure A’ (i.e., is Figure A ~ Figure A’)?
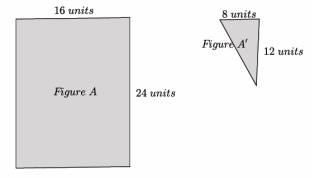
→ No. Even though we could say that the corresponding sides are in proportion, there exists no single rigid motion or sequence of rigid motions that would map a four-sided figure to a three-sided figure. Therefore, the figures do not fulfill the congruence part of the definition for similarity, and Figure A is not similar to Figure A’.
Eureka Math Grade 8 Module 3 Lesson 8 Exercise Answer Key
Exercises
Allow students to work in pairs to describe sequences that map one figure onto another.
Exercise 1.
Triangle ABC was dilated from center O by scale factor r=\(\frac{1}{2}\). The dilated triangle is noted by A’B’C’. Another triangle A”B”C” is congruent to triangle A’B’C’ (i.e., △A”B”C”≅△A’B’C’). Describe a dilation followed by the basic rigid motion that would map triangle A”B”C” onto triangle ABC.
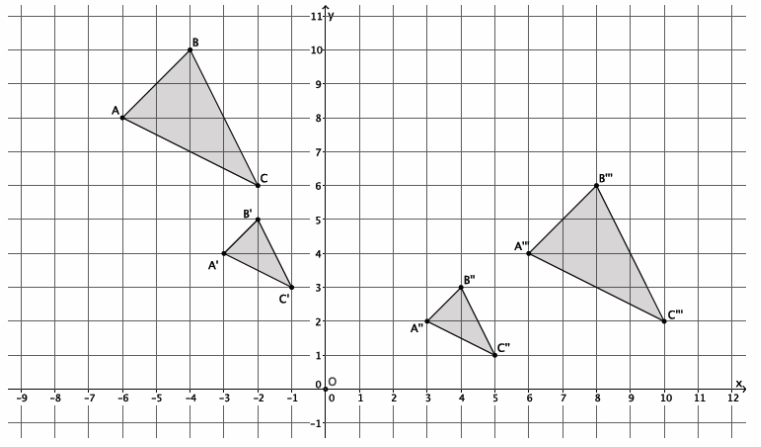
Answer:
Triangle A”B”C” needs to be dilated from center O, by scale factor r=2 to bring it to the same size as triangle ABC. This produces a triangle noted by A”’B”’C”’. Next, triangle A”’B”’C”’ needs to be translated 4 units up and 12 units left. The dilation followed by the translation maps triangle A”B”C” onto triangle ABC.
Exercise 2.
Describe a sequence that would show △ABC ~△A’ B’ C’.
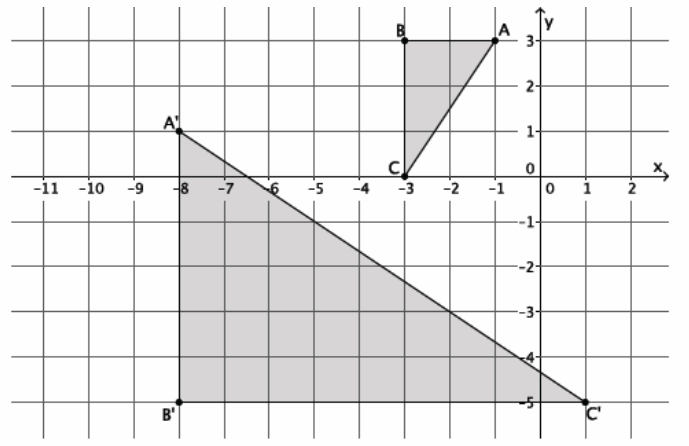
Answer:
Since r|AB|=|A’ B’ |, then r⋅2=6, and r=3. A dilation from the origin by scale factor r=3 makes △ABC the same size as △A’B’C’. Then, a translation of the dilated image of △ABC ten units right and five units down, followed by a rotation of 90 degrees around point C’, maps △ABC onto △A’ B’ C’, proving the triangles to be similar.
Exercise 3.
Are the two triangles shown below similar? If so, describe a sequence that would prove △ABC ~△A’B’C’. If not, state how you know they are not similar.
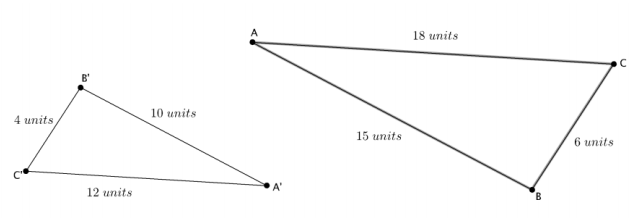
Answer:
Yes, △ABC ~△A’B’C’. The corresponding sides are in proportion and equal to the scale factor:
\(\frac{10}{15}\)=\(\frac{4}{6}\)=\(\frac{12}{18}\)=\(\frac{2}{3}\)=r
To map triangle ABC onto triangle A’B’C’, dilate triangle ABC from center O, by scale factor r=\(\frac{2}{3}\). Then, translate triangle ABC along vector \(\overrightarrow{A A^{\prime}}\). Next, rotate triangle ABC d degrees around point A.
Exercise 4.
Are the two triangles shown below similar? If so, describe the sequence that would prove △ABC ~△A’B’C’. If not, state how you know they are not similar.
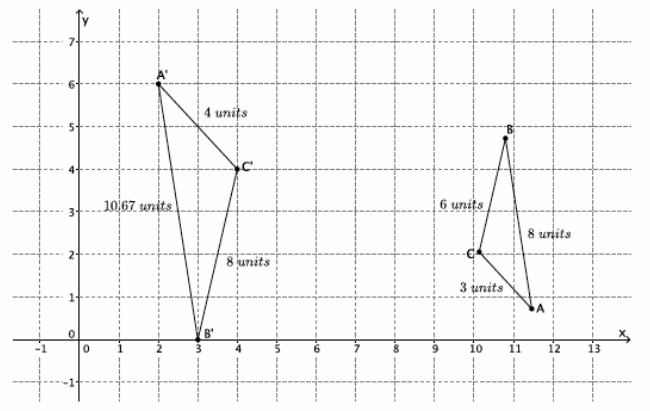
Answer:
Yes, triangle △ABC ~△A’B’C’. The corresponding sides are in proportion and equal to the scale factor:
\(\frac{4}{3}\)=\(\frac{8}{6}\)=\(\frac{4}{3}\)=\(1.3 \overline{3}\); \(\frac{10.67}{8}\)=1.33375; therefore, r=1.33 which is approximately equal to \(\frac{4}{3}\)
To map triangle ABC onto triangle A’B’C’, dilate triangle ABC from center O, by scale factor r=\(\frac{4}{3}\). Then, translate triangle ABC along vector \(\overrightarrow{A A^{\prime}}\). Next, rotate triangle ABC 180 degrees around point A’.
Eureka Math Grade 8 Module 3 Lesson 8 Problem Set Answer Key
Students practice dilating a curved figure and describing a sequence of a dilation followed by a congruence that maps one figure onto another.
Question 1.
In the picture below, we have triangle DEF that has been dilated from center O by scale factor r=4. It is noted by D’E’F’. We also have triangle D”E”F”, which is congruent to triangle D’E’F’ (i.e., △D’E’F’≅△D”E”F”). Describe the sequence of a dilation, followed by a congruence (of one or more rigid motions), that would map triangle D”E”F” onto triangle DEF.
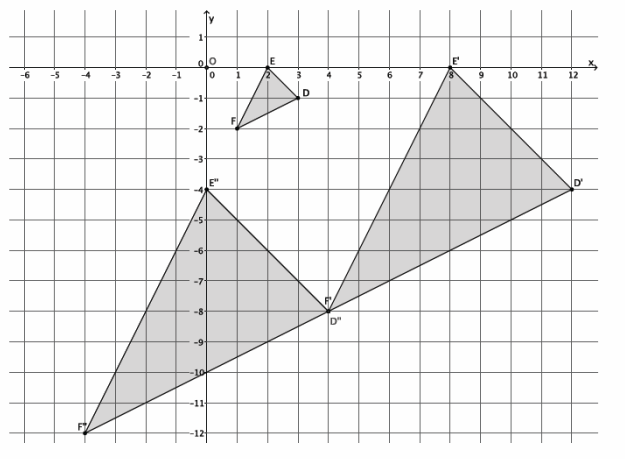
Answer:
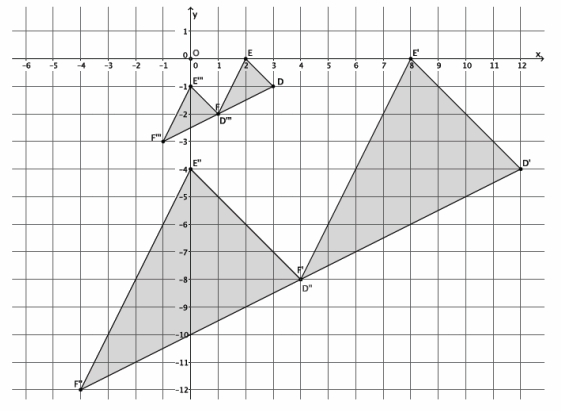
First, we must dilate triangle D”E”F” by scale factor r=\(\frac{1}{4}\) to shrink it to the size of triangle DEF. Next, we must translate the dilated triangle, noted by D”’E”’F”’, one unit up and two units to the right. This sequence of the dilation followed by the translation would map triangle D”E”F” onto triangle DEF.
Question 2.
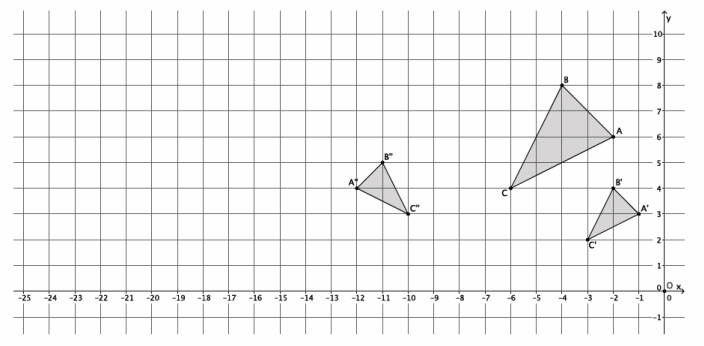
Triangle ABC was dilated from center O by scale factor r=\(\frac{1}{2}\). The dilated triangle is noted by A’B’C’. Another triangle A”B”C” is congruent to triangle A’B’C’ (i.e., △A”B”C”≅△A’B’C’). Describe the dilation followed by the basic rigid motions that would map triangle A”B”C” onto triangle ABC.
Answer:
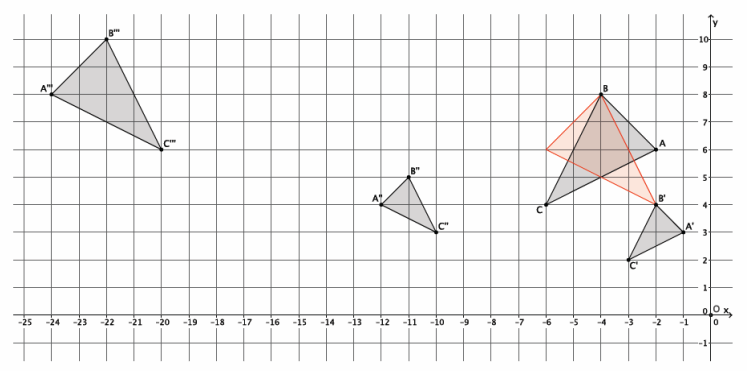
Triangle A”B”C” needs to be dilated from center O by scale factor r=2 to bring it to the same size as triangle ABC. This produces a triangle noted by A”’B”’C”’. Next, triangle A”’B”’C”’ needs to be translated 18 units to the right and two units down, producing the triangle shown in red. Next, rotate the red triangle d degrees around point B so that one of the segments of the red triangle coincides completely with segment BC. Then, reflect the red triangle across line BC. The dilation, followed by the congruence described, maps triangle A”B”C” onto triangle ABC.
Question 3.
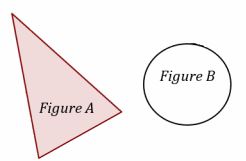
Are the two figures shown below similar? If so, describe a sequence that would prove the similarity. If not, state how you know they are not similar.
Answer:
No, these figures are not similar. There is no single rigid motion, or sequence of rigid motions, that would map Figure A onto Figure B.
Question 4.
Triangle ABC is similar to triangle A’B’C’ (i.e., △ABC ~△A’B’C’). Prove the similarity by describing a sequence that would map triangle A’B’C’ onto triangle ABC.
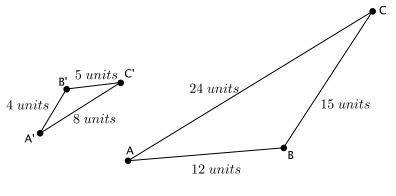
Answer:
The scale factor that would magnify triangle A’B’C’ to the size of triangle ABC is r=3. The sequence that would prove the similarity of the triangles is a dilation from center O by a scale factor of r=3, followed by a translation along vector \(\overrightarrow{A^{\prime} A}\), and finally, a reflection across line AC.
Question 5.
Are the two figures shown below similar? If so, describe a sequence that would prove △ABC ~△A’B’C’. If not, state how you know they are not similar.
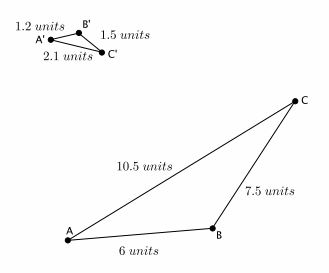
Answer:
Yes, the triangles are similar. The scale factor that triangle ABC has been dilated is r=\(\frac{1}{5}\). The sequence that proves the triangles are similar is as follows: dilate triangle A’B’C’ from center O by scale factor r=5; then, translate triangle A’B’C’ along vector \(\overrightarrow{C^{\prime} C}\); next, rotate triangle A’B’C’ d degrees around point C; and finally, reflect triangle A’B’C’ across line AC.
Question 6.
Describe a sequence that would show △ABC ~△A’ B’ C’.
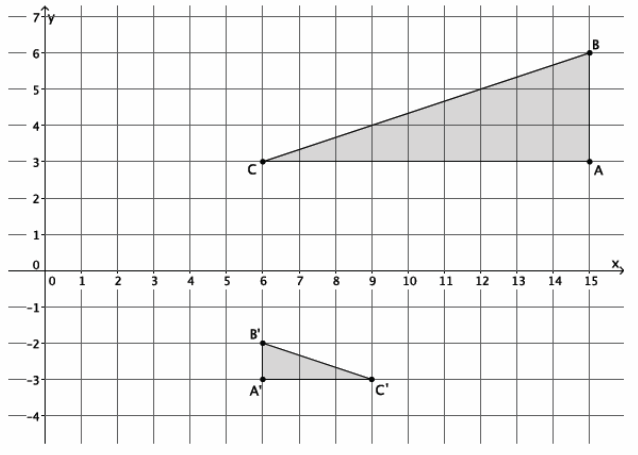
Answer:
Since r|AB|=|A’ B’|, then r∙3=1 and r = \(\frac{1}{3}\). A dilation from the origin by scale factor r\(\frac{1}{3}\) makes △ABC the same size as △A’B’C’. Then, a translation of the dilated image of △ABC four units down and one unit to the right, followed by a reflection across line A’ B’, maps △ABC onto △A’ B’ C’, proving the triangles to be similar.
Eureka Math Grade 8 Module 3 Lesson 8 Exit Ticket Answer Key
In the picture below, we have triangle DEF that has been dilated from center O by scale factor r=\(\frac{1}{2}\). The dilated triangle is noted by D’E’F’. We also have a triangle D”EF, which is congruent to triangle DEF (i.e., △DEF≅△D”EF). Describe the sequence of a dilation, followed by a congruence (of one or more rigid motions), that would map triangle D’E’F’ onto triangle D”EF.
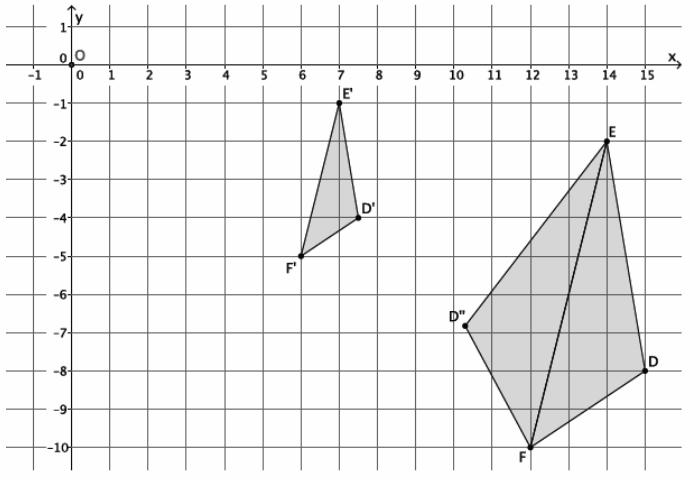
Answer:
Triangle D’E’F’ needs to be dilated from center O by scale factor r=2 to bring it to the same size as triangle DEF. This produces the triangle noted by DEF. Next, triangle DEF needs to be reflected across line EF. The dilation followed by the reflection maps triangle D’E’F’ onto triangle D”EF.