Engage NY Eureka Math 8th Grade Module 4 Lesson 15 Answer Key
Eureka Math Grade 8 Module 4 Lesson 15 Opening Exercise Answer Key
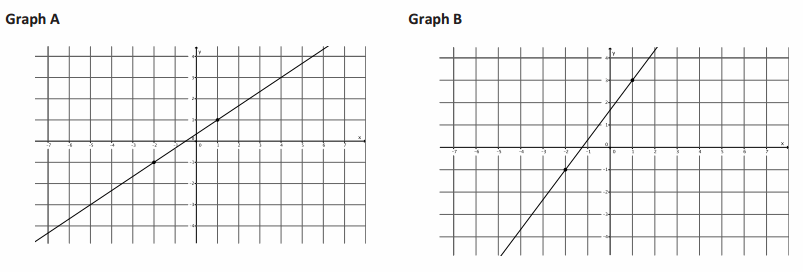
a. Which graph is steeper?
Answer:
It looks like Graph B is steeper.
b. Write directions that explain how to move from one point on the graph to the other for both Graph A and Graph B.
Answer:
For Graph A, move 2 units up and 3 units right. For Graph B, move 4 units up and 3 units right.
c. Write the directions from part (b) as ratios, and then compare the ratios. How does this relate to which graph was steeper in part (a)?
Answer:
\(\frac{2}{3}\)<\(\frac{4}{3}\).
Pair 1:
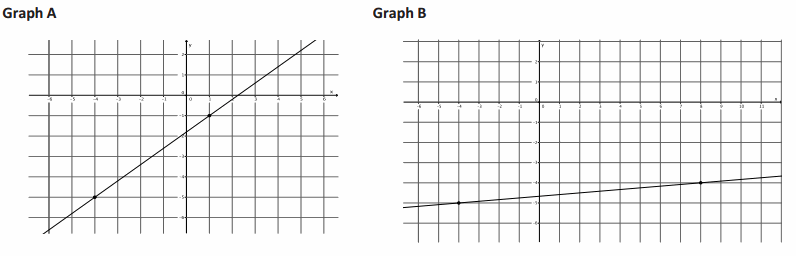
a. Which graph is steeper?
Answer:
It looks like Graph A is steeper.
b. Write directions that explain how to move from one point on the graph to the other for both Graph A and Graph B.
Answer:
For Graph A, move 4 units up and 5 units right. For Graph B, move 1 unit up and 12 units right.
c. Write the directions from part (b) as ratios, and then compare the ratios. How does this relate to which graph was steeper in part (a)?
Answer:
\(\frac{4}{5}\)>\(\frac{1}{12}\). Graph A was steeper and had the greater ratio.
Pair 2:
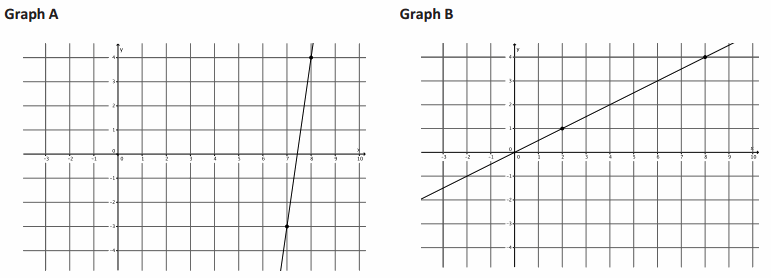
a. Which graph is steeper?
Answer:
It looks like Graph A is steeper.
b. Write directions that explain how to move from one point on the graph to the other for both Graph A and Graph B.
Answer:
For Graph A, move 7 units up and 1 unit right. For Graph B, move 3 units up and 6 units right.
c. Write the directions from part (b) as ratios, and then compare the ratios. How does this relate to which graph was steeper in part (a)?
Answer:
\(\frac{7}{1}\)>\(\frac{3}{6}\). Graph A was steeper and had the greater ratio.
Pair 3:
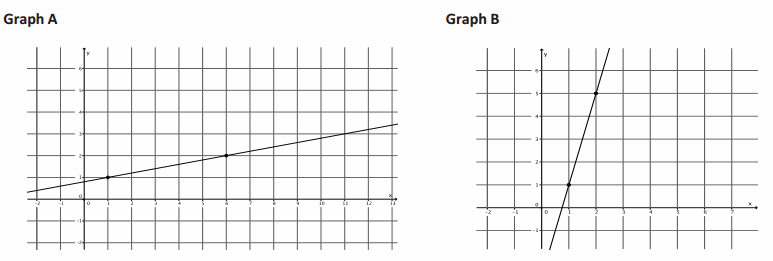
a. Which graph is steeper?
Answer:
It looks like Graph B is steeper.
b. Write directions that explain how to move from one point on the graph to the other for both Graph A and Graph B.
Answer:
For Graph A, move 1 unit up and 5 units right. For Graph B, move 4 units up and 1 unit right.
c. Write the directions from part (b) as ratios, and then compare the ratios. How does this relate to which graph was steeper in part (a)?
\(\frac{1}{5}\)<\(\frac{4}{1}\). Graph B was steeper and had the greater ratio.
Pair 4:
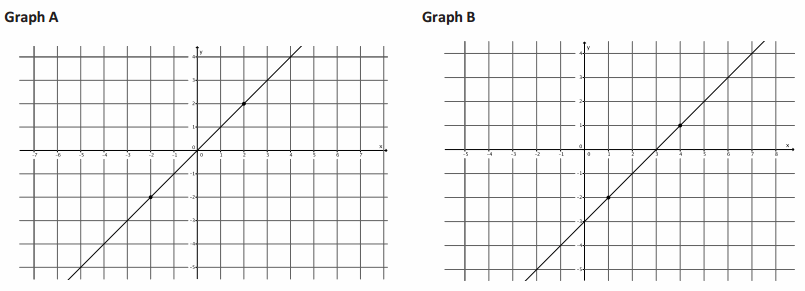
a. Which graph is steeper?
Answer:
They look about the same steepness.
b. Write directions that explain how to move from one point on the graph to the other for both Graph A and Graph B.
Answer:
For Graph A, move 4 units up and 4 units right. For Graph B, move 3 units up and 3 units right.
c. Write the directions from part (b) as ratios, and then compare the ratios. How does this relate to which graph was steeper in part (a)?
Answer:
\(\frac{4}{4}\)=\(\frac{3}{3}\). The graphs have equal ratios, which may explain why they look like the same steepness.
Eureka Math Grade 8 Module 4 Lesson 15 Exercise Answer Key
Use your transparency to find the slope of each line if needed.
Exercise 1.
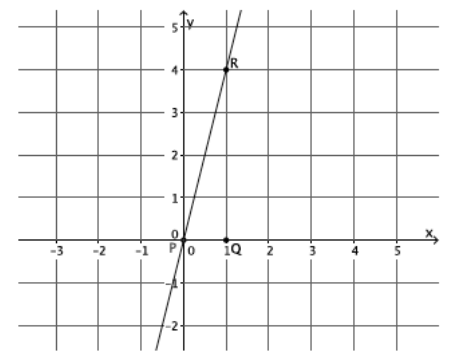
What is the slope of this non-vertical line?
Answer:
The slope of this line is 4, m=4.
Exercise 2.
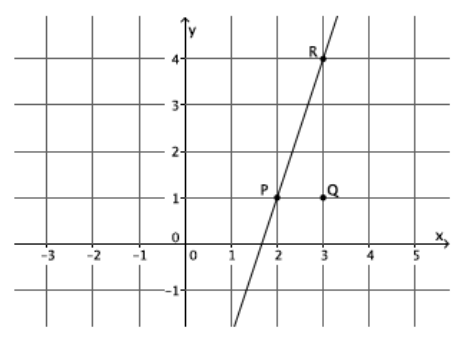
What is the slope of this non-vertical line?
Answer:
The slope of this line is 3, m=3.
Exercise 3.
Which of the lines in Exercises 1 and 2 is steeper? Compare the slopes of each of the lines. Is there a relationship between steepness and slope?
Answer:
The graph in Exercise 1 seems steeper. The slopes are 4 and 3. It seems like the greater the slope, the steeper the line.
Exercise 4.
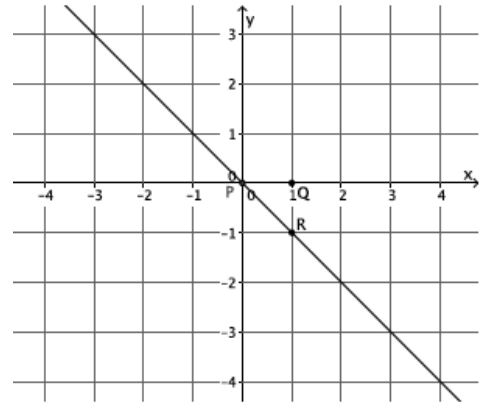
What is the slope of this non-vertical line?
Answer:
The slope of this line is -1, m=-1.
Exercise 5.
What is the slope of this non-vertical line?
Answer:
The slope of this line is -4, m=-4.
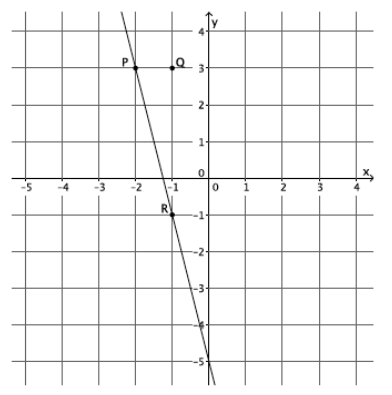
Exercise 6.
What is the slope of this non-vertical line?
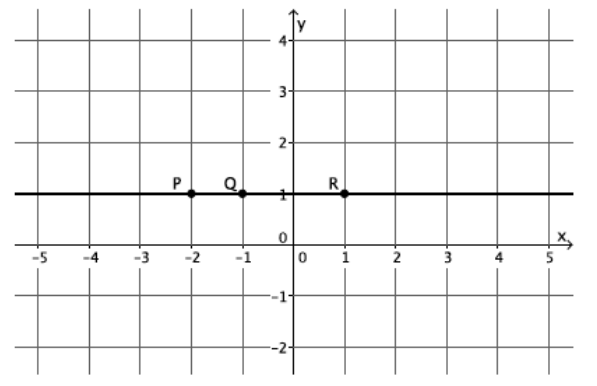
Answer:
The slope of this line is 0, m=0.
Eureka Math Grade 8 Module 4 Lesson 15 Problem Set Answer Key
Students practice identifying lines as having positive or negative slope. Students interpret the unit rate of a graph as the slope of the graph.
Question 1.
Does the graph of the line shown below have a positive or negative slope? Explain.
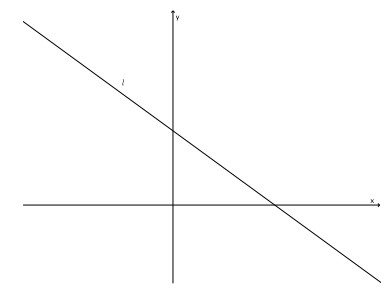
Answer:
The graph of this line has a negative slope. First of all, it is left-to-right declining, which is an indication of negative slope. Also, if we were to mark a point P and a point Q one unit to the right of P and then draw a line parallel to the y-axis through Q, then the intersection of the two lines would be below Q, making the number that represents slope negative.
Question 2.
Does the graph of the line shown below have a positive or negative slope? Explain.
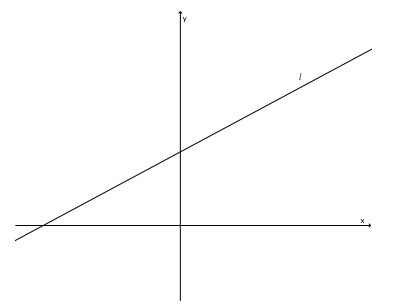
Answer;
The graph of this line has a positive slope. First of all, it is left-to-right inclining, which is an indication of positive slope. Also, if we were to mark a point P and a point Q one unit to the right of P and then draw a line parallel to the y-axis through Q, then the intersection of the two lines would be above Q, making the number that represents slope positive.
Question 3.
What is the slope of this non-vertical line? Use your transparency if needed.
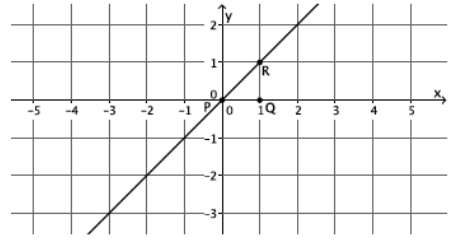
Answer:
The slope of this line is 1, m=1.
Question 4.
What is the slope of this non-vertical line? Use your transparency if needed.
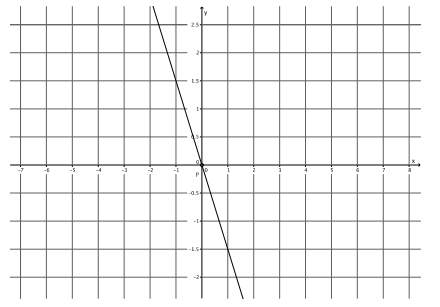
Answer:
The slope of this line is –\(\frac{3}{2}\), m=-\(\frac{3}{2}\).
Question 5.
What is the slope of this non-vertical line? Use your transparency if needed.
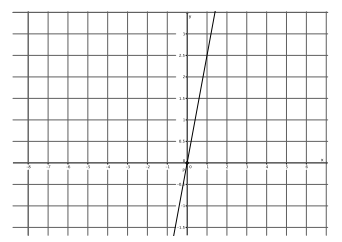
Answer:
The slope of this line is \(\frac{5}{2}\), m=\(\frac{5}{2}\).
Question 6.
What is the slope of this non-vertical line? Use your transparency if needed.
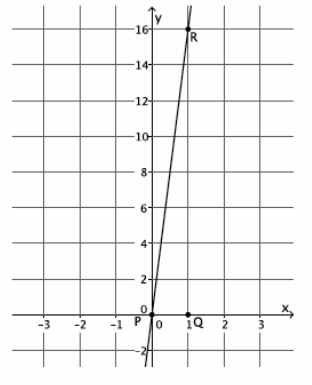
Answer:
The slope of this line is 16, m=16.
Question 7.
What is the slope of this non-vertical line? Use your transparency if needed.
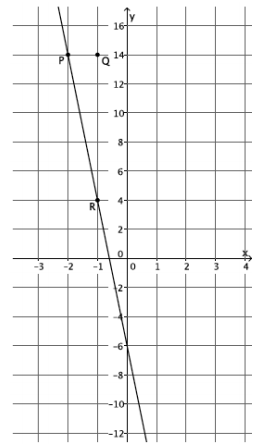
Answer:
The slope of this line is -10, m=-10.
Question 8.
What is the slope of this non-vertical line? Use your transparency if needed.
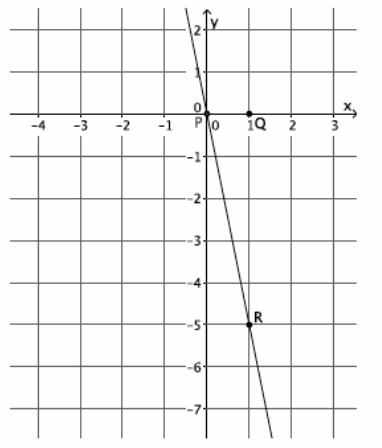
Answer:
The slope of this line is -5, m=-5.
Question 9.
What is the slope of this non-vertical line? Use your transparency if needed.
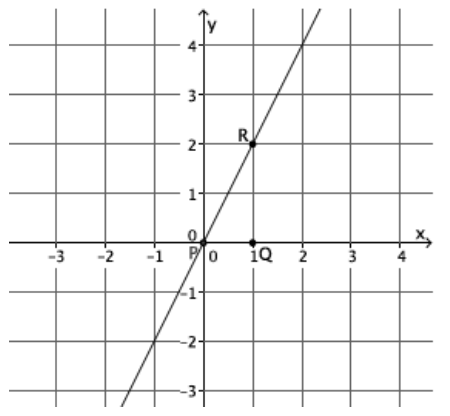
Answer:
The slope of this line is 2, m=2.
Question 10.
What is the slope of this non-vertical line? Use your transparency if needed.
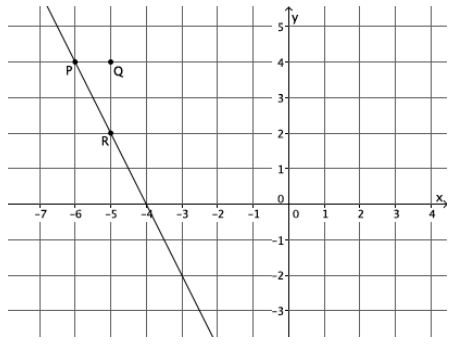
Answer:
The slope of this line is -2, m=-2.
Question 11.
What is the slope of this non-vertical line? Use your transparency if needed.
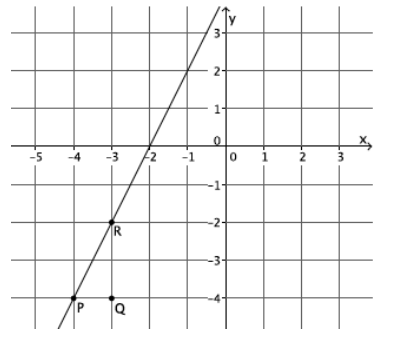
Answer:
The slope of this line is 2, m=2.
Question 12.
What is the slope of this non-vertical line? Use your transparency if needed.
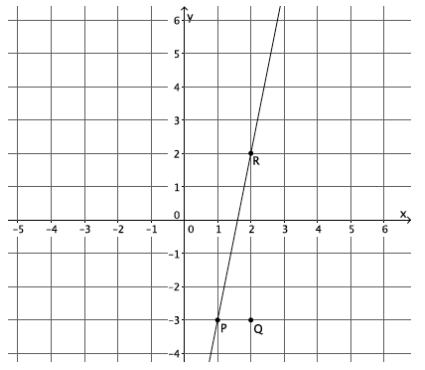
Answer:
The slope of this line is 5, m=5.
Question 13.
What is the slope of this non-vertical line? Use your transparency if needed.
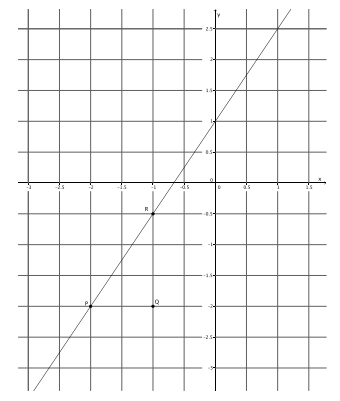
Answer:
The slope of this line is \(\frac{3}{2}\), m=\(\frac{3}{2}\).
Question 14
What is the slope of this non-vertical line? Use your transparency if needed.
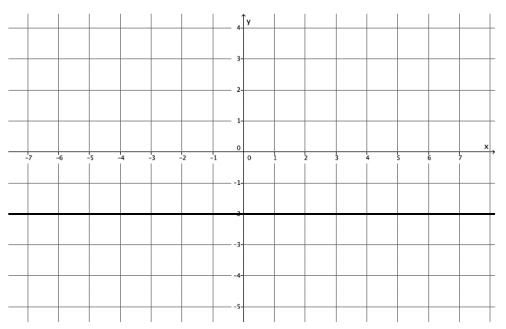
Answer:
The slope of this line is 0, m=0.
In Lesson 11, you did the work below involving constant rate problems. Use the table and the graphs provided to answer the questions that follow.
Question 15.
Suppose the volume of water that comes out in three minutes is 10.5 gallons.
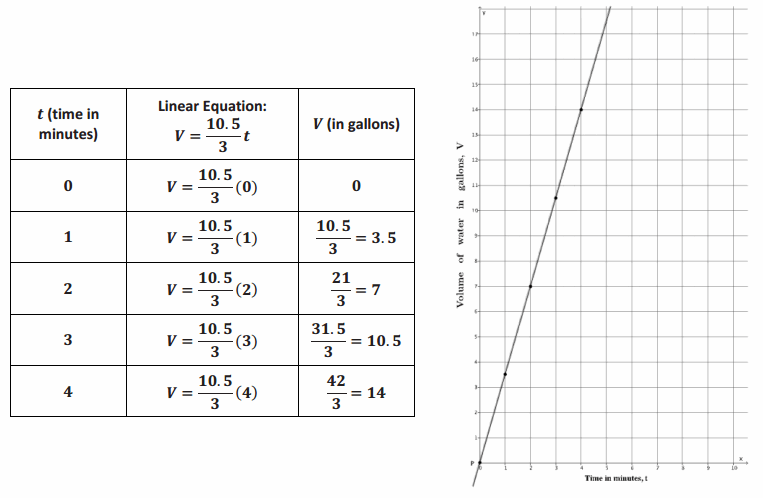
a. How many gallons of water flow out of the faucet per minute? In other words, what is the unit rate of water flow?
Answer:
The unit rate of water flow is 3.5 gallons per minute.
b. Assume that the graph of the situation is a line, as shown in the graph. What is the slope of the line?
Answer:
The slope of the line is 3.5, m=3.5.
Question 16.
Emily paints at a constant rate. She can paint 32 square feet in five minutes.
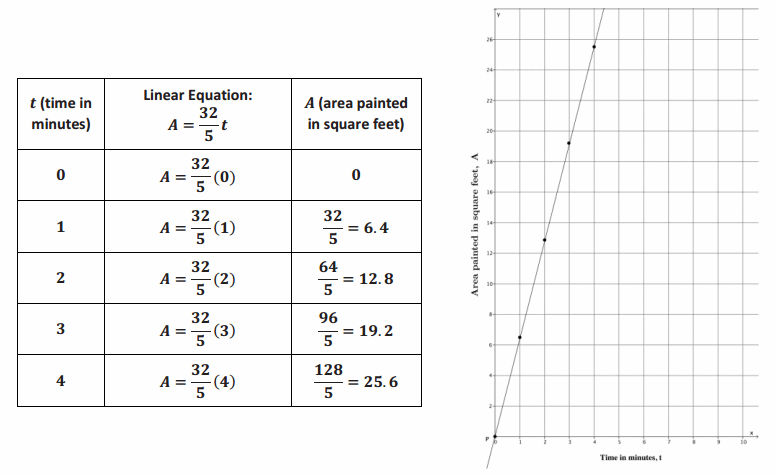
a. How many square feet can Emily paint in one minute? In other words, what is her unit rate of painting?
Answer:
The unit rate at which Emily paints is 6.4 square feet per minute.
b. Assume that the graph of the situation is a line, as shown in the graph. What is the slope of the line?
Answer:
The slope of the line is 6.4, m=6.4.
Question 17.
A copy machine makes copies at a constant rate. The machine can make 80 copies in 2 1/2 minutes.
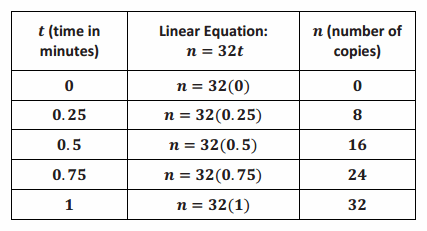
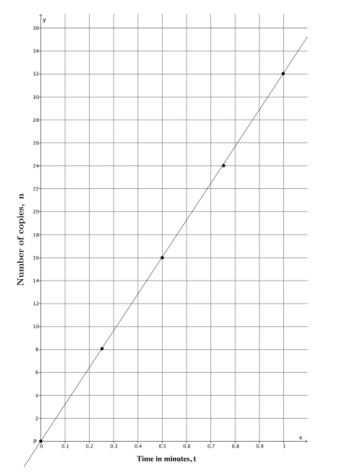
a. How many copies can the machine make each minute? In other words, what is the unit rate of the copy machine?
Answer:
The unit rate of the copy machine is 32 copies per minute.
b. Assume that the graph of the situation is a line, as shown in the graph. What is the slope of the line?
Answer:
The slope of the line is 32, m=32.
Eureka Math Grade 8 Module 4 Lesson 15 Exit Ticket Answer Key
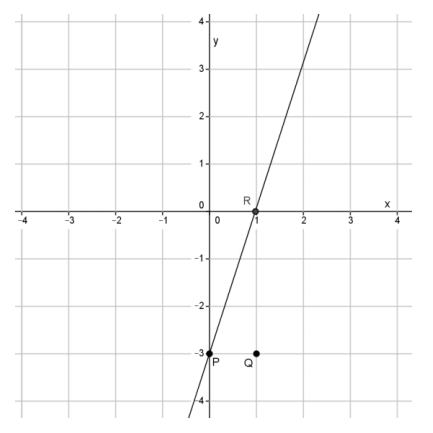
Question 1.
What is the slope of this non-vertical line? Use your transparency if needed.
Answer:
The slope of the line is 3, m=3.
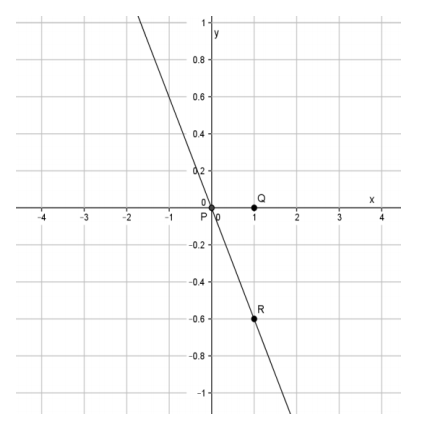
Question 2.
What is the slope of this non-vertical line? Use your transparency if needed.
Answer:
The slope of the line is -0.6, which is equal to –\(\frac{3}{5}\), m=-\(\frac{3}{5}\).