Engage NY Eureka Math 8th Grade Module 4 Lesson 28 Answer Key
Eureka Math Grade 8 Module 4 Lesson 28 Example Answer Key
Example 1.
Use what you noticed about adding equivalent expressions to solve the following system by elimination:
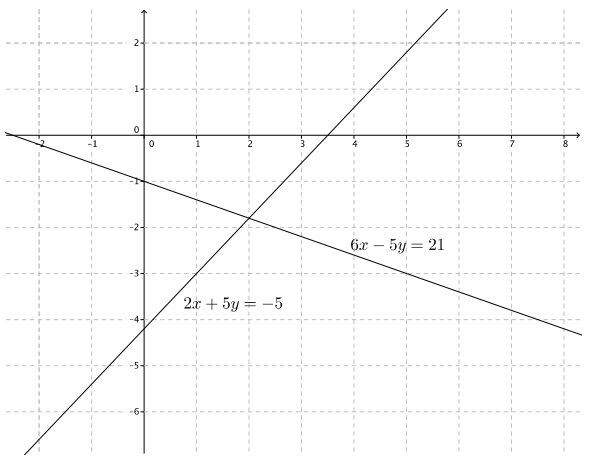
6x – 5y = 21
2x + 5y = – 5
Answer:
Show students the three examples of adding integer equations together. Ask students to verbalize what they notice in the examples and to generalize what they observe. The goal is for students to see that they can add equivalent expressions and still have an equivalence.
Example 1: If 2 + 5 = 7 and 1 + 9 = 10, does 2 + 5 + 1 + 9 = 7 + 10?
Example 2: If 1 + 5 = 6 and 7 – 2 = 5, does 1 + 5 + 7 – 2 = 6 + 5?
Example 3: If – 3 + 11 = 8 and 2 + 1 = 3, does – 3 + 11 + 2 + 1 = 8 + 3?
Use what you noticed about adding equivalent expressions to solve the following system by elimination:
6x – 5y = 21
2x + 5y = – 5
Provide students with time to attempt to solve the system by adding the equations together. Have students share their work with the class. If necessary, use the points belows to support students.
Notice that terms – 5y and 5y are opposites; that is, they have a sum of zero when added. If we were to add the equations in the system, the y would be eliminated.
6x – 5y + 2x + 5y = 21 + ( – 5)
6x + 2x – 5y + 5y = 16
8x = 16
x = 2
Just as before, now that we know what x is, we can substitute it into either equation to determine the value of y.
2(2) + 5y = – 5
4 + 5y = – 5
5y = – 9
y = – \(\frac{9}{5}\)
The solution to the system is (2, – \(\frac{9}{5}\)).
We can verify our solution by sketching the graphs of the system.
Example 2.
Solve the following system by elimination:
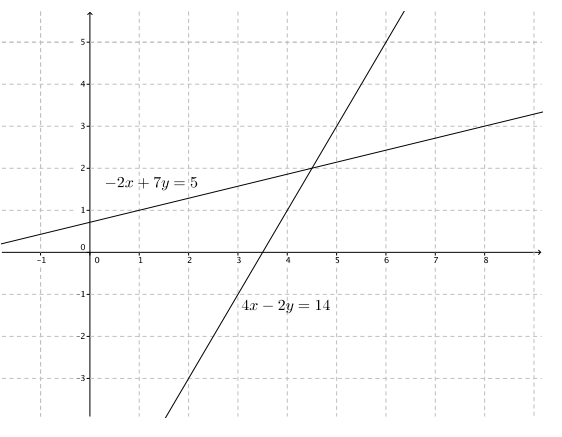
– 2x + 7y = 5
4x – 2y = 14
Answer:
We will solve the following system by elimination:
– 2x + 7y = 5
4x – 2y = 14
In this example, it is not as obvious which variable to eliminate. It will become obvious as soon as we multiply the first equation by 2.
2( – 2x + 7y = 5)
– 4x + 14y = 10
Now we have the system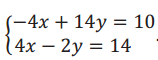 
. It is clear that when we add – 4x + 4x, the x will be eliminated. Add the equations of this system together, and determine the solution to the system.
Sample student work:
– 4x + 14y + 4x – 2y = 10 + 14
14y – 2y = 24
12y = 24
y = 2
4x – 2(2) = 14
4x – 4 = 14
4x = 18
x = \(\frac{18}{4}\)
x = \(\frac{9}{2}\)
The solution to the system is (\(\frac{9}{2}\), 2).
We can verify our solution by sketching the graphs of the system.
Example 3.
Solve the following system by elimination:
7x – 5y = – 2
3x – 3y = 7
Answer:
We will solve the following system by elimination:
7x – 5y = – 2
3x – 3y = 7
Provide time for students to solve this system on their own before discussing it as a class.
In this case, it is even less obvious which variable to eliminate. On these occasions, we need to rewrite both equations. We multiply the first equation by – 3 and the second equation by 7.
– 3(7x – 5y = – 2)
– 21x + 15y = 6
7(3x – 3y = 7)
21x – 21y = 49
Now we have the system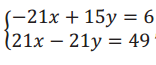 
, and it is obvious that the x can be eliminated.
Look at the system again.
7x – 5y = – 2
3x – 3y = 7
What would we do if we wanted to eliminate the y from the system?
We could multiply the first equation by 3 and the second equation by – 5.
Students may say to multiply the first equation by – 3 and the second equation by 5. Whichever answer is given first, ask if the second is also a possibility. Students should answer yes. Then have students solve the system.
Sample student work:
– 21x + 15y = 6
21x – 21y = 49
15y – 21y = 6 + 49
– 6y = 55
y = – \(\frac{55}{6}\)
7x – 5( – \(\frac{55}{6}\)) = – 2
7x + \(\frac{275}{6}\) = – 2
7x = – \(\frac{287}{6}\)
x = – \(\frac{287}{42}\)
The solution to the system is ( – \(\frac{287}{42}\), – \(\frac{55}{6}\)).
Eureka Math Grade 8 Module 4 Lesson 28 Exercise Answer Key
Exercises
Each of the following systems has a solution. Determine the solution to the system by eliminating one of the variables. Verify the solution using the graph of the system.
Exercise 1.
6x – 7y = – 10
3x + 7y = – 8
Answer:
6x – 7y + 3x + 7y = – 10 + ( – 8)
9x = – 18
x = – 2
3( – 2) + 7y = – 8
– 6 + 7y = – 8
7y = – 2
y = – \(\frac{2}{7}\)
The solution is ( – 2, – \(\frac{2}{7}\)).
Exercise 2.
x – 4y = 7
5x + 9y = 6
Answer:
– 5(x – 4y = 7)
– 5x + 20y = – 35
– 5x + 20y = – 35
5x + 9y = 6
– 5x + 20y + 5x + 9y = – 35 + 6
29y = – 29
y = – 1
x – 4( – 1) = 7
x + 4 = 7
x = 3
The solution is (3, – 1).
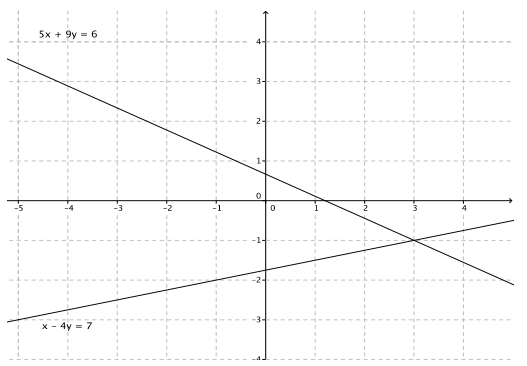
Exercise 3.
2x – 3y = – 5
3x + 5y = 1
Answer:
– 3(2x – 3y = – 5)
– 6x + 9y = 15
2(3x + 5y = 1)
6x + 10y = 2
– 6x + 9y = 15
6x + 10y = 2
– 6x + 9y + 6x + 10y = 15 + 2
19y = 17
y = \(\frac{17}{19}\)
2x – 3(\(\frac{17}{19}\)) = – 5
2x – \(\frac{51}{19}\) = – 5
2x = – 5 + \(\frac{51}{19}\)
2x = – \(\frac{44}{19}\)
x = – \(\frac{44}{38}\)
x = – \(\frac{22}{19}\)
The solution is ( – \(\frac{22}{19}\), \(\frac{17}{19}\)).
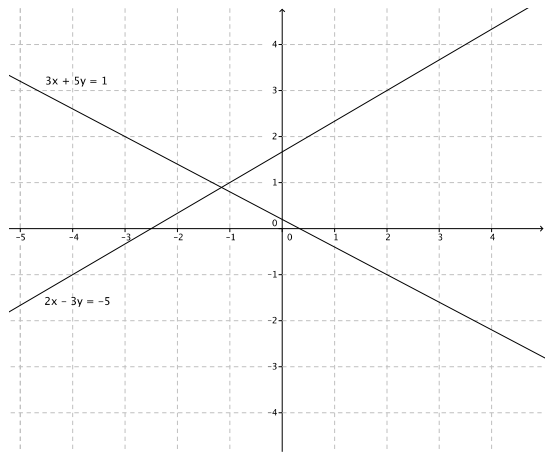
Eureka Math Grade 8 Module 4 Lesson 28 Problem Set Answer Key
Determine the solution, if it exists, for each system of linear equations. Verify your solution on the coordinate plane.
Question 1.
\(\frac{1}{2}\) x + 5 = y
2x + y = 1
Answer:
2x + \(\frac{1}{2}\) x + 5 = 1
\(\frac{5}{2}\) x + 5 = 1
\(\frac{5}{2}\) x = – 4
x = – \(\frac{8}{5}\)
2( – \(\frac{8}{5}\)) + y = 1
– \(\frac{16}{5}\) + y = 1
y = \(\frac{21}{5}\)
The solution is ( – \(\frac{8}{5}\), \(\frac{21}{5}\)).
Question 2.
9x + 2y = 9
– 3x + y = 2
Answer:
3( – 3x + y = 2)
– 9x + 3y = 6
9x + 2y = 9
– 9x + 3y = 6
9x + 2y – 9x + 3y = 15
5y = 15
y = 3
– 3x + 3 = 2
– 3x = – 1
x = \(\frac{1}{3}\)
The solution is (\(\frac{1}{3}\), 3).
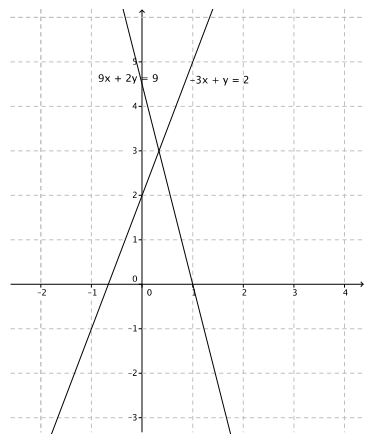
Question 3.
y = 2x – 2
2y = 4x – 4
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.
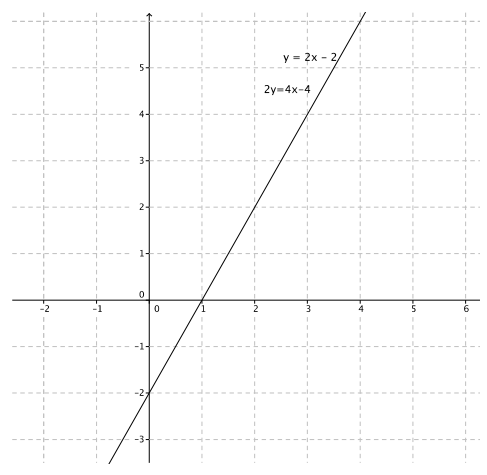
Question 4.
8x + 5y = 19
– 8x + y = – 1
Answer:
8x + 5y – 8x + y = 19 – 1
5y + y = 18
6y = 18
y = 3
8x + 5(3) = 19
8x + 15 = 19
8x = 4
x = \(\frac{1}{2}\)
The solution is (\(\frac{1}{2}\), 3)
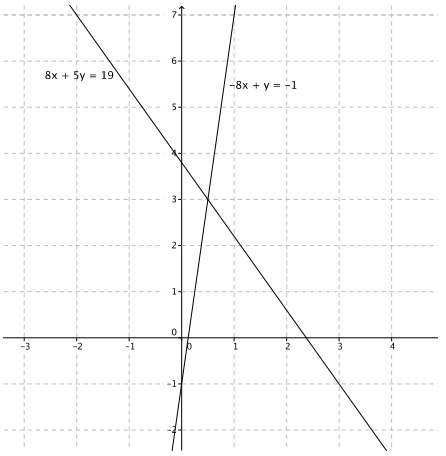
Question 5.
x + 3 = y
3x + 4y = 7
Answer:
3x + 4(x + 3) = 7
3x + 4x + 12 = 7
7x + 12 = 7
7x = – 5
x = – \(\frac{5}{7}\)
– \(\frac{5}{7}\) + 3 = y
\(\frac{16}{7}\) = y
The solution is ( – \(\frac{5}{7}\), \(\frac{16}{7}\)).
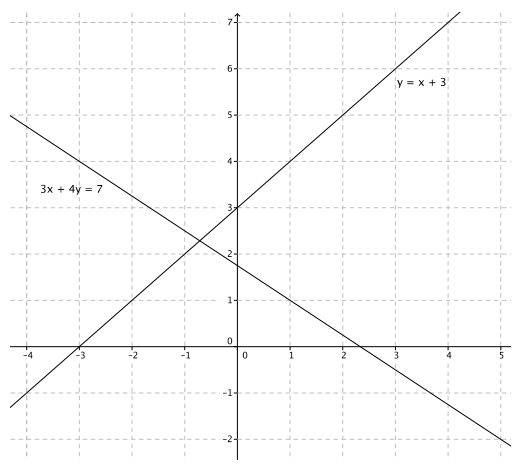
Question 6.
y = 3x + 2
4y = 12 + 12x
Answer:
The equations graph as distinct lines. The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.
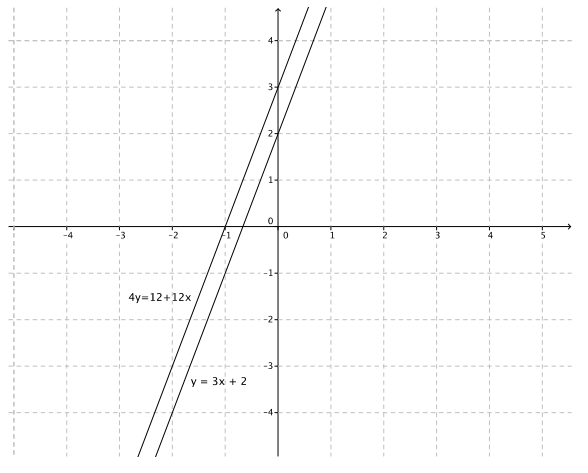
Question 7.
4x – 3y = 16
– 2x + 4y = – 2
Answer:
2( – 2x + 4y = – 2)
– 4x + 8y = – 4
4x – 3y = 16
– 4x + 8y = – 4
4x – 3y – 4x + 8y = 16 – 4
– 3y + 8y = 12
5y = 12
y = \(\frac{12}{5}\)
4x – 3(\(\frac{12}{5}\)) = 16
4x – \(\frac{36}{5}\) = 16
4x = \(\frac{116}{5}\)
x = \(\frac{29}{5}\)
The solution is (\(\frac{29}{5}\), \(\frac{12}{5}\)).
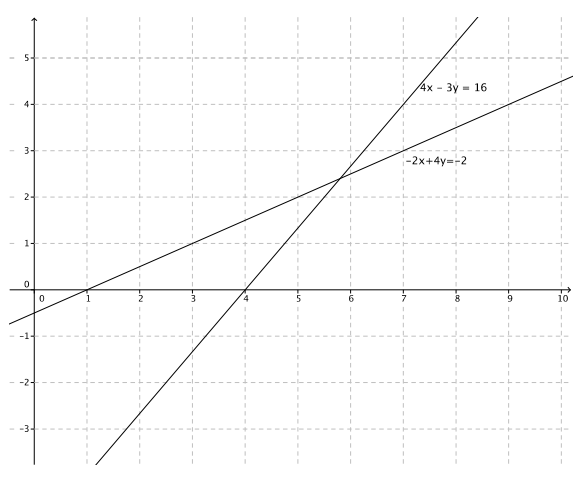
Question 8.
2x + 2y = 4
12 – 3x = 3y
Answer:
The equations graph as distinct lines. The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.
Question 9.
y = – 2x + 6
3y = x – 3
Answer:
3(y = – 2x + 6)
3y = – 6x + 18
3y = – 6x + 18
3y = x – 3
– 6x + 18 = x – 3
18 = 7x – 3
21 = 7x
\(\frac{21}{7}\) = x
x = 3
y = – 2(3) + 6
y = – 6 + 6
y = 0
The solution is (3, 0).
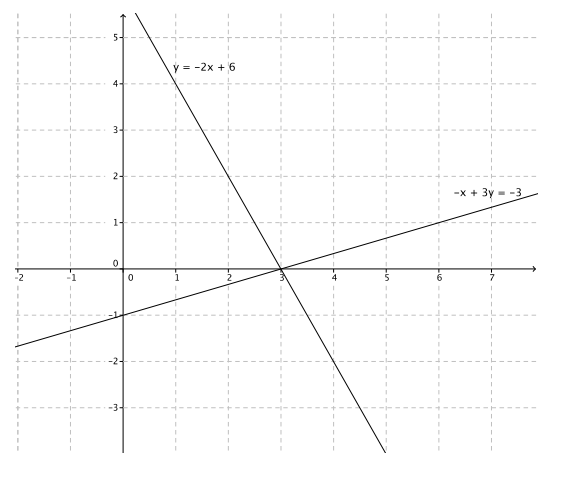
Question 10.
y = 5x – 1
10x = 2y + 2
Answer:
These equations define the same line. Therefore, this system will have infinitely many solutions.
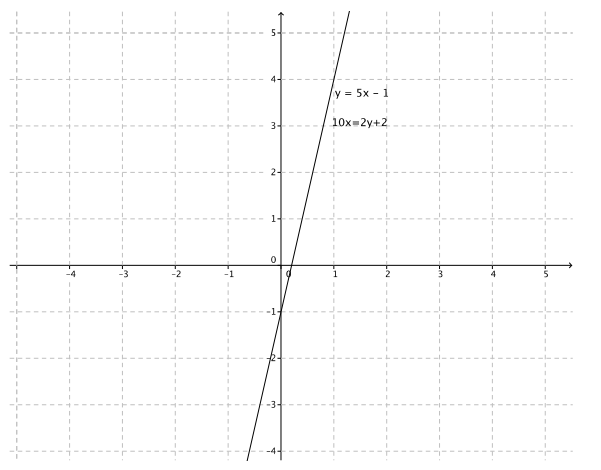
Question 11.
3x – 5y = 17
6x + 5y = 10
Answer:
3x – 5y + 6x + 5y = 17 + 10
9x = 27
x = 3
3(3) – 5y = 17
9 – 5y = 17
– 5y = 8
y = – \(\frac{8}{5}\)
The solution is (3, – \(\frac{8}{5}\)).
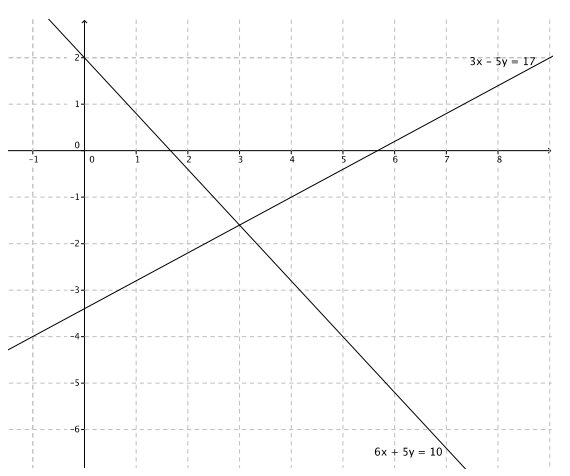
Question 12.
y = \(\frac{4}{3}\) x – 9
y = x + 3
Answer:
\(\frac{4}{3}\) x – 9 = x + 3
\(\frac{1}{3}\) x – 9 = 3
\(\frac{1}{3}\) x = 12
x = 36
y = 36 + 3
y = 39
The solution is (36, 39).
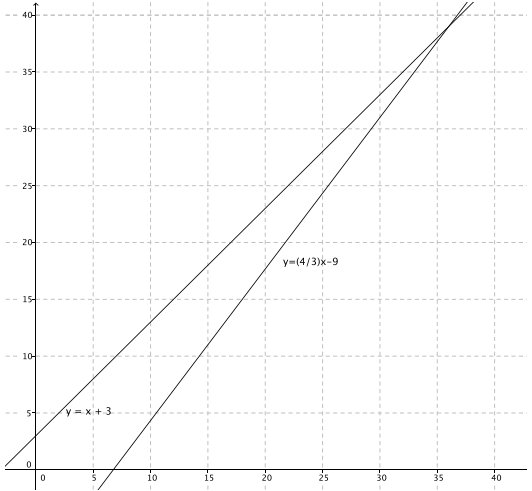
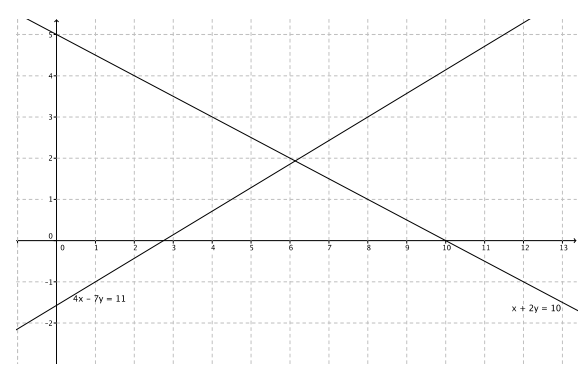
Question 13.
4x – 7y = 11
x + 2y = 10
Answer:
– 4(x + 2y = 10)
– 4x – 8y = – 40
4x – 7y = 11
– 4x – 8y = – 40
4x – 7y – 4x – 8y = 11 – 40
– 15y = – 29
y = \(\frac{29}{15}\)
x + 2(\(\frac{29}{15}\)) = 10
x + \(\frac{58}{15}\) = 10
x = \(\frac{92}{15}\)
The solution is (\(\frac{92}{15}\), \(\frac{29}{15}\)).
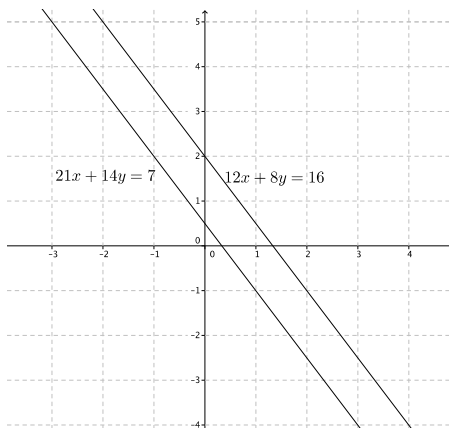
Question 14.
21x + 14y = 7
12x + 8y = 16
Answer:
The slopes of these two equations are the same, and the y – intercept points are different, which means they graph as parallel lines. Therefore, this system will have no solution.
Answer:
Eureka Math Grade 8 Module 4 Lesson 28 Exit Ticket Answer Key
Determine the solution, if it exists, for each system of linear equations. Verify your solution on the coordinate plane.
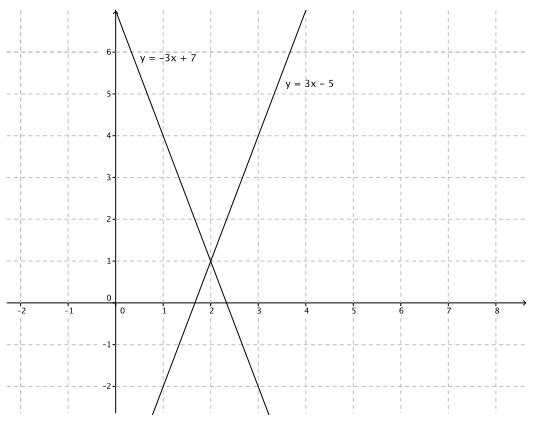
Question 1.
y = 3x – 5
y = – 3x + 7
Answer:
3x – 5 = – 3x + 7
6x = 12
x = 2
y = 3(2) – 5
y = 6 – 5
y = 1
The solution is (2, 1).
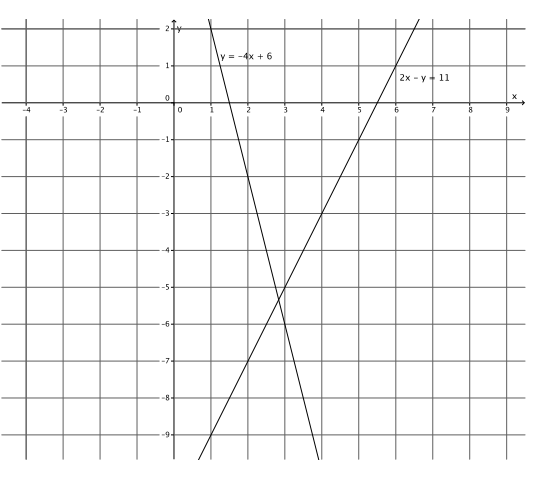
Question 2.
y = – 4x + 6
2x – y = 11
Answer:
2x – ( – 4x + 6) = 11
2x + 4x – 6 = 11
6x = 17
x = \(\frac{17}{6}\)
y = – 4(\(\frac{17}{6}\)) + 6
y = – \(\frac{34}{3}\) + 6
y = – \(\frac{16}{3}\)
The solution is (\(\frac{17}{6}\), – \(\frac{16}{3}\)).