Engage NY Eureka Math 8th Grade Module 4 Lesson 8 Answer Key
Eureka Math Grade 8 Module 4 Lesson 8 Example Answer Key
Example 1.
→ Given a linear equation in disguise, we will try to solve it. To do so, we must first assume that the following equation is true for some number x.
\(\frac{x-1}{2}\) = \(\frac{x+\frac{1}{3}}{4}\)
We want to make this equation look like the linear equations we are used to. For that reason, we will multiply both sides of the equation by 2 and 4, as we normally do with proportions:
2(x+\(\frac{1}{3}\))=4(x-1).
→ Is this a linear equation? How do you know?
→ Yes, this is a linear equation because the expressions on the left and right of the equal sign are linear expressions.
→ Notice that the expressions that contained more than one term were put in parentheses. We do that so we do not make a mistake and forget to use the distributive property.
→ Now that we have a linear equation, we will use the distributive property and solve as usual.
2(x+\(\frac{1}{3}\))=4(x-1)
2x+\(\frac{2}{3}\)=4x-4
2x-2x+\(\frac{2}{3}\)=4x-2x-4
\(\frac{2}{3}\)=2x-4
\(\frac{2}{3}\)+4=2x-4+4
\(\frac{14}{3}\)=2x
\(\frac{1}{2}\)∙\(\frac{14}{3}\)=\(\frac{1}{2}\)∙2x
\(\frac{7}{3}\)=x
→ How can we verify that \(\frac{7}{3}\) is the solution to the equation?
→ We can replace x with \(\frac{7}{3}\) in the original equation.
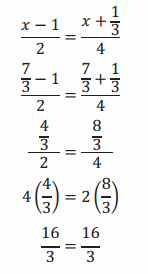
Since \(\frac{7}{3}\) made the equation true, we know it is a solution to the equation.
Example 2.
→ Can we solve the following equation? Explain.
\(\frac{\frac{1}{5}-x}{7}\) = \(\frac{2 x+9}{3}\)
→ We need to multiply each numerator with the other fraction’s denominator.
→ So,
\(\frac{\frac{1}{5}-x}{7}\) = \(\frac{2 x+9}{3}\)
7(2x+9)=3(\(\frac{1}{5}\)-x).
→ What would be the next step?
→ Use the distributive property.
→ Now we have
7(2x+9)=3(\(\frac{1}{5}\)-x)
14x+63=\(\frac{3}{5}\)-3x
14x+3x+63=\(\frac{3}{5}\)-3x+3x
17x+63=\(\frac{3}{5}\)
17x+63-63=\(\frac{3}{5}\)-63
17x=\(\frac{3}{5}\)–\(\frac{315}{5}\)
17x=-\(\frac{312}{5}\)
\(\frac{1}{17}\) (17x)=(-\(\frac{312}{5}\))\(\frac{1}{17}\)
x=-\(\frac{312}{85}\).
→ Is this a linear equation? How do you know?
→ Yes, this is a linear equation because the left and right side are linear expressions.
Example 3.
Can this equation be solved?
\(\frac{6+x}{7 x+\frac{2}{3}}\)=\(\frac{3}{8}\)
Give students a few minutes to work. Provide support to students as needed.
→ Yes, we can solve the equation because we can multiply each numerator with the other fraction’s denominator and then use the distributive property to begin solving it.
Answer:
\(\frac{6+x}{7 x+\frac{2}{3}}\)=\(\frac{3}{8}\)
(6+x)8=(7x+\(\frac{2}{3}\))3
48+8x=21x+2
48+8x-8x=21x-8x+2
48=13x+2
48-2=13x+2-2
46=13x
\(\frac{46}{13}\)=x
Example 4.
Can this equation be solved?
\(\frac{7}{3 x+9}\)=\(\frac{1}{8}\)
Give students a few minutes to work. Provide support to students as needed.
→ Yes, we can solve the equation because we can multiply each numerator with the other fraction’s denominator and then use the distributive property to begin solving it.
Answer:
\(\frac{7}{3 x+9}\)=\(\frac{1}{8}\)
7(8)=(3x+9)1
56=3x+9
56-9=3x+9-9
47=3x
\(\frac{47}{3}\)=x
Example 5.
In the diagram below, △ABC~ △A’ B’ C’. Using what we know about similar triangles, we can determine the value of x.
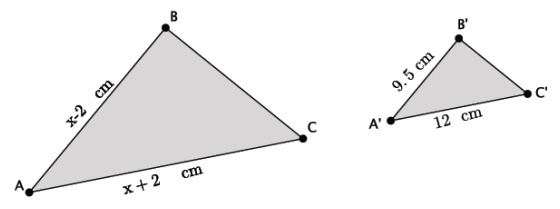
→ Begin by writing the ratios that represent the corresponding sides.
Answer:
\(\frac{x-2}{9.5}\) = \(\frac{x+2}{12}\)
It is possible to write several different proportions in this case. If time, discuss this fact with students.
→ Now that we have the ratios, solve for x and find the lengths of \(\overline{A B}\) and \(\overline{A C}\).
Answer:
\(\frac{x-2}{9.5}\) = \(\frac{x+2}{12}\)
(x-2)12=9.5(x+2)
12x-24=9.5x+19
12x-24+24=9.5x+19+24
12x=9.5x+43
12x-9.5x=9.5x-9.5x+43
2.5x=43
x=\(\frac{43}{2.5}\)
x=17.2
|AB|=15.2 cm, and |AC|=19.2 cm.
Eureka Math Grade 8 Module 4 Lesson 8 Exercise Answer Key
Solve the following equations of rational expressions, if possible.
Question 1.
\(\frac{2 x+1}{9}\)=\(\frac{1-x}{6}\)
Answer:
\(\frac{2 x+1}{9}\)=\(\frac{1-x}{6}\)
9(1-x)=(2x+1)6
9-9x=12x+6
9-9x+9x=12x+9x+6
9=21x+6
9-6=21x+6-6
3=21x
\(\frac{3}{21}\)=\(\frac{21}{2}\)1 x
\(\frac{1}{7}\)=x
Question 2.
\(\frac{5+2 x}{3 x-1}\)=\(\frac{6}{7}\)
Answer:
\(\frac{5+2 x}{3 x-1}\)=\(\frac{6}{7}\)
(5+2x)7=(3x-1)6
35+14x=18x-6
35-35+14x=18x-6-35
14x=18x-41
14x-18x=18x-18x-41
-4x=-41
\(\frac{-4}{-4}\) x=\(\frac{-41}{-4}\)
x=\(\frac{41}{4}\)
Question 3.
\(\frac{x+9}{12}\)=\(\frac{-2 x-\frac{1}{2}}{3}\)
Answer:
\(\frac{x+9}{12}\)=\(\frac{-2 x-\frac{1}{2}}{3}\)
12(-2x-\(\frac{1}{2}\))=(x+9)3
-24x-6=3x+27
-24x+24x-6=3x+24x+27
-6=27x+27
-6-27=27x+27-27
-33=27x
\(\frac{-33}{27}\)=\(\frac{27}{27}\) x
–\(\frac{11}{9}\)=x
Question 8.
\(\frac{8}{3-4 x}\) = \(\frac{5}{2 x+\frac{1}{4}}\)
Answer:
\(\frac{8}{3-4 x}\) = \(\frac{5}{2 x+\frac{1}{4}}\)
8(2x+\(\frac{1}{4}\))=(3-4x)5
16x+2=15-20x
16x+2-2=15-2-20x
16x=13-20x
16x+20x=13-20x+20x
36x=13
\(\frac{36}{36}\) x=\(\frac{13}{36}\)
x=\(\frac{13}{36}\)
Eureka Math Grade 8 Module 4 Lesson 8 Problem Set Answer Key
Students practice solving equations with rational expressions, if a solution is possible.
Solve the following equations of rational expressions, if possible. If an equation cannot be solved, explain why.
Question 1.
\(\frac{5}{6 x-2}\) = \(\frac{-1}{x+1}\)
Answer:
\(\frac{5}{6 x-2}\) = \(\frac{-1}{x+1}\)
5(x+1)=-1(6x-2)
5x+5=-6x+2
5x+5-5=-6x+2-5
5x=-6x-3
5x+6x=-6x+6x-3
11x=-3
x=-\(\frac{3}{11}\)
Question 2.
\(\frac{4-x}{8}\) = \(\frac{7 x-1}{3}\)
Answer:
\(\frac{4-x}{8}\) = \(\frac{7 x-1}{3}\)
8(7x-1)=(4-x)3
56x-8=12-3x
56x-8+8=12+8-3x
56x=20-3x
56x+3x=20-3x+3x
59x=20
\(\frac{59}{59}\) x=\(\frac{20}{59}\)
x=\(\frac{20}{59}\)
Question 3.
\(\frac{3 x}{x+2}\) = \(\frac{5}{9}\)
Answer:
\(\frac{3 x}{x+2}\) = \(\frac{5}{9}\)
9(3x)=(x+2)5
27x=5x+10
27x-5x=5x-5x+10
22x=10
\(\frac{22}{22}\) x=\(\frac{10}{22}\)
x=\(\frac{5}{11}\)
Question 4.
\(\frac{\frac{1}{2} x+6}{3}\) = \(\frac{x-3}{2}\)
Answer:
\(\frac{\frac{1}{2} x+6}{3}\) = \(\frac{x-3}{2}\)
3(x-3)=2(\(\frac{1}{2}\) x+6)
3x-9=x+12
3x-9+9=x+12+9
3x=x+21
3x-x=x-x+21
2x=21
x=\(\frac{21}{2}\)
Question 5.
\(\frac{7-2 x}{6}\) = \(\frac{x-5}{1}\)
Answer:
\(\frac{7-2 x}{6}\) = \(\frac{x-5}{1}\)
6(x-5)=(7-2x)1
6x-30=7-2x
6x-30+30=7+30-2x
6x=37-2x
6x+2x=37-2x+2x
8x=37
\(\frac{8}{8}\) x=\(\frac{37}{8}\)
x=\(\frac{37}{8}\)
Question 6.
\(\frac{2 x+5}{2}\) = \(\frac{3 x-2}{6}\)
Answer:
\(\frac{2 x+5}{2}\) = \(\frac{3 x-2}{6}\)
2(3x-2)=6(2x+5)
6x-4=12x+30
6x-4+4=12x+30+4
6x=12x+34
6x-12x=12x-12x+34
-6x=34
x=-\(\frac{34}{6}\)
x=-\(\frac{17}{3}\)
Question 7.
\(\frac{6 x+1}{3}\) = \(\frac{9-x}{7}\)
Answer:
\(\frac{6 x+1}{3}\) = \(\frac{9-x}{7}\)
(6x+1)7=3(9-x)
42x+7=27-3x
42x+7-7=27-7-3x
42x=20-3x
42x+3x=20-3x+3x
45x=20
\(\frac{45}{45}\)x=\(\frac{20}{45}\)
x=\(\frac{4}{9}\)
Question 8.
\(\frac{\frac{1}{3} x-8}{12}\) = \(\frac{-2-x}{15}\)
Answer:
\(\frac{\frac{1}{3} x-8}{12}\) = \(\frac{-2-x}{15}\)
12(-2-x)=(\(\frac{1}{3}\) x-8)15
-24-12x=5x-120
-24-12x+12x=5x+12x-120
-24=17x-120
-24+120=17x-120+120
96=17x
\(\frac{96}{17}\)=\(\frac{17}{17}\) x
\(\frac{96}{17}\)=x
Question 9.
\(\frac{3-x}{1-x}\)=\(\frac{3}{2}\)
Answer:
\(\frac{3-x}{1-x}\)=\(\frac{3}{2}\)
(3-x)2=(1-x)3
6-2x=3-3x
6-2x+2x=3-3x+2x
6=3-x
6-3=3-3-x
3=-x
-3=x
Question 10.
In the diagram below, △ABC~ △A’ B’ C’. Determine the lengths of \(\overline{A C}\) and \(\overline{B C}\).
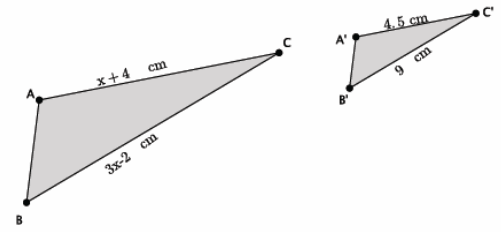
Answer:
\(\frac{x+4}{4.5}\) = \(\frac{3 x-2}{9}\)
9(x+4)=4.5(3x-2)
9x+36=13.5x-9
9x+36+9=13.5x-9+9
9x+45=13.5x
9x-9x+45=13.5x-9x
45=4.5x
10=x
|AC|=14 cm, and |BC|=28 cm.
Eureka Math Grade 8 Module 4 Lesson 8 Exit Ticket Answer Key
Solve the following equations for x.
Question 1.
\(\frac{5 x-8}{3}\) = \(\frac{11 x-9}{5}\)
Answer:
\(\frac{5 x-8}{3}\) = \(\frac{11 x-9}{5}\)
5(5x-8)=3(11x-9)
25x-40=33x-27
25x-25x-40=33x-25x-27
-40=8x-27
-40+27=8x-27+27
-13=8x
–\(\frac{13}{8}\)=x
Question 2.
\(\frac{x+11}{7}\)=\(\frac{2 x+1}{-8}\)
Answer:
\(\frac{x+11}{7}\)=\(\frac{2 x+1}{-8}\)
7(2x+1)=-8(x+11)
14x+7=-8x-88
14x+7-7=-8x-88-7
14x=-8x-95
14x+8x=-8x+8x-95
22x=-95
x=-\(\frac{95}{22}\)
Question 3.
\(\frac{-x-2}{-4}\) = \(\frac{3 x+6}{2}\)
Answer:
\(\frac{-x-2}{-4}\) = \(\frac{3 x+6}{2}\)
-4(3x+6)=2(-x-2)
-12x-24=-2x-4
-12x-24+24=-2x-4+24
-12x=-2x+20
-12x+2x=-2x+2x+20
-10x=20
x=-2