Engage NY Eureka Math 8th Grade Module 5 Lesson 9 Answer Key
Eureka Math Grade 8 Module 5 Lesson 9 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge 1/Exercises 1–4
As you complete Exercises 1–4, record the information in the table below.
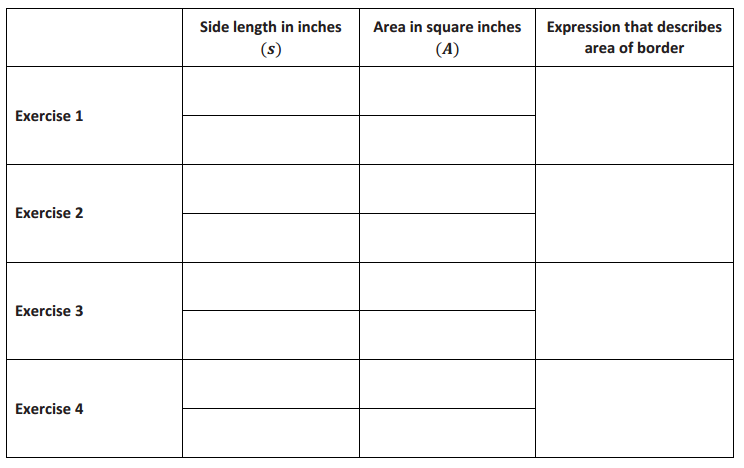
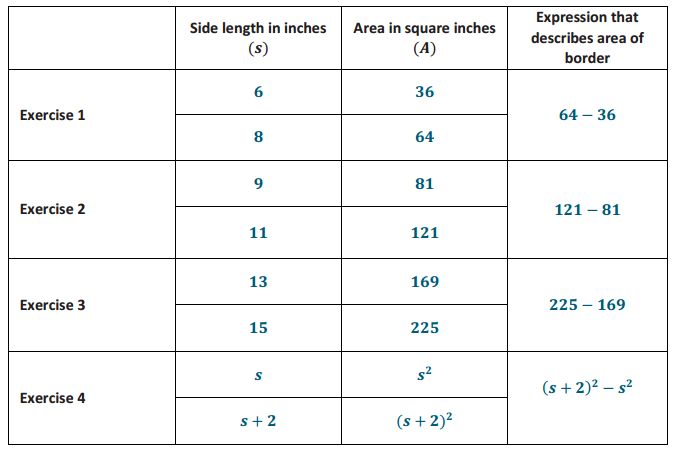
Answer:
Exercise 1.
Use the figure below to answer parts (a)–(f).
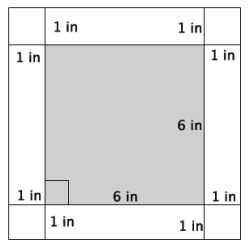
a. What is the length of one side of the smaller, inner square?
Answer:
The length of one side of the smaller square is 6 in.
b. What is the area of the smaller, inner square?
Answer:
62 = 36
The area of the smaller square is 36 in2.
c. What is the length of one side of the larger, outer square?
Answer:
The length of one side of the larger square is 8 in.
d. What is the area of the larger, outer square?
Answer:
82 = 64
The area of the larger square is 64 in2.
e. Use your answers in parts (b) and (d) to determine the area of the 1 – inch white border of the figure.
Answer:
64 – 36 = 28
The area of the 1 – inch white border is 28 in2.
f. Explain your strategy for finding the area of the white border.
Answer:
First, I had to determine the length of one side of the larger, outer square. Since the inner square is 6 in. and the border is 1 in. on all sides, then the length of one side of the larger square is (6 + 2) in = 8 in. Then, the area of the larger square is 64 in2. Next, I found the area of the smaller, inner square. Since one side length is 6 in., the area is 36 in2. To find the area of the white border, I needed to subtract the area of the inner square from the area of the outer square.
Exercise 2.
Use the figure below to answer parts (a)–(f).
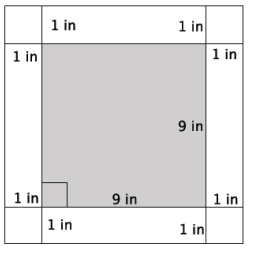
a. What is the length of one side of the smaller, inner square?
Answer:
The length of one side of the smaller square is 9 in.
b. What is the area of the smaller, inner square?
Answer:
92 = 81
The area of the smaller square is 81 in2.
c. What is the length of one side of the larger, outer square?
Answer:
The length of one side of the larger square is 11 in.
d. What is the area of the larger, outer square?
Answer:
112 = 121
The area of the larger square is 121 in2.
e. Use your answers in parts (b) and (d) to determine the area of the 1 – inch white border of the figure.
Answer:
121 – 81 = 40
The area of the 1 – inch white border is 40 in2.
f. Explain your strategy for finding the area of the white border.
Answer:
First, I had to determine the length of one side of the larger, outer square. Since the inner square is 9 in. and the border is 1 in. on all sides, the length of one side of the larger square is (9 + 2) in = 11 in. Therefore, the area of the larger square is 121 in2. Then, I found the area of the smaller, inner square. Since one side length is 9 in., the area is 81 in2. To find the area of the white border, I needed to subtract the area of the inner square from the area of the outer square.
Exercise 3.
Use the figure below to answer parts (a)–(f).
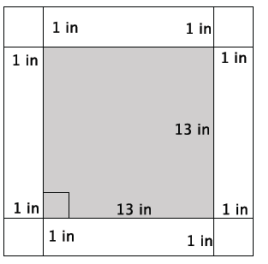
a. What is the length of one side of the smaller, inner square?
Answer:
The length of one side of the smaller square is 13 in.
b. What is the area of the smaller, inner square?
Answer:
132 = 169
The area of the smaller square is 169 in2.
c. What is the length of one side of the larger, outer square?
Answer:
The length of one side of the larger square is 15 in.
d. What is the area of the larger, outer square?
Answer:
152 = 225
The area of the larger square is 225 in2.
e. Use your answers in parts (b) and (d) to determine the area of the 1 – inch white border of the figure.
Answer:
225 – 169 = 56
The area of the 1 – inch white border is 56 in2.
f. Explain your strategy for finding the area of the white border.
Answer:
First, I had to determine the length of one side of the larger, outer square. Since the inner square is 13 in. and the border is 1 in. on all sides, the length of one side of the larger square is (13 + 2) in = 15 in. Therefore, the area of the larger square is 225 in2. Then, I found the area of the smaller, inner square. Since one side length is 13 in., the area is 169 in2. To find the area of the white border, I needed to subtract the area of the inner square from the area of the outer square.
Exercise 4.
Write a function that would allow you to calculate the area of a 1 – inch white border for any sized square picture measured in inches.
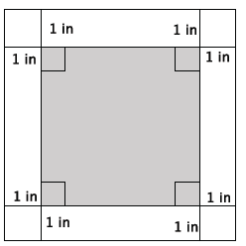
a. Write an expression that represents the side length of the smaller, inner square.
Answer:
Symbols used will vary. Expect students to use s or x to represent one side of the smaller, inner square. Answers that follow will use s as the symbol to represent one side of the smaller, inner square.
b. Write an expression that represents the area of the smaller, inner square.
Answer:
s2
c. Write an expression that represents the side lengths of the larger, outer square.
Answer:
s + 2
d. Write an expression that represents the area of the larger, outer square.
Answer:
(s + 2)2
e. Use your expressions in parts (b) and (d) to write a function for the area A of the 1 – inch white border for any sized square picture measured in inches.
Answer:
A = (s + 2)2 – s2
Exercises 5–6
Exercise 5.
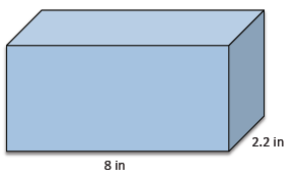
The volume of the prism shown below is 61.6 in3. What is the height of the prism?
Answer:
Let x represent the height of the prism.
61.6 = 8(2.2)x
61.6 = 17.6x
3.5 = x
The height of the prism is 3.5 in.
Exercise 6.
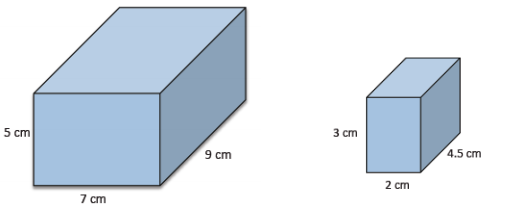
Find the value of the ratio that compares the volume of the larger prism to the smaller prism.
Answer:
Volume of larger prism:
V = 7(9)(5)
= 315
The volume of the larger prism is 315 cm3.
Volume of smaller prism:
V = 2(4.5)(3)
= 27
The volume of the smaller prism is 27 cm3.
The ratio that compares the volume of the larger prism to the smaller prism is 315:27. The value of the ratio is \(\frac{315}{27}\) = \(\frac{35}{3}\).
Exploratory Challenge 2/Exercises 7–10
As you complete Exercises 7–10, record the information in the table below. Note that base refers to the bottom of the prism.
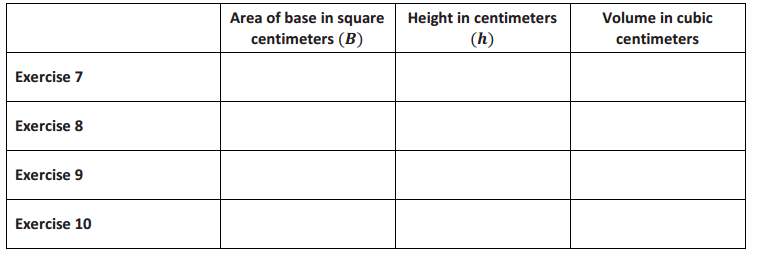
Answer:
Exercise 7.
Use the figure to the right to answer parts (a)–(c).
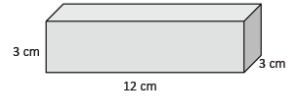
a. What is the area of the base?
Answer:
The area of the base is 36 cm2.
b. What is the height of the figure?
Answer:
The height is 3 cm.
c. What is the volume of the figure?
Answer:
The volume of the rectangular prism is 108 cm3.
Exercise 8.
Use the figure to the right to answer parts (a)–(c).
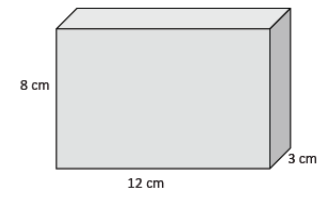
a. What is the area of the base?
Answer:
The area of the base is 36 cm2.
b. What is the height of the figure?
Answer:
The height is 8 cm.
c. What is the volume of the figure?
Answer:
The volume of the rectangular prism is 288 cm3.
Exercise 9.
Use the figure to the right to answer parts (a)–(c).
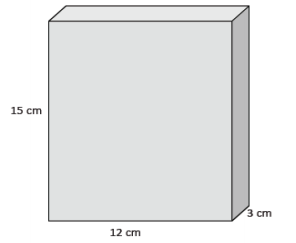
a. What is the area of the base?
Answer:
The area of the base is 36 cm2.
b. What is the height of the figure?
Answer:
The height is 15 cm.
c. What is the volume of the figure?
Answer:
The volume of the rectangular prism is 540 cm3.
Exercise 10.
Use the figure to the right to answer parts (a)–(c).
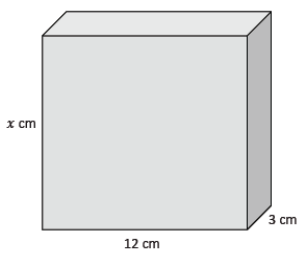
a. What is the area of the base?
Answer:
The area of the base is 36 cm2.
b. What is the height of the figure?
Answer:
The height is x cm.
c. Write and describe a function that will allow you to determine the volume of any rectangular prism that has a base area of
Answer:
36 cm2.
The rule that describes the function is V = 36x, where V is the volume and x is the height of the rectangular prism. The volume of a rectangular prism with a base area of 36 cm2 is a function of its height.
Eureka Math Grade 8 Module 5 Lesson 9 Problem Set Answer Key
Question 1.
Calculate the area of the 3 – inch white border of the square figure below.
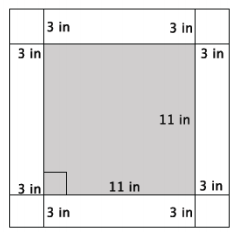
Answer:
172 = 289
112 = 121
The area of the 3 – inch white border is 168 in2.
Question 2.
Write a function that would allow you to calculate the area, A, of a 3 – inch white border for any sized square picture measured in inches.
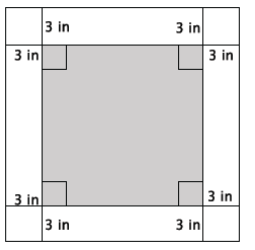
Answer:
Let s represent the side length of the inner square in inches. Then, the area of the inner square is s2 square inches. The side length of the outer square, in inches, is s + 6, which means that the area of the outer square, in square inches, is (s + 6)2. The function that describes the area, A, of the 3 – inch border is in square inches
A = (s + 6)2 – s2.
Question 3.
Dartboards typically have an outer ring of numbers that represent the number of points a player can score for getting a dart in that section. A simplified dartboard is shown below. The center of the circle is point A. Calculate the area of the outer ring. Write an exact answer that uses π (do not approximate your answer by using 3.14 for π).
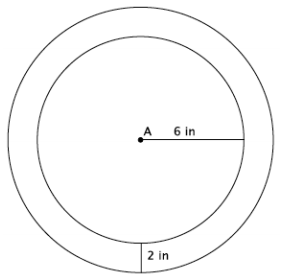
Answer:
Inner ring area: πr2 = π(62 ) = 36 π
Outer ring: πr2 = π(6 + 2)2 = π(82 ) = 64 π
Difference in areas: 64 π – 36 π = (64 – 34)π = 28 π
The inner ring has an area of 36π in2. The area of the inner ring including the border is 64π in2. The difference is the area of the border, 28π in2.
Question 4.
Write a function that would allow you to calculate the area, A, of the outer ring for any sized dartboard with radius r. Write an exact answer that uses π (do not approximate your answer by using 3.14 for π).
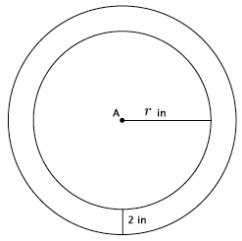
Answer:
Inner ring area: πr2
Outer ring: πr2 = π(r + 2)2
Difference in areas: Inner ring area: π(r + 2)2 – πr2
The inner ring has an area of πr2 in2. The area of the inner ring including the border is π(r + 2)2 in2. Let A be the area of the outer ring. Then, the function that would describe that area in square inches is
A = π(r + 2)2 – πr2.
Question 5.
The shell of the solid shown was filled with water and then poured into the standard rectangular prism, as shown. The height that the volume reaches is 14.2 in. What is the volume of the shell of the solid?
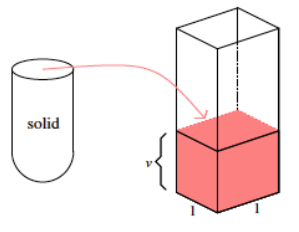
Answer:
V = Bh
= 1(14.2)
= 14.2
The volume of the shell of the solid is 14.2 in3.
Question 6.
Determine the volume of the rectangular prism shown below.
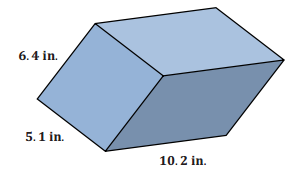
Answer:
6.4 × 5.1 × 10.2 = 332.928
The volume of the prism is 332.928 in3.
Question 7.
The volume of the prism shown below is 972 cm3. What is its length?

Answer:
Let x represent the length of the prism.
972 = 8.1(5)x
972 = 40.5x
24 = x
The length of the prism is 24 cm.
Question 8.
The volume of the prism shown below is 32.7375 ft3. What is its width?
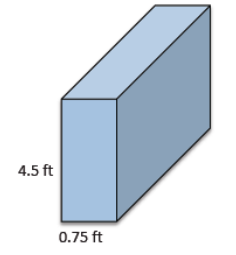
Answer:
Let x represent the width.
32.7375 = (0.75)(4.5)x
32.7375 = 3.375x
9.7 = x
The width of the prism is 9.7 ft.
Question 9.
Determine the volume of the three – dimensional figure below. Explain how you got your answer.
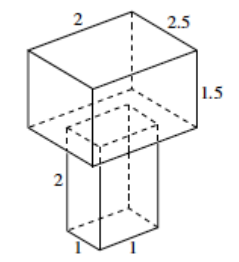
Answer:
2 × 2.5 × 1.5 = 7.5
2 × 1 × 1 = 2
The volume of the top rectangular prism is 7.5 units3. The volume of the bottom rectangular prism is 2 units3. The figure is made of two rectangular prisms, and since the rectangular prisms only touch at their boundaries, we can add their volumes together to obtain the volume of the figure. The total volume of the three – dimensional figure is 9.5 units3.
Eureka Math Grade 8 Module 5 Lesson 9 Exit Ticket Answer Key
Question 1.
Write a function that would allow you to calculate the area in square inches, A, of a 2 – inch white border for any sized square figure with sides of length s measured in inches.
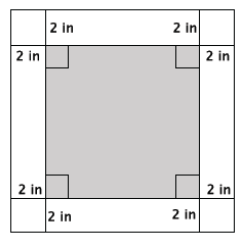
Answer:
Let s represent the side length of the inner square in inches. Then, the area of the inner square is s2 square inches. The side length of the larger square, in inches, is s + 4, and the area in square inches is (s + 4)2. If A is the area of the 2 – inch border, then the function that describes A in square inches is
A = (s + 4)2 – s2.
Question 2.
The volume of the rectangular prism is 295.68 in3. What is its width?
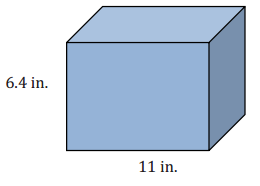
Answer:
Let x represent the width of the prism.
295.68 = 11(6.4)x
295.68 = 70.4x
4.2 = x
The width of the prism is 4.2 in.