Engage NY Eureka Math 8th Grade Module 7 Lesson 13 Answer Key
Eureka Math Grade 8 Module 7 Lesson 13 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge/Exercises 1–11
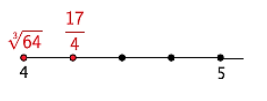
Exercise 1.
Rodney thinks that \(\sqrt [ 3 ]{ 64 }\) is greater than \(\frac{17}{4}\). Sam thinks that \(\frac{17}{4}\) is greater. Who is right and why?
\(\sqrt [ 3 ]{ 64 }\) = \(\sqrt[3]{4^{3}}\) = 4
and
\(\frac{17}{4}\) = \(\frac{16}{4}\) + \(\frac{1}{4}\)
= 4 + \(\frac{1}{4}\)
= 4 \(\frac{1}{4}\)
We see that \(\sqrt [ 3 ]{ 64 }\) < \(\frac{17}{4}\). Sam is correct.
Exercise 2.
Which number is smaller, \(\sqrt [ 3 ]{ 27 }\) or 2.89? Explain.
Answer:
\(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{3^{3}}\) = 3
We see that 2.89 is smaller than \(\sqrt [ 3 ]{ 27 }\).
Exercise 3.
Which number is smaller, \(\sqrt{121}\) or \(\sqrt [ 3 ]{ 125 }\)? Explain.
Answer:
\(\sqrt{121}\) = \(\sqrt{11^{2}}\) = 11
\(\sqrt [ 3 ]{ 125 }\) = \(\sqrt[3]{5^{3}}\) = 5
We see that \(\sqrt [ 3 ]{ 125 }\) is smaller than \(\sqrt{121}\).
Exercise 4.
Which number is smaller, \(\sqrt{49}\) or \(\sqrt [ 3 ]{ 216 }\)? Explain.
Answer:
\(\sqrt{49}\) = \(\sqrt{7^{2}}\) = 7
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{6^{3}}\) = 6
We see that \(\sqrt [ 3 ]{ 216 }\) is smaller than \(\sqrt{49}\).
Exercise 5.
Which number is greater, \(\sqrt{50}\) or \(\frac{319}{45}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{319}{45}\) is equal to\(7.0 \overline{8}\).
The number \(\sqrt{50}\) is between 7 and 8 because 72 < 50 < 82. The number \(\sqrt{50}\) is between 7.0 and 7.1 because 72 < 50 < 7.12. The number \(\sqrt{50}\) is between 7.07 and 7.08 because 7.072 < 50 < 7.082. The approximate decimal value of \(\sqrt{50}\) is 7.07. Since 7.07 < \(7.0 \overline{8}\), then \(\sqrt{50}\) < \(\frac{319}{45}\); therefore, the fraction \(\frac{319}{45}\) is greater than \(\sqrt{50}\) .
Alternately: (\(\sqrt{50}\))2 = 50 and (\(\frac{319}{45}\))2 = 101761/2025>101250/2025 = 50. So, 319/45 must be larger.
Exercise 6.
Which number is greater, \(\frac{5}{11}\) or \(0. \overline{4}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{5}{11}\) is equal to \(0. \overline{45}\). Since 0.44444… < 0.454545…, then \(0. \overline{4}\) < \(\frac{5}{11}\); therefore, the fraction \(\frac{5}{11}\) is greater than 0.4 ̅.
Alternately: 0.444… = \(\frac{4}{9}\), and we can compare the fractions \(\frac{4}{9}\) and \(\frac{5}{11}\) using their equivalents, \(\frac{44}{99}\) and \(\frac{45}{99}\) to see that \(\frac{5}{11}\) is larger.
Exercise 7.
Which number is greater, \(\sqrt{38}\) or \(\frac{154}{25}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
\(\frac{154}{25}\) = \(\frac{154 \times 4}{25 \times 4} = \frac{616}{10^{2}}\) = 6.16
The number \(\sqrt{38}\) is between 6 and 7 because 62 < 38 < 72. The number \(\sqrt{38}\) is between 6.1 and 6.2 because
6.12 < 38 < 6.22. The number \(\sqrt{38}\) is between 6.16 and 6.17 because 6.162 < 38 < 6.172. Since \(\sqrt{38}\) is greater than 6.16, then \(\sqrt{38}\) is greater than 154/25.
Alternately: (\(\sqrt{38}\))2 = 38 and (\(\frac{154}{25}\))2 = \(\frac{23716}{625}\) < \(\frac{23750}{625}\) = 38. So, \(\sqrt{38}\) must be larger.
Exercise 8.
Which number is greater, \(\sqrt{2}\) or \(\frac{15}{9}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{15}{9}\) is equal to\(1 . \overline{6}\).
The number \(\sqrt{2}\) is between 1 and 2 because 12 < 2 < 22. The number \(\sqrt{2}\) is between 1.4 and 1.5 because
1.42 < 2 < 1.52. Therefore, \(\sqrt{2}\) < \(\frac{15}{9}\); the fraction \(\frac{15}{9}\) is greater.
Alternately: (\(\sqrt{2}\))2 = 2 and (\(\frac{15}{9}\))2 = (\(\frac{5}{3}\))2 = \(\frac{28}{9}\)>2. So, \(\frac{15}{9}\) must be larger.
Exercise 9.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{25}\), \(\sqrt{28}\), \(\sqrt{30}\), \(\sqrt{32}\), \(\sqrt{35}\), and \(\sqrt{36}\).
Answer:
The solutions are shown in red:

The number \(\sqrt{25}\) = \(\sqrt{5^{2}}\) = 5.
The numbers \(\sqrt{28}\),\(\sqrt{30}\),\(\sqrt{32}\), and \(\sqrt{35}\) are between 5 and 6. The number \(\sqrt{28}\) is between 5.2 and 5.3 because 5.22 < 28 < 5.32. The number \(\sqrt{30}\) is between 5.4 and 5.5 because 5.42 < 30 < 5.52. The number \(\sqrt{32}\) is between 5.6 and 5.7 because 5.62 < 32 < 5.72. The number \(\sqrt{35}\) is between 5.9 and 6.0 because
5.92 < 35 < 62.
The number\(\sqrt{36}\) = \(\sqrt{6^{2}}\) = 6.
Exercise 10.
Challenge: Which number is larger, \(\sqrt{5}\) or \(\sqrt [ 3 ]{ 11 }\)?
Answer:
The number \(\sqrt{5}\) is between 2 and 3 because 22 < 5 < 32. The number \(\sqrt{5}\) is between 2.2 and 2.3 because
2.22 < 5 < 2.32. The number \(\sqrt{5}\) is between 2.23 and 2.24 because 2.232 < 5 < 2.242. The number \(\sqrt{5}\) is between 2.236 and 2.237 because 2.2362 < 5 < 2.2372. The decimal expansion of \(\sqrt{5}\) is approximately 2.236….
The number \(\sqrt [ 3 ]{ 11 }\) is between 2 and 3 because 2^3 < 11 < 3^3. The number \(\sqrt [ 3 ]{ 11 }\) is between 2.2 and 2.3 because 2.2^3 < 11 < 2.3^3. The number \(\sqrt [ 3 ]{ 11 }\) is between 2.22 and 2.23 because 2.22^3 < 11 < 2.23^3. The decimal expansion of \(\sqrt [ 3 ]{ 11 }\) is approximately 2.22…. Since 2.22″…” < 2.236″…” , then \(\sqrt [ 3 ]{ 11 }\) < \(\sqrt{5}\); therefore, \(\sqrt{5}\) is larger.
Alternately:
(\(\sqrt [ 3 ]{ 11 }\))^6 = 112 = 121
(\(\sqrt{5}\))^6 = 5^3 = 125
We see that \(\sqrt{5}\) must be larger.
Exercise 11.
A certain chessboard is being designed so that each square has an area of 3 in2. What is the length of one edge of the board rounded to the tenths place? (A chessboard is composed of 64 squares as shown.)

Answer:
The area of one square is 3 in2. So, if x is the length of one side of one square,
x2 = 3
\(\sqrt{x^{2}}\) = \(\sqrt{3}\)
x = \(\sqrt{3}\).
There are 8 squares along one edge of the board, so the length of one edge is 8×\(\sqrt{3}\). The number \(\sqrt{3}\) is between 1 and 2 because
12 < 3 < 22. The number \(\sqrt{3}\) is between 1.7 and 1.8 because 1.72 < 3 < 1.82. The number \(\sqrt{3}\) is between 1.73 and 1.74 because 1.732 < 3 < 1.742. The number \(\sqrt{3}\) is approximately 1.73. So, the length of one edge of the chessboard is about
8×1.73 inches, which is approximately 13.8 in.
Note: Some students may determine the total area of the board, 64×3 = 192, and then determine the approximate value of \(\sqrt{192}\) as 13.8 to answer the question.
Eureka Math Grade 8 Module 7 Lesson 13 Problem Set Answer Key
Question 1.
Which number is smaller, \(\sqrt [ 3 ]{ 343 }\) or \(\sqrt{48}\) ? Explain.
Answer:
√(3&343) = \(\sqrt[3]{7^{3}}\) = 7
The number \(\sqrt{48}\) is between 6 and 7 but definitely less than 7. Therefore, \(\sqrt{48}\) < \(\sqrt [ 3 ]{ 343 }\), and √\(\sqrt{48}\) is smaller.
Question 2.
Which number is smaller, \(\sqrt{100}\) or \(\sqrt [ 3 ]{ 1000 }\)? Explain.
Answer:
\(\sqrt{100}\) = \(\sqrt{10^{2}}\) = 10
\(\sqrt [ 3 ]{ 1000 }\) = \(\sqrt[3]{10^{3}}\) = 10
The numbers \(\sqrt{100}\) and \(\sqrt [ 3 ]{ 1000 }\) are equal because both are equal to 10.
Question 3.
Which number is larger, \(\sqrt{87}\) or \(\frac{929}{99}\)? Explain.
Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\frac{929}{99}\) is equal to \(9 . \overline{38}\).
The number \(\sqrt{87}\) is between 9 and 10 because 92 < 87 < 102. The number \(\sqrt{87}\) is between 9.3 and 9.4 because 9.32 < 87 < 9.42. The number \(\sqrt{87}\) is between 9.32 and 9.33 because 9.322 < 87 < 9.332. Since \(\sqrt{87}\) < 9.3, then \(\sqrt{87}\) < \(\frac{929}{99}\). The fraction \(\frac{929}{99}\) is larger.
Question 4.
Which number is larger, \(\frac{9}{13}\) or \(0 . \overline{692}\)? Explain.
Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\frac{9}{13}\) is equal to \(0 . \overline{692307}\). Since 0.692307… < 0.692692…, then we see that 9/13 < \(0 . \overline{692}\).
The decimal \(0 . \overline{692}\) is larger.
Question 5.
Which number is larger, 9.1 or \(\sqrt{82}\)? Explain.
Answer:
The number \(\sqrt{82}\) is between 9 and 10 because 92 < 82 < 102. The number \(\sqrt{82}\) is between 9.0 and 9.1 because 9.02 < 82 < 9.12. Since \(\sqrt{82}\) < 9.1, then the number 9.1 is larger than the number \(\sqrt{82}\).
Question 6.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{144}\), \(\sqrt [ 3 ]{ 1000 }\), \(\sqrt{130}\), \(\sqrt{110}\), \(\sqrt{120}\), \(\sqrt{115}\), and \(\sqrt{133}\). Explain how you knew where to place the numbers.

Answer:
The solutions are shown in red:

The number \(\sqrt{144}\) = \(\sqrt{12^{2}}\) = 12.
The number \(\sqrt [ 3 ]{ 1000 }\) = \(\sqrt[3]{10^{3}}\) = 10.
The numbers \(\sqrt{110}\), \(\sqrt{115}\), and \(\sqrt{120}\) are all between 10 and 11 because when squared, their value falls between 102 and 112. The number \(\sqrt{110}\) is between 10.4 and 10.5 because 10.42 < 110 < 10.52. The number \(\sqrt{115}\) is between 10.7 and 10.8 because 10.72 < 115 < 10.82. The number \(\sqrt{120}\) is between 10.9 and 11 because 10.92 < 120 < 112.
The numbers √130 and \(\sqrt{133}\) are between 11 and 12 because when squared, their value falls between 112 and 122. The number √130 is between 11.4 and 11.5 because 11.42 < 130 < 11.52. The number \(\sqrt{133}\) is between 11.5 and 11.6 because 11.52 < 133 < 11.62.
Question 7.
Which of the two right triangles shown below, measured in units, has the longer hypotenuse? Approximately how much longer is it?
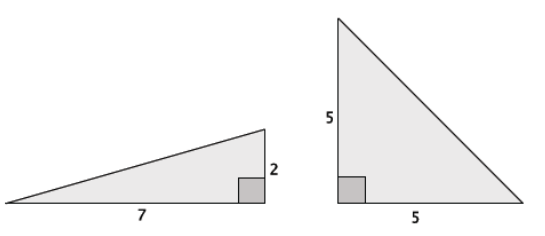
Answer:
Let x represent the length of the hypotenuse of the triangle on the left.
72 + 22 = x2
49 + 4 = x2
53 = x2
\(\sqrt{53}\) = x
The number \(\sqrt{53}\) is between 7 and 8 because 72 < 53 < 82. The number \(\sqrt{53}\) is between 7.2 and 7.3 because 7.22 < 53 < 7.32. The number \(\sqrt{53}\) is between 7.28 and 7.29 because 7.282 < 53 < 7.292. The approximate decimal value of \(\sqrt{53}\) is 7.28.
Let y represent the length of the hypotenuse of the triangle on the right.
52 + 52 = y2
25 + 25 = y2
50 = y2
\(\sqrt{50}\) = y
The number \(\sqrt{50}\) is between 7 and 8 because 72 < 50 < 82. The number \(\sqrt{50}\) is between 7.0 and 7.1 because 7.02 < 50 < 7.12. The number \(\sqrt{50}\) is between 7.07 and 7.08 because 7.072 < 50 < 7.082. The approximate decimal value of \(\sqrt{50}\) is 7.07.
The triangle on the left has the longer hypotenuse. It is approximately 0.21 units longer than the hypotenuse of the triangle on the right.
Note: Based on their experience, some students may reason that \(\sqrt{50}\) < \(\sqrt{53}\). To answer completely, students must determine the decimal expansion to approximate how much longer one hypotenuse is than the other.
Eureka Math Grade 8 Module 7 Lesson 13 Exit Ticket Answer Key
Question 1.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{12}\), \(\sqrt{16}\), \(\frac{20}{6}\), \(3 . \overline{53}\), and \(\sqrt [ 3 ]{ 27 }\).

Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\sqrt{12}\) is between 3.4 and 3.5 since 3.42 < 12 < 3.52.
The number \(\sqrt{16}\) = \(\sqrt{4^{2}}\) = 4.
The number \(\frac{20}{6}\) is equal to \(3 . \overline{3}\).
The number \(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{3^{3}}\) = 3.
The solutions are shown in red:
