Engage NY Eureka Math 8th Grade Module 7 Mid Module Assessment Answer Key
Eureka Math Grade 8 Module 7 Mid Module Assessment Task Answer Key
Question 1.
a. What is the decimal expansion of the number \(\frac{35}{7}\)? Is the number \(\frac{35}{7}\) rational or irrational? Explain.
Answer:
\(\frac{35}{7}\) = 5.000….
The number \(\frac{35}{7}\) is a rational number. Rational numbers have decimal expansions that repeat. In this case, the decimal that repeats is a zero.
b. What is the decimal expansion of the number \(\frac{4}{33}\)? Is the number \(\frac{4}{33}\) rational or irrational? Explain.
Answer:
\(\frac{4}{33}\) = 0.1212……… = \(0 . \overline{12}\)

The number \(\frac{4}{33}\) is a rational number. Rational numbers have decimal expansions that repeat. The digits 12 repeat in the decimal expansion of \(\frac{4}{33}\). So, \(\frac{4}{33}\) is rational.
Question 2.
a. Write \(0 . \overline{345}\) as a fraction.
Answer:
Let x be \(0 . \overline{345}\)
103x = 103(\(0 . \overline{345}\))
1000 x = 1000(\(0 . \overline{345}\))
1000x = \(345 . \overline{345}\)
1000x = 345 + x
1000x – x = 345 + x – x
999x = 345
x = \(\frac{345}{999}\) = \(\frac{115}{333}\)
b. Write \(2.8 \overline{40}\) as a fraction.
Answer:
Let x be \(2.8 \overline{40}\)
10x = \(2.8 \overline{40}\)
10x = 28 + \(0. \overline{40}\)
10x = \(\frac{(28)(99)+40}{99}\)
x = \(\frac{2812}{99}\)(\(\frac{1}{10}\))
x = \(\frac{2812}{990}\) = \(\frac{1406}{495}\)
Let y be \(0. \overline{40}\)
102y = 102 (\(0. \overline{40}\))
100y = \(40. \overline{40}\)
100y = 40 + y
100y – y = 40 + y – y
99y = 40
y = \(\frac{40}{99}\)
\(2.8 \overline{40}\) = \(\frac{2812}{990}\) = \(\frac{1406}{495}\)
c. Brandon stated that 0.66 and \(\frac{2}{3}\) are equivalent. Do you agree? Explain why or why not.
Answer:
No, I do not agree with brandon. The decimal 0.66 is equal to the fraction \(\frac{66}{100}\) = \(\frac{33}{50}\), not \(\frac{2}{3}\). Also, the number \(\frac{2}{3}\) is equal to the infinit decimal \(0 . \overline{6}\). The number 0.66 is a finite decimal. Therefore, 0.66 and \(\frac{2}{3}\) are not equivlent.
d. Between which two positive integers does \(\sqrt{33}\) lie?
Answer:
The number \(\sqrt{33}\) is between 5 and 6 because
52 < (\(\sqrt{33}\))2 < 62
e. For what integer x is \(\sqrt{x}\) closest to 5.25? Explain.
Answer:
(5.25)2 = 27.5625
Since \(\sqrt{x}\) is the square root of x, then x2 will give me the integer that belongs in the square root.
(5.25)2 = 27.5625, which is closest to the integer 28.
Question 3.
Identify each of the following numbers as rational or irrational. If the number is irrational, explain how you know.
a. \(\sqrt{29}\)
Answer:
Irrational because 29 is not a perfect square and \(\sqrt{29}\) has an infinite decimal expansion that does not repeat.
b. \(5 . \overline{39}\)
Answer:
Rational
c. \(\frac{12}{4}\)
Answer:
Rational
d. \(\sqrt{36}\)
Answer:
Rational
e. \(\sqrt{5}\)
Answer:
Irrational because 5 is not a perfect square and \(\sqrt{5}\) has an infinite decimal expansion that does not repeat.
f. \(\sqrt [ 3 ]{ 27 }\)
Answer:
Rational
g. π=3.141592…
Answer:
Irrational because pi has a decimal expansion that does not repeat.
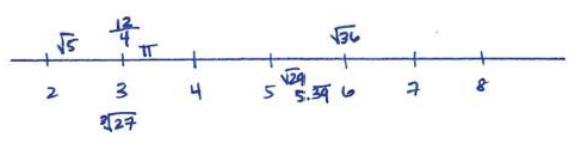
h. Order the numbers in parts (a)–(g) from least to greatest, and place them on a number line.
Answer:
\(\sqrt{29}\) : 52 < (\(\sqrt{29}\))2 < 62, 5.32 < (\(\sqrt{29}\))2 < 5.42, 5.382 < (\(\sqrt{29}\))2 < 5.392
Question 4.
Circle the greater number in each of the pairs (a)–(e) below.
a. Which is greater, 8 or \(\sqrt{60}\) ?
Answer:
8
b. Which is greater, 4 or \(\sqrt{26}\) ?
Answer:
\(\sqrt{26}\)
c. Which is greater, \(\sqrt [ 3 ]{ 64 }\) or \(\sqrt{16}\) ?
Answer:
The numbers are equal: \(\sqrt [ 3 ]{ 64 }\) = 4, \(\sqrt{16}\) = 4
d. Which is greater, \(\sqrt [ 3 ]{ 125 }\)5 or \(\sqrt{30}\) ?
Answer:
\(\sqrt{30}\)
e. Which is greater, -7 or –\(\sqrt{42}\) ?
Answer:
–\(\sqrt{42}\)
f. Put the numbers 9, \(\sqrt{52}\) , and \(\sqrt [ 3 ]{ 216 }\) in order from least to greatest. Explain how you know which order to put them in.
Answer:
\(\sqrt{52}\) is between 7 and 8
\(\sqrt [ 3 ]{ 216 }\) = 6
In order from least to greatest:
\(\sqrt [ 3 ]{ 216 }\), \(\sqrt{52}\), 9
Question 5.
Answer:
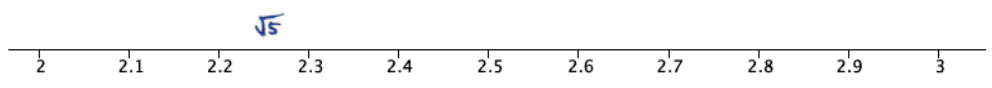
a. Between which two labeled points on the number line would \(\sqrt{5}\) be located?
Answer:
The number \(\sqrt{5}\) is between 2.2 and 2.3.
b. Explain how you know where to place \(\sqrt{5}\) on the number line.
Answer:
I knew that \(\sqrt{5}\) was between 2 and 3 but closer to 2. So next, I checked intervals of tenths beginning with 2.0 to 2.1. The interval that \(\sqrt{5}\) fit between was 2.2 and 2.3 because 2.22 < (\(\sqrt{5}\))2 < 2.32, 4.84 < 5 < 5.29.
c. How could you improve the accuracy of your estimate?
Answer:
To improve the estimate, I would have to continue with the method of rational approximation to determine which interval of hundreths \(\sqrt{5}\) fits between. Once I knew the interval of hundreths, I would check the interval of thousandths, and so on.
\(\sqrt{5}\) : 22 < (\(\sqrt{5}\))2 < 32, 2.22 < (\(\sqrt{5}\))2 < 2.32 4 < 5 < 9
4.84 < 5 < 5.29
Question 6.
Determine the positive solution for each of the following equations.
a. 121 = x2
Answer:
\(\sqrt{121}\) = \(\sqrt{x^{2}}\)
11 = x
112 = 121
121 = 121
b. x3=1000
Answer:
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 1000 }\)
x = 10
103 = 1000
1000 = 1000
c. 17 + x2 = 42
Answer:
17 – 17 + x2 = 42 – 17
x2 = 25
\(\sqrt{x^{2}}\) = \(\sqrt{25}\)
x = 5
17 + 52 = 42
17 + 25 = 42
42 = 42
d. x3 + 3x – 9 = x – 1 + 2x
Answer:
x3 + 3x – 3x – 9 = x – 1 + 2x – 3x
x3 – 9 = -1
x3 – 9 + 9 = -1 + 9
x3 = 8
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 8 }\)
x = 2
23 + (3)(2) – 9 = 2 – 1 + (2)(2)
8 + 6 – 9 = 2 – 1 + 4
14 – 9 = 1 + 4
5 = 5
e. The cube shown has a volume of 216 cm3.
i. Write an equation that could be used to determine the length, l, of one side.
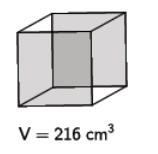
Answer:
V = l3
216 = l3
ii. Solve the equation, and explain how you solved it.
Answer:
216 = l3
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{l^{3}}\)
6 = l
The length of one side is 6 cm.
To solve the equation, I had to take the cube root of both sides of the equation. The cube root of l3, \(\sqrt[3]{l^{3}}\), is l. The cube root of 216, \(\sqrt [ 3 ]{ 216 }\), is 6 because 63 = 216.
Therefore, the length of one side of the cube is 6 cm.