Examine your Preparation and understanding level towards chapter 11 concepts with the help of the Go Math Grade 4 Answer Key Chapter 11 Angles Assessment Test. All you need to do is just click on the links provided here and assess your weak areas and strong areas. So that you can allot time accordingly & fill up the knowledge gaps using the 4th Grade HMH Go Math Homework Practice FL Answer Key Ch 11 Angles. With regular practice, you can secure more marks in your exam.
Go Math Grade 4 Answer Key Chapter 11 Angles
Go Math Grade 4 Answer Key Chapter 11 includes all standard topics of angles. Improve your math skills by taking help from 4th Grade HMH Go Math Solutions Key Chapter 11 Angles Practice FL, Homework practice FL. Educators and Instructors must use of these Grade 4 Go Math Chapter 11 Angles Answer Key & educate their students to understand the topics clearly. Step by step Solutions are given for all the concepts of angles and you can refer to them to easily and clear all your doubts. Utilize these links and begin your practice right away.
Lesson 1:
- Investigate • Angles and Fractional Parts of a Circle Page No. 605
- Investigate • Angles and Fractional Parts of a Circle Lesson Check Page No. 606
Lesson 2:
Lesson 3: Measure and Draw Angles
- Common Core – New Measure and Draw Angles Page No. 611
- Common Core – New Measure and Draw Angles Lesson Check Page No. 612
- Measure and Draw Angles Page No. 615
- Measure and Draw Angles Page No. 616
- Measure and Draw Angles Page No. 617
- Measure and Draw Angles Lesson Check Page No. 618
Mid-Chapter Checkpoint
Lesson 4:
- Investigate • Join and Separate Angles Page No. 623
- Investigate • Join and Separate Angles Lesson Check Page No. 624
Common Core – New
Lesson 5:
- Problem Solving • Unknown Angle Measures Page No. 629
- Problem Solving • Unknown Angle Measures Page No. 630
Common Core – New
- Problem Solving Unknown Angle Measures Common Core – New – Page No. 631
- Problem Solving Unknown Angle Measures Common Core – New Lesson Check – Page No. 632
Chapter 11 Review/Test
- Review/Test Page No. 633
- Review/Test Page No. 634
- Review/Test Page No. 635
- Review/Test Page No. 636
- Review/Test Page No. 637
- Review/Test Page No. 638
- Review/Test Page No. 643
- Review/Test Page No. 644
Common Core – New – Page No. 605
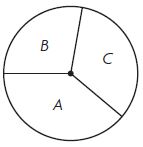
Angles and Fractional Parts of a Circle
Tell what fraction of the circle the shaded angle represents.
Question 1.
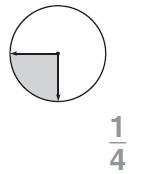
The figure shows that the \(\frac{1}{4}\)th part of the circle is shaded. So, the fraction of the shaded angle is \(\frac{1}{4}\)
Question 2.
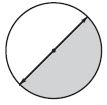
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
Explanation:
Half of the circle is shaded. Thus the fraction of the shaded angle is \(\frac{1}{2}\)
Question 3.
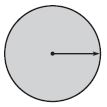
\(\frac{□}{□}\)
Answer: \(\frac{1}{1}\)
Explanation:
From the above figure, we can observe that the complete circle is shaded. So, the fraction of the shaded angle is \(\frac{1}{1}\) or 1.
Tell whether the angle on the circle shows a \(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}\), or 1 full turn clockwise or counterclockwise.
Question 4.
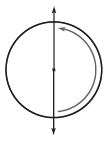
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\) turn counter clockwise
Explanation:
From the figure, we can see that the circle is rotating in the anti-clockwise direction. And it has completed the half turn.
Thus the fraction is \(\frac{1}{2}\) turn counter clockwise
Question 5.
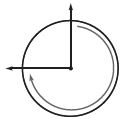
\(\frac{□}{□}\)
Answer: \(\frac{3}{4}\) turn clockwise
Explanation:
The arrow is turned in a clockwise direction. It has completed \(\frac{3}{4}\) turn. So, the angle with direction is \(\frac{3}{4}\) turn clockwise.
Question 6.
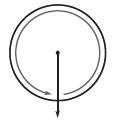
_________
Answer: 1 full turn counter clockwise
Explanation:
From the above picture, we can observe that the circle has completed the full turn in the counter clockwise direction.
Problem Solving
Question 7.
Shelley exercised for 15 minutes. Describe the turn the minute hand made.
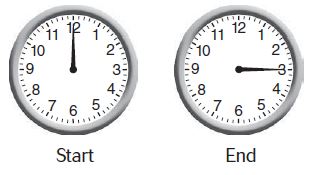
Type below:
_________
Answer: The minute hand made a turn of \(\frac{1}{4}\) clockwise.
Explanation:
Given that,
Shelley exercised for 15 minutes.
So, the fraction of the minute hand made is \(\frac{1}{4}\).
The direction of the minute hand made is clockwise.
So, the answer is the minute hand made a turn of \(\frac{1}{4}\) clockwise.
Question 8.
Mark took 30 minutes to finish lunch. Describe the turn the minute hand made.
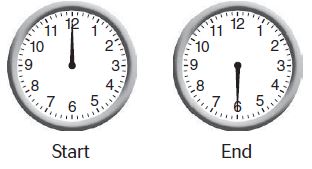
Type below:
_________
Answer: The minute hand made a turn of \(\frac{1}{2}\) clockwise.
Explanation:
Given, Mark took 30 minutes to finish lunch.
The minute hand made a turn in the clockwise direction from 12 to 6.
That means the fraction of the angle is \(\frac{1}{2}\).
Thus the turn minute hand made is \(\frac{1}{2}\) clockwise.
Common Core – New – Page No. 606
Lesson Check
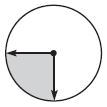
Question 1.
What fraction of the circle does the shaded angle represent
Options:
a. \(\frac{1}{1}\) or 1
b. \(\frac{3}{4}\)
c. \(\frac{1}{2}\)
d. \(\frac{1}{4}\)
Answer: \(\frac{1}{4}\)
Explanation:
From the figure we can say that the fraction of the shaded angle is \(\frac{1}{4}\).
Thus the answer is option D.
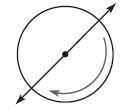
Question 2.
Which describes the turn shown below?
Options:
a. \(\frac{1}{4}\) turn clockwise
b. \(\frac{1}{2}\) turn clockwise
c. \(\frac{1}{4}\) turn counterclockwise
d. \(\frac{1}{2}\) turn counterclockwise
Answer: \(\frac{1}{2}\) turn clockwise
Explanation:
From the figure, we can see that the circle is rotating in the clockwise direction. And it has completed the half turn.
So, the answer is \(\frac{1}{2}\) turn clockwise.
Spiral Review
Question 3.
Which shows \(\frac{2}{3}\) and \(\frac{3}{4}\) written as a pair of fractions with a common denominator?
Options:
a. \(\frac{2}{3} \text { and } \frac{4}{3}\)
b. \(\frac{6}{9} \text { and } \frac{6}{8}\)
c. \(\frac{2}{12} \text { and } \frac{3}{12}\)
d. \(\frac{8}{12} \text { and } \frac{9}{12}\)
Answer: \(\frac{8}{12} \text { and } \frac{9}{12}\)
Explanation:
\(\frac{2}{3}\) and \(\frac{3}{4}\)
The denomintors are different here. So you have to make the denominators common.
\(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
So the answer is option D.
Question 4.
Raymond bought \(\frac{3}{4}\) of a dozen rolls. How many rolls did he buy?
Options:
a. 3
b. 6
c. 7
d. 9
Answer: 9
Explanation:
Raymond bought \(\frac{3}{4}\) of a dozen rolls.
Dozen = 12
\(\frac{3}{4}\) × 12 = 9
Thus the correct answer is option D.
Question 5.
Which of the following lists all the factors of 18?
Options:
a. 1, 2, 4, 9, 18
b. 1, 2, 3, 6, 9, 18
c. 2, 3, 6, 9
d. 1, 3, 5, 9, 18
Answer: 1, 2, 3, 6, 9, 18
Explanation:
The factors of 18 are
1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
6 × 3 = 18
9 × 2 = 18
18 × 1 = 18
Thus the correct answer is option B.
Question 6.
Jonathan rode 1.05 miles on Friday, 1.5 miles on Saturday, 1.25 miles on Monday, and 1.1 miles on Tuesday. On which day did he ride the shortest distance?
Options:
a. Monday
b. Tuesday
c. Friday
d. Saturday
Answer: Friday
Explanation:
Jonathan rode 1.05 miles on Friday, 1.5 miles on Saturday, 1.25 miles on Monday, and 1.1 miles on Tuesday.
The shortest among all is 1.05 miles.
Therefore the answer is option C.
Page No. 609
Question 1.
Find the measure of the angle.
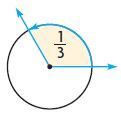
Through what fraction of a circle does the angle turn?
\(\frac{1}{3}=\frac{■}{360}\)
Think: 3 × 12 = 36, so 3 × _____ = 360.
So, the measure of the angle is _____.
_____ degrees
Answer: 120°
Explanation:
The fraction of the shaded angle is \(\frac{1}{3}\)
To measure the angle we have to multiply the fraction of the shaded angle with the total angle.
That means, \(\frac{1}{3}\) × 360
360/3 = 120 degrees.
Thus the angle of the shaded part is 120°
Tell the measure of the angle in degrees.
Question 2.
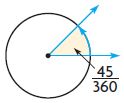
____ °
Answer: 45°
Explanation:
The fraction of the shaded angle is \(\frac{45}{360}\)
Multiply the fraction with the complete angle
\(\frac{45}{360}\) × 360° = 45°
Thus the angle of the above figure is 45°
Question 3.
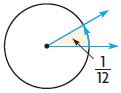
____ degrees
Answer: 30°
Explanation:
The figure shows the fraction of the shaded angle is \(\frac{1}{12}\)
Multiply the fraction with the complete angle
\(\frac{1}{12}\) × 360° = 30°
Therefore the measure of the shaded angle is 30°
Tell the measure of the angle in degrees.
Question 4.
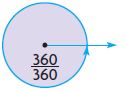
____ °
Answer: 360°
Explanation:
We observe that the circle is shaded completely.
\(\frac{360}{360}\) × 360° = 360°
Thus the above figure is the complete angle.
Question 5.
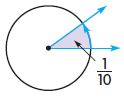
____ °
Answer: 36°
Explanation:
The fraction of the shaded angle is \(\frac{1}{10}\)
Multiply the fraction with the complete angle
\(\frac{1}{10}\) × 360° = 36°
Therefore the measure of the shaded angle is 36°
Classify the angle. Write acute, obtuse, right, or straight.
Question 6.
_________
Answer: Obtuse
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees. However, A reflex angle measures more than 180 degrees but less than 360 degrees.
Question 7.
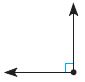
_________
Answer: Right
A right angle is an angle of exactly 90° (degrees), corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles.
Question 8.
_________
Answer: Acute
The acute angle is the small angle which is less than 90°.
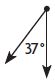
Question 9.
_________
Answer: Straight
A straight angle is 180 degrees. A straight angle changes the direction to point the opposite way.
Question 10.
Is this an obtuse angle? Explain.
Type below:
_________
Answer: Obtuse
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees. However, A reflex angle measures more than 180 degrees but less than 360 degrees.
Question 11.
Alex cut a circular pizza into 8 equal slices. He removed 2 of the slices of pizza. What is the measure of the angle made by the missing slices of pizza?

____ °
Answer: 90°
Explanation:
Alex cut a circular pizza into 8 equal slices.
He removed 2 of the slices of pizza.
The fraction of the missing slices = \(\frac{2}{8}\) = \(\frac{1}{4}\)
The fraction of the missing slices is \(\frac{1}{4}\)
To know the angle we have to multiply the fraction with complete angle i.e., 360°
\(\frac{1}{4}\) × 360° = 90°
Thus the angle of the missing slices is 90°
Page No. 610
Question 12.
Ava started reading at 3:30 p.m. She stopped for a snack at 4:15 p.m. During this time, through what fraction of a circle did the minute hand turn? How many degrees did the minute hand turn?

a. What are you asked to find?
Type below:
_________
Answer: I am asked to find the fraction of a circle did the minute hand turn and how many degrees did the minute hand turn
Question 12.
b. What information can you use to find the fraction of a circle through which the minute hand turned?
Type below:
_________
Answer: The fraction of a circle through which the minute hand-turned \(\frac{3}{4}\) Clockwise.
Question 12.
c. How can you use the fraction of a circle through which the minute hand turned to find how many degrees it turned?
Type below:
_________
Answer:
The figure shows that the fraction of a circle through which the minute hand turned is \(\frac{3}{4}\) Clockwise.
Let the shaded part be x
And the nonshaded part is 90°
x + 90° = 360°
x = 360°- 90°
x = 270°
Therefore the minute hand turns 270° clockwise.
Question 12.
d. Show the steps to solve the problem.
Step 1:
\(\frac{3 × ■}{4 × ■}=\frac{?}{360}\)
Step 2:
\(\frac{3 × 90}{4 × 90}=\frac{■}{360}\)
Type below:
_________
Answer:
\(\frac{3 × 90}{4 × 90}=\frac{■}{360}\)
\(\frac{270}{360} = \frac{■}{360}\)
If the denominators are equal then the numerators must be equated.
■ = 270
Question 12.
e. Complete the sentences. From 3:30 p.m. to 4:15 p.m., the minute hand made a ______ turn clockwise. The minute hand turned ______ degrees.
Type below:
_________
Answer:
From 3:30 p.m. to 4:15 p.m., the minute hand made a \(\frac{3}{4}\) turn clockwise. The minute hand turned 270 degrees.
Question 13.
An angle represents \(\frac{1}{15}\) of a circle. Select the number to show how to find the measure of the angle in degrees.
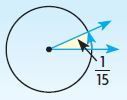
![]()
\(\frac{1}{15}=\frac{1 × □}{15 × □}=\frac{□}{360}\)
Type below:
_________
Answer: 24°
\(\frac{1}{15} × 360° = 24°
Common Core – New – Page No. 611
Degrees
Tell the measure of the angle in degrees.
Question 1.
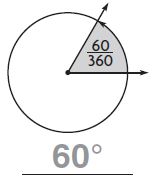
Answer: 60°
Explanation:
Given that the fraction of the shaded angle is [latex]\frac{60}{360}\)
\(\frac{60}{360}\) × 360 = 60°
Thus the angle for the above figure is 60°
Question 2.
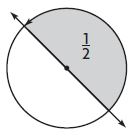
____ °
Answer: 180°
Explanation:
Half of the circle is shaded. The fraction of the shaded angle is \(\frac{1}{2}\)
\(\frac{1}{2}\) × 360 = 360/2 = 180°
Question 3.
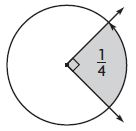
____ °
Answer: 90°
Explanation:
The fraction of the shaded angle is \(\frac{1}{4}\)
To find the angle we need to multiply the fraction with the total angle.
\(\frac{1}{4}\) × 360° = 90°
Classify the angle. Write acute, obtuse, right, or straight.
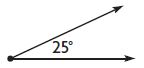
Question 4.
_________
Answer: Acute
Explanation:
25° < 90°
So, the above figure is an acute angle.
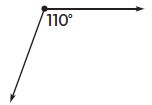
Question 5.
_________
Answer: Obtuse
Explanation:
110° > 90°
So, the figure shown above is an obtuse angle.
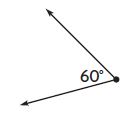
Question 6.
_________
Answer: Acute
Explanation:
60° < 90°
Acute angles measure less than 90 degrees. Thus the above angle is an acute angle.
Classify the triangle. Write acute, obtuse, or right.
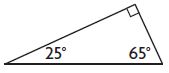
Question 7.
_________
Answer: Right
Explanation:
65 + 25 = 90
The sum of two angles = 90°
Thus the above figure is a right-angled triangle.
Question 8.
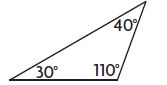
_________
Answer: Obtuse
Explanation:
110° > 90°
So, the above triangle is an obtuse angle.
Question 9.
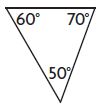
_________
Answer: Acute
Explanation:
50° is less than 90°
Thus the above triangle is an acute angle triangle.
Problem Solving
Ann started reading at 4:00 P.M. and finished at 4:20 P.M.
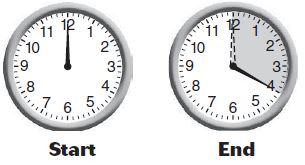
Question 10.
Through what fraction of a circle did the minute hand turn?
\(\frac{□}{□}\)
Answer: \(\frac{1}{3}\) turn clockwise
Explanation:
The fraction of the shaded clock is \(\frac{12}{4}\)
\(\frac{12}{4}\) = \(\frac{1}{3}\)
The minute hand turn clockwise direction.
So, the answer is \(\frac{1}{3}\) turn clockwise
Question 11.
How many degrees did the minute hand turn?
____ °
Answer: 120°
Explanation:
The fraction of the minute hand turn is \(\frac{1}{3}\)
\(\frac{1}{3}\) × 360° = 120°
The minute hand turn 120°
Common Core – New – Page No. 612
Lesson Check
Question 1.
What kind of angle is shown?
![]()
Options:
a. acute
b. obtuse
c. right
d. straight
Answer: straight
A straight angle is 180 degrees. This is a straight angle. A straight angle changes the direction to point the opposite way.
So, the answer is option D.
Question 2.
How many degrees are in an angle that turns through \(\frac{1}{4}\) of a circle?
Options:
a. 45°
b. 90°
c. 180°
d. 270°
Answer: 90°
Explanation:
\(\frac{1}{4}\) × 360°
\(\frac{360}{4}\) = 90°
Thus the correct answer is option B.
Spiral Review
Question 3.
Mae bought 15 football cards and 18 baseball cards. She separated them into 3 equal groups. How many sports cards are in each group?
Options:
a. 5
b. 6
c. 11
d. 12
Answer: 11
Explanation:
Mae bought 15 football cards and 18 baseball cards.
She separated them into 3 equal groups.
Total number of cards = 15 + 18 = 33
33/3 = 11
There are 11 sports cards in each group.
Question 4.
Each part of a race is \(\frac{1}{10}\) mile long. Marsha finished 5 parts of the race. How far did Marsha race?
Options:
a. \(\frac{1}{10}\) mile
b. \(\frac{5}{12}\) mile
c. \(\frac{1}{2}\) mile
d. 5 \(\frac{1}{10}\) miles
Answer: \(\frac{1}{2}\) mile
Explanation:
Each part of a race is \(\frac{1}{10}\) mile long.
Marsha finished 5 parts of the race.
\(\frac{1}{10}\) × 5 = 5/10 = \(\frac{1}{2}\) mile
Thus the correct answer is option C.
Question 5.
Jeff said his city got \(\frac{11}{3}\) inches of snow. Which shows this fraction written as a mixed number?
Options:
a. 3 \(\frac{2}{3}\)
b. 3 \(\frac{1}{3}\)
c. 2 \(\frac{2}{3}\)
d. 1 \(\frac{2}{3}\)
Answer: 3 \(\frac{2}{3}\)
Explanation:
Jeff said his city got \(\frac{11}{3}\) inches of snow.
The mixed fraction of \(\frac{11}{3}\) is 3 \(\frac{2}{3}\)
The correct answer is option A.
Question 6.
Amy ran \(\frac{3}{4}\) mile. Which decimal shows how many miles she ran?
Options:
a. 0.25 mile
b. 0.34 mile
c. 0.5 mile
d. 0.75 mile
Answer: 0.75 mile
Explanation:
Amy ran \(\frac{3}{4}\) mile.
\(\frac{3}{4}\) = \(\frac{75}{100}\)
The decimal form of \(\frac{75}{100}\) is 0.75
So, the answer is option D.
Page No. 615
Question 1.
Measure ∠ABC.
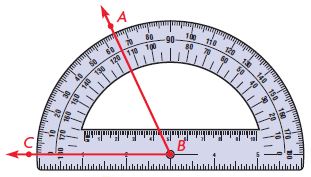
Place the center of the protractor on point ____.
Align ray BC with ____ .
Read where ____ intersects the same scale.
So, m∠ABC is _____.
Type below:
_________
Answer: 65°
Use a protractor to find the angle measure.
Question 2.
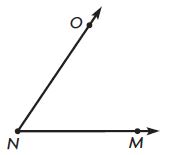
m∠ONM = ____ °
Answer: 55°
Question 3.
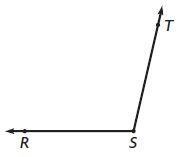
m∠TSR = ____ °
Answer: 105°
Use a protractor to draw the angle.
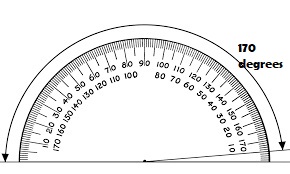
Question 4.
170°
Type below:
_________
Answer:
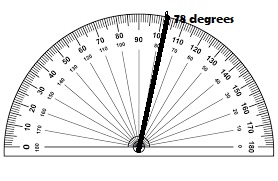
Question 5.
78°
Type below:
_________
Answer:
Use a protractor to find the angle measure.
Question 6.
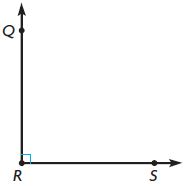
m∠QRS = ____ °
Answer: 90°
Question 7.
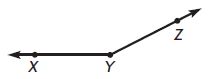
m∠XYZ = ____ °
Answer: 155°
Use a protractor to draw the angle.
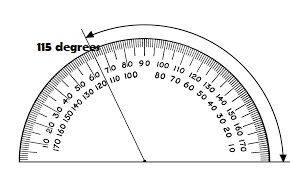
Question 8.
115°
Type below:
_________
Answer:
Question 9.
67°
Type below:
_________
Answer:
Draw an example of each. Label the angle with its measure.
Question 10.
an acute angle
Type below:
_________
Answer:

Question 11.
an obtuse angle
Type below:
_________
Answer:

Question 12.
Elizabeth is making a quilt with scraps of fabric. What is the difference between m∠ABC and m∠DEF?
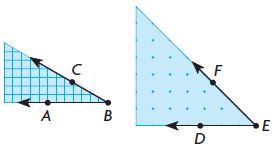
____ °
Answer: 15°
Question 13.
Draw an angle with a measure of 0°.
Describe your drawing.
Type below:
_________
Answer:
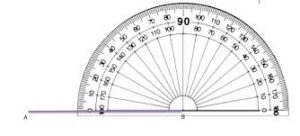
Page No. 616
Question 14.
Hadley wants to divide this angle into three angles with equal measure. What will the measure of each angle be?
____ °
Answer: 30°
Explanation:
Given,
Hadley wants to divide this angle into three angles with equal measure.
The above figure is a right angle = 90°
If he divides into three equal angles
90/3 = 30°
So, the measure of angle will be 30°
Question 15.
Tracy measured an angle as 50° that was actually 130°. Explain her error.
Type below:
_________
Answer: She has measured the angle in the counterclockwise direction. So, that is why she got 50°.
Question 16.
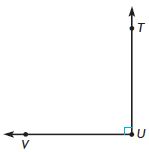
Choose the word or number to complete a true statement about ∠QRS.
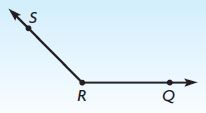
∠QRS is a(n)  angle that has a measure of
angle that has a measure of 
Type below:
_________
Answer: ∠QRS is an obtuse angle that has a measure of 135°.
Earth’s Axis Earth revolves around the sun yearly. The Northern Hemisphere is the half of Earth that is north of the equator. The seasons of the year are due to the tilt of Earth’s axis.
Use the diagrams and a protractor for 17–18.
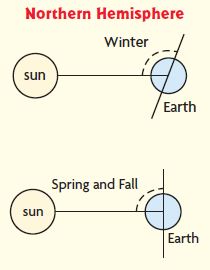
Question 17.
In the Northern Hemisphere, Earth’s axis is tilted away from the sun on the first day of winter, which is often on December 21. What is the measure of the marked angle on the first day of winter, the shortest day of the year?
____ °
Answer: 115°
Explanation:
By seeing the above figure we can say that the angle is an obtuse angle. The mark is above 90° and the marked angle is 115°.
Therefore the measure of the marked angle on the first day of winter, the shortest day of the year is 115°.
Question 18.
Earth’s axis is not tilted away from or toward the sun on the first days of spring and fall, which are often on March 20 and September 22. What is the measure of the marked angle on the first day of spring or fall?
____ °
Answer: 90°
Explanation:
The mark is exactly 90°. So, the angle on the first day of spring or fall is 90°
Common Core – New – Page No. 617
Measure and Draw Angles
Use a protractor to find the angle measure.
Question 1.
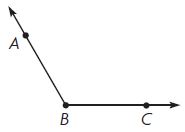
m∠ABC = 120°
By using the protractor we can measure the angle m∠ABC i.e., 120°
Question 2.
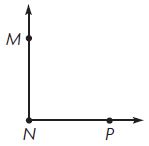
m∠MNP = ____ °
Answer: m∠MNP = 90°
By observing the above figure we can say that the angle of m∠MNP is 90°
Question 3.
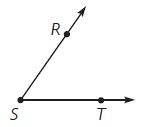
m∠RST = ____ °
Answer: m∠RST = 65°
By using the protractor we can measure m∠RST = 65°
Use a protractor to draw the angle.
Question 4.
40°
Answer:
Question 5.
170°
Answer:

Draw an example of each. Label the angle with its measure.
Question 6.
a right angle
Answer:
A right angle is an angle of exactly 90°

Question 7.
an acute angle
Answer:
The acute angle is the small angle which is less than 90°.

Problem Solving
The drawing shows the angles a stair tread makes with a support board along a wall. Use your protractor to measure the angles.
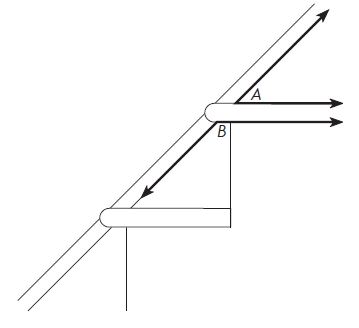
Question 8.
What is the measure of ∠A?
____ °
Answer: 45°
By using the protractor we can measure the angle for A = 45°
Question 9.
What is the measure of ∠B?
____ °
Answer: 135°
The same process is used to measure ∠B = 135°
Common Core – New – Page No. 618
Lesson Check
Question 1.
What is the measure of ∠ABC?
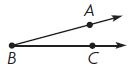
Options:
a. 15°
b. 25°
c. 155°
d. 165°
Answer: 15°
Explanation:
Step 1: Place the center point of the protractor on the point B.
Step 2: Align the 0° mark on the scale of the protractor with ray BC.
Step 3: Find the point where AC meet. Read the angle measure on that scale.
So, the measure of ∠ABC is 15°
Thus the correct answer is option A.
Question 2.
What is the measure of ∠XYZ?
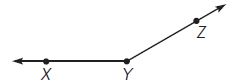
Options:
a. 20°
b. 30°
c. 150°
d. 160°
Answer: 150°
Explanation:
Step 1: Place the center point of the protractor on the point Y.
Step 2: Align the 0° mark on the scale of the protractor with ray XY.
Step 3: Find the point where YZ meet. Read the angle measure on that scale.
So, ∠XYZ = 150°
Therefore the correct answer is option C.
Spiral Review
Question 3.
Derrick earned $1,472 during the 4 weeks he had his summer job. If he earned the same amount each week, how much did he earn each week?
Options:
a. $360
b. $368
c. $3,680
d. $5,888
Answer: $368
Explanation:
Given that, Derrick earned $1,472 during the 4 weeks he had his summer job.
Let the amount he earned per week = x
x × 4 = $1,472
x = 1472 ÷ 4
x = 1472/4 = 368
So, Derrick earned $368 per week.
Question 4.
Arthur baked 1 \(\frac{7}{12}\) dozen muffins. Nina baked 1 \(\frac{1}{12}\) dozen muffins. How many dozen muffins did they bake in all?
Options:
a. 3 \(\frac{2}{3}\)
b. 2 \(\frac{2}{3}\)
c. 2 \(\frac{1}{2}\)
d. \(\frac{6}{12}\)
Answer: 2 \(\frac{2}{3}\)
Explanation:
Given:
Arthur baked 1 \(\frac{7}{12}\) dozen muffins. Nina baked 1 \(\frac{1}{12}\) dozen muffins.
Add both the fractions
Convert mixed fraction into normal fractions
1 \(\frac{7}{12}\) = \(\frac{19}{12}\)
1 \(\frac{1}{12}\) = \(\frac{13}{12}\)
\(\frac{19}{12}\) + \(\frac{13}{12}\) = \(\frac{32}{12}\)
= \(\frac{8}{3}\)
Convert \(\frac{8}{3}\) into mixed fraction = 2 \(\frac{2}{3}\)
So, the answer is option B.
Question 5.
Trisha drew the figure below. What figure did she draw?
![]()
Options:
a. line segment ST
b. ray ST
c. ray TS
d. line TS
Answer: ray TS
A ray can be defined as a part of a line that has a fixed starting point but no endpoint.
Here the point starts from T and ends at S.
So, the figure Trisha drew is ray TS.
The correct answer is option C.
Question 6.
Which describes the turn shown by the angle?
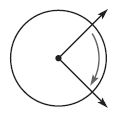
Options:
a. 1 full turn clockwise
b. \(\frac{3}{4 }\) turn clockwise
c. \(\frac{1}{2}\) turn clockwise
d. \(\frac{1}{4}\) turn clockwise
Answer: \(\frac{1}{4}\) turn clockwise
Explanation:
The figure shows that the point turned \(\frac{1}{4}\) in clockwise direction.
So, the answer is option D.
Page No. 619
Choose the best term from the box.
Question 1.
The unit used to measure an angle is called a ________.
________
Answer: The unit used to measure an angle is called a degree.
Question 2.
________ is the opposite of the direction in which the hands of a clock move.
________
Answer: Counterclockwise is the opposite of the direction in which the hands of a clock move.
Question 3.
A ________ is a tool for measuring the size of an angle.
________
Answer: A protractor is a tool for measuring the size of an angle.
Tell whether the angle on the circle shows a \(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}\), or 1 full turn clockwise or counterclockwise.
Question 4.
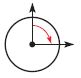
\(\frac{□}{□}\)
Answer: \(\frac{1}{4}\) turn clockwise
The figure shows that the angle turn \(\frac{1}{4}\) in the clockwise direction.
Question 5.
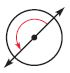
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\) turn counterclockwise
From the above figure, we can see that the angle turn \(\frac{1}{2}\) in the counterclockwise direction.
Question 6.
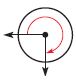
\(\frac{□}{□}\)
Answer: \(\frac{3}{4}\) turn clockwise
The figure shows that the angle turn \(\frac{3}{4}\) in the clockwise direction.
Question 7.
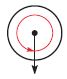
____
Answer: \(\frac{1}{1}\) or 1 turn counterclockwise
From the above figure, we can see that the angle turn \(\frac{1}{1}\) or 1 in the counterclockwise direction.
Tell the measure of the angle in degrees.
Question 8.
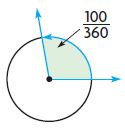
____ °
Answer: 100°
\(\frac{100}{360}\) × 360° = 100°
Question 9.
____ °
Use a protractor to draw the angle.
Question 10.
75°
Type below:
________
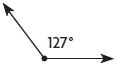
Question 11.
127°
Type below:
________
Page No. 620
Question 12.
Phillip watched a beach volleyball game from 1:45 p.m. to 2:00 p.m. How many degrees did the minute hand turn?

____ °
Answer: 90°
Explanation:
Phillip watched a beach volleyball game from 1:45 p.m. to 2:00 p.m.
The minute hand turned for 15 minutes.
That means \(\frac{1}{4}\) turn clockwise.
Complete angle = 360°
\(\frac{1}{4}\) × 360° = 360°/4 = 90°
Therefore the minute hand turn 90°
Question 13.
What angle does this piece of pie form?

____ °
Answer: 180°
From the above figure, we can see that half of the pie is completed.
Complete angle = 360°
\(\frac{1}{2}\) × 360°
= 180°
The angle for the piece of pie form is 180°
Question 14.
What is m∠CBT? Use a protractor to help you.
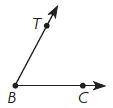
____ °
Answer: 60°
By using the protractor we can say that the angle for the above figure is 60°
Question 15.
Matt cut a circle into 8 equal sections. He drew an angle that measures the same as the total measure of 3 of the sections in the circle. What is the measure of the angle Matt drew?
____ °
Answer: 135°
Explanation:
Matt cut a circle into 8 equal sections.
He drew an angle that measures the same as the total measure of 3 of the sections in the circle.
Complete angle = 360°
Divide the total number of sections by 360°
\(\frac{360}{8}\) = 45°
So, the angle for each section is 45°
The angle for 3 of the sections in the circle = 3 × 45° = 135°
Thus the measure of the angle Matt drew is 135°
Page No. 623
Add to find the measure of the angle. Write an equation to record your work.
Question 1.
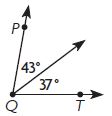
∠PQT = ____ °
Answer: 80°
To find the ∠PQT you have to add 43° and 37°
∠PQT = 43° + 37°
∠PQT = 80°
Question 2.
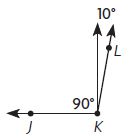
∠JKL = ____ °
Answer: 100°
Let ∠JKL = x°
∠JKL = 90° + 10°
∠JKL = 100°
Question 3.
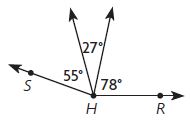
∠RHT = ____ °
Answer:
Let ∠RHT = x°
x = 55° + 27° + 78°
x = 160°
Therefore ∠RHT = 160°
Use a protractor to find the measure of each angle. Label each angle with its measure.
Write the sum of the angle measures as an equation.
Question 4.
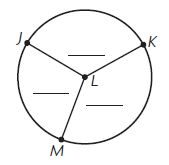
Type below:
________
Answer:
By using the protractor we can measure the angles of the above figures.
m∠KLM = 160°
m∠KLJ = 80°
m∠LMJ = 120°
Question 5.
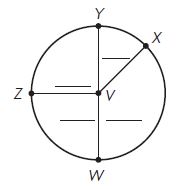
Type below:
________
Answer:
By using the protractor we can measure the angles of the above figures.
m∠WVZ = 90°
m∠YVZ = 90°
m∠WVX = 140°
m∠YVX = 40°
Question 6.
Use Diagrams What is m∠QRT?
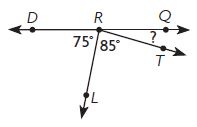
∠QRT = ____ °
Answer: 20°
The above figure is a straight angle.
∠QRT + ∠LRD + ∠RLT = 180
∠QRT + 75° + 85° = 180°
∠QRT + 160° = 180°
∠QRT = 180°- 160°
∠QRT = 20°
Question 7.
Look back at Exercise 1. Suppose you joined an angle measuring 10° to ∠PQT. Draw the new angle, showing all three parts. What type of angle is formed?
Type below:
________
Page No. 624
Question 8.
Stephanie, Kay, and Shane each ate an equal-sized piece of a pizza. The measure of the angle of each piece was 45°. When the pieces were together, what is the measure of the angle they formed?

a. What are you asked to find?
Type below:
________
Answer: What is the measure of the angle for the pizza leftover?
Question 8.
b. What information do you need to use?
Type below:
________
Answer: I need the information about the angle for each piece of pizza.
Question 8.
c. Tell how you can use addition to solve the problem.
Type below:
________
Answer:
The measure of the angle of each piece was 45°
There are 3 pieces of pizza = 45° + 45° + 45° = 135°
Question 8.
d. Complete the sentence. The three pieces of pizza formed a _________ angle.
________
Answer: Obtuse angle
Question 9.
What is the measure of ∠XZW?
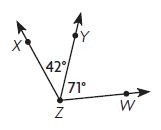
____ °
Answer: 113°
Explanation:
∠XZW = ∠XZY + ∠YZW
∠XZY = 42°
∠YZW = 71°
∠XZW = 42° + 71°
∠XZW = 113°
Question 10.
What is m∠PRS? Use equations to explain and check your answer.
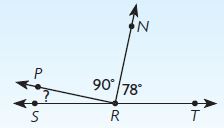
____ °
Answer: 12°
Explanation:
The above figure is a straight angle.
The sum of the three angles must be equal to 180°
m∠PRS + m∠PRN + m∠TRN = 180°
m∠PRS + 90° + 78° = 180°
m∠PRS = 180° – 90° – 78°
m∠PRS = 12°
Common Core – New – Page No. 625
Join and Separate Angles
Add to find the measure of the angle. Write an equation to record your work.
Question 1.
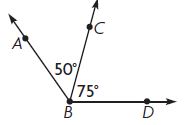
50°+75° = 125°
m∠ABD = 125°
Explanation:
m∠ABC = 50°
m∠CBD = 75°
To find the measure of m∠ABD we have to add m∠ABC and m∠CBD
m∠ABD = 50°+75°
m∠ABD = 125°
Question 2.
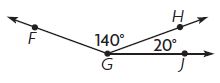
____ ° + ____ ° = ____ ° ; m∠FGJ = ____ °
Answer: 140° + 20° = 160°
m∠FGJ = 160°
Explanation:
m∠FGH = 140°
m∠JGH = 20°
To find the measure of m∠FGJ we need to add m∠FGH and m∠JGH
m∠FGJ = 140° + 20°
m∠FGJ = 160°
Question 3.
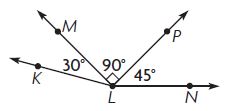
____ ° + ____ ° = ____ ° ; m∠KLN = ____ °
Answer: 30° + 90° + 45° = 165°
m∠KLN = 165°
Explanation:
m∠KLM = 30°
m∠MLP = 90°
m∠PLN = 45°
To find the measure of m∠KLN we need to add m∠KLM, m∠MLP and m∠PLN
m∠KLN = 30° + 90° + 45° = 165°
m∠KLN = 165°
Use a protractor to find the measure of each angle in the circle.
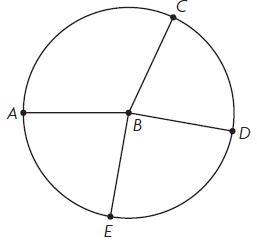
Question 4.
m∠ABC = ____ °
Answer: 115°
Question 5.
m∠DBE = ____ °
Answer: 90°
Question 6.
m∠CBD = ____ °
Answer: 75°
Question 7.
m∠EBA = ____ °
Answer: 80°
Question 8.
Write the sum of the angle measures as an equation.
____ ° + ____ ° + ____ ° + ____ ° = ____ °
Answer:
Sum all the angles = m∠DBE + m∠ABC + m∠CBD + m∠EBA
= 115° + 90° + 75° + 80° = 360°
Problem Solving
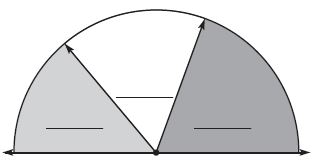
Question 9.
Ned made the design at the right. Use a protractor. Find and write the measure of each of the 3 angles.
____ ° ; ____ ° ; ____ ° ;
Answer: 50°; 60°; 70°
The above figure is a straight angle.
By using the protractor we can measure the angles of the above figure.
The angle of above 3 shades is 50°; 60°; 70°
Question 10.
Write an equation to find the measure of the total angle.
____ ° + ____ ° + ____ ° = ____ °
Answer: Sum of three angles = 50° + 60° + 70° = 180°
Common Core – New – Page No. 626
Lesson Check
Question 1.
What is the measure of m∠WXZ?
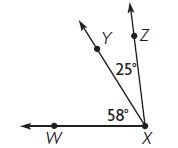
Options:
a. 32°
b. 83°
c. 88°
d. 97°
Answer: 83°
Explanation:
m∠WXZ = m∠WXY + m∠YXZ
Let m∠WXZ be x°
x° = 58° + 25°
x° = 83°
Thus the correct answer is option B.
Question 2.
Which equation can you use to find the m∠MNQ?
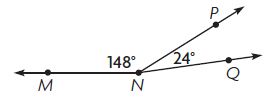
Options:
a. 148° – 24° = ■
b. 148° × 24° = ■
c. 148° ÷ 24° = ■
d. 148° + 24° = ■
Answer: 148° + 24° = ■
Explanation:
To measure the unknown angle we need to add both the angles
m∠MNQ = m∠MNP + m∠PNQ
■ = 148° + 24°
So, the correct answer is option D.
Spiral Review
Question 3.
Joe bought 6 packages of envelopes. Each package contains 125 envelopes. How many envelopes did he buy?
Options:
a. 750
b. 723
c. 720
d. 650
Answer: 750
Explanation:
Joe bought 6 packages of envelopes.
Each package contains 125 envelopes.
To find the total number of envelopes in all 6 packages
We have to multiply number of packages and number of envelopes
= 125 × 6 =750
Thus Joe bought 750 envelopes.
The correct answer is option A.
Question 4.
The Lake Trail is \(\frac{3}{10}\) mile long and the Rock Trail is \(\frac{5}{10}\) long. Bill hiked each trail once. How many miles did he hike in all?
Options:
a. \(\frac{1}{5}\) mile
b. \(\frac{4}{10}\) mile
c. \(\frac{1}{2}\) mile
d. \(\frac{8}{10}\) mile
Answer: \(\frac{8}{10}\) mile
Explanation:
The Lake Trail is \(\frac{3}{10}\) mile long and the Rock Trail is \(\frac{5}{10}\) long. Bill hiked each trail once.
We need to both the fractions
\(\frac{3}{10}\) +\(\frac{5}{10}\)
The denominators are common. So add the numerators.
= \(\frac{8}{10}\)
Bill hiked \(\frac{8}{10}\) miles in all.
Thus the correct answer is option D.
Question 5.
Ron drew a quadrilateral with 4 right angles and 4 sides with the same length. Which best describes the figure he drew?
Options:
a. square
b. rhombus
c. trapezoid
d. parallelogram
Answer: square
Explanation:
A square has got 4 sides of equal length and 4 right angles (right angle = 90 degrees).
So, the answer is option A.
Question 6.
How many degrees are in an angle that turns through \(\frac{3}{4}\) of a circle?
Options:
a. 45°
b. 90°
c. 180°
d. 270°
Answer: 270°
Explanation:
Complete angle = 360°
To measure the angle that turns through is \(\frac{3}{4}\)
multiply \(\frac{3}{4}\) with 360°
360° × \(\frac{3}{4}\) = 270°
So, the answer is option D.
Page No. 629
Question 1.
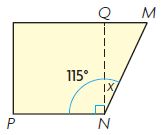
Laura cuts a square out of scrap paper as shown. What is the angle measure of the piece left over?
First, draw a bar model to represent the problem.
Type below:
_________
Question 1.
Next, write the equation you need to solve.
Type below:
_________
Answer:
m∠MNQ + m∠QNP = m∠MNP
x + 90° = 115°
x = 115° – 90°
Question 1.
Last, find the angle measure of the piece left over.
m∠MNQ =
So, the angle measure of the piece left over is _____.
____ °
Answer:
x + 90° = 115°
x = 115° – 90°
x = 25°
So, the angle measure of the piece left over is 25°
Question 2.
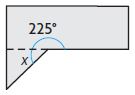
Jackie trimmed a piece of scrap metal to make a straight edge as shown. What is the measure of the piece she trimmed off?
x = ____ °
Answer:
x + 180° = 225°
x = 225°- 180°
x = 45°
Thus the measure of the piece she trimmed off is 45°
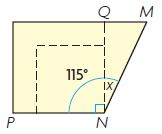
Question 3.
What if Laura cut a smaller square as shown? Would m∠MNQ be different? Explain.
Type below:
_________
Answer: No
m∠MNQ would still be 25°. Only the size of the square changed the angle will be the same.
m∠PNQ and m∠MNP did not change.
Question 4.
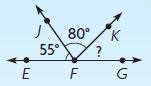
The map shows Marco’s paper route. When Marco turns right onto Center Street from Main Street, what degree turn does he make? Hint: Draw a dashed line to extend Oak Street to form a 180° angle.
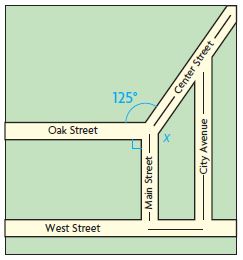
Answer:
x° + 125° + 180° = 360°
x° = 360° – 125° – 180°
x° = 360° – 215°
x° = 145°
Page No. 630
Question 5.
Write an Equation Two angles form a straight angle. One angle measures 89°. What is the measure of the other angle? Explain.
____ °
Answer: 91°
A straight angle measures 180°, so you can subtract 89° from 180°
180° – 89° = 91°
Question 6.
Pose a Problem Look back at Problem 5. Write a similar problem about two angles that form a right angle.
____ °
Answer: Two angles form a right angle. The measure of one angle is 25°. What is the measure of the other angle?
x + 25° = 90°
x °= 90° – 25°
x° = 65°
The measure of other angle is 65°
Question 7.
Sam paid $20 for two T-shirts. The price of each T-shirt was a multiple of 5. What are the possible prices of the T-shirts?
Type below:
_________
Answer:
Sam paid $20 for two T-shirts.
The price of each T-shirt was a multiple of 5.
$20 – 2 T-shirts
x – 1 T-shirt
x = $10
The possible prices of the T-shirts are $10, $10
Another possible price of the T-shirts are $5, $15
Question 8.
Zayna has 3 boxes with 15 art books in each box. She has 2 bags with 11 math books in each bag. If she gives 30 books away, how many art and math books does she have left?
_____ books
Answer: 37 art and math books
Explanation:
Zayna has 3 boxes with 15 art books in each box = 15 × 3 = 45
She has 2 bags with 11 math books in each bag = 11 × 2 = 22
Total number of books = 45 + 22 = 67
If she gives 30 books away, then we have to subtract 30 from 67
67 – 30 = 37
37 art and math books are left.
Question 9.
What’s the Question? It measures greater than 0° and less than 90°.
Type below:
_________
Answer: What is an acute angle?
Question 10.
Two angles, ∠A and ∠B, form a straight angle. ∠A measures 65°. For numbers 10a–10c, select True or False for the statement.
a. ∠B is an acute angle.
i. True
ii. False
Answer: False
Explanation:
Two angles, ∠A and ∠B, form a straight angle. ∠A measures 65°.
65° + ∠B = 180°
∠B = 180° – 65°
∠B = 115°
115° is not an acute angle.
So, the above statement is false.
Question 10.
b. The equation 180° – 65° = x° can be used to find the measure of ∠B.
i. True
ii. False
Answer: True
Question 10.
c. The measure of ∠B is 125°.
i. True
ii. False
Answer: False
65° + ∠B = 180°
∠B = 180° – 65°
∠B = 115°
So, the above statement is false.
Common Core – New – Page No. 631
Problem Solving Unknown Angle Measures
Solve each problem. Draw a diagram to help.
Question 1.

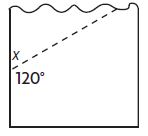
Question 2.
An artist is cutting a piece of metal as shown. What is the angle measure of the piece left over?
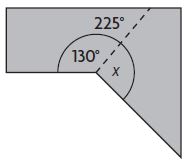
x = ____ °
Answer: 95°
x + 130° = 225°
x = 225° – 130°
x = 95°
Therefore the angle of the piece leftover is 95°.
Question 3.
Joan has a piece of material for making a costume. She needs to cut it as shown. What is the angle measure of the piece left over?
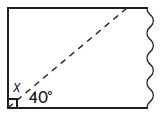
x = ____ °
Answer: 50°
Joan has a piece of material for making a costume. She needs to cut it as shown.
By seeing the above figure we can say that it is a right angle.|
The sum of two must be equal to 90°
Let the unknown angle be x
x + 40° = 90°
x = 90° – 40°
x = 50°
Thue the angle measure of the piece leftover is 50°
Common Core – New – Page No. 632
Lesson Check
Question 1.
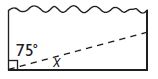
Angelo cuts a triangle from a sheet of paper as shown. What is the measure of ∠x in the triangle?
Options:
a. 15°
b. 25°
c. 75°
d. 105°
Answer: 15°
Explanation:
The above figure is a right angle.
So, to measure the ∠x we have to subtract 75° from 90°
∠x + 75° = 90°
∠x = 90° – 75°
∠x = 15°
Thus the correct answer is option A.
Question 2.
Cindy cuts a piece of wood as shown. What is the angle measure of the piece left over?

Options:
a. 30°
b. 90°
c. 120°
d. 150°
Answer: 120°
Explanation:
x + 90° = 210°
x = 210° – 90°
x = 120°
120° is the measure of the piece leftover.
So, the correct answer is option C.
Spiral Review
Question 3.
Tyronne worked 21 days last month. He earned $79 each day. How much did Tyronne earn last month?
Options:
a. $869
b. $948
c. $1,659
d. $2,169
Answer: $1,659
Explanation:
Tyronne worked 21 days last month.
He earned $79 each day.
$79 × 21 = 1659
Thus Tyronne earned $1,659 last month.
So, the correct answer is option C.
Question 4.
Meg inline skated for \(\frac{7}{10}\) mile. Which shows this distance written as a decimal?
Options:
a. 0.07 mile
b. 0.1 mile
c. 0.7 mile
d. 7.1 miles
Answer: 0.7 mile
Explanation:
Meg inline skated for \(\frac{7}{10}\) mile.
The decimal of the fraction \(\frac{7}{10}\) is 0.7
So, the answer is option C.
Question 5.
Kerry ran 34 mile. Sherrie ran \(\frac{1}{2}\) mile. Marcie ran \(\frac{2}{3}\) mile. Which list orders the friends from least to greatest distance
run?
Options:
a. Kerry, Sherrie, Marcie
b. Kerry, Marcie, Sherrie
c. Sherrie, Kerry, Marcie
d. Sherrie, Marcie, Kerry
Answer: Sherrie, Marcie, Kerry
Explanation:
Kerry ran 34 miles. Sherrie ran \(\frac{1}{2}\) mile. Marcie ran \(\frac{2}{3}\) mile.
The order of the above fractions is Sherrie ran \(\frac{1}{2}\), \(\frac{2}{3}\), 34
The distance from least to greatest is Sherrie, Marcie, Kerry.
so, the correct answer is option D.
Question 6.
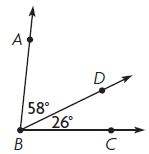
What is the measure of m∠ABC?
Options:
a. 32°
b. 84°
c. 88°
d. 94°
Answer: 84°
Explanation:
m∠ABC = m∠ABD + m∠DBC
m∠ABC = 58° + 26°
m∠ABC = 84°
So, the correct answer is option B.
Page No. 633
Question 1.
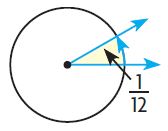
An angle represents \(\frac{1}{12}\) of a circle. Use the numbers to show how to find the measure of the angle in degrees.

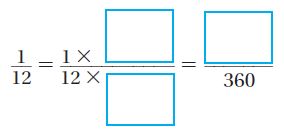
The angle measure is ____ °
Answer: 30°
\(\frac{1}{12}\) × \(\frac{30}{30}\) = \(\frac{30}{360}\)
Thus the angle measure is 30°
Question 2.
Match the measure of each ∠C with the measure of ∠D that forms a straight angle.
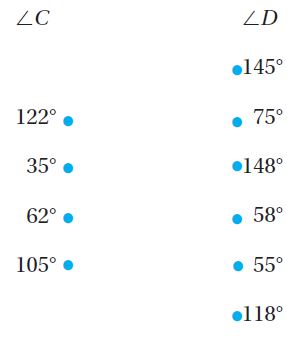
Type below:
_________
i. 122° + 58° = 180°
ii. 35° + 145° = 180°
iii. 62° + 118° = 180°
iv. 105° + 75° = 180°
Question 3.
Katie drew an obtuse angle. Which could be the measure of the angle she drew? Mark all that apply.
Options:
a. 35°
b. 157°
c. 180°
d. 92°
Answer: 157° and 92°
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees.
From the above options, B and D are more than 90°
So, the answer is option B and D.
Question 4.
Draw an angle that represents a \(\frac{1}{4}\) turn counterclockwise on the circle.
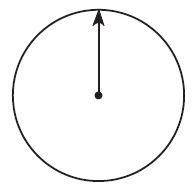
Type below:
_________
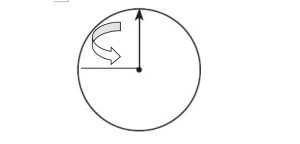
Page No. 634
Question 5.
Renee drew the figure shown. For 5a–5c, select Yes or No to tell whether the statement is true.
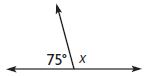
a. The measure of a straight angle is 180°.
i. yes
ii. no
Answer: Yes
By seeing the above figure we can say that the angle is a straight angle.
So, the above statement is true.
Question 5.
b. To find the measure of x, Renee can subtract 75° from 180°.
i. yes
ii. no
Answer: Yes
To know the value of x we have to subtract 75° from 180°.
x = 180° – 75°
Thus the above statement is true.
Question 5.
c. The measure of x is 115°.
i. yes
ii. no
Answer: No
x = 180° – 75°
x = 105°
Thus the above statement is false.
So, the answer is no.
Question 6.
Trey drew this figure with a protractor.
Part A
Write an equation that can be used to find m∠KFG.
Type below:
_________
Answer: 55° + 80° + x = 180°
The figure is a straight angle.
So, the sum of the three angles must be equal to 180°
Let m∠KFG = x
55° + 80° + x = 180°
Question 6.
Part B
What is the measure of m∠KFG? Describe how you solved the equation and how you can check your answer.
____ °
Explain:
_________
Answer: 45°
Explanation:
55° + 80° + x = 180°
x = 180° – 80° – 55°
x = 45°
Question 7.
Use a protractor to find the measure of the angle.
The angle measures ____ °
Answer: 40°
By using a protractor we can measure the angle.
The angle of the above figure is 40°
Page No. 635
Question 8.
Alex drew this angle on the circle. Which describes the angle? Mark all that apply.
Options:
a. \(\frac{1}{4}\) turn
b. clockwise
c. \(\frac{1}{2}\) turn
d. counterclockwise
Answer: \(\frac{1}{2}\) turn
The above figure shows that it is straight angle. So, the fraction of the circle is \(\frac{1}{2}\) turn.
The correct answer is option C.
Question 9.
Miles has a piece of paper that is \(\frac{1}{4}\) of a large circle. He cuts the paper into three equal parts from the center point of the circle. What is the angle measure of each part?
The angle measure is ____ °
Answer: 30°
Explanation:
Miles has a piece of paper that is \(\frac{1}{4}\) of a large circle. He cuts the paper into three equal parts from the center point of the circle.
\(\frac{1}{4}\) of a large circle = 90°
Given that he cut into 3 equal parts = \(\frac{90}{3}\) = 30°
So, the angle for each part is 30°
Question 10.
Use a protractor to find the measure of each angle. Write each angle and its measure in a box ordered by the measure of the angles from least to greatest.

Answer:

Question 11.
Use the numbers and symbols to write an equation that can be used to find the measure of the unknown angle.
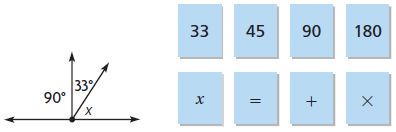
What is the measure of the unknown angle?
____ °
Answer: 57°
Explanation:
Let the unknown angle be x
It is a straight angle.
The sum of three angles = 180°
90° + 33° + x = 180°
x = 180° – 90° – 33°
x = 57°
Page No. 636
Question 12.
Choose the word or number to complete a true statement about m∠JKL.
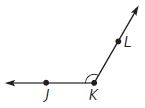

m∠JKL is a(n) ______ angle that has a measure of ____ °.
Answer: m∠JKL is an Obtuse angle that has a measure of 120°.
Question 13.
Vince began practicing piano at 5:15 p.m. He stopped at 5:35 p.m. How many degrees did the minute hand turn during Vince’s practice time?
Explain how you found your answer.
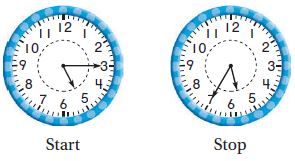
____ °
Explain:
_________
Answer: 120°
I shaded the part of the clock that the minute hand turned from 5:15 p.m. to 5:35 p.m. anmd found that it is \(\frac{1}{3}\) of the circle.
Next, I multiplied \(\frac{1}{3}\) × 360° = 120°
Thus the minute hand moved 120°
Question 14.
An angle measures 125°. Through what fraction of a circle does the angle turn?
\(\frac{□}{□}\) of a circle
Answer: \(\frac{125}{360}\)
The fraction of the circle the angle turned is \(\frac{125}{360}\)
Question 15.
Write the letter for each angle measure in the correct box.

Type below:
__________
Answer:

Page No. 637
Question 16.
For numbers 16a–16b, select the fraction that makes a true statement about the figure.
Question 16.
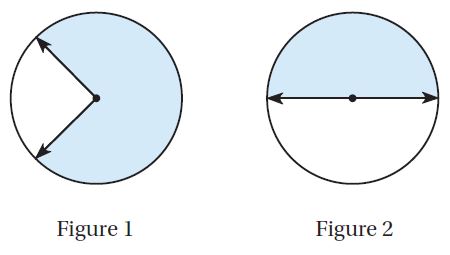
a. The angle in Figure 1 represents a 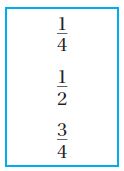 turn.
turn.
\(\frac{□}{□}\) turn
Answer: The angle in Figure 1 represents a \(\frac{3}{4}\) turn
The above figure shows that \(\frac{3}{4}\) part of the circle is shaded. So, the angle represents \(\frac{3}{4}\) turn.
Question 16.
b. The angle in Figure 2 represents a  turn.
turn.
\(\frac{□}{□}\) turn
Answer: The angle in Figure 2 represents a \(\frac{1}{2}\) turn.
From the second figure, we observe that half of the circle is shaded. So, The angle in Figure 2 represents a \(\frac{1}{2}\) turn.
Question 17.
Melanie cuts a rectangle out of a piece of scrap paper as shown. She wants to calculate the angle measure of the piece that is left over.
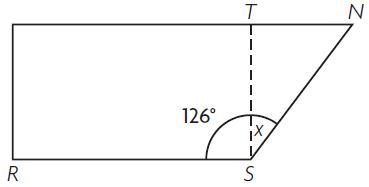
Part A
Draw a bar model to represent the problem.
Question 17.
Part B
Write and solve an equation to find x.
The angle measures ____ °.
Answer: 36°
m∠RST = 90°
m∠RSN = 126°
m∠TSN = x°
x + 90° = 126°
x = 126° – 90°
x = 36°
m∠TSN = 36°
Page No. 638
Question 18.
Two angles, m∠A and m∠B, form a right angle. m∠A measures 32°.
For numbers, 18a–18c, select True or False for the statement.
a. m∠B is an acute angle.
i. True
ii. False
Answer: True
If the sum of two angles is 90°, if one angle is acute then the other angle will be acute.
So, the above statement is true.
Question 18.
b. The equation 180° − 32° = x° can be used to find the measure of m∠B.
i. True
ii. False
Answer: False
Explanation:
Given that the sum of 2 angles is 90°
The sum of m∠A and m∠B = 90°
90° – 32° = x°
So, the above statement is false.
Question 18.
c. The measure of m∠B is 58°.
i. True
ii. False
Answer: True
Explanation:
Let m∠B = x
x° + 32° = 90°
x = 90 – 32
x = 58°.
So, the above statement is true.
Question 19.
A circle is divided into parts. Which sum could represent the angle measures that make up the circle? Mark all that apply.
Options:
a. 120° + 120° + 120° + 120°
b. 25° + 40° + 80° + 105° + 110°
c. 33° + 82° + 111° + 50° + 84°
d. 40° + 53° + 72° + 81° + 90° + 34°
Answer: 25° + 40° + 80° + 105° + 110°; 33° + 82° + 111° + 50° + 84°
Explanation:
The sum of all the angles must be equal to 360°
i. 120° + 120° + 120° + 120° = 480° ≠ 360°
ii. 25° + 40° + 80° + 105° + 110° = 360°
iii. 33° + 82° + 111° + 50° + 84° = 360°
iv. 40° + 53° + 72° + 81° + 90° + 34° = 370° ≠ 360°
So, the correct answers are option B, C.
Question 20.
Use a protractor to find the measures of the unknown angles.
What do you notice about the measures of the unknown angles? Is this what you would have expected? Explain your reasoning.
m∠x = ____ ° m∠y = ____ °
Answer: m∠x = 70°; m∠y = 110°
By using a protractor we can find the measure of m∠y
m∠y = 110°
Let m∠x = x°
Sum of supplementary angles = 180°
110° + x = 180°
x = 180° – 110°
x = 70°
Therefore m∠x = 70°
Page No. 643
Use benchmarks to choose the metric unit you would use to measure each.

Question 1.
mass of a strawberry
__________
Answer: gram
The metric unit used to measure the mass of a strawberry is the gram.
Question 2.
length of a cell phone
__________
Answer: Centimeter
The metric unit used to measure the length of a cell phone is Centimeter.
Circle the better estimate.
Question 3.
width of a teacher’s desk
10 meters or 1 meter
__________
Answer: 1 meter
The estimation of the width of the teacher’s desk is 1 meter.
Question 4.
the amount of liquid a punch bowl holds
2 liters or 20 liters
__________
Answer: 2 liters
20 liters is greater than 2 liters.
The estimation of the amount of liquid a punch bowl holds is 2 liters.
Question 5.
distance between Seattle and San Francisco
6 miles or 680 miles
__________
Answer: 680 miles
The distance between Seattle and San Francisco is 680 miles.
Use benchmarks to choose the customary unit you would use to measure each.

Question 6.
length of a football field
__________
Answer: Yard
The units to measure the length of a football field is Yards.
Question 7.
weight of a pumpkin
__________
Answer: Pound
The customary unit I use to measure the weight of a pumpkin is pounds.
Circle the better estimate.
Question 8.
weight of a watermelon
4 pounds or 4 ounces
__________
Answer: 4 pounds
The estimation of the weight of watermelon is 4 pounds.
Question 9.
the amount of liquid a fish tank holds
10 cups or 10 gallons
__________
Answer: 10 gallons
The estimation of the amount of liquid a fish tank holds is 10 gallons.
Complete the sentence. Write more or less.
Question 10.
Matthew’s large dog weighs ________ than one ton.
________
Answer: Less
1 ton = 1000 kgs
The weight of dogs can’t be more than a ton.
So, Matthew’s large dog weighs less than one ton.
Question 11.
The amount of liquid a sink can hold is _______ than one cup of water.
________
Answer: More
1 cup holds very less amount of water.
So, The amount of liquid a sink can hold is more than one cup of water.
Question 12.
A paper clip has a mass of _______ than one kilogram.
________
Answer: Less
The weight of a paper clip is about 1 gram.
So, A paper clip has a mass of less than one kilogram.
Page No. 644
For 13–15, use benchmarks to explain your answer.

Question 13.
Cristina is making macaroni and cheese for her family. Would Cristina use 1 pound of macaroni or 1 ounce of macaroni?
__________
Answer: Cristina should use 1 pound of macaroni.
Question 14.
Which is the better estimate for the length of a kitchen table, 200 centimeters or 200 meters?
__________
Answer: 200 centimeters
Centimeters are less than meters. The length of the kitchen will be measured in centimeters.
So, the answer is 200 centimeters.
Question 15.
Jodi wants to weigh her cat and measure its standing height. Which two units should she use?
weight: ________
height: ________
Answer:
The weight of the cat should be measured in Kilograms.
The height of the cat should be measured in Centimeters.
Question 16.
Evaluate Reasonableness Dalton used benchmarks to estimate that there are more cups than quarts in one gallon. Is Dalton’s estimate reasonable? Explain.
Type below:
__________
Answer: Dalton’s reasoning is correct because the measurement of cups is smaller than the measurement of quarts, therefore there would be more cups in a gallon than quarts.
Question 17.
Select the correct word to complete the sentence. Justine is thirsty after running two miles.
She should  of water.
of water.
__________
Answer: 1 pint
The suitable word for the above sentence is the pint. Pint is a measure for liquid equal to about half a liter. There are eight pints in a gallon.
Conclusion
Hoping that the data provided here has shed some light on the students of grade 4. If teachers & parents want to make their kids learn all angles concepts properly then make sure they refer to these Go Math Grade 4 Chapter 11 Angles Answer Key. Need any assistance then check our other articles such as HMH Go Math 4th Grade Chapter 11 Homework Practice FL Angles.
