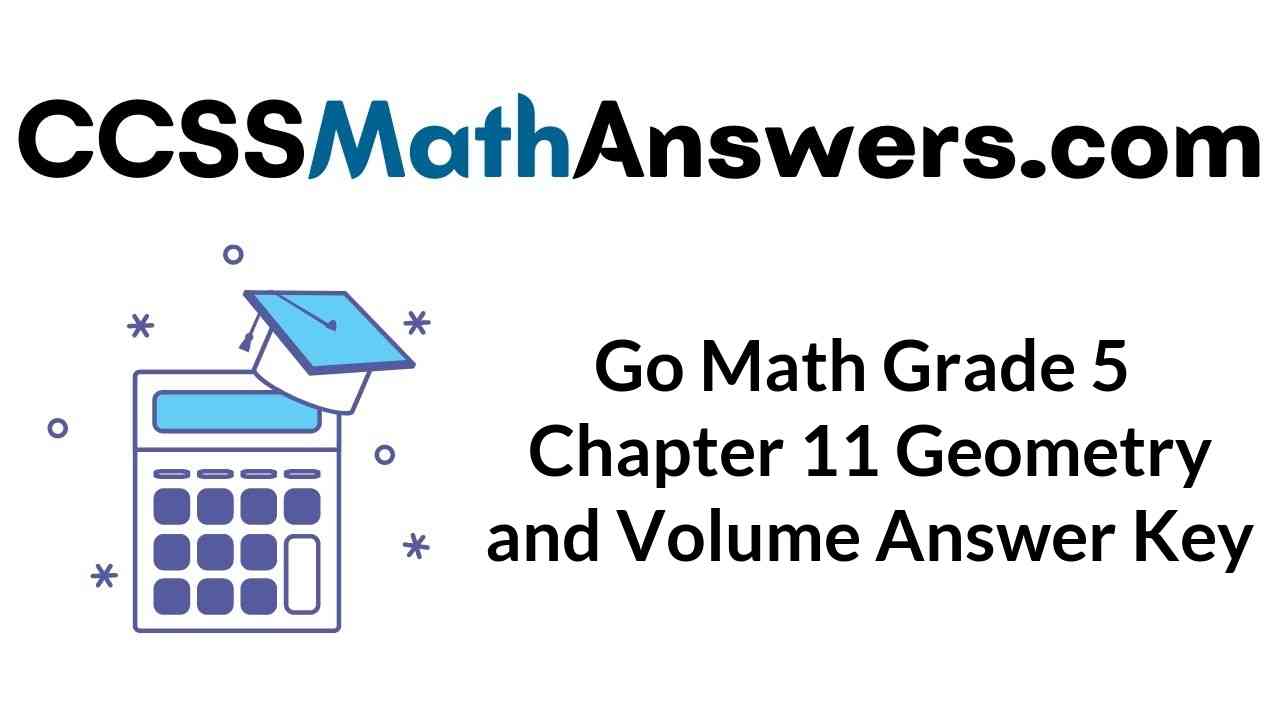Go Math Grade 5 Answer Key Chapter 11 Geometry and Volume comes with Crystal Clear Solutions and makes it easy for you to grasp the topics in it. Get Acquainted with the Geometry and Volume of Rectangular Prisms in the later sections. We provide Go Math Grade 5 Answer Key by Subject experts and explained them clearly so that students will no longer feel the concepts of Geometry and Volume difficult anymore.
Go Math Grade 5 Answer Key Chapter 11 Geometry and Volume
Anyone who wishes to know the Procedure on How to find the Geometry and Volume of different shapes can get them using the 5th Grade Go Math Answer Key for Ch 11 Geometry and Volume. You can access the Topics of 5th Grade Go Math Answer Key Chapter 11 through the direct links available out there. The Topics Covered in the Geometry and Volume Chapter include polygons, quadrilaterals, triangles, understand volume, estimate volume, the volume of the rectangular prism, etc.
Lesson 1: Polygons
- Share and Show – Lesson 1: Polygons – Page No. 639
- Problem Solving – Lesson 1: Polygons – Page No. 640
Lesson 2: Triangles
- Share and Show – Lesson 2: Triangles – Page No. 645
- Problem Solving – Lesson 2: Triangles – Page No. 646
Lesson 3: Quadrilaterals
- Share and Show – Lesson 3: Quadrilaterals – Page No. 651
- Problem Solving – Lesson 3: Quadrilaterals – Page No. 652
Lesson 4: Properties of Two-Dimensional Figures
- Share and Show – Lesson 4: Properties of Two-Dimensional Figures – Page No. 455
- On Your Own – Lesson 4: Properties of Two-Dimensional Figures – Page No. 456
- Share and Show – Lesson 4: Properties of Two-Dimensional Figures – Page No. 656
- Problem Solving – Lesson 4: Properties of Two-Dimensional Figures – Page No. 657
Mid-Chapter Checkpoint
Lesson 5: Unit Cubes and Solid Figures
- Share and Show – Lesson 5: Unit Cubes and Solid Figures – Page No. 665
- Lesson 5: Unit Cubes and Solid Figures – Page No. 666
Lesson 6: Understand Volume
- Share and Show – Lesson 6: Understand Volume – Page No. 671
- Problem Solving – Lesson 6: Understand Volume – Page No. 672
Lesson 7: Estimate Volume
- Share and Show – Lesson 7: Estimate Volume – Page No. 677
- Problem Solving – Lesson 7: Estimate Volume – Page No. 678
Lesson 8: Volume of Rectangular Prisms
- Share and Show – Lesson 8: Volume of Rectangular Prisms – Page No. 683
- UNLOCK the Problem – Lesson 8: Volume of Rectangular Prisms – Page No. 684
Lesson 9: Algebra Apply Volume Formulas
- Share and Show – Lesson 9: Algebra Apply Volume Formulas – Page No. 689
- Problem Solving – Lesson 9: Algebra Apply Volume Formulas – Page No. 690
Lesson 10: Problem Solving Compare Volumes
- Share and Show – Lesson 10: Problem Solving Compare Volumes – Page No. 695
- On Your Own – Lesson 10: Problem Solving Compare Volumes – Page No. 696
Lesson 11: Find Volume of Composed Figures
- Share and Show – Lesson 11: Find Volume of Composed Figures – Page No. 701
- Problem Solving – Lesson 11: Find Volume of Composed Figures – Page No. 702
Chapter Review/Test
- Chapter Review/Test – Page No. 705
- Chapter Review/Test – Page No. 706
- Chapter Review/Test – Page No. 707
- Chapter Review/Test – Page No. 708
- Chapter Review/Test – Page No. 709
- Chapter Review/Test – Page No. 710
- Chapter Review/Test – Page No. 4910
- Chapter Review/Test – Page No. 4920
- Chapter Review/Test – Page No. 4930
- Chapter Review/Test – Page No. 4940
Share and Show – Lesson 1: Polygons – Page No. 639
Question 1.
Name the polygon. Then use the markings on the figure to tell whether it is a regular polygon or not a regular polygon.
a. Name the polygon.
__________
Answer: Triangle
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of three sides. So, the name of the polygon is a triangle.
Question 1.
b. Are all the sides and all the angles congruent?
_____
Answer: Yes
Explanation:
When line segments have the same length or when angles have the same measure, they are congruent. All sides are equal in the above figure.
Thus the above figure is congruent.
Question 1.
c. Is the polygon a regular polygon?
_____
Answer: Yes
Explanation:
In a regular polygon, all sides are congruent and all angles are congruent.
The above figure has the same sides and same angles. Thus the above figure is a regular polygon.
Name each polygon. Then tell whether it is a regular polygon or not a regular polygon.
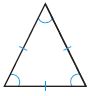
Question 2.
Name: __________
Type: __________
Answer:
i. Hexagon
ii. Regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 6 sides. So, the name of the polygon is Hexagon.
In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above figure is a regular polygon.
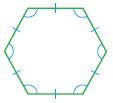
Question 3.
Name: __________
Type: __________
Answer:
i. Quadrilateral
ii. Not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 4 sides. So, the name of the polygon is Quadrilateral.
The above figure doesn’t have the same sides thus the above figure is not a regular polygon.
Question 4.
Name: __________
Type: __________
Answer:
i. Octagon
ii. Regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 8 sides. So, the name of the polygon is Octagon.
In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Octagon is a regular polygon.
Name each polygon. Then tell whether it is a regular polygon or not a regular polygon.
Question 5.
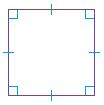
Name: __________
Type: __________
Answer:
i. Quadrilateral
ii. Regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 4 sides. So, the name of the polygon is Quadrilateral.
In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Quadrilateral is a regular polygon.
Question 6.
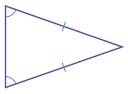
Name: __________
Type: __________
Answer:
i. Triangle
ii. Not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of three sides. So, the name of the polygon is a triangle.
The above figure doesn’t have the same sides thus the above figure is not a regular polygon.
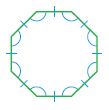
Question 7.
Name: __________
Type: __________
Answer:
i. Heptagon
ii. Regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of 7 sides. So, the name of the polygon is Heptagon.
In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Heptagon is a regular polygon.
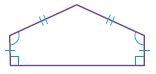
Question 8.
Name: __________
Type: __________
Answer:
i. Hexagon
ii. Not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of six sides. So, the name of the polygon is a Hexagon.
The above figure doesn’t have the same sides and angles thus the above figure is not a regular polygon.
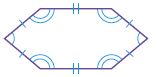
Question 9.
Name: __________
Type: __________
Answer:
i. Pentagon
ii. Not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of five sides. So, the name of the polygon is a Pentagon.
The above figure doesn’t have the same sides and angles thus the above figure is not a regular polygon.
Question 10.
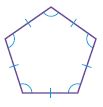
Name: __________
Type: __________
Answer:
i. Pentagon
ii. Regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has. The above figure consists of five sides. So, the name of the polygon is a Pentagon.
In a regular polygon, all sides are congruent and all angles are congruent. The above figure has the same sides and same angles. Thus the above Pentagon is a regular polygon.
Problem Solving – Lesson 1: Polygons – Page No. 640
For 11–12, use the Castel del Monte floor plan at the right.
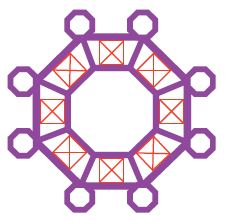
Question 11.
Which polygons in the floor plan have four equal sides and four congruent angles? How many of these polygons are there?
polygon: __________
The number of polygons: __________
Answer:
polygon: Quadrilateral
The number of polygons: 8
Explanation:
By seeing the above figure we can say that there are eight Quadrilaterals in the octagon. And the number of polygons is 8.
Question 12.
Is there a quadrilateral in the floor plan that is not a regular polygon? Name the quadrilateral and tell how many of the quadrilaterals are in the floor plan.
Name of quadrilateral: __________
The number of quadrilaterals: __________
Answer:
Name of quadrilateral: Trapezoid
The number of quadrilaterals: 8
Explanation:
The name of the Quadrilateral for the above figure is Trapezoid. There is 8 number of quadrilaterals in the floor plan.
Question 13.
Sketch eight points. Then connect the points to draw a closed plane figure.
What kind of polygon did you draw?
__________
Answer: Octagon

Question 14.
Look at the angles for all regular polygons. As the number of sides increases, do the measures of the angles increase or decrease? What pattern do you see?
angles measures __________
Answer: Increase
Explanation:
As the number of sides increases, the measures of the angles increase.
we know that
The measure of the interior angle in a regular polygon is equal to
x = (n-2)/n(180°)
where
n is the number of sides of the regular polygon.
x is the measure of the interior angle in a regular polygon.
Question 15.
Test Prep Which of the following is a regular hexagon?
Options:
a. 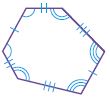
b. 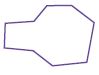
c. 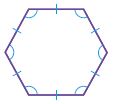
d. 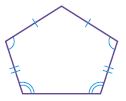
Answer: 
Share and Show – Lesson 2: Triangles – Page No. 645
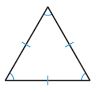
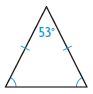
Classify each triangle. Write isosceles, scalene, or equilateral.
Then write acute, obtuse, or right.
Question 1.
△ __________
∠ __________
Answer:
△ – Scalene
∠ – Acute
Explanation:
The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. The angles are less than 90° thus the angle is known as an acute angle.
Question 2.
△ __________
∠ __________
Answer:
△ – Equilateral
∠ – Acute
Explanation:
The 3 sides of the triangle are equal. If three sides of the triangle are equal it is known as the equilateral triangle. The angles are less than 90° thus the angle is known as an acute angle.
Question 3.
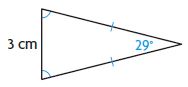
△ __________
∠ __________
Answer:
△ – Isosceles
∠ – Acute
Explanation:
The 2 sides of the triangle are equal and the third side is not equal. If two sides of the triangle are different it is known as Isosceles.
The angles are less than 90° thus the angle is known as an acute angle.
On Your Own
Classify each triangle. Write isosceles, scalene, or equilateral.
Then write acute, obtuse, or right.
Question 4.
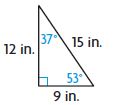
△ __________
∠ __________
Answer:
△ – Scalene
∠ – Right
Explanation:
The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. One of the angle is 90° thus the angle is known as a right angle.
Question 5.
△ __________
∠ __________
Answer:
△ – Isosceles
∠ – Acute
Explanation:
The 2 sides of the triangle are equal and the third side is not equal. If two sides of the triangle are different it is known as Isosceles.
The angles are less than 90° thus the angle is known as an acute angle.
Question 6.
△ __________
∠ __________
Answer:
△ – Scalene
∠ – Obtuse
Explanation:
The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. The angles are more than 90° thus the angle is known as an obtuse angle.
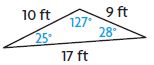
A triangle has sides with the lengths and angle measures given.
Classify each triangle. Write isosceles, scalene, or equilateral.
Then write acute, obtuse, or right.
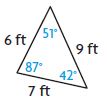
Question 7.
sides: 3.5 cm, 6.2 cm, 3.5 cm
angles: 27°, 126°, 27°
△ __________
∠ __________
Answer:
△ – Isosceles
∠ – Obtuse
Explanation:
The 2 sides of the triangle are equal and the third side is not equal. If two sides of the triangle are different it is known as Isosceles. One of the angle is more than 90° thus the angle is known as an obtuse angle.
Question 8.
sides: 2 in., 5 in., 3.8 in.
angles: 43°, 116°, 21°
△ __________
∠ __________
Answer:
△ – Scalene
∠ – Obtuse
Explanation:
The 3 sides of the triangle are unequal. If three sides of the triangle are different it is known as Scalene. One of the angle is more than 90° thus the angle is known as an obtuse angle.
Question 9.
Circle the figure that does not belong.
Type below:
__________
Answer:
Problem Solving – Lesson 2: Triangles – Page No. 646
Question 10.
Draw 2 equilateral triangles that are congruent and share a side. What polygon is formed? Is it a regular polygon?
What polygon is formed? __________
Is it a regular polygon? __________
Answer:
The name for the polygon is Quadrilateral.
In a regular polygon, all sides are congruent and all angles are congruent.
Question 11.
What’s the Error? Shannon said that a triangle with exactly 2 congruent sides and an obtuse angle is an equilateral obtuse triangle. Describe her error.
Type below:
__________
Answer: All angles of an equilateral triangle are acute. You cannot have an obtuse angle in an equilateral angle. And all of the angles must be congruent.
Question 12.
Test Prep Which kind of triangle has exactly 2 congruent sides?
Options:
a. isosceles
b. equilateral
c. scalene
d. right
Answer: isosceles
Explanation:
An isosceles triangle, therefore, has both two equal sides and two equal angles.
Thus the correct answer is option A.
Connect to Science
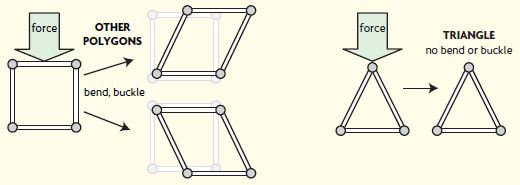
Classify the triangles in the structures below. Write isosceles, scalene, or equilateral. Then write acute, obtuse, or right.
Question 13.

△ __________
∠ __________
Answer:
△ – Equilateral triangle
∠ – Acute
Explanation:
From the figure, we can see an equilateral triangle. In an equilateral triangle, all sides will be less than 90°. So it is an acute angle.
Question 14.

△ __________
∠ __________
Answer:
△ – Scalene triangle
∠ – Right
Explanation:
In the above figure, we can see a right-angle triangle. The three sides of the above triangle is different. So, it is known as the scalene triangle.
Share and Show – Lesson 3: Quadrilaterals – Page No. 651
Question 1.
Use quadrilateral ABCD to answer each question. Complete the sentence.
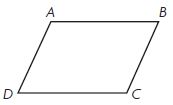
a. Measure the sides. Are any of the sides congruent?
Mark any congruent sides.
_____
Answer: Yes
Explanation:
The above figure consists of same sides. Thus the above Quadrilateral is congruent.
Question 1.
b. How many right angles, if any, does the quadrilateral have?
_____
Answer: 0
The above figure doesn’t have any straight line. Thus the above figure has 0 right angles.
Question 1.
c. How many pairs of parallel sides, if any, does the quadrilateral have?
_____ pairs
Answer: 2
Explanation:
The above has two parallel sides. Yes, the Quadrilateral has the parallel sides.
Question 1.
So, quadrilateral ABCD is a ______________ .
_________
Answer: Parallelogram
Explanation:
A parallelogram is a special trapezoid with opposite sides are equal.
Classify the quadrilateral in as many ways as possible.
Write quadrilateral, parallelogram, rectangle, rhombus, square, or trapezoid.
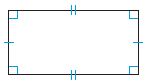
Question 2.
1. _________
2. _________
3. _________
Answer:
The possible ways of Quadrilateral are:
1. Rectangle
2. Parallelogram
3. Quadrilateral
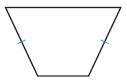
Question 3.
1. _________
2. _________
Answer:
The possible ways of Quadrilateral are:
1. Quadrilateral
2. Trapezoid
On Your Own
Classify the quadrilateral in as many ways as possible.
Write quadrilateral, parallelogram, rectangle, rhombus, square, or trapezoid.
Question 4.
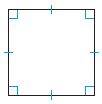
1. _________
2. _________
3. _________
4. _________
5. _________
Answer:
The possible ways of Quadrilateral for the above figure are:
1. Square
2. Quadrilateral
3. Parallelogram
4. Rectangle
5. Rhombus
Question 5.
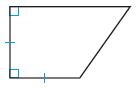
1. _________
2. _________
Answer:
The possible ways of Quadrilateral for the above figure are:
1. Trapezoid
2. Parallelogram
Question 6.
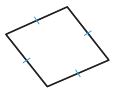
1. _________
2. _________
3. _________
Answer:
The possible ways of Quadrilateral for the above figure are:
1. Rhombus
2. Parallelogram
3. Square
Question 7.
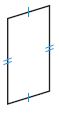
1. _________
2. _________
Answer:
The possible ways of Quadrilateral for the above figure are:
1. Rectangle
2. Parallelogram
Problem Solving – Lesson 3: Quadrilaterals – Page No. 652
Solve the problems.
Question 8.
A quadrilateral has exactly 2 congruent sides. Which quadrilateral types could it be? Which quadrilaterals could it not be?
Type below:
_________
Answer: A rectangle has 2 congruent sides.
Explanation:
The type of quadrilateral that has two congruent sides is a rectangle.
Question 9.
What’s the Error? A quadrilateral has exactly 3 congruent sides. Davis claims that the figure must be a rectangle. Why is his claim incorrect? Use a diagram to explain your answer.
Type below:
_________
Answer: Daviss’s claim is incorrect because a rectangle does not have three congruent sides.
Question 10.
The opposite corners of a quadrilateral are right angles. The quadrilateral is not a rhombus. What kind of quadrilateral is this figure? Explain how you know.
Type below:
_________
Answer:
It depends, is it just one set of opposite angles that are right angles? Then it could be just a quadrilateral, or it could be a kite, or it could be a rectangle. Because a Quadrilateral is the least restrictive, the best answer is. “It is a quadrilateral”.
Or is it both sets of opposite angles are right angles? Then it can only be a “rectangle, that is not a square”.
Question 11.
I am a figure with four sides. I can be placed in the following categories: quadrilateral, parallelogram, rectangle, rhombus, and square. Draw me. Explain why I fit into each category.
Type below:
_________
Answer: Square

Question 12.
Test Prep A quadrilateral has exactly 1 pair of parallel sides and no congruent sides. What type of quadrilateral is it?
Options:
a. rectangle
b. rhombus
c. parallelogram
d. trapezoid
Answer: Trapezoid
Explanation:
A quadrilateral with one pair of parallel sides is a trapezoid.
Thus the correct answer is option D.
Share and Show – Lesson 4: Properties of Two-Dimensional Figures – Page No. 455
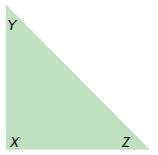
Question 1.
Erica thinks that triangle X Y Z, below, has two congruent sides, but she does not have a ruler to measure the sides. Are two sides congruent?
First, trace the triangle and cut out the tracing.
Type below:
_________
Answer:
Question 1.
Then, fold the triangle to match each pair of sides to determine if at least two of the sides are congruent. As you test the sides, record or draw the results for each pair to make sure that you have checked all pairs of sides. Possible drawings are shown.
Type below:
_________
Question 1.
Finally, answer the question.
______
Answer: Yes
Question 2.
What if Erica also wants to show, without using a protractor, that the triangle has one right angle and two acute angles? Explain how she can show this.
Answer:
The sum of three angles = 180
If one of the angles is 90 then the other two angles will be acute angles.
Question 3.
December, January, and February were the coldest months in Kristen’s town last year. February was the warmest of these months. December was not the coldest. What is the order of these months from coldest to warmest?
Coldest: _________
_________
Warmest: _________
_________
Answer:
Coldest: January
December
Warmest: February
Explanation:
January and December are the coldest months of the year depending on the direction of the wind. February is the warmest month among these months.
Question 4.
Jan enters a 20-foot by 30-foot rectangular room. The long sides face north and south. Jan enters the exact center of the south side and walks 10 feet north. Then she walks 8 feet east. How far is she from the east side of the room?
______ ft
Answer: 7 feet
Explanation:
Given that,
Jan enters a 20-foot by 30-foot rectangular room.
The long sides face north and south.
Jan enters the exact center of the south side and walks 10 feet north.
Then she walks 8 feet east.
Jan is 7 feet from the east wall in the room.
On Your Own – Lesson 4: Properties of Two-Dimensional Figures – Page No. 456
Question 5.
Max drew a grid to divide a piece of paper into 18 congruent squares, as shown. What is the least number of lines Max can draw to divide the grid into 6 congruent rectangles?
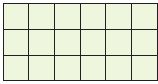
______ lines
Answer: 3 lines
Explanation:
From the above figure, we can see that there are 18 congruent squares.
To find the least number of lines Max can draw we have to divide number of squares by number of congruent rectangles
18 ÷ 6 = 3
Thus the least number of lines that Max can Draw is 3 lines.
Question 6.
Of the 95 fifth and sixth graders going on a field trip, there are 27 more fifth-graders than sixth graders. How many fifth graders are going on the field trip?
5th graders = ______
Answer: 61
Explanation:
Since we are not told how many 6th graders are going on the trip let’s use a variable, the letter x.
Now let’s understand the problem in the “math” language.
x= the number of 6th graders.
X+27= the number of 5th graders since there are 27 more fifth-graders than sixth graders.
x+x+27 = 95
2x+27=95
-27 -27
2x+ 0 =68
2x=68
divide by 2 on both sides.
x = 34
Now, remember how x+27 = the number of 5th graders going on the trip?
Since we know that x=34, substitute the x as 34+27 which = 61 fifth graders going on the trip.
Use the map to solve 7–8.
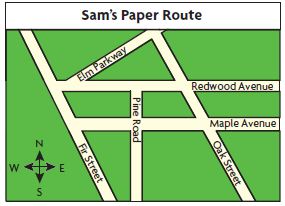
Question 7.
Sam’s paper route begins and ends at the corner of Redwood Avenue and Oak Street. His route is made up of 4 streets, and he makes no 90° turns. What kind of polygon do the streets of Sam’s paper route form? Name the streets in Sam’s route.
_________
Answer: Parallelogram
Explanation:
Given that, Sam’s paper route begins and ends at the corner of Redwood Avenue and Oak Street. His route is made up of 4 streets, and he makes no 90° turns.
By following the route map we can say that the polygon is a parallelogram.
Question 8.
Sam’s paper route includes all 32 houses on two pairs of parallel streets. If each street has the same number of houses, how many houses are on each street?
Name the parallel streets.
______ houses on each street
Answer: 8
Explanation:
Given,
Sam’s paper route includes all 32 houses on two pairs of parallel streets.
If each street has same number of houses we have to divide 32 by 4
32 ÷ 4 = 8
Thus there are 8 houses on each street.
Question 8.
Test Prep Which figure below is a quadrilateral that has opposite sides that are congruent and parallel?
Options:
a. 
b. 
c. 
d. 
Answer: 
Explanation:
Square is a type of quadrilateral that has opposite sides that are congruent and parallel.
Thus the correct answer is option B.
Share and Show – Lesson 4: Properties of Two-Dimensional Figures – Page No. 656
Classify the solid figure. Write prism, pyramid, cone, cylinder, or sphere.
Question 1.
_________
Answer: Triangular prism
Explanation:
A triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise, it is oblique.
Question 2.
_________
Answer: Sphere
Explanation:
A sphere has no bases and 1 curved surface.
Question 3.
_________
Answer: Hexagonal Base Pyramid
Explanation:
A pyramid that has a hexagonal base, that is, base with six sides and 6 triangular lateral faces, then it is a hexagonal pyramid.
Question 4.
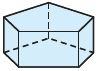
_________
Answer: Pentagonal prism
Explanation:
A pentagonal prism is a prism that has two pentagonal bases like top and bottom and five rectangular sides. It is a type of heptahedron with 7 faces, 10 vertices, and 15 edges.
Question 5.

_________
Answer: Pentagonal Base Pyramid
Explanation:
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point.
Question 6.
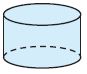
_________
Answer: Cylinder
Explanation:
A cylinder has 2 congruent circular bases and 1 curved surface.
On Your Own
Classify the solid figure. Write prism, pyramid, cone, cylinder, or sphere.
Question 7.
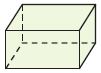
_________
Answer: Rectangular prism
Explanation:
A rectangular prism is a polyhedron with two congruent and parallel bases. It is also a cuboid. It has six faces, and all the faces are in a rectangle shape and have twelve edges. Because of its cross-section along the length, it is said to be a prism.
Question 8.
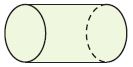
_________
Answer: Cylinder
Explanation:
A cylinder has 2 congruent circular bases and 1 curved surface.
Question 9.
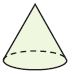
_________
Answer: Cone
Explanation:
A cone has 1 circular base and 1 curved surface.
Question 10.
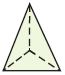
_________
Answer: Triangle base pyramid
Explanation:
A triangle-based pyramid has four triangular sides. The base can be any shape or size of the triangle but usually, it is an equilateral triangle. This means the three sides of the pyramid are the same size as each other and the pyramid looks the same if you rotate it.
Question 11.
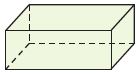
_________
Answer: Rectangular prism
Explanation:
A rectangular prism is a polyhedron with two congruent and parallel bases. It is also a cuboid. It has six faces, and all the faces are in a rectangle shape and have twelve edges. Because of its cross-section along the length, it is said to be a prism.
Question 12.
![]()
_________
Answer: Triangular prism
Explanation:
A prism’s base shape is used to name the solid figure. The base shape of this prism is a triangle. The prism is a triangular prism.
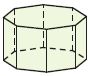
Question 13.
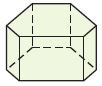
_________
Answer: Hexagonal Prism
Explanation:
In geometry, the hexagonal prism is a prism with a hexagonal base. This polyhedron has 8 faces, 18 edges, and 12 vertices. Since it has 8 faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces.
Question 14.
_________
Answer: Square Pyramid
Explanation:
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid and has symmetry. If all edges are equal, it is an equilateral square pyramid.
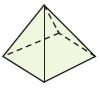
Question 15.
_________
Answer: Octogonal Prism
Explanation:
In geometry, the octagonal prism is the sixth in an infinite set of prisms, formed by square sides and two regular octagon caps. If faces are all regular, it is a semiregular polyhedron.
Problem Solving – Lesson 4: Properties of Two-Dimensional Figures – Page No. 657
Question 16.
Mario is making a sculpture out of stone. He starts by carving a base with five sides. He then carves five triangular lateral faces that all meet at a point at the top. What three-dimensional figure does Mario make?
_________
Answer: Pentagonal Pyramid
Explanation:
Given,
Mario is making a sculpture out of stone.
He starts by carving a base with five sides.
He then carves five triangular lateral faces that all meet at a point at the top.
The polygon which has 5 sides is a pentagon.
The three-dimensional figure which meets at the same point is the pyramid.
The 3-dimensional figure that Mario makes is Pentagonal Pyramid
So, the answer to the above question is Pentagonal Pyramid.
Question 17.
What is another name for a cube? Explain your reasoning.
Type below:
_________
Answer: The cube can also be called a regular hexahedron. It is one of the five regular polyhedrons, which are also sometimes referred to as the Platonic solids.
Connect to Reading
Example Read the description. Underline the details you need to identify the solid figure that will name the correct building.
This building is one of the most identifiable structures in its city’s skyline. It has a square foundation and 28 floors. The building has four triangular exterior faces that meet at a point at the top of the structure.



Identify the solid figure and name the correct building.
Question 18.
Solve the problem in the Example.
Solid figure: _________
Building: _________
Answer:
i. Pyramid
ii. Luxor Hotel-Las Vegas-Nevada
Explanation:
The 3rd figure is in the form of a pyramid. The name of the pyramid-shaped building is Luxor Hotel-Las Vegas-Nevada.
Question 19.
This building was completed in 1902. It has a triangular foundation and a triangular roof that are the same size and shape. The three sides of the building are rectangles.
Solid figure: _________
Building: _________
Answer:
i. prism
ii. Flatiron Building-New York City-New York
Explanation:
The triangle-shaped figure is in the form of a prism. The name of the triangular prism building is Flatiron Building-New York, City-New York.
Mid-Chapter Review – Vocabulary – Page No. 661
Choose the best term from the box.

Question 1.
A closed plane figure with all sides congruent and all angles congruent is called a ________ .
_________
Answer: Regular Polygon
Question 2.
Line segments that have the same length or angles that have the same measure are __________ .
_________
Answer: Congruent
Concepts and Skills
Name each polygon. Then tell whether it is a regular polygon or not a regular polygon.
Question 3.
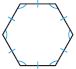
Name: _________
Type: _________
Answer:
i. Hexagon
ii. Regular Polygon
Question 4.
Name: _________
Type: _________
Answer:
i. Triangle
ii. Non-Regular
Question 5.
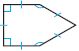
Name: _________
Type: _________
Answer:
i. Pentagon
ii. Not Regular
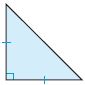
Classify each triangle. Write isosceles, scalene, or equilateral.
Then write acute, obtuse, or right.
Question 6.
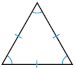
△ _________
∠ _________
Answer:
i. Equilateral
ii. Acute
Question 7.
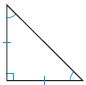
△ _________
∠ _________
Answer:
i. Isosceles
ii. Right
Question 8.
![]()
△ _________
∠ _________
Answer:
i. Isosceles
ii. Obtuse
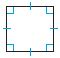
Classify the quadrilateral in as many ways as possible. Write quadrilateral, parallelogram, rectangle, rhombus, square, or trapezoid.
Question 9.
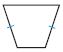
1. _________
2. _________
Answer:
1. Quadrilateral
2. Trapezoid
Question 10.
![]()
1. _________
2. _________
3. _________
Answer:
1. Quadrilateral
2. Parallelogram
3. Rectangle
Question 11.
1. _________
2. _________
3. _________
4. _________
5. _________
Answer:
1. Quadrilateral
2. Parallelogram
3. Rhombus
4. Rectangle
5. Square
Mid-Chapter Review – Page No. 662
Fill in the bubble completely to show your answer.
Question 12.
What type of triangle is shown below?
Options:
a. right isosceles
b. right scalene
c. equilateral
d. obtuse scalene
Answer: right isosceles
Explanation:
The above figure is a right angle and the two sides of the triangle are equal. The above figure is a right isosceles.
Thus the correct answer is option A.
Question 13.
Classify the quadrilateral in as many ways as possible.
Options:
a. quadrilateral, parallelogram, rhombus
b. quadrilateral, parallelogram, rhombus, trapezoid
c. quadrilateral, parallelogram, rhombus, rectangle, trapezoid, square
d. quadrilateral, parallelogram, rhombus, rectangle, square
Answer: quadrilateral, parallelogram, rhombus, rectangle, square
Question 14.
Classify the following figure.
Options:
a. cone
b. cube
c. rectangular prism
d. rectangular pyramid
Answer: rectangular prism
Explanation:
The 3-dimensional figure of the above rectangle is a rectangular prism.
Thus the correct answer is option C.
Share and Show – Lesson 5: Unit Cubes and Solid Figures – Page No. 665
Count the number of cubes used to build each solid figure.
Question 1.
The rectangular prism is made up of _____ unit cubes.
![]()
______
Answer: 3
Explanation:
By seeing the above figure we can say that the rectangular prism has 3 unit cubes.
Question 2.
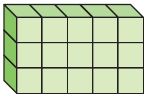
______ unit cubes
Answer: 15
Explanation:
The above figure shows that there are 5 congruent squares of 3 lines.
5 × 3 = 15 unit cubes
Question 3.
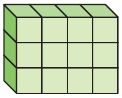
______ unit cubes
Answer: 12
Explanation:
The above figure shows that there are 4 congruent squares of 3 lines.
4 × 3 = 12 unit cubes
Question 4.
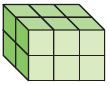
______ unit cubes
Answer: 12
Explanation:
The above figure shows that there are 6 congruent squares of 2 lines.
6 × 2 = 12
Question 5.
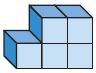
______ unit cubes
Answer: 5
Explanation:
By seeing the above figure we can say that there are 5 unit cubes.
Question 6.
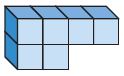
______ unit cubes
Answer: 6
Explanation:
There are 6 congruent squares in the above figure.
Question 7.
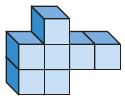
______ unit cubes
Answer: 7
Explanation:
The figure shows that there are 7 unit cubes.
Question 8.
How are the rectangular prisms in Exercises 3–4 related? Can you show a different rectangular prism with the same relationship? Explain.
Type below:
_________
Answer:
A rectangular prism is a polyhedron with two congruent and parallel bases. It is also a cuboid. It has six faces, and all the faces are in a rectangle shape and have twelve edges. Because of its cross-section along the length, it is said to be a prism.
Compare the number of unit cubes in each solid figure. Use < , > or =.
Question 9.
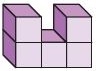 ______
______ 
Answer:  =
= 
Explanation:
There are 5 cubes in the first figure and there are 5 cubes in the second figure.
Thus the figures  is equal to
is equal to 
Question 10.
![]() ______
______ 
Answer: ![]() <
< 
Explanation:
There are 4 cubes in the first figure and there are 5 cubes in the second figure.
4 is less than 5
![]() is less than
is less than 
Lesson 5: Unit Cubes and Solid Figures – Page No. 666
Use the information to answer the questions.
The Cube Houses of Rotterdam, Netherlands

The Nakagin Capsule Tower, Tokyo, Japan

Question 11.
There are 38 Cube Houses. Each house could hold 1,000 unit cubes that are 1 meter by 1 meter by 1 meter. Describe the dimensions of a cube house using unit cubes. Remember that the edges of a cube are all the same length.
Each dimension = ______ meters
Answer: 10 meters
Explanation:
So each house can hold 1000 cubes that are 1 meter in length.
The house is also shaped like a cube, so you need to cube-root 1000.
The cube-root of 1000 is 10. So the cube house has a length, width, and height of 10 meters.
V = lbh
V = 10 m × 10 m × 10 m = 1000 cu. meter
Thus Each dimension is 10 meters.
Question 12.
The Nakagin Capsule Tower has 140 modules and is 14 stories high. If all of the modules were divided evenly among the number of stories, how many modules would be on each floor? How many different rectangular prisms could be made from that number?
Type below:
_________
Answer: 10 modules on each floor
Explanation:
The Nakagin Capsule Tower has 140 modules and is 14 stories high.
Divide 140 modules by 14
140 ÷ 14 = 10
Thus 10 modules would be on each floor.
The factors of 10 are 1, 2, 5.
1 × 10 = 10
2 × 5 = 10
Thus 2 different rectangular prisms can be made from 10 unit cubes.
Share and Show – Lesson 6: Understand Volume – Page No. 671
Use the unit given. Find the volume.
Question 1.
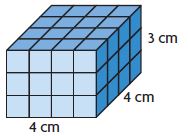
Each cube = 1 cu cm
Volume = ______ cu ______
Answer: 48 cu. cm
Explanation:
Given that,
L = 4cm
B = 4cm
H = 3 cm
We know that,
The volume of the cuboid is lbh
V = 4 cm × 4 cm × 3 cm = 48 cubic cm
Thus the volume for the above cube is 48 cubic cm.
Question 2.
Each cube = 1 cu in.
Volume = ______ cu ______
Answer: 24 cu. in.
Explanation:
Given that,
L = 3 in
B = 2 in
H = 4 in.
We know that,
The volume of the cuboid is lb
V = 3 in × 2 in × 4 in = 24 cubic inches
Therefore the volume for the above cube is 24 cubic inches.
Question 3.
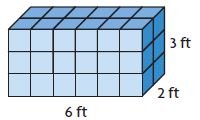
Each cube = 1 cu ft
Volume = ______ cu ______
Answer: 36 cu. ft
Explanation:
Given that,
L = 6 ft
B = 2 ft
H = 3 ft
We know that,
The volume of the cuboid is lbh
V = 6 ft × 2 ft × 3 ft = 36 cubic feet
V = 36 cu. ft
Therefore the volume for the above figure is 36 cu. ft
Question 4.
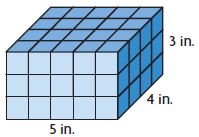
Each cube = 1 cu in.
Volume = ______ cu ______
Answer: 60 cu. in
Given that,
L = 5 in.
B = 4 in.
H = 3 in.
We know that,
The volume of the cuboid is lbh
V = 5 in × 4 in × 3 in = 60 cubic inches
Thus the volume for the above figure is 60 cu. in.
Compare the volumes. Write < , >, or =.
Question 5.
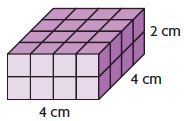 ______
______ 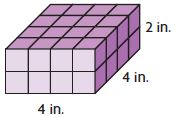
Answer:  <
< 
Explanation:
Figure 1:
L = 4 cm
B = 4 cm
H = 2 cm
V = 4 × 4 × 2 = 32 cu. cm
Figure 2:
L = 4 in
B = 4 in
H = 2 in
V = 4 × 4 × 2 = 32 cu. in
32 cu. cm is less than 32 cu. in
Thus  <
< 
Question 6.
 ______
______ 
Answer:  >
> 
Explanation:
Let us find the volume for both the figures,
Figure 1:
L = 9 ft
B = 4 ft
H = 3 ft
Volume of the cuboid = lbh
V = 9 × 4 × 3 = 108 cu. ft
Figure 2:
L = 8 ft
B = 5 ft
H = 2 ft
Volume of the cuboid = lbh
V = 8 ft × 5 ft × 3 ft = 120 cu. ft
By seeing the volume for both the figures we can say that 120 cu. ft is greater than 108 cu. ft
Thus,  >
> 
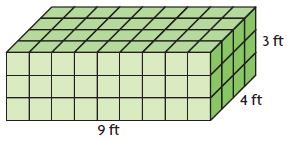
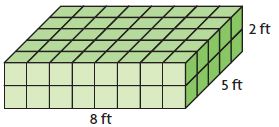
Problem Solving – Lesson 6: Understand Volume – Page No. 672
Question 7.
What’s the Error? Jerry says that a cube with edges that measure 10 centimeters has a volume that is twice as much as a cube with sides that measure 5 centimeters. Explain and correct Jerry’s error.
Type below:
__________
Answer:
Let v1 equal the 10 cm sided cube’s volume.
Let v2 equal the 5 cm sided cube’s volume.
v1 = 10 × 10 10 = 1000 cu. cm
v2 = 5 × 5 × 5 = 125 cu. cm
To find the relationship between the two volumes, divide the first volume by the second.
r = v1 ÷ v2
r = 1000 ÷ 125 = 8
The volume differ by a factor of 8.
Thus the volume differs by a factor of 8, not by a factor of 2.
Question 8.
Pattie built a rectangular prism with cubes. The base of her prism has 12 centimeter cubes. If the prism was built with 108 centimeter cubes, how many layers does her prism have? What is the height of her prism?
layers: ______ the height of the prism: ______ cm
Answer: 9 layers, the height of the prism is 9 cm
Explanation:
Given:
Pattie built a rectangular prism with cubes.
The base of her prism has 12-centimeter cubes.
The prism was built with 108 cm cubes.
To find the layers divide the number of cubes by base of the prism
That means 108 ÷ 12
108/12 = 9
Thus the prism has 9 layers.
Now we have to find the base of the prism
108 = b × h
12 × h = 108
h = 108/12 = 9
Therefore the height of the prism = 9 cm
Question 9.
A packing company makes boxes with edges each measuring 3 feet. What is the volume of the boxes? If 10 boxes are put in a larger, rectangular shipping container and completely fill it with no gaps or overlaps, what is the volume of the shipping container?
volume of the boxes: __________ cu ft
volume of the shipping container = __________ cu ft
Answer:
the volume of the boxes: 27 cu ft
the volume of the shipping container = 27 cu ft
Explanation:
A packing company makes boxes with edges each measuring 3 feet.
Volume of the cube = lbh
V = 3 × 3 × 3 = 27 cubic feet
Thus the volume of the boxes is 27 feet.
The volume of the boxes for 10 boxes is 27 × 10 = 270 cubic feet
Therefore the volume of the shipping container is 27 cu ft
Question 10.
Test Prep Find the volume of the rectangular prism.
Each cube = 1 cu cm
Options:
a. 25 cubic feet
b. 25 cubic meters
c. 75 cubic meters
d. 75 cubic centimeters
Answer: 75 cubic centimeters
Explanation:
L = 5 cm
B = 3 cm
H = 5 cm
Volume of the rectangular prism is lbh
V = 5 cm × 3 cm × 5 cm = 75 cubic centimeter
V = 75 cu. cm
Thus the correct answer is option D.
Share and Show – Lesson 7: Estimate Volume – Page No. 677
Estimate the volume.
Question 1.
Each tissue box has a volume of 125 cubic inches.

There are _______ tissue boxes in the larger box.
The estimated volume of the box holding the tissue
boxes is ______ × 125 = _____ cu in.
_____ tissue boxes _____ cu in.
Answer:
Given that the volume of each box is 125 cubic inches.
By seeing the above figure we can say that there are 9 boxes in the larger box.
Thus there are 9 tissue boxes in the larger box.
Now to find the volume of the tissue boxes.
We have to multiply the number of boxes with the volume of the box
V = 125 × 9 = 1125 cubic inches.
Therefore The estimated volume of the box holding the tissue boxes is 1125 cubic inches.
Question 2.
Volume of chalk box: 16 cu in.

Volume of large box: ______________ .
_____ cu in.
Answer:
Given that, the volume of the chalk box is 16 cubic inches.
From the figure, we can see that there are 24 boxes.
The volume of the large box is 24 × 16 = 384 cubic inches.
Therefore the estimated volume of the large box is 384 cu in.
Question 3.
Volume of small jewelry box: 30 cu cm

Volume of large box: __________
_____ cu cm
Answer:
Given, the volume of the small jewelry box is 30 cu cm
There are 10 small jewelry boxes.
V = 30 × 10 = 300 cu. cm
Thus the estimated volume of large box is 300 cu. cm
On Your Own
Estimate the volume.
Question 4.
Volume of book: 80 cu in.

Volume of large box: __________
_____ cu in.
Answer:
Given that, the volume of the book is 80 cu. in
There are 12 books in the figure.
Multiply the number of books with the volume of each book
= 12 × 80 = 960 cu. inches
Thus the estimated volume of large books is 960 cu in.
Question 5.
Volume of spaghetti box: 750 cu cm

Volume of large box: ________
_____ cu cm
Answer:
Volume of spaghetti box is 750 cu. cm
Volume = 2 × 5 × 4 = 40
Number of boxes = 40
Now multiply 40 with 750 cu. cm to find the volume of large box
V = 40 × 750 cu. cm
V = 30000 cubic cm
Therefore the estimated Volume of large box is 30000 cubic cm
Question 6.
Volume of cereal box: 324 cu in.

Volume of large box: __________
cu in.
Answer:
Given, Volume of a cereal box is 324 cu. in
Number of boxes is 2 × 3 × 3 = 18
The volume of large box is 18 × 324 cu. in
V = 18 × 324 cu. in = 5832 cubic inches
Thus the estimated Volume of large box is 5832 cubic inches.
Question 7.
Volume of pencil box: 4,500 cu cm

Volume of large box: ________
_____ cu cm
Answer:
Volume of pencil box is 4500 cu cm
Number of pencil boxes = 2 × 5 = 10
The volume of large box is 4500 × 10 = 45000 cu cm
Thus the estimated volume of large box is 45000 cu cm
Problem Solving – Lesson 7: Estimate Volume – Page No. 678
Sense or Nonsense?
Question 8.
Marcelle estimated the volume of the two boxes below, using one of his books. His book has a volume of 48 cubic inches. Box 1 holds about 7 layers of books, and Box 2 holds about 14 layers of books. Marcelle says that the volume of either box is about the same.

Does Marcelle’s statement make sense or is it nonsense?
Explain your answer.
Type below:
_________
Answer:
Calculate the books in box 1
V = lbh
V1 = 2 × 4 × 7 = 56 books
Calculate the volume of books in box 2
V = lbh
V2 = 1 × 4 × 14 = 56 books
So, both boxes hold the same number of books.
Thus Marcelle’s statement make sense.
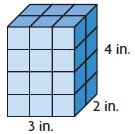
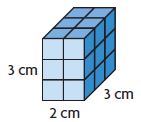
Share and Show – Lesson 8: Volume of Rectangular Prisms – Page No. 683
Find the volume.
Question 1.
The length of the rectangular prism is ______.
The width is ______. So, the area of the base is ______.
The height is ______. So, the volume of the prism is ______.
Type below:
_________
Answer: 120 cu. in
Explanation:
From the figure, we can say that the length of the rectangular prism is 4 in
The width of the rectangular prism is 5 in
The height of the rectangular prism is 6 in.
The volume of the rectangular prism is l × w × h
V = 4 in × 6 in × 5 in = 120 cu. in
So, the volume of the prism is 120 cu. in
Question 2.
Volume: ______ cu cm
Answer: 18
Explanation:
From the figure, we can say that the length of the rectangular prism is 2 cm
The width of the rectangular prism is 3 cm
The height of the rectangular prism is 3 cm
The volume of the rectangular prism is l × w × h
V = 2 cm × 3 cm × 3 cm = 18 cu. cm
Thus the volume of the rectangular prism is 18 cu. cm
Question 3.
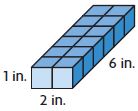
Volume: ______ cu in.
Answer: 12
Explanation:
From the figure, we can say that the length of the rectangular prism is 2 in.
The width of the rectangular prism is 6 in.
The height of the rectangular prism is 1 in.
The volume of the rectangular prism is l × w × h
V = 2 in × 6 in × 1 in
V = 12 Cu in.
Thus the volume of the rectangular prism is 12 Cu in.
On Your Own
Find the volume.
Question 4.
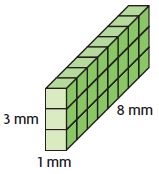
Volume: ______ cu mm
Answer: 24
Explanation:
From the figure, we can say that the length of the rectangular prism is 1 mm
The width of the rectangular prism is 8 mm
The height of the rectangular prism is 3 mm
The volume of the rectangular prism is l × w × h
V = 1 mm × 8 mm × 3 mm
V = 24 Cu. mm
Thus the volume of the rectangular prism is 24 Cu. mm
Question 5.
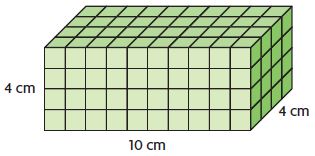
Volume: ______ cu cm
Answer: 160
Explanation:
From the figure, we can say that the length of the rectangular prism is 10 cm
The width of the rectangular prism is 4 cm
The height of the rectangular prism is 4 cm
The volume of the rectangular prism is l × w × h
V = 10 cm × 4 cm × 4 cm = 160 Cu. cm
Thus the volume of the rectangular prism is 160 Cu. cm
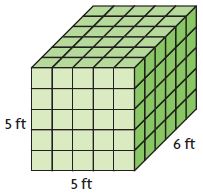
Question 6.
Volume: ______ cu ft
Answer: 150
Explanation:
From the figure, we can say that the length of the rectangular prism is 5 ft
The width of the rectangular prism is 6 ft
The height of the rectangular prism is 5 ft
The volume of the rectangular prism is l × w × h
V = 5 ft × 6 ft × 5 ft
V = 150 Cu. ft
Thus the volume of the rectangular prism is 150 Cu. ft
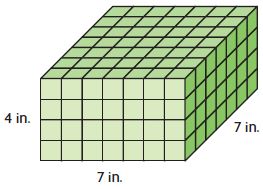
Question 7.
Volume: ______ cu in.
Answer: 196
Explanation:
From the figure, we can say that the length of the rectangular prism is 7 in.
The width of the rectangular prism is 7 in.
The height of the rectangular prism is 4 in.
The volume of the rectangular prism is l × w × h
V = 7 in × 7 in × 4 in = 196 Cu. in
Thus the volume of the rectangular prism is 196 Cu. in
UNLOCK the Problem – Lesson 8: Volume of Rectangular Prisms – Page No. 684
Question 8.
Rich is building a travel crate for his dog, Thomas, a beagle mix who is about 30 inches long, 12 inches wide, and 24 inches tall. For Thomas to travel safely, his crate needs to be a rectangular prism that is about 12 inches greater than his length and width, and 6 inches greater than his height. What is the volume of the travel crate that Rich should build?

a. What do you need to find to solve the problem?
Type below:
_________
Answer: We need to find the volume of the travel crate that Rich should build.
Question 8.
b. How can you use Thomas’s size to help you solve the problem?
Type below:
_________
Answer: Thomas’s size helps to find the length, width and height of the dog crate.
Question 8.
c. What steps can you use to find the size of Thomas’s crate?
Type below:
_________
Answer:
Rich is building a travel crate for his dog, Thomas, a beagle mix who is about 30 inches long, 12 inches wide, and 24 inches tall.
For Thomas to travel safely, his crate needs to be a rectangular prism that is about 12 inches greater than his length and width, and 6 inches greater than his height.
Length of the dog crate is 30 in + 12 in = 42 inches
Width of the dog crate is 12 inches more than width of Thomas crate = 12 in + 12 in = 24 inches
Height of the dog crate is 24 in + 6 in = 30 inches
V = 42 in × 24 in × 30 in
V = 30,240 cu in
Question 8.
d. Fill in the blanks for the dimensions of the dog crate.
length: _____
width: _____
height: _____
area of base: _____
Type below:
_________
Answer:
Crate length = 30 + 12 = 42 in
Crate width = 12 + 12 = 24 in
Crate height = 24 + 6 = 30 in
Area of base = l × w
A = 42 in × 24 in = 1008 sq in.
Question 8.
e. Find the volume of the crate by multiplying the base area and the height.
______ × ______ = ______
So, Rich should build a travel crate for Thomas that has a volume of ______ .
Type below:
_________
Answer:
Area of base = l × w
A = 42 in × 24 in = 1008 sq in.
Height = 30 in
V = 1008 sq in × 30 in = 30240 cu. in
So, Rich should build a travel crate for Thomas that has a volume of 30240 cu. in
Question 9.
What is the volume of the rectangular prism at the right?

Options:
a. 35 in.3
b. 125 in.3
c. 155 in.3
d. 175 in.3
Answer: 175 in.3
Explanation:
Length = 5 in
Width = 7 in
Height = 5 in
Volume of the rectangular prism is l × w × h
V = 5 in × 7 in × 5 in
V = 175 in.3
The volume of the rectangular prism is 175 in.3
Therefore the correct answer is option D.
Share and Show – Lesson 9: Algebra Apply Volume Formulas – Page No. 689
Find the volume.
Question 1.
V =____ cu ft
Answer: 40
Explanation:
length = 2 ft
width = 4 ft
height = 5 ft
Volume of the rectangular prism is l × w × h
V = 2 ft × 4 ft × 5 ft
V = 40 cu ft
Volume of the rectangular prism is 40 cu. ft
Question 2.
V =____ cu cm
Answer: 144
Explanation:
length = 4 cm
width = 4 cm
height = 9 cm
Volume of the rectangular prism is l × w × h
V = 4 cm × 4 cm × 9 cm
V = 144 cu cm
Volume of the rectangular prism is 144 cu cm
On Your Own
Find the volume.
Question 3.
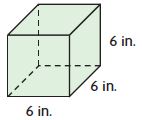
V =____ cu in.
Answer: 216
Explanation:
length = 6 in
width = 6 in
height = 6 in
Volume of the prism is l × w × h
V = 6 in × 6 in × 6 in
V = 216 cu. in
Thus the Volume of the prism is 216 cu. in.
Question 4.
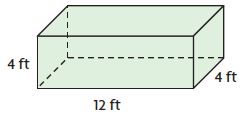
V =____ cu ft
Answer: 192
Explanation:
length = 12 ft
width = 4 ft
height = 4 ft
Volume of the rectangular prism is l × w × h
V = 12 ft × 4 ft × 4 ft
V = 192 cu ft
Therefore, the Volume of the rectangular prism is 192 cu ft.
Question 5.
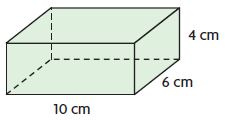
V =____ cu cm
Answer: 240
Explanation:
length = 10 cm
width = 6 cm
height = 4 cm
Volume of the rectangular prism is l × w × h
V = 10 cm × 6 cm × 4 cm
V = 240 Cu. cm
Therefore, the Volume of the rectangular prism is 240 Cu. cm.
Question 6.
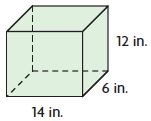
V =____ cu in.
Answer: 1008
Explanation:
length = 14 in.
width = 6 in.
height = 12 in.
Volume of the rectangular prism is l × w × h
V = 14 in × 6 in × 12 in
V = 1008 cu. in
Thus the Volume of the rectangular prism is 1008 cu. in
Question 7.
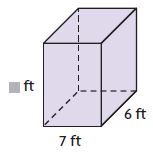
V =420 cu ft
■ = ____ ft
Answer: 10
Explanation:
length = 7 ft
width = 6 ft
height = ■ ft
Volume of the rectangular prism is l × w × h
420 cu ft = 7 ft × 6 ft × ■
■ × 42 sq ft = 420 cu ft
■ = 420 cu ft ÷ 42 sq ft
■ = 10 ft
Question 8.
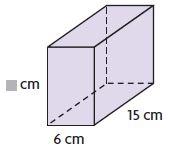
V =900 cu cm
■ = ____ cm
Answer: 10
Explanation:
length = 6 cm
width = 15 cm
height = ■ cm
Volume of the rectangular prism is l × w × h
V = 900 cu cm
900 cu cm = 6 cm × 15 cm × ■ cm
900 cu cm = 90 sq cm × ■ cm
■ cm = 900 cu cm ÷ 90 sq cm
■ cm = 10 cm
Problem Solving – Lesson 9: Algebra Apply Volume Formulas – Page No. 690
Question 9.
The Jade Restaurant has a large aquarium on display in its lobby. The base of the aquarium is 5 feet by 2 feet. The height of the aquarium is 4 feet. How many cubic feet of water are needed to completely fill the aquarium?

V =____ cu ft of water
Answer: 40 cu ft of water
Explanation:
The Jade Restaurant has a large aquarium on display in its lobby.
The base of the aquarium is 5 feet by 2 feet.
The height of the aquarium is 4 feet.
Volume = b × w × h
V = 5 feet × 2 feet× 4 feet
V = 40 Cu. ft
Therefore, the volume of the aquarium is 40 cu ft of water.
Question 10.
The Pearl Restaurant put a larger aquarium in its lobby. The base of their aquarium is 6 feet by 3 feet, and the height is 4 feet. How many more cubic feet of water does the Pearl Restaurant’s aquarium hold than the Jade Restaurant’s aquarium?
____ cu ft
Answer: 32 cu ft
Explanation:
The Pearl Restaurant put a larger aquarium in its lobby.
The base of their aquarium is 6 feet by 3 feet, and the height is 4 feet.
Volume = b × w × h
V = 6 feet × 3 feet × 4 feet = 72 cu. feet
Thus the Volume of Pearl Restaurant’s aquarium is 72 cu. feet
The volume of the Jade Restaurant’s aquarium is 40 cu ft of water
V = Vp – Vj
V = 72 – 40 = 32 cu feet
Question 11.
Eddie measured his aquarium using a small fish food box. The box has a base area of 6 inches and a height of 4 inches. Eddie found that the volume of his aquarium is 3,456 cubic inches. How many boxes of fish food could fit in the aquarium? Explain your answer.
____ boxes
Answer: 144 boxes
Explanation:
Volume = b × h
V = 6 in × 4 in = 24 cu in
To find out how many boxes will fit, divide the aquarium volume by the food box volume.
numfit = Vaq/Vbox
numfit = 3456/24 = 144
144 fish food boxes fir inside the aquarium.
Question 12.
Describe the difference between area and volume.
Type below:
_________
Answer: The surface area is the sum of the areas of all the faces of the solid figure. It is measured in square units. Volume is the number of cubic units that make up a solid figure.
Question 13.
Test Prep Adam stores his favorite CDs in a box like the one at the right. What is the volume of the box?
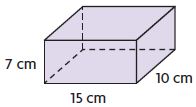
Options:
a. 150 cubic centimeters
b. 750 cubic centimeters
c. 1,050 cubic centimeters
d. 1,150 cubic centimeters
Answer: 1,050 cubic centimeters
Explanation:
L = 15 cm
W = 10 cm
H = 7 cm
V = lwh
V = 15 cm × 10 cm × 7 cm = 1050 cubic centimeters
Thus the correct answer is option C.
Share and Show – Lesson 10: Problem Solving Compare Volumes – Page No. 695
Question 1.
Mr. Price makes cakes for special occasions. His most popular-sized cakes have a volume of 360 cubic inches. The cakes have a height, or thickness, of 3 inches, and have different whole number lengths and widths. No cakes have a length or width of 1 or 2 inches. How many different cakes, each with a different-size base, have a volume of 360 cubic inches?
First, think about what the problem is asking you to solve, and the information that you are given.
Next, make a table using the information from problem.
Finally, use the table to solve the problem.
Type below:
_________
Answer: There are total of 8 different possible combination of length and width
Explanation:
Volume = 360 cubic inches
Height = 3 inches
Volume = l x w x h
360 = l x w x 3
l x w = 120
The factors of 120 are,
1 x 120,
2x 60,
3 x 40,
4 x 30,
5 x 24,
6 x 20,
8 x 15,
10 x 12
Question 2.
What if the 360 cubic-inch cakes are 4 inches thick and any whole number length and width are possible? How many different cakes could be made? Suppose that the cost of a cake that size is $25, plus $1.99 for every 4 cubic inches of cake. How much would the cake cost?
Type below:
_________
Answer:
Since the store have a volume of 360 cu in and a height of 4 in.
We need to find the number of different stones which have a base of 90 sq in.
V = b × h
B = 360 cu in/4 in
B = 90 sq in.
Consider the factors of 90.
The factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Make a table with the base, height and volume for each pair of factors
Height = 4 in
1 × 90 × 4 = 360 cu in
2 × 45 × 4 = 360 cu in
3 × 30 × 4 = 360 cu in
5 × 18 × 4 = 360 cu in
6 × 15 × 4 = 360 cu in
9 × 10 × 4 = 360 cu in
6 different sized paving stones.
Remember that each store has a volume of 360 cu in.
Divide by 4 to find how many 4 cu in per stone
Concrete = $0.18 × (360/4)
= $0.18 × 90 = $18.70
The cost of the stone plus the concrete
cost = $2.50 + concrete
Cost = $2.50 + $16.20 = $18.70
Question 3.
One company makes inflatable swimming pools that come in four sizes of rectangular prisms. The length of each pool is twice the width and twice the depth. The depth of the pools are each a whole number from 2 to 5 feet. If the pools are filled all the way to the top, what is the volume of each pool?
Type below:
_________
Answer:
If the depth of the pool is 2 feet
then the length of the pool is twice the width and twice the depth
That means 2 feet × 2 × 2 = 8 feet
Width is twice the depth
W = 2 feet × 2 = 4 feet
The volume of the rectangular swimming pool is l × w × h
V = 8 ft × 4 feet × 2 ft
V = 64 cu ft
If the depth of the pool is 3 feet
then the length of the pool is twice the width and twice the depth
That means 3 feet × 2 × 2 = 12 feet
Width is twice the depth
W = 3 feet × 2 = 6 feet
The volume of the rectangular swimming pool is l × w × h
V = 12 ft × 6 feet × 2 ft
V = 144 cu ft
If the depth of the pool is 4 feet
then the length of the pool is twice the width and twice the depth
That means 4 feet × 2 × 2 = 16 feet
Width is twice the depth
W = 4 feet × 2 = 8 feet
The volume of the rectangular swimming pool is l × w × h
V = 16 ft × 8 feet × 2 ft
V = 256 cu ft
If the depth of the pool is 5 feet
then the length of the pool is twice the width and twice the depth
That means 5 feet × 2 × 2 = 20 feet
Width is twice the depth
W = 5 feet × 2 = 10 feet
The volume of the rectangular swimming pool is l × w × h
V = 20 ft × 10 feet × 2 ft
V = 400 cu ft
On Your Own – Lesson 10: Problem Solving Compare Volumes – Page No. 696
Question 4.
Ray wants to buy the larger of two aquariums. One aquarium has a base that is 20 inches by 20 inches and a height that is 18 inches. The other aquarium has a base that is 40 inches by 12 inches and a height that is 12 inches. Which aquarium has a greater volume? By how much?
Type below:
_________
Answer: 1440 cu. in
Explanation:
Volume = l × w × h
Volume of Aquarium 1 = 20 in × 20 in × 18 in
V = 7200 cu. in
Volume = l × w × h
Volume of Aquarium 2 is 40 in × 12 in × 12 in
V for A2 = 5760 cu in
A1 > A2
A1 has a greater volume.
Subtract A2 from A1
A1 – A2 = 7200 cu in – 5760 cu in
= 1440 cu in
The volume of Aquarium 1 is 1440 cu in more than Volume of Aquarium 2.
Question 5.
Ken owns 13 CDs. His brother Keith has 7 more CDs than he does. Their brother, George, has more CDs than either of the younger brothers. Together, the three brothers have 58 CDs. How many CDs does George have?
______ CDs
Answer: 25 CDs
Explanation:
Given that,
Ken owns 13 CDs.
His brother Keith has 7 more CDs than he does.
Their brother, George, has more CDs than either of the younger brothers.
Together, the three brothers have 58 CDs.
Keith has 7 more CDs than Ken
That means he has 7 + 13 = 20 CDs
Now subtract Ken’s CDs, Keith CDs from the total number of CDs.
= 58 – 20 – 13 = 25 CDs.
Thus George has 25 CDs.
Question 6.
Kathy has ribbons that have lengths of 7 inches, 10 inches, and 12 inches. Explain how she can use these ribbons to measure a length of 15 inches.
Type below:
_________
Answer: She could take the 10-inch ribbon and then use 5 inches from the 7-inch ribbon
Question 7.
A park has a rectangular playground area that has a length of 66 feet and a width of 42 feet. The park department has 75 yards of fencing material. Is there enough fencing material to enclose the playground area? Explain.
______
Answer: Yes
Explanation:
A park has a rectangular playground area that has a length of 66 feet and a width of 42 feet.
The park department has 75 yards of fencing material.
Area of the rectangular playground = l × w
A = 66 feet × 42 feet
A = 2772 sq. ft
Perimeter of the rectangular playground = 2l + 2w
P = 2 × 66 + 2 × 42
P = 216 ft
Now convert from feet to yard
We know that 1 yard = 3 feet
216 ft = 1/3 × 216 = 72 yard
72 yard is less than 75 yard
Thus the park department has enough fencing material.
Question 8.
Test Prep John is making a chest that will have a volume of 1,200 cubic inches. The length is 20 inches and the width is 12 inches. How many inches tall will his chest be?
Options:
a. 4 in.
b. 5 in.
c. 6 in.
d. 7 in.
Answer: 5 in
Explanation:
John is making a chest that will have a volume of 1,200 cubic inches.
The length is 20 inches and the width is 12 inches.
Volume = l × w × h
1200 cu in = 20 in × 12 in × h
240 sq in × h = 1200 cu in
h = 1200 cu in ÷ 240 sq in
h = 5 in
Thus John’s chest will be 5 inches tall.
The correct answer is option B.
Share and Show – Lesson 11: Find Volume of Composed Figures – Page No. 701
Find the volume of the composite figure.
Question 1.
V = ______ cu in.
Answer: 88 cu in.
Explanation:
Split the figure into 2 parts
Volume of figure 1:
b = 2 in
h = 3 in
w = 4 in
V = 2 in × 4 in × 3 in
V = 24 cu. in
Volume of figure 2:
b = 8 in
w = 4 in
h = 2 in
V = 8 in × 4 in × 2 in
V = 64 in
Volume of the composite figure = 24 cu in + 64 cu. in = 88 cu. in
Question 2.
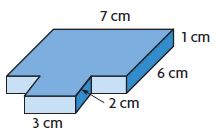
V = ______ cu cm
Answer: 48 cu cm
Explanation:
Split the figure into 2 parts
Volume of figure 1:
b = 3 cm
h = 1 cm
w = 2 cm
V = 3 cm × 2 cm × 1 cm
V = 6 cu. cm
Volume of figure 2:
b = 7 cm
w = 6 cm
h = 1 cm
V = 7 cm × 6 cm × 1 cm
V = 42 cu. cm
Volume of the composite figure = 42 cu. cm + 6 cu. cm = 48 cu cm
On Your Own
Find the volume of the composite figure.
Question 3.
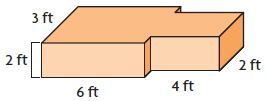
V = ______ cu ft
Answer: 52 cu ft
Explanation:
Split the figure into 2 parts
Volume of figure 1:
b = 6 ft
h = 2 ft
w = 3 ft
V = 6 ft × 3 ft × 2 ft
V = 36 cu. ft
Volume of figure 2:
b = 4 ft
w = 2 ft
h = 2 ft
V = 4 ft × 2 ft × 2 ft
V = 16 cu. ft
Volume of the composite figure = 36 cu. ft + 16 cu. ft = 52 cu ft
Question 4.
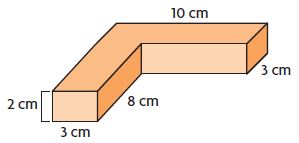
V = ______ cu cm
Answer: 108 cu. cm
Explanation:
Split the figure into 2 parts
Volume of figure 1:
b = 3 cm
w = 8 cm
h = 2 cm
V = 3 cm × 8 cm × 2 cm
V = 48 cu cm
Volume of figure 2:
b = 10 cm
w = 3 cm
h = 2 cm
V = 10 cm × 3 cm × 2 cm
V = 60 cu cm
Volume of the composite figure = 48 cu cm + 60 cu cm = 108 cu. cm
Question 5.
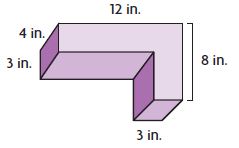
V = ______ cu in.
Answer: 204 cu. in
Explanation:
Split the figure into 2 parts
Volume of figure 1:
b = 3 in
h = 5 in
w = 4 in
V = 3 in × 4 in × 5 in
V = 60 cu. in
Volume of figure 2:
b = 12 in
w = 4 in
h = 3 in
V = 12 in × 4 in × 3 in
V = 144 cu. in
Volume of the composite figure = 60 cu in + 144 cu. in = 204 cu. in
Question 6.
V = ______ cu ft
Answer: 96 cu ft
Explanation:
Split the figure into 3 parts.
Figure 1:
V1 = 9 ft × 4 ft × 2 ft
V1 = 72 cu. ft
Figure 2:
V2 = 3 ft × 4 ft × 2 ft
V2 = 24 cu. ft
V = V1 + V2
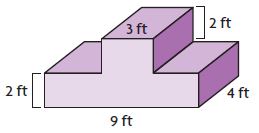
V = 72 cu. ft + 24 cu. ft = 96 cu. ft
Thus the volume of the composite figure is 96 cu. ft
Question 7.
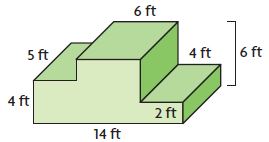
V = ______ cu ft
Answer: 300 cu. ft
Explanation:
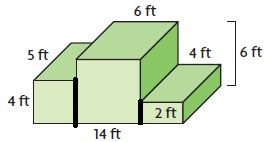
Split the figure into 3 parts.
Figure 1:
V1 = 5 ft × 4 ft × 4 ft
V1 = 80 cu. ft
Figure 2:
V2 = 6 ft × 5 ft × 6 ft
V2 = 180 cu ft
Figure 3:
V3 = 4 ft × 5 ft × 2 ft
V3 = 40 cu. ft
V = V1 + V2 + V3
V = 80 cu. ft + 180 cu ft + 40 cu ft = 300 cu. ft
Question 8.
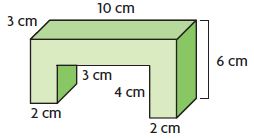
V = ______ cu cm
Answer: 102 cu cm
Explanation:
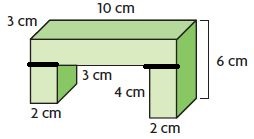
Figure 1:
V1 = 10 cm × 3 cm × 2 cm = 60 cu cm
V1 = 60 cu. cm
Figure 2:
V2= 2 cm × 3 cm × 4 cm
V2 = 24 cu. cm
Figure 3:
V3 = 2 cm × 3 cm × 3 cm
V3 = 18 cu. cm
V = V1 + V2 + V3
V = 60 cu. cm + 24 cu. cm + 18 cu. cm = 102 cu. cm
Problem Solving – Lesson 11: Find Volume of Composed Figures – Page No. 702
Use the composite figure at the right for 9–11.
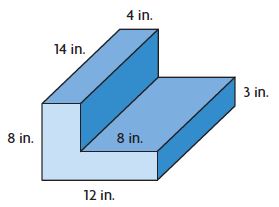
Question 9.
As part of a wood-working project, Jordan made the figure at the right out of wooden building blocks. How much space does the figure he made take up?
______ cu in.
Answer: 784 cu. in
Explanation:
Split the figure into 2 parts
Figure 1:
V1 = 14 in × 4 in × 5 in
V1 = 280 cu. in
Figure 2:
V2 = 12 in × 14 in × 3 in
V2 = 504 cu. in
V = V1 + V2
V = 280 cu. in + 504 cu. in
V = 784 cu. in
Question 10.
What are the dimensions of the two rectangular prisms you used to find the volume of the figure? What other rectangular prisms could you have used?
Type below:
________
Answer:
Dimensions for figure 1:
Base = 14 in
Width = 4 in
Height = 5 in
Dimensions for figure 2:
Base = 12 in
Width = 14 in
Height = 3 in
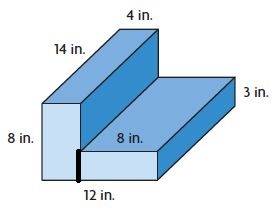
Question 11.
If the volume is found using subtraction, what is the volume of the empty space that is subtracted? Explain.
______ cu in.
Answer: 560 cu. in
Explanation:
B = 8 in
H = 5 in
W = 14 in
V = 8 in × 14 in × 5 in
V = 560 cu. in
Thus the volume of the empty space is 560 cu. in
Question 12.
Explain how you can find the volume of composite figures that are made by combining rectangular prisms.
Type below:
________
Answer:
Split the figure into 2 parts
Figure 1:
V1 = 14 in × 4 in × 5 in
V1 = 280 cu. in
Figure 2:
V2 = 12 in × 14 in × 3 in
V2 = 504 cu. in
V = V1 + V2
V = 280 cu. in + 504 cu. in
V = 784 cu. in
Question 13.
Test Prep What is the volume of the composite figure?
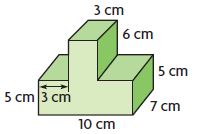
Options:
a. 126 cubic centimeters
b. 350 cubic centimeters
c. 450 cubic centimeters
d. 476 cubic centimeters
Answer: 476 cubic centimeters
Explanation:
Split the figure into 2 parts
Figure 1:
V1 = 10 cm × 7 cm × 5 cm
V1 = 350 cu. cm
Figure 2:
V2 = 3 cm × 7 cm × 6 cm
V2 = 126 cu. cm
V = V1 + V2
V = 350 cu. cm + 126 cu. cm
V = 476 cu. cm
Chapter Review/Test – Page No. 705
Question 1.
Fran drew a triangle with no congruent sides and 1 right angle. Which term accurately describes the triangle? Mark all that apply.
Options:
a. isosceles
b. scalene
c. acute
d. right
Answer: Right
Explanation:
A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.
Thus the correct answer is option D.
Question 2.
Jose stores his baseball cards in a box like the one shown.
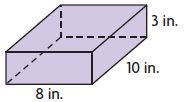
Use the numbers and symbols on the tiles to write a formula that represents the volume of the box. Symbols may be used more than once or not at all.

What is the volume of the box?
V = ______ cubic inches
Answer:
Volume of the box is l × w × h
V = 8 in × 10 in × 3 in
V = 240 cu. in
Thus the volume of the box is 240 cu. in
Question 3.
Mr. Delgado sees this sign while he is driving. For 3a–3b, choose the values and term that correctly describes the shape Mr. Delgado saw.

3a. The figure has  sides and
sides and  angles.
angles.
Type below:
________
Answer: The figure has 3 sides and 3 angles.
Explanation:
From the above figure we can say that there are three sides and three angles.
Question 3.
3b. All of the sides are congruent, so the figure is 
________
Answer: a regular polygon
If all the sides are congruent then the polygon is a regular polygon.
Chapter Review/Test – Page No. 706
Question 4.
What is the volume of the composite figure?
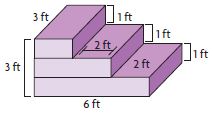
______ cubic feet
Answer: 36 cubic feet
Explanation:
Figure 1:
length = 2 ft
width = 3 ft
height = 1 ft
Volume of 1st figure = l × w × h
V = 2 ft × 3 ft × 1 ft = 6 cu. ft
Figure 2:
length = 4 ft
width = 3 ft
height = 1 ft
Volume of 1st figure = l × w × h
V = 4 ft × 3 ft × 1 ft = 12 cu. ft
Figure 3:
length = 6 ft
width = 3 ft
height = 1 ft
Volume of 1st figure = l × w × h
V = 6 ft × 3 ft × 1 ft = 18 cu. ft
Add all the volumes = 6 cu. ft + 12 cu. ft + 18 cu. ft
Volume = 36 cu. ft
Question 5.
Match the figure with the number of unit cubes that would be needed to build each figure. Not every number of unit cubes will be used.
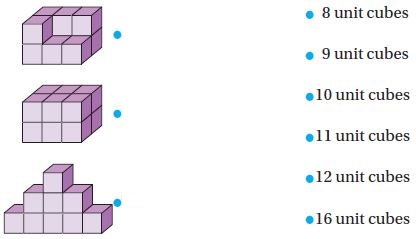
Answer:
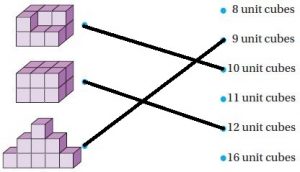
Explanation:
Count the number of unit cubes in the first figure.
There are 10 unit cubes in figure 1 so match the figure 1 to 10 unit cubes.
Count the number of unit cubes in the second figure.
There are 12 unit cubes in figure 2 so match figure 2 to 12 unit cubes.
Count the number of unit cubes in the third figure.
There are 9 unit cubes in figure 3 so match figure 3 to 9 unit cubes.
Question 6.
Chuck is making a poster about polyhedrons for his math class. He will draw figures and organize them in different sections of the poster.
Part A
Chuck wants to draw three-dimensional figures whose lateral faces are rectangles. He says he can draw prisms and pyramids. Do you agree?
Explain your answer.
i. yes
ii. no
Answer: No
Explanation:
The lateral faces of a pyramid are triangles.
The lateral faces of a prism are rectangles.
Question 6.
Part B
Chuck says that he can draw a cylinder on his polyhedron poster because it has a pair of bases that are congruent. Is Chuck correct?
Explain your reasoning.
i. yes
ii. no
Answer: No
Explanation:
A cylinder does have 2 congruent bases, but a cylinder is not a polyhedron.
A cylinder has 1 curved surface, while a polyhedron has faces that are polygons
Chapter Review/Test – Page No. 707
Question 7.
Javier drew the shape shown. For 7a–7b, choose the values and term that correctly describe the shape Javier drew.
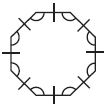
7a. The figure has  sides and
sides and  angles.
angles.
Type below:
_________
Answer: 8, 8
The above figure has 8 sides and 8 angles.
Question 7.
7b. The figure is a 
Type below:
_________
Answer: The polygon with 8 sides is known as the octagon. The above figure is congruent thus it is a regular octagon.
Question 8.
Victoria used 1-inch cubes to build the rectangular prism shown. Find the volume of the rectangular prism Victoria built.
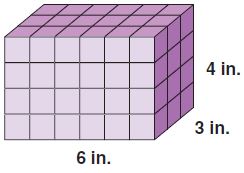
______ cubic inches
Answer: 72
Explanation:
Given,
l = 6 in
w = 3 in
h = 4 in
The volume of the rectangular prism is l × w × h
V = 6 in × 3 in × 4in
V = 72 cu in.
Hence, the volume of the rectangular prism Victoria built is 72 cu. in.
Question 9.
Nathan drew a scalene, obtuse triangle. For 9a–9c, choose Yes or No to indicate whether the figure shown could be the triangle that Nathan drew.
a. 
i. yes
ii. no
Answer: Yes
Explanation:
The above different have different sizes thus the triangle is scalene. The angle for the above triangle is more than 90° thus the angle is an obtuse angle. So, the answer is yes.
Question 9.
b. 
i. yes
ii. no
Answer: No
Explanation:
The above different have different sizes thus the triangle is scalene. It has one right angle thus the statement is not correct.
Question 9.
c. 
Answer: No
Explanation:
The above different have different sizes thus the triangle is scalene. It has one right angle thus the statement is not correct.
Chapter Review/Test – Page No. 708
Question 10.
A shipping crate holds 20 shoeboxes. The dimensions of a shoebox are 6 inches by 4 inches by 12 inches. For 10a–10b, select True or False for each statement.
a. Each shoebox has a volume of 22 cubic inches.
i. True
ii. False
Answer: False
Explanation:
Shoebox volume:
V = 6 in × 4 in × 12 in
V = 288 cu. in
Thus the statement is false.
Question 10.
b. Each crate has a volume of about 440 cubic inches.
i. True
ii. False
Answer: False
Explanation:
Crate Volume:
V = 288 cu. in × 20
V = 5760 cu. in
Thus the statement is false.
Question 10.
c. If the crate could hold 27 shoeboxes the volume of the crate would be about 7,776 cubic inches.
i. True
ii. False
Answer: True
Explanation:
Crate Volume:
V = 288 cu. in × 27
V = 7776 cu. in
Thus the statement is true.
Question 11.
Mario is making a diagram that shows the relationship between different kinds of quadrilaterals. In the diagram, each quadrilateral on a lower level can also be described by the quadrilateral(s) above it on higher levels.
Part A
Complete the diagram by writing the name of one figure from the tiles in each box. Not every figure will be used.
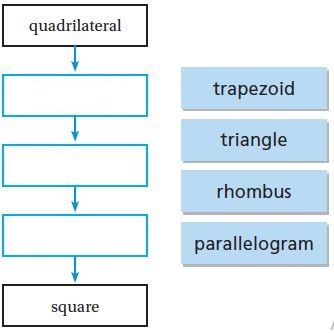
Answer:
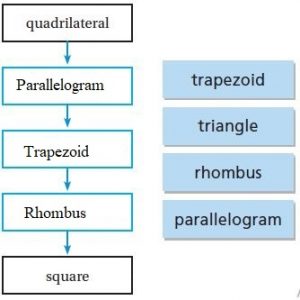
Question 11.
Part B
Mario claims that a rhombus is sometimes a square, but a square is always a rhombus. Is he correct? Explain your answer.
i. yes
ii. no
Answer: Yes
Explanation:
A square is a quadrilateral with all sides equal in length and all interior angles right angles. A square however is a rhombus since all four of its sides are of the same length.
Chapter Review/Test – Page No. 709
Question 12.
Write the letter in the box that correctly describes the three-dimensional figure.
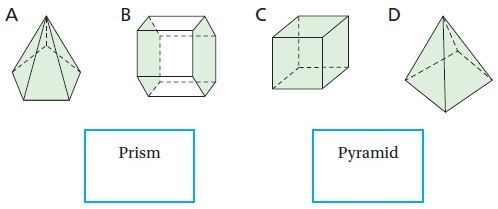
Type below:
___________
Answer:
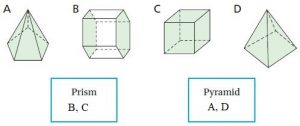
Explanation:
Prism: In geometry, a prism is a polyhedron comprising an n-sided polygonal base, a second base which is a translated copy of the first, and n other faces joining corresponding sides of the two bases.
Figure B and C are prisms
Pyramid: In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle called a lateral face. All the edges meet at the same point in the pyramid. Thus the figures A and D are pyramids.
Question 13.
Mark packed 1-inch cubes into a box with a volume of 120 cubic inches. How many layers of 1-inch cubes did Mark pack?
______ layers
Answer: 5
Explanation:
Mark packed 1-inch cubes into a box with a volume of 120 cubic inches.
By seeing the figure we can say that there are 24 unit cubes.
To find the number of layers we need to divide 120 by 24
= 120 ÷ 24 = 5
There are 5 layers of 1-inch cubes.
Question 14.
A composite figure is shown. What is the volume of the composite figure?
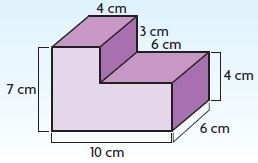
Volume = ______ cubic centimeters
Answer: 312
Explanation:
Split the figure into 2 parts.
Figure 1:
h = 3 cm
w = 6 cm
b = 4 cm
V = 4 cm × 6 cm × 3 cm = 72 cu. cm
Figure 2:
b = 10 cm
w = 6 cm
h = 4 cm
V = 10 cm × 6 cm × 4 cm = 240 cu. cm
Now add the volume of 2 figures
72 cu. cm + 240 cu. cm = 312 cu cm
Thus the volume of the composite figure is 312 cu. cm
Chapter Review/Test – Page No. 710
Question 15.
For 15a–15c, write the name of one quadrilateral from the tiles to complete a true statement. Use each quadrilateral once only.
a. A  is always a parallelogram.
is always a parallelogram.
_________
Answer: rectangle
Explanation: Parallelograms are quadrilaterals with two sets of parallel sides. Since squares must be quadrilaterals with two sets of parallel sides, then all squares are parallelograms.
Question 15.
b. A  is always a rhombus.
is always a rhombus.
_________
Answer: square
Explanation: A square is a quadrilateral with all sides equal in length and all interior angles right angles.
Question 15.
c. A  is sometimes a parallelogram.
is sometimes a parallelogram.
_________
Answer: trapezoid
Explanation: A trapezoid has one pair of parallel sides and a parallelogram has two pairs of parallel sides. So a parallelogram is also a trapezoid.
Question 16.
Megan’s aquarium has a volume of 4,320 cubic inches. Which could be the dimensions of the aquarium? Mark all that apply.
Options:
a. 16 in. by 16 in. by 18 in.
b. 14 in. by 18 in. by 20 in.
c. 12 in. by 15 in. by 24 in.
d. 8 in. by 20 in. by 27 in.
Answer: C, D
Explanation:
The volume of a prism = l × w × h
1. V = 16 in × 16 in × 16 in
V = 4608 cu. in
2. V = 14 in × 18 in × 20 in = 5040 cu. in
3. V = 12 in × 15 in × 24 in = 4320 cu. in
4. V = 8 in × 20 in × 27 in = 4320 cu in
Thus the suitable answers are C and D.
Question 17.
Ken keeps paper clips in a box that is the shape of a cube. Each side of the cube is 3 inches. What is the volume of the box?
______ cubic inches
Answer: 27
Explanation:
Ken keeps paper clips in a box that is the shape of a cube.
Each side of the cube is 3 inches.
The volume of a cube = 3 in × 3 in × 3 in = 27 cu. in
Therefore the volume of the box is 27 cubic inches.
Question 18.
Monica used 1-inch cubes to make the rectangular prism shown. For 18a–18d, write the value that makes each statement true. Each value can be used more than once or not at all.
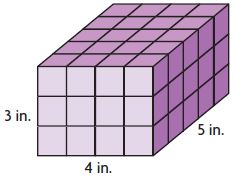

a. Each cube has a volume of ____ cubic inch(es).
Answer: 1
Explanation:
Monica used 1-inch cubes to make the rectangular prism
Volume = 1 in × 1 in × 1 in = 1 cu. in.
Each cube has a volume of 1 cubic inch.
Question 18.
b. Each layer of the prism is made up of ____ cubes.
______ cubes
Answer: 20
Explanation:
We can calculate the layer by calculating the base and width
4 × 5 = 20 cubes
Each layer of the prism is made up of 20 cubes.
Question 18.
c. There are ____ layers of cubes.
______ layers
Answer: 3
By seeing the figure we can say that there are 3 layers of the cube.
You can also find the layers of the cube by calculating the height of the figure.
Question 18.
d. The volume of the prism is ____ cubic inches.
______ cubic inches
Answer: 60
Explanation:
The volume of a prism = l × w × h
V = 4 in × 5 in × 3 in
Volume = 60 cu. inches
Therefore, the volume of the prism is 60 cubic inches.
Chapter Review/Test – Vocabulary – Page No. 4910
Choose the best term from the box.
Question 1.
A _____ has two congruent polygons as bases and rectangular lateral faces.
__________
Answer: prism
A prism has two congruent polygons as bases and rectangular lateral faces.
Question 2.
A _____ has only one base and triangular lateral faces.
__________
Answer: pyramid
A pyramid has only one base and triangular lateral faces.
Concepts and Skills
Name each polygon. Then tell whether it is a regular polygon or not a regular polygon.
Question 3.
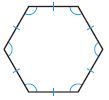
Name: __________
Type: __________
Answer:
i. hexagon
ii. regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has.
The above figure has six sides and 6 angles. Thus the name of the polygon is hexagon.
Two polygons are congruent when they have the same size and the same shape. The above figure has same size and angles. Thus it is a regular polygon.
Question 4.
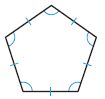
Name: __________
Type: __________
Answer:
i. pentagon
ii. regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has.
The above figure has five sides and 5 angles. Thus the name of the polygon is pentagon.
Two polygons are congruent when they have the same size and the same shape. The above figure has same size and angles. Thus it is a regular polygon.
Question 5.
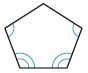
Name: __________
Type: __________
Answer:
i. pentagon
ii. not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has.
The above figure has five sides and 5 angles. Thus the name of the polygon is the pentagon.
Two polygons are congruent when they have the same size and the same shape. The above figure does not have the same size and angles. Thus it is not a regular polygon.
Question 6.
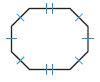
Name: __________
Type: __________
Answer:
i. octagon
ii. not regular
Explanation:
A polygon is a closed plane figure formed by three or more line segments that meet at points called vertices. It is named by the number of sides and angles it has.
The above figure has 8 sides and 8 angles. Thus the name of the polygon is octagon.
Two polygons are congruent when they have the same size and the same shape. The above figure does not have same size and angles. Thus it is not a regular polygon.
Classify each figure in as many ways as possible.
Question 7.
1. __________
2. __________
Answer:
1. quadrilateral
2. trapezoid
Explanation:
1. A general quadrilateral has 4 sides and 4 angles.
2. A trapezoid is a 4-sided flat shape with straight sides that has a pair of opposite sides parallel.
Question 8.
△ __________
∠ __________
Answer:
△ – scalene
∠ – right
Explanation:
The above triangle has different sides. Thus the triangle is a scalene triangle.
The triangle with one right angle is known as a right angled triangle.
Classify the solid figure. Write prism, pyramid, cone, cylinder, or sphere.
Question 9.
__________
Answer: prism
Explanation:
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.
Question 10.
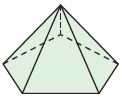
__________
Answer: pyramid
Explanation:
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the vertex). Like any pyramid, it is self-dual.
Count the number of cubes used to build each solid figure.
Question 11.
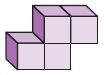
_____ unit cubes
Answer: 4
Explanation:
The figure shows that there are 4 unit cubes.
Question 12.
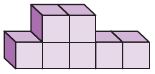
_____ unit cubes
Answer: 7
Explanation:
By seeing the above figure we can say that there are 7 unit cubes.
Question 13.
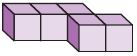
_____ unit cubes
Answer: 5
Explanation:
The figure above shows that there are 5 unit cubes.
Chapter Review/Test – Page No. 4920
Fill in the bubble completely to show your answer.
Question 14.
What type of triangle is shown below?
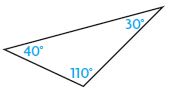
Options:
a. acute; isosceles
b. acute; scalene
c. obtuse; scalene
d. obtuse; isosceles
Answer: obtuse; scalene
Explanation:
The sides of the triangle is different. Thus it is a scalene triangle. The angle of the triangle is an obtuse angle.
Thus the correct answer is option C.
Question 15.
Angela buys a paperweight at the local gift shop. The paperweight is in the shape of a hexagonal pyramid.
Which of the following represents the correct number of faces, edges, and vertices in a hexagonal pyramid?
Options:
a. 6 faces, 12 edges, 18 vertices
b. 7 faces, 7 edges, 12 vertices
c. 7 faces, 12 edges, 7 vertices
d. 8 faces, 18 edges, 12 vertices
Answer: 7 faces, 12 edges, 7 vertices
Explanation:
In geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point.
The hexagonal pyramid has 7 faces, 12 edges and 7 vertices.
Therefore the correct answer is option C.
Question 16.
A manufacturing company constructs a shipping box to hold its cereal boxes. Each cereal box has a volume of 40 cubic inches. If the shipping box holds 8 layers with 4 cereal boxes in each layer, what is the volume of the shipping box?
Options:
a. 160 cu in.
b. 320 cu in.
c. 480 cu in.
d. 1,280 cu in.
Answer: 1,280 cu in.
Explanation:
A manufacturing company constructs a shipping box to hold its cereal boxes.
Each cereal box has a volume of 40 cubic inches.
If the shipping box holds 8 layers with 4 cereal boxes in each layer
Multiply the number of layers with boxes
= 8 × 4 = 32
The volume of 8 layers is 40 × 32 = 1280 cubic inches
Thus the correct answer is option D.
Chapter Review/Test – Page No. 4930
Fill in the bubble completely to show your answer.
Question 17.
Sharri packed away her old summer clothes in a storage tote that had a length of 3 feet, a width of 4 feet, and a height of 3 feet. What was the volume of the tote that Sharri used?
Options:
a. 36 cu ft
b. 24 cu ft
c. 21 cu ft
d. 10 cu ft
Answer: 36 cu ft
Explanation:
Given,
Sharri packed away her old summer clothes in a storage tote that had a length of 3 feet, a width of 4 feet, and a height of 3 feet.
Volume = l × w × h
V = 3 ft × 4 ft × 3 ft
V = 36 cu. ft
Thus the volume of the tote that Sharri used is 36 cu. ft.
The correct answer is option A.
Question 18.
Which quadrilateral is NOT classified as a parallelogram?
Options:
a. 
b. 
c. 
d. 
Answer: 
Explanation:
The opposite sides of figure b are not parallel. Thus the figure b quadrilateral is NOT classified as a parallelogram.
Question 19.
What is the volume of the composite figure below?
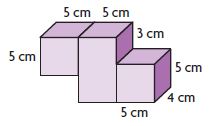
Options:
a. 1,875 cm3
b. 480 cm3
c. 360 cm3
d. 150 cm3
Answer:
Volume of 1st cube is 5 cm × 4 cm × 5 cm = 100 cu. cm
Volume of 2nd cube is 5 cm × 4 cm × 8 cm = 160 cu. cm
Volume of 3rd cube is 5 cm × 4 cm × 5 cm = 100 cu. cm
Add all the volumes to find the volume of the composite figure
That means 100 cu. cm + 160 cu. cm + 100 cu. cm = 360 cu. cm
Therefore the volume of the composite figure is 360 cm3
The correct answer is option C.
Chapter Review/Test – Page No. 4940
Constructed Response
Question 20.
a. A video game store made a display of game console boxes shown at the right. The length, width, and height of each game console box is 2 feet.
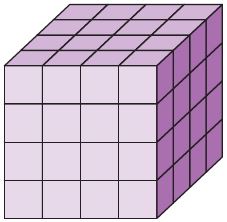
What is the volume of the display of game console boxes? Show your work and explain your answer.
_____ cu ft.
Answer: 512 cu. ft
Explanation:
length = 2 ft
width = 2 ft
height = 2 ft
Volume of the display of game console boxes = 2 ft × 2 ft × 2 ft = 8 cu. ft
Number of console boxes = 64
64 × 8 cu. ft = 512 cu ft
The volume of the display of game console boxes = 512 cu ft
Question 20.
b. On a busy Saturday, the video game store sold 22 game consoles.
What is the volume of the game console boxes that are left?
_____ cu ft.
Answer: 336 cu. ft
length = 2 ft
width = 2 ft
height = 2 ft
The volume of the display of game console boxes = 2 ft × 2 ft × 2 ft = 8 cu. ft
Number of console boxes = 22
The volume of the game console boxes that are left
22 × 8 cu. ft = 176 cu. ft
The volume of the game console boxes that are left = 512 – 176 = 336 cu. ft
Performance Task
Question 21.
Look for two pictures of three-dimensional buildings in newspapers and magazines. The buildings should be rectangular prisms.
A. Paste the pictures on a large sheet of paper. Leave room to write information near the picture.
B. Label each building with their name and location.
C. Research the buildings, if the information is available. Find things that are interesting about the buildings or their location. Also find their length, width, and height to the nearest foot. If the information is not available, measure the buildings on the page in inches or centimeters, and make a good estimate of their width (such as 1/2 the height, rounded to the nearest whole number). Find their volumes.
D. Make a class presentation, choosing one of the buildings you found.
Conclusion
Hoping the knowledge shared about Go Math Grade 5 Answer Key Chapter 11 Geometry and Volume has helped you clear your queries to the possible extent. Download the 5th Grade Go Math Ch 11 Geometry and Volume Answer Key free of cost and take your preparation to next level.