Students who are in search of the Answer Key of Go Math Grade 6 Chapter 1 Divide Multi Digit Numbers can get them on this page. Refer to our Go Math Grade 6 Answer Key and solve the problems. We provide the step by step explanations for all the question by using the pictures here. By using Go Math 6th Grade Chapter, 1 Answer Key the scholars will not find any difficulty in solving the questions.
Go Math Grade 6 Answer Key Chapter 1 Divide Multi-Digit Numbers
In order to excel in exam we suggest the students of 6th standard to refer the Go Math Answer Key Chapter 1 Divide Multi-Digit Numbers. The solutions in Go Math Grade 6 Answer Key Chapter 1 Divide Multi-Digit Numbers are prepared by the math experts. You can understand the concepts in depth with the help of Go Math Grade 6 Solution Key.
Lesson 1: Divide Multi-Digit Numbers
- Page No. 7
- Problem Solving + Applications – Page No. 8
- Divide Multi-Digit Numbers – Page No. 9
- Lesson Check – Page No. 10
Lesson 2: Prime Factorization
- Find the prime factorization – Page No. 13
- Problem Solving + Applications – Page No. 14
- Prime Factorization – Page No. 15
- Lesson Check – Page No. 16
Lesson 3: Least Common Multiple
- Find the LCM – Page No. 19
- Unlock The Problem – Page No. 20
- Least Common Multiple – Page No. 21
- Lesson Check – Page No. 22
Lesson 4: Greatest Common Factor
- Share and Show – Page No. 25
- Problem Solving + Applications – Page No. 26
- Greatest Common Factor – Page No. 27
- Lesson Check – Page No. 28
Lesson 5: Problem Solving • Apply the Greatest Common Factor
- Share and Show – Page No. 31
- On Your Own – Page No. 32
- Problem Solving Apply the Greatest Common Factor – Page No. 33
- Lesson Check – Page No. 34
Mid-Chapter Checkpoint
Lesson 6: Add and Subtract Decimals
- Share and Show – Page No. 39
- Page No. 40
- Add and Subtract Decimals – Page No. 41
- Lesson Check – Page No. 42
Lesson 7: Multiply Decimals
- Share and Show – Page No. 45
- Unlock the Problem – Page No. 46
- Multiply Decimals – Page No. 47
- Lesson Check – Page No. 48
Lesson 8: Divide Decimals by Whole Numbers
- Then find the quotient – Page No. 51
- Problem Solving + Applications – Page No. 52
- Divide Decimals by Whole Numbers – Page No. 53
- Lesson Check – Page No. 54
Lesson 9: Divide with Decimals
- Share and Show – Page No. 57
- Page No. 58
- Divide with Decimals – Page No. 59
- Lesson Check – Page No. 60
Chapter 1 Review/Test
Page No. 7
Estimate. Then find the quotient. Write the remainder, if any, as a fraction.
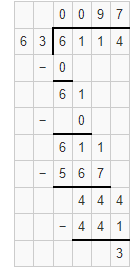
Question 3.
6,114 ÷ 63
Answer: Quotient is 97 3/63= 97 1/21 and the remainder is 3
Explanation:
Question 4.
11050 ÷ 26
Answer: Quotient is 425 and the remainder is 0.
Explanation:
On Your Own
Estimate. Then find the quotient. Write the remainder, if any, as a fraction.
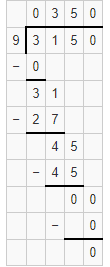
Question 5.
3150 ÷ 9
Answer: Quotient is 350 and the remainder is 0.
Explanation:
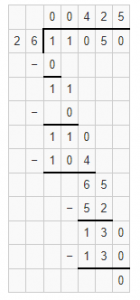
Question 6.
2115 ÷ 72
Answer: Quotient is 29 27/72= 29 3/8 and the remainder is 27.
Explanation:
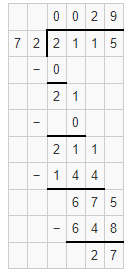
Question 7.
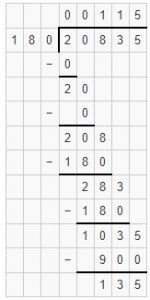
20835 ÷ 180
Answer: Quotient is 115 135/180= 115 3/4 and the remainder is 135
Explanation:
Question 8.
Find the least whole number that can replace ? to make the statement true.
110 < ? ÷ 47
Answer: Least whole number is 5,171.
Explanation: 110×47= 5,170
Question 9.
Use Reasoning Name two whole numbers that can replace ? to make both statements true.
2 × ? < 1800 ÷ 12 ? > 3744 ÷ 52
Answer:
Explanation:
Question 10.
The 128 employees of a company volunteer 12,480 hours in 26 weeks. On average, how many hours do they all volunteer per week? On average, how many hours does each employee volunteer per week?
Answer: 3.75 hours.
Explanation: In 26 weeks 128 employees volunteer 12,480 hours, so in 1 week they volunteer 12,480÷26= 480 hours.
And each employee volunteer per week is 480÷128= 3.75 hours.
Question 11.
A factory produces 30,480 bolts in 12 hours. If the same number of bolts are produced each hour, how many bolts does the factory produce in 5 hours?
Answer: 12,700.
Explanation: As the factory produces 30,480 bolts in 12 hours, so in a 1-hour company produces 30,480÷12= 2,450 boults and in 5 hours it produces 2,450×5= 12,700.
Problem Solving + Applications – Page No. 8
Use the table for 12-15.
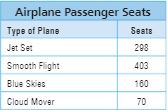
Question 12.
A Smooth Flight jet carried 6,045 passengers last week, and all of its flights were full. How many flights did the jet make last week?
Answer: 15 flights.
Explanation: As there are 403 seats in Smooth flight and 6,045 passengers are carried in last week, so no.of flights did the jet make in last week are 6045÷403= 15
Question 13.
Last month an airline made 6,322 reservations for flights from Newark, New Jersey, to Frankfurt, Germany. If there were 21 full flights and 64 reservations cancelled, which airplane made the flights?
Answer: Jet Set.
Explanation: Total reservations made by the airline are 6,322 and cancelled are 64, so completed reservations are 6,322-64= 6,258 and 21 flights are full so 6258÷21= 298 passengers in each flight and that airplane is Jet set
Question 14.
An airline carries about 750 passengers from Houston to Chicago each day. How many Blue Sky jets would be needed to carry this many passengers, and how many empty seats would there be?
Answer: 5 Sky jets would be needed and 50 empty seats would be there.
Explanation: Let’s round off 750 to 800, As there are 800 passengers each day so no. of Sky jets needed are 800÷160= 5. and 50 empty seats would be there.
Question 15.
Pose a Problem Refer back to Problem 12. Use the information in the table to write a similar problem involving airplane passenger seats.
Answer:
Explanation:
Question 16.
For numbers 16a – 16d, choose Yes or No to indicate whether the equation is correct.
16a. 1,350 ÷ 5 = 270 O Yes O No
16b. 3,732 ÷ 4 = 933 O Yes O No
16c. 4,200 ÷ 35 = 12 O Yes O No
16d. 1,586 ÷ 13 = 122 O Yes O No
16a. Answer: Yes
Explanation: 1,350÷5= 270.
16b. Answer: Yes
Explanation: 3732÷4= 933
16c. Answer: No
Explanation: 4200÷35= 120
16d. Answer: Yes
Explanation: 1586÷13= 122.
Divide Multi-Digit Numbers – Page No. 9
Estimate. Then find the quotient. Write the remainder, if any, with an r.
Question 1.
180)\(\overline { 20835 } \)
Answer: Quotient is 115 and remainder r135
Explanation:
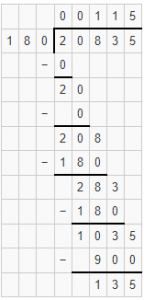
Question 2.
19)\(\overline { 800 } \)
Answer: Quotient is 42 and remainder r2
Explanation:
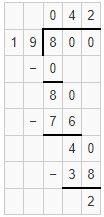
Question 3.
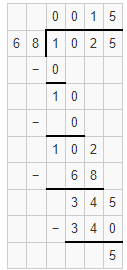
68)\(\overline { 1025 } \)
Answer: Quotient is 15 and remainder r5
Explanation:
Estimate. Then find the quotient. Write the remainder, if any, as a fraction.
Question 4.
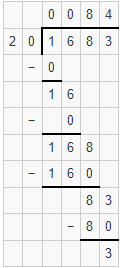
20)\(\overline { 1683 } \)
Answer: Quotient is 84 and remainder r3.
Explanation:
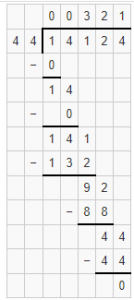
Question 5.
14124 ÷ 44
Answer: Quotient is 321 and remainder r0
Explanation:
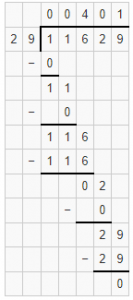
Question 6.
11629 ÷ 29
Answer: Quotient is 401 and remainder r0
Explanation:
Find the least whole number that can replace ? to make the statement true.
Question 7.
? ÷ 7 > 800
Answer: The least whole number to makes the statement true is 5600
Explanation: 5600÷7> 800
Question 8.
? ÷ 21 > 13
Answer: The least whole number to makes the statement true is 273
Explanation: 273÷21>13
Question 9.
15 < ? ÷ 400
Answer: The least whole number to makes the statement true is 6000
Explanation: 15< 6000÷400
Problem Solving
Question 10.
A plane flew a total of 2,220 miles. Its average speed was 555 miles per hour. How many hours did the plane fly?
Answer: 4 hours
Explanation: Total miles does a plane flew is 2,220 miles and average speed is 555 miles per hour. So total hours did plane fly are 2,220÷555= 4 hours
Question 11.
A van is carrying 486 pounds. There are 27 boxes in the van. What is the average weight of each box in the van?
Answer: 18 lbs
Explanation: No.of pounds did the van carry are 486 pounds and no.of boxes in a van are 27. So the average weight of each box is 486÷27= 18
Question 12.
Find 56,794 ÷ 338. Write the quotient twice, once with the remainder as a fraction and once with an r.
Answer: 56,794÷338= 168 10/338= 168 5/169, r=10.
Explanation: 56,794÷338= 168 10/338= 168 5/169 and reminder is 10
Lesson Check – Page No. 10
Question 1.
A caterer’s fee is based on the number of meals she provides. How much is the price per meal if the total fee is $1,088 for 64 meals?
Answer: $17.
Explanation: No.of meals are 64 and the total fee is $1,088. Therefore the price per meal is $1,088÷64= $17.
Question 2.
Amelia needs 24 grains of beads to make a bracelet. She has 320 grams of beads. How many bracelets can she make?
Answer: 13 bracelets.
Explanation: No.of grains of beads Amelia need are 24 and she has 320 grams of beads. So no.of bracelets can Amelia make are 320÷24= 13.33 will round off to 13.
Spiral Review
Question 3.
Hank bought 2.4 pounds of apples. Each pound cost $1.95. How much did Hank spend on the apples?
Answer: $4.68
Explanation: No.of pounds of apples Hank bought is 2.4 pounds and each pound cost is $ 1.95, so total Hank spend on apples is 2.4×$1.95= $4.68
Question 4.
Gavin bought 4 packages of cheese. Each package weighed 1.08 kilograms. How many kilograms of cheese did Gavin buy?
Answer: 4.32kg
Explanation: No.of cheese packages Gavin bought are 4 and each package weight is 1.08 kg. So total weight of cheese is 4×1.08= 4.32 kg
Question 5.
Mr. Thompson received a water bill for $85.98. The bill covered three months of service. He used the same amount of water each month. How much does Mr. Thompson pay for water each month?
Answer: $28.66
Explanation: Water bill received to Mr. Thompson is $85.98 as he covered for 3 months the amount Mr.Thompson paid for each month is $85.98÷3= $28.66
Question 6.
Layla used 0.482 gram of salt in her experiment. Maurice use 0.51 gram of salt. Who used the greater amount of salt?
Answer: Maurice as 0.51 is greater than 0.482.
Explanation: Salt used by Layla is 0.482 grams and salt used by Maurice is 0.51 grams, so the greatest amount of salt used is Maurice as 0.51 is greater than 0.482.
Find the prime factorization – Page No. 13
Question 3.
75
Answer: 5×5×3.
Explanation: 75
15 5
5×3 5
5×5×3
Question 4.
12
Answer: 3×2×2.
Explanation: 12
6×2
3×2×2
Question 3.
65
Answer: 13×5
Explanation: 65
13×5
On Your Own
Write the number whose prime factorization is given.
Question 6.
2 × 2 × 2 × 7
Answer: 56
Question 7.
2 × 2 × 5 × 5
Answer: 100
Question 8.
2 × 2 × 2 × 2 × 3 × 3
Answer: 144
Practice: Copy and Solve Find the prime factorization.
Question 9.
45
Answer: 5×3×3
Explanation:
45
5×9
5×3×3
Question 10.
50
Answer: 5×5×2
Explanation:
50
5×10
5×5×2
Question 11.
32
Answer: 2×2×2×2×2
Explanation:
32
2×16
2×2×8
2×2×2×4
2×2×2×2×2
Question 12.
76
Answer: 2×2×19
Explanation:
76
2×38
2×2×19
Question 13.
108
Answer: 2×2×3×3×3
Explanation:
108
2×54
2×2×27
2×2×3×9
2×2×3×3×3
Question 14.
126
Answer: 2×7×3×3
Explanation:
126
2×63
2×7×9
2×7×3×3
Question 15.
The area of a rectangle is the product of its length and width. A rectangular poster has an area of 260 square inches. The width of the poster is greater than 10 inches and is a prime number. What is the width of the poster?
Answer: Width is 13.
Explanation: Area of a rectangular poster is 260 square inches i.e width×length= 260 sq inches. And the width of the poster is greater than 10 inches and it is a prime number, so the width will be 13 as 13 is a prime number and also 260 is divisible by 13, and length is 13×length= 260 in which length is 260÷13= 20.
Question 16.
Look for Structure Dani says she is thinking of a secret number. As a clue, she says the number is the least whole number that has three different prime factors. What is Dani’s secret number? What is its prime factorization?
Answer: Dani’s secret number is 30 and the prime factorization is 2,3,5.
Explanation: The least three prime numbers are 2,3,5, so the product of three prime numbers is 2×3×5= 30.
Problem Solving + Applications – Page No. 14
Use the table for 17–19. Agent Sanchez must enter a code on a keypad to unlock the door to her office.

Question 17.
In August, the digits of the code number are the prime factors of 150. What is the code number for the office door in August?
Answer: 2355.
Explanation: Prime Factors of 150 are 2×3×5×5, so code number for office door in August is 2355
Question 18.
In September, the fourth digit of the code number is 2 more than the fourth digit of the code number based on the prime factors of 225. The prime factors of what number were used for the code in September?
Answer: 315.
Explanation: Prime factors of 225 are 3×3×5×5 which is 3355 as the fourth digit of the code number is 2 more than the fourth digit, s0 5+2=7 and by replacing 7 in 3×3×5×5, then 3×3×5×7= 315.
Question 19.
One day in October, Agent Sanchez enters the code 3477. How do you know that this code is incorrect and will not open the door?
Answer: 4 is not a prime number.
Explanation: The code 3477 is incorrect as the code contains only a prime number and 4 is not a prime number.
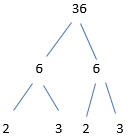
Question 20.
Use the numbers to complete the factor tree. You may use a number more than once.
2 3 6 9 18
Answer: 36= 2×2×3×3
Explanation:
Prime Factorization – Page No. 15
Find the prime factorization.
Question 1.
44
Answer: 2×2×11
Explanation:
44
2×22
2×2×11
Question 2.
90
Answer: 2×3×3×5
Explanation:
90
2×45
2×3×15
2×3×3×5
Question 3.
48
Answer:
Explanation:
48
2×24
2×2×12
2×2×2×6
2×2×2×2×3
Question 4.
204
Answer: 2×2×3×17
Explanation:
204
2×102
2×2×51
2×2×3×17
Question 5.
400
Answer: 2×2×2×2×5×5
Explanation:
400
2×200
2×2×100
2×2×2×50
2×2×2×2×25
2×2×2×2×5×5
Question 6.
112
Answer: 2×2×2×2×7
Explanation:
112
2×56
2×2×28
2×2×2×14
2×2×2×2×7
Problem Solving
Question 7.
A computer code is based on the prime factorization of 160. Find the prime factorization of 160.
Answer: 2×2×2×2×2×5
Explanation: Prime factors of 160 is 2×2×2×2×2×5
Question 8.
The combination for a lock is a 3-digit number. The digits are the prime factors of 42 listed from least to greatest. What is the combination for the lock?
Answer: 237.
Explanation: Prime factors of 42 is 2×3×7.
Question 9.
Describe two methods for finding the prime factorization of a number.
Answer:
1. Divison Method.
2. Factor Tree Method.
Explanation:
1. Division Method: In Division method first we will divide the number by smallest prime number, and repeat the process until the quotient became 1.
2. Factor Tree Method: In Factor Tree Method we will write a pair of factors as the branches of the tree and then we will factorize.
Lesson Check – Page No. 16
Question 1.
Maritza remembers her PIN because it is between 1,000 and 1,500 and it is the product of two consecutive prime numbers. What is her PIN?
Answer: Two consecutive prime numbers are 31 and 37 and PIN is 1147.
Explanation: As 31 and 37 are two consecutive prime numbers and their product is 1147 which is between 1,000 to 1,500.
Question 2.
Brent knows that the 6 -digit number he uses to open his computer is the prime factorization of 5005. If each digit of the code increases from left to right, what is his code?
Answer: 111357.
Explanation: Factors of 5005 are 5×7×11×13, as the increases from left to right so the code is 111357
Spiral Review
Question 3.
Piano lessons cost $15. What expressions could be used to find the cost in dollars of 5 lessons?
Answer: $15×5= $75
Explanation: We will use multiplication to find the cost in dollars of 5 lessons.
Question 4.
A jet plane costs an airline $69,500,000. What is the place value of the digit 5 in this number?
Answer: Hundred thousand.
Explanation: The place value of 5 in $69,500,000 is 500,000.
Question 5.
A museum has 13,486 butterflies, 1,856 ants, and 13,859 beetles. What is the order of the insects from least number to greatest number?
Answer: Ants, Butterflies, Beetles.
Explanation: The order of insects from least to greatest are Ants, Butterflies, Beetles.
Question 6.
Juan is reading a 312-page book for school. He reads 12 pages each day. How long will it take him to finish the book?
Answer: 26 days.
Explanation: As Juan reads 12 pages each day and the book has 312 pages, so he will finish in 312÷12= 26 days
Find the LCM – Page No. 19
Question 2.
3, 5
Answer: 15
Explanation:
Multiples of 3: 3,6,9,12,15
Multiples of 5: 5,10,15.
LCM is 15
Question 3.
3, 9
Answer: 9
Explanation:
Multiples of 3: 3,6,9
Multiples of 9: 9
LCM is 9
Question 4.
9, 15
Answer: 135
Explanation:
Multiples of 9: 9,18,27,36,45,54,63,72,81,90,99,108,117,126,135.
Multiples of 15: 15,30,45,60,75,90,105,120,135.
LCM is 135
On Your Own
Find the LCM.
Question 5.
5, 10
Answer: 10
Explanation:
Multiples of 5: 5,10
Multiples of 10: 10
LCM is 10
Question 6.
3, 8
Answer: 24
Explanation:
Multiples of 3: 3,6,92,15,18,21,24
Multiples of 8: 8,16,24
LCM is 24
Question 7.
9, 12
Answer: 108
Explanation:
Multiples of 9: 9,18,27,36,45,54,63,72,81,90,99,108
Multiples of 12: 12,24,36,48,60,72,84,96,108
LCM is 108
Use Reasoning Algebra Write the unknown number for ?.
Question 8.
5, 8 LCM : ?
? =
Answer: 40
Explanation:
Multiples of 5: 5,10,15,20,25,30,35,40
Multiples of 8: 8,16,24,32,40
LCM is 40
Question 9.
?, 6 LCM : 42
? =
Answer: 7
Explanation: 6×7= 42
Question 10.
How can you tell when the LCM of two numbers will equal one of the numbers or equal the product of the numbers?
Answer: If the other number is 1 then the LCM of two numbers will equal one.
Question 11.
Verify the Reasoning of Others Mr. Haigwood is shopping for a school picnic. Veggie burgers come in packages of 15, and buns come in packages of 6. He wants to serve veggie burgers on buns and wants to have no items left over. Mr. Haigwood says that he will have to buy at least 90 of each item, since 6 × 15 = 90. Do you agree with his reasoning? Explain.
Answer: No. We must find the least number of burgers and buns, so we must find LCM of 15 and 6.
Explanation:
Multiples of 15: 15,30
Multiples of 6: 6,12,18,24,30
LCM is 30.
Question 12.
A deli has a special one -day event to celebrate its anniversary. On the day of the event, every eighth customer receives a free drink. Every twelfth customer receives a free sandwich. If 200 customers show up for the event, how many of the customers will receive both a free drink and a free sandwich?
Answer: 24,48,72,96,120,144,168,192 are the customers who get both free drink and free sandwich.
Explanation: To find how many customers have received both a free drink and a sandwich, first we have to find who got a free sandwich and a free drink separately, so
Multiples of 8 are 8,16,24,32,40,48,56,64,72,80,88,96,104,112,120,128, 136,144,152,160,168,176,184,192 and 200 and
Multiples of 12 are 12,24,36,48,60,72,84,96,108,120,132,144,156,168,180 and 192. So common customers are 24,48,72,96,120,144,168,192 are the customers who get both free drink and free sandwich.
Unlock The Problem – Page No. 20
Question 13.
Katie is making hair clips to sell at the craft fair. To make each hair clip, she uses 1 barrette and 1 precut ribbon. The barrettes are sold in packs of 12, and the precut ribbons are sold in packs of 9. How many packs of each item does she need to buy to make the least number of hair clips with no supplies left over?
a. What information are you given?
Answer: 3 packs of barrettes and 4 packs of precut ribbons.
Explanation: As barrettes are sold in packs of 12 and precut ribbons are sold in packs of 9, so we need to find the number of packs of each item does she need to make the least number of hair clips with no supplies left over. So the LCM of 12 and 9.
Multiples of 12 are: 12,24,36
Multiples of 9 are: 9,18,27,36
LCM is 36
So Katie needs 36 barrettes and ribbons to make the least number of hair clips with no supplies left over, and she needs 3 packs of barrettes and 4 packs of precut ribbons.
Question 13.
b. What problem are you being asked to solve?
Answer: To find the number of packs of each item does she need to make the least number of hair clips with no supplies left over
Question 13.
c. Show the steps you use to solve the problem.
Answer:
Multiples of 12 are: 12,24,36
Multiples of 9 are: 9,18,27,36
LCM is 36
Question 13.
d. Complete the sentences.
The least common multiple of 12 and 9 is _____ .
Katie can make _____ hair clips with no supplies left over.
To get 36 barrettes and 36 ribbons, she needs to buy _____ packs of barrettes and _____ packs of precut ribbons.
Answer: 36, 3, 4.
Explanation:
The least common multiple of 12 and 9 is 36.
Katie can make 36 hair clips with no supplies left over.
To get 36 barrettes and 36 ribbons, she needs to buy 3 packs of barrettes and 4 packs of precut ribbons.
Question 14.
Reptile stickers come in sheets of 6 and fish stickers come in sheets of 9. Antonio buys the same number of both types of stickers and he buys at least 100 of each type. What is the least number of sheets of each type he might buy?
Answer: 108
Explanation: As Reptile stickers come in sheets of 6 and fish stickers come in sheets of 9, so we will find the LCM of 6 and 9 to get the least number of sheets,
Multiples of 6 are 6,12,18
Multiples of 9 are 9,18
LCM is 18
As Antonio buys at least 100 of each type, so multiples of 18 are 18,36,54,72,90,108 as 108 is the least number and more than 100 and nearest to 100, so the least number of sheets he might buy= 108
Question 15.
For numbers 15a -15d, choose Yes or No to indicate whether the LCM of the two numbers is 16.
15a. 2,8 O Yes O No
15b. 2,16 O Yes O No
15c. 4,8 O Yes O No
15d. 8,16 O Yes O No
15a. 2,8 O Yes O No
Answer: No
Explanation:
Multiples of 2 are 2,4,6,8
Multiples of 8 are 8
LCM is 8
15b. 2,16 O Yes O No
Answer: Yes
Explanation:
Multiples of 2 are 2,4,6,8,10,12,14,16
Multiples of 16 are 16
LCM is 16
15c. 4,8 O Yes O No
Answer: No
Explanation:
Multiples of 4 are 4,8
Multiples of 8 are 8
LCM is 8
15d. 8,16 O Yes O No
Answer: 16
Explanation:
Multiples of 8 are 8,16
Multiples of 16 are 16
LCM is 16
Least Common Multiple – Page No. 21
Find the LCM.
Question 1.
2, 7
Answer: 14
Explanation:
Multiples of 2 are 2,4,6,8,10,12,14.
Multiples of 7 are 7,14.
LCM is 14.
Question 2.
4, 12
Answer: 12
Explanation:
Multiples of 4 are 4,8,12
Multiples of 12 are 12
LCM is 12
Question 3.
6, 9
Answer: 54
Explanation:
Multiples of 6 are 6,12,18,24,30,36,42,48,54
Multiples of 9 are 9,18,27,36,45,54
LCM is 54
Question 4.
5, 4
Answer: 8
Explanation:
Multiples of 5 are 5,10,15
Multiples of 4 are 8
LCM is 8
Question 5.
5, 8, 4
Answer: 40
Explanation:
Multiples of 5 are 5,10,15,20,25,30,35,40
Multiples of 8 are 8,16,24,32,40
Multiples of 4 are 4,8,12,16,20,24,28,32,36,40
LCM is 40
Question 6.
12, 8, 24
Answer: 24
Explanation:
Multiples of 12 are 12,24
Multiples of 8 are 8,16,24
Multiples of 24 are 24
LCM is 24
Write the unknown number for the?
Question 7.
3, ? LCM : 21
? =
Answer: 7
Explanation: 3×7= 21
Question 8.
?, 7 LCM : 63
? =
Answer: 9
Explanation: 9×7=63
Question 9.
10, 5 LCM : ?
? =
Answer: 10
Explanation:
Multiples of 10 are 10
Multiples of 5 are 5,10
LCM is 10
Problem Solving
Question 10.
Juanita is making necklaces to give as presents. She plans to put 15 beads on each necklace. Beads are sold in packages of 20. What is the least number of packages she can buy to make necklaces and have no beads left over?
Answer: 3 packages.
Explanation:
Multiples of 15: 15,30,45,60
Multiples of 20: 20,40,60
LCM is 60
As beads are sold in packages of 20 Juanita needs 3 least number of packages to make necklaces with no beads leftover.
Question 11.
Pencils are sold in packages of 10, and erasers are sold in packages of 6. What is the least number of pencils and erasers you can buy so that there is one pencil for each eraser with none left over?
Answer: 30 pencils and 30 erasers are the least numbers we can buy without any leftover.
Explanation:
Multiples of 10: 10,20,30.
Multiples of 6: 6,12,18,24,30.
LCM is 30.
So 30 pencils and 30 erasers are the least numbers we can buy without any leftover.
Question 12.
Explain when you would use each method (finding multiples or prime factorization) for finding the LCM and why.
Answer: When the numbers are smaller we can use finding multiples and when the numbers are larger then we can use prime factorization.
Lesson Check – Page No. 22
Question 1.
Martha is buying hot dogs and buns for the class barbecue. The hot dogs come in packages of 10. The buns come in packages of 12. What is the least number she can buy of each so that she has exactly the same number of hot dogs and buns? How many packages of each should she buy?
_________ packages of hot dogs
_________ packages of buns
Answer: 6 packages of hot dogs and 5 packages of buns she can buy.
Explanation:
Multiples of 10: 10,20,30,40,50,60.
Multiples of 12: 12,24,36,48,60.
LCM is 60.
So 60 is the least number she can buy and 6 packages of hot dogs and 5 packages of buns she can buy.
Question 2.
Kevin makes snack bags that each contain a box of raisins and a granola bar. Each package of raisins contains 9 boxes. The granola bars come 12 to a package. What is the least number he can buy of each so that he has exactly the same number of granola bars and boxes of raisins? How many packages of each should he buy?
_________ packages of raisins
_________ packages of granola bars
Answer: 4 packages of raisins and 3 packages of granola bars he should buy.
Explanation: Kevin’s every package contains 9 raisins boxes and 12 granola bars in each package, so LCM of 9 and 12 are
Multiples of 9: 9,18,21,36
Multiples of 12: 12,24,36
LCM is 36.
So 4 packages of raisins and 3 packages of granola bars he should buy.
Spiral Review
Question 3.
John has 2,456 pennies in his coin collection. He has the same number of pennies in each of 3 boxes. Estimate to the nearest hundred the number of pennies in each box.
Answer: 800 pennies.
Explanation: Let’s round off 2,456 to 2400, as he has the same no. of pennies in each of 3 boxes, so in each box no.of pennies are 2400÷3= 800 pennies.
Question 4.
What is the distance around a triangle that has sides measuring 2 \(\frac{1}{8}\) feet, 3 \(\frac{1}{2}\) feet, and 2 \(\frac{1}{2}\) feet?
Answer: 8 1/8 feet
Explanation: Distance around the triangle is 2 1/8+3 1/2+ 2 1/2= 8 1/8 feet
Question 5.
The 6th grade class collects $1,575. The class wants to give the same amount of money to each of 35 charities. How much will each charity receive?
Answer: $45
Explanation: The 6th-grade class collects $1575 and wants to give the same amount to 35 charities each, so each charity receives $1575÷35= $45.
Question 6.
Jean needs \(\frac{1}{3}\) cup of walnuts for each serving of salad she makes. She has 2 cups of walnuts. How many servings can she make?
Answer: 6.
Explanation: No.of servings made by 1/3 cup of walnuts is 1, so for 1 cup Jean serves 1/(1/3+1/3+1/3)= 3. So for 2 cups, no.of servings can she make are 3×2= 6.
Share and Show – Page No. 25
Question 1.
List the factors of 12 and 20. Circle the GCF.
Factors of 12 : __________
Factors of 20 : __________
Answer: 4
Explanation:
Factors of 12: 1,2,3,4,6,12
Factors of 20: 1,2,4,5,10,20
Common factors are 1,2,4
GCF is 4
Find the GCF.
Question 2.
16, 18
Answer: 2
Explanation:
Factors of 16: 1,2,4,8,16
Factors of 18: 1,2,3,6,9,18
Common factors are 1,2
GCF is 2
Question 3.
25, 40
Answer: 5
Explanation:
Factors of 25: 1,2,5,25
Factors of 40: 1,2,4,5,8,10,20,40
Common factors are 1,2,5
GCF is 5
Question 4.
24, 40
Answer: 8
Explanation:
Factors of 24: 1,2,3,4,6,8,12,24
Factors of 40: 1,2,4,5,8,10,20,40
Common factors are 1,2,4,8
GCF is 8
Question 5.
14, 35
Answer: 7
Explanation:
Factors of 14: 1,2,7,14
Factors of 35: 1,2,5,7,35
Common factors are 1,2,7
GCF is 7
Use the GCF and the Distributive Property to express the sum as a product.
Question 6.
21 + 28
Answer: 7×(3+4)
Explanation:
21+28= (7×3)+(7×4)
=7×(3+4)
Question 7.
15 + 27
Answer: 3×(5+9)
Explanation:
15+27= (3×5)+(3×9)
=3×(5+9)
Question 8.
40 + 15
Answer: 5×(8+3)
Explanation:
40+15= (5×8)+(5×3)
= 5×(8+3)
Question 9.
32 + 20
Answer: 4×(8+5)
Explanation:
32+20= (4×8)+(4×5)
= 4×(8+5)
On Your Own
Find the GCF.
Question 10.
8, 25
Answer: 1
Explanation:
Factors of 8: 1,2,4,8
Factors of 25: 1,5,25
Common factors are 1
GCF is 1
Question 11.
31, 32
Answer: 1
Explanation:
Factors of 31: 1,31
Factors of 32: 1,2,4,8,16,32
Common Factors are 1
GCF is 1
Question 12.
56, 64
Answer: 8
Explanation:
Factors of 56: 1,2,4,7,8,14,28,56
Factors of 64: 1,2,4,8,16,32,64
Common Factors are 1,2,4,8
GCF is 8
Question 13.
150, 275
Answer: 25
Explanation:
Factors of 150: 1,2,3,5,6,10,15,25,30,50,75,150
Factors of 275: 1,5,11,25,55,275
Common Factors are 1,5,25.
GCF is 25.
Use the GCF and the Distributive Property to express the sum as a product.
Question 14.
24 + 30
Answer: 6×(4+5)
Explanation:
24+30= (6×4)+(6×5)
=6×(4+5)
Question 15.
49 + 14
Answer: 7×(7+2)
Explanation:
49+14= (7×7)+(7×2)
=7×(7+2)
Question 16.
63 + 81
Answer: 9×(7+9)
Explanation:
63+81= (9×7)+(9×9)
=9×(7+9)
Question 17.
60 + 12
Answer: 12×(5+1)
Explanation:
60+12= (12×5)+(12×1)
=12×(5+1)
Question 18.
Describe the difference between the LCM and the GCF of two numbers.
Answer: In LCM we will get the Least Common Multiples of two numbers, and in GCF we will get Greatest Common Factor.
Problem Solving + Applications – Page No. 26
Use the table for 19-22. Teachers at the Scott School of Music teach only one instrument in each class. No students take classes for more than one instrument.
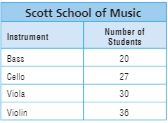
Question 19.
Francisco teaches group lessons to all of the violin and viola students at the Scott School of Music. All of his classes have the same number of students. What is the greatest number of students he can have in each class?
Answer: 6
Explanation: No. of students for Viola instrument is 30 and 36 for Violin,
Factors of 30: 1,2,3,5,6,10,15,30
Factors of 36: 1,2,3,4,6,9,12,18,36
GCF is 6
So the greatest number of students he can have in each class is 6
Question 20.
Amanda teaches all of the bass and viola students. All her classes have the same number of students. Each class has the greatest possible number of students. How many of these classes does she teach?
__________ bass classes
__________ viola classes
Answer: 2 bass classes and 3 viola classes.
Explanation:
Factors of 20: 1,2,4,5,10,20
Factors of 30: 1,2,3,5,6,10,15,30
GCF is 10
As the greatest number of possible students in each class is 10, So Amanda teaches 2 bass classes and 3 viola classes.
Question 21.
Mia teaches jazz classes. She has 9 students in each class, and she teaches all the classes for two of the instruments. Which two instruments does she teach, and how many students are in her classes?
Answer: 63 students.
Explanation:
Factors of 27: 1,3,9,27
Factors of 36: 1,2,3,4,6,9,12,18,36
GCF is 9
As 9 is the GCF of 27 and 36, So Mia teaches Cello and Violin classes for a total of 63 students.
Question 22.
Explain how you could use the GCF and the Distributive Property to express the sum of the number of bass students and the number of violin students as a product.
Answer: GCF is 4
Distributive property is 4×(5+9)
Explanation: The no.of bass students are 20 and no.of violin students are 36,
Factors of 20: 1,2,4,5,10,20
Factors of 36: 1,2,3,4,6,12,18,36
GCF is 4
And the Distributive property is 20+36
= (4×5)+(4×9)
= 4×(5+9)
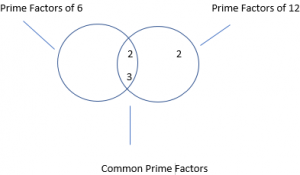
Question 23.

Answer: 6
Explanation:
Factors of 6: 1,2,3,6
Factors of 12: 1,2,3,4,6
GCF is 6
Greatest Common Factor – Page No. 27
List the common factors. Circle the greatest common factor.
Question 1.
25 and 10
Answer: 5
Explanation:
Factors of 25: 1,5,25.
Factors of 10: 1,2,5,10
Common factors are 1,5
GCF is 5
Question 2.
36 and 90
Answer: 18
Explanation:
Factors of 36: 1,2,3,4,6,9,12,18,36
Factors of 90: 1,2,3,5,6,9,10,15,18,30,45,90
Common Factors are 1,2,3,6,9,18
GCF is 18
Question 3.
45 and 60
Answer: 15
Explanation:
Factors of 45: 1,3,5,9,15,45
Factors of 60: 1,2,3,4,5,6,10,12,15,20,30,60
Common Factors are 1,3,5,15
GCF is 15
Find the GCF.
Question 4.
14, 18
Answer: 2
Explanation:
Factors of 14: 1,2,7,14
Factors of 18: 1,2,3,6,9,18
Common Factors are 1,2
GCF is 2
Question 5.
6, 48
Answer: 6
Explanation:
Factors of 6: 1,2,3,6
Factors of 48: 1,2,3,4,6,8,12,24,48
Common Factors are 1,2,3,6
GCF is 6
Question 6.
16, 100
Answer: 4
Explanation:
Factors of 16: 1,2,4,8,16
Factors of 100: 1,2,4,5,10,20,25,50,100
Common Factors are 1,2,4
GCF is 4
Use the GCF and the Distributive Property to express the sum as a product.
Question 7.
20 + 35
Answer: 5×(4+7)
Explanation:
20+35= (5×4)+(5×7)
=5×(4+7)
Question 8.
18 + 27
Answer: 9×(2+3)
Explanation:
18+27= (9×2)+(9×3)
=9×(2+3)
Question 9.
64 + 40
Answer: 8×(8+5)
Explanation:
64+40= (8×8)+(8×5)
= 8×(8+5)
Problem Solving
Question 10.
Jerome is making prizes for a game at the school fair. He has two bags of different pins, one with 15 square pins and one with 20 round pins. Every prize will have one kind of pin. Each prize will have the same number of pins. What is the greatest number of pins Jerome can put in each prize?
Answer: 5
Explanation:
Factors of 15: 1,3,5,15
Factors of 20: 1,2,4,5,10,20
Common factors are 1,5
So the greatest number of pins Jerome can put in each prize is 5
Question 11.
There are 24 sixth graders and 40 seventh graders. Mr. Chan wants to divide both grades into groups of equal size, with the greatest possible number of students in each group. How many students should be in each group?
Answer: 8.
Explanation:
Factors of 24: 1,2,3,4,6,8,12,24
Factors of 40: 1,2,4,5,8,10,20,40
Common Factors are 1,2,4,8
So the greatest possible number of students are 8
Question 12.
Write a short paragraph to explain how to use prime factorization and the Distributive Property to express the sum of two whole numbers as a product.
Answer:
Prime Factorization is the product of prime numbers
Lesson Check – Page No. 28
Question 1.
There are 15 boys and 10 girls in Miss Li’s class. She wants to group all the students so that each group has the same number of boys and the same number of girls. What is the greatest number of groups she can have?
Answer: 5
Explanation:
Factors of 15: 1,3,5,15
Factors of 10: 1,2,5,10
Common Factors are 1,5
The greatest number of groups she can have is 5.
Question 2.
A pet shop manager wants the same number of birds in each cage. He wants to use as few cages as possible, but can only have one type of bird in each cage. If he has 42 parakeets and 18 canaries, how many birds will he put in each cage?
Answer: 6
Explanation:
Factors of 42: 1,2,3,6,7,14,21,42
Factors of 18: 1,2,3,6,9,18
Common Factors are 1,2,3,6
GCF is 6
So he will put 6 birds in each cage.
Spiral Review
Question 3.
There are 147 people attending a dinner party. If each table can seat 7 people, how many tables are needed for the dinner party?
Answer: 21 tables.
Explanation: Total no.of people attending a dinner party are 147 and 7 people can seat in each table, so 147÷7= 21 tables are needed for a dinner party.
Question 4.
Sammy has 3 pancakes. He cuts each one in half. How many pancake halves are there?
Answer: 6
Explanation: Sammy has 3 pancakes, as he cut each one into half so there are 3×2= 6 pancake halves.
Question 5.
The Cramer Company had a profit of $8,046,890 and the Coyle Company had a profit of $8,700,340 last year. Which company had the greater profit?
Answer: Coyle company
Explanation: Coyle company had a profit of $8,700,340 and Cramer Company had $8,046,890, So $8,700,340-$8,046,890= $653,450 Coyle company have greater profits.
Question 6.
There are 111 guests attending a party. There are 15 servers. Each server has the same number of guests to serve. Jess will serve any extra guests. How many guests will Jess be serving?
Answer: 6.
Explanation:
Total guests attending a party are 111 and no.of servers are 15, as each server has the same number of guests to serve so we will divide total guests by the number of servers 111÷15= 7.4 round off to 6. Therefore, no.of guests, will Jess be serving is 6.
Share and Show – Page No. 31
Question 1.
Toby is packaging 21 baseball cards and 12 football cards to sell at a swap meet. Each packet will have the same number of cards. Each packet will have cards for only one sport. What is the greatest number of cards he can place in each packet? How many packets will there be for each sport?
Answer: 7 packets of baseball cards and 4 packets of football cards and each packet contains 3 cards.
Explanation: The GCF of 21 and 12 are
Factors of 21: 1,3,7,21
Factors of 12: 1,2,3,4,6,12
GCF is 3
By Distributive property 21+12
= (3×7)+(3×4)
= 3×(7+4)
So there will be 7 packets of baseball cards and 4 packets of football cards and each packet contains 3 cards.
Question 2.
What if Toby had decided to keep one baseball card for himself and sell the rest? How would your answers to the previous problem have changed?
Answer: 5 packets of baseball cards and 3 football and each packet contains 4 cards.
Explanation: If Toby had decided to keep one baseball card for himself, so he will have 20 baseball cards and 12 football cards
Factors of 20: 1,2,4,5,10,20
Factors of 12: 1,2,3,4,6,12
GCF is 4
By Distributive property 20+12
= (4×5)+(4×3)
=4×(5+3)
So there will be 5 packets of baseball cards and 3 football and each packet contains 4 cards.
Question 3.
Melissa bought 42 pine seedlings and 30 juniper seedlings to plant in rows on her tree farm. She wants each row to have the same number of seedlings. She wants only one type of seedling in each row. What is the greatest number of seedlings she can plant in each row? How many rows of each type of tree will there be?
Answer: 7 rows of pine seedlings and 5 rows of juniper seedling with 6 seedlings in each row.
Explanation:
Factors of 42: 1,2,3,6,7,14,21,42
Factors of 30: 1,2,3,6,10,15,30
GCF is 6
By Distributive 42+30
=(6×7)+(6×5)
=6×(7+5)
So there will be 7 rows of pine seedlings and 5 rows of juniper seedling with 6 seedlings in each row.
On Your Own – Page No. 32
Question 4.
Make Sense of Problems A drum and bugle marching band has 45 members who play bugles and 27 members who play drums. When they march, each row has the same number of players. Each row has only bugle players or only drummers. What is the greatest number of players there can be in each row? How many rows of each type of player can there be?
Answer: 9 people in each row, And there will be 5 rows of bugle players and 3 rows of drummers.
Explanation:
Factors of 45: 1,3,5,9,15,45
Factors of 27: 1,3,9,27
GCF is 9
So there will be 9 people in each row and by the distributive law 45+27
= (9×5)+(9×3)
= 9×(5+3)
And there will be 5 rows of bugle players and 3 rows of drummers.
Question 5.
The “color guard” of a drum and bugle band consists of members who march with flags, hoops, and other props. How would your answers to Exercise 4 change if there were 21 color guard members marching along with the bugle players and drummers?
Answer: 15 rows of bugle players, 9 rows of drummers, and 7 rows color guard members with 3 marchers in each row.
Explanation:
Factors of 21: 1,3,7,21
Factors of 45: 1,3,5,9,15,45
Factors of 27: 1,3,9,27
GCF is 3
So there would be 15 rows of bugle players, 9 rows of drummers, and 7 rows color guard members with 3 marchers in each row.
Question 6.
If you continue the pattern below so that you write all of the numbers in the pattern less than 500, how many even numbers will you write?
4, 9, 14, 19, 24, 29…
Answer: 50
Explanation: You can write 50 numbers.
Question 7.
Mr. Yaw’s bookcase holds 20 nonfiction books and 15 fiction books. Each shelf holds the same number of books and contains only one type of book. How many books will be on each shelf if each shelf has the greatest possible number of books? Show your work.
Answer: 5
Explanation:
Factors of 15: 1,3,5,15
Factors of 20: 1,2,4,5,10,20.
GCF is 5
5 books will be on each self.
Problem Solving Apply the Greatest Common Factor – Page No. 33
Read the problem and solve.
Question 1.
Ashley is bagging 32 pumpkin muffins and 28 banana muffins for some friends. Each bag will hold only one type of muffin. Each bag will hold the same number of muffins. What is the greatest number of muffins she can put in each bag? How many bags of each type of muffin will there be?
Answer: 8 pumpkin muffins and 7 banana muffins with 4 greatest number of muffins in each bag.
Explanation:
Factors of 32: 1,2,4,8,16,32
Factors of 28: 1,2,4,7,14,28
GCF is 4
By distributive property 32+28
= (4×8)+(4×7)
=4×(8+7)
So there will be 8 pumpkin muffins and 7 banana muffins with 4 greatest number of muffins in each bag.
Question 2.
Patricia is separating 16 soccer cards and 22 baseball cards into groups. Each group will have the same number of cards, and each group will have only one kind of sports card. What is the greatest number of cards she can put in each group? How many groups of each type will there be?
Answer: Patricia has 8 soccer cards and 11 baseball cards and 2 groups each.
Explanation:
Factors of 16: 1,2,4,8,16
Factors of 22: 1,2,11,22
GCF is 2
By distributive property 16+22
= (2×8)+(2×11)
=2×(8+11)
Patricia has 8 soccer cards and 11 baseball cards and 2 groups each.
Question 3.
Bryan is setting chairs in rows for a graduation ceremony. He has 50 black chairs and 60 white chairs. Each row will have the same number of chairs, and each row will have the same color chair. What is the greatest number of chairs that he can fit in each row? How many rows of each color chair will there be?
Answer: 10 chairs per row and 5 black chairs and 6 white chairs.
Explanation:
By distributive law 50+60
= (10×5)+(10×60)
= 10×(5+6)
So there will 10 chairs per row and 5 black chairs and 6 white chairs.
Question 4.
A store clerk is bagging spices. He has 18 teaspoons of cinnamon and 30 teaspoons of nutmeg. Each bag needs to contain the same number of teaspoons, and each bag can contain only one spice. What is the maximum number of teaspoons of spice the clerk can put in each bag? How many bags of each spice will there be?
Answer: 6 no. of teaspoons of spices and 3 teaspoons of cinnamon 5 teaspoons of nutmeg.
Explanation:
By distributive property (18+30)
= (6×3)+(6×5)
= 6×(3+5)
So there will be 6 no. of teaspoons of spices and 3 teaspoons of cinnamon 5 teaspoons of nutmeg.
Question 5.
Write a problem in which you need to put as many of two different types of objects as possible into equal groups. Then use the GCF, Distributive Property, and a diagram to solve your problem
Answer: Jack has a bag full of 20 red apples and 32 green apples. Each bag needs to contain same number of apples and each bag can contain only one type of apple. What is the maximum number of apples can Jack put in each bag? How many bags of each apple will be there?
Explanation: By distributive property (20+32)
= (4×5)+(4×8)
= 4×(5+8)
So there will be 4 bags and in that 5 red apples and 8 green apples.
Lesson Check – Page No. 34
Question 1.
Fred has 36 strawberries and 42 blueberries. He wants to use them to garnish desserts so that each dessert has the same number of berries, but only one type of berry. He wants as much fruit as possible on each dessert. How many berries will he put on each dessert? How many desserts with each type of fruit will he have?
Answer: 6 berries on each dessert and 6 strawberries and 7 blueberries in each type of fruit.
Explanation:
By distributive property 36+42
= (6×6)+(6×7)
= 6×(6+7)
So he put 6 berries on each dessert and 6 strawberries and 7 blueberries in each type of fruit.
Question 2.
Dolores is arranging coffee mugs on shelves in her shop. She wants each shelf to have the same number of mugs. She only wants one color of mug on each shelf. If she has 49 blue mugs and 56 red mugs, what is the greatest number she can put on each shelf? How many shelves does she need for each color?
__________ shelves for blue mugs
__________ shelves for red mugs
Answer: 7 blue mugs and 8 red mugs.
Explanation:
By distributive property 49+56
= (7×7)+(7×8)
= 7×(7+8)
So the greatest number she can put on each shelf is 7, 7 blue mugs and 8 red mugs.
Spiral Review
Question 3.
A rectangle is 3 \(\frac{1}{3}\) feet long and 2 \(\frac{1}{3}\) feet wide. What is the distance around the rectangle?
_____ \(\frac{□}{□}\)
Answer: 11 1/3 feet
Explanation: Distance of a rectangle= 2(L+W)
= 2(3 1/3+ 2 1/3)
= 2(10/3+7/3)
= 2(17/3)
= 34/3
= 11 1/3 feet.
Question 4.
Lowell bought 4 \(\frac{1}{4}\) pounds of apples and 3 \(\frac{3}{5}\) pounds of oranges. How many pounds of fruit did Lowell buy?
_____ \(\frac{□}{□}\)
Answer: 7 17/20 pounds
Explanation: Lowell bought 4 1/4 pounds of apples and 3 3/5 pounds of oranges, so total pounds of fruits Lowell bought is 4 1/4+ 3 3/5=
= 17/4+ 18/5
= 157/20
= 7 17/20 pounds
Question 5.
How much heavier is a 9 \(\frac{1}{8}\) pound box than a 2 \(\frac{5}{6}\) pound box?
_____ \(\frac{□}{□}\)
Answer: 6 7/4 much heavier.
Explanation: 9 1/8 – 2 5/6
= 73/8 – 17/6
= 151/24
= 6 7/4
Question 6.
The combination of Clay’s locker is the prime factors of 102 in order from least to greatest. What is the combination of Clay’s locker?
Answer: 2317.
Explanation:
Prime Factors of 102 are 2,3,17, so the combination of Clay’s locker is 2317
Vocabulary – Page No. 35
Choose the best term from the box to complete the sentence.

Question 1.
The _____ of two numbers is greater than or equal to the numbers.
Answer: LCM
Question 2.
The _____ of two numbers is less than or equal to the numbers.
Answer: Greatest Common
Concepts and Skills
Estimate. Then find the quotient. Write the remainder, if any, with an r.
Question 3.
2,800 ÷ 25
Answer: Quotient is 112 and remainder is 0
Explanation:
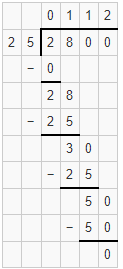
Question 4.
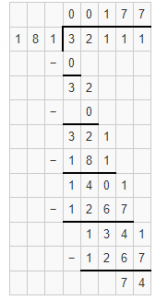
19,129 ÷ 37
Answer: Quotient is 517 and remainder is 0
Explanation:
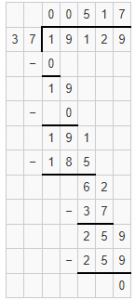
Question 5.
32,111 ÷ 181
Answer: Quotient is 177 and the remainder is 74
Explanation:
Find the prime factorization.
Question 6.
44
Answer: 2×2×11
Explanation:
44= 4×11
2×2×11
Question 7.
36
Answer: 2×2×3×3
Explanation:
36= 2×18
=2×2×9
=2×2×3×3
Question 8.
90
Answer: 3×3×5×2
Explanation:
90= 9×10
=3×3×10
=3×3×5×2
Find the LCM.
Question 9.
8, 10
Answer: 40
Explanation:
Multiples of 8: 8,16,24,32,40
Multiples of 10: 10,20,30,40
LCM is 40
Question 10.
4, 14
Answer: 28
Explanation:
Multiples of 4: 4,8,12,16,20,24,28
Multiples of 14: 14,28
LCM is 28
Question 11.
6, 9
Answer: 18
Explanation:
Multiples of 6: 6,12,18
Multiples of 9: 9,18
LCM is 18
Find the GCF.
Question 12.
16, 20
Answer: 4
Explanation:
Factors of 16: 1,2,4,8,16
Factors of 20: 1,2,4,5,10,20
Common Factors are 1,2,4
GCF is 4
Question 13.
8, 52
Answer: 4
Explanation:
Factors of 8: 1,2,4,8
Factors of 52: 1,2,4,13,26,52
Common Factors are 1,2,4
GCF is 4
Question 14.
36, 54
Answer: 18
Explanation:
Factors of 36: 1,2,3,4,6,9,12,18,36
Factors of 54: 1,2,3,6,9,18,27,54
Common Factors are 1,2,3,6,9,18
GCF is 18
Page No. 36
Question 15.
A zookeeper divided 2,440 pounds of food equally among 8 elephants. How many pounds of food did each elephant receive?
Answer: 305 Pounds.
Explanation: Zookeeper divides 2,440 pounds of food equally among 8 elephants, so no. of pounds is
2,440÷8= 305 pounds.
Question 16.
DVD cases are sold in packages of 20. Padded mailing envelopes are sold in packets of 12. What is the least number of cases and envelopes you could buy so that there is one case for each envelope with none left over?
Answer: 60
Explanation:
Multiples of 20: 20,40,60
Multiples of 12: 12,24,36,48,60
LCM is 60
So the Least number of cases and envelopes without any leftover is 60.
Question 17.
Max bought two deli sandwich rolls measuring 18 inches and 30 inches. He wants them to be cut into equal sections that are as long as possible. Into what lengths should the rolls be cut? How many sections will there be in all?
Answer: 6 inches and 8 sections.
Explanation:
By distributive property 18+30
= (6×3)+(6×5)
= 6(3+5)
So Length of the rolls should cut at 6 inches and sections are (3+5)= 8 sections.
Question 18.
Susan is buying supplies for a party. If spoons only come in bags of 8 and forks only come in bags of 6, what is the least number of spoons and the least number of forks she can buy so that she has the same number of each?
Answer: So least no. of forks and spoons are 24.
Explanation:
Multiples of 8: 8,16,24
Multiples of 6: 6,2,18,24
LCM is 24
So least no. of forks and spoons are 24.
Question 19.
Tina is placing 30 roses and 42 tulips in vases for table decorations in her restaurant. Each vase will hold the same number of flowers. Each vase will have only one type of flower. What is the greatest number of flowers she can place in each vase? If Tina has 24 tables in her restaurant, how many flowers can she place in each vase?
Answer: Maximum flowers in a vase is 3.
Explanation: Tina is placing 30 roses and 42 tulips, so total flowers are 30+42= 72 flowers. The total number of tables are 24, as each vase hold same no. of flowers, Let the no. of flowers in each vase be X, so total no.of flowers to be decorate 24X,
24X = 72
X= 3.
So maximum flowers in a vase is 3.
Share and Show – Page No. 39
Question 1.
Find 3.42 − 1.9.
Answer: 1.52
Explanation: 3.42 − 1.9= 1.52.
Estimate. Then find the sum or difference.
Question 2.
2.3 + 5.68 + 21.047
Answer: 29.027
Explanation: 2.3 + 5.68 + 21.047= 29.027
Question 3.
33.25 − 21.463
Answer: 11.787
Explanation: 33.25 − 21.463= 11.787
Question 4.
Evaluate (8.54 + 3.46) − 6.749.
Answer: 5.251
Explanation:
(8.54 + 3.46) − 6.749= (12)-6.749
= 5.251
On Your Own
Estimate. Then find the sum or difference.
Question 5.
57.08 + 34.71
Answer: 91.79
Explanation:
57.08 + 34.71= 91.79
Question 6.
20.11 − 13.27
Answer: 33.38
Explanation:
20.11−13.27= 33.38
Question 7.
62 − 9.817
Answer: 52.183
Explanation:
62 − 9.817= 52.183
Question 8.
35.1 + 4.89
Answer: 39.99
Explanation:
35.1 + 4.89= 39.99
Practice: Copy and Solve Evaluate using the order of operations.
Question 9.
8.01 − (2.2 + 4.67)
Answer: 1.14
Explanation:
8.01 − (2.2 + 4.67)
= 8.01-(6.87)
= 1.14
Question 10.
54 + (9.2 − 1.413)
Answer: 61.787
Explanation: 54 + (9.2 − 1.413)
= 54+(7.787)
=61.787
Question 11.
21.3 − (19.1 − 3.22)
Answer: 5.42
Explanation: 21.3 − (19.1 − 3.22)
= 21.3-(15.88)
=5.42
Question 12.
Make Arguments A student evaluated 19.1 + (4.32 + 6.9) and got 69.2. How can you use estimation to convince the student that this answer is not reasonable?
Answer: The answer is not reasonable, because 19.1+4.32+6.9= 30.32
Explanation: 19.1 + (4.32 + 6.9)
= 19.1+(11.22)
= 30.32
Question 13.
Lynn paid $4.75 for cereal, $8.96 for chicken, and $3.25 for soup. Show how she can use properties and compatible numbers to evaluate (4.75 + 8.96) + 3.25 to find the total cost.
Answer: 16.96
Explanation: Total cost is (4.75 + 8.96) + 3.25
= (13.71)+3.25
= 16.96
Page No. 40
Question 14.
For numbers 14a–14d, select True or False for each equation.
14a. 3.76 + 2.7 = 6.46 True False
14b. 4.14 + 1.8 = 4.32 True False
14c. 2.01 – 1.33 = 0.68 True False
14d. 51 – 49.2 = 1.8 True False
14a. 3.76 + 2.7 = 6.46
Answer: True
Explanation: 3.76 + 2.7 = 6.46
14b. 4.14 + 1.8 = 4.32
Answer: False
Explanation: 4.14 + 1.8 = 5.94
14c. 2.01 – 1.33 = 0.68
Answer: True
Explanation: 2.01 – 1.33 = 0.68
14d. 51 – 49.2 = 1.8
Answer: True
Explanation: 51 – 49.2 = 1.8
Comparing Eggs
Different types of birds lay eggs of different sizes. Small birds lay eggs that are smaller than those that are laid by larger birds. The table shows the average lengths and widths of five different birds’ eggs.
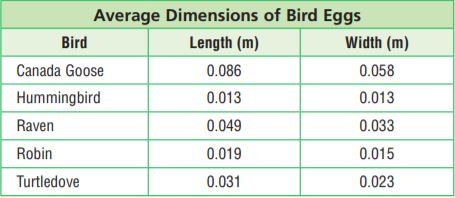
Use the table for 15–17.
Question 15.
What is the difference in average length between the longest egg and the shortest egg?
Answer: 0.073
Explanation: The length of the longest egg is 0.086 and the shortest egg is 0.013, so the difference is
0.086-0.013= 0.073
Question 16.
Which egg has a width that is eight thousandths of a meter shorter than its length?
Answer: Turtledove
Explanation: The length of the turtledove egg is 0.031 and the width is 0.023, so 0.031-0.023= 0.08m shorter than length.
Question 17.
How many robin eggs, laid end to end, would be about equal in length to two raven eggs? Justify your answer
Answer: 5 robin eggs should be laid.
Explanation: The length of Two raven eggs is 0.049+0.049=0.098, so 5 robin eggs should be laid.
Add and Subtract Decimals – Page No. 41
Estimate. Then find the sum or difference.
Question 1.
43.53 + 27.67
Answer: 71.2
Explanation: 43.53 + 27.67=71.2
Question 2.
17 + 3.6 + 4.049
Answer: 24.649
Explanation: 17 + 3.6 + 4.049
=17+7.649
=24.649
Question 3.
3.49 − 2.75
Answer: 0.74
Explanation:
3.49-2.75= 0.74
Question 4.
5.07 − 2.148
Answer: 2.922
Explanation:
5.07-2.148= 2.922
Question 5.
3.92 + 16 + 0.085
Answer: 20.005
Explanation: 3.92 + 16 + 0.085
= 3.92+16.085
= 20.005
Question 6.
41.98 + 13.5 + 27.338
Answer: 82.818
Explanation: 41.98 + 13.5 + 27.338
= 41.98+ 40.838
Evaluate using the order of operations.
Question 7.
8.4 + (13.1 − 0.6)
Answer: 20.9
Explanation: 8.4 + (13.1 − 0.6)
= 8.4+(12.5)
= 20.9
Question 8.
34.7 − (12.07 + 4.9)
Answer: 17.73
Explanation: 34.7 − (12.07 + 4.9)
= 34.7-(16.97)
= 17.73
Question 9.
(32.45 − 4.8) − 2.06
Answer: 25.59
Explanation: (32.45 − 4.8) − 2.06
= 27.65- 2.06
= 25.59
Problem Solving
Question 10.
The average annual rainfall in Clearview is 38 inches. This year, 29.777 inches fell. How much less rain fell this year than falls in an average year?
Answer: 8.23
Explanation: Average annual rainfall in last year is 38 inches and this year is 29.777 inches, so 38-29.77= 8.23 inches less rainfall
Question 11.
At the theater, the Worth family spent $18.00 on adult tickets, $16.50 on children’s tickets, and $11.75 on refreshments. How much did they spend in all?
Answer: $46.25
Explanation: As the family spent $18.00 on adult tickets, $16.50 on children’s tickets, and $11.75 on refreshments,
So the total spent by the family is $18.00+$16.50+$11.75= $46.25
Question 12.
Write a word problem that involves adding or subtracting decimals. Include the solution.
Answer: Mark and Jack went to the park and cost of ticket is $6.50. Mark has $20. How much remaining did mark has left?
Explanation: As MArk and jack went to the park where ticket price is $6.50, so for both it will be
$6.50+$6.50= $13.00. As Mark has $20, remaining amount left with Mark is $20-$13= $7
Lesson Check – Page No. 42
Question 1.
Alden fills his backpack with 0.45 kg of apples, 0.18 kg of cheese, and a water bottle that weighs 1.4 kg. How heavy are the contents of his backpack?
Answer: 2.03kg
Explanation: The total weight of a backpack is 0.45+0.18+1.4= 2.03kg
Question 2.
Gabby plans to hike 6.3 kilometers to see a waterfall. She stops to rest after hiking 4.75 kilometers. How far does she have left to hike?
Answer: 1.55kms
Explanation: Gobby hikes 6.3kms and stops at 4.75kms, so she left at 6.3-4.75= 1.55kms
Spiral Review
Question 3.
A 6-car monorail train can carry 78 people. If one train makes 99 trips during the day, what is the greatest number of people the train can carry in one day?
Answer: 7,722.
Explanation: The greatest number of people the train can carry in one day is 78×99= 7,722.
Question 4.
An airport parking lot has 2,800 spaces. If each row has 25 spaces, how many rows are there?
Answer: 112 rows
Explanation: As parking lot has 2,800 spaces and each row has 25 spaces, no. of rows is 2800÷25= 112 rows
Question 5.
Evan brought 6 batteries that cost $10 each and 6 batteries that cost $4 each. The total cost was the same as he would have spent buying 6 batteries that cost $14 each. So, 6 × $14 = (6 × 10) + (6 × 4). What property does the equation illustrate?
Answer: Distributive property
Explanation: By distributive property (a×b)+(a×c)= a×(b+c), here a= 6, b=10, c=4.
Question 6.
Cups come in packages of 12 and lids come in packages of 15. What is the least number of cups and lids that Corrine can buy if she wants to have the same number of cups and lids?
Answer: 60 cups and 60 lids.
Explanation:
Multiples of 12: 12,24,36,48,60
Multiples of 15: 15,30,45,60
LCM is 60
So the least number of cups and lids she can buy is 60 cups and 60 lids.
Share and Show – Page No. 45
Estimate. Then find the product.
Question 1.
12.42 × 28.6
Answer: 355.212
Explanation: 12.42 × 28.6
= 355.212
Question 2.
32.5 × 7.4
Answer: 240.5
Explanation: 32.5 × 7.4
=240.5
Attend to Precision Algebra Evaluate using the order of operations.
Question 3.
0.24 × (7.3 + 2.1)
Answer: 2.256
Explanation: 0.24 × (7.3 + 2.1)
= 0.24×9.4
= 2.256
Question 4.
0.075 × (9.2 − 0.8)
Answer: 0.63
Explanation: 0.075 × (9.2 − 0.8)
= 0.075×(8.4)
= 0.63
Question 5.
2.83 + (0.3 × 2.16)
Answer: 3.478
Explanation: 2.83 + (0.3 × 2.16)
= 2.83+0.648
= 3.478
On Your Own
Estimate. Then find the product.
Question 6.
29.14 × 5.2
Answer: 151.528
Explanation: 29.14 × 5.2
= 151.528
Question 7.
6.95 × 12
Answer: 83.4
Explanation: 6.95 × 12
= 83.4
Question 8.
0.055 × 1.82
Answer: 0.1001
Explanation: 0.055 × 1.82
= 0.1001
Attend to Precision Algebra Evaluate using the order of operations.
Question 9.
(3.62 × 2.1) − 0.749
Answer: 6.853
Explanation: (3.62 × 2.1) − 0.749
= 7.602- 0.749
= 6.853
Question 10.
5.8 − (0.25 × 1.5)
Answer: 5.425
Explanation: 5.8 − (0.25 × 1.5)
= 5.8- (0.375)
= 5.425
Question 11.
(0.83 + 1.27) × 6.4
Answer: 13.44
Explanation: (0.83 + 1.27) × 6.4
= (2.1)×6.4
= 13.44
Question 12.
Jamal is buying ingredients to make a large batch of granola to sell at a school fair. He buys 3.2 pounds of walnuts for $4.40 per pound and 2.4 pounds of cashews for $6.25 per pound. How much change will he receive if he pays with two $20 bills?
Answer: $40-$29.08= $10.92.
Explanation: Jamal bought 3.2 pounds of walnuts for $4.40 per pound, so for 3.2 pounds it will be 3.2×4.40= 14.08,
and 2.4 pounds of cashew for $6.25 per pound, so for 2.4 pounds it will be 2.4×6.25= 15. Total Jamal spend is 14.08+15= 29.08. As he have two $20 so he will receive $40-$29.08= $10.92.
Unlock the Problem – Page No. 46
The table shows some currency exchange rates for 2009.
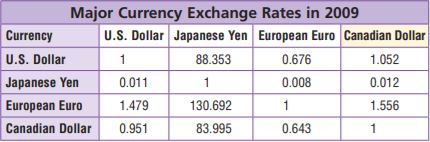
Question 13.
When Cameron went to Canada in 2007, he exchanged 40 U.S. dollars for 46.52 Canadian dollars. If Cameron exchanged 40 U.S. dollars in 2009, did he receive more or less than he received in 2007? How much more or less?
a. What do you need to find?
Answer: We need how much or less 40 US dollars are worth in Canadian dollars in 2009 compared to 2007.
Question 13.
b. How will you use the table to solve the problem?
Answer: The table provides exchange rates for 2009, will multiply to find the value of 40 US dollars in Canadian dollars in 2009.
Question 13.
c. Complete the sentences.
40 U.S. dollars were worth _____ Canadian dollars in 2009.
So, Cameron would receive _____ Canadian dollars in 2009.
Answer: 42.08 Canadian dollars in 2009
4.44 Canadian dollars in 2009
Explanation: In 2009 1 US dollar is 1.052, so 40 US dollars is 40×1.052= 42.08 and in 2007 Cameron received 46.52, so in 2009 Cameron would receive 46.52-42.08= 4.44 Canadian dollars in 2009.
Question 14.
At a convenience store, the Jensen family puts 12.4 gallons of gasoline in their van at a cost of $3.80 per gallon. They also buy 4 water bottles for $1.99 each, and 2 snacks for $1.55 each. Complete the table to find the cost for each item.
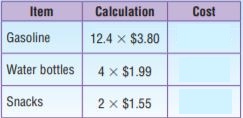
Mrs. Jensen says the total cost for everything before tax is $56.66. Do you agree with her? Explain why or why not.
Answer: No, the answer is not reasonable.
Explanation: As the total cost is 58.18
12.4×3.80= 47.12
4×1.99= 7.96
2×1.55= 3.1
So 47.12+7.96+3.1= $58.18
Multiply Decimals – Page No. 47
Estimate. Then find the product.
Question 1.
5.69 × 7.8
Answer: 44.382
Explanation: 5.69 × 7.8
= 44.382
Question 2.
3.92 × 0.051
Answer: 0.19992
Explanation: 3.92 × 0.051
= 0.19992
Question 3.
2.365 × 12.4
Answer: 29.326
Explanation: 2.365 × 12.4
= 29.326
Question 4.
305.08 × 1.5
Answer: 457.62
Explanation: 305.08 × 1.5
= 457.62
Evaluate the expression using the order of operations.
Question 5.
(61.8 × 1.7) + 9.5
Answer: 114.56
Explanation: (61.8 × 1.7) + 9.5
= 105.06+ 9.5
= 114.56
Question 6.
205 − (35.80 × 5.6)
Answer: 4.52
Explanation: 205 − (35.80 × 5.6)
= 205- 200.48
= 4.52
Question 7.
1.9 × (10.6 − 2.17)
Answer: 16.017
Explanation: 1.9 × (10.6 − 2.17)
= 1.9×( 8.43)
= 16.017
Problem Solving
Question 8.
Blaine exchanges $100 for yen before going to Japan. If each U.S. dollar is worth 88.353 yen, how many yen should Blaine receive?
Answer: 8835.3 yen
Explanation: As 1 US dollar is 88.353 yen, so when Blaine exchanges $100 to yen it will be $100×88.353=8835.3 yen
Question 9.
A camera costs 115 Canadian dollars. If each Canadian dollar is worth 0.952 U.S. dollars, how much will the camera cost in U.S. dollars?
Answer: 109.48.
Explanation: As 1 Canadian dollar is 0.952 US dollars, so camers cost is 115×0.952= 109.48.
Question 10.
Explain how to mentally multiply a decimal number by 100.
Answer: Move the decimal point two places right.
Lesson Check – Page No. 48
Question 1.
A gallon of water at room temperature weighs about 8.35 pounds. Lena puts 4.5 gallons in a bucket. How much does the water weigh?
Answer: 37.575
Explanation: As 1 gallon= 8.35 pounds, Lena put 4.5 gallons in a bucket. So water weight is 4.5×8.35= 37.575
Question 2.
Shawn’s rectangular mobile home is 7.2 meters wide and 19.5 meters long. What is its area?
Answer: 140.4
Explanation: Area= Length×wide, so 7.2×19.5= 140.4
Spiral Review
Question 3.
Last week, a store sold laptops worth a total of $3,885. Each laptop cost $555. How many laptops did the store sell last week?
Answer: 7 Laptops.
Explanation: Total Laptops sold is $3885 and each laptop cost is $555, so 3885÷555= 7 laptops were sold by the store.
Question 4.
Kyle drives his truck 429 miles on 33 gallons of gas. How many miles can Kyle drive on 1 gallon of gas?
Answer: 13 miles.
Explanation: As Kyle drives 429 miles on 33 gallons gas, so 429÷33= 13 miles he can drive on 1 gallon of gas.
Question 5.
Seven busloads each carrying 35 students arrived at the game, joining 23 students who were already there. Evaluate the expression 23 + (7 × 35) to find the total number of students at the game.
Answer: 268 students.
Explanation: 23+(7×35)
=23+(245)
=268.
Total students are 268.
Question 6.
A store is giving away a $10 coupon to every 7th person to enter the store and a $25 coupon to every 18th person to enter the store. Which person will be the first to get both coupons?
Answer: 126th person will get both coupons.
Explanation: LCM of 7 and 18 is 18×7= 126. So 126th person will get both coupons.
Estimate. Then find the quotient – Page No. 51
Question 2.
7)\(\overline { $17.15 } \)
Answer: 2.45
Explanation: $17.15÷7= 2.45
Question 3.
4)\(\overline { 1.068 } \)
Answer: 0.267
Explanation: 1.068÷4= 0.267
Question 4.
12)\(\overline { 60.84 } \)
Answer: 5.07
Explanation: 60.84÷12= 5.07
Question 5.
18.042 ÷ 6
Answer: 3.007
Explanation: 18.042÷6= 3.007
On Your Own
Estimate. Then find the quotient.
Question 6.
$21.24 ÷ 6
Answer: 3.54
Explanation: $21.24 ÷ 6= 3.54
Question 7.
28.63 ÷ 7
Answer: 4.09
Explanation: 28.63 ÷ 7= 4.09
Question 8.
1.505 ÷ 35
Answer: 0.043
Explanation: 1.505 ÷ 35= 0.043
Question 9.
0.108 ÷ 18
Answer: 0.006
Explanation: 0.108 ÷ 18= 0.006
Attend to Precision Algebra Evaluate using the order of operations.
Question 10.
(3.11 + 4.0) ÷ 9
Answer: 0.79
Explanation: (3.11 + 4.0) ÷ 9
= (7.11)+9
= 0.79
Question 11.
(6.18 − 1.32) ÷ 3
Answer: 1.62
Explanation: (6.18 − 1.32) ÷ 3
= (4.86)÷3
= 1.62
Question 12.
(18 − 5.76) ÷ 6
Answer: 2.04
Explanation: (18 − 5.76) ÷ 6
= (12.24)÷6
= 2.04
Question 13.
Use Appropriate Tools Find the length of a dollar bill to the nearest tenth of a centimeter. Then show how to use division to find the length of the bill when it is folded in half along the portrait of George Washington
Answer: 3.07 inches or 7.8 centimeter.
Explanation: As the length of a dollar bill to the nearest tenth of a centimeter is 15.6 cm, and length of the bill when it is folded in half along the portrait of George Washington is 3.07 inches or 7.8 centimeter.
Question 14.
Emilio bought 5.65 pounds of green grapes and 3.07 pounds of red grapes. He divided the grapes equally into 16 bags. If each bag of grapes has the same weight, how much does each bag weigh?
Answer: 0.545 pounds.
Explanation: Total weight of grapes is 5.65+3.07= 8.72 pounds, so each bag weight is 8.72÷16= 0.545 pounds.
Problem Solving + Applications – Page No. 52
Pose a Problem
Question 15.
This table shows the average height in inches for girls and boys at ages 8, 10, 12, and 14 years. To find the average growth per year for girls from age 8 to age 12, Emma knew she had to find the amount of growth between age 8 and age 12, then divide that number by the number of years between age 8 and age 12.
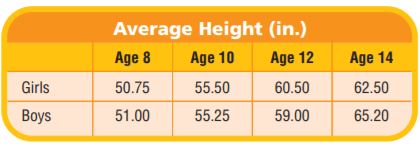
Emma used this expression: (60.50−50.75)÷4
She evaluated the expression using the order of operations.
Write the expression. (60.50−50.75)÷4
Perform operations in parentheses. 9.75÷4
Divide. 2.4375
So, the average annual growth for girls ages 8 to 12 is 2.4375 inches. Write a new problem using the information in the table for the average height for boys. Use division in your problem.
Answer: Find the average growth per year for girls 8 to 14.
Explanation: As (62.50-50.75)÷6
= (11.75)÷6
= 1.96
So the average annual growth for girls age 8 to age 14 is 1.96 inches.
Question 16.
The table shows the number of books each of three friends bought and the cost. On average, which friend spent the most per book? Use numbers and words to explain your answer
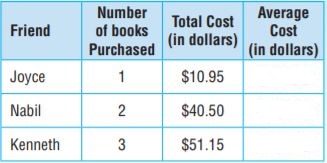
Answer: Nabil spent the most per book.
Explanation:
Joyce purchased 1 book which costs $10.95
Nabil purchased 2 books which costs $40.50, so 1 book cost is 40.50÷2= $20.26
Kenneth purchased 3 books for $51.15 , so 1 book cost is 51.15÷3= $17.05
So, Nabil spent the most per book.
Divide Decimals by Whole Numbers – Page No. 53
Estimate. Then find the quotient.
Question 1.
1.284 ÷ 12
Answer: 0.107
Explanation: 1.284÷12= 0.107
Question 2.
9)\(\overline { 2.43 } \)
Answer: 0.27
Explanation: 2.43÷9 = 0.27
Question 3.
25.65 ÷ 15
Answer: 1.71
Explanation: 25.65÷15= 1.71
Question 4.
12)\(\overline { 2.436 } \)
Answer: 0.203
Explanation: 2.436÷12 = 0.203
Evaluate using the order of operations.
Question 5.
(8 − 2.96) ÷ 3
Answer: 1.68
Explanation: (8 − 2.96) ÷ 3
= (5.04)÷3
= 1.68
Question 6.
(7.772 − 2.38) ÷ 8
Answer: 0.674
Explanation: (7.772 − 2.38) ÷ 8
= (5.392)÷8
= 0.674
Question 7.
(53.2 + 35.7) ÷ 7
Answer: 12.7
Explanation: (53.2 + 35.7) ÷ 7
= (88.9)÷7
= 12.7
Problem Solving
Question 8.
Jake earned $10.44 interest on his savings account for an 18-month period. What was the average amount of interest Jake earned on his savings account per month?
Answer: $0.58.
Explanation: Jake earned $10.44 interest on his savings account for an 18 month period, so average amount interest is 10.44÷18= $0.58.
Question 9.
Gloria worked for 6 hours a day for 2 days at the bank and earned $114.24. How much did she earn per hour?
Answer: $9.52.
Explanation: As gloria worked for 6 hours for 2 days, so total hours is 6×2= 12 hours earned $114.24. So per hour she earns $114.24÷12= $9.52.
Question 10.
Explain the importance of correctly placing the decimal point in the quotient of a division problem.
Answer: If you don’t have the decimals in right spot your answer could be differ.
Lesson Check – Page No. 54
Estimate each quotient. Then find the exact quotient for each question.
Question 1.
Ron divided 67.6 fluid ounces of orange juice evenly among 16 glasses. How much did he pour into each glass?
Answer: 4.225 ounces.
Explanation: As there are 16 glasses, he pours into each glass 67.6÷16= 4.225 ounces.
Question 2.
The cost of a $12.95 pizza was shared evenly by 5 friends. How much did each person pay?
Answer: $2.59.
Explanation: The cost of pizza is $12.95 which was shared by 5 friends, so each person pays $12.95÷5= $2.59
Spiral Review
Question 3.
What is the value of the digit 6 in 968,743,220?
Answer: 60 Lakhs.
Explanation: The place value of 6 is 60,00,000.
Question 4.
The Tama, Japan, monorail carries 92,700 riders each day. If the monorail runs 18 hours each day, what is the average number of passengers riding each hour?
Answer: 5150 passengers.
Explanation: No. of riders each day is 92,700 and he runs for 18 hours in each day, so average no. of passengers riding each hour is 92,700÷18= 5150 passengers.
Question 5.
Ray paid $812 to rent music equipment that costs $28 per hour. How many hours did he have the equipment?
Answer: 29 hours.
Explanation: As Ray paid $812 which costs $28 per hour, so no.of hours did he have the equipment is
$812÷$28= 29 hours.
Question 6.
Jan has 35 teaspoons of chocolate cocoa mix and 45 teaspoons of french vanilla cocoa mix. She wants to put the same amount of mix into each jar, and she only wants one flavor of mix in each jar. She wants to fill as many jars as possible. How many jars of french vanilla cocoa mix will Jan fill?
Answer: 9 jars.
Explanation: By distributive property (35+45)
= (5×7)+(5×9)
= 5(7+9)
So she will fill 9 jars.
Share and Show – Page No. 57
Question 1.
Find the quotient.
14.8)\(\overline { 99.456 } \)
Answer: 6.72
Explanation: 99.456÷14.8= 6.72
Estimate. Then find the quotient.
Question 2.
$10.80 ÷ $1.35
Answer: 8
Explanation:
$10.80 ÷ $1.35
= 8
Question 3.
26.4 ÷ 1.76
Answer: 15.113
Explanation:
26.4 ÷ 1.76
= 15.113
Question 4.
8.7)\(\overline { 53.07 } \)
Answer: 6.1
Explanation: 53.07÷8.7= 6.1
On Your Own
Estimate. Then find the quotient.
Question 5.
75 ÷ 12.5
Answer: 6
Explanation:
Question 6.
544.6 ÷ 1.75
Answer: 311.2
Explanation:
Question 7.
0.78)\(\overline { 0.234 } \)
Answer: 0.3.
Explanation: 0.234÷0.78= 0.3.
Attend to Precision Algebra Evaluate using the order of operations.
Question 8.
36.4 + (9.2 − 4.9 ÷ 7)
Answer: 44.9
Explanation: By BODMAS rule
36.4+(9.2−4.9÷ 7)
= 36.4+(9.2−(4.9÷7))
= 36.4+(9.2-(0.7))
= 36.4+(8.5)
= 44.9
Question 9.
16 ÷ 2.5 − 3.2 × 0.043
Answer: 6.2624
Explanation: 16 ÷ 2.5 − 3.2 × 0.043
= (16÷2.5) − (3.2 × 0.043)
= (6.4)-(3.2 × 0.043)
= 6.4 – 0.1376
= 6.2624
Question 10.
142 ÷ (42 − 6.5) × 3.9
Answer: 15.6
Explanation: 142 ÷ (42 − 6.5) × 3.9
= (142÷ 35.5) × 3.9
= 4×3.9
= 15.6
Question 11.
Marcus can buy 0.3 pound of sliced meat from a deli for $3.15. How much will 0.7 pound of sliced meat cost?
Answer: $7.35
Explanation: As 0.3 pound of sliced meat is $3.15, so cost of 1 pound of sliced meat is 3.15÷0.3= $10.5. And for 0.7 pound of sliced meat cost is 10.5×0.7= $7.35
Page No. 58
Question 12.
The table shows the earnings and the number of hours worked for three employees. Complete the table by finding the missing values. Which employee earned the least per hour? Explain.
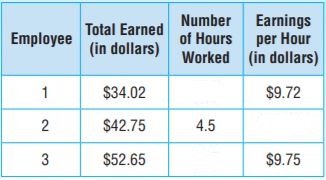
Answer: Employee 2 has earned least per hour.
Explanation:
1. No. of hours worked is 34.02÷ 9.72= 3.5 hours.
2. Earnings per hour is 42.75÷4.5= $9.5
3. No.of hours worked is 52.65÷9.75= 5.4 hours
Employee 2 has earned least per hour.
Amoebas
Amoebas are tiny one-celled organisms. Amoebas can range in size from 0.01 mm to 5 mm in length. You can study amoebas by using a microscope or by studying photographic enlargements of them.
Jacob has a photograph of an amoeba that has been enlarged 1,000 times. The length of the amoeba in the photo is 60 mm. What is the actual length of the amoeba?
Divide 60 ÷ 1,000 by looking for a pattern.
60 ÷ 1 = 60
60 ÷ 10 = 6.0 The decimal point moves _____ place to the left.
60 ÷ 100 = ____ The decimal point moves _____ place to the left.
60 ÷ 1000 =____ The decimal point moves _____ place to the left.
So, the actual length of the amoeba is _____ mm.
Answer: 0.06mm
Explanation:
60 ÷ 10 = 6.0 The decimal point moves one place to the left.
60 ÷ 100 =0.6 The decimal point moves two place to the left.
60 ÷ 1000 =0.06 The decimal point moves three place to the left.
Actual length of amoeba is 0.06mm
Question 13.
Explain the pattern.
Answer: 0.06mm
Explanation: 60÷1000= 0.06mm.
Question 14.
Pelomyxa palustris is an amoeba with a length of 4.9 mm. Amoeba proteus has a length of 0.7 mm. How many Amoeba proteus would you have to line up to equal the length of three Pelomyxa palustris? Explain.
Answer: 21
Explanation:
Let N be the number, then
N×(proteus length)= 3× (palustris length)
N× 0.7= 3× 4.9
N×0.7= 14.7
N= 14.7÷0.7
N= 21
Divide with Decimals – Page No. 59
Estimate. Then find the quotient.
Question 1.
43.18 ÷ 3.4
Answer: 12.7
Explanation: 43.18 ÷ 3.4= 12.7
Question 2.
4.185 ÷ 0.93
Answer: 4.5
Explanation: 4.185 ÷ 0.93= 4.5
Question 3.
6.3)\(\overline { 25.83 } \)
Answer: 0.244
Explanation: 6.3÷25.83= 0.244
Question 4.
0.143 ÷ 0.55
Answer: 0.26
Explanation: 0.143 ÷ 0.55= 0.26
Evaluate using the order of operations.
Question 5.
4.92 ÷ (0.8 – 0.12 ÷ 0.3)
Answer: 12.3
Explanation: 4.92 ÷ (0.8 – 0.12 ÷ 0.3)
= 4.92÷(0.8-(0.12÷0.3))
= 4.92÷(0.8-(0.4))
= 4.92÷(0.4)
= 12.3
Question 6.
0.86 ÷ 5 – 0.3 × 0.5
Answer: 0.022
Explanation: 0.86 ÷ 5 – 0.3 × 0.5
= (0.86÷5) – (0.3 × 0.5)
= (0.172)-(0.3 × 0.5)
= 0.172 – (0.15)
= 0.022
Question 7.
17.28 ÷ (1.32 – 0.24) × 0.6
Answer: 9.6
Explanation: 17.28 ÷ (1.32 – 0.24) × 0.6
= (17.28 ÷ (1.32 – 0.24))× 0.6
= (17.28 ÷( 1.08))×0.6
= (16)×0.6
= 9.6
Problem Solving
Question 8.
If Amanda walks at an average speed of 2.72 miles per hour, how long will it take her to walk 6.8 miles?
Answer: 2.5 hours.
Explanation: Amanda walks at an average speed of 2.72 miles per hour, so for 6.8 miles it will be
6.8÷2.72= 2.5 hours.
Question 9.
Chad cycled 62.3 miles in 3.5 hours. If he cycled at a constant speed, how far did he cycle in 1 hour?
Answer: 17.8 miles.
Explanation: Chad cycled 62.3 miles in 3.5 hours, so in 1 hour 62.3÷3.5= 17.8 miles.
Question 10.
Explain how dividing by a decimal is different from dividing by a whole number and how it is similar.
Answer: By moving the decimals first the dividing will be different, and after that it will be same.
Lesson Check – Page No. 60
Question 1.
Elliot drove 202.8 miles and used 6.5 gallons of gasoline. How many miles did he travel per gallon of gasoline?
Answer: 31.2 miles.
Explanation: Elliot drove 202.8 miles and used 6.5 gallons of gasoline, so per gallon of gasoline he will travel 202.8÷6.5= 31.2 miles.
Question 2.
A package of crackers weighing 8.2 ounces costs $2.87. What is the cost per ounce of crackers?
Answer: 0.35 per ounce.
Explanation: As 8.2 ounces costs $2.87, so per ounce of crackers it will be 2.87÷8.2= 0.35 per ounce.
Spiral Review
Question 3.
Four bags of pretzels were divided equally among 5 people. How much of a bag did each person get?
\(\frac{□}{□}\)
Answer: 0.8
Explanation: As 4 bags were divided equally among 5 people, so each person gets 4÷5= 0.8 of a bag
Question 4.
A zebra ran at a speed of 20 feet per second. What operation should you use to find the distance the zebra ran in 10 seconds?
Answer: Multiplication.
Explanation: Per second zebra ran at a speed of 20 feet, so for 10 seconds 20×10= 200 feet.
Question 5.
Nira has $13.50. She receives a paycheck for $55. She spends $29.40. How much money does she have now?
Answer: $39.10.
Explanation: As Nira has $13.50 and she receives paycheck of $55, so total she had is $13.50+$55= $68.5. As she spent $29.40, so she has now $68.5-$29.40= $39.10.
Question 6.
A piece of cardboard is 24 centimeters long and 15 centimeters wide. What is its area?
_____ cm2
Answer: 360 cm2
Explanation:
Area= Length×wide
= 24×15
= 360 cm2
Chapter 1 Review/Test – Page No. 61
Question 1.
Use the numbers to complete the factor tree. You may use a number more than once.

Write the prime factorization of 54
Answer: 54=2×3×3×3
Explanation:
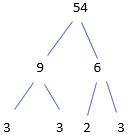
Question 2.
For numbers 2a–2d, choose Yes or No to indicate whether the LCM of the two numbers is 15.
2a. 5, 3 Yes No
2b. 5, 10 Yes No
2c. 5, 15 Yes No
2d. 5, 20 Yes No
2a. 5, 3
Answer: Yes
Explanation:
Multiples of 5: 5,10,15
Multiples of 3: 53,6,9,12,15
LCM of 5,3 is 15
2b. 5, 10
Answer: No
Explanation:
Multiples of 5: 5,10
Multiples of 10: 10
LCM of 5,10 is 10
2c. 5, 15
Answer: Yes
Explanation:
Multiples of 5: 5,10,15
Multiples of 15: 15
LCM is 15
2d. 5, 20
Answer: No
Explanation:
Multiples of 5: 5,10,15,20
Multiples of 20: 20
LCM is 20
Question 3.
Select two numbers that have 9 as their greatest common factor. Mark all that apply.
Options:
a. 3, 9
b. 3, 18
c. 9, 18
d. 9, 36
e. 18, 27
Answer: c,d,e
Explanation:
a. 3,9
Factors of 3: 1,3.
Factors of 9: 1,3,9.
GCF is 3
b. 3,18
Factors of 3: 1,3
Factors of 18: 1,2,3,6,9,18
GCF is 3
c. 9,18
Factors of 9: 1,3,9
Factors of 18: 1,2,3,6,9,18.
GCF is 9
d. 9,36
Factors of 9: 1,3,9
Factors of 36: 1,2,3,4,6,9,18,36
GCF is 9
e. 18,27
Factors of 18: 1,2,3,6,9,18
Factors of 27: 1,3,9,27
GCF is 9
Page No. 62
Question 4.
The prime factorization of each number is shown.
15 = 3 × 5
18 = 2 × 3 × 3
Part A
Using the prime factorization, complete the Venn diagram
Answer:
Prime factors of 15: 3×5
Prime factors of 18: 2×3×3
Common factors are: 3
Explanation:
Question 4.
Part B
Find the GCF of 15 and 18.
Answer: 3
Explanation:
Factors of 15: 1,3,5
Factors of 18: 1,2,3,6,9,18
GCF is 3
Question 5.
For numbers 5a–5d, choose Yes or No to indicate whether each equation is correct.
5a. 222.2 ÷ 11 = 22.2 Yes No
5b. 400 ÷ 50 = 8 Yes No
5c. 1,440 ÷ 36 = 40 Yes No
5d. 7,236 ÷ 9 = 804 Yes No
5a. 222.2 ÷ 11 = 22.2
Answer: No
Explanation:
222.2 ÷ 11 = 20.2
5b. 400 ÷ 50 = 8
Answer: Yes
Explanation:
400 ÷ 50 = 8
5c. 1,440 ÷ 36 = 40
Answer: Yes
Explanation:
1,440 ÷ 36 = 40
5d. 7,236 ÷ 9 = 804
Answer: Yes
Explanation:
7,236 ÷ 9 = 804
Page No. 63
Question 6.
For numbers 6a–6d, select True or False for each equation.
6a. 1.7 + 4.03 = 6 True False
6b. 2.58 + 3.5 = 6.08 True False
6c. 3.21 − 0.98 = 2.23 True False
6d. 14 − 1.3 = 0.01 True False
6a. 1.7 + 4.03 = 6
Answer: False
Explanation:
1.7 + 4.03 = 5.73
6b. 2.58 + 3.5 = 6.08
Answer: True
Explanation:
2.58 + 3.5 = 6.08
6c. 3.21 − 0.98 = 2.23
Answer: True
Explanation:
3.21 − 0.98 = 2.23
6d. 14 − 1.3 = 0.01
Answer: False
Explanation:
6d. 14 − 1.3 = 12.7
Question 7.
Four friends went shopping at a music store. The table shows the number of CDs each friend bought and the total cost. Complete the table to show the average cost of the CDs each friend bought.
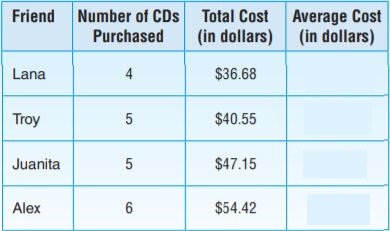
What is the average cost of all the CDs that the four friends bought? Show your work.
Answer: $8.94.
Explanation:
Lana purchased 4 CDs and total cost is $36.68, so cost of 1 CD is $36.68÷4= $9.17
Troy purchased 5 CDs and total cost is $40.55, so cost of 1 CD is $40.55÷5= $8.11
Juanita purchased 5 CDs and total cost is $47.15, so cost of 1 CD is $47.15÷5= $9.43
Alex purchased 6 CDs and total cost is $54.42, so cost of 1 CD is $54.42÷6= $9.07
Average cost of all CD’s i= (cost of all CD’s)÷(No.of CD’S)
=($36.68+$40.55+$47.15+$54.42)÷20
= (178.8) ÷20
= $8.94
Question 8.
The table shows the earnings and the number of hours worked for five employees. Complete the table by finding the missing values.
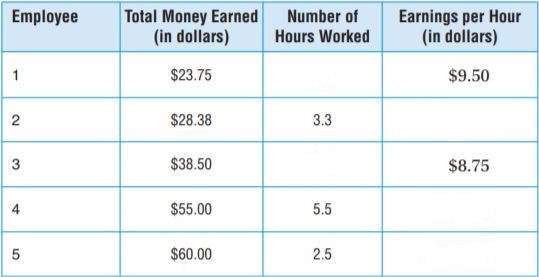
Answer:
1. No. of hours worked is 2.5 hours.
2. Earnings per hour is $93.654.
3. No. of hours worked is 4.4 hours.
4. Earnings per hour is $302.5.
5. Earnings per hour is $150.
Explanation:
1. No. of hours worked is $23.75÷$9.50= 2.5 hours.
2. Earnings per hour is $28.38×3.3= $93.654.
3. No. of hours worked is $38.50÷8.75= 4.4 hours.
4. Earnings per hour is $55×5.5= $302.5.
5. Earnings per hour is $60×2.5= $150.
Page No. 64
Question 9.
The distance around the outside of Cedar Park is 0.8 mile. Joanie ran 0.25 of the distance during her lunch break. How far did she run? Show your work.
Answer: 0.2 miles.
Explanation: Joanie ran 0.25 miles and the distance around the outside of cedar park is 0.8 mile, so she ran
0.25×0.8= 0.2 miles.
Question 10.
A one-celled organism measures 32 millimeters in length in a photograph. If the photo has been enlarged by a factor of 100, what is the actual length of the organism? Show your work.
Answer: 3200 millimeters.
Explanation: Length of one celled organism is 32 millimeters, as the photo was enlarged by a factor of 100, it’s actual length is 32×100= 3200 millimeters.
Question 11.
You can buy 5 T-shirts at Baxter’s for the same price that you can buy 4 T-shirts at Bixby’s. If one T-shirt costs $11.80 at Bixby’s, how much does one T-shirt cost at Baxter’s? Use numbers and words to explain your answer.
Answer: $9.44.
Explanation: As one T-shirt costs $11.80, so 4 T-shirts cost is 4×$11.80= 47.2. So 5 T-shirts at Baxter’s is 47.2 and one T-shirt cost is 47.2÷5= $9.44.
Page No. 65
Question 12.
Crackers come in packages of 24. Cheese slices come in packages of 18. Andy wants one cheese slice for each cracker. Patrick made the statement shown.
If Andy doesn’t want any crackers or cheese slices left over, he needs to buy at least 432 of each.
Is Patrick’s statement correct? Use numbers and words to explain why or why not. If Patrick’s statement is incorrect, what should he do to correct it?
Answer: Patrick’s statement is wrong.
Explanation:
Multiples of 18: 18,36,54,72
Multiples of 24: 24,48,72
LCM is 72
So the least packages he need to buy is 72.
Question 13.
There are 16 sixth graders and 20 seventh graders in the Robotics Club. For the first project, the club sponsor wants to organize the club members into equal-size groups. Each group will have only sixth graders or only seventh graders.
Part A
How many students will be in each group if each group has the greatest possible number of club members? Show your work.
Answer: Each group will have 4 members, and 4 groups of sixth grade and 5 groups of seventh grade.
Explanation: By distributive property 16+20
=(4×4)+(4×5)
=4×(4+5)
So each group will have 4 members, and 4 groups of sixth grade and 5 groups of seventh grade.
Question 13.
Part B
If each group has the greatest possible number of club members, how many groups of sixth graders and how many groups of seventh graders will there be? Use numbers and words to explain your answer
__________ groups of sixth graders
__________ groups of seventh graders
Answer: Each group will have 4 members, and 4 groups of sixth grade and 5 groups of seventh grade.
Explanation: By distributive property 16+20
=(4×4)+(4×5)
=4×(4+5)
So each group will have 4 members, and 4 groups of sixth grade and 5 groups of seventh grade.
Page No. 66
Question 14.
The Hernandez family is going to the beach. They buy sun block for $9.99, 5 snacks for $1.89 each, and 3 beach toys for $1.49 each. Before they leave, they fill up the car with 13.1 gallons of gasoline at a cost of $3.70 per gallon.
Part A
Complete the table by calculating the total cost for each item.
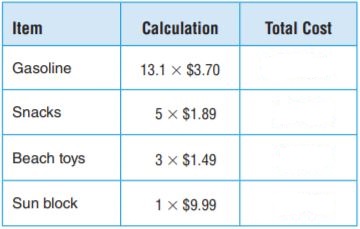
Answer: Total cost is $48.47+$9.45++$4.47+$9.99= $72.38
Explanation:
Gasoline 13.1×$3.70= $48.47
Snacks 5×$1.89= $9.45
Beach toys 3×$1.49= $4.47
Sun block 1×$9.99= $9.99
Total cost is $48.47+$9.45++$4.47+$9.99= $72.38
Question 14.
Part B
What is the total cost for everything before tax? Show your work.
Answer: $72.38.
Explanation: Total cost is $48.47+$9.45++$4.47+$9.99= $72.38.
Question 14.
Part C
Mr. Hernandez calculates the total cost for everything before tax using this equation.
Total cost = 13.1 + 3.70 × 5 + 1.89 × 3 + 1.49 × 9.99
Do you agree with his equation? Use numbers and words to explain why or why not. If the equation is not correct, write a correct equation.
Answer: No
Explanation: Mr. Hernandez calculated in a wrong way.
Total cost is (13.1×$3.70)+(5×$1.89)+(3×$1.49)+(1×$9.99)= $72.38.
Conclusion:
I hope the information provided in the Go Math Grade 6 Answer Key Chapter 1 Chapter 1 Divide Multi-Digit Numbers. For any queries you can post your comments in the below comment section.
