Are you browsing the net to get the best material to score well in the exams? Then you are on the right page. Here you can get the best Go Math Grade 7 Answer Key for Chapter 2 Multiplying and Dividing Integers. Refer to Chapter 2 Multiplying and Dividing Integers Go Math Grade 7 Answer Key to enhance your math skills.
Go Math Grade 7 Answer Key Chapter 2 Multiplying and Dividing Integers
Go through the topics covered in Multiplying and Dividing Integers before you start your preparation. Just tap the link and start preparing now. In addition to the exercise problems, you can also get a detailed explanation for all the questions in Module Review. So, first, practice the exercise problems and then try to solve the questions given in the module review. With the help of this Go Math 7th Grade Answer Key Chapter 2 Multiplying and Dividing Integers, you can improve the knowledge in the following topics.
Chapter 2 – Multiplying Integers
- Multiplying Integers – Guided Practice – Page No. 40
- Multiplying Integers – Independent Practice – Page No. 41
- Multiplying Integers – Page No. 42
Chapter 2 – Dividing Integers
- Dividing Integers – Guided Practice – Page No. 46
- Dividing Integers – Independent Practice – Page No. 47
- Dividing Integers – Page No. 48
Chapter 2- Applying Integer Operations
- Applying Integer Operations – Guided Practice – Page No. 52
- Applying Integer Operations – Independent Practice – Page No. 53
- Applying Integer Operations – Page No. 54
Chapter 2 – Module Review
- MODULE QUIZ – 2.1 Multiplying Integers – Page No. 55
- MIXED REVIEW – Selected Response – Page No. 56
- Module 2 Review – Multiplying and Dividing Integers – Page No. 104
Multiplying Integers – Guided Practice – Page No. 40
Find each product.
Question 1.
-1(9)
_______
Answer: -9
Explanation:
We have to find the product:
-1(9)
1. Determine the sign of the product
-1 < 0 and 9 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-1| = 1
|9| = 9
1 × 9 =9
3. We assign the correct sign to the product:
-1 × 9 = -9
Question 2.
14(-2)
_______
Answer: -28
Explanation:
We have to find the product:
14(-2)
1. Determine the sign of the product
-2 < 0 and 14 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-2| = 2
|14| = 14
2 × 14 = 28
3. We assign the correct sign to the product:
-2 × 14 = -28
Question 3.
(-9)(-6)
_______
Answer: 54
Explanation:
We have to find the product:
(-9)(-6)
1. Determine the sign of the product
-9 < 0 and -6 < 0
Since the numbers have the same signs, the product will be positive.
2. We find the absolute value of the numbers and multiply them:
|-9| = 9
|-6| = 6
3. We assign the correct sign to the product:
-9 × -6 = 54
Question 4.
(-2)(50)
_______
Answer: -100
Explanation:
We have to find the product:
(-2)(50)
1. Determine the sign of the product
-2 < 0 and 50 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-2| = 2
|50| = 50
3. We assign the correct sign to the product:
-2 × 50 = -100
Question 5.
(-4)(15)
_______
Answer: -60
Explanation:
We have to find the product:
(-4)(15)
1. Determine the sign of the product
-4 < 0 and 15 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-4| = 4
|15| = 15
3. We assign the correct sign to the product:
-4 × 15 = -60
Question 6.
-18(0)
_______
Answer: 0
Explanation:
We have to find the product:
-18(0)
Since one of the factors is zero, the product is zero.
-18 × 0 = 0
Question 7.
(-7)(-7)
_______
Answer: 49
Explanation:
We have to find the product:
(-7)(-7)
1. Determine the sign of the product
-7 < 0
Since the numbers have the same signs, the product will be positive.
2. We find the absolute value of the numbers and multiply them:
|-7| = 7
|-7| = 7
3. We assign the correct sign to the product:
-7 × -7 = 49
Question 8.
-15(9)
_______
Answer: -125
Explanation:
We have to find the product:
-15(9)
1. Determine the sign of the product
-15 < 0 and 9 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-15| = 15
|9| = 9
3. We assign the correct sign to the product:
-15 × 9 = -125
Question 9.
(8)(-12)
_______
Answer: -96
Explanation:
We have to find the product:
(8)(-12)
1. Determine the sign of the product
8 > 0 and -12 < 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|8| = 8
|-15| = 15
3. We assign the correct sign to the product:
8 × -15 = -96
Question 10.
-3(-100)
_______
Answer: 300
Explanation:
We have to find the product:
-3 < 0 and -100 < 0
Since the numbers have the same signs, the product will be positive.
2. We find the absolute value of the numbers and multiply them:
|-3| = 3
|-100| = 100
3. We assign the correct sign to the product:
-3 × -100 = 300
Question 11.
0(-153)
_______
Answer: 0
Explanation:
We have to find the product:
0(-153)
Since one of the factors is zero, the product is zero.
0 × -153 = 0
Question 12.
-6(32)
_______
Answer: -192
Explanation:
We have to find the product:
-6(32)
1. Determine the sign of the product
-6 < 0 and 32 > 0
Since the numbers have opposite signs, the product will be negative.
2. We find the absolute value of the numbers and multiply them:
|-6| = 6
|32| = 32
3. We assign the correct sign to the product:
-6 × 32 = -192
Question 13.
Flora made 7 withdrawals of $75 each from her bank account. What was the overall change in her account?
$ _______
Answer: -525
Explanation:
Flora made 7 withdrawals of $75 each from her bank account.
Since she withdrew 7 amounts of money, the overall change in the account will be:
(-7)(75)
-7 < 0 and 75 > 0
The numbers have the opposite signs, so the product will be negative.
7 × 75 = 525
We assign the correct sign to the product:
-7 × 75 = -525
Question 14.
A football team lost 5 yards on each of 3 plays. Explain how you could use a number line to find the team’s change in field position after the 3 plays.
Type below:
_____________
Answer: -15 yards
Explanation:
A football team lost 5 yards on each of 3 plays.
The team lost 5 yards 3 times.
3(-5) = (-5) + (-5) + (-5)
To graph 3(-5) we start at 0 and move 5 units to the left 3 times:
-15
The result is -15 yards.
Question 15.
The temperature dropped 2 °F every hour for 6 hours. What was the total number of degrees the temperature changed in the 6 hours?
_______ °F
Answer: -12°F
Explanation:
Since the temperature dropped 2 °F every hour for 6 hours, the total number of degrees the temperature changed in the 6 hours is:
6(-2) = (-2) + (-2) + (-2) + (-2) + (-2) + (-2)
To graph 6(-2) we start at 0 and move 2 units to the left 6 times.
6 × -2 = -12
Question 16.
The price of one share of Acme Company declined $5 per day for 4 days in a row. How much did the price of one share change in total after the 4 days?
$ _______
Answer: -20
Explanation:
The price declined $5 4 times, thus the total change in the price after the 4 days is:
4(-5)
4(-5) = (-5) + (-5) + (-5) + (-5)
To graph 4(-5) we start at 0 and move 5 units to the left 4 times:
4 × -5 = $-20
Question 17.
A mountain climber climbed down a cliff 50 feet at a time. He did this 5 times in one day. What was the overall change in his elevation?
_______ feet
Answer: -250 feet
Explanation:
A mountain climber climbed down a cliff 50 feet at a time. He did this 5 times in one day.
5(-50)
5(-50) = (-50) + (-50) + (-50) + (-50) + (-50)
To graph 5(-50) we start at 0 and move 50 units to the left 5 times:
5 × -50 = -250 feet
Thus the overall change in his elevation is -250 feet.
Question 18.
Explain the process for finding the product of two integers.
Type below:
_____________
Answer: Determine the sign of the product, multiply the absolute value of the numbers then attach the sign to the product. If one of the numbers is zero then the product is zero.
Multiplying Integers – Independent Practice – Page No. 41
Question 19.
Critique Reasoning Lisa used a number line to model –2(3). Does her number line make sense? Explain why or why not.
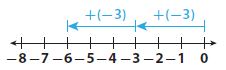
_______
Answer:
Lisa used the number line incorrectly since in her number line she multiplied -3 twice.
The number line should show 2 movements to the left three times.
Question 20.
Represent Real-World Problems Mike got on an elevator and went down 3 floors. He meant to go to a lower level, so he stayed on the elevator and went down 3 more floors. How many floors did Mike go down altogether?
_______ floors
Answer: 6 floors
Explanation:
Mike got on an elevator and went down 3 floors. He meant to go to a lower level, so he stayed on the elevator and went down 3 more floors.
2(-3) = -6
This means he went down 6 floors.
Solve. Show your work.
Question 21.
When Brooke buys lunch at the cafeteria, money is withdrawn from a lunch account. The table shows amounts withdrawn in one week. By how much did the amount in Brooke’s lunch account change by the end of that week?
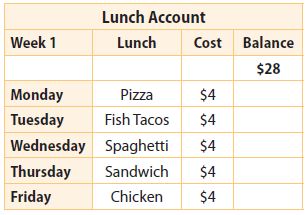
$ _______ decrease
Answer: $-20 decrease
Explanation:
He withdrew $4 each day, which means 5 times $4 each time. By the end of the week, his account will mark a decrease of: -$20
Question 22.
Adam is scuba diving. He descends 5 feet below sea level. He descends the same distance 4 more times. What is Adam’s final elevation?
_______ feet
Answer: -20 feet
Explanation:
Since he descends 4 times 5 feet each time, his final elevation will be:
4(-5) = -20 feet
Question 23.
The price of jeans was reduced $6 per week for 7 weeks. By how much did the price of the jeans change over the 7 weeks?
$ _______
Answer: $42
Explanation:
The price of the jeans was reduced $6 per week for 7 weeks.
After 7 weeks the price will be reduced by 7 times $6:
7(-6) = -42
Thus the price will be reduced by $42.
Question 24.
Casey uses some of his savings on batting practice. The cost of renting a batting cage for 1 hour is $6. He rents a cage for 9 hours in each of two months. What is the change in Casey’s savings after two months?
$ _______
Answer: $108
Explanation:
Given,
Casey uses some of his savings on batting practice.
The cost of renting a batting cage for 1 hour is $6.
He rents a cage for 9 hours in each of two months.
9(-6) = -54
For 2 months = -54 × 2 = -108
Question 25.
Volunteers at Sam’s school use some of the student council’s savings for a special project. They buy 7 backpacks for $8 each and fill each backpack with paper and pens that cost $5. By how much did the student council’s savings change because of this project?
$ _______
Answer: $91
Explanation:
They buy 7 backpacks for $8 each and fill each backpack with paper and pens that cost $5
Cost of 1 backpack = $8
cost of 7 backpacks = 8 × 7 = $56
Cost to fill each backpack with paper and pens = $5
Cost to fill each 7 backpacks with paper and pens = 5 × 7=$35
Total cost = $56 + $35 = $91
the students councils savings change by $91
Multiplying Integers – Page No. 42
Question 26.
Communicate Mathematical Ideas Describe a real-world situation that can be represented by the product 8(–20). Then find the product and explain what the product means in terms of the real-world situation.
_______ points
Answer: -160
Example:
Irene has some savings in an account. Each of 8 months she uses $20 to pay a rate for a bicycle. What is the change in her account after the 8 months?
8(-20) = -160
The change in the account consists of 8 times $20:
Her account diminished by $160.
Question 27.
What If? The rules for multiplying two integers can be extended to a product of 3 or more integers. Find the following products by using the Associative Property to multiply 2 numbers at a time.
a. 3(3)(–3)
_______
Answer: -27
Explanation:
3 × 3 × (-3) = 9(-3) = -27
Question 27.
b. 3(–3)(–3)
_______
Answer: 27
3((-3)(-3))
3 × 9 = 27
Question 27.
c. –3(–3)(–3)
_______
Answer: -27
(-3)(–3)(–3)
(-3)(9)
9 × -3 = -27
Question 27.
d. 3(3)(3)(–3)
_______
Answer: -81
(3 × 3)(3 × -3)
9 × -9 = -81
Question 27.
e. 3(3)(–3)(–3)
_______
Answer: 81
(3 × 3)(-3 × -3)
9 × 9 = 81
Question 27.
f. 3(–3)(–3)(–3)
_______
Answer: -81
3(-3)(-3 × -3)
-9 × 9 = -81
Question 27.
g. Make a Conjecture Based on your results, complete the following statements:
When a product of integers has an odd number of negative factors, then the sign of the product is ____________.
____________
Answer: negative
Explanation:
When a product of integers has an odd number of negative factors, then the sign of the product is negative.
Question 27.
When a product of integers has an even number of negative factors, then the sign of the product is ___________ .
____________
Answer: positive
Explanation:
When a product of integers has an even number of negative factors, then the sign of the product is positive.
FOCUS ON HIGHER ORDER THINKING
Question 28.
Multiple Representations The product of three integers is –3. Determine all of the possible values for the three factors.
Type below:
_______________
Answer:
We are given the product:
a . b . c = -3
a, b, c integers
a = -1, b = 1, c = 3
a = -3, b = c = 1
a = -1, b = -1, c = -3
The elements of the product can be 1, -1, 3, -3. Since the result is negative, it means that the number of negative factors is odd. Thus we can have either one negative number or three. The possibilities are:
-1, 1, 3
-3, 1 , 1
-1, -1, -3
Question 29.
Analyze Relationships When is the product of two nonzero integers less than or equal to both of the two factors?
Type below:
_______________
Answer:
Let a, b be the two integers.
We are given the data:
a.b ≤ a
a.b ≤ b
a > 0, b> 0
Case 1: both are positive numbers
a = 1, b = 1
= a.b = 1.1 = a = b
The product is greater than any of the two numbers except for the case in which both numbers are 1:
Case 2: both numbers are negative.
a < 0, b< 0
a.b > 0
a . b > a
a . b > b
The product is positive, thus it cannot be smaller than any of the numbers.
Case 3: the numbers have different signs
a . b < 0
a. b < a
a . b ≤ b
The product is negative, therefore smaller than the positive number. The product is also smaller than the negative number as it represents a times the number b:
a = b = 1
a > 0, b < 0
Question 30.
Justify Reasoning The sign of the product of two integers with the same sign is positive. What is the sign of the product of three integers with the same sign? Explain your thinking.
Type below:
_______________
Answer: The product will have the sign of the third number.
Explanation:
Let a, b, c be three integers. a, b have the same sign.
We have to find the sign of a. b . c
a . b > 0
Because a, b have the same sign, their product is positive:
The product a.b.c will have the same sign of c because the sign a.b is positive and multiplying it by a positive number leads to a positive number, while multiplying it by a negative number leads to a negative number.
c > 0
a.b.c = (a.b).c > 0
c < 0 = a.b.c = (a.b).c < 0
Dividing Integers – Guided Practice – Page No. 46
Find each quotient.
Question 1.
\(\frac{-14}{2}\) = _______
Answer: -7
Explanation:
We have to find the quotient:
-14 < 0
2 > 0
Since the numbers have opposite signs, the quotient will be negative.
-14/2 = -7
Question 2.
21 ÷ (−3) = _______
Answer: -7
Explanation:
We have to find the quotient:
21 ÷ (−3)
21 > 0
-3 < 0
Since the numbers have opposite signs, the quotient will be negative.
21/(-3) = -7
Question 3.
\(\frac{26}{-13}\) = _______
Answer: -2
Explanation:
We have to find the quotient:
\(\frac{26}{-13}\)
26 > 0
-13 < 0
Since the numbers have opposite signs, the quotient will be negative.
\(\frac{26}{-13}\) = -2
Question 4.
0 ÷ (−4) = _______
Answer: 0
Explanation:
We have to find the quotient:
0 ÷ (−4)
If one of the numbers is zero answer will be zero.
0 ÷ (−4) = 0
Question 5.
\(\frac{-45}{-5}\) = _______
Answer: 9
Explanation:
We have to find the quotient:
\(\frac{-45}{-5}\)
Since the numbers have the same sign, the quotient will be positive.
\(\frac{-45}{-5}\) = 9
Question 6.
-30 ÷ (10) = _______
Answer: -3
Explanation:
We have to find the quotient:
-30 ÷ (10)
Since the numbers have opposite signs, the quotient will be negative.
-30 ÷ (10) = 3
Question 7.
\(\frac{-11}{-1}\) = _______
Answer: 11
Explanation:
We have to find the quotient:
\(\frac{-11}{-1}\)
Since the numbers have the same sign, the quotient will be positive.
\(\frac{-11}{-1}\) = 11
Question 8.
-31 ÷ (-31) = _______
Answer: 1
Explanation:
We have to find the quotient:
-31 ÷ (-31)
Since the numbers have the same sign, the quotient will be positive.
-31 ÷ (-31) = 1
Question 9.
\(\frac{0}{-7}\) = _______
Answer: 0
Explanation:
We have to find the quotient:
\(\frac{0}{-7}\)
If one of the numbers is zero answer will be zero.
0/-7 = 0
Question 10.
\(\frac{-121}{-11}\) = _______
Answer: 11
Explanation:
We have to find the quotient:
\(\frac{-121}{-11}\)
Since the numbers have the same sign, the quotient will be positive.
\(\frac{-121}{-11}\) = 11
Question 11.
84 ÷ (-7) = _______
Answer: -12
Explanation:
We have to find the quotient:
84 ÷ (-7)
Since the numbers have opposite signs, the quotient will be negative.
84 ÷ (-7)
7 divides 84 twelve times.
So, the answer is -12.
Question 12.
\(\frac{500}{-25}\) = _______
Answer: -20
Explanation:
We have to find the quotient:
\(\frac{500}{-25}\)
Since the numbers have opposite signs, the quotient will be negative.
\(\frac{500}{-25}\) = -20
Question 13.
-6 ÷ 0 =
__________
Answer: undefined
Explanation:
We have to find the quotient:
-6 ÷ 0
Any number divided by 0 is undefined.
Question 14.
\(\frac{-63}{-21}\) = _______
Answer: 3
Explanation:
We have to find the quotient:
\(\frac{-63}{-21}\)
Since the numbers have the same sign, the quotient will be positive.
\(\frac{-63}{-21}\) = 3
Write a division expression for each problem. Then find the value of the expression.
Question 15.
Clark made four of his truck payments late and was fined four late fees. The total change to his savings from late fees was -$40. How much was one late fee?
$ _______
Answer: 10
Explanation:
Clark made four of his truck payments late and was fined four late fees.
The total change to his savings from late fees was -$40.
We determine one late fee by dividing the total change in his savings by the number of late fees|:
-10 ÷ 4 = -10
One late fee was $10.
Question 16.
Jan received -22 points on her exam. She got 11 questions wrong out of 50 questions. How much was Jan penalized for each wrong answer?
_______ points
Answer: 2 points
Explanation:
Jan received -22 points on her exam. She got 11 questions wrong out of 50 questions.
We determine the number of points on the exam to the number of wrong questions:
-22 ÷ 11 = -2
Thus a wrong answer was penalized by 2 points.
Question 17.
Allen’s score in a video game was changed by -75 points because he missed some targets. He got -15 points for each missed target. How many targets did he miss?
_______ targets
Answer: 5 targets
Explanation:
Allen’s score in a video game was changed by -75 points because he missed some targets.
He got -15 points for each missed target.
We divide the change in the score by the number of points for a missed target:
-75 ÷ -15 = 5
Thus he missed 5 targets.
Question 18.
Louisa’s savings change by -$9 each time she goes bowling. In all, it changed by -$99 during the summer. How many times did she go bowling in the summer?
_______
Answer: 11 times
Explanation:
Given,
Louisa’s savings change by -$9 each time she goes bowling.
In all, it changed by -$99 during the summer.
We divide the change in the savings by the amount she spends each time at bowling:
-99 ÷ -9 = 11
She was bowling 11 times.
ESSENTIAL QUESTION CHECK-IN
Question 19.
How is the process of dividing integers similar to the process of multiplying integers?
Type below:
____________
Answer: The process of dividing integers is similar to the process of multiplying integers about the sign of the result which is positive in case both numbers have the same sign and negative when they have different signs.
Dividing Integers – Independent Practice – Page No. 47
Question 20.
Walter buys a bus pass for $30. Every time he rides the bus, money is deducted from the value of the pass. He rode 12 times and $24 was deducted from the value of the pass. How much does each bus ride cost?
$ _______
Answer: 2
Explanation:
We divide the total amount deducted fro the value of the pass by the number of times he rode the bus:
-24 ÷ 12 = -2
The price of a bus ride is $2.
Question 21.
Analyze Relationships Elisa withdrew $20 at a time from her bank account and withdrew a total of $140. Francis withdrew $45 at a time from his bank account and withdrew a total of $270. Who made the greater number of withdrawals? Justify your answer.
___________
Answer: Elisa
Explanation:
We divide the total withdrew Elisa made by the amount she withdrew each time:
-140 ÷ -20 = 7
We divide the total withdraw Francis made by the amount he withdrew each time:
-270 ÷ -45 = 6
Since Elisa made 7 withdrawals and Francis only 6, it means Elisa made a greater number of withdrawals.
Question 22.
Multistep At 7 p.m. last night, the temperature was 10 °F. At 7 a.m. the next morning, the temperature was -2 °F.
a. By how much did the temperature change from 7 p.m. to 7 a.m.?
_______ degrees
Answer: 12 degrees
Explanation:
We are given the data:
7 p.m: 10°F.
7 a.m: -2 °F.
We determine by how much the temperature changed from 7 p.m to 7 a.m by subtraction the initial temperature from the final temperature:
-2 – 10 = -12
Thus the temperature decreased by 12 degrees.
Question 22.
b. The temperature changed by a steady amount overnight. By how much did it change each hour?
_______ degrees each hour
Answer: 1
Explanation:
We divide the total change of temperature by the number of hours to determine by how much the temperature changed each hour:
-12 ÷ 12 = -1
The temperature decreased by 1°F each hour.
Question 23.
Analyze Relationships Nola hiked down a trail at a steady rate for 10 minutes. Her change in elevation was -200 feet. Then she continued to hike down for another 20 minutes at a different rate. Her change in elevation for this part of the hike was -300 feet. During which portion of the hike did she walk down at a faster rate? Explain your reasoning.
___________ was faster
Answer:
First trail: -200 feet in 10 minutes
Second trail -300 feet in 20 minutes
we determine the rate she walked down on the first trail by dividing the elevation by the time she walked on that trail:
-200 ÷ 10 = -20
The rate was 20 feet/minute.
we determine the rate she walked down on the second trail by dividing the elevation by the time she walked on that trail:
-300 ÷ 20 = -15
The rate was 15 feet/minute.
Question 24.
Write a real world description to fit the expression -50 ÷ 5.
Type below:
___________
Answer:
Example:
Mary planned to lose 50 pounds at a constant rate for 5 months. How much she lose each month?
-50 ÷ 5 = -10
Thus she should lose 10 pounds each month.
Dividing Integers – Page No. 48
Question 25.
Communicate Mathematical Ideas Two integers, a and b, have different signs. The absolute value of integer a is divisible by the absolute value of integer b. Find two integers that fit this description. Then decide if the product of the integers is greater than or less than the quotient of the integers. Show your work.
product ___________ quotient
Answer:
Let’s consider two positive numbers to represent |a| and |b|
Case 1: a = 12, b = -4
a . b = 12 . (-4) = -48
a ÷ b = 12 ÷ (-4) = 3
or
Case 2: a = -12, b = 4
a . b = -12 . 4 = -48
a ÷ b = -12 ÷ 4 = -3
In both the cases the product is smaller than the quotient and the happens because one number is positive and the other negative and because |a| is divisible by |b|
a . b ≤ a ÷ b
Determine if each statement is true or false. Justify your answer.
Question 26.
For any two nonzero integers, the product and quotient have the same sign.
___________
Answer: True
The statement is true because both division and multiplication operate in the same way about signs, the difference being that the absolute values are either multiplied or divided which doesn’t make any difference regarding the signs.
Question 27.
Any nonzero integer divided by 0 equals 0.
___________
Answer: False
The statement is false because the divisor cannot be zero, division is undefined in this case no matter the dividend.
FOCUS ON HIGHER ORDER THINKING
Question 28.
Multi-step A perfect score on a test with 25 questions is 100. Each question is worth the same number of points.
a. How many points is each question on the test worth?
_______ points
Answer: 4
Explanation:
We determine the number of points each question worth by dividing the perfect score to the number of questions:
100 ÷ 25 = 4
Question 28.
b. Fred got a score of 84 on the test. Write a division sentence using negative numbers where the quotient represents the number of questions Fred answered incorrectly.
_______ questions
Answer: 4
Explanation:
The number of questions Fred answered incorrectly is:
(84 – 100) ÷ (-4) = -16 ÷ -4 = 4
The number of questions Fred answered incorrectly is 4.
Question 29.
Persevere in Problem Solving Colleen divided integer a by -3 and got 8. Then she divided 8 by integer b and got -4. Find the quotient of integer a and integer b.
a ÷ b = _______
Answer: 12
Explanation:
a ÷ (-3) = 8
8 ÷ b = -4
a = 8(-3) = -24
a = -24
b = 8 ÷ (-4)
b = -2
a ÷ b = -24 ÷ -2 = 12
Question 30.
Justify Reasoning The quotient of two negative integers results in an integer. How does the value of the quotient compare to the value of the original two integers? Explain.
Type below:
___________
Answer: Since the quotient of two negative numbers is positive, it will always be greater than the original two integers.
Applying Integer Operations – Guided Practice – Page No. 52
Evaluate each expression.
Question 1.
−6(−5) + 12 =
_______
Answer: 42
Explanation:
We are given the expression:
−6(−5) + 12
First, multiply -6 and -5
−6(−5) + 12 = 30 + 12 = 42
Question 2.
3(−6) − 3 =
_______
Answer: -21
Explanation:
We are given the expression:
3(−6) − 3 = -18 – 3
= -21
3(−6) − 3 = -21
Question 3.
(−2)8 + 7 =
_______
Answer: -9
Explanation:
We are given the expression:
(−2)8 + 7 = -2 × 8 + 7
= -16 + 7 = -9
Question 4.
4(−13) + 20 =
_______
Answer: -32
Explanation:
We are given the expression:
4(−13) + 20 = -52 + 20 = -32
Question 5.
(−4)(0) − 4 =
_______
Answer: -4
Explanation:
We are given the expression:
(−4)(0) − 4 = 0 – 4 = -4
Question 6.
−3(−5) − 16 =
_______
Answer: -1
Explanation:
We are given the expression:
−3(−5) − 16 = 15 – 16 = -1
Write an expression to represent the situation. Evaluate the expression and answer the question.
Question 7.
Bella pays 7 payments of $5 each to a game store. She returns one game and receives 20 dollars back. What is the change to the amount of money she has?
$ _______
Answer: 15 less
Explanation:
Given that,
Bella pays 7 payments of $5 each to a game store. She returns one game and receives 20 dollars back.
7(-5) + 20 = -35 + 20 = -15
Thus she will have $15 less.
Question 8.
Ron lost 10 points seven times playing a video game. He then lost an additional 100 points for going over the time limit. What was the total change in his score?
_______ points
Answer: 170 points
Explanation:
We use negative numbers for the number of points he losses.
7(-10) + (-100) = -70 – 100 = -170
Thus he will have 170 points less.
Question 9.
Ned took a test with 25 questions. He lost 4 points for each of the 6 questions he got wrong and earned an additional 10 points for answering a bonus question correctly. How many points did Ned receive or lose overall?
_______ points
Answer: He lost 14 points
Explanation:
Given,
Ned took a test with 25 questions. He lost 4 points for each of the 6 questions he got wrong and earned an additional 10 points for answering a bonus question correctly.
6(-4) + 10 = -24 + 10 = -14
Since he lost the same number of points for each of the 6 questions he answered incorrectly, we use multiplication to determine the number of points he lost, then we add the number of points he received as a bonus.
Thus he lost 14 points.
Question 10.
Mr. Harris has some money in his wallet. He pays the babysitter $12 an hour for 4 hours of babysitting. His wife gives him 10, and he puts the money in his wallet. By how much does the amount in his wallet change?
$ _______
Answer: $38 less
Explanation:
Given,
Mr. Harris has some money in his wallet. He pays the babysitter $12 an hour for 4 hours of babysitting.
His wife gives him 10, and he puts the money in his wallet.
Since she paid 4 times the amount of $12, we use multiplication to determine the money he spent paying the babysitter, then we add the money received from his wife.
The change to the amount of money he has is:
4(12) + 10 = -48 + 10 = -38
Thus he will have $38 less.
Compare the values of the two expressions using <, =, or >.
Question 11.
-3(-2) + 3 _______ 3(-4) + 9
Answer: -3(-2) + 3 > 3(-4) + 9
Explanation:
-3(-2) + 3 = 6 + 3 = 9
3(-4) + 9 = -12 + 9 = -3
9 is greater than -3
So, -3(-2) + 3 > 3(-4) + 9
Question 12.
-8(-2) – 20 _______ 3(-2) + 2
Answer: -8(-2) – 20 = 3(-2) + 2
Explanation:
-8(-2) – 20 = 16 – 20 = -4
3(-2) + 2 = -6 + 2 = -4
-4 = -4
Thus, -8(-2) – 20 = 3(-2) + 2
Question 13.
-7(5) – 9 _______ -3(20) + 10
Answer: -7(5) – 9 > -3(20) + 10
Explanation:
-7(5) – 9 = -35 – 9 = -44
-3(20) + 10 = -60 + 10 = -50
-44 is greater than -50
So, -7(5) – 9 > -3(20) + 10
Question 14.
-16(0) – 3 _______ -8(-2) – 3
Answer: -16(0) – 3 < -8(-2) – 3
Explanation:
-16(0) – 3 = 0 – 3 = -3
-8(-2) – 3 = 16 – 3 = 13
-3 is less than 13.
Thus -16(0) – 3 < -8(-2) – 3
Essential Question Check-In
Question 15.
When you solve a problem involving money, what can a negative answer represent?
Type below:
___________
Answer:
A negative answer in a problem involving money can represent:
– an amount of money spent on something
– a stolen amount of money
– a lent amount of money
– a donated amount of money
– an amount of money given for fines, fees
Applying Integer Operations – Independent Practice – Page No. 53
Evaluate each expression.
Question 16.
−12(−3) + 7
_______
Answer: 43
Explanation:
We are given the expression:
−12(−3) + 7
We perform multiplication first, then addition:
-12(-3) + 7 = 36 + 7 = 43
Question 17.
(−42) ÷ (−6) + 5 − 8
_______
Answer: 4
Explanation:
We are given the expression:
(−42) ÷ (−6) + 5 − 8
((−42) ÷ (−6)) + 5 − 8 = 7 + 5 – 8
12 – 8 = 4
Question 18.
10(−60) − 18
_______
Answer: -618
Explanation:
We are given the expression:
10(−60) − 18
We perform multiplication first, then subtraction:
-600 – 18 = -618
Question 19.
(−11)(−7) + 5 − 82
_______
Answer: 0
Explanation:
We are given the expression:
(−11)(−7) + 5 − 82
We perform multiplication first, then subtraction:
77 + 5 – 82
82 – 82 = 0
(−11)(−7) + 5 − 82 = 0
Question 20.
35 ÷ (−7) + 6
_______
Answer: 1
Explanation:
We are given the expression:
35 ÷ (−7) + 6
We perform division first, then addition:
35 ÷ (−7) + 6 = -5 + 6 = 1
35 ÷ (−7) + 6 = 1
Question 21.
−13(−2) − 16 − 8
_______
Answer: 2
Explanation:
We are given the expression:
−13(−2) − 16 − 8
We perform multiplication first, then subtraction:
26 – 16 – 8
10 – 8 = 2
−13(−2) − 16 − 8 = 2
Question 22.
Multistep
Lily and Rose are playing a game. In the game, each player starts with 0 points and the player with the most points at the end wins. Lily gains 5 points two times, loses 12 points, and then gains 3 points. Rose loses 3 points two times, loses 1 point, gains 6 points, and then gains 7 points.
a. Write and evaluate an expression to find Lily’s score
_______ point(s)
Answer: 1 point
Explanation:
We write and evaluate an expression to find Lily’s score:
2(5) – 12 + 3 = 10 – 12 + 3 = -2 + 3 = 1
Question 22.
b. Write and evaluate an expression to find Rose’s score.
_______ point(s)
Answer: 6 points
Explanation:
We write and evaluate an expression to find Rose’s score:
2(-3) – 1 + 6 + 7 = -6 – 1 + 6 + 7 = -7 + 6 + 7
= 0 + 6 = 6
Question 22.
c. Who won the game?
___________
Answer: Rose
Explanation:
6 > 1
So, Rose won the game because her score is greater than Lily’s score.
Write an expression from the description. Then evaluate the expression.
Question 23.
8 less than the product of 5 and -4.
_______
Answer: -28
Explanation:
The phrase product means multiplication and less than means subtraction.
So, the expression is 5(-4) – 8 = -20 – 8 = -28
Question 24.
9 more than the quotient of -36 and -4.
_______
Answer: 18
Explanation:
The phrase quotient means division and more than means addition.
So, we write the expression as -36 ÷ (-4) + 9
= 9 + 9 =18
Question 25.
Multistep
Arleen has a gift card for a local lawn and garden store. She uses the gift card to rent a tiller for 4 days. It costs 35 dollars per day to rent the tiller. She also buys a rake for $9.
a. Find the change to the value on her gift card.
$ _______
Answer: -149
Explanation:
We determine the change to the value on her gift card:
4(-35) + (-9) = -140 – 9 = – 149
Question 25.
b. The original amount on the gift card was $200. Does Arleen have enough left on the card to buy a wheelbarrow for $50? Explain.
________________
Answer: yes
Explanation:
We determine the amount of money she has left on the gift card after renting the tiler and buying the rake.
200 – 149 = 51
Since she has got $51 on the gift card and a wheelbarrow is $50 she is able to but it.
51 > 50
Applying Integer Operations – Page No. 54
Question 26.
Carlos made up a game where, in a deck of cards, the red cards (hearts and diamonds) are negative and the black cards (spades and clubs) are positive. All face cards are worth 10 points, and number cards are worth their value.
a. Samantha has a king of hearts, a jack of diamonds, and a 3 of spades. Write an expression to find the value of her cards.
_______
Answer: -17
Explanation:
We use negative values for hearts and diamonds and positive values for spades and clubs
1(-10) + 1(-10) + 1(3)
-10 – 10 + 3 = -17
Question 26.
b. Warren has a 7 of clubs, a 2 of spades, and a 7 of hearts. Write an expression to find the value of his cards.
_______
Answer: 2
Explanation:
We use negative values for hearts and diamonds and positive values for spades and clubs
1(7) + 1(2) + 1(-7)
7 + 2 – 7 = 0 + 2 = 2
Question 26.
c. If the greater score wins, who won?
___________
Answer: Warren
2 > -17
Question 26.
d. If a player always gets three cards, describe two different ways to receive a score of 7.
Type below:
___________
Answer:
10 – 2 – 1 = 7 (a queen of spades, a 2 of hearts and an ace of diamonds)
1 + 2 + 4 = 7 (an ace of clubs, a 2 of spades and a 4 of clubs)
-10 + 10 + 7 = 7 (a king of diamonds, a jack of spades and a 7 of clubs)
H.O.T.
Focus On Higher Order Thinking
Question 27.
Represent Real-World Problems
Write a problem that the expression 3(-7) – 10 + 25 = -6 could represent.
Type below:
___________
Answer: -6
Explanation:
We are given the expression:
3(-7) – 10 + 25 = -6
Example:
Adrian has some savings from which he buys 3 books $7 each and a video game for which he pays $10. His sister gives him $5. Whats is the total change in his savings?
3(-7) – 10 + 25 = -21 – 10 + 25 = -31 + 25 = -6
Question 28.
Critique Reasoning
Jim found the quotient of two integers and got a positive integer. He added another integer to the quotient and got a positive integer. His sister Kim says that all the integers Jim used to get this result must be positive. Do you agree? Explain.
___________
Answer: Kim is wrong
Explanation:
Let a, b, c be three integers.
We note by a, b the first two integers and by c the third one.
a ÷ b > 0
a ÷ b + c > 0
Because the quotient a ÷ b is positive it means that either a, b are both positive or they are both negative.
Adding the third number to the positive quotient gives a positive result either if c positive or is negative, but having an absolute value smaller than that of the quotient a ÷ b.
Example:
a = -12
b = -2
c = -3
a ÷ b + c = (-12) ÷ (-2) + (-3) = 6 + (-3)
6 – 3 = 3
3 > 0
Thus kim is wrong.
Question 29.
Persevere in Problem Solving
Lisa is standing on a dock beside a lake. She drops a rock from her hand into the lake. After the rock hits the surface of the lake, the rock’s distance from the lake’s surface changes at a rate of -5 inches per second. If Lisa holds her hand 5 feet above the lake’s surface, how far from Lisa’s hand is the rock 4 seconds after it hits the surface?
________ inches
Answer: 80 inches
Explanation:
We use negative values for the distances the rock gets into the water and the distance from Lisa’s hand until the water’s surface as both go down.
Convert from feet to inches.
1 feet = 12 inches
5 feet = 5 × 12 = 60 inches
After 4 seconds the distance from Lisa’s hand will be given by the sum between the distance from Lisa’s hand until the water’s surface and the distance traveled by the rock below the water’s surface.
4(-5) + (-60) = -20 – 60 = -80
Thus the rock will be 80 inches from Lisa’s hand.
MODULE QUIZ – 2.1 Multiplying Integers – Page No. 55
Find each product.
Question 1.
(−2)(3)
______
Answer: -6
Explanation:
We have to determine the product
(−2)(3)
The numbers have different signs, thus the result will be negative.
We multiply the absolute values of the numbers and assign the negative sign.
-2 × 3 = -6
Question 2.
(−5)(−7)
______
Answer: 35
Explanation:
We have to determine the product
(−5)(−7)
The numbers have the same signs, thus the result will be positive.
We multiply the absolute values of the numbers and assign a positive sign.
(−5)(−7) = 35
Question 3.
8(−11)
______
Answer: -88
Explanation:
We have to determine the product
8(−11)
The numbers have different signs, thus the result will be negative.
We multiply the absolute values of the numbers and assign the negative sign.
8(−11) = -88
Question 4.
(−3)2(−2)
______
Answer: 12
Explanation:
We have to determine the product
(−3)2(−2)
The numbers have the same signs, thus the result will be positive.
We multiply the absolute values of the numbers and assign a positive sign.
(−3)2(−2) = -6 × -2 = 12
Question 5.
The temperature dropped 3 °C every hour for 5 hours. Write an integer that represents the change in temperature.
______ °C
Answer: -15°C
Explanation:
Given that,
The temperature dropped 3 °C every hour for 5 hours.
We use negative numbers for the drop in temperature. Since the temperature dropped with the same number of degrees each hour, the change in temperature will be represented by the result of the multiplication.
5 × -3 = -15 °C
2.2 Dividing Integers
Find each quotient.
Question 6.
\(\frac{-63}{7}\)
______
Answer: -9
Explanation:
We have to determine the quotient:
\(\frac{-63}{7}\)
The numbers have different signs, thus the result will be negative.
We divide the absolute values of the numbers and assign the negative sign.
\(\frac{-63}{7}\) = -9
Thus the quotient of \(\frac{-63}{7}\) is -9
Question 6.
\(\frac{-15}{-3}\)
______
Answer: 5
Explanation:
We have to determine the quotient:
\(\frac{-15}{-3}\)
The numbers have the same signs, thus the result will be positive.
We divide the absolute values of the numbers and assign a positive sign.
\(\frac{-15}{-3}\) = 5
Thus the quotient of \(\frac{-15}{-3}\) is 5.
Question 8.
0 ÷ (−15)
______
Answer: 0
Explanation:
We have to determine the quotient:
0 ÷ (−15)
If one of the numbers is zero then the quotient will be 0.
0 ÷ (−15) = 0
Question 9.
96 ÷ (−12)
______
Answer: -8
Explanation:
We have to determine the quotient:
96 ÷ (−12)
The numbers have different signs, thus the result will be negative.
We divide the absolute values of the numbers and assign the negative sign.
12 divides 96 eight times
So, 96 ÷ (−12) = -8
Question 10.
An elephant at the zoo lost 24 pounds over 6 months. The elephant lost the same amount of weight each month. Write an integer that represents the change in the elephant’s weight each month.
______ pounds
Answer: – 4 pounds
Explanation:
Given that,
An elephant at the zoo lost 24 pounds over 6 months.
The elephant lost the same amount of weight each month.
We use the negative numbers for the drop in weight.
Since the elephant’s weight decreased each month with the same amount, the change in the elephant’s weight each month will be represented by the result of the division:
-24 ÷ 6 = – 4
Thus the change in the elephant’s weight each month is -4 pounds.
2.3 Applying Integer Operations
Evaluate each expression.
Question 11.
(−4)(5) + 8
______
Answer: -12
Explanation:
Given the expression
(−4)(5) + 8
We have to perform multiplication first and then addition
-20 + 8 = -12
So, (−4)(5) + 8 is -12.
Question 12.
(−3)(−6) − 7
______
Answer: 11
Explanation:
Given the expression
(−3)(−6) − 7
We have to perform multiplication first and then subtraction
18 – 7 = 11
Thus (−3)(−6) − 7 = 11
Question 13.
−27 ÷ 9 − 11
______
Answer: -14
Explanation:
Given the expression
−27 ÷ 9 − 11
We have to perform division first and then subtraction
-3 – 11 = -14
So the answer for the expression −27 ÷ 9 − 11 is -14
Question 14.
\(\frac{-24}{-3}\) − (−2)
Answer: 10
Explanation:
Given the expression
\(\frac{-24}{-3}\) − (−2)
We have to perform division first and then subtraction
The numbers have the same signs, thus the result will be positive.
We divide the absolute values of the numbers and assign a positive sign.
\(\frac{-24}{-3}\) = 8
8 – (-2) = 8 + 2 = 10
Essential Question
Question 15.
Write and solve a real-world problem that can be represented by the expression (–3)(5) + 10.
Type below:
___________
Answer: $5
Example:
Lily bought 5 DVDs $3 each and was given a prize of $ 10 for winning a competition. What is the change in her account after these events?
Answer:
5(-3) + 10 = -15 + 10 = -5
Thus she has $5 less in her account.
MIXED REVIEW – Selected Response – Page No. 56
Question 1.
A diver is at an elevation of -18 feet relative to sea level. The diver descends to an undersea cave that is 4 times as far from the surface. What is the elevation of the cave?
Options:
a. -72 feet
b. -22 feet
c. -18 feet
d. -14 feet
Answer: -72 feet
Explanation:
A diver is at an elevation of -18 feet relative to sea level.
The diver descends to an undersea cave that is 4 times as far from the surface.
We determine the elevation of the cave using multiplication as the diver descends 4 times the distance of -18 feet:
4 × -18 = -72
Thus the correct answer is option A.
Question 2.
The football team lost 4 yards on 2 plays in a row. Which of the following could represent the change in field position?
Options:
a. -12 yards
b. -8 yards
c. -6 yards
d. -2 yards
Answer: -8 yards
Explanation:
We determine the change in field position using multiplication as the team lost twice the distance of 4 yards:
2 × -4 = -8 yards
Thus the correct answer is option B.
Question 3.
Clayton climbed down 50 meters. He climbed down in 10-meter intervals. In how many intervals did Clayton make his climb?
Options:
a. 5
b. 10
c. 40
d. 500
Answer: 5
Explanation:
We determine the number of intervals using division as Clayton climbed down the total distance in equal 10 meter intervals
-50 ÷ -10 = 5
Thus the correct answer is option A.
Question 4.
Which expression results in a negative answer?
Options:
a. a negative number divided by a negative number
b. a positive number divided by a negative number
c. a negative number multiplied by a negative number
d. a positive number multiplied by a positive number
Answer:
a. a negative number divided by a negative number gives a positive result.
b. a positive number divided by a negative number gives a negative result.
c. a negative number multiplied by a negative number gives a positive result.
d. a positive number multiplied by a positive number gives a positive result.
The only situation in which we get a negative result is in case B, thus the correct answer is option B.
Question 5.
Clara played a video game before she left the house to go on a walk. She started with 0 points, lost 6 points 3 times, won 4 points, and then lost 2 points. How many points did she have when she left the house to go on the walk?
Options:
a. -20
b. -16
c. 12
d. 20
Answer: -16
Explanation:
Clara played a video game before she left the house to go on a walk.
She started with 0 points, lost 6 points 3 times, won 4 points, and then lost 2 points.
3(-6) + 4 – 2 = -18 + 2 = -16
Thus the correct answer is option B.
Question 6.
Which expression is equal to 0?
Options:
a. \(\frac{-24}{6}\) − 4
b. \(\frac{-24}{-6}\) + 4
c. \(\frac{24}{6}\) + 4
d. \(\frac{-24}{-6}\) − 4
Answer: \(\frac{-24}{-6}\) − 4
Explanation:
a. \(\frac{-24}{6}\) − 4
– 4 – 4 = -8
b. \(\frac{-24}{-6}\) + 4
4 + 4 = 8
c. \(\frac{24}{6}\) + 4
4 + 4 = 8
d. \(\frac{-24}{-6}\) − 4
4 – 4 = 0
Thus the correct answer is option D.
Mini-Task
Question 7.
Rochelle and Denae started with the same amount of money in their bank accounts. Rochelle made three withdrawals of $25 and then wrote a $100 check. Denae deposited $5 and then wrote a $200 check.
a. Find the total change in the amount of money in Rochelle’s account.
$ _______
Answer: -175
Explanation:
We use positive values for deposited money and negative values for withdrawals and written checks.
3(-25) – 100 = -75 – 100 = -175
Question 7.
b. Find the total change in the amount of money in Denae’s account.
$ _______
Answer: -195
Explanation:
We find the total change in the amount of money in Rochelle’s account:
5 + (-200) = -195
Question 7.
c. Compare the amounts of money the two women have in their accounts now.
Type below:
___________
Answer: 20
Explanation:
Since they started with the same amount of money and Rochelle’s account decreased by $175, while Denae’s account decreased by $195, it means Rochelle has an account greater than Denae’s by the sum of
195 – 175 = 20
Module 2 Review – Multiplying and Dividing Integers – Page No. 104
EXERCISES
Question 1.
−9 × (−5) =
________
Answer: 45
Explanation:
Given,
−9 × (−5)
Since the two integers have the same sign, the answer will be positive.
Multiply both the numbers.
−9 × (−5) = 45
Question 2.
0 × (−10) =
________
Answer: 0
Explanation:
Given,
Any number multiplied with zero will be zero.
0 × (−10) = 0
Question 3.
12 × (−4) =
________
Answer: -48
Explanation:
Given,
12 × (−4)
Since the two integers have different signs, the answer will be negative.
12 × (−4) = -48
Question 4.
−32 ÷ 8 =
________
Answer: -4
Explanation:
Given,
−32 ÷ 8
Since the two integers have different signs, the answer will be negative.
−32 ÷ 8 = -4
Question 5.
−9 ÷ (−1) =
________
Answer: 9
Explanation:
Given,
Since the two integers have the same sign, the answer will be positive.
Divide both the numbers.
−9 ÷ (−1) = 9
Question 6.
−56 ÷ 8 =
________
Answer: -7
Explanation:
Given,
Since the two integers have different signs, the answer will be negative.
Divide both the numbers.
−56 ÷ 8 = -7
Question 7.
−14 ÷ 2 − 3 =
________
Answer: -10
Explanation:
Given,
−14 ÷ 2 − 3 = (−14 ÷ 2) − 3
– 7 – 3 = -10
Question 8.
8 + (−20) × 3 =
________
Answer: -52
Explanation:
Given,
8 + (−20) × 3 = 8 – 60 = -52
Question 9.
36 ÷ (−6) − 15 =
________
Answer: -21
Explanation:
Given,
36 ÷ (−6) − 15 = (36 ÷ (−6)) − 15
– 6 – 15 = -21
Question 10.
Tony bought 3 packs of pencils for 4 each and a pencil box for 7. Mario bought 4 binders for 6 each and used a coupon for 6 off. Write and evaluate expressions to find who spent more money.
_____________
Answer: Tony
Explanation:
Tony bought 3 packs of pencils for 4 each and a pencil box for 7.
Mario bought 4 binders for 6 each and used a coupon for 6 off.
Find the total amount that Tony spent
3 × 4 + 7 = 12 + 7 = $19
Find the total amount that Mario spent this is less than Tony’s amount so Tony spent more.
4 × 6 – 6 = 24 – 6 = $18
Compare the amount that Tony and Mario spent
Tony spent more.
Conclusion:
The solutions provided in the Go Math Grade 7 Answer Key Chapter 2 Multiplying and Dividing Integers pdf are prepared by the math experts. This Go Math Answer Key Grade 7 Chapter 2 helps the students to score the highest marks in the exams. It also helps the teachers and parents to help their children in solving the problems in Go Math Grade 7 Key Chapter 2 Multiplying and Dividing Integers.
