Students who are in search of the HMH Go Math Chapter 4 Rates and Proportionality Answer Key can get them on this page. With the help of the Go Math Grade 7 Answer Key 4th Chapter Rates and Proportionality parents can teach simple methods to solve the problems to their children. So, Download Go Math Grade 7 Rates and Proportionality Chapter 4 pdf for free of cost.
Go Math Grade 7 Answer Key Chapter 4 Rates and Proportionality
It is important for the students to learn the concepts given in Go Math Grade 7 Chapter 4 Answer Key to score the highest marks in the exams. The quick way of solving the problems will help you to save time in the exam. The topics covered in this chapter are Unit rates, Constant Rates of Change, Proportional Relationships, and Graphs. Click on the below-provided links and go through all the questions and answers.
Chapter 4 – Unit Rates
- Unit Rates – Guided Practice – Page No. 120
- Unit Rates – Independent Practice – Page No. 121
- Unit Rates – Page No. 122
Chapter 4 – Constant Rates of Change
- Constant Rates of Change – Guided Practice – Page No. 126
- Constant Rates of Change – Page No. 127
- Constant Rates of Change – Page No. 128
Chapter 4 – Proportional Relationships and Graphs
- Proportional Relationships and Graphs – Guided Practice – Page No. 132
- Proportional Relationships and Graphs – Guided Practice – Page No. 133
- Proportional Relationships and Graphs – Page No. 134
Chapter 4 – Module 4
- MODULE QUIZ – 4.1 Unit Rates – Page No. 135
- MIXED REVIEW – Selected Response – Page No. 136
- Module 4 – Page No. 161
Unit Rates – Guided Practice – Page No. 120
Question 1.
Brandon enters bike races. He bikes 8 \(\frac{1}{2}\) miles every \(\frac{1}{2}\) hour. Complete the table to find how far Brandon bikes for each time interval

Type below:
____________
Answer:
1 hour: 8 \(\frac{1}{2}\) + 8 \(\frac{1}{2}\) = 17
1 \(\frac{1}{2}\) hour: 17 + 8 \(\frac{1}{2}\) = 25 \(\frac{1}{2}\)
2 hour: 25 \(\frac{1}{2}\) + 8 \(\frac{1}{2}\) = 34
2 \(\frac{1}{2}\) hour: 34 + 8 \(\frac{1}{2}\) = 42 \(\frac{1}{2}\)

Find each unit rate.
Question 2.
Julio walks 3 \(\frac{1}{2}\) miles in 1 \(\frac{1}{4}\) hours.
________ \(\frac{□}{□}\)
Answer: 2 \(\frac{4}{5}\)
Explanation:
Divide the number of miles by the number of hours to find the unit rate in miles per hour.
3 \(\frac{1}{2}\) ÷ 1 \(\frac{1}{4}\) = \(\frac{7}{2}\)/\(\frac{5}{4}\)
\(\frac{7}{2}\) × \(\frac{4}{5}\) = \(\frac{14}{5}\)
Convert from improper fraction to the mixed fraction.
\(\frac{14}{5}\) = 2 \(\frac{4}{5}\) miles per hour
Question 3.
Kenny reads \(\frac{5}{8}\) page in \(\frac{2}{3}\) minute.
________ \(\frac{□}{□}\)
Answer: \(\frac{15}{16}\)
Explanation:
Divide the number of pages by the number of minutes to find the unit rate in pages per minute.
\(\frac{5}{8}\) ÷ \(\frac{2}{3}\)
= \(\frac{5}{8}\) × \(\frac{3}{2}\) = \(\frac{15}{16}\)
Thus Kenny read \(\frac{15}{16}\) pages per minute.
Question 4.
A garden snail moves \(\frac{1}{6}\) foot in \(\frac{1}{3}\) hour.
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
Explanation:
Given that,
A garden snail moves \(\frac{1}{6}\) foot in \(\frac{1}{3}\) hour.
Divide the number of feet by the number of hours to find the unit rate in feet per hour.
\(\frac{1}{6}\) ÷ \(\frac{1}{3}\)
\(\frac{1}{6}\) × \(\frac{3}{1}\) = \(\frac{1}{2}\)
Therefore A garden snail moves \(\frac{1}{2}\) feet per hour.
Question 5.
A fertilizer covers \(\frac{5}{8}\) square foot in \(\frac{1}{4}\) hour.
________ \(\frac{□}{□}\)
Answer: 2 \(\frac{1}{2}\) square feet per hour
Explanation:
Given,
A fertilizer covers \(\frac{5}{8}\) square foot in \(\frac{1}{4}\) hour.
Divide the number of square feet, which is \(\frac{5}{8}\) by the number of hours, which is \(\frac{1}{4}\), to find the unit rate in square feet per hour.
\(\frac{5}{8}\) ÷ \(\frac{1}{4}\)
\(\frac{5}{8}\) × \(\frac{4}{1}\) =\(\frac{5}{2}\)
Convert from improper fraction to the mixed fraction.
\(\frac{5}{2}\) = 2 \(\frac{1}{2}\) square feet per hour
Thus A fertilizer covers 2 \(\frac{1}{2}\) square feet per hour.
Find each unit rate. Determine which is lower.
Question 6.
Brand A: 240 mg sodium for \(\frac{1}{3}\) pickle or Brand B: 325 mg sodium for \(\frac{1}{2}\) pickle.
____________
Answer:
Find the unit rates in mg per pickle for each brand by dividing the number of mg by the number of pickles.
Brand A: 240 mg ÷ \(\frac{1}{3}\) = 240 × 3 = 720
Brand B: 325 mg ÷ \(\frac{1}{2}\) = 325 × 2 = 650
650 is less than 720 so Brand B has a lower unit rate.
Question 7.
Ingredient C: \(\frac{1}{4}\) cup for \(\frac{2}{3}\) serving or Ingredient D: \(\frac{1}{3}\) cup for \(\frac{3}{4}\) serving.
____________
Answer: Find the unit rates in cups per serving by dividing the number of cups by the number of servings.
Ingredient C: \(\frac{1}{4}\) ÷ \(\frac{2}{3}\)
\(\frac{1}{4}\) × \(\frac{3}{2}\) = \(\frac{3}{8}\)
Ingredient D: \(\frac{1}{3}\) ÷ \(\frac{3}{4}\)
\(\frac{1}{3}\) × \(\frac{4}{3}\) = \(\frac{4}{9}\)
\(\frac{3}{8}\) is less than \(\frac{4}{9}\), ingredient C has a lower unit rate.
Essential Question Check-In
Question 8.
How can you find a unit rate when given a rate?
Type below:
____________
Answer: To find a unit rate when given a rate such as 25 miles per 5 minutes, divide the first quantity by the second quantity.
In the example I gave, this would mean the unit rate is 25 ÷ 5 = 5 miles per minute.
Unit Rates – Independent Practice – Page No. 121

Question 9.
The information for two pay-as-you-go cell phone companies is given.
a. What is the unit rate in dollars per hour for each company?
On Call: ____________ dollars per hour
Talk Time: ____________ dollars per hour
Answer:
Divide the cost by the number of hours for each company to find the unit rates.
On Call: 10 ÷ 3.5 = 2 \(\frac{6}{7}\) ≈ 2.86
Talk Time: 1.25 ÷ \(\frac{1}{2}\) = 2.50
Question 9.
b. Analyze Relationships
Which company offers the best deal? Explain your answer.
____________
Answer: Talk time has the lowest unit rate so it offers the best deal.
Question 9.
c. What If?
Another company offers a rate of $0.05 per minute. How would you find the unit rate per hour?
____________ dollars per hour
Answer:
Since there are 60 minutes in 1 hour, $.0.05 per minute is
60 × 0.05 = $3 per hour.
Thus the unit rate per hour is $3.
Question 9.
d. Draw Conclusions
Is the rate in part c a better deal than On Call or Talk Time? Explain.
____________
Answer:
The unit rate in part c is greater than the unit rates from part a so it is not a better deal than the other two companies.
Question 10.
Represent Real-World Problems
Your teacher asks you to find a recipe that includes two ingredients with a rate of \(\frac{2 \text { units }}{3 \text { units }}\).
a. Give an example of two ingredients in a recipe that would meet this requirement.
Type below:
____________
Answer: A rate of 2/3 units means that there need to be 2 units of 1 ingredient for every 3 units of a second ingredient.
One example could then be 2 eggs per 3 cups of flour.
Another example could 2 teaspoons of vanilla per 3 teaspoons of sugar.
Question 10.
b. If you needed to triple the recipe, would the rate change? Explain.
____________
Answer: No, the rate would not change. Using the example I gave in
part a) of 2 eggs per 3 cups of flour, tripling the recipe would require using 3(2 eggs) = 6 eggs
3(3 cups of sugar) = 9 cups of flour.
Since 6 eggs/9 cups of flour = 2 eggs/3 cups of flour, the rate is still the same.
Question 11.
A radio station requires DJs to play 2 commercials for every 10 songs they play. What is the unit rate of songs to commercials?
____________ songs per commercials
Answer: 10 ÷ 2 = 5
Divide the number of songs by the number of commercials.
Thus the radio requires 5 songs per commercial.
Question 12.
Multistep
Terrance and Jesse are training for a long-distance race. Terrance trains at a rate of 6 miles every half hour and Jesse trains at a rate of 2 miles every 15 minutes.
a. What is the unit rate in miles per hour for each runner?
Terrance: ____________ mi per hour
Jesse: ____________ mi per hour
Answer:
Find the unit rates for each runner by dividing the number of miles by the number of hours. Remember that 15 minutes is 1/4 of an hour since there are 60 minutes in an hour
15 ÷ 60 = 1/4
a) Terrance: 6 ÷ 1/2 = 6 × 2 = 12 miles per hour.
Jesse: 2 ÷ 1/4 = 2 × 4 = 8 miles per hour.
Question 12.
b. How long will each person take to run a total of 50 miles at the given rates?
Terrance: ______ \(\frac{□}{□}\)
Jesse: ______ \(\frac{□}{□}\)
Answer:
Divide the number of miles by the unit rates found in part a to find the time.
Terrance: 50 ÷ 12 = 50/12 = 4 \(\frac{1}{6}\) hours
Jesse: 50 ÷ 8 = 50/8 = 6 \(\frac{1}{4}\) hours
Question 12.
c. Sandra runs at a rate of 8 miles in 45 minutes. How does her unit rate compare to Terrance’s and to Jesse’s?
______ \(\frac{□}{□}\) mi per hour
Answer:
We need to find the unit rate for Sandra by dividing the number of miles by the number of hours.
Remember that 45 minutes is 3/4 of an hour.
Since 45/60 = 3/4.
Sandra’s unit rate is smaller than Terrance’s but larger than Jesse’s.
Unit Rates – Page No. 122
Question 13.
Analyze Relationships
Eli takes a typing test and types all 300 words in \(\frac{1}{10}\) hour. He takes the test a second time and types the words in \(\frac{1}{12}\) hour. Was he faster or slower on the second attempt? Explain.
____________
Answer:
We need to find the unit rates for each time he took the test.
1st time: 300 ÷ 1/10 = 300 × 10 = 3000
2nd time: 300 ÷ 1/12 = 300 × 12 = 3600
The second time has a faster unit rate since 3600 > 3000.
Question 14.
Justify Reasoning
An online retailer sells two packages of protein bars.

a. Which package has the better price per bar?
____________
Answer:
Find the unit rates per bar by dividing the costs by the number of bars. the 12 pack has the better price per bar.
10-pack: 15.37 ÷ 10 = 1.537 ≈ 1.54
12-pack: 15.35 ÷ 12 ≈ 1.30
Question 14.
b. Which package has the better price per ounce?
____________
Answer:
First, find the total number of ounces by multiplying the number of bars times the number of ounces per bar. then find the unit rates per ounce by dividing the costs by the total number of ounces the 10-pack has the better price per ounce.
10-pack: 10 × 2.1 = 21 ounces
12-pack: 12 × 1.4 = 16.8 ounces
10-pack: 15.37 ÷ 21 ≈ 0.73
12-pack: 15.35 ÷ 16.8 ≈ 0.91
Question 14.
c. Which package do you think is a better buy? Justify your reasoning.
____________
Answer:
The 10-pack is a better deal since the price per ounce is a better measure to use than price per bar. The number of bars doesn’t tell you how you are actually buying since the bars can be very small meaning the number of ounces you are actually buying is small.
Question 15.
Check for Reasonableness
A painter painted about half a room in half a day. Coley estimated the painter would paint 7 rooms in 7 days. Is Coley’s estimate reasonable? Explain.
____________
Answer:
If a painter can paint half a room in a half day, then he can paint 1 room in 1 day.
This would be equivalent to painting 7 rooms in 7 days so his estimate is reasonable.
7 rooms ÷ 7 days = 1/2 room ÷ 1/2 days
Question 16.
Communicate Mathematical
Ideas If you know the rate of a water leak in gallons per hour, how can you find the number of hours it takes for 1 gallon to leak out? Justify your answer.
Type below:
____________
Answer: If you know the rate in gallons per hour, then the rate in hours per gallon is the reciprocal of the rate in gallons per hour.
Example:
If water is leaking at a rate of 5 gallons per hour, then it is leaking at 1/5 hour per gallon.
Constant Rates of Change – Guided Practice – Page No. 126
Question 1.
Based on the information in the table, is the relationship between time and the number of words typed a proportional relationship?

The relationship ____________ proportional
Answer: is proportional
Explanation:
Since 45 ÷ 1 = 45, 90 ÷ 2 = 45, 135 ÷ 3 = 45 and 180 ÷ 4 = 45, the relationship is proportional.
Thus the relationship for the above table is proportional.
Find the constant of proportionality k. Then write an equation for the relationship between x and y.
Question 2.

k = _______
Answer: 5
Explanation:
The equation is of the form y = kx so k = y/x.
Substituting values of x and y from the table gives k = 10/2 = 5.
Plugging this value into y = kx gives the equation y = 5x.
The relationship between x and y is y = 5x.
Question 3.

k = \(\frac{□}{□}\)
Answer: k = \(\frac{1}{4}\)
Explanation:
The equation is of the form y = kx so k = y/x.
Substituting values of x and y from the table gives k = 2/8 = \(\frac{1}{4}\).
Plugging this value into y = kx gives the equation y = \(\frac{1}{4}\)x.
Essential Question Check-In
Question 4.
How can you represent a proportional relationship using an equation?
Type below:
____________
Answer: y = kx
Explanation:
A proportional relationship can always be represented by an equation of the form y = kx
where ks is the constant of proportionality and represents the rate of the change in the y quantity in relation to the x quantity.
Constant Rates of Change – Page No. 127
Information on three car-rental companies is given.
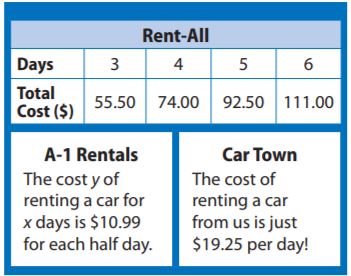
Question 5.
Write an equation that gives the cost y of renting a car for x days from Rent-All.
y = _______ x
Answer: 18.50
Explanation:
Find the constant of proportionality by dividing the total costs by the number of days.
k = 55.50/3 = 18.50
The equation is y = 18.50x
Question 6.
What is the cost per day of renting a car from A-1?
$ _______ per day
Answer: $21.98
Explanation:
Since the cost of each half day is $10.99, the cost for each day is 2 × 10.99 = 21.98
The cost per day of renting a car from A-1 is $21.98
Question 7.
Analyze Relationships
Which company offers the best deal? Why?
The company that offers the best deal is ____________
Answer: Rent all
Explanation:
The costs per day were $18.50 for Rent-All, $21.98 for A-1 Rentals, and $19.25 for Car Town so Reant All offers the best deal since it offers the lowest cost per day.
Thus the company that offers the best deal is Rent-All.
Question 8.
Critique Reasoning
A skydiver jumps out of an airplane. After 0.8 second, she has fallen 100 feet. After 3.1 seconds, she has fallen 500 feet. Emtiaz says that the skydiver should fall about 187.5 feet in 1.5 seconds. Is his answer reasonable? Explain.
_______
Answer: No. He assumed the rate of descent was proportional but the rate is increasing as time increases.
Explanation:
Since 100 ÷ 0.8 = 125 the skydiver fell at a speed of 125 ft per second for the first 0.8 second.
Since 500 ÷ 3.1 = 161, the skydiver fell at a speed of about 161 ft per second for the first 3.1 seconds.
The rate of descent is then increased as time increases and is not proportional since 125 ≠ 161.
Since 187.5 ÷ 1.5 = 125, he assumed the rate of descent was proportional. His estimate is then not reasonable. The actual rate of descent should be between 125 and 161.3 since 1.5 seconds is between 0.8 and 3.1 seconds.
Steven earns extra money babysitting. He charges $31.25 for 5 hours and $50 for 8 hours.
Question 9.
Explain why the relationship between how much Steven charges and time is a proportional relationship.
Type below:
____________
Answer: The relationship is proportional since the ratios are equal.
Explanation:
Since 31.25 ÷ 5 = 6.25 and 50 ≈ 8 = 6.25 the relationship is proportional since the ratios are equal.
Question 10.
Interpret the Answer
Explain what the constant rate of change means in the context.
Type below:
____________
Answer: The rate of change means he charges $6.25.
Explanation:
The constant rate of change of 6.25 means he charges $6.25 per hour since the rate was found by dividing the charge by the number of hours.
The rate of change means he charges $6.25.
Question 11.
Write an equation to represent the relationship. Tell what the variables represent.
Type below:
____________
Answer: The equation is y = 6.25x
where x is the number of hours and ys is the total charge.
Explanation:
The rate of change is 6.25 so k = 6.25.
This gives an equation of y = 6.25x where x is the number of hours and y is the total charge.
Question 12.
How much would Steven charge for 3 hours?
$ _______
Answer: $18.75
Explanation:
y = 6.25 × 3 = 18.75
Thus Steve charges $18.75 for 3 hours.
Constant Rates of Change – Page No. 128
A submarine dives 300 feet every 2 minutes, and 6,750 feet every 45 minutes.
Question 13.
Find the constant rate at which the submarine dives. Give your answer in feet per minute and in feet per hour.
____________ feet per minute
____________ feet per hour
Answer: 150 feet per minute, 9000 feet per hour
Explanation:
Since 300 ÷ 2 = 150, the submarine is diving at 150 feet per minute.
Since 45 minutes = 3/4 of an hour and 6750 ÷ 3/4 = 9000, the submarine is diving at a rate of 9000 feet per hour.
Question 14.
Let x represent the time of the dive. Let y represent the depth of the submarine. Write an equation for the proportional relationship using the rate in feet per minute.
Type below:
____________
Answer: y = 150x
Explanation:
The submarine was diving at a rate of 150 feet per minute so k = 150.
The equation is then y = 150x.
Question 15.
Draw Conclusions
If you wanted to find the depth of a submarine during a dive, would it be more reasonable to use an equation with the rate in feet per minute or feet per hour? Explain your reasoning.
____________
Answer: Feet per minute
Explanation:
Since a submarine would only dive for a few minutes at a time and not dive for hours at a time, it is more reasonable to use the rate in feet per minute.
H.O.T.
Focus on Higher Order Thinking
Question 16.
Make a Conjecture
There is a proportional relationship between your distance from a thunderstorm and the time from when you see lightning and hear thunder. If there are 9 seconds between lightning and thunder, the storm is about 3 kilometers away. If you double the amount of time between lightning and thunder, do you think the distance in kilometers also double? justify your reasoning.
_______
Answer: Yes the distance will also double. If the relationship is proportional then distance/time = k
where k is the constant of proportionality.
Since the time was 9 seconds for 3km, then for 18 seconds the distance would be 6 km since 3/9 = 6/18.
6 is double 3 so the distance doubles when the time doubles.
Question 17.
Communicate Mathematical Ideas
A store sells 3 ears of corn for $1. They round prices to the nearest cent as shown in the table. Tell whether you would describe the relationship between cost and number of ears of corn as a proportional relationship. Justify your answer.

_______
Answer:
Since 0.33 ÷ 1 = 0.33, 0.67 ÷ 2 = 0.335, 1.00 ÷ 3 = 0.33.., 1.34 ÷ 4 = 0.335, the relationship is approximately proportional since all the ratios are approximately equal. The difference in the ratios com from rounding the amount charged to the nearest cent.
Question 18.
Jack is 12 and his sister Sophia is 16. Jack says that the relationship between his age and Sophia’s age is proportional and the constant of proportionality is \(\frac{12}{16}\) Do you agree? Explain.
____________
Answer:
Given that current age of Jack = 12 years
Given that current age of Sophia = 16 years
Jack says that the relationship between his age and Sophia‘s is proportional
If Jack’s age is represented by y and Sophia’s age by x then we can write y=kx as they are in proportion
where k is called constant of proportion
Now let’s plug given ages of each that is y=12 and x=16 into y=kx to find the constant of proportionality
12=k×16
12/16=k
Which is the same as the given value of the constant of proportionality?
Hence Jack is right about his statement.
But if you think about practical life situation then the age of both will not be in proportion
For example, after 1 year Jack’s age will be 13 and Sophie’s age will be 17
then constant of proportionality using new values will be 13/17
Clearly 12/16 and 13/17 are not same.
So in practical life, the age of both will not in proportion.
Question 19.
Luke’s turkey chili recipe calls for 1.5 pounds of ground turkey for every 6 servings. How many servings can he make if he has 5 pounds of ground turkey? Show your work.
____________ servings
Answer: 20 servings
Explanation:
Given,
Luke’s turkey chili recipe calls for 1.5 pounds of ground turkey for every 6 servings.
So if 1.5 pounds of turkey can get you 6 servings
1.5 = 6
3 = 12
4.5 = 18
5 =?
to find what 5 pounds are equal to we must do 1.5/6 to find the unit rate of 0.25. We then add 0.25 to 18.25 servings or if you round you can get about 18 servings.
18 + 0.25 × 8 = 18 + 2 = 20
Proportional Relationships and Graphs – Guided Practice – Page No. 132
Complete each table. Tell whether the relationship is a proportional relationship. Explain why or why not.
Question 1.
A student reads 65 pages per hour.
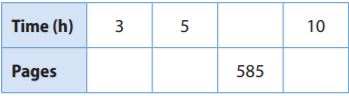
____________
Answer:
Given that,
A student reads 65 pages per hour.
3 hours: 3 × 65 = 195 pages
5 hours: 5 × 65 = 325 pages
10 hours: 10 × 65 = 650 pages
We need to find the number of hours for 585 pages by dividing the number of pages by 65 since the students read 65 pages per hour:
585 pages: 585 ÷ 65 = 9 hours
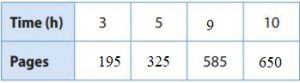
A relationship is proportional if the quotient of each ordered pair is constant. Since the student is reading at a constant rate of 65 pages per hour, and the quotient of each ordered pair in the table is 65, the relationship is proportional.
Question 2.
A babysitter makes $7.50 per hour.
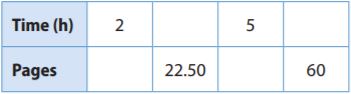
____________
Answer:
2 hours = 2 × 7.50 = 15
22.50 = 22.50 ÷ 7.50 = 3 hours
5 hours = 5 × 7.50 = 37.50
6. = 60 ÷ 7.50 = 8 hours
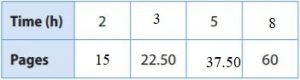
Tell whether the relationship is a proportional relationship. Explain why or why not.
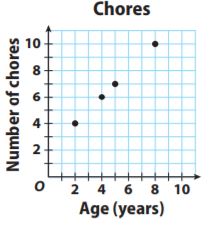
Question 3.
____________
Answer:
The relationship has the points (2, 4) and (8, 10).
Since 4 ÷ 2 = 2 and 10 ÷ 8 = 1.25, the relationship is not proportional since the ratios are not equal.
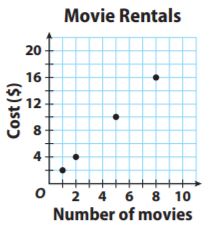
Question 4.
____________
Answer:
The relationship appears to be proportional since the points appear to form a line that goes through the origin. That line would go through the points (1,2), (2, 4), (5, 10), and (8, 16).
Since 2 ÷ 1 = 2, 4 ÷ 2 = 2, 10 ÷ 5 = 2, and 16 ÷ 8 = 2, the relationship is proportional since all the ratios are equal.
Write an equation of the form y = kx for the relationship shown in each graph.
Question 5.
y = ____________ x
Answer: y = 3.5x
Explanation:
One of the points is (8, 28) so k = 28/8 = 7/2. The equation is the y = 7/2 = 3.5x
Question 6.
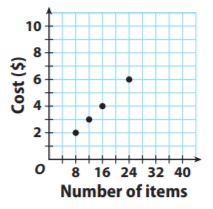
y = ____________ x
Answer: y = 0.25x
Explanation:
One of the points is (8,2) so k = 2/8 = 1/4.
The equation is the ya = 1/4x = 0.25 x.
Essential Question Check-In
Question 7.
How does a graph show a proportional relationship?
Type below:
____________
Answer:
A proportional relationship between two variables, x and y, exists if y = kx.
This equation is a line that passes through the origin and has a slope of k. The slope can be positive or negative. Therefore is the points lie on a line that goes through the origin, the graph shows a proportional relationship. If the points lie on a line that does not go through the origin, that is, has a non zero y-intercept, then the relationship is not proportional.
Proportional Relationships and Graphs – Guided Practice – Page No. 133
For Exercises 8–12, the graph shows the relationship between time and distance run by two horses.
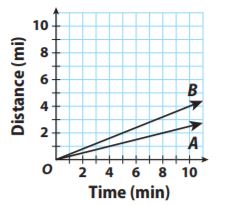
Question 8.
Explain the meaning of the point (0,0).
Type below:
____________
Answer: The point (0, 0) represents a distance of 0 miles in 0 min.
Question 9.
How long does it take each horse to run a mile?
Horse A runs 1 mile in ____________ minutes
Horse B runs 1 mile in ____________ minutes
Answer: Horse A: 4 min per mile.
Horse B: 2.5 min per mile
Explanation:
Line A goes through the point (8, 2) which gives a rate of 8/2 = 4 min per mile. Line B goes through the point (10, 4) which gives a rate of 10/4 = 2.5 min per mile.
Question 10.
Multiple Representations
Write an equation for the relationship between time and distance for each horse.
For Horse A : y = ____________ x
For Horse B : y = ____________ x
Answer: A: y = 1/4x, B: y = 2/5x
Explanation:
The graph has x representing the time in minutes and y representing the distance in miles so the slope of the line has units of miles per minute.
Since horse A runs 4 min per mile, it runs at a rate of 1/4 mi per min.
This gives the equation y = 1/4x.
Since horse B runs at a rate of 2.5 min per mi, it runs at a rate of 1/2.5 = 2/5 miles per min.
The equation is then y = 2/5x.
Question 11.
Draw Conclusions
At the given rates, how far would each horse run in 12 minutes?
Horse A will run ____________ miles
Horse B will run ____________ miles
Answer: Horse A will run 3 miles.
Horse B will run 4.8 miles.
Explanation:
Multiply the rates in mi per min from the above problem by the number of minutes.
A: 1/4 mi per min × 12 min = 3 miles
B: 2/5 mi per min × 12 min = 4.8 miles
Question 12.
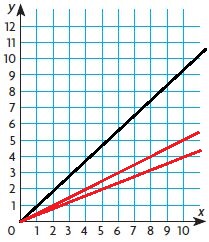
Analyze Relationships
Draw a line on the graph representing a horse than runs faster than horses A and B.
Type below:
____________
Answer:
To have a line representing at the rate of the horse faster than horses A and B, the line should be a little bit steeper than the other two lines. This can be represented in the graph as:
Question 13.
A bullet train can travel at 170 miles per hour. Will a graph representing the distance in miles compared to the time in hours show a proportional relationship? Explain.
____________
Answer: Yes
Since the train is travelling at a constant rate, a graph representing distance in miles compared to time in hours will show a proportional relationship.
Question 14.
Critical Thinking
When would it be more useful to represent a proportional relationship with a graph rather than an equation?
Type below:
____________
Answer: It is more useful to represent a proportional relationship with a graph when comparing different and various situations.
Question 15.
Multiple Representations
Bargain DVDs cost $5 each at Mega Movie.
a. Graph the proportional relationship that gives the cost y in dollars of buying x bargain DVDs.
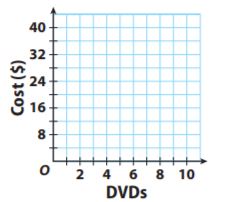
Type below:
____________
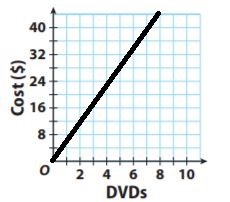
Answer:
Since each DVD is $5 each, make sure to graph a line that corresponds to this rate.
Question 15.
b. Give an ordered pair on the graph and explain its meaning in the real world context.
Type below:
____________
Answer: An ordered pair in the graph is (3, 15) and this means that three DVDs cost $15.
Proportional Relationships and Graphs – Page No. 134
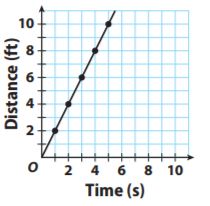
The graph shows the relationship between distance and time as Glenda swims.
Question 16.
How far did Glenda swim in 4 seconds?
______ feet
Answer: 8 ft
Explanation:
The graph goes through the point (4, 8) so she swam 8 ft in 4 sec.
Question 17.
Communicate Mathematical Ideas
Is this a proportional relationship? Explain your reasoning.
____________
Answer: The relationship is proportional since the points lie on a line and the line connecting the points goes through the origin.
Question 18.
Multiple Representations
Write an equation that shows the relationship between time and distance.
Type below:
____________
Answer: y = 2x
Explanation:
The line goes through the point (4, 8) which means k = 8/4 = 2.
This give an equation of y = 2x.
H.O.T.
Focus on Higher Order Thinking
Question 19.
Make a Conjecture
If you know that a relationship is proportional and are given one ordered pair that is not (0,0), how can you find another pair?
Type below:
____________
Answer:
If you are given a point (a, b) that is not (0, 0) and that the relationship is proportional, then you can find k since k = y/x = b/a.
Then you can write the equation as y = b/ax. From there, you can plug in any value for x to find the corresponding y-coordinate.
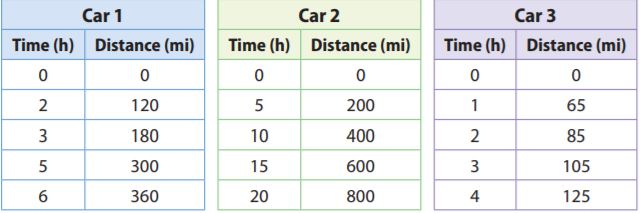
The tables show the distance traveled by three cars.
Question 20.
Communicate Mathematical Ideas
Which car is not traveling at a constant speed? Explain your reasoning.
____________
Answer:
Since 120 ÷ 2 = 180 ÷ 3 = 300 ÷ 5 = 360 ÷ 6 = 60, Car 1 is travelling at a constant speed.
Since 200 ÷ 5 = 400 ÷ 10 = 600 ÷ 15 = 800 ÷ 20 = 40, Car 2 is travelling at a constant speed.
Since 65 ÷ 1 ≠ 85 ÷ 2, Car 3 is not traveling at a constant speed.
Question 21.
Make a Conjecture
Car 4 is traveling at twice the rate of speed of car 2. How will the table values for car 4 compare to the table values for car 2?
Type below:
____________
Answer:
From problem 20, car 2 is traveling at 40 miles per hour. If car 4 is traveling twice that rate, then it is traveling at 80 miles per hour. This means all the values for the distances for car 4 will be double the values for the distances for car 2.
MODULE QUIZ – 4.1 Unit Rates – Page No. 135
Find each unit rate. Round to the nearest hundredth, if necessary.
Question 1.
$140 for 18 ft2
$ ______
Answer: $7.78 per ft2
Explanation:
Divide the cost of $140 by the number of square feet, 18 sq. ft, using a calculator:
140 ÷ 18 ≈ $7.78 per sq. ft.
If you are required by your teacher to do the division by hand, divide to three decimal points as shown below:
Since the dollar amounts must be rounded to two decimal places, then $7.77.. ≈ $7.78 so the cost per square foot is $7.78 sq. ft.
Question 1.
14 lb for $2.99
$ ______
Answer: $0.21 per lb
Explanation:
Divide the cost by the number of pounds.
2.99 ÷ 14 = $0.21
Circle the better deal in each pair. Then give the unit rate for the better deal.
Question 3.
\(\frac{\$ 56}{25 \text { gal }} or \frac{\$ 32.05}{15 \text { gal }}\)
____________
Answer:
Better deal: $32.05/15 gal
Unit rate: $2.14 per gal
Explanation:
Find the unit rates by dividing the cost by the number of gallons:
$56/25 gal = $2.24 per gal
$32.05/15 gal ≈ $2.14 per gal
Since 2.14 < 2.24, then the better deal is $32.25/15 gal.
Question 4.
\(\frac{\$ 160}{5 \mathrm{g}} \text { or } \frac{\$ 315}{9 \mathrm{g}}\)
____________
Answer:
Better deal: $160/5g
Unit rate: $32 per gram
Explanation:
Find the unit rates by dividing the cost by the number of grams:
$160/5 g = $32 per gram
$315/9 g = $35 per gram
Since 32 < 35, then the better deal is $160/5 g.
4.2 Constant Rates of Change
Question 5.
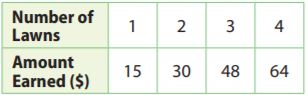
The table shows the amount of money Tyler earns for mowing lawns. Is the relationship a proportional relationship? Why or why not?
____________
Answer: not proportional
Explanation:
Since 15 ÷ 1 = 15 but 48 ÷ 3 = 16, the relationship is not proportional.
Question 6.
On a recent day, 8 euros were worth $9 and 24 euros were worth $27. Write an equation of the form y = kx to show the relationship between the number of euros and the value in dollars.
Type below:
____________
Answer: y = \(\frac{9}{8}\)x
Explanation:
k = \(\frac{value in dollars}{number of euros}\) = \(\frac{9}{8}\)
so, the equation is y = \(\frac{9}{8}\)x
4.3 Proportional Relationships and Graphs
Question 7.
The graph shows the number of servings in different amounts of frozen yogurt listed on a carton. Write an equation that gives the number of servings y in x pints.
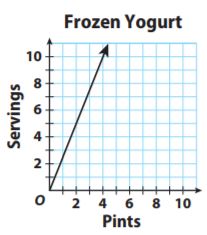
Type below:
____________
Answer: y = \(\frac{5}{2}\)x
Explanation:
The graph goes through the point (2, 5) so k = \(\frac{5}{2}\).
This gives an equation of y = \(\frac{5}{2}\)x
Question 8.
A refreshment stand makes 2 large servings of frozen yogurt from 3 pints. Add the line to the graph and write its equation.
Type below:
____________
Answer: y = \(\frac{2}{3}\)x
Explanation:
If the situation states that 2 servings of frozen yogurt can be made from 3 pints, then we can say that k = \(\frac{2}{3}\), and therefore the equation of the line is y = \(\frac{2}{3}\)x. The graph of the line is shown below.
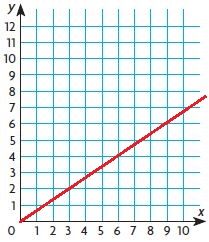
Essential Question
Question 9.
How can you use rates to determine whether a situation is a proportional relationship?
Type below:
____________
Answer: If the rate is constant, then the situation is a proportional relationship. If the rate is not constant, the situation cannot be a proportional relationship.
MIXED REVIEW – Selected Response – Page No. 136
Question 1.
Kori spent $46.20 on 12 gallons of gasoline. What was the price per gallon?
Options:
a. $8.35
b. $3.85
c. $2.59
d. $0.26
Answer: $3.85
Explanation:
Given that,
Kori spent $46.20 on 12 gallons of gasoline.
Divide the cost by the number of gallons to find the price per gallon.
46.20/12 = 3.85
Thus the correct answer is option B.
Question 2.
A rabbit can run short distances at a rate of 35 miles per hour. A fox can run short distances at a rate of 21 miles per half hour. Which animal is faster, and by how much?
Options:
a. The rabbit; 7 miles per hour
b. The fox; 7 miles per hour
c. The rabbit; 14 miles per hour
d. The fox; 14 miles per hour
Answer: The fox; 7 miles per hour
Explanation:
Given that,
A rabbit can run short distances at a rate of 35 miles per hour. A fox can run short distances at a rate of 21 miles per half hour.
If a fox runs 21 miles for half an hour then it can 42 miles per hour.
42 – 35 = 7 miles per hour
The fox is faster by 7 miles per hour.
Therefore the correct answer is option B.
Question 3.
A pet survey found that the ratio of dogs to cats is 25. Which proportion shows the number of dogs if the number of cats is 140?
Options:
a. \(\frac{2 \mathrm{dogs}}{5 \mathrm{cats}}=\frac{140 \mathrm{dogs}}{350 \mathrm{cats}}\)
b. \(\frac{2 \mathrm{dogs}}{5 \mathrm{cats}}=\frac{140 \mathrm{cats}}{350 \mathrm{dogs}}\)
c. \(\frac{2 \mathrm{dogs}}{5 \mathrm{cats}}=\frac{28 \mathrm{dogs}}{140 \mathrm{cats}}\)
d. \(\frac{2 \mathrm{dogs}}{5 \mathrm{cats}}=\frac{56 \mathrm{dogs}}{140 \mathrm{cats}}\)
Answer: \(\frac{2 \mathrm{dogs}}{5 \mathrm{cats}}=\frac{56 \mathrm{dogs}}{140 \mathrm{cats}}\)
Explanation:
Given,
A pet survey found that the ratio of dogs to cats is 25.
Since 5 × 25 = 140 and
2 × 28 = 56
= 56/140
Thus the correct answer is option D.
Question 4.
What is the cost of 2 kilograms of flour if 3 kilograms cost $4.86 and the unit price for each package of flour is the same?
Options:
a. $0.81
b. $2.86
c. $3.24
d. $9.72
Answer: $3.24
Explanation:
We need to find the unit price.
4.86/3 = 1.62
multiply the unit price by 2 to find the cost of 2 kg
1.62 × 2 = 3.24
Therefore the correct answer is option C.
Question 5.
One gallon of paint covers about 450 square feet. How many square feet will 1.5 gallons of paint cover?
Options:
a. 300ft2
b. 451.5ft2
c. 675ft2
d. 900ft2
Answer: 675ft2
Explanation:
Given,
One gallon of paint covers about 450 square feet.
We need to find how many square feet will 1.5 gallons of paint cover.
For that, we have to multiply the number of gallons by the number of square feet covered by each gallon.
1.5 × 450 = 675 sq. ft.
Thus the correct answer is option C.
Question 6.
The graph shows the relationship between the late fines the library charges and the number of days late.
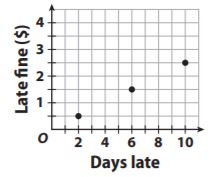
Options:
a. y = 0.25x
b. y = 0.40x
c. y = 0.50x
d. y = 0.75x
Answer: y = 0.25x
Explanation:
The graph shows the relationship between the late fines the library charges and the number of days late
One of the points is (2, 0.5) so k = 0.5/2 = 0.25.
This gives an equation of y = 0.25x
Thus the correct answer is option A.
Mini-Task
Question 7.
School is 2 miles from home along a straight road. The table shows your distance from home as you walk home at a constant rate.
a. Is the relationship in the table proportional?
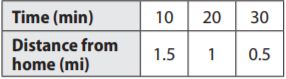
___________
Answer: no
Since 1.5/10 = 0.15 and 1/20 = 0.05, the relationship is not proportional since the ratios are not equal.
Question 7.
b. Find your distance from school for each time in the table.
Type below:
___________
Answer: Since the distance between school and home is 2 mi, the distance from school when the distance from home is 1.5 mi is 2 – 1.5 = 0.5 mi, for 1 mi its 2 – 1 = 1 mi, and for 0.5 mi its 2 – 0.5 = 1.5 mi.
Question 7.
c. Write an equation representing the relationship between the distance from school and time walking.
Type below:
___________
Answer: y = -0.05 x + 2
Explanation:
At time t = 0, you are 2 mi from home since the distance from home to school is 2 mi. This means the y-intercept, b is 2.
To find the slope of the line, find the rate of change:
m = (y2 – y1)/(x2 – x1) = (1 – 1.5)/(20 – 10) = -0.5/10 = -0.05
The line is then y = mx + b
y = 0.5x + 2.
Module 4 – Page No. 161
EXERCISES
Question 1.
Steve uses \(\frac{8}{9}\) gallon of paint to paint 4 identical birdhouses. How many gallons of paint does he use for each birdhouse?
\(\frac{□}{□}\)
Answer: \(\frac{2}{9}\) gallons
Explanation:
Given that,
Steve uses \(\frac{8}{9}\) gallon of paint to paint 4 identical birdhouses.
Divide the number of gallons by the number of birdhouses.
\(\frac{8}{9}\) ÷ 4 = \(\frac{8}{9}\) × \(\frac{1}{4}\)
= \(\frac{2}{9}\) gallons
Thus Steve uses \(\frac{2}{9}\) gallons of paint for each birdhouse.
Question 2.
Ron walks 0.5 mile on the track in 10 minutes. Stevie walks 0.25 mile on the track in 6 minutes. Find the unit rate for each walker in miles per hour. Who is the faster walker?
Ron: ___________ miles per hour
Stevie: ___________ miles per hour
___________ is the faster walker.
Answer: Ron
Explanation:
Given,
Ron walks 0.5 miles on the track in 10 minutes.
Stevie walks 0.25 miles on the track in 6 minutes.
We can find each unit rate by dividing the number of miles by the number of minutes then multiply by 60 to get the number of miles per hour.
Ron: 0.5 ÷ 10 = 0.05 miles = 3 miles per hour
Stevie: 0.25/6 = 1/24 mi per min = 2.5 mi per hour
Question 3.
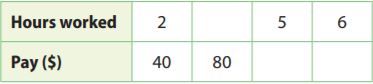
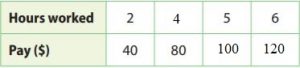
The table below shows the proportional relationship between Juan’s pay and the hours he works. Complete the table. Plot the data and connect the points with a line.
Type below:
____________
Answer:
First, find the constant of proportionality.
Let y represents pay and x represents the number of hours worked.
The constant of proportionality = y/x = 40/2 = 20
Hence, for 1 hour of work, he earns $20.
To find how many hours he needs to work $80, we divide 80 by the constant of proportionality.
80/20 = 4
For 1 hour he earns $20, so for 5 hours he earns 5 × 20 = $100.
For 1 hour he earns $20, so for 6 hours he earns 6 × 20 = $120.
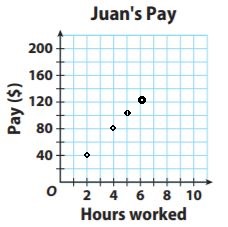
Conclusion:
After the preparation of Go Math Grade 7 Answer Key Chapter 4 Rates and Proportionality, we suggest the students solve the questions given in the Module Quiz. Test yourself by solving the questions given at the end of this chapter. By this, you can enhance your math skills and secure good marks in the exams. If you have any doubts regarding the solutions you can post your comment in the below comment section.
