In Geometry Topics, the most commonly solved topic is Rotations. A Rotation is a circular motion of any figure or object around an axis or a center. If we talk about the real-life examples, then the known example of rotation for every person is the Earth, it rotates on its own axis. However, Rotations can work in both directions ie., Clockwise and Anticlockwise or Counterclockwise. 90° and 180° are the most common rotation angles whereas 270° turns about the origin occasionally.
Here, in this article, we are going to discuss the 90 Degree Clockwise Rotation like definition, rule, how it works, and some solved examples. So, Let’s get into this article!
90 Degree Clockwise Rotation
If a point is rotating 90 degrees clockwise about the origin our point M(x,y) becomes M'(y,-x). In short, switch x and y and make x negative.
| Before Rotation | After Rotation |
| (x, y) | (y,-x) |
Rule of 90 Degree Rotation about the Origin
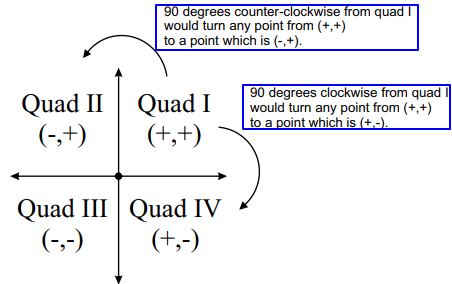
- When the object is rotating towards 90° clockwise then the given point will change from (x,y) to (y,-x).
- When the object is rotating towards 90° anticlockwise then the given point will change from (x,y) to (-y,x).
Solved Examples:
Example 1:
Solve the given coordinates of the points obtained on rotating the point through a 90° clockwise direction?
(i) A (4, 7)
(ii) B (-8, -9)
(iii) C (-2, 8)
Solution:
When the point rotated through 90º about the origin in the clockwise direction, then the new place of the above coordinates are as follows:
(i) The current position of point A (4, 7) will change into A’ (7, -4)
(ii) The current position of point B (-8, -9) will change into B’ (-9, 8)
(iii) The current position of point C (-2, 8) will change into C’ (8, 2)
Example 2:
Let P (-6, 3), Q (9, 6), R (2, 7) S (3, 8) be the vertices of a closed figure. If this figure is rotated 90° about the origin in a clockwise direction, find the vertices of the rotated figure.
Solution:
Given vertices are P (-6, 3), Q (9, 6), R (2, 7) S (3, 8)
Now, we will solve this closed figure when it rotates in a 90° clockwise direction,
In step 1, we have to apply the rule of 90 Degree Clockwise Rotation about the Origin
(x, y) → (-y, x)
Next, find the new position of the points of the rotated figure by using the rule in step 1.
(x, y) → (y, -x)
P (-6, 3) → P'(3, 6)
Q (9, 6) → Q’ (6, -9)
R (2, 7) → R'(7, -2)
S (3, 8) → S'(8, -3)
Finally, the Vertices of the rotated figure are P'(3, 6), Q’ (6, -9), R'(7, -2), S'(8, -3).
Example 3:
Find the new position of the given coordinates A(-5,6), B(3,7), and C(2,1) after rotating 90 degrees clockwise about the origin?
Solution:
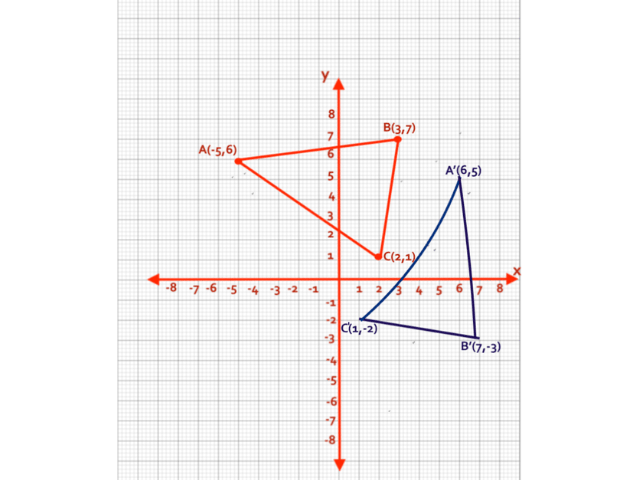
Given Coordinates are A(-5,6), B(3,7), and C(2,1)
The rule/formula for 90 degree clockwise rotation is (x, y) —> (y, -x).
After applying this rule for all coordinates, it changes into new coordinates and the result is as follows:
A(-5,6) –> A'(6,5)
B(3,7) –> B'(7,-3)
C(2,1) –> C'(1,-2)
I believe that the above graph clears all your doubts regarding the 90 degrees rotation about the origin in a clockwise direction. At last, the result of the coordinates is A'(6,5), B'(7,-3), C'(1,-2).
FAQs on 90 Degree Clockwise Rotation
1. Is a 90 Degree rotation clockwise or counterclockwise?
Considering that the rotation is 90 Degree, you should rotate the point in a clockwise direction.
2. What are the types of rotation?
You can see the rotation in two ways ie., clockwise or counterclockwise. In case, there is an object which is rotating that can rotate in different ways as shown below:
- 90 degrees counterclockwise
- 90 degrees clockwise
- 180 degrees counterclockwise
- 180 degrees clockwise
3. What is the rule of Rotation by 90° about the origin?
The rule for a rotation by 90° Counterclockwise about the origin is (x,y)→(−y,x)
The rule for a rotation by 90° Clockwise about the origin is (x,y)→(y,−x)