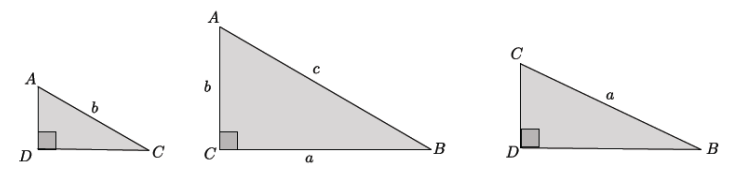
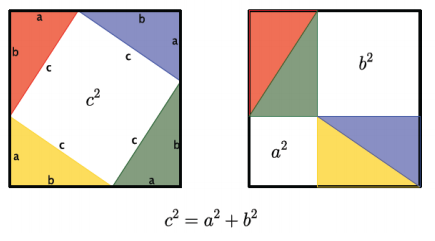
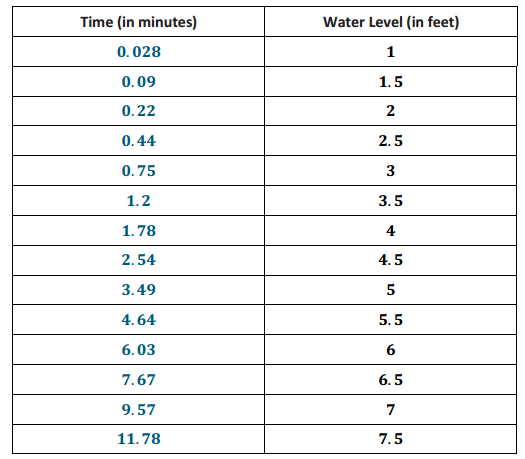
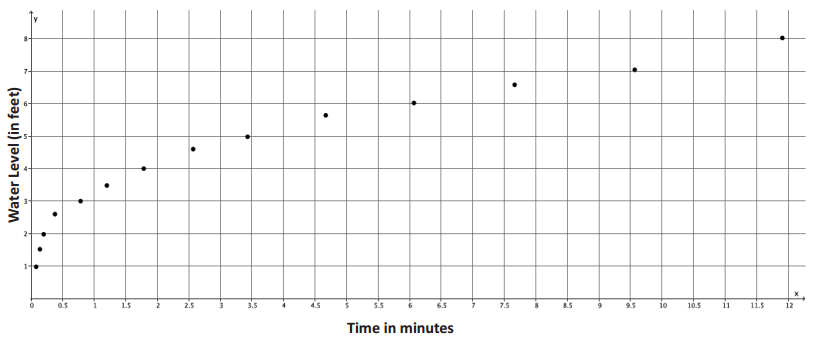
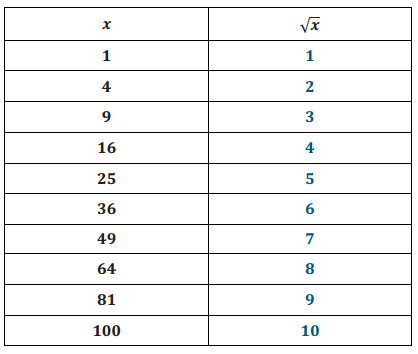
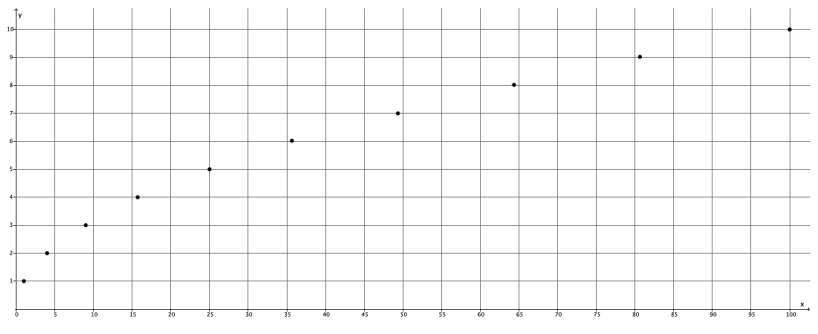
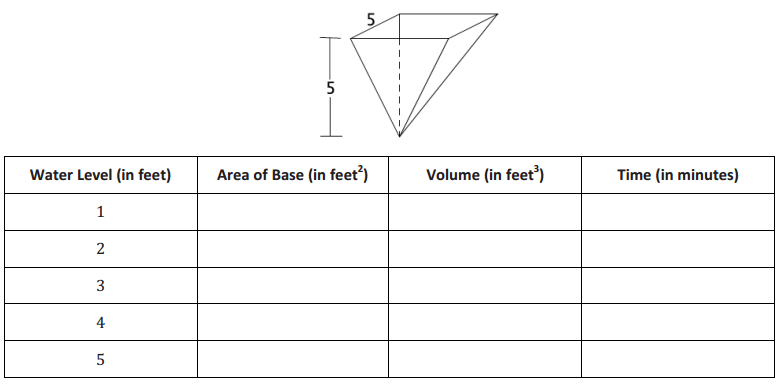
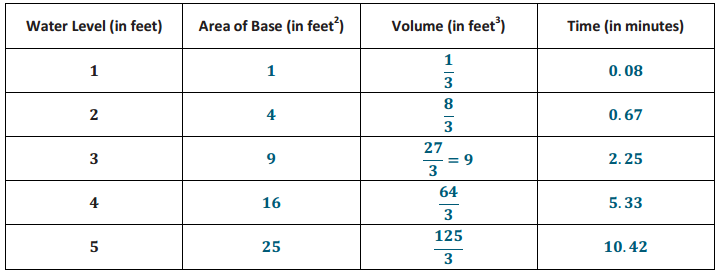
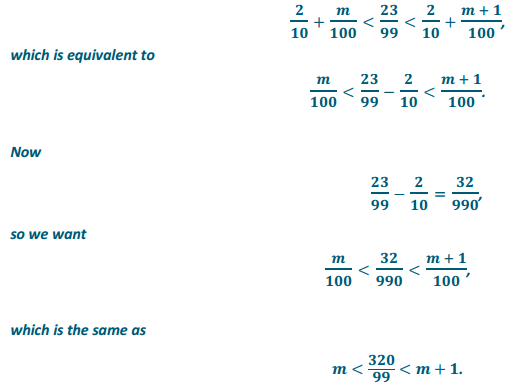Engage NY Eureka Math 8th Grade Module 7 Lesson 18 Answer Key
Eureka Math Grade 8 Module 7 Lesson 18 Exercise Answer Key
Exercises
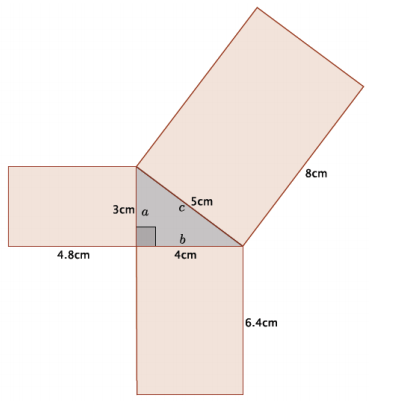
Exercise 1.
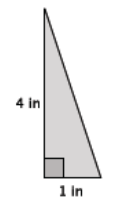
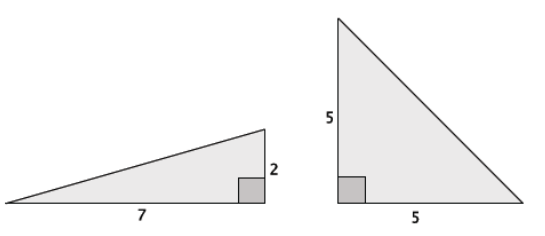
The area of the right triangle shown below is 26.46 in2. What is the perimeter of the right triangle? Round your answer to the tenths place.
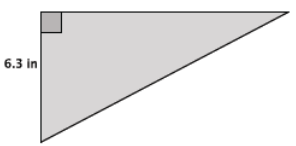
Answer:
Let b in. represent the length of the base of the triangle where
h = 6.3.
A = latex]\frac{bh}{2}[/latex]
26.46 = \(\frac{6.3b}{2}\)
52.92 = 6.3b
\(\frac{52.92}{6.3}\) = \(\frac{6.3b}{6.3}\)
8.4 = b
Let c in. represent the length of the hypotenuse.
6.32 + 8.42 = c2
39.69 + 70.56 = c2
110.25 = c2
\(\sqrt{110.25}\) = \(\sqrt{c^{2}}\)
\(\sqrt{11.025}\) = c
The number √(110.25) is between 10 and 11. When comparing with tenths, the number is actually equal to 10.5 because 10.52 = 110.25. Therefore, the length of the hypotenuse is 10.5 in. The perimeter of the triangle is 6.3 in. + 8.4 in. + 10.5 in. = 25.2 in.
Exercise 2.
The diagram below is a representation of a soccer goal.
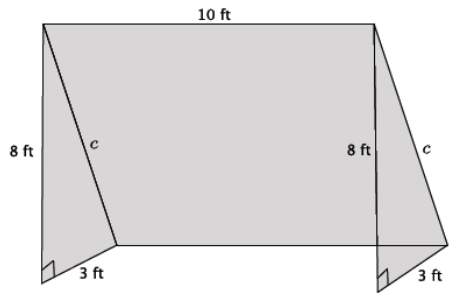
a. Determine the length of the bar, c, that would be needed to provide structure to the goal. Round your answer to the tenths place.
Answer:
Let c ft. represent the hypotenuse of the right triangle.
82 + 32 = c2
64 + 9 = c2
73 = c2
\(\sqrt{73}\) = \(\sqrt{c^{2}}\)
The number \(\sqrt{73}\) is between 8 and 9. In the sequence of tenths, it is between 8.5 and 8.6 because 8.52 < (\(\sqrt{73}\))2 < 8.62. In the sequence of hundredths, the number is between 8.54 and 8.55 because 8.542 < (\(\sqrt{73}\))2 < 8.552. Since the number \(\sqrt{73}\) is between 8.54 and 8.55, it would round to 8.5. The length of the bar that provides structure for the goal is approximately 8.5 ft.
b. How much netting (in square feet) is needed to cover the entire goal?
Answer:
The areas of the triangles are each 12 ft2. The area of the rectangle in the back is approximately 85 ft2. The total area of netting required to cover the goal is approximately 109 ft2.
Exercise 3.
The typical ratio of length to width that is used to produce televisions is 4:3.
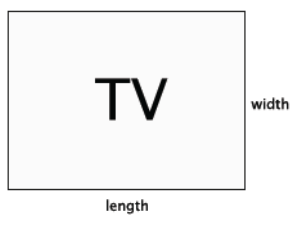
A TV with length 20 inches and width 15 inches, for example, has sides in a 4:3 ratio; as does any TV with length 4x inches and width 3x inches for any number x.
a. What is the advertised size of a TV with length 20 inches and width 15 inches?
Answer:
Let c in. be the length of the diagonal.
202 + 152 = c2
400 + 225 = c2
625 = c2
\(\sqrt{625}\) = \(\sqrt{c^{2}}\)
25 = c
Since the TV has a diagonal length of 25 inches, then it is a 25″ TV.
b. A 42″ TV was just given to your family. What are the length and width measurements of the TV?
Answer:
Let x be the factor applied to the ratio 4:3.
(3x)2 + (4x)2 = 422
9x2 + 16x2 = 1764
(9 + 16) x2 = 1764
25x2 = 1764
\(\frac{25 x^{2}}{25}\) = \(\frac{1764}{25}\)
x2 = 70.56
\(\sqrt{x^{2}}\) = \(\sqrt{70.56}\)
x = \(\sqrt{70.56}\)
The number \(\sqrt{70.56}\) is between 8 and 9. In working with the sequence of tenths, I realized the number \(\sqrt{70.56}\) is actually equal to 8.4 because 8.42 = 70.56. Therefore, x = 8.4, and the dimensions of the TV are (4 × 8.4) inches , which is 33.6 inches, and (3 × 8.4) inches, which is 25.2 inches.
c. Check that the dimensions you got in part (b) are correct using the Pythagorean theorem.
Answer:
33.62 + 25.22 = 422
1128.96 + 635.04 = 1764
1764 = 1764
d. The table that your TV currently rests on is 30″ in length. Will the new TV fit on the table? Explain.
Answer:
The dimension for the length of the TV is 33.6 inches. It will not fit on a table that is 30 inches in length.
Exercise 4.
Determine the distance between the following pairs of points. Round your answer to the tenths place. Use graph paper if necessary.
a. (7,4) and ( – 3, – 2)
Answer:
Let c represent the distance between the two points.
102 + 62 = c2
100 + 36 = c2
136 = c2
\(\sqrt{136}\) = \(\sqrt{c^{2}}\)
\(\sqrt{136}\) = c
The number \(\sqrt{136}\) is between 11 and 12. In the sequence of tenths, it is between 11.6 and 11.7 because 11.62 < (\(\sqrt{136}\))2 < 11.72. In the sequence of hundredths, it is between 11.66 and 11.67, which means the number will round in tenths to 11.7. The distance between the two points is approximately 11.7 units.
b. ( – 5,2) and (3,6)
Answer:
Let c represent the distance between the two points.
82 + 42 = c2
64 + 16 = c2
80 = c2
\(\sqrt{80}\) = \(\sqrt{c^{2}}\)
\(\sqrt{80}\) = c
The number \(\sqrt{80}\) is between 8 and 9. In the sequence of tenths, it is between 8.9 and 9 because
8.92 < (\(\sqrt{80}\))2 < 92. In the sequence of hundredths, it is between 8.94 and 8.95, which means it will round to 8.9. The distance between the two points is approximately 8.9 units.
c. Challenge: (x1,y1) and (x2,y2). Explain your answer.
Answer:
Note: Deriving the distance formula using the Pythagorean theorem is not part of the standard but does present an interesting challenge to students. Assign it only to students who need a challenge.
Let c represent the distance between the two points.
(x1 – x2 )2 + (y1 – y2 )2 = c2
\(\sqrt{\left(x_{1} – x_{2}\right)^{2} + \left(y_{1} – y_{2}\right)^{2}}\) = \(\sqrt{c^{2}}\)
\(\sqrt{\left(x_{1} – x_{2}\right)^{2} + \left(y_{1} – y_{2}\right)^{2}}\) = c
I noticed that the dimensions of the right triangle were equal to the difference in x – values and the difference in y – values. Using those expressions and what I knew about solving radical equations, I was able to determine the length of c.
Exercise 5.
What length of ladder is needed to reach a height of 7 feet along the wall when the base of the ladder is 4 feet from the wall? Round your answer to the tenths place.
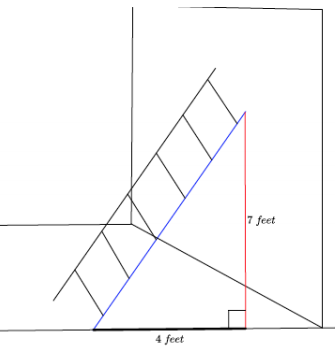
Answer:
Let c feet represent the length of the ladder.
72 + 42 = c2
49 + 16 = c2
65 = c2
\(\sqrt{65}\) = \(\sqrt{c^{2}}\)
\(\sqrt{65}\) = c
The number \(\sqrt{65}\) is between 8 and 9. In the sequence of tenths, it is between 8 and 8.1 because 82 < (\(\sqrt{65}\))2 < 8.12. In the sequence of hundredths, it is between 8.06 and 8.07, which means the number will round to 8.1. The ladder must be approximately 8.1 feet long to reach 7 feet up a wall when placed 4 feet from the wall.
Eureka Math Grade 8 Module 7 Lesson 18 Problem Set Answer Key
Question 1.
A 70″ TV is advertised on sale at a local store. What are the length and width of the television?
Answer:
The TV is in the ratio of 4:3 and has measurements of 4x:3x, where x is the scale factor of enlargement.
(3x)2 + (4x)2 = 702
9x2 + 16x2 = 4,900
25x2 = 4,900
\(\frac{25 x^{2}}{25}\) = \(\frac{4,900}{25}\)
x2 = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = 14
The length of the TV is (4 × 14) inches, which is 56 inches, and the width is (3 × 14) inches, which is 42 inches.
Question 2.
There are two paths that one can use to go from Sarah’s house to James’ house. One way is to take C Street, and the other way requires you to use A Street and B Street. How much shorter is the direct path along C Street?
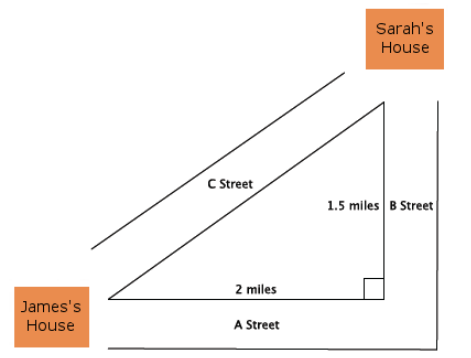
Answer:
Let c miles represent the length of the hypotenuse of the right triangle.
22 + 1.52 = c2
4 + 2.25 = c2
6.25 = c2
\(\sqrt{6.225}\) = \(\sqrt{c^{2}}\)
2.5 = c
The path using A Street and B Street is 3.5 miles. The path along C Street is 2.5 miles. The path along C Street is exactly 1 mile shorter than the path along A Street and B Street.
Question 3.
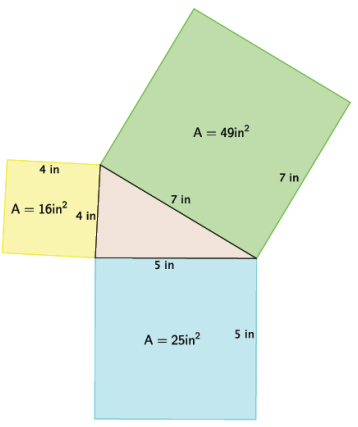
An isosceles right triangle refers to a right triangle with equal leg lengths, s, as shown below.
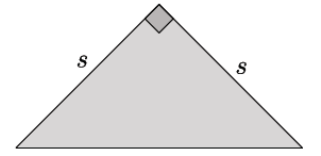
What is the length of the hypotenuse of an isosceles right triangle with a leg length of 9 cm? Write an exact answer using a square root and an approximate answer rounded to the tenths place.
Answer:
Let c be the length of the hypotenuse of the isosceles triangle in centimeters.
92 + 92 = c2
81 + 81 = c2
162 = c2
\(\sqrt{162}\) = \(\sqrt{c^{2}}\)
\(\sqrt{81 \times 2}\) = c
\(\sqrt{81}\) × \(\sqrt{2}\) = c
9\(\sqrt{2}\) = c
The number \(\sqrt{2}\) is between 1 and 2. In the sequence of tenths, it is between 1.4 and 1.5 because 1.42 < (\(\sqrt{2}\))2 < 1.52. Since the number 2 is closer to 1.42 than 1.52, it would round to 1.4. 9 × 1.4 = 12.6.
So, 12.6 cm is the approximate length of the hypotenuse, and 9\(\sqrt{2}\) cm is the exact length.
Question 4.
The area of the right triangle shown to the right is 66.5 cm2.
a. What is the height of the triangle?
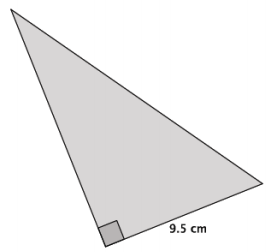
Answer:
A = \(\frac{bh}{2}\)
66.5 = \(\frac{9.5h}{2}\)
133 = 9.5h
\(\frac{133}{9.5}\) = \(\frac{9.5h}{9.5}\)
14 = h
The height of the triangle is 14 cm.
b. What is the perimeter of the right triangle? Round your answer to the tenths place.
Answer:
Let c represent the length of the hypotenuse in centimeters.
9.52 + 142 = c2
90.25 + 196 = c2
286.25 = c2
\(\sqrt{286.25}\) = \(\sqrt{c^{2}}\)
\(\sqrt{286.25}\) = c
The number \(\sqrt{286.25}\) is between 16 and 17. In the sequence of tenths, the number is between 16.9 and 17 because 16.92 < (\(\sqrt{286.25}\))2 < 172. Since 286.25 is closer to 16.92 than 172, then the approximate length of the hypotenuse is 16.9 cm.
The perimeter of the triangle is 9.5 cm + 14 cm + 16.9 cm = 40.4 cm.
Question 5.
What is the distance between points (1,9) and ( – 4, – 1)? Round your answer to the tenths place.
Answer:
Let c represent the distance between the points.
102 + 52 = c2
100 + 25 = c2
125 = c2
\(\sqrt{125}\) = \(\sqrt{c^{2}}\)
\(\sqrt{125}\) = c
11.2 ≈ c
The distance between the points is approximately 11.2 units.
Question 6.
An equilateral triangle is shown below. Determine the area of the triangle. Round your answer to the tenths place.
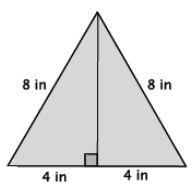
Answer:
Let h in. represent the height of the triangle.
42 + h2 = 82
16 + h2 = 64
h2 = 48
\(\sqrt{h^{2}}\) = \(\sqrt{48}\)
h = \(\sqrt{48}\)
h ≈ 6.9
A = \(\frac{(8)(6.9)}{2}\) = (4)(6.9) = 27.6
The area of the triangle is approximately 27.6 in2.
Eureka Math Grade 8 Module 7 Lesson 18 Exit Ticket Answer Key
Use the diagram of the equilateral triangle shown below to answer the following questions. Show the work that leads to your answers.
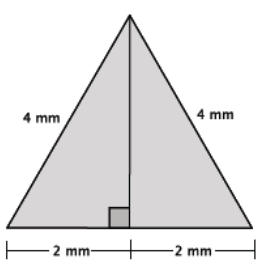
a. What is the perimeter of the triangle?
Answer:
4 + 4 + 4 = 12
The perimeter is 12 mm.
b. What is the height, h mm, of the equilateral triangle? Write an exact answer using a square root and an approximate answer rounded to the tenths place.
Answer:
Using the fact that the height is one leg length of a right triangle, and I know the hypotenuse is 4 mm and the other leg length is 2 mm, I can use the Pythagorean theorem to find h.
22 + h2 = 42
4 + h2 = 16
4 – 4 + h2 = 16 – 4
h2 = 12
h = \(\sqrt{12}\)
h = \(\sqrt{4 \times 3}\)
h = \(\sqrt{4}\) × \(\sqrt{3}\)
h = 2\(\sqrt{3}\)
The number \(\sqrt{3}\) is between 1 and 2. In the sequence of tenths, it is between 1.7 and 1.8 because
1.72 < (\(\sqrt{3}\))2 < 1.82. In the sequence of hundredths, it is between 1.73 and 1.74. This would put h between 2 × 1.73 mm, which is 3.46 mm, and 2 × 1.74 mm, which is 3.48 mm. In terms of tenths, the approximate height is 3.5 mm. The exact height is \(\sqrt{12}\) mm, or 2\(\sqrt{3}\) mm.
c. Using the approximate height found in part (b), estimate the area of the equilateral triangle
Answer:
A = \(\frac{bh}{2}\)
A = \(\frac{4(3.5)}{2}\)
A = \(\frac{14}{2}\)
A = 7
The approximate area of the equilateral triangle is 7 mm2.
Eureka Math Grade 8 Module 7 Lesson 18 Area and Volume II Answer Key
Question 1.
Find the area of the square shown below.
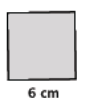
Answer:
A = (6 cm)2
= 36 cm2
Question 2.
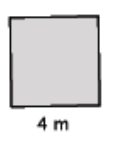
Find the volume of the cube shown below.
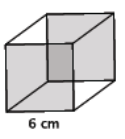
Answer:
V = (6 cm)3
= 216 cm3
Question 3.
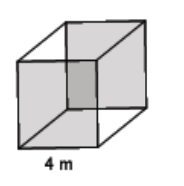
Find the area of the rectangle shown below.
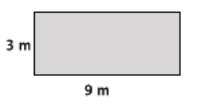
Answer:
A = (9 m)(3 m)
= 27 m2
Question 4.
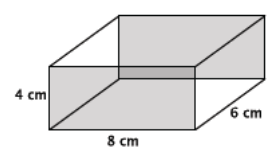
Find the volume of the rectangular prism shown below.
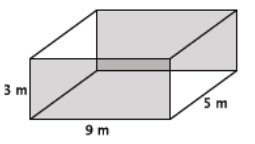
Answer:
V = (27 m2)(5 m)
= 135 m3
Question 5.
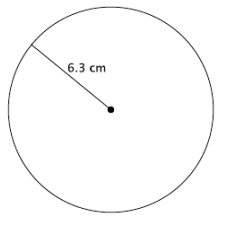
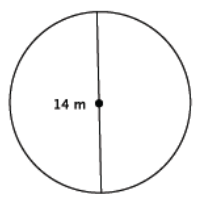
Find the area of the circle shown below.
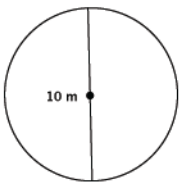
Answer:
A = (5 m)2 π
= 25π m2
Question 6.
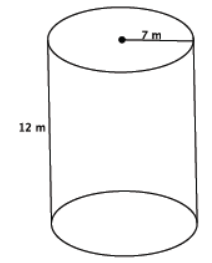
Find the volume of the cylinder shown below.
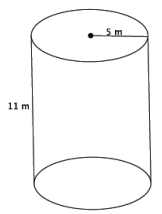
Answer:
V = (25π m2 )(11 m)
= 275π m3
Question 7.
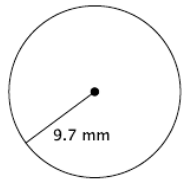
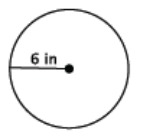
Find the area of the circle shown below.
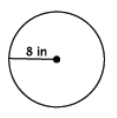
Answer:
A = (8 in.)2 π
= 64π in2
Question 8.
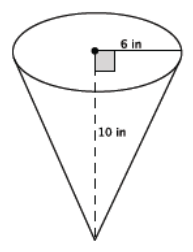
Find the volume of the cone shown below.
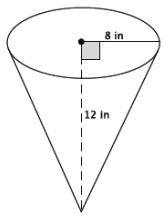
Answer:
V = (\(\frac{1}{3}\))(64π in2)(12 in.)
= 256π in3
Question 9.
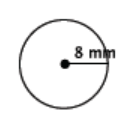
Find the area of the circle shown below.
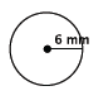
Answer:
A = (6 mm)2 π
= 36π mm2
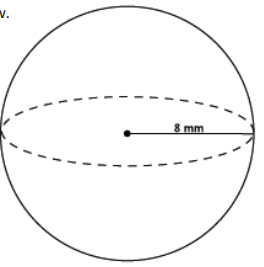
Question 10.
Find the volume of the sphere shown below.
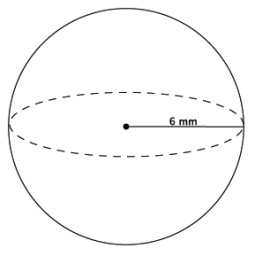
Answer:
V = (\(\frac{4}{3}\))π(6 mm)3
= \(\frac{864 \mathrm{~mm}^{3}}{3}\) π
= 288π mm3