Prasanna

Engage NY Eureka Math 8th Grade Module 7 Lesson 7 Answer Key

Eureka Math Grade 8 Module 7 Lesson 7 Example Answer Key

Example 1.
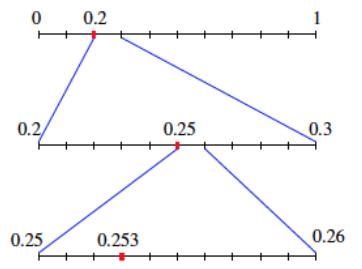
The number 0.253 is represented on the number line below.

Answer:
How can we locate the number 0.253 = \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) on the number line?
We can see that 0.253 is a tad larger than 0.2 and is smaller than 0.3. So if we divide the line segment from 0 to 1 into tenths, 0.253 lies somewhere in the segment between 0.2 and 0.3.

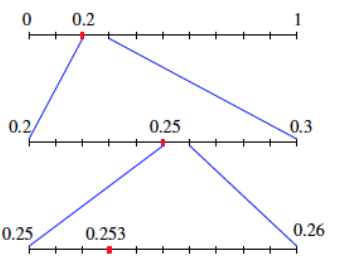
Now divide this segment into ten equal parts. (Those parts are hundredths of the original unit length.) We know that 0.253 is larger than 0.25 but smaller than 0.26, and so lies in the segment between these two values.

Now divide this small segment into tenths again. (We are now dealing with thousandths of the original unit length.) We can now see where exactly to pin 0.253 on the number line.

Writing 0.253 in its expanded decimal form of \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) illustrates this process:
The first decimal digit of 0.253 is 0.2, or \(\frac{2}{10}\), and this tells us within which tenth we are to place 0.253.
The first two decimal digits of 0.253 are 0.25 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) , or \(\frac{25}{10^{2}}\), and this tells us within which hundredth we are to place 0.253.

The first three decimal digits of 0.253 are 0.253 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) + \(\frac{3}{10^{3}}\), or \(\frac{253}{10^{3}}\), and this tells us within which thousandth we are to place 0.253. And since the decimal terminates here, we are done.
Have the students explain this process again in their own words, referring to the number line diagram as they do so.

How do you think this process would change if we tried to locate an infinite decimal on the number line?
The sequence for an infinite decimal would never end; it would go on infinitely.
We need to introduce some notation. If a decimal has a repeating pattern, as for 0.3333… or 7.45454545…, for instance, then a horizontal bar is used to indicate that a block of digits is being repeated. For example, 0.3333… is written as \(0 . \overline{3}\) and 7.45454545… as \(7 . \overline{45}\). It is conceivable that an infinite decimal could have no repeating pattern.

Example 2.
The number \(\frac{5}{6}\), which is equal to 0.833333…, or \(0 . \overline{83}\) is partially represented on the number line below.

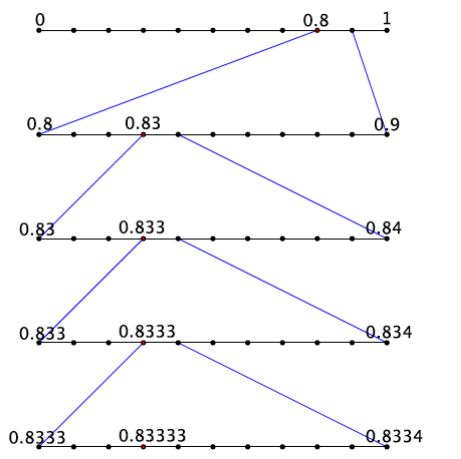
Answer:
Now, consider the equality \(\frac{5}{6}\) = 0.833333″…” = \(0 . \overline{83}\). Notice that at the second step, the work feels as though it repeats, which coincides with the fact that the decimal digit of 3 repeats.

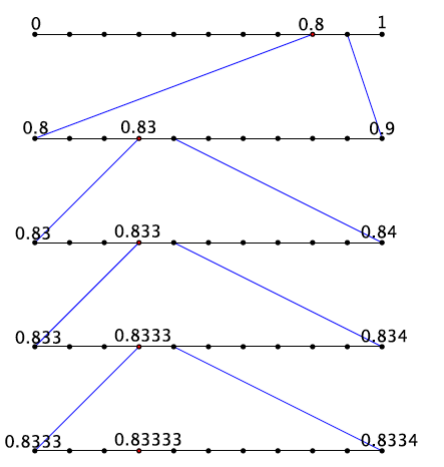
What is the expanded form of the decimal 0.833333…?
0.833333″…” = \(\frac{8}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\) + …………
We see again that at the second step the work begins to repeat.
Each step can be represented by increasing powers of 10 in the denominator: \(\frac{8}{10}, \frac{83}{10^{2}}, \frac{833}{10^{3}}, \frac{8333}{10^{4}}, \frac{83333}{10^{5}}, \frac{833333}{10^{6}}\), and so on. When will it end? Explain.
It will never end because the decimal is infinite.

As we step through this process we are pinning the exact location of 0.8333… into smaller and smaller intervals, intervals with sizes shrinking to zero: an interval of a tenth, and then a hundredth, then a thousandth, and, if we kept going, an interval of size \(\frac{1}{10^{20}}\), and later on to an interval of size \(\frac{1}{10^{100}}\), and so on, supposedly forever!
Okay. Let’s now think deeply about 0.9999…. Where do we find this number on the number line?

Draw on the board a sequence of number-line segments akin to those in Example 2, and have students give instructions on how to pin down the location of 0.9999…. In which tenth does it lie? In which hundredth? In which thousandth? And so on. Ask: At any stage of this process is 0.9999… right at the number 1 on the number line?
No. We are always just to the left of 1.
Right. And that makes sense as 0.9 is smaller than 1, and 0.99 is smaller than 1, as are 0.999 and 0.9999. At every stage of the process we are just shy of the number 1.

Eureka Math Grade 8 Module 7 Lesson 7 Exercise Answer Key

Opening Exercise
a. Write the expanded form of the decimal 0.3765 using powers of 10.
Answer:
0.3765 = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{6}{10^{3}} + \frac{5}{10^{4}}\)

b. Write the expanded form of the decimal 0.3333333… using powers of 10.
Answer:
0.333333″…” = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\)

c. Have you ever wondered about the value of 0.99999…? Some people say this infinite decimal has a value of 1. Some disagree. What do you think?
Answer:
Answers will vary. Have a brief discussion with students about this exercise. The answer will be revisited in the discussion below.

Exercises 1–5

Exercise 1.
a. Write the expanded form of the decimal 0.125 using powers of 10.
Answer:
0.125 = \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)

b. Show on the number line the placement of the decimal 0.125.

Answer:

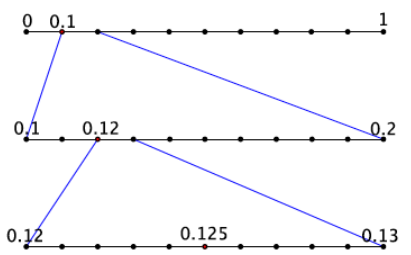
Exercise 2.
a. Write the expanded form of the decimal 0.3875 using powers of 10.
Answer:
0.3875 = \(\frac{3}{10} + \frac{8}{10^{2}} + \frac{7}{10^{3}} + \frac{5}{10^{4}}\)

b. Show on the number line the placement of the decimal 0.3875.

Answer:

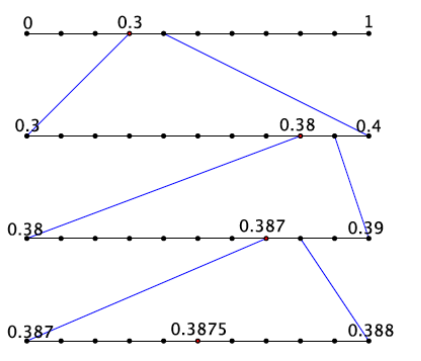
Exercise 3.
a. Write the expanded form of the decimal 0.777777… using powers of 10.
Answer:
0.777777… = \(\frac{7}{10} + \frac{7}{10^{2}} + \frac{7}{10^{3}} + \frac{7}{10^{4}} + \frac{7}{10^{5}} + \frac{7}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.777777… on the number line.

Answer:

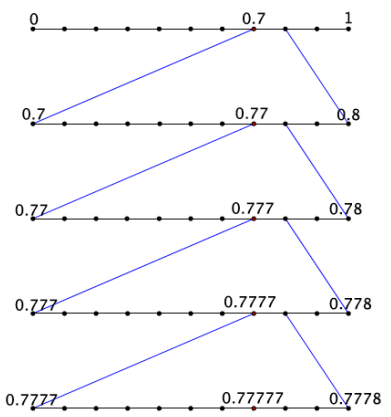
Exercise 4.
a. Write the expanded form of the decimal \(0 . \overline{45}\) using powers of 10.
Answer:
\(0 . \overline{45}\) = \(\frac{4}{10} + \frac{5}{10^{2}} + \frac{4}{10^{3}} + \frac{5}{10^{4}} + \frac{4}{10^{5}} + \frac{5}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal \(0 . \overline{45}\) on the number line.

Answer:

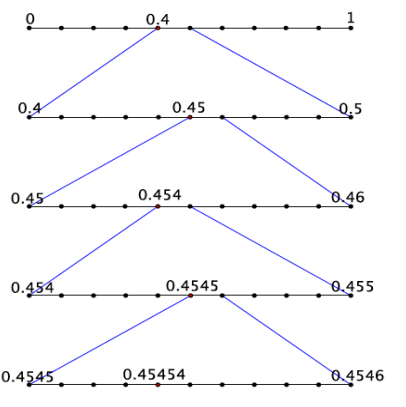
Exercise 5.
a. Order the following numbers from least to greatest: 2.121212, 2.1, 2.2, and \(2 . \overline{12}\).
Answer:
2.1, 2.121212, \(2 . \overline{12}\), and 2.2

b. Explain how you knew which order to put the numbers in.
Answer:
Each number is the sum of the whole number 2 and a decimal. When you write each number in this manner, you get the following expansions.
2.121212 = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}}\)
2.1 = 2 + \(\frac{1}{10}\)
2.2 = 2 + \(\frac{2}{10}\)
\(2 . \overline{12}\) = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}} + \frac{1}{10^{7}} + \frac{2}{10^{8}} + \cdots\)
In this form, it is clear that 2.1 is the least of the four numbers, followed by the finite decimal 2.121212, then the infinite decimal \(2 . \overline{12}\), and finally 2.2.

Eureka Math Grade 8 Module 7 Lesson 7 Problem Set Answer Key

Question 1.
a. Write the expanded form of the decimal 0.625 using powers of 10.
Answer:
0.625 = \(\frac{6}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)

b. Place the decimal 0.625 on the number line.

Answer:

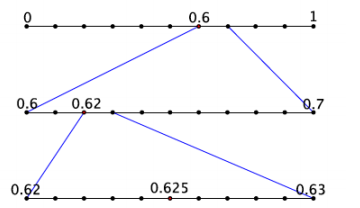
Question 2.
a. Write the expanded form of the decimal \(0 . \overline{370}\) using powers of 10.
Answer:
\(0 . \overline{370}\) = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{0}{10^{3}} + \frac{3}{10^{4}} + \frac{7}{10^{5}} + \frac{0}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.370370… on the number line.

Answer:

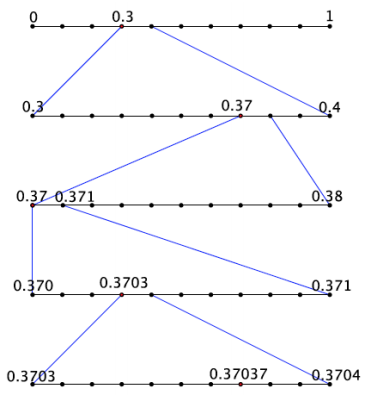
Question 3.
Which is a more accurate representation of the fraction \(\frac{2}{3}\): 0.6666 or \(0 . \overline{6}\)? Explain. Which would you prefer to compute with?
Answer:
The number \(\frac{2}{3}\) is more accurately represented by the decimal 0.6 ̅ compared to 0.6666. The long division algorithm with \(\frac{2}{3}\) shows that the digit 6 repeats. Then, the expanded form of the decimal \(0 . \overline{6}\) is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}} + \frac{6}{10^{5}} + \frac{6}{10^{6}} + \cdots\), and the expanded form of the decimal 0.6666 is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}}\). For this reason, \(0 . \overline{6}\) is precise, but 0.6666 is an approximation. For computations, I would prefer to use 0.6666. My answer would be less precise, but at least I would be able to compute with it. When attempting to compute with an infinite number, you would never finish writing it; thus, you could never compute with it.

Question 4.
Explain why we shorten infinite decimals to finite decimals to perform operations. Explain the effect of shortening an infinite decimal on our answers.
Answer:
We often shorten infinite decimals to finite decimals to perform operations because it would be impossible to represent an infinite decimal precisely since the sequence that describes infinite decimals has an infinite number of steps. Our answers are less precise; however, they are not that much less precise because with each additional digit we include in the sequence, we are adding a very small amount to the value of the number. The more decimals we include, the closer the value we add approaches zero. Therefore, it does not make that much of a difference with respect to our answer.

Question 5.
A classmate missed the discussion about why \(0 . \overline{9}\) = 1. Convince your classmate that this equality is true.
Answer:
Answers will vary. Accept any reasonable explanation. One is provided below.
Ask: Could there be any space between the locations of 0.9999… and 1 on the number line? We have that 0.9999… is larger than 0.9 and so is within one-tenth of 1 on the number line. We also have that 0.9999… is larger than 0.99 and so is within one-hundredth of 1 on the number line. And 0.9999… is larger than 0.999 and so is within one-thousandth of 1 on the number line, and so on. There can be no space between 0.9999… and 1 on the number line, as we can always argue that 0.9999… must be within any given distance from 1. Thus, 0.9999… and 1 must sit at the same location on the number line and so are the same number.

Question 6.
Explain why 0.3333 < 0.33333.
Answer:
0.3333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}}\), and 0.33333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}}\). That means that 0.33333 is exactly \(\frac{3}{10^{5}}\) larger than 0.3333. If we examined the numbers on the number line, 0.33333 is to the right of 0.3333, meaning that it is larger than 0.3333.

Eureka Math Grade 8 Module 7 Lesson 7 Exit Ticket Answer Key

Question 1.
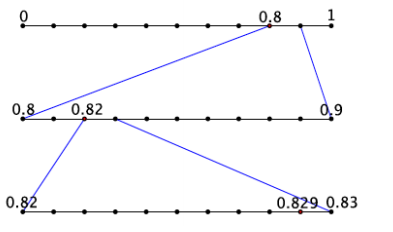
a. Write the expanded form of the decimal 0.829 using powers of 10.
Answer:
0.829 = \(\frac{8}{10} + \frac{2}{10^{2}} + \frac{9}{10^{3}}\)

b. Show the placement of the decimal 0.829 on the number line.

Answer:

Question 2.
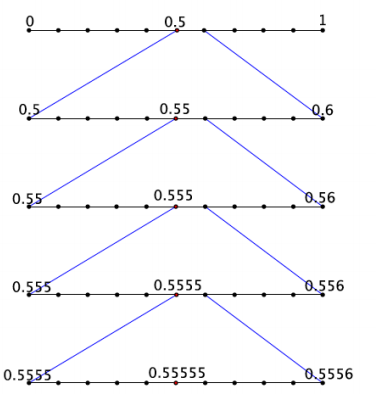
a. Write the expanded form of the decimal 0.55555… using powers of 10.
Answer:
0.55555″…” = \(\frac{5}{10} + \frac{5}{10^{2}} + \frac{5}{10^{3}} + \frac{5}{10^{4}} + \frac{5}{10^{5}} + \frac{5}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.555555… on the number line.

Answer:

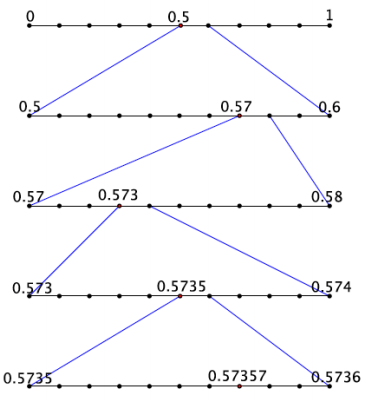
Question 3.
a. Write the expanded form of the decimal \(0 . \overline{573}\) using powers of 10.
Answer:
\(0 . \overline{573}\) = \(\frac{5}{10} + \frac{7}{10^{2}} + \frac{3}{10^{3}} + \frac{5}{10^{4}} + \frac{7}{10^{5}} + \frac{3}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal \(0 . \overline{573}\) on the number line.

Answer:

Engage NY Eureka Math 8th Grade Module 7 Lesson 5 Answer Key

Eureka Math Grade 8 Module 7 Lesson 5 Example Answer Key

Example 1.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
Answer:
Now that we know about square roots and cube roots, we can combine that knowledge with our knowledge of the properties of equality to begin solving nonlinear equations like x³ + 9x = \(\frac{1}{2}\) (18x + 54). Transform the equation until you can determine the positive value of x that makes the equation true.
Challenge students to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
x³ + 9x = 9x + 27
x³ + 9x – 9x = 9x – 9x + 27
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = \(\sqrt[3]{3^{3}}\)
x = 3
Now, we verify our solution is correct.
3³ + 9(3) = \(\frac{1}{2}\) (18(3) + 54)
27 + 27 = \(\frac{1}{2}\) (54 + 54)
54 = \(\frac{1}{2}\) (108)
54 = 54
Since the left side is the same as the right side, our solution is correct.

Example 2.
x(x – 3) – 51 = – 3x + 13
Answer:
Let’s look at another nonlinear equation. Find the positive value of x that makes the equation true: x(x – 3) – 51 = – 3x + 13.
Provide students with time to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
Sample response:
x(x – 3) – 51 = – 3x + 13
x² – 3x – 51 = – 3x + 13
x² – 3x + 3x – 51 = – 3x + 3x + 13
x² – 51 = 13
x² – 51 + 51 = 13 + 51
x² = 64
\(\sqrt{x^{2}}\) = ±\(\sqrt{64}\)
x = ±\(\sqrt{64}\)
x = ±8
Now we verify our solution is correct.
Provide students time to check their work.
Let x = 8.
8(8 – 3) – 51 = – 3(8) + 13
8(5) – 51 = – 24 + 13
40 – 51 = – 11
– 11 = – 11

Let x = – 8.
– 8( – 8 – 3) – 51 = – 3( – 8) + 13
– 8( – 11) – 51 = 24 + 13
88 – 51 = 37
37 = 37
Now it is clear that the left side is exactly the same as the right side, and our solution is correct.

Eureka Math Grade 8 Module 7 Lesson 5 Exercise Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Exercise 1.
a. Solve x² – 14 = 5x + 67 – 5x.
Answer:
x² – 14 = 5x + 67 – 5x
x² – 14 = 67
x² – 14 + 14 = 67 + 14
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±\(\sqrt{81}\)
x = ±9

Check:
9² – 14 = 5(9) + 67 – 5(9)
81 – 14 = 45 + 67 – 45
67 = 67

( – 9)² – 14 = 5( – 9) + 67 – 5( – 9)
81 – 14 = – 45 + 67 + 45
67 = 67

b. Explain how you solved the equation.
Answer:
To solve the equation, I had to first use the properties of equality to transform the equation into the form of x² = 81. Then, I had to take the square root of both sides of the equation to determine that x = 9 since the number x is being squared.

Exercise 2.
Solve and simplify: x(x – 1) = 121 – x.
Answer:
x(x – 1) = 121 – x
x² – x = 121 – x
x² – x + x = 121 – x + x
x² = 121
\(\sqrt{x^{2}}\) = ±\(\sqrt{121}\)
x = ±\(\sqrt{121}\)
x = ±11

Check:
11(11 – 1) = 121 – 11
11(10) = 110
110 = 110

– 11( – 11 – 1) = 121 – ( – 11)
– 11( – 12) = 121 + 11
132 = 132

Exercise 3.
A square has a side length of 3x inches and an area of 324 in². What is the value of x?
Answer:
(3x)² = 324
3² x² = 324
9x² = 324
\(\frac{9 x^{2}}{9}\) = \(\frac{324}{9}\)
x² = 36
\(\sqrt{x^{2}}\) = \(\sqrt{36}\)
x = 6

Check:
(3(6)) ² = 324
18² = 324
324 = 324
A negative number would not make sense as a length, so x = 6.

Exercise 4.
– 3x³ + 14 = – 67
Answer:
– 3x³ + 14 = – 67
– 3x³ + 14 – 14 = – 67 – 14
– 3x³ = – 81
\(\frac{ – 3 x^{3}}{3}\) = \(\frac{ – 81}{ – 3}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
– 3(3)³ + 14 = – 67
– 3(27) + 14 = – 67
– 81 + 14 = – 67
– 67 = – 67

Exercise 5.
x(x + 4) – 3 = 4(x + 19.5)
Answer:
x(x + 4) – 3 = 4(x + 19.5)
x² + 4x – 3 = 4x + 78
x² + 4x – 4x – 3 = 4x – 4x + 78
x² – 3 = 78
x² – 3 + 3 = 78 + 3
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±9

Check:
9(9 + 4) – 3 = 4(9 + 19.5)
9(13) – 3 = 4(28.5)
117 – 3 = 114
114 = 114

– 9( – 9 + 4) – 3 = 4( – 9 + 19.5)
– 9( – 5) – 3 = 4(10.5)
45 – 3 = 42
42 = 42

Exercise 6.
216 + x = x(x² – 5) + 6x
Answer:
216 + x = x(x² – 5) + 6x
216 + x = x³ – 5x + 6x
216 + x = x³ + x
216 + x – x = x³ + x – x
216 = x³
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{x^{3}}\)
6 = x

Check:
216 + 6 = 6(6² – 5) + 6(6)
222 = 6(31) + 36
222 = 186 + 36
222 = 222

Exercise 7.
a. What are we trying to determine in the diagram below?

Answer:
We need to determine the value of x so that its square root, multiplied by 4, satisfies the equation
5² + (4\(\sqrt{x}\))² = 11².

b. Determine the value of x, and check your answer.
Answer:
5² + (4\(\sqrt{x}\))² = 11²
25 + 4² (\(\sqrt{x}\))² = 121
25 – 25 + 4² (\(\sqrt{x}\))² = 121 – 25
16x = 96
\(\frac{16x}{16}\) = \(\frac{96}{16}\)
x = 6
The value of x is 6.

Check:
5² + (4\(\sqrt{6}\))² = 11²
25 + 16(6) = 121
25 + 96 = 121
121 = 121

Eureka Math Grade 8 Module 7 Lesson 5 Problem Set Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Question 1.
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
Answer:
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
x³ + 7x² = 7x² + 8
x³ + 7x² – 7x² = 7x² – 7x² + 8
x³ = 8
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 8 }\)
x = 2

Check:
2² (2 + 7) = \(\frac{1}{2}\) (14(2² ) + 16)
4(9) = \(\frac{1}{2}\) (56 + 16)
36 = \(\frac{1}{2}\) (72)
36 = 36

Question 2.
x³ = 1331 ^{– 1}
Answer:
x³ = 1331 ^{– 1}
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{1331^{ – 1}}\)
x = \(\sqrt[3]{\frac{1}{1331}}\)
x = \(\sqrt[3]{\frac{1}{11^{3}}}\)
x = \(\frac{1}{11}\)

Check:
(\(\left(\frac{1}{11}\right)^{3}\))³ = 1331 ^{– 1}
\(\frac{1}{11^{3}}\) = 1331 ^{– 1}
\(\frac{1}{1331}\) = 1331 ^{– 1}
1331 ^{– 1} = 1331 ^{– 1}

Question 3.
Determine the positive value of x that makes the equation true, and then explain how you solved the equation.
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
Answer:
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
x² – 49 = 0
x² – 49 + 49 = 0 + 49
x² = 49
\(\sqrt{x^{2}}\) = \(\sqrt{49}\)
x = 7

Check:
7² – 49 = 0
49 – 49 = 0
0 = 0
To solve the equation, I first had to simplify the expression \(\frac{x^{9}}{x^{7}}\) to x². Next, I used the properties of equality to transform the equation into x² = 49. Finally, I had to take the square root of both sides of the equation to solve for x.

Question 4.
Determine the positive value of x that makes the equation true.
(8x)² = 1
Answer:
(8x)² = 1
64x² = 1
\(\sqrt{64^{2}}\) = \(\sqrt{1}\)
8x = 1
\(\frac{8x}{8}\) = \(\frac{1}{8}\)
x = \(\frac{1}{8}\)

Check:
(8(\(\frac{1}{8}\)))² = 1
1² = 1
1 = 1

Question 5.
(9\(\sqrt{x}\))² – 43x = 76
Answer:
(9\(\sqrt{x}\))² – 43x = 76
9² (√x)² – 43x = 76
81x – 43x = 76
38x = 76
\(\frac{38x}{38}\) = \(\frac{76}{38}\)
x = 2

Check:
(9(\(\sqrt{2}\)))² – 43(2) = 76
9² (\(\sqrt{2}\))² – 86 = 76
81(2) – 86 = 76
162 – 86 = 76
76 = 76

Question 6.
Determine the length of the hypotenuse of the right triangle below.

Answer:
3² + 7² = x²
9 + 49 = x²
58 = x²
\(\sqrt{58}\) = \(\sqrt{x^{2}}\)
\(\sqrt{58}\) = x

Check:
3² + 7² = (\(\sqrt{52}\))²
9 + 49 = 58
58 = 58
Since x = \(\sqrt{58}\), the length of the hypotenuse is \(\sqrt{58}\) mm.

Question 7.
Determine the length of the legs in the right triangle below.

Answer:
x² + x² = (14\(\sqrt{2}\))²
2x² = 14² (\(\sqrt{2}\))²
2x² = 196(2)
\(\frac{2 x^{2}}{2}\) = \(\frac{196(2)}{2}\)
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = \(\sqrt{14^{2}}\)
x = 14

Check:
14² + 14² = (14\(\sqrt{2}\))²
196 + 196 = 14² (\(\sqrt{2}\))²
392 = 196(2)
392 = 392
Since x = 14, the length of each of the legs of the right triangle is 14 cm.

Question 8.
An equilateral triangle has side lengths of 6 cm. What is the height of the triangle? What is the area of the triangle?

Answer:
Note: This problem has two solutions, one with a simplified root and one without. Choose the appropriate solution for your classes based on how much simplifying you have taught them.
Let h cm represent the height of the triangle.
3² + h² = 6²
9 + h² = 36
9 – 9 + h² = 36 – 9
h² = 27
\(\sqrt{h^{2}}\) = \(\sqrt{27}\)
h = \(\sqrt{27}\)
h = \(\sqrt{3^{3}}\)
h = \(\sqrt{3^{2}}\)×\(\sqrt{3}\)
h = 3\(\sqrt{3}\)

Let A represent the area of the triangle.
A = \(\frac{6(3 \sqrt{3})}{2}\))
A = 3(3\(\sqrt{3}\))
A = 9\(\sqrt{3}\)
Simplified: The height of the triangle is 3\(\sqrt{3}\) cm, and the area is 9\(\sqrt{3}\) cm².
Unsimplified: The height of the triangle is \(\sqrt{27}\) cm, and the area is 3\(\sqrt{27}\) cm²

Question 9.
Challenge: Find the positive value of x that makes the equation true.
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
Answer:
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
\(\frac{1}{4}\) x² – 3x = – 3x + 8
\(\frac{1}{4}\) x² – 3x + 3x = – 3x + 3x + 8
\(\frac{1}{4}\) x² = 8
4(\(\frac{1}{4}\)) x² = 8(4)
x² = 32
\(\sqrt{x^{2}}\) = \(\sqrt{32}\)
x = \(\sqrt{2^{5}}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2}\)
x = 4\(\sqrt{2}\)

Check:
(\(\frac{1}{2}\) (4\(\sqrt{2}\)))² – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) + 8 – 10(4\(\sqrt{2}\))
\(\frac{1}{4}\) (16)(2) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
\(\frac{32}{4}\) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = (7 – 10)(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8
8 – 8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8 – 8
– 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\))

Question 10.
Challenge: Find the positive value of x that makes the equation true.
11x + x(x – 4) = 7(x + 9)
Answer:
11x + x(x – 4) = 7(x + 9)
11x + x² – 4x = 7x + 63
7x + x² = 7x + 63
7x – 7x + x² = 7x – 7x + 63
x² = 63
\(\sqrt{x^{2}}\)) = \(\sqrt{63}\)
x = \(\sqrt{\left(3^{2}\right)(7)}\)
x = \(\sqrt{3^{2}}\) ⋅ \(\sqrt{7}\)
x = 3\(\sqrt{7}\)

Check:
11(3\(\sqrt{7}\)) + 3\(\sqrt{7}\) (3\(\sqrt{7}\) – 4) = 7(3\(\sqrt{7}\) + 9)
33\(\sqrt{7}\) + 3² (\(\sqrt{7}\))² – 4(3\(\sqrt{7}\)) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 4(3\(\sqrt{7}\)) + 9(7) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 12\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
(33 – 12) \(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 – 63 = 21\(\sqrt{7}\) + 63 – 63
21\(\sqrt{7}\) = 21\(\sqrt{7}\)

Eureka Math Grade 8 Module 7 Lesson 5 Exit Ticket Answer Key

Question 1.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
x² + 4x = 4(x + 16)
Answer:
x² + 4x = 4(x + 16)
x² + 4x = 4x + 64
x² + 4x – 4x = 4x – 4x + 64
x² = 64
\(\sqrt{x^{2}}\) = \(\sqrt{64}\)
x = 8

Check:
8² + 4(8) = 4(8 + 16)
64 + 32 = 4(24)
96 = 96

Question 2.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
(4x)³ = 1728
Answer:
(4x)³ = 1728
64x³ = 1728
\(\frac{1}{64}\)(64x³) = (1728)\(\frac{1}{64}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
(4(3))³ = 1728
12³ = 1728
1728 = 1728

Engage NY Eureka Math 8th Grade Module 7 Lesson 4 Answer Key

Eureka Math Grade 8 Module 7 Lesson 4 Example Answer Key

Example 1.
Simplify the square root as much as possible.
\(\sqrt{50}\) =
Answer:
→ Is the number 50 a perfect square? Explain.
The number 50 is not a perfect square because there is no integer squared that equals 50.

→ Since 50 is not a perfect square, when we need to simplify \(\sqrt{50}\), we write the factors of the number 50 looking specifically for those that are perfect squares. What are the factors of 50?
50 = 2 × 5²
Since 50 = 2 × 5², then \(\sqrt{50}\) = \(\sqrt{2 \times 5^{2}}\). We can rewrite \(\sqrt{50}\) as a product of its factors:
\(\sqrt{50}\) = \(\sqrt{2}\) × \(\sqrt{5^{2}}\).

→ Obviously, 5² is a perfect square. Therefore, \(\sqrt{5^{2}}\) = 5, so \(\sqrt{50}\) = 5 × \(\sqrt{2}\) = 5\(\sqrt{2}\). Since \(\sqrt{2}\) is not a perfect square, we leave it as it is. We have simplified this expression as much as possible because there are no other perfect square factors remaining in the square root.

→ The number \(\sqrt{50}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 5\(\sqrt{2}\) is the simplified form of \(\sqrt{50}\).
Now that we know \(\sqrt{50}\) can be expressed as a product of its factors, we also know that we can multiply expressions containing square roots. For example, if we are given \(\sqrt{2}\) × \(\sqrt{5^{2}}\), we can rewrite the expression as √(2 × 5² ) = \(\sqrt{50}\).

Example 2.
Simplify the square root as much as possible.
\(\sqrt{28}\) =
Answer:
→ Is the number 28 a perfect square? Explain.
The number 28 is not a perfect square because there is no integer squared that equals 28.

→ What are the factors of 28?
28 = 2² × 7
Since 28 = 2² × 7, then \(\sqrt{28}\) = \(\sqrt{2^{2} \times 7}\). We can rewrite \(\sqrt{28}\) as a product of its factors:
\(\sqrt{28}\) = \(\sqrt{2^{2}}\) × \(\sqrt{7}\).

→ Obviously, 2² is a perfect square. Therefore, \(\sqrt{2^{2}}\) = 2, and \(\sqrt{28}\) = 2 × \(\sqrt{7}\) = 2\(\sqrt{7}\). Since \(\sqrt{7}\) is not a perfect square, we leave it as it is.

→ The number \(\sqrt{28}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 2\(\sqrt{7}\) is the simplified form of \(\sqrt{28}\).

Example 3.
Simplify the square root as much as possible.
\(\sqrt{128}\) =
Answer:
→ In this example, students may or may not recognize 128 as 64 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{128}\) = \(\sqrt{64 \times 2}\) = \(\sqrt{64}\) × \(\sqrt{2}\) = 8 × \(\sqrt{2}\) = 8\(\sqrt{2}\).

→ Is the number 128 a perfect square? Explain.
The number 128 is not a perfect square because there is no integer squared that equals 128.

→ What are the factors of 128?
128 = 2⁷
→ Since 128 = 2⁷, then \(\sqrt{128}\) = √(2⁷ ). We know that we can simplify perfect squares, so we can rewrite 2⁷ as 2² × 2² × 2² × 2 because of what we know about the laws of exponents. Then,
\(\sqrt{128}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\).
Each 2² is a perfect square. Therefore, \(\sqrt{128}\) = 2 × 2 × 2 × \(\sqrt{2}\) = 8\(\sqrt{2}\).

Example 4.
Simplify the square root as much as possible.
\(\sqrt{288}\) =
Answer:
In this example, students may or may not recognize 288 as 144 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{288}\) = \(\sqrt{144 \times 2}\) = \(\sqrt{144}\) × \(\sqrt{2}\) = 12 × \(\sqrt{2}\) = 12\(\sqrt{2}\).

→ Is the number 288 a perfect square? Explain.
The number 288 is not a perfect square because there is no integer squared that equals 288.
→ What are the factors of 288?
288 = 2⁵ × 3²
Since 288 = 2⁵ × 3², then \(\sqrt{288}\) = √(2⁵ × 3² ). What do we do next?
Use the laws of exponents to rewrite 2⁵ as 2² × 2² × 2.

→ Then, \(\sqrt{288}\) is equivalent to
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\).

→ What does this simplify to?
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\)) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) ) × \(\sqrt{2}\) = 2 × 2 × 3 × \(\sqrt{2}\) = 12\(\sqrt{2}\)

Eureka Math Grade 8 Module 7 Lesson 4 Exercise Answer Key

Opening Exercise
a.
i. What does \(\sqrt{16}\) equal?
Answer:
4

ii. What does 4 × 4 equal?
Answer:
16

iii. Does \(\sqrt{16}\) = \(\sqrt{4 \times 4}\)?
Answer:
Yes

b.
i. What does \(\sqrt{36}\) equal?
Answer:
6

ii. What does 6 × 6 equal?
Answer:
36

iii. Does \(\sqrt{36}\) = \(\sqrt{6 \times 6}\)?
Answer:
Yes

c.
i. What does \(\sqrt{121}\) equal?
Answer:
11

ii. What does 11 × 11 equal?
Answer:
121

iii. Does \(\sqrt{121}\) = \(\sqrt{11 \times 11}\)?
Yes

d.
i. What does \(\sqrt{81}\) equal?
Answer:
9

ii. What does 9 × 9 equal?
Answer:
81

iii. Does \(\sqrt{81}\) = \(\sqrt{9 \times 9}\)?
Answer:
Yes

e. Rewrite \(\sqrt{20}\) using at least one perfect square factor.
Answer:
\(\sqrt{20}\) = \(\sqrt{4 \times 5}\)

f. Rewrite \(\sqrt{28}\) using at least one perfect square factor.
Answer:
\(\sqrt{28}\) = \(\sqrt{4 \times 7}\)

Exercises 1–4
Simplify the square roots as much as possible.

Exercise 1.
\(\sqrt{18}\)
Answer:
\(\sqrt{18}\) = \(\sqrt{2 \times 3^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{2}\)

Exercise 2.
\(\sqrt{44}\)
Answer:
\(\sqrt{44}\) = \(\sqrt{2^{2} \times 11}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11}\)
= 2\(\sqrt{11}\)

Exercise 3.
\(\sqrt{169}\)
Answer:
\(\sqrt{169}\) = \(\sqrt{13^{2}}\)
= 13

Exercise 4.
\(\sqrt{75}\)
Answer:
\(\sqrt{75}\) = \(\sqrt{3 \times 5^{2}}\)
= \(\sqrt{3}\) × \(\sqrt{5^{2}}\)
= 5\(\sqrt{3}\)

Exercises 5–8

Exercise 5.
Simplify \(\sqrt{108}\).
Answer:
\(\sqrt{108}\) = \(\sqrt{2^{2} \times 3^{3}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\)
= 2 × 3\(\sqrt{3}\)
= 6\(\sqrt{3}\)

Exercise 6.
Simplify \(\sqrt{250}\).
Answer:
\(\sqrt{250}\) = \(\sqrt{2 \times 5^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{5^{2}}\) × \(\sqrt{5}\)
= 5\(\sqrt{2}\) × \(\sqrt{5}\)
= 5\(\sqrt{10}\)

Exercise 7.
Simplify \(\sqrt{200}\).
Answer:
\(\sqrt{200}\) = \(\sqrt{2^{3} \times 5^{2}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{5^{2}}\)
= 2 × 5\(\sqrt{2}\)
= 10\(\sqrt{2}\)

Exercise 8.
Simplify \(\sqrt{504}\).
Answer:
\(\sqrt{504}\) = \(\sqrt{2^{3} \times 3^{2} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{7}\)
= 6\(\sqrt{14}\)

Eureka Math Grade 8 Module 7 Lesson 4 Problem Set Answer Key

Simplify each of the square roots in Problems 1–5 as much as possible.

Question 1.
\(\sqrt{98}\)
\(\sqrt{98}\) = \(\sqrt{2 \times 7^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{7^{2}}\)
= 7\(\sqrt{2}\)

Question 2.
\(\sqrt{54}\)
\(\sqrt{54}\) = \(\sqrt{2 \times 3^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{3}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{6}\)

Question 3.
\(\sqrt{144}\)
\(\sqrt{144}\) = \(\sqrt{12^{2}}\)
= 12

Question 4.
\(\sqrt{512}\)
\(\sqrt{512}\) = \(\sqrt{2^{9}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\)
= 2 × 2 × 2 × 2\(\sqrt{2}\)
= 16\(\sqrt{2}\)

Question 5.
\(\sqrt{756}\)
\(\sqrt{756}\) = \(\sqrt{2^{2} \times 3^{3} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{21}\)
= 6\(\sqrt{21}\)

Question 6.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c units represent the length of the hypotenuse.
(\(\sqrt{27}\))² + (\(\sqrt{48}\))² = c²
27 + 48 = c²
75 = c²
\(\sqrt{75}\) = \(\sqrt{c^{2}}\)
\(\sqrt{5^{2}}\) × \(\sqrt{3}\) = c
5\(\sqrt{3}\) = c
The length of the hypotenuse is 5\(\sqrt{3}\) units.

Question 7.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c cm represent the length of the hypotenuse.
3² + 8² = c²
9 + 64 = c²
73 = c²
\(\sqrt{73}\) = \(\sqrt{c^{2}}\)
\(\sqrt{73}\) = c
The length of the unknown side is \(\sqrt{73}\) cm.

Question 8.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c mm represent the length of the hypotenuse.
3² + 3² = c²
9 + 9 = c²
18 = c²
\(\sqrt{18}\) = \(\sqrt{c^{2}}\)
\(\sqrt{18}\) = c
\(\sqrt{3^{2}}\) × \(\sqrt{2}\) = c
3\(\sqrt{2}\) = c
The length of the unknown side is 3\(\sqrt{2}\) mm.

Question 9.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let x in. represent the unknown length.
x² + 8² = 12²
x² + 64 = 144
x² + 64 – 64 = 144 – 64
x² = 80
\(\sqrt{x^{2}}\) = \(\sqrt{80}\)
x = \(\sqrt{80}\)
x = \(\sqrt{2^{4} \cdot 5}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{5}\)
x = 2 ⋅ 2\(\sqrt{5}\)
x = 4\(\sqrt{5}\)
The length of the unknown side is 4\(\sqrt{5}\) in.

Question 10.
Josue simplified \(\sqrt{450}\) as 15\(\sqrt{2}\) Is he correct? Explain why or why not.
Answer:
\(\sqrt{450}\) = \(\sqrt{2 \times 3^{2} \times 5^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5^{2}}\)
= 3 × 5 × \(\sqrt{1}\)
= 15\(\sqrt{1}\)
Yes, Josue is correct because the number 450 = 2 × 3² × 5². The factors that are perfect squares simplify to 15 leaving just the factor of 2 that cannot be simplified. Therefore, \(\sqrt{450}\) = 15\(\sqrt{2}\).

Question 11.
Tiah was absent from school the day that you learned how to simplify a square root. Using \(\sqrt{360}\), write Tiah an explanation for simplifying square roots.
Answer:
To simplify \(\sqrt{360}\), first write the factors of 360. The number 360 = 2³ × 3² × 5. Now, we can use the factors to write \(\sqrt{360}\) = \(\sqrt{2^{3} \times 3^{2} \times 5}\)), which can then be expressed as \(\sqrt{360}\) = \(\sqrt{2^{3}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5}\). Because we want to simplify square roots, we can rewrite the factor \(\sqrt{2^{3}}\) as \(\sqrt{2^{2}}\) × \(\sqrt{2}\) because of the laws of exponents. Now, we have
\(\sqrt{360}\) = \(\sqrt{2^{2}}\) × √2 × \(\sqrt{3^{2}}\) × \(\sqrt{5}\).
Each perfect square can be simplified as follows:
\(\sqrt{360}\) = 2 × \(\sqrt{2}\) × 3 × \(\sqrt{5}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{5}\)
= 6\(\sqrt{10}\).
The simplified version of \(\sqrt{360}\) = 6\(\sqrt{10}\).

Eureka Math Grade 8 Module 7 Lesson 4 Exit Ticket Answer Key

Simplify the square roots as much as possible.
Question 1.
\(\sqrt{24}\)
Answer:
\(\sqrt{24}\) = \(\sqrt{2^{2} \times 6}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{6}\)
= 2\(\sqrt{6}\)

Question 2.
\(\sqrt{338}\)
Answer:
\(\sqrt{338}\) = \(\sqrt{13^{2} \times 2}\)
= \(\sqrt{13^{2}}\) × \(\sqrt{24}\)
= 13\(\sqrt{2}\)

Question 3.
\(\sqrt{196}\)
Answer:
\(\sqrt{196}\) = \(\sqrt{14^{2}}\)
= 14

Question 4.
\(\sqrt{2420}\)
Answer:
\(\sqrt{2420}\) = \(\sqrt{2^{2} \times 11^{2} \times 5}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11^{2}}\) × \(\sqrt{5}\)
= 2 × 11 × \(\sqrt{5}\)
= 22\(\sqrt{5}\)

Engage NY Eureka Math 8th Grade Module 7 Lesson 3 Answer Key

Eureka Math Grade 8 Module 7 Lesson 3 Exercise Answer Key

Opening
The numbers in each column are related. Your goal is to determine how they are related, determine which numbers belong in the blank parts of the columns, and write an explanation for how you know the numbers belong there.

Answer:

Exercises
Find the positive value of x that makes each equation true. Check your solution.

Exercise 1.
x² = 169
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve the equation, and check your answer.
Answer:
x² = 169
\(\sqrt{x^{2}}\) = \(\sqrt{169}\)
x = \(\sqrt{169}\)
x = 13

Check:
13² = 169
169 = 169

Exercise 2.
A square-shaped park has an area of 324 yd². What are the dimensions of the park? Write and solve an equation.
x² = 324
\(\sqrt{x^{2}}\) = \(\sqrt{324}\)
x = \(\sqrt{324}\)
x = 18

Check:
18² = 324
324 = 324
The square park is 18 yd. in length and 18 yd. in width.

Exercise 3.
625 = x²
625 = x²
\(\sqrt{625}\) = \(\sqrt{x^{2}}\)
\(\sqrt{625}\) = x
25 = x

Check:
625 = 25²
625 = 625

Exercise 4.
A cube has a volume of 27 in³. What is the measure of one of its sides? Write and solve an equation.
27 = x³
\(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{x^{3}}\)
\(\sqrt [ 3 ]{ 27 }\) = x
3 = x

Check:
27 = 3³
27 = 27
The cube has side lengths of 3 in.

Exercise 5.
What positive value of x makes the following equation true: x² = 64? Explain.
x² = 64
\(\sqrt{x^{2}}\) = \(\sqrt{64}\)
x = \(\sqrt{64}\)
x = 8

Check:
8² = 64
64 = 64
To solve the equation, I need to find the positive value of x so that when it is squared, it is equal to 64. Therefore, I can take the square root of both sides of the equation. The square root of x², \(\sqrt{52}\), is x because x² = x ∙ x. The square root of 64, \(\sqrt{64}\), is 8 because 64 = 8 ∙ 8. Therefore, x = 8.

Exercise 6.
What positive value of x makes the following equation true: x³ = 64? Explain.
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4 Check:
4³ = 64
64 = 64
To solve the equation, I need to find the positive value of x so that when it is cubed, it is equal to 64. Therefore, I can take the cube root of both sides of the equation. The cube root of x³, \(\sqrt[3]{x^{3}}\), is x because x³ = x ∙ x ∙ x. The cube root of 64, \(\sqrt [ 3 ]{ 64 }\), is 4 because 64 = 4 ∙ 4 ∙ 4. Therefore, x = 4.

Exercise 7.
Find the positive value of x that makes the equation true: x² = 256^-1.
Answer:
x² = 256^-1
\(\sqrt{x^{2}}\) = \(\sqrt{256^{-1}}\)
x = \(\sqrt{256^{-1}}\)
x = \(\sqrt{\frac{1}{256}}\)
x = \(\frac{1}{16}\)
x = 16^-1

Check:
(16^-1)² = 256^-1
16^-2 = 256^-1
\(\frac{1}{16^{2}}\) = 256^-1
\(\frac{1}{256}\) = 256^-1
256^-1 = 256^-1

Exercise 8.
Find the positive value of x that makes the equation true: x³ = 343^-1.
x³ = 343^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{343^{-1}}\)
x = \(\sqrt[3]{343^{-1}}\)
x = \(\sqrt[3]{\frac{1}{343}}\)
x = \(\frac{1}{7}\)
x = 7^-1

Check:
(7^-1)³ = 343^-1
7³ = 343^-1
(\(\frac{1}{7}\))³ = 343^-1
\(\frac{1}{343}\) = 343^-1
343^-1 = 343^-1

Exercise 9.
Is 6 a solution to the equation x² – 4 = 5x? Explain why or why not.
Answer:
6² – 4 = 5(6)
36 – 4 = 30
32 ≠ 30
No, 6 is not a solution to the equation x² – 4 = 5x. When the number is substituted into the equation and simplified, the left side of the equation and the right side of the equation are not equal; in other words, it is not a true number sentence. Since the number 6 does not satisfy the equation, it is not a solution to the equation.

Eureka Math Grade 8 Module 7 Lesson 3 Problem Set Answer Key

Find the positive value of x that makes each equation true. Check your solution.
Question 1.
What positive value of x makes the following equation true: x² = 289? Explain.
Answer:
x² = 289
\(\sqrt{x^{2}}\) = \(\sqrt{289}\)
x = \(\sqrt{289}\)
x = 17

Check:
17² = 289
289 = 289
To solve the equation, I need to find the positive value of x so that when it is squared, it is equal to 289. Therefore, I can take the square root of both sides of the equation. The square root of x², \(\sqrt{x^{2}}\), is x because x² = x ⋅ x. The square root of 289, \(\sqrt{289}\) , is 17 because 289 = 17 ⋅ 17. Therefore, x = 17.

Question 2.
A square-shaped park has an area of 400 yd². What are the dimensions of the park? Write and solve an equation.
Answer:
x² = 400
\(\sqrt{x^{2}}\) = \(\sqrt{400}\)
x = \(\sqrt{400}\)
x = 20

Check:
20² = 400
400 = 400
The square park is 20 yd. in length and 20 yd. in width.

Question 3.
A cube has a volume of 64 in³. What is the measure of one of its sides? Write and solve an equation.
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4

Check:
4³ = 64
64 = 64
The cube has a side length of 4 in.

Question 4.
What positive value of x makes the following equation true: 125 = x³? Explain.
Answer:
125 = x³
\(\sqrt [ 3 ]{ 125 }\) = \(\sqrt[3]{x^{3}}\)
\(\sqrt [ 3 ]{ 125 }\) = x
5 = x

Check:
125 = 5³
125 = 125
To solve the equation, I need to find the positive value of x so that when it is cubed, it is equal to 125. Therefore, I can take the cube root of both sides of the equation. The cube root of x³, \(\sqrt[3]{x^{3}}\), is x because x³ = x ⋅ x ⋅ x. The cube root of 125, \(\sqrt [ 3 ]{ 125 }\), is 5 because 125 = 5 ⋅ 5 ⋅ 5. Therefore, x = 5.

Question 5.
Find the positive value of x that makes the equation true: x² = 441^-1.
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve and check your solution.
x² = 441^-1
\(\sqrt{x^{2}}\) = \(\sqrt{144^{-1}}\)
x = \(\sqrt{144^{-1}}\)
x = \(\sqrt{\frac{1}{441}}\)
x = \(\frac{1}{21}\)
x = 21^-1

Check:
(21^-1 )² = 441^-1
21^-2 = 441^-1
\(\frac{1}{21^{2}}\) = 441^-1
\(\frac{1}{441}\) = 441^-1
441^-1 = 441^-1

Question 6.
Find the positive value of x that makes the equation true: x³ = 125^-1.
Answer:
x³ = 125^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{125^{-1}}\)
x = \(\sqrt[3]{125^{-1}}\)
x = \(\sqrt[3]{\frac{1}{125}}\)
x = \(\frac{1}{5}\)
x = 5^-1

Check:
(5^-1)³ = 125^-1
5^-3 = 125^-1
\(\frac{1}{5^{3}}\) = 125^-1
\(\frac{1}{125}\) = 125^-1
125^-1 = 125^-1

Question 7.
The area of a square is 196 in². What is the length of one side of the square? Write and solve an equation, and then check your solution.
Answer:
Let x in. represent the length of one side of the square.
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = \(\sqrt{196}\)
x = 14

Check:
14² = 196
196 = 196
The length of one side of the square is 14 in.

Question 8.
The volume of a cube is 729 cm³. What is the length of one side of the cube? Write and solve an equation, and then check your solution.
Answer:
Let x cm represent the length of one side of the cube.
x³ = 729
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 729 }\)
x = \(\sqrt [ 3 ]{ 729 }\)
x = 9

Check:
9³ = 729
729 = 729
The length of one side of the cube is 9 cm.

Question 9.
What positive value of x would make the following equation true: 19 + x² = 68?
Answer:
19 + x² = 68
19 – 19 + x² = 68 – 19
x² = 49
x = 7
The positive value for x that makes the equation true is 7.

Eureka Math Grade 8 Module 7 Lesson 3 Exit Ticket Answer Key

Find the positive value of x that makes each equation true. Check your solution.
Question 1.
x² = 225
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve and check your solution.
Answer:
x² = 225
\(\sqrt{x^{2}}\) = \(\sqrt{225}\)
x = \(\sqrt{225}\)
x = 15

Check:
15² = 225
225 = 225

Question 2.
x³ = 64
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4

Check:
4³ = 64
64 = 64

Question 3.
x² = 361^-1
Answer:
x² = 361^-1
\(\sqrt{x^{2}}\) = \(\sqrt{361^{-1}}\)
x = \(\sqrt{361^{-1}}\)
x = \(\sqrt{\frac{1}{361}}\)
x = \(\frac{1}{19}\)
x = 19^-1

Check:
(19^-1)² = 361^-1
19^-2 = 361^-1
\(\frac{1}{19^{2}}\) = 361^-1
\(\frac{1}{361}\) = 361^-1
361^-1 = 361^-1

Question 4.
x³ = 1000^-1
Answer:
x³ = 1000^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{1000^{-1}}\)
x = \(\sqrt[3]{1000^{-1}}\)
x = \(\sqrt[3]{\frac{1}{1000}}\)
x = \(\frac{1}{10}\)
x = 10^-1

Check:
(10^-1 )³ = 1000^-1
10^-3 = 1000^-1
\(\frac{1}{10^{3}}\) = 1000^-1
\(\frac{1}{1000}\) = 1000^-1
1000^-1 = 1000^-1

Engage NY Eureka Math 8th Grade Module 7 Lesson 2 Answer Key

Eureka Math Grade 8 Module 7 Lesson 2 Exercise Answer Key

Exercise 1.
Determine the positive square root of 81, if it exists. Explain.
Answer:
The square root of 81 is 9 because 9²=81.

Exercise 2.
Determine the positive square root of 225, if it exists. Explain.
Answer:
The square root of 225 is 15 because 15²=225.

Exercise 3.
Determine the positive square root of -36, if it exists. Explain.
Answer:
The number -36 does not have a square root because there is no number squared that can produce a negative number.

Exercise 4.
Determine the positive square root of 49, if it exists. Explain.
Answer:
The square root of 49 is 7 because 7²=49.

Discussion

Answer:
Place the numbers \(\sqrt{1}\), \(\sqrt{4}\), \(\sqrt{9}\), and \(\sqrt{1}\)6 on the number line, and explain how you knew where to place them.
Solutions are shown below in red.

Place the numbers \(\sqrt{2}\) and \(\sqrt{3}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. Students should reason that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) belong on the number line between \(\sqrt{1}\) and \(\sqrt{4}\). They might be more specific and suggest that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) sit equally spaced in the interval between 1 and 2. This idea suggests that 1 \(\frac{1}{3}\) might be a good approximation for \(\sqrt{2}\) and 1 \(\frac{2}{3}\) for \(\sqrt{3}\). Of course, this suggested spacing is just speculation for now.

Place the numbers \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), and \(\sqrt{8}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

Place the numbers \(\sqrt{1}\)0, \(\sqrt{1}\)1, \(\sqrt{1}\)2, \(\sqrt{1}\)3, \(\sqrt{1}\)4, and \(\sqrt{1}\)5 on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

Our work on the number line shows that there are many more square roots of whole numbers that are not perfect squares than those that are perfect squares. On the number line above, we have four perfect square numbers and twelve that are not! After we do some more work with roots, in general, we will cover exactly how to describe these numbers and how to approximate their values with greater precision. For now, we will estimate their locations on the number line using what we know about perfect squares.

Determine the positive square root of the number given. If the number is not a perfect square, determine which whole number the square root would be closest to, and then use guess and check to give an approximate answer to one or two decimal places.
Exercise 5.
\(\sqrt{49}\)
Answer:
7

Exercise 6.
\(\sqrt{62}\)
Answer:
The square root of 62 is close to 8. The square root of 62 is approximately 7.9 because 7.9²=62.41.

Exercise 7.
\(\sqrt{122}\)
Answer:
The square root of 122 is close to 11. Students may guess a number between 11 and 11.1 because 11.05²=122.1025.

Exercise 8.
\(\sqrt{400}\)
Answer:
20

Exercise 9.
Which of the numbers in Exercises 5–8 are not perfect squares? Explain.
Answer:
The numbers 62 and 122 are not perfect squares because there is no integer x to satisfy x²=62 or x²=122.

Eureka Math Grade 8 Module 7 Lesson 2 Problem Set Answer Key

Determine the positive square root of the number given. If the number is not a perfect square, determine the integer to which the square root would be closest.
Question 1.
\(\sqrt{169}\)
Answer:
13

Question 2.
\(\sqrt{256}\)
Answer:
16

Question 3.
\(\sqrt{81}\)
Answer:
9

Question 4.
\(\sqrt{147}\)
Answer:
The number 147 is not a perfect square. It is between the perfect squares 144 and 169 but closer to 144. Therefore, the square root of 147 is close to 12.

Question 5.
\(\sqrt{8}\)
Answer:
The number 8 is not a perfect square. It is between the perfect squares 4 and 9 but closer to 9. Therefore, the square root of 8 is close to 3.

Question 6.
Which of the numbers in Problems 1–5 are not perfect squares? Explain.
Answer:
The numbers 147 and 8 are not perfect squares because there is no integer x so that x²=147 or x²=8.

Question 7.
Place the following list of numbers in their approximate locations on a number line.
\(\sqrt{32}\), \(\sqrt{12}\), \(\sqrt{27}\), \(\sqrt{18}\), \(\sqrt{23}\), and \(\sqrt{50}\)
Answer:
Answers are noted in red.

Question 8.
Between which two integers will \(\sqrt{45}\) be located? Explain how you know.
Answer:
The number 45 is not a perfect square. It is between the perfect squares 36 and 49 but closer to 49. Therefore, the square root of 45 is between the integers 6 and 7 because \(\sqrt{36}\) = 6 and \(\sqrt{49}\) = 7 and \(\sqrt{36}\) < \(\sqrt{45}\) < \(\sqrt{49}\).

Eureka Math Grade 8 Module 7 Lesson 2 Exit Ticket Answer Key

Question 1.
Write the positive square root of a number x in symbolic notation.
Answer:
\(\sqrt{x}\)

Question 2.
Determine the positive square root of 196. Explain.
Answer:
\(\sqrt{196}\) = 14 because 14² = 196.

Question 3.
The positive square root of 50 is not an integer. Which whole number does the value of \(\sqrt{50}\) lie closest to? Explain.
Answer:
\(\sqrt{50}\) is between 7 and 8 but closer to 7. The reason is that 7²=49, and 8²=64. The number 50 is between 49 and 64 but closer to 49. Therefore, the square root of 50 is close to 7.

Question 4.
Place the following numbers on the number line in approximately the correct positions: \(\sqrt{16}\), \(\sqrt{9}\), \(\sqrt{11}\), and 3.5.

Answer:
Solutions are shown in red below.

Engage NY Eureka Math 8th Grade Module 2 Lesson 14 Answer Key

Eureka Math Grade 8 Module 2 Lesson 14 Example Answer Key

Example 1
Find the measure of angle x.

Answer:
We need to find the sum of the measures of the remote interior angles to find the measure of the exterior angle x:
14+30=44. Therefore, the measure of ∠x is 44°.

→ Present an informal argument that proves you are correct.
→ We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ABC must be 136°, which means that ∠x is 44°.

Example 2.
Find the measure of angle x.

Answer:
We need to find the sum of the measures of the remote interior angles to find the measure of the exterior angle x: 44+32=76. Therefore, the measure of ∠x is 76°.

→ Present an informal argument that proves you are correct.
→ We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 104°, which means that ∠x is 76°.

Example 3.
Find the measure of angle x.

Answer:
180-121=59. Therefore, the measure of ∠x is 59°.

Students should notice that they are not given the two remote interior angles associated with the exterior angle x.
For that reason, they must use what they know about straight angles (or supplementary angles) to find the measure of
angle x.

Example 4.
Find the measure of angle x.

Answer:
129-45=84. Therefore, the measure of ∠x is 84°.

Eureka Math Grade 8 Module 2 Lesson 14 Exercise Answer Key

Exercises 1–4
Use the diagram below to complete Exercises 1–4.

Exercise 1.
Name an exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠ZYP, and the related remote interior angles are ∠YZX and ∠ZXY.

Exercise 2.
Name a second exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠XZQ, and the related remote interior angles are ∠ZYX and ∠ZXY.

Exercise 3.
Name a third exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠RXY, and the related remote interior angles are ∠ZYX and ∠XZY.

Exercise 4.
Show that the measure of an exterior angle is equal to the sum of the measures of the related remote interior angles.
Answer:
Triangle XYZ has interior angles ∠XYZ, ∠YZX, and ∠ZXY. The sum of those angles is 180°. The straight angle ∠XYP also has a measure of 180° and is made up of angles ∠XYZ and ∠ZYP. Since the triangle and the straight angle have the same number of degrees, we can write the sum of their respective angles as an equality:
∠XYZ+∠YZX+∠ZXY=∠XYZ+ZYP.
Both the triangle and the straight angle share ∠XYZ. We can subtract the measure of that angle from the triangle and the straight angle. Then, we have
∠YZX+∠ZXY=∠ZYP,
where the angle ∠ZYP is the exterior angle, and the angles ∠YZX and ∠ZXY are the related remote interior angles of the triangle. Therefore, the sum of the measures of the remote interior angles of a triangle are equal to the measure of the exterior angle.

Exercise 5–10

Question 5.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 89+28 = 117, the measure of angle x is 117°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 63°, which means that ∠x is 117°.

Question 6.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 59+52=111, the measure of angle x is 111°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CAB must be 69°, which means that ∠x is 111°.

Question 7.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 180-79=101, the measure of angle x is 101°. We know that straight angles are 180°, and the straight angle in the diagram is made up of ∠ABC and ∠x. ∠ABC is 79°, which means that ∠x is 101°.

Question 8.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 71+74=145, the measure of angle x is 145°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 35°, which means that ∠x is 145°.

Question 9.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 107+32=139, the measure of angle x is 139°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CBA must be 41°, which means that x is 139°.

Question 10.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 156-81 = 75, the measure of angle x is 75°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 24° because it is part of the straight angle. Then, ∠x=180°-(81°+24°), which means ∠x is 75°.

Eureka Math Grade 8 Module 2 Lesson 14 Exit Ticket Answer Key

Question 1.
Find the measure of angle p. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle p is 67°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 113°, which means that ∠p is 67°.

Question 2.
Find the measure of angle q. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle q is 27°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CAB must be 25°, which means that ∠q is 27°.

Question 3.
Find the measure of angle r. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle r is 121°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BCA must be 59°, which means that ∠r is 121°.

Eureka Math Grade 8 Module 2 Lesson 14 Problem Set Answer Key

Students practice finding missing angle measures of triangles.

For each of the problems below, use the diagram to find the missing angle measure. Show your work.

Question 1.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 26+13=39, the measure of angle x is 39°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BCA must be 141°, which means that ∠x is 39°.

Question 2.
Find the measure of angle x.

Answer:
Since 52+44=96, the measure of angle x is 96°.

Question 3.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 76-25=51, the measure of ∠x is 51°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 104° because it is part of the straight angle. Then, x=180°-(104°+25°), which means ∠x is 51°.

Question 4.
Find the measure of angle x.

Answer:
Since 27+52 =79, the measure of angle x is 79°.

Question 5.
Find the measure of angle x.

Answer:
Since 180-104=76, the measure of angle x is 76°.

Question 6.
Find the measure of angle x.

Answer:
Since 52+53=105, the measure of angle x is 105°.

Question 7.
Find the measure of angle x.

Answer:
Since 48+83=131, the measure of angle x is 131°.

Question 8.
Find the measure of angle x.

Answer:
Since 100+26=126, the measure of angle x is 126°.

Question 9.
Find the measure of angle x.

Answer:
Since 126-47=79, the measure of angle x is 79°.

Question 10.
Write an equation that would allow you to find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since y+z=x, the measure of angle x is (y+z)°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°.
Then, ∠y+∠z+∠BAC=180°, and ∠x+∠BAC=180°. Since both equations are equal to 180°,
then ∠y+∠z+∠BAC=∠x+∠BAC. Subtract ∠BAC from each side of the equation, and you get ∠y+∠z=∠x.

Engage NY Eureka Math 8th Grade Module 2 Lesson 13 Answer Key

Eureka Math Grade 8 Module 2 Lesson 13 Exploratory Challenge Answer Key

Classwork
Concept Development

m∠1+m∠2+m∠3=m∠4+m∠5+m∠6=m∠7+m∠8+m∠9=180°
Note that the sum of the measures of angles 7 and 9 must equal 90° because of the known right angle in the right triangle.

We want to prove that the angle sum of any triangle is 180°. To do so, we use some facts that we already know about geometry:
→ A straight angle is 180° in measure.
→ Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).
→ Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).

Exploratory Challenge 1.
Let triangle ABC be given. On the ray from B to C, take a point D so that C is between B and D. Through point C, draw a segment parallel to \(\overline{A B}\), as shown. Extend the segments AB and CE. Line AC is the transversal that intersects the parallel lines.

a. Name the three interior angles of triangle ABC.
Answer:
∠ABC, ∠BAC, ∠BCA

b. Name the straight angle.
Answer:
∠BCD
Our goal is to show that the measures of the three interior angles of triangle ABC are equal to the measures of the angles that make up the straight angle. We already know that a straight angle is 180° in measure.
If we can show that the interior angles of the triangle are the same as the angles of the straight angle, then we will have proven that the sum of the measures of the interior angles of the triangle have a sum of 180°.

c. What kinds of angles are ∠ABC and ∠ECD? What does that mean about their measures?
Answer:
∠ABC and ∠ECD are corresponding angles. Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{\boldsymbol{C E}}\)).

d. What kinds of angles are ∠BAC and ∠ECA? What does that mean about their measures?
Answer:
∠BAC and ∠ECA are alternate interior angles. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{\boldsymbol{A B}}\) || \(\overline{\boldsymbol{C E}}\)).

d. We know that m∠BCD=m∠BCA+m∠ECA+m∠ECD=180°. Use substitution to show that the measures of the three interior angles of the triangle have a sum of 180°.
Answer:
m∠BCD=m∠BCA+m∠BAC+m∠ABC=180° (∠ sum of △)

Exploratory Challenge 2.
The figure below shows parallel lines L₁ and L₂ . Let m and n be transversals that intersect L₁ at points B and C, respectively, and L₂ at point F, as shown. Let A be a point on L₁ to the left of B, D be a point on L₁ to the right of C, G be a point on L₂ to the left of F, and E be a point on L₂ to the right of F.

a. Name the triangle in the figure.
Answer:
△BCF

b. Name a straight angle that will be useful in proving that the sum of the measures of the interior angles of the triangle is 180°.
Answer:
∠GFE
As before, our goal is to show that the sum of the measures of the interior angles of the triangle are equal to the measure of the straight angle. Use what you learned from Exploratory Challenge 1 to show that the measures of the interior angles of a triangle have a sum of 180°.

c. Write your proof below.
Answer:
The straight angle ∠GFE is comprised of ∠GFB, ∠BFC, and ∠EFC. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A D}\) || \(\overline{C E}\)). For that reason, ∠BCF=∠EFC and ∠CBF=∠GFB. Since ∠GFE is a straight angle, it is equal to 180°. Then, ∠GFE=∠GFB+∠BFC+∠EFC=180°.
By substitution, ∠GFE=∠CBF+∠BFC+∠BCF=180°. Therefore, the sum of the measures of the interior angles of a triangle is 180° (∠ sum of △).

Eureka Math Grade 8 Module 2 Lesson 13 Exit Ticket Answer Key

Question 1.
If L₁ || L₂ , and L₃ || L₄ , what is the measure of ∠1? Explain how you arrived at your answer.

Answer:
The measure of angle 1 is 29°. I know that the angle sum of triangles is 180°. I already know that two of the angles of the triangle are 90° and 61°.

Question 2.
Given that line AB is parallel to line CE, present an informal argument to prove that the measures of the interior angles of triangle ABC have a sum of 180°.

Answer:
Since \(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C E}\), the corresponding angles ∠BAC and ∠ECD are equal in measure. Similarly, ∠ABC and ∠ECB are equal in measure because they are alternate interior angles. Since ∠ACD is a straight angle (i.e., equal to 180° in measure), substitution shows that triangle ABC has a sum of 180°. Specifically, the straight angle is made up of ∠ACB, ∠ECB, and ∠ECD. ∠ACB is one of the interior angles of the triangle and one of the angles of the straight angle. We know that ∠ABC has the same measure as ∠ECB and that ∠BAC has the same measure as ∠ECD. Therefore, the sum of the measures of the interior angles will be the same as the sum of the measures of the angles of the straight angle, which is 180°.

Eureka Math Grade 8 Module 2 Lesson 13 Problem Set Answer Key

Students practice presenting informal arguments about the sum of the angles of a triangle using the theorem to find the measures of missing angles.

Question 1.
In the diagram below, line AB is parallel to line CD, that is, L_AB ∥L_CD. The measure of ∠ABC is 28° and the measure of ∠EDC is 42°. Find the measure of ∠CED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle.

Answer:
The measure of ∠CED is 110°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(28°+42°) and ∠CED is 110°.

Question 2.
In the diagram below, line AB is parallel to line CD, that is, L_AB || L_CD . The measure of ∠ABE is 38°, and the measure of ∠EDC is 16°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Find the measure of ∠CED first, and then use that measure to find the measure of ∠BED.)

Answer:
The measure of ∠BED is 54°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(38°+16°)=126°. The straight angle ∠BEC is made up of ∠CED and ∠BED. Since we know straight angles measure 180° and ∠CED=126°, then ∠BED is 54°.

Question 3.
In the diagram below, line AB is parallel to line CD, that is, L_AB || L_CD . The measure of ∠ABE is 56°, and the measure of ∠EDC is 22°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Extend the segment BE so that it intersects line CD.)

Answer:
The measure of ∠BED is 78°. This is the correct measure for the angle because ∠ABE and ∠DFE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠FED=180°-(56°+22°)=102°. The straight angle ∠BEF is made up of ∠FED and ∠BED. Since straight angles measure 180° and ∠FED is 102°, then ∠BED is 78°.

Question 4.
What is the measure of ∠ACB?

Answer:
The measure of ∠ACB is 180°-(83°+64°), which is equal to 33°.

Question 5.
What is the measure of ∠EFD?

Answer:
The measure of ∠EFD is 180°-(101°+40°), which is equal to 39°.

Question 6.
What is the measure of ∠HIG?

Answer:
The measure of ∠HIG is 180°-(154°+14°), which is equal to 12°.

Question 7.
What is the measure of ∠ABC?

Answer:
The measure of ∠ABC is 60° because 60°+60°+60°, which is equal to 180°.

Question 8.
Triangle DEF is a right triangle. What is the measure of ∠EFD?

Answer:
The measure of ∠EFD is 90°-57°, which is equal to 33°.

Question 9.
In the diagram below, Lines L₁ and L₂ are parallel. Transversals r and s intersect both lines at the points shown below. Determine the measure of ∠JMK. Explain how you know you are correct.

Answer:
The Lines L₁ and L₂ are parallel, which means that the alternate interior angles formed by the transversals are equal. Specifically, ∠LMK=∠JKM=72°. Since △JKM has a sum of interior angles equal to 180°,
∠KJM+∠JMK+∠JKM=180°. By substitution, we have 39°+∠JMK+72°=180°; therefore, ∠JMK is 69°.

Engage NY Eureka Math 8th Grade Module 2 Lesson 12 Answer Key

Eureka Math Grade 8 Module 2 Lesson 12 Exploratory Challenge Answer Key

Exploratory Challenge 1.
In the figure below, L₁ is not parallel to L₂, and m is a transversal. Use a protractor to measure angles 1–8. Which, if any, are equal in measure? Explain why. (Use your transparency if needed.)

Answer:

The following angle measures are equal: ∠1=∠3, ∠2=∠4, ∠5=∠7, and ∠6=∠8. The pairs of angles listed are equal because they are vertical angles. Vertical angles are always equal because a rotation of 180° around the vertex of the angle will map it to its opposite angle.

Exploratory Challenge 2.
In the figure below, L₁ || L₂, and m is a transversal. Use a protractor to measure angles 1–8. List the angles that are equal in measure.

Answer:

∠1=∠3=∠5=∠7 and ∠2=∠4=∠6=∠8

a. What did you notice about the measures of ∠1 and ∠5? Why do you think this is so? (Use your transparency if needed.)
Answer:
∠1 and ∠5 are equal in measure. We can translate ∠1 along a vector on line m so that the vertex of ∠1 maps onto the vertex of ∠5. Translations are angle-preserving, so the two angles will coincide.

b. What did you notice about the measures of ∠3 and ∠7? Why do you think this is so? (Use your transparency if needed.) Are there any other pairs of angles with this same relationship? If so, list them.
Answer:
∠3 and ∠7 are equal in measure. We can translate ∠3 along a vector on line m so that the vertex of ∠3 maps onto the vertex of ∠7. Translations are angle-preserving, so the two angles will coincide. Other pairs of angles with this same relationship are ∠4 and ∠8 and ∠2 and ∠6.

c. What did you notice about the measures of ∠4 and ∠6? Why do you think this is so? (Use your transparency if needed.) Is there another pair of angles with this same relationship?
Answer:
The measures of ∠4 and ∠6 are equal. A rotation of 180° around a center would map ∠4 to ∠6. Rotations are angle-preserving, so we know that ∠4 and ∠6 are equal. ∠3 and ∠5 have the same relationship.

Eureka Math Grade 8 Module 2 Lesson 12 Problem Set Answer Key

Students practice identifying corresponding, alternate interior, and alternate exterior angles from a diagram.

Use the diagram below to do Problems 1–10.

Question 1.
Identify all pairs of corresponding angles. Are the pairs of corresponding angles equal in measure? How do you know?
Answer:
∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7
There is no information provided about the lines in the diagram being parallel. For that reason, we do not know if the pairs of corresponding angles are equal in measure. If we knew the lines were parallel, we could use translation to map one angle onto another.

Question 2.
Identify all pairs of alternate interior angles. Are the pairs of alternate interior angles equal in measure? How do you know?
Answer:
∠4 and ∠5, ∠3 and ∠6
There is no information provided about the lines in the diagram being parallel. For that reason, we do not know if the pairs of alternate interior angles are equal in measure. If the lines were parallel, we could use rotation to show that the pairs of angles would map onto one another, proving they are equal in measure.

Question 3.
Use an informal argument to describe why ∠1 and ∠8 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 1 and angle 8 are equal in measure when the lines are parallel is because you can rotate around the midpoint of the segment between the parallel lines. A rotation would then map angle 1 onto angle 8, showing that they are congruent and equal in measure.

Question 4.
Assuming L₁∥L₂, if the measure of ∠4 is 73°, what is the measure of ∠8? How do you know?
Answer:
The measure of ∠8 is 73°. This must be true because they are corresponding angles of parallel lines.

Question 5.
Assuming L₁ || L₂, if the measure of ∠3 is 107° degrees, what is the measure of ∠6? How do you know?
Answer:
The measure of ∠6 is 107°. This must be true because they are alternate interior angles of parallel lines.

Question 6.
Assuming L₁ || L₂, if the measure of ∠2 is 107°, what is the measure of ∠7? How do you know?
Answer:
The measure of ∠7 is 107°. This must be true because they are alternate exterior angles of parallel lines.

Question 7.
Would your answers to Problems 4–6 be the same if you had not been informed that L₁ || L₂? Why or why not?
Answer:
No. The fact that the lines are parallel is the reason we can state that specific pairs of angles are equal in measure. We can use basic rigid motions to prove that angles associated with parallel lines have the property of being equal in measure when they are corresponding, alternate interior, or alternate exterior angles. If the lines are not parallel, then we could still classify the angles, but we would not know anything about their measures.

Question 8.
Use an informal argument to describe why ∠1 and ∠5 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 1 and angle 5 are equal in measure when the lines are parallel is because you can translate along a vector equal in length of the segment between the parallel lines; then, angle 1 would map onto angle 5.

Question 9.
Use an informal argument to describe why ∠4 and ∠5 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 4 and angle 5 are equal in measure when the lines are parallel is because when you rotate angle 4 around the midpoint of the segment between the parallel lines, angle 4 will map onto angle 5.

Question 10.
Assume that L₁ is not parallel to L₂. Explain why ∠3≠∠7.
Answer:
If the lines are not parallel, then all we know about angle 3 and angle 7 is that they are corresponding angles. If the lines are parallel, we could use translation to map one angle onto the other to show that they are equal in measure. However, we are to assume that the lines are not parallel, which means that their corresponding angles will not be equal in measure.

Eureka Math Grade 8 Module 2 Lesson 12 Exit Ticket Answer Key

Use the diagram to answer Questions 1 and 2. In the diagram, lines L₁ and L₂ are intersected by transversal m, forming angles 1–8, as shown.

Question 1.
If L₁ || L₂, what do you know about ∠2 and ∠6? Use informal arguments to support your claim.
Answer:
They are alternate interior angles because they are on opposite sides of the transversal and inside of lines L₁
and L₂. Also, the angles are equal in measure because the lines L₁ and L₂ are parallel. If we rotated angle 2 180° around the midpoint of the segment between the parallel lines, then it would map onto angle 6.

Question 2.
If L₁ || L₂, what do you know about ∠1 and ∠3? Use informal arguments to support your claim.
Answer:
They are corresponding angles because they are on the same side of the transversal and above each of lines L₁
and L₂. Also, the angles are equal in measure because the lines L₁ and L₂ are parallel. If we translated angle 1 along a vector (the same length as the segment between the parallel lines), then it would map onto angle 3.

Engage NY Eureka Math 8th Grade Module 2 Lesson 11 Answer Key

Eureka Math Grade 8 Module 2 Lesson 11 Example Answer Key

Example 1.
The advantage of the scientific notation becomes even more pronounced when we have to compute how many times heavier a proton is than an electron. Instead of writing the value of the ratio, r, as

we express it as
r=\(\frac{1.672622 \times 10^{-27}}{9.10938291 \times 10^{-31}}\).
→ Should we eliminate the power of 10 in the numerator or denominator? Explain.
→ Using the theorem on generalized equivalent fractions, we can eliminate the negative power of 10 in the numerator and denominator to see what we are doing more clearly. Anticipating that
10^-31×10³¹=1, we can multiply the numerator and denominator of the (complex) fraction by 10³¹

Using the first law of exponents (10) presented in Lesson 5, we get

Note that since we are using scientific notation, we can interpret an approximate value of r right away. For example, we see

so that r is approximately \(\frac{1}{5}\) ×10,000, which is 2,000. Thus, we expect a proton to be about two thousand times heavier than an electron.

Example 2.
The U.S. national debt as of March 23, 2013, rounded to the nearest dollar, is $16,755,133,009,522. According to the 2012 U.S. census, there are about 313,914,040 U.S. citizens. What is each citizen’s approximate share of the debt?
Answer:
\(\frac{1.6755 \times 10^{13}}{3.14 \times 10^{8}}\)=\(\frac{1.6755}{3.14}\)×\(\frac{10^{13}}{10^{8}}\)
=\(\frac{1.6755}{3.14}\)×10⁵
=0.533598…×10⁵
≈0.5336×10⁵
=53360
Each U.S. citizen’s share of the national debt is about $53,360.

Eureka Math Grade 8 Module 2 Lesson 11 Exercise Answer Key

Exercise 1.
The mass of a proton is
0.000 000 000 000 000 000 000 000 001 672 622 kg.
In scientific notation it is
Answer:
1.672622×10^-27 kg.

Exercise 2.
The mass of an electron is
0.000 000 000 000 000 000 000 000 000 000 910 938 291 kg.
In scientific notation it is
Answer:
9.10938291×10^-31 kg.

Exercise 3.
Write the ratio that compares the mass of a proton to the mass of an electron.
Answer:
Ratio: (1.672622×10^-27) :(9.10938291×10^-31)

Exercise 4.
Compute how many times heavier a proton is than an electron (i.e., find the value of the ratio). Round your final answer to the nearest one.
Answer:
Let r= the value of the ratio, then:
r=\(\frac{1.672622 \times 10^{-27}}{9.10938291 \times 10^{-31}}\)
=\(\frac{1.672622 \times 10^{-27} \times 10^{31}}{9.10938291 \times 10^{-31} \times 10^{31}}\)
=\(\frac{1.672622 \times 10^{4}}{9.10938291}\)×10⁴
=\(\frac{1.672622 \times 10^{8}}{9.10938291 \times 10^{8}}\) ×10⁴
=\(\frac{167,262,200}{910,938,291}\)×10⁴
=0.183615291675×10⁴
=1836.15291675
≈1836

Exercise 5.
The geographic area of California is 163,696 sq.mi., and the geographic area of the U.S. is 3,794,101 sq.mi. Let’s round off these figures to 1.637×10⁵ and 3.794×10⁶. In terms of area, roughly estimate how many Californias would make up one U.S. Then compute the answer to the nearest ones.
Answer:
\(\frac{3.794 \times 10^{6}}{1.637 \times 10^{5}}\)=\(\frac{3.794}{1.637}\)×\(\frac{10^{6}}{10^{5}}\)
=\(\frac{3.794}{1.637}\)×10
=2.3176…×10
≈2.318×10
=23.18
It would take about 23 Californias to make up one U.S.

Exercise 6.
The average distance from Earth to the moon is about 3.84×10⁵ km, and the distance from Earth to Mars is approximately 9.24×10⁷ km in year 2014. On this simplistic level, how much farther is traveling from Earth to Mars than from Earth to the moon?
9.24×10⁷-3.84×10⁵=924×10⁵-3.84×10⁵
=(924-3.84)×10⁵
=920.16×10⁵
=92 016 000
It is 92,016,000 km further to travel from Earth to Mars than from Earth to the moon.

Eureka Math Grade 8 Module 2 Lesson 11 Problem Set Answer Key

Question 1.
There are approximately 7.5×10¹⁸ grains of sand on Earth. There are approximately 7×10²7 atoms in an average human body. Are there more grains of sand on Earth or atoms in an average human body? How do you know?
Answer:
There are more atoms in the average human body. When comparing the order of magnitude of each number,
27>18; therefore, 7×10²⁷>7.5×10¹⁸.

Question 2.
About how many times more atoms are in a human body compared to grains of sand on Earth?
Answer:
\(\frac{7 \times 10^{27}}{7.5 \times 10^{18}}\)=\(\frac{7}{7.5}\)×\(\frac{10^{27}}{10^{18}}\)
≈1×10^27-18
≈1×10⁹
≈10⁹
There are about 1,000,000,000 times more atoms in the human body compared to grains of sand on Earth.

Question 3.
Suppose the geographic areas of California and the U.S. are 1.637×10⁵ and 3.794×10⁶ sq.mi., respectively. California’s population (as of 2012) is approximately 3.804×10⁷ people. If population were proportional to area, what would be the U.S. population?
Answer:
We already know from Exercise 5 that it would take about 23 Californias to make up one U.S. Then the population of the U.S. would be 23 times the population of California, which is
23×3.804×10⁷=87.492×10⁷
=8.7492×10⁸
=874,920,000.

Question 4.
The actual population of the U.S. (as of 2012) is approximately 3.14×10⁸. How does the population density of California (i.e., the number of people per square mile) compare with the population density of the U.S.?
Answer:
Population density of California per square mile:
\(\frac{3.804 \times 10^{7}}{1.637 \times 10^{5}}\)=\(\frac{3.804}{1.637}\)×\(\frac{10^{7}}{10^{5}}\)
=2.32376…×10²
≈2.32×10²
=232
Population density of the U.S. per square mile:
\(\frac{3.14 \times 10^{8}}{3.794 \times 10^{6}}\)=\(\frac{3.14}{3.794}\)×\(\frac{10^{8}}{10^{6}}\)
=0.8276…×10²
≈0.83×10²
=83
Population density of California compared to the population density of the U.S.:
\(\frac{232}{83}\)=2.7951…
≈2.8
California is about 3 times as dense as the U.S. in terms of population.

Eureka Math Grade 8 Module 2 Lesson 11 Exit Ticket Answer Key

Question 1.
Two of the largest mammals on earth are the blue whale and the elephant. An adult male blue whale weighs about 170 tonnes or long tons. (1 tonne = 1000 kg)
Show that the weight of an adult blue whale is 1.7×10⁵ kg.
Answer:
Let x (or any other symbol) represent the number of kilograms an adult blue whale weighs.
170×1000=x
1.7×10⁵=x

Question 2.
An adult male elephant weighs about 9.07×10³ kg.
Compute how many times heavier an adult male blue whale is than an adult male elephant (i.e., find the value of the ratio). Round your final answer to the nearest one.
Answer:
Let r be the value of the ratio.
r=\(\frac{1.7 \times 10^{5}}{9.07 \times 10^{3}}\)
=\(\frac{1.7}{9.07}\)×10²
=0.18743×10²
=18.743
≈19
The blue whale is 19 times heavier than the elephant.

Engage NY Eureka Math 8th Grade Module 2 Lesson 10 Answer Key

Eureka Math Grade 8 Module 2 Lesson 10 Example Answer Key

Example 1.
The world population is about 7 billion. There are 4.6× 10⁷ ants for every human on the planet. About how many ants are there in the world?
First, write 7 billion in scientific notation: (7× 10⁹).
To find the number of ants in the world, we need to multiply the world population by the known number of ants for each person: (7× 10⁹)(4.6× 10⁷ ).
(7× 10⁹)(4.6× 10⁷ )=(7×4.6)( 10⁹× 10⁷) By repeated use of the associative and commutative properties
=32.2× 10¹⁶ By the first law of exponents
=3.22×10× 10¹⁶
=3.22× 10¹⁷ By the first law of exponents
There are about 3.22× 10¹⁷ ants in the world!

Example 2.
A certain social media company processes about 990 billion likes per year. If the company has approximately 8.9× 10⁸ users of the social media, about how many likes is each user responsible for per year? Write your answer in scientific and standard notation.
First, write 990 billion in scientific notation: 9.9× 10¹¹.
To find the number of likes per person, divide the total number of likes by the total number of users: \(\frac{9.9 \times 10^{11}}{8.9 \times 10^{8}}\)
\(\frac{9.9 \times 10^{11}}{8.9 \times 10^{8}}\) = \(\frac{9.9}{8.9}\)×\(\frac{10^{11}}{10^{8}}\) By the product formula
=1.11235…× 10³ By the first law of exponents
≈1.1× 10³
≈1100
Each user is responsible for about 1.1× 10³, or 1,100, likes per year.

Example 3.
In 2010, Americans generated 2.5× 10⁸ tons of garbage. There are about 2,000 landfills in the United States. Assuming that each landfill is the same size and that trash is divided equally among them, determine how many tons of garbage were sent to each landfill in 2010.
First, write 2,000 in scientific notation: 2× 10³.
To find the number of tons of garbage sent to each landfill, divide the total weight of the garbage by the number of landfills: \(\frac{2.5 \times 10^{8}}{2 \times 10^{3}}\).
\(\frac{2.5 \times 10^{8}}{2 \times 10^{3}}\) = \(\frac{2.5}{2}\)× \(\frac{10^{8}}{10^{3}}\) By the product formula
=1.25× 10⁵ By the first law of exponents
Each landfill received 1.25× 10⁵ tons of garbage in 2010.
Actually, not all garbage went to landfills. Some of it was recycled and composted. The amount of recycled and composted material accounted for about 85 million tons of the 2.5× 10⁸ tons of garbage. Given this new information, how much garbage was actually sent to each landfill?
First, write 85 million in scientific notation: 8.5× 10⁷.
Next, subtract the amount of recycled and composted material from the garbage: 2.5× 10⁸-8.5× 10⁷. To subtract, we must give each number the same order of magnitude and then use the distributive property.
2.5× 10⁸-8.5× 10⁷=(2.5×10)× 10⁷-8.5× 10⁷ By the first law of exponents
=(2.5×10)-8.5))× 10⁷ By the distributive property
=(25-8.5)× 10⁷
=16.5× 10⁷
=1.65×10× 10⁷
=1.65× 10⁸ By the first law of exponents
Now, divide the new amount of garbage by the number of landfills: \(\frac{1.65 \times 10^{8}}{2 \times 10^{3}}\).
\(\frac{1.65 \times 10^{8}}{2 \times 10^{3}}\) = \(\frac{1.65}{2}\)× \(\frac{10^{8}}{10^{3}}\) By the product formula
=0.825× 10⁵ By the first law of exponents
=0.825×10× 10⁴ By the first law of exponents
=8.25× 10⁴
Each landfill actually received 8.25× 10⁴ tons of garbage in 2010.

Eureka Math Grade 8 Module 2 Lesson 10 Exercise Answer Key

Exercise 1.
The speed of light is 300,000,000 meters per second. The sun is approximately 1.5× 10¹¹ meters from Earth. How many seconds does it take for sunlight to reach Earth?
Answer:
300 000 000=3× 10⁸
\(\frac{1.5 \times 10^{11}}{3 \times 10^{8}}\) = \(\frac{1.5}{3}\)×\(\frac{10^{11}}{10^{8}}\)
=0.5× 10³
=0.5×10× 10²
=5× 10²
It takes 500 seconds for sunlight to reach Earth.

Exercise 2.
The mass of the moon is about 7.3× 10²² kg. It would take approximately 26,000,000 moons to equal the mass of the sun. Determine the mass of the sun.
Answer:
26 000 000=2.6× 10⁷
(2.6× 10⁷ )(7.3× 10²²)=(2.6×7.3)( 10⁷× 10²²)
=18.98× 10²⁹
=1.898×10× 10²⁹
=1.898× 10³⁰
The mass of the sun is 1.898× 10³⁰ kg.

Exercise 3.
The mass of Earth is 5.9× 10²4 kg. The mass of Pluto is 13,000,000,000,000,000,000,000 kg. Compared to Pluto, how much greater is Earth’s mass than Pluto’s mass?
Answer:
13 000 000 000 000 000 000 000=1.3× 10²²
5.9× 10²⁴-1.3× 10²²=(5.9× 10² )× 10²²-1.3× 10²²
=(590-1.3)× 10²²
=588.7× 10²²
=5.887× 10²× 10²²
=5.887× 10²⁴
The mass of Earth is 5.887× 10²⁴ kg greater than the mass of Pluto.

Exercise 4.
Using the information in Exercises 2 and 3, find the combined mass of the moon, Earth, and Pluto.
Answer:
7.3× 10²²+1.3× 10²²+5.9× 10²⁴=(7.3× 10²²+1.3× 10²²)+5.9× 10²⁴
=8.6× 10²²+5.9× 10²⁴
=(8.6+590)× 10²²
=598.6× 10²²
=5.986× 10²× 10²²
=5.986× 10²⁴
The combined mass of the moon, Earth, and Pluto is 5.986× 10²⁴ kg.

Exercise 5.
How many combined moon, Earth, and Pluto masses (i.e., the answer to Exercise 4) are needed to equal the mass of the sun (i.e., the answer to Exercise 2)?
Answer:
\(\frac{1.898 \times 10^{30}}{5.986 \times 10^{24}}\)=\(\frac{1.898}{5.986}\) × \(\frac{10^{30}}{10^{24}}\)
≈0.32× 10⁶
=0.32×10× 10⁵
=3.2× 10⁵
It would take 3.2× 10⁵ combined masses of the moon, Earth, and Pluto to equal the mass of the sun.

Eureka Math Grade 8 Module 2 Lesson 10 Problem Set Answer Key

Have students practice operations with numbers written in scientific notation and standard notation.

Question 1.
The sun produces 3.8× 10²⁷ joules of energy per second. How much energy is produced in a year? (Note: a year is approximately 31,000,000 seconds).
Answer:
31 000 000=3.1× 10⁷
(3.8× 10²7 )(3.1× 10⁷ )=(3.8×3.1)( 10²7× 10⁷ )
=11.78× 10³⁴
=1.178×10× 10³⁴
=1.178× 10³⁵
The sun produces 1.178× 10³⁵ joules of energy in a year.

Question 2.
On average, Mercury is about 57,000,000 km from the sun, whereas Neptune is about 4.5× 10⁹ km from the sun. What is the difference between Mercury’s and Neptune’s distances from the sun?
Answer:
57 000 000=5.7× 10⁷
4.5× 10⁹-5.7× 10⁷=(4.5× 10² )× 10⁷-5.7× 10⁷
=450× 10⁷-5.7× 10⁷
=(450-5.7)× 10⁷
=444.3× 10⁷
=4.443× 10²× 10⁷
=4.443× 10⁹
The difference in the distance of Mercury and Neptune from the sun is 4.443× 10⁹ km.

Question 3.
The mass of Earth is approximately 5.9× 10²⁴ kg, and the mass of Venus is approximately 4.9× 10²⁴ kg.
a. Find their combined mass.
Answer:
5.9× 10²⁴+4.9× 10²⁴=(5.9+4.9)× 10²⁴
=10.8× 10²⁴
=1.08×10× 10²⁴
=1.08× 10²⁵
The combined mass of Earth and Venus is 1.08× 10²⁵ kg.

b. Given that the mass of the sun is approximately 1.9× 10³⁰ kg, how many Venuses and Earths would it take to equal the mass of the sun?
Answer:
\(\frac{1.9 \times 10^{30}}{1.08 \times 10^{25}}\) = \(\frac{1.9}{1.08}\) × \(\frac{10^{30}}{10^{25}}\)
=1.75925…× 10⁵
≈1.8× 10⁵
It would take approximately 1.8× 10⁵ Venuses and Earths to equal the mass of the sun.

Eureka Math Grade 8 Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
The speed of light is 3× 10⁸ meters per second. The sun is approximately 230,000,000,000 meters from Mars. How many seconds does it take for sunlight to reach Mars?
Answer:
230 000 000 000=2.3× 10¹¹
\(\frac{2.3 \times 10^{11}}{3 \times 10^{8}}\) =\(\frac{2.3}{3}\)×\(\frac{10^{11}}{10^{8}}\)
=0.7666″…”× 10³
≈0.77×10× 10²
≈7.7× 10²
It takes approximately 770 seconds for sunlight to reach Mars.

Question 2.
If the sun is approximately 1.5× 10¹¹ meters from Earth, what is the approximate distance from Earth to Mars?
Answer:
(2.3× 10¹¹ )-(1.5× 10¹¹ )=(2.3-1.5)× 10¹¹
=0.8× 10¹¹
=0.8×10× 10¹⁰
=8× 10¹⁰
The distance from Earth to Mars is 8× 10¹⁰ meters.

Engage NY Eureka Math 8th Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 8 Module 2 Lesson 9 Exercise Answer Key

Are the following numbers written in scientific notation? If not, state the reason.
Exercise 1
1.908×10¹⁷
Answer:
yes

Exercise 2.
0.325×10^-2
Answer:
no, d<1

Exercise 3.
7.99×10³²
Answer:
yes

Exercise 4.
4.0701+10⁷
Answer:
no, it must be a product

Exercise 5.
18.432×5⁸
Answer:
no, d>10 and it is ×5 instead of ×10

Exercise 6.
8×10^-11
Answer:
yes

Use the table below to complete Exercises 7 and 8.

The table below shows the debt of the three most populous states and the three least populous states.

Exercise 7.
a. What is the sum of the debts for the three most populous states? Express your answer in scientific notation.
Answer:
(4.07×10¹¹ )+(3.37×10¹¹ )+(2.76×10¹¹ )=(4.07+3.37+2.76)×10¹¹
=10.2×10¹¹
=(1.02×10)×10¹¹
=1.02×10¹²

b. What is the sum of the debt for the three least populous states? Express your answer in scientific notation.
Answer:
(4×10⁹ )+(4×10⁹ )+(2×10⁹ )=(4+4+2)×10⁹
=10×10⁹
=(1×10)×10⁹
=1×10¹⁰

c. How much larger is the combined debt of the three most populous states than that of the three least populous states? Express your answer in scientific notation.
Answer:
(1.02×10¹² )-(1×10¹⁰ )=(1.02×10²×10¹⁰ )-(1×10¹⁰ )
=(102×10¹⁰ )-(1×10¹⁰ )
=(102-1)×10¹⁰
=101×10¹⁰
=(1.01×10²)×10¹⁰
=1.01×10¹²

Exercise 8.
a. What is the sum of the population of the three most populous states? Express your answer in scientific notation.
Answer:
(3.8×10⁷ )+(1.9×10⁷ )+(2.6×10⁷ )=(3.8+1.9+2.6)×10⁷
=8.3×10⁷

b. What is the sum of the population of the three least populous states? Express your answer in scientific notation.
Answer:
(6.9×10⁵ )+(6.26×10⁵ )+(5.76×10⁵ )=(6.9+6.26+5.76)×10⁵
=18.92×10⁵
=(1.892×10)×10⁵
=1.892×10⁶

c. Approximately how many times greater is the total population of California, New York, and Texas compared to the total population of North Dakota, Vermont, and Wyoming?
Answer:
\(\frac{8.3 \times 10^{7}}{1.892 \times 10^{6}}\) = \(\frac{8.3}{1.892}\) × \(\frac{10^{7}}{10^{6}}\)
≈4.39×10
=43.9
The combined population of California, New York, and Texas is about 43.9 times greater than the combined population of North Dakota, Vermont, and Wyoming.

Exercise 9.
All planets revolve around the sun in elliptical orbits. Uranus’s furthest distance from the sun is approximately 3.004×10⁹ km, and its closest distance is approximately 2.749×10⁹ km. Using this information, what is the average distance of Uranus from the sun?
Answer:
average distance = \(\frac{\left(3.004 \times 10^{9}\right)+\left(2.749 \times 10^{9}\right)}{2}\)
= \(\frac{(3.004+2.749) \times 10^{9}}{2}\)
= \(\frac{5.753 \times 10^{9}}{2}\)
=2.8765×10⁹
On average, Uranus is 2.8765×10⁹ km from the sun.

Eureka Math Grade 8 Module 2 Lesson 9 Problem Set Answer Key

Students practice working with numbers written in scientific notation.

Question 1.
Write the number 68,127,000,000,000,000 in scientific notation. Which of the two representations of this number do you prefer? Explain.
Answer:
68 127 000 000 000 000=6.8127×10¹⁶
Most likely, students will say that they like the scientific notation better because it allows them to write less. However, they should also take note of the fact that counting the number of zeros in 68,127,000,000,000,000 is a nightmare. A strong reason for using scientific notation is to circumvent this difficulty: right away, the exponent 16 shows that this is a 17-digit number.

Question 2.
Here are the masses of the so-called inner planets of the solar system.
Mercury: 3.3022×10²³ kg
Earth: 5.9722×10²⁴ kg
Venus: 4.8685×10²⁴ kg
Mars: 6.4185×10²³ kg
What is the average mass of all four inner planets? Write your answer in scientific notation.
Answer:

= 29.531925×10²³
= 2.9531925×10²⁴
The average mass of the inner planets is 2.9531925×10²⁴ kg.

Eureka Math Grade 8 Module 2 Lesson 9 Exit Ticket Answer Key

Question 1.
The approximate total surface area of Earth is 5.1×10⁸ km². All the salt water on Earth has an approximate surface area of 352,000,000 km², and all the fresh water on Earth has an approximate surface area of
9×10⁶ km². How much of Earth’s surface is covered by water, including both salt and fresh water? Write your answer in scientific notation.
Answer:
(3.52×10⁸ )+(9×10⁶ )=(3.52×10²×10⁶ )+(9×10⁶ )
=(352×10⁶ )+(9×10⁶ )
=(352+9)×10⁶
=361×10⁶
=3.61×10⁸
The Earth’s surface is covered by 3.61×10⁸ km² of water.

Question 2.
How much of Earth’s surface is covered by land? Write your answer in scientific notation.
Answer:
(5.1×10⁸ )-(3.61×10⁸ )=(5.1-3.61)×10⁸
=1.49×10⁸
The Earth’s surface is covered by 1.49×10⁸ km² of land.

Question 3.
Approximately how many times greater is the amount of Earth’s surface that is covered by water compared to the amount of Earth’s surface that is covered by land?
Answer:
\(\frac{3.61 \times 10^{8}}{1.49 \times 10^{8}}\)≈2.4
About 2.4 times more of the Earth’s surface is covered by water than by land.

Engage NY Eureka Math 8th Grade Module 2 Lesson 16 Answer Key

Engage NY Math 8th Grade Module 2 Lesson 16 Example Answer Key

Example 1.
Given a right triangle with a hypotenuse with length 13 units and a leg with length 5 units, as shown, determine the length of the other leg.

Answer:
5² +b² =13²
5² – 5² + b² =13² -5²
b² =13² -5²
b² =169-25
b² =144
b=12
The length of the leg is 12 units.

→ Let b represent the missing leg of the right triangle; then, by the Pythagorean theorem:
5² +b² =13².
→ If we let a represent the missing leg of the right triangle, then by the Pythagorean theorem:
a² +5² =13².
→ Which of these two equations is correct: 5² +b² =13² or a² +5² =13² ?

→ It does not matter which equation we use as long as we are showing the sum of the squares of the legs as equal to the square of the hypotenuse.
→ Using the first of our two equations, 5² +b² =13², what can we do to solve for b in the equation?
→ We need to subtract 5² from both sides of the equation.
5² + b² =13²
5² – 5² + b² =13² -5²
b² =13² -5²
→ Point out to students that we are looking at the Pythagorean theorem in a form that allows us to find the length of one of the legs of the right triangle. That is, b² =c² -a² .
→ The length of the leg of the right triangle is 12 units.

Example 2.
The Pythagorean theorem as it applies to missing side lengths of triangles in a real-world problem:
→ Suppose you have a ladder of length 13 feet. Suppose that to make it sturdy enough to climb, you must place the ladder exactly 5 feet from the wall of a building. You need to post a banner on the building 10 feet above the ground. Is the ladder long enough for you to reach the location you need to post the banner?

The ladder against the wall forms a right angle. For that reason, we can use the Pythagorean theorem to find out how far up the wall the ladder will reach. If we let h represent the height the ladder can reach, what equation will represent this problem?
→ 5² +h² =13² or h² =13² -5²

→ Using either equation, we see that this is just like Example 1. We know that the missing side of the triangle is 12 feet. Is the ladder long enough for you to reach the 10-foot banner location?
→ Yes, the ladder allows us to reach 12 feet up the wall.

Example 3.
Pythagorean theorem as it applies to missing side lengths of a right triangle:
→ Given a right triangle with a hypotenuse of length 15 units and a leg of length 9, what is the length of the other leg?

→ If we let the length of the missing leg be represented by a, what equation will allow us to determine its value?
→ a² +9² =15² or a² =15² -9²
→ Finish the computation:
a² =225-81
a² =144
a=12
→ The length of the missing leg of this triangle is 12 units.

Eureka Math Grade 8 Module 2 Lesson 16 Exercise Answer Key

Exercises 1–2

Exercise 1.
Use the Pythagorean theorem to find the missing length of the leg in the right triangle.
Answer:

Let b represent the missing leg length; then,
15² +b² =25²
15² -15² +b² =25² -15²
b² =625-225
b² =400
b=20
The length of the leg is 20 units.

Exercise 2.
You have a 15-foot ladder and need to reach exactly 9 feet up the wall. How far away from the wall should you place the ladder so that you can reach your desired location?
Answer:

Let a represent the distance the ladder must be placed from the wall; then,
a² +9² =15²
a² +9² -9² =15² -9²
a² =225-81
a² =144
a=12.
The ladder must be placed exactly 12 feet from the wall.

Exercises 3–6

Exercise 3.
Find the length of the segment AB, if possible.

Answer:
If we let the length of segment AB be represented by c, then
3² +4² =c²
9+16=c²
25=c²
5=c.
The length of segment AB is 5 units.

Exercise 4.
Given a rectangle with dimensions 5 cm and 10 cm, as shown, find the length of the diagonal, if possible.

Answer:
Let c represent the length of the diagonal; then,
c² =5² +10²
c² =25+100
c² =125.
The measure of the length of the hypotenuse in centimeters is the positive number c that satisfies c² =125.

Exercise 5.
A right triangle has a hypotenuse of length 13 in. and a leg with length 4 in. What is the length of the other leg?
Answer:
If we let a represent the length of the other leg, then
a² +4² =13²
a² +4² -4² =13² -4²
a² =13² -4²
a² =169-16
a² =153
The measure of the length of the leg in inches is the positive number a that satisfies a² =153.

Exercise 6.
Find the length of b in the right triangle below, if possible.

Answer:
By the Pythagorean theorem,
4² +b² =11²
4² -4² +b² =11² -4²
b² =11² -4²
b² =121-16
a² =105.
The length of side AC is the positive number b that satisfies b² =105.

Eureka Math Grade 8 Module 2 Lesson 16 Problem Set Answer Key

Students practice using the Pythagorean theorem to find missing lengths in right triangles.

Question 1.
Find the length of the segment AB shown below, if possible.

Answer:
If we let the length of segment AB be represented by c units, then by the Pythagorean theorem
6² +8² =c²
36+48=c²
100=c²
10=c
The length of the segment AB is 10 units.

Question 2.
A 20-foot ladder is placed 12 feet from the wall, as shown. How high up the wall will the ladder reach?

Answer:
Let the height up the wall that the ladder will reach be a feet. Then,
a² +12² =20²
a² +12² -12² =20² -12²
a² =20² -12²
a² =400-144
a² =256
a=16
The ladder will reach 16 feet up the wall.

Question 3.
A rectangle has dimensions 6 in. by 12 in. What is the length of the diagonal of the rectangle?
Answer:
Let the length of the diagonal be c inches. Then c is a positive number that satisfies
6² +12² =c²
36+144=c²
80=c² .
The measure of the length of the diagonal in inches is the positive number c that satisfies c² =180.

Use the Pythagorean theorem to find the missing side lengths for the triangles shown in Problems 4–8.

Question 4.
Determine the length of the missing side, if possible.

12²+b²=13²
12²-12²+b²=〖13²-12²
b² =13²-12²
b²=169-144
b²=25
b=5
The length of the missing side is 5 units.

Question 5.
Determine the length of the missing side, if possible.

Answer:
a²+3²=8²
a²+3²-3²=8²-3²
a²=8²-3²
a²=64-9
a²=55)
The number of units of the side is given by the positive number a that satisfies a²=55.

Question 6.
Determine the length of the missing side, if possible.

Answer:
7²+b²=10²
7²-7²+b²=10²-7²
b²=10²-7²
b²=100-49
b²=51
The number of units of the side is given by the positive number b that satisfies b²=51.

Question 7.
Determine the length of the missing side, if possible.

Answer:
a²+1²=5²
a²+1²-1²=5²-1²
a²=5²-1²
a²=25-1
a²=24
The number of units of the side is given by the positive number a that satisfies a²=24.

Question 8.
Determine the length of the missing side, if possible.

Answer:
a²+9²=14²
a²+9²-9²=14²-9²
a²=14²-9²
a²=196-81
a²=115
The number of units of the side is given by the positive number a that satisfies a²=115.

Eureka Math Grade 8 Module 2 Lesson 16 Exit Ticket Answer Key

Question 1.
Find the length of the missing side of the rectangle shown below, if possible.

Answer:
Let the length of the unknown leg be a units. Then,
a² +7² =12²
a² +7² -7² =12² -7²
a² =12² -7²
a² =144-49
a² =95.
The number of units of the side is given by the positive number a that satisfies a² =95.

Question 2.
Find the length of all three sides of the right triangle shown below, if possible.

Answer:

The two legs are each 5 units in length. If the hypotenuse is c units in length, then c is a positive number that satisfies
5²+5²=c²
25+25=c²
50=c².
The length of the hypotenuse is given by the positive number c that satisfies c² =50 units.

Engage NY Eureka Math 8th Grade Module 2 Lesson 15 Answer Key

Eureka Math Grade 8 Module 2 Lesson 15 Example Answer Key

Example 1.
Now that we know what the Pythagorean theorem is, let’s practice using it to find the length of a hypotenuse of a right triangle.
Determine the length of the hypotenuse of the right triangle.

The Pythagorean theorem states that for right triangles a² +b² =c² , where a and b are the legs, and c is the hypotenuse. Then,
a² +b² =c²
6² +8² =c²
36+64=c²
100=c².
Since we know that 100=10², we can say that the hypotenuse c is 10.

Example 2.
Determine the length of the hypotenuse of the right triangle.

→ Based on our work in the last example, what should we do to find the length of the hypotenuse?
→ Use the Pythagorean theorem, and replace a and b with 3 and 7. Then,
a² + b² = c²
3² +7² =c²
9+49=c²
58=c²
→ Since we do not know what number times itself produces 58, for now we can leave our answer as 58=c² . Later this year, we learn how to determine the actual value for c for problems like this one.

Eureka Math Grade 8 Module 2 Lesson 15 Exercise Answer Key

Exercises 1–5
For each of the exercises, determine the length of the hypotenuse of the right triangle shown. Note: Figures are not drawn to scale.

Question 1.

Answer:
a² +b² =c²
3² +4² =c²
9+16=c²
25=c²
5=c

Question 2.

Answer:
a² +b² =c²
8² +11² =c²
64+121=c²
185=c²

Question 3.

Answer:
a² +b² =c²
4² +9² =c²
16+81=c²
97=c²

Question 4.

Answer:
a² +b² =c²
2² +5² =c²
4+25=c²
29=c²

Question 5.

Answer:
a² +b² =c²
1² +9² =c²
1+81=c²
82=c²

Eureka Math Grade 8 Module 2 Lesson 15 Problem Set Answer Key

Students practice using the Pythagorean theorem to find the length of the hypotenuse of a right triangle.

For each of the problems below, determine the length of the hypotenuse of the right triangle shown. Note: Figures are not drawn to scale.

Question 1.

Answer:
a² +b² =c²
3² +9² =c²
9+81=c²
90=c²

Question 2.

Answer:
a² +b² =c²
8² +2² =c²
64+4=c²
68=c²

Question 3.

Answer:
a² +b² =c²
9² +2² =c²
81+4=c²
85=c²

Question 4.

Answer:
a² +b² =c²
7² +1² =c²
49+1=c²
50=c²

Question 5.

Answer:
a² +b² =c²
6² +3² =c²
36+9=c²
45=c²

Question 6.

Answer:
a² +b² =c²
4² +3² =c²
16+9=c²
25=c²
5=c

Question 7.

Answer:
a² +b² =c²
4² +2² =c²
16+4=c²
20=c²

Question 8.

Answer:
a² +b² =c²
12² +5² =c²
144+25=c²
169=c²
13=c

Question 9.

Answer:
a² +b² =c²
13² +8² =c²
169+64=c²
233=c²

Question 10.

Answer:
a² +b² =c²
10² +7² =c²
100+49=c²
149=c²

Question 11.

Answer:
a² +b² =c²
12² +9² =c²
144+81=c²
225=c²
15=c

Question 12.

Answer:
a² +b² =c²
5² +1² =c²
25+1=c²
26=c²

Eureka Math Grade 8 Module 2 Lesson 15 Exit Ticket Answer Key

Question 1.
Label the sides of the right triangle with leg, leg, and hypotenuse.

Answer:

Question 2.
Determine the length of c in the triangle shown.

Answer:
a² +b² =c²
6² +8² =c²
36+64=c²
100=c²
10=c

Question 3.
Determine the length of c in the triangle shown.

Answer:
a² +b² =c²
4² +7² =c²
16+49=c²
65=c²

Engage NY Eureka Math 8th Grade Module 2 Lesson 7 Answer Key

Eureka Math Grade 8 Module 2 Lesson 7 Exercise Answer Key

Exercise 1.
Let M=993,456,789,098,765. Find the smallest power of 10 that will exceed M.
Answer:
M=993 456 789 098 765<999 999 999 999 999 < 1 000 000 000 000 000=10¹⁵. Because M has 15 digits, 10¹⁵ will exceed it.

Exercise 2.
Let M=78,491\(\frac{899}{987}\). Find the smallest power of 10 that will exceed M.
Answer:
M=78491\(\frac{899}{987}\)<78492<99999<100 000=10⁵.
Therefore, 10⁵ will exceed M.

Exercise 3.
Let M be a positive integer. Explain how to find the smallest power of 10 that exceeds it.
Answer:
If M is a positive integer, then the power of 10 that exceeds it will be equal to the number of digits in M. For example, if M were a 10-digit number, then 10¹⁰ would exceed M. If M is a positive number, but not an integer, then the power of 10 that would exceed it would be the same power of 10 that would exceed the integer to the right of M on a number line. For example, if M=5678.9, the integer to the right of M is 5,679. Then based on the first explanation, 10⁴ exceeds both this integer and M; this is because M=5678.9<5679<10 000=10⁴.

Exercise 4.
The chance of you having the same DNA as another person (other than an identical twin) is approximately 1 in 10 trillion (one trillion is a 1 followed by 12 zeros). Given the fraction, express this very small number using a negative power of 10.
\(\frac{1}{10000000000000}\)=
Answer:
\(\frac{1}{10000000000000}\)=\(\frac{1}{10^{13}}\) =10¹³

Exercise 5.
The chance of winning a big lottery prize is about 10^-8, and the chance of being struck by lightning in the U.S. in any given year is about 0.000 001. Which do you have a greater chance of experiencing? Explain.
Answer:
0.000 001=10^-6
There is a greater chance of experiencing a lightning strike. On a number line, 10^-8 is to the left of 10^-6. Both numbers are less than one (one signifies 100% probability of occurring). Therefore, the probability of the event that is greater is 10^-6—that is, getting struck by lightning.

Exercise 6.
There are about 100 million smartphones in the U.S. Your teacher has one smartphone. What share of U.S. smartphones does your teacher have? Express your answer using a negative power of 10.
Answer:
\(\frac{1}{100000000}\) = \(\frac{1}{10^{8}}\) = 10^-8

Eureka Math Grade 8 Module 2 Lesson 7 Exit Ticket Answer Key

Question 1.
Let M=118,526.65902. Find the smallest power of 10 that will exceed M.
Answer:
Since M=118,526.65902<118,527<1,000,000<10⁶, then 10⁶will exceed M.

Question 2.
Scott said that 0.09 was a bigger number than 0.1. Use powers of 10 to show that he is wrong.
Answer:
We can rewrite 0.09 as \(\frac{9}{10^{2}}\) =9×10^-2 and rewrite 0.1 as \(\frac{1}{10^{1}}\) =1×10^-1. Because 0.09 has a smaller power of 10, 0.09 is closer to zero and is smaller than 0.1.

Eureka Math Grade 8 Module 2 Lesson 7 Problem Set Answer Key

Question 1.
What is the smallest power of 10 that would exceed 987,654,321,098,765,432?
Answer:
987 654 321 098 765 432<999 999 999 999 999 999<1 000 000 000 000 000 000=10¹⁸

Question 2.
What is the smallest power of 10 that would exceed 999,999,999,991?
Answer:
999 999 999 991<999 999 999 999<1 000 000 000 000=10¹²

Question 3.
Which number is equivalent to 0.000 000 1: 10⁷or 10^-7? How do you know?
Answer:
0.000 000 1=10^-7. Negative powers of 10 denote numbers greater than zero but less than 1. Also, the decimal 0.000 000 1 is equal to the fraction \(\frac{1}{10^{7}}\), which is equivalent to 10^-7.

Question 4.
Sarah said that 0.000 01 is bigger than 0.001 because the first number has more digits to the right of the decimal point. Is Sarah correct? Explain your thinking using negative powers of 10 and the number line.
Answer:
0.000 01= \(\frac{1}{100000}\) =10^-5 and 0.001= \(\frac{1}{1000}\) =10^-3. On a number line, 10^-5 is closer to zero than 10^-3; therefore, 10^-5 is the smaller number, and Sarah is incorrect.

Question 5.
Order the following numbers from least to greatest:

Answer:
10^-99<10^-17<10^-5<10⁵<10¹⁴<10³⁰