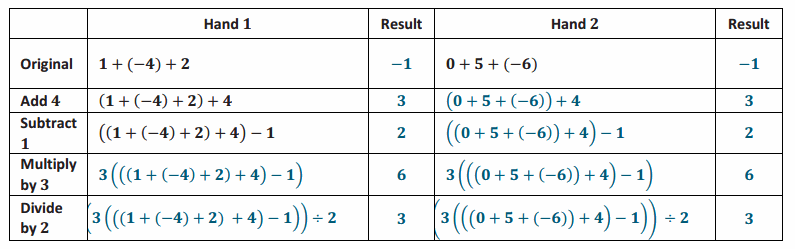
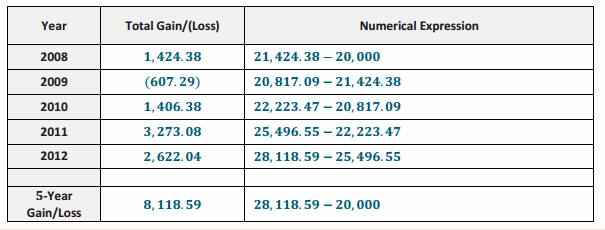
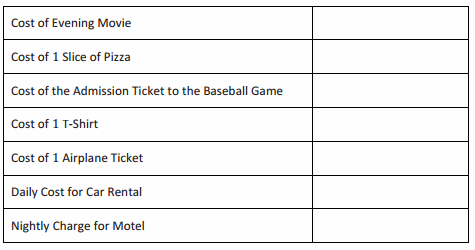
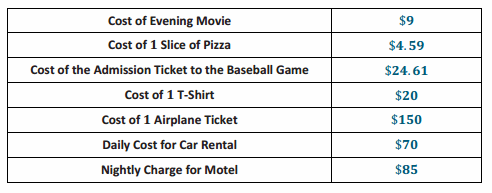
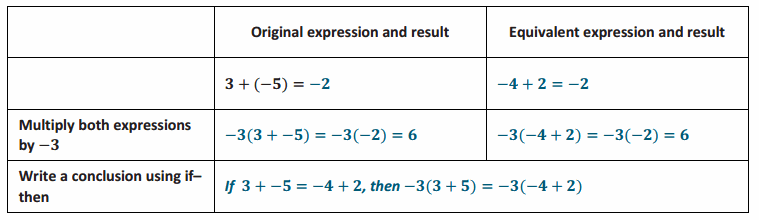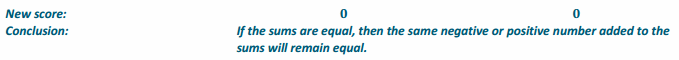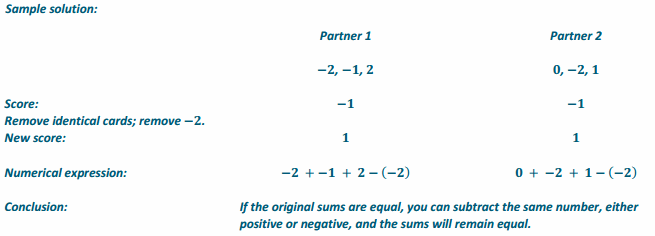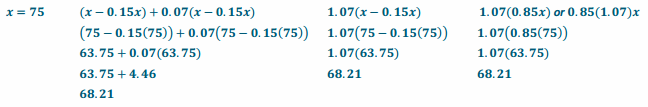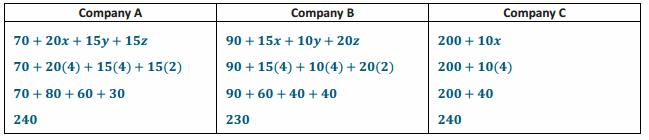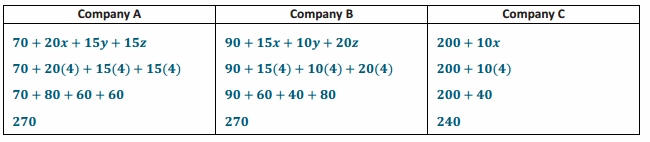Engage NY Eureka Math 7th Grade Module 3 Lesson 2 Answer Key
Eureka Math Grade 7 Module 3 Lesson 2 Example Answer Key
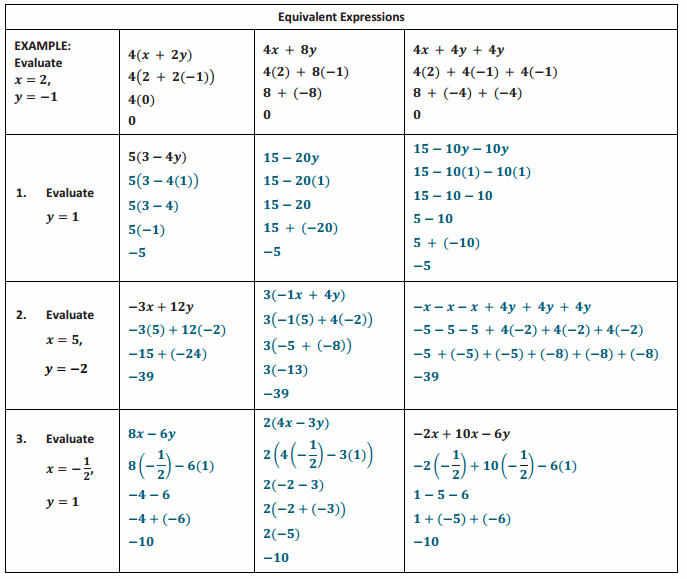
Example 1.
Subtracting Expressions
a. Subtract: (40 + 9) – (30 + 2).
Answer:
The opposite of a sum is the sum of its opposites. Order of operations
40 + 9 + (- (30 + 2))
40 + 9 + (- 30) + (- 2)
49 + (- 30) + (- 2)
19 + (- 2)
17
(40 + 9)- (30 + 2)
(49)- (32)
17
b. Subtract: (3x + 5y – 4) – (4x + 11).
Answer:
3x + 5y + ( – 4) + ( – (4x + 11)) Subtraction as adding the opposite
3x + 5y + ( – 4) + ( – 4x) + ( – 11) The opposite of a sum is the sum of its opposites.
3x + ( – 4x) + 5y + ( – 4) + ( – 11) Any order, any grouping
– x + 5y + ( – 15) Combining like terms
– x + 5y – 15 Subtraction replaces adding the opposite.
Have students check the equivalency of the expressions by substituting 2 for x and 6 for y.
(3x + 5y – 4) – (4x + 11)
(3(2) + 5(6) – 4) – (4(2) + 11)
(6 + 30 – 4) – (8 + 11)
(36 – 4) – (19)
32 – 19
13
– x + 5y – 15
– (2) + 5(6) – 15
– 2 + 30 + ( – 15)
28 + ( – 15)
13
→ When writing the difference as adding the expression’s opposite in Example 1(b), what happens to the grouped terms that are being subtracted?
→ When the subtraction is changed to addition, every term in the parentheses that follows must be converted to its opposite.
Example 2.
Combining Expressions Vertically
a. Find the sum by aligning the expressions vertically.
(5a + 3b – 6c) + (2a – 4b + 13c)
Answer:
(5a + 3b + ( – 6c)) + (2a + ( – 4b) + 13c) Subtraction as adding the opposite

7a – b + 7c Adding the opposite is equivalent to subtraction.
b. Find the difference by aligning the expressions vertically.
(2x + 3y – 4) – (5x + 2)
Answer:
(2x + 3y + ( – 4)) + ( – 5x + ( – 2)) Subtraction as adding the opposite

– 3x + 3y – 6 Adding the opposite is equivalent to subtraction.
Students should recognize that the subtracted expression in Example 1(b) did not include a term containing the variable y, so the 3y from the first grouped expression remains unchanged in the answer.
Example 3.
Using Expressions to Solve Problems
A stick is x meters long. A string is 4 times as long as the stick.
a. Express the length of the string in terms of x.
Answer:
The length of the stick in meters is x meters, so the string is 4∙x, or 4x, meters long.
b. If the total length of the string and the stick is 15 meters long, how long is the string?
Answer:
The length of the stick and the string together in meters can be represented by x + 4x, or 5x. If the length of the stick and string together is 15 meters, the length of the stick is 3 meters, and the length of the string is 12 meters.
Example 4.
Expressions from Word Problems
It costs Margo a processing fee of $3 to rent a storage unit, plus $17 per month to keep her belongings in the unit. Her friend Carissa wants to store a box of her belongings in Margo’s storage unit and tells her that she will pay her $1 toward the processing fee and $3 for every month that she keeps the box in storage. Write an expression in standard form that represents how much Margo will have to pay for the storage unit if Carissa contributes. Then, determine how much Margo will pay if she uses the storage unit for 6 months.
Answer:
Let m represent the number of months that the storage unit is rented.
(17m + 3) – (3m + 1) Original expression
17m + 3 + ( – (3m + 1)) Subtraction as adding the opposite
17m + 3 + ( – 3m) + ( – 1) The opposite of the sum is the sum of its opposites.
17m + ( – 3m) + 3 + ( – 1) Any order, any grouping
14m + 2 Combined like terms
This means that Margo will have to pay only $2 of the processing fee and $14 per month that the storage unit is used.
14(6) + 2
84 + 2
86
Margo will pay $86 toward the storage unit rental for 6 months of use.
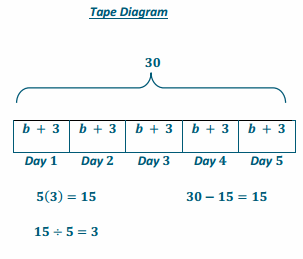
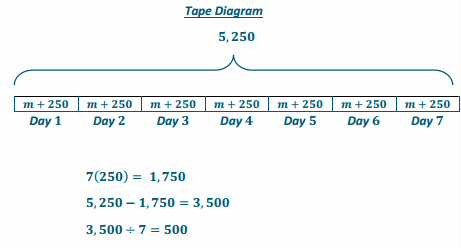
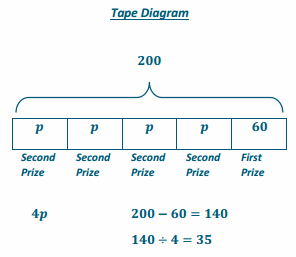
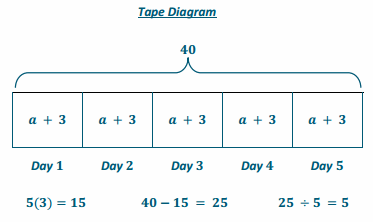
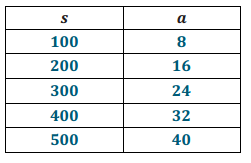
Example 5.
Extending Use of the Inverse to Division

Answer:
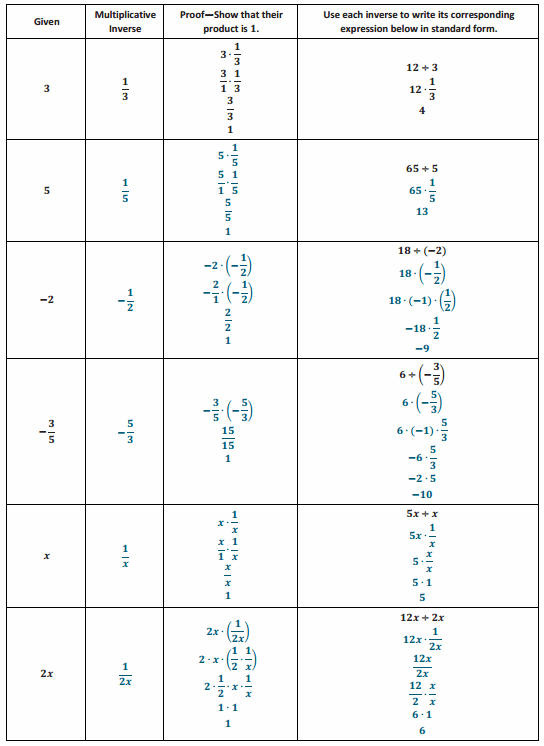
Eureka Math Grade 7 Module 3 Lesson 2 Opening Exercise Answer Key
Opening Exercise
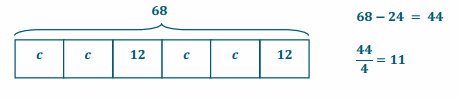
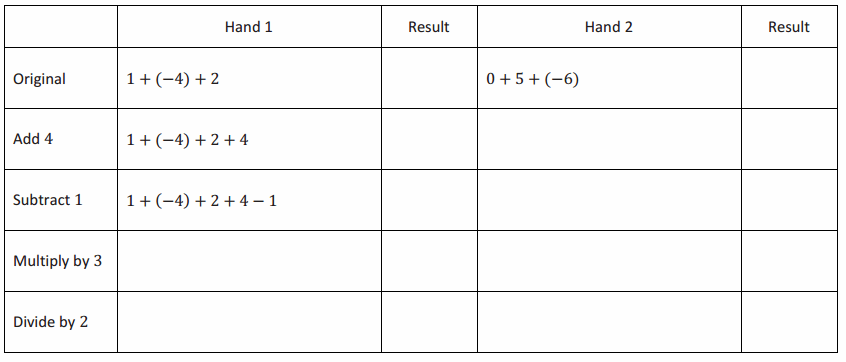
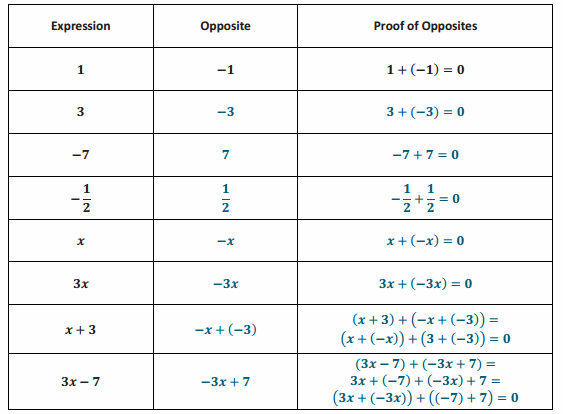
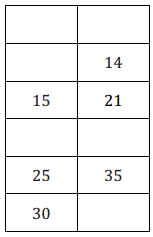
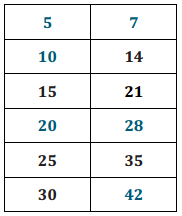
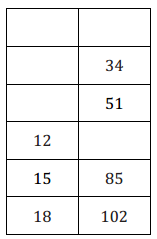
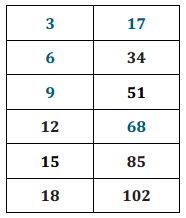
Additive inverses have a sum of zero. Fill in the center column of the table with the opposite of the given number or expression, then show the proof that they are opposites. The first row is completed for you.
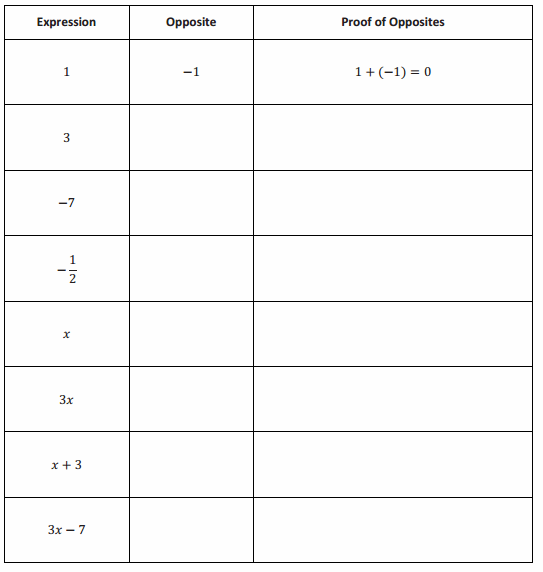
Answer:
Eureka Math Grade 7 Module 3 Lesson 2 Problem Set Answer Key
Question 1.
Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating each expression using x=5.
a. 3x + (2 – 4x)
Answer:
3x + (2 – 4x)
– x + 2
– 5 + 2
– 3
3(5) + (2 – 4(5))
15 + (2 + ( – 20))
15 + ( – 18)
– 3
b. 3x + ( – 2 + 4x)
Answer:
3x + ( – 2 + 4x)
7x – 2
7(5) – 2
35 – 2
33
3(5) + ( – 2 + 4(5))
15 + ( – 2 + 20)
15 + 18
33
c. – 3x + (2 + 4x)
Answer:
– 3x + (2 + 4x)
x + 2
5 + 2
7
– 3(5) + (2 + 4(5))
– 15 + (2 + 20)
– 15 + 22
7
d. 3x + ( – 2 – 4x)
Answer:
3x + ( – 2 – 4x)
– x – 2
– 5 – 2
– 7
3(5) + ( – 2 – 4(5))
15 + ( – 2 + ( – 4(5)))
15 + ( – 2 + ( – 20))
15 + ( – 22)
– 7
e. 3x – (2 + 4x)
Answer:
3x – (2 + 4x)
– x – 2
– 5 – 2
– 7
3(5) – (2 + 4(5))
15 – (2 + 20)
15 – 22
15 + ( – 22)
– 7
f. 3x – ( – 2 + 4x)
Answer:
3x – ( – 2 + 4x)
– x + 2
– 5 + 2
– 3
3(5) – ( – 2 + 4(5))
15 – ( – 2 + 20)
15 – (18)
15 + ( – 18)
– 3
g. 3x – ( – 2 – 4x)
Answer:
3x – ( – 2 – 4x)
7x + 2
7(5) + 2
35 + 2
37
3(5) – ( – 2 – 4(5))
15 – ( – 2 + ( – 4(5)))
15 – ( – 2 + ( – 20))
15 – ( – 22)
15 + 22
37
h. 3x – (2 – 4x)
Answer:
3x – (2 – 4x)
7x – 2
7(5) – 2
35 – 2
33
3(5) – (2 – 4(5))
15 – (2 + ( – 4(5)))
15 – (2 + ( – 20))
15 – ( – 18)
15 + 18
33
i. – 3x – ( – 2 – 4x)
Answer:
– 3x – ( – 2 – 4x)
x + 2
5 + 2
7
– 3(5) – ( – 2 – 4(5))
– 15 – ( – 2 + ( – 4(5)))
– 15 – ( – 2 + ( – 20))
– 15 – ( – 22)
– 15 + 22
7
j. In problems (a)–(d) above, what effect does addition have on the terms in parentheses when you removed the parentheses?
Answer:
By the any grouping property, the terms remained the same with or without the parentheses.
k. In problems (e)–(i), what effect does subtraction have on the terms in parentheses when you removed the parentheses?
Answer:
The opposite of a sum is the sum of the opposites; each term within the parentheses is changed to its opposite.
Question 2.
Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating each expression for the given value of the variable.
a. 4y – (3 + y); y=2
Answer:
4y – (3 + y)
3y – 3
3(2) – 3
6 – 3
3
4(2) – (3 + 2)
8 – 5
8 + ( – 5)
3
b. (2b + 1) – b; b= – 4
Answer:
(2b + 1) – b
b + 1
– 4 + 1
– 3
(2( – 4) + 1) – ( – 4)
( – 8 + 1) + 4
( – 7) + 4
– 3
c. (6c – 4) – (c – 3); c= – 7
Answer:
(6c – 4) – (c – 3)
5c – 1
5( – 7) – 1
– 35 – 1
– 36
(6( – 7) – 4) – ( – 7 – 3)
( – 42 – 4) – ( – 10)
– 42 + ( – 4) + (10)
– 46 + 10
– 36
d. (d + 3d) – ( – d + 2); d=3
Answer:
(d + 3d) – ( – d + 2)
5d – 2
5(3) – 2
15 – 2
13
(3 + 3(3)) – ( – 3 + 2)
(3 + 9) – ( – 1)
12 + 1
13
e. ( – 5x – 4) – ( – 2 – 5x); x=3
Answer:
– 2
( – 5(3) – 4) – ( – 2 – 5(3))
( – 15 – 4) – ( – 2 – 15)
( – 19) – ( – 17)
( – 19) + 17
– 2
f. 11f – ( – 2f + 2); f=\(\frac{1}{2}\)
13f – 2
13(\(\frac{1}{2}\) ) – 2
\(\frac{13}{2}\) – 2
6 \(\frac{1}{2}\) – 2
4 \(\frac{1}{2}\)
11(\(\frac{1}{2}\) ) – ( – 2(\(\frac{1}{2}\) ) + 2)
1\(\frac{1}{2}\) – ( – 1 + 2)
1\(\frac{1}{2}\) – 1
1\(\frac{1}{2}\) + ( – \(\frac{2}{2}\) )
\(\frac{9}{2}\)
4 \(\frac{1}{2}\)
g. – 5g + (6g – 4); g= – 2
Answer:
– 5g + (6g – 4)
g – 4
– 2 – 4
– 6
– 5( – 2) + (6( – 2) – 4)
10 + ( – 12 – 4)
10 + ( – 12 + ( – 4))
10 + ( – 16)
– 6
h. (8h – 1) – (h + 3); h= – 3
Answer:
(8h – 1) – (h + 3)
7h – 4
7( – 3) – 4
– 21 – 4
– 25
(8( – 3) – 1) – ( – 3 + 3)
( – 24 – 1) – (0)
( – 25) – 0
– 25
i. (7 + w) – (w + 7); w= – 4
Answer
(7 + w) – (w + 7)
0
(7 + ( – 4)) – ( – 4 + 7)
3 – 3
3 + ( – 3)
0
j. (2g + 9h – 5) – (6g – 4h + 2); g= – 2 and h=5
Answer:
(2g + 9h – 5) – (6g – 4h + 2)
– 4g + 13h – 7
– 4( – 2) + 13(5) – 7
8 + 65 + ( – 7)
73 + ( – 7)
66
(2( – 2) + 9(5) – 5) – (6( – 2) – 4(5) + 2)
( – 4 + 45 – 5) – ( – 12 + ( – 4(5)) + 2)
(41 – 5) – ( – 12 + ( – 20) + 2)
(41 + ( – 5)) – ( – 32 + 2)
36 – ( – 30)
36 + 30
66
Question 3.
Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating both expressions for the given value of the variable.
a. – 3(8x); x=\(\frac{1}{4}\)
Answer:
– 3(8x)
– 24x
– 24(\(\frac{1}{4}\) )
– 24/4
– 6
– 3(8(\(\frac{1}{4}\) ))
– 3(2)
– 6
b. 5∙k∙( – 7); k=\(\frac{3}{5}\)
Answer:
5∙k∙( – 7)
– 35k
– 35(\(\frac{3}{5}\) )
– 105/5
– 21
5(\(\frac{3}{5}\) )( – 7)
3( – 7)
– 21
c. 2( – 6x)∙2; x=\(\frac{3}{4}\)
Answer:
2( – 6x)∙2
– 24x
– 24(\(\frac{3}{4}\) )
– \(\frac{72}{4}\)
– 18
2( – 6(\(\frac{3}{4}\) ))∙2
2( – 3(\(\frac{3}{2}\) ))∙2
2( – 3)(\(\frac{3}{2}\) )(2)
– 6(3)
– 18
d. – 3(8x) + 6(4x); x=2
Answer:
– 3(8x) + 6(4x)
0
– 3(8(2)) + 6(4(2))
– 3(16) + 6(8)
– 48 + 48
0
e. 8(5m) + 2(3m); m= – 2
Answer:
8(5m) + 2(3m)
46m
46( – 2)
– 92
8(5( – 2)) + 2(3( – 2))
8( – 10) + 2( – 6)
– 80 + ( – 12)
– 92
f. – 6(2v) + 3a(3); v=\(\frac{1}{3}\) ; a=\(\frac{2}{3}\)
Answer:
– 6(2v) + 3a(3); v=\(\frac{1}{3}\)
– 6(2v) + 3a(3)
– 12v + 9a
– 12(\(\frac{1}{3}\) ) + 9(\(\frac{2}{3}\) )
– 1\(\frac{2}{3}\) + \(\frac{18}{3}\)
– 4 + 6
2
– 6(2(\(\frac{1}{3}\) )) + 3(\(\frac{2}{3}\) )(3)
– 6(\(\frac{2}{3}\) ) + 2(3)
– 4 + 6
2
Question 4.
Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating both expressions for the given value of the variable
a. 8x ÷ 2; x= – \(\frac{1}{4}\)
Answer:
8x ÷ 2
4x
4( – \(\frac{1}{4}\) )
– 1
8( – \(\frac{1}{4}\) ) ÷ 2
– 2 ÷ 2
– 1
b. 18w ÷ 6; w=6
Answer:
18w ÷ 6
3w
3(6)
18
18(6) ÷ 6
108 ÷ 6
18
c. 25r ÷ 5r; r= – 2
Answer:
25r ÷ 5r
5
25( – 2) ÷ (5( – 2))
– 50 ÷ ( – 10)
5
d. 33y ÷ 11y; y= – 2
Answer:
33y ÷ 11y
3
33( – 2) ÷ (11( – 2))
( – 66) ÷ ( – 22)
3
e. 56k ÷ 2k; k=3
Answer:
56k ÷ 2k
28
56(3) ÷ (2(3))
168 ÷ 6
28
f. 24xy ÷ 6y; x= – 2;y=3
Answer:
24xy ÷ 6y
4x
4( – 2)
– 8
24( – 2)(3) ÷ (6(3))
– 48(3) ÷ 18
– 144 ÷ 18
– 8
Question 5.
For each problem (a)–(g), write an expression in standard form.
a. Find the sum of – 3x and 8x.
Answer:
– 3x + 8x
5x
b. Find the sum of – 7g and 4g + 2.
Answer:
– 7g + (4g + 2)
– 3g + 2
c. Find the difference when 6h is subtracted from 2h – 4.
Answer:
(2h – 4) – 6h
– 4h – 4
d. Find the difference when – 3n – 7 is subtracted from n + 4.
Answer:
(n + 4) – ( – 3n – 7)
4n + 11
e. Find the result when 13v + 2 is subtracted from 11 + 5v.
Answer:
(11 + 5v) – (13v + 2)
– 8v + 9
f. Find the result when – 18m – 4 is added to 4m – 14.
Answer:
(4m – 14) + ( – 18m – 4)
– 14m – 18
g. What is the result when – 2x + 9 is taken away from – 7x + 2?
Answer:
( – 7x + 2) – ( – 2x + 9)
– 5x – 7
Question 6.
Marty and Stewart are stuffing envelopes with index cards. They are putting x index cards in each envelope. When they are finished, Marty has 15 stuffed envelopes and 4 extra index cards, and Stewart has 12 stuffed envelopes and 6 extra index cards. Write an expression in standard form that represents the number of index cards the boys started with. Explain what your expression means.
Answer:
They inserted the same number of index cards in each envelope, but that number is unknown, x. An expression that represents Marty’s index cards is 15x + 4 because he had 15 envelopes and 4 cards left over. An expression that represents Stewart’s index cards is 12x + 6 because he had 12 envelopes and 6 left over cards. Their total number of cards together would be:
15x + 4 + 12x + 6
15x + 12x + 4 + 6
27x + 10
This means that altogether, they have 27 envelopes with x index cards in each, plus another 10 leftover index cards.
Question 7.
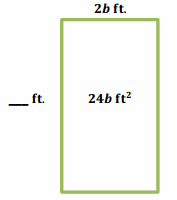
The area of the pictured rectangle below is 24b ft2. Its width is 2b ft. Find the height of the rectangle and name any properties used with the appropriate step.
Answer:
24b ÷ 2b
24b∙\(\frac{1}{2b}\) Multiplying the reciprocal
\(\frac{27b}{2b}\) Multiplication
\(\frac{24}{2}\) ∙\(\frac{b}{b}\) Any order, any grouping in multiplication
12∙1
12
The height of the rectangle is 12 ft.
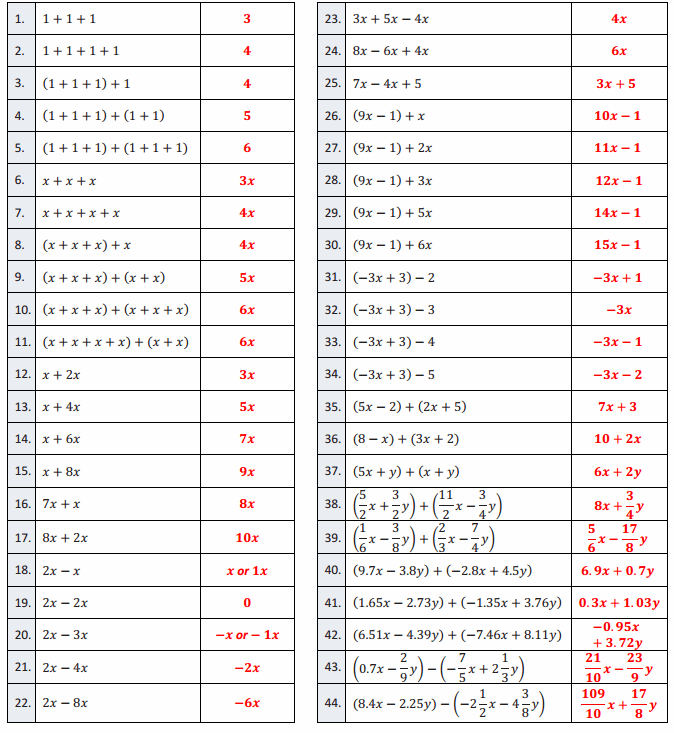
Eureka Math Grade 7 Module 3 Lesson 2 Generating Equivalent Expressions—Round 1 Answer Key
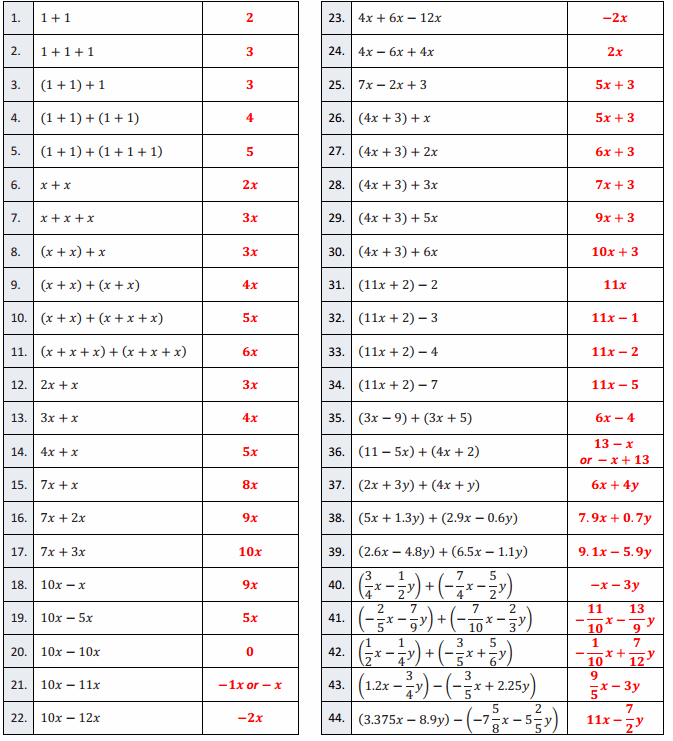
Directions: Write each as an equivalent expression in standard form as quickly and as accurately as possible within the allotted time.
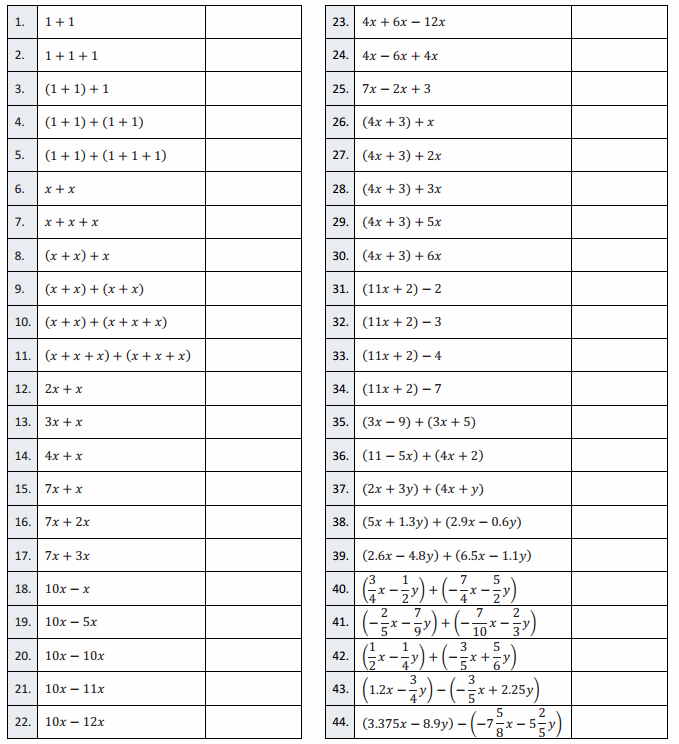
Answer:
Eureka Math Grade 7 Module 3 Lesson 2 Generating Equivalent Expressions—Round 2 Answer Key
Directions: Write each as an equivalent expression in standard form as quickly and as accurately as possible within the allotted time.

Answer:
Eureka Math Grade 7 Module 3 Lesson 2 Exit Ticket Answer Key
Question 1.
Write the expression in standard form.
Answer:
(4f – 3 + 2g) – ( – 4g + 2)
4f + ( – 3) + 2g + ( – ( – 4g + 2)) Subtraction as adding the opposite
4f + ( – 3) + 2g + 4g + ( – 2) The opposite of a sum is the sum of its opposites.
4f + 2g + 4g + ( – 3) + ( – 2) Any order, any grouping
4f + 6g + ( – 5) Combined like terms
4f + 6g – 5 Subtraction as adding the opposite
Question 2.
Find the result when 5m + 2 is subtracted from 9m.
Answer:
9m – (5m + 2) Original expression
9m + ( – (5m + 2)) Subtraction as adding the opposite
9m + ( – 5m) + ( – 2) The opposite of a sum is the sum of its opposites.
4m + ( – 2) Combined like terms
4m – 2 Subtraction as adding the opposite
Question 3.
Write the expression in standard form.
27h ÷ 3h
Answer:
27h∙\(\frac{1}{3 h}\) Multiplying by the reciprocal
\(\frac{27h}{3 h}\) Multiplication
\(\frac{27}{3}\)∙\(\frac{h}{h}\) Any order, any grouping
9∙1
9














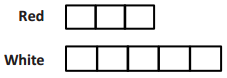
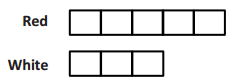
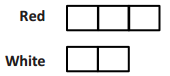
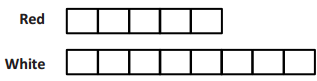
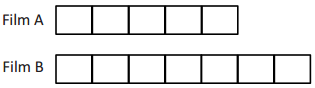
 of the length of Film B.
of the length of Film B.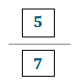 of the length of Film B.
of the length of Film B. of the length of Film A.
of the length of Film A.