Prasanna

Engage NY Eureka Math 6th Grade Module 1 Lesson 6 Answer Key

Eureka Math Grade 6 Module 1 Lesson 6 Exercise Answer Key

Exercise 1.
The Business Direct Hotel caters to people who travel for different types of business trips. On Saturday night there is not a lot of business travel, so the ratio of the number of occupied rooms to the number of unoccupied rooms is 2: 5. However, on Sunday night the ratio of the number of occupied rooms to the number of unoccupied rooms is 6: 1 due to the number of business people attending a large conference in the area. If the Business Direct Hotel has 432 occupied rooms on Sunday night, how many unoccupied rooms does it have on Saturday night?
Answer:

Exercise 2.
Peter is trying to work out by completing sit-ups and push-ups in order to gain muscle mass. Originally, Peter was completing five sit-ups for every three push-ups, but then he injured his shoulder. After the injury, Peter completed the same number of repetitions as he did before his injury, but he completed seven sit-ups for every one push-up. During a training session after his injury, Peter completed eight push-ups. How many push-ups was Peter completing before his injury?
Answer:
Peter was completing 24 push-ups before his injury.

Exercise 3.
Tom and Rob are brothers who like to make bets about the outcomes of different contests between them. Before the last bet, the ratio of the amount of Tom’s money to the amount of Rob’s money was 4: 7. Rob lost the latest competition, and now the ratio of the amount of Tom’s money to the amount of Rob’s money is 8: 3. If Rob had $280 before the last competition, how much does Rob have now that he lost the bet?
Answer:
Rob has $ 120.

Exercise 4.
A sporting goods store ordered new bikes and scooters. For every 3 bikes ordered, 4 scooters were ordered. However, bikes were way more popular than scooters, so the store changed its next order. The new ratio of the number of bikes ordered to the number of scooters ordered was 5: 2. If the same amount of sporting equipment was ordered in both orders and 64 scooters were ordered originally, how many bikes were ordered as part of the new order?
Answer:
80 bikes were ordered as part of the new order.

Exercise 5.
At the beginning of Grade 6, the ratio of the number of advanced math students to the number of regular math students was 3: 8. However, after taking placement tests, students were moved around changing the ratio of the number of advanced math students to the number of regular math students to 4: 7. How many students started in regular math and advanced math if there were 92 students in advanced math after the placement tests?
Answer:
There were 69 students in advanced math and 184 students in regular math before the placement tests,

Exercise 6.
During first semester, the ratio of the number of students in art class to the number of students in gym class was 2: 7. However, the art classes were really small, and the gym classes were large, so the principal changed students’ classes for second semester. In second semester, the ratio of the number of students in art class to the number of students in gym class was 5: 4. If 75 students were in art class second semester, how many were in art class and gym class first semester?
Answer:
There were 30 students in art class and 105 students in gym class during first semester.

Exercise 7.
Jeanette wants to save money, but she has not been good at it in the past. The ratio of the amount of money in Jeanette’s savings account to the amount of money in her checking account was 1: 6. Because Jeanette is trying to get better at saving money, she moves some money out of her checking account and into her savings account. Now, the ratio of the amount of money in her savings account to the amount of money in her checking account is 4: 3. If Jeanette had $936 in her checking account before moving money, how much money does Jeanette have in each account after moving money?
Answer:
Jeanette has $624 in her savings account and $468 in her checking account after moving money.

Eureka Math Grade 6 Module 1 Lesson 6 Problem Set Answer Key

Question 1.
Shelley compared the number of oak trees to the number of maple trees as part of a study about hardwood trees in a woodlot. She counted 9 maple trees to every 5 oak trees. Later in the year there was a bug problem and many trees died. New trees were planted to make sure there was the same number of trees as before the bug problem. The new ratio of the number of maple trees to the number of oak trees is 3: 11. After planting new trees, there were 132 oak trees. How many more maple trees were in the woodlot before the bug problem than after the bug problem? Explain.
Answer:
There were 72 more maple trees before the bug problem than after because there were 108 maples trees before the bug problem and 36 maple trees after the bug problem.

Question 2.
The school band is comprised of middle school students and high school students, but it always has the same maximum capacity. Last year the ratio of the number of middle school students to the number of high school students was 1: 8. However, this year the ratio of the number of middle school students to the number of high school students changed to 2: 7. If there are 18 middle school students in the band this year, how many fewer high school students are in the band this year compared to last year? Explain.
Answer:
There are 9 fewer high school students in the band this year when compared to last year because last year there were 72 high school students in the band, and this year there are only 63 high school students in the band.

Eureka Math Grade 6 Module 1 Lesson 6 Exit Ticket Answer Key

Question 1.
Students surveyed boys and girls separately to determine which sport was enjoyed the most. After completing the boy survey, it was determined that for every 3 boys who enjoyed soccer, 5 boys enjoyed basketball. The girl survey had a ratio of the number of girls who enjoyed soccer to the number of girls who enjoyed basketball of 7: 1. If the same number of boys and girls were surveyed, and 90 boys enjoy soccer, how many girls enjoy each sport?
Answer:
The girl survey would show that 210 girls enjoy soccer, and 30 girls enjoy basketball.

Engage NY Eureka Math 6th Grade Module 1 Lesson 5 Answer Key

Eureka Math Grade 6 Module 1 Lesson 5 Example Answer Key

Example 1.
A County Superintendent of Highways is interested in the numbers of different types of vehicles that regularly travel within his county. In the month of August, a total of 192 registrations were purchased for passenger cars and pickup trucks at the local Department of Motor Vehicles (DMV). The DMV reported that in the month of August, for every 5 passenger cars registered, there were 7 pickup trucks registered. How many of each type of vehicle were registered in the county in the month of August?
a. Using the information in the problem, write four different ratios and describe the meaning of each.
Answer:
The ratio of cors to trucks is 5: 7 and is a part-to-part ratio. The ratio of trucks to cors is 7:5, and that is a
part-to-part ratio. The ratio of cars to total vehicles is 5 to 12, and that is a part-to-whole ratio. The ratio of
trucks to total vehicles is 7 to 12, and that is a part-to-whole ratio.

b. Make a tape diagram that represents the quantities in the part-to-part ratios that you wrote.
Answer:

c. How many equal-sized parts does the tape diagram consist of?
Answer:
12

d. What total quantity does the tape diagram represent?
Answer:
192 vehicles

e. What value does each individual part of the tape diagram represent?
Answer:
Divide the total quantity into 12 equal-sized parts:
\(\frac{192}{12}\) = 16

f. How many of each type of vehicle were registered in August?
Answer:
5 . 16 = 80 passenger cars
7 . 16 = 112 pickup trucks

Example 2.
The Superintendent of Highways is further interested in the numbers of commercial vehicles that frequently use the county’s highways. He obtains information from the Department of Motor Vehicles for the month of September and finds that for every 14 non-commercial vehicles, there were 5 commercial vehicles. If there were 108 more non commercial vehicles than commercial vehicles, how many of each type of vehicle frequently use the county’s highways during the month of September?
Answer:

Eureka Math Grade 6 Module 1 Lesson 5 Exercise Answer Key

Exercise 1.
The ratio of the number of people who own a smartphone to the number of people who own a flip phone is 4: 3. If 500 more people own a smartphone than a flip phone, how many people own each type of phone?
Answer:
2,000 people own a smartphone, and 1,500 people own a flip phone.

Exercise 2.
Sammy and David were selling water bottles to raise money for new football uniforms. Sammy sold 5 water bottles for every 3 water bottles David sold. Together they sold 160 water bottles. How many did each boy sell?
Answer:
Sammy sold 100 Water bottles, and David sold 60 water bottles.

Exercise 3.
Ms. Johnson and Ms. Siple were folding report cards to send home to parents. The ratio of the number of report cards Ms. Johnson folded to the number of report cards Ms. Siple folded is 2: 3. At the end of the day, Ms. Johnson and Ms. Siple folded a total of 300 report cards. How many did each person fold?
Answer:
Ms. Johnson folded 120 report cards, and Ms. Siple folded 180 report cards.

Exercise 4.
At a country concert, the ratio of the number of boys to the number of girls is 2: 7. If there are 250 more girls than boys, how many boys are at the concert?
Answer:
There are 100 boys at the country concert.

Eureka Math Grade 6 Module 1 Lesson 5 Problem Set Answer Key

Question 1.
Last summer, at Camp Okey-Fun-Okey, the ratio of the number of boy campers to the number of girl campers was 8: 7. If there were a total of 195 campers, how many boy campers were there? How many girl campers?
Answer:
104 boys and 91 girls are at Camp Okey-Fun-Okey.

Question 2.
The student-to-faculty ratio at a small college is 17: 3. The total number of students and faculty is 740. How many faculty members are there at the college? How many students?
Answer:
111 faculty members and 629 students are at the college.

Question 3.
The Speedy Fast Ski Resort has started to keep track of the number of skiers and snowboarders who bought season passes. The ratio of the number of skiers who bought season passes to the number of snowboarders who bought season passes is 1: 2. If 1,250 more snowboarders bought season passes than skiers, how many snowboarders and how many skiers bought season passes?
Answer:
1,250 skiers bought season passes, and 2,500 snowboarders bought season passes.

Question 4.
The ratio of the number of adults to the number of students at the prom has to be 1: 10. Last year there were
477 more students than adults at the prom. If the school is expecting the same attendance this year, how many
adults have to attend the prom?
Answer:
53 adults have to be at the prom to keep the 1: 10 ratio.

Eureka Math Grade 6 Module 1 Lesson 5 Exit Ticket Answer Key

Question 1.
When Carla looked out at the school parking lot, she noticed that for every 2 minivans, there were 5 other types of vehicles. If there are 161 vehicles in the parking lot, how many of them are not minivans?
Answer:
5 out of 7 vehicles are not minivans. 7 × 23 = 161. So, 5 × 23 = 115. 115 of the vehicles are not minivans.

Engage NY Eureka Math 6th Grade Module 1 Lesson 4 Answer Key

Eureka Math Grade 6 Module 1 Lesson 4 Example Answer Key

Example 1.
The morning announcements said that two out of every seven sixth-grade students In the school have an overdue library book. Jasmine said, “That would mean 24 of us have overdue books!” Grace argued, “No way. That is way too high.” How can you determine who is right?
Answer:
You would have to know the total number of sixth-grade students, and then see if the ratio 24: total is equivalent to 2: 7.

Answer:

Eureka Math Grade 6 Module 1 Lesson 4 Exercise Answer Key

Exercise 1.
Decide whether or not each of the following pairs of ratios is equivalent.
→ If the ratios are not equivalent, find a ratio that is equivalent to the first ratio.
→ If the ratios are equivalent, identify the nonzero number, c, that could be used to multiply each number of the first ratio by in order to get the numbers for the second ratio.
a. 6: 11 and 42: 88
________ Yes, the value, c, is ________
________ No, an equivalent ratio would be ________
Answer:

________ Yes, the value, c, is ________
  x    No, an equivalent ratio would be    42: 77   
Answer:

b. 0: 5 and 0: 20
________ Yes, the value, c, is ________
________ No, an equivalent ratio would be ________
Answer:

  x _  Yes, the value, c, is   4   
________ No, an equivalent ratio would be ________

Exercise 2.
In a bag of mixed walnuts and cashews, the ratio of the number of walnuts to the number of cashews is 5: 6. Determine the number of walnuts that are in the bag if there are 54 cashews. Use a tape diagram to support your work. Justify your answer by showing that the new ratio you created of the number of walnuts to the number of cashews is equivalent to 5: 6.
Answer:

54 divided by 6 equals 9.
5 times 9 equals 45.
There are 45 walnuts in the bag.
The ratio of the number of walnuts to the number of cashews is 45: 54. That ratio is equivalent to 5: 6.

Answer:

Eureka Math Grade 6 Module 1 Lesson 4 Problem Set Answer Key

Question 1.
Use diagrams or the description of equivalent ratios to show that the ratios 2: 3, 4: 6, and 8: 12 are equivalent.
Answer:

Question 2.
Prove that 3: 8 is equivalent to 12: 32.
a. Use diagrams to support your answer.
Answer:

b. Use the description of equivalent ratios to support your answer.
Answer:
Answers will vary. Descriptions should include multiplicative comparisons, such as 12 is 3 times 4 and 32 is 8 times 4. The constant number, c, is 4.

Question 3.
The ratio of Isabella’s money to Shane’s money is 3: 11. If Isabella has $33, how much money do Shane and Isabella have together? Use diagrams to illustrate your answer.
Answer:
Isabella has $33, and Shane has $121. $33 + $121 = $154. Together, Isabella and Shane have $154. 00.

Eureka Math Grade 6 Module 1 Lesson 4 Exit Ticket Answer Key

Question 1.
There are 35 boys in the sixth grade. The number of girls in the sixth grade is 42. Lonnie says that means the ratio of the number of boys in the sixth grade to the number of girls in sixth grade is 5: 7. Is Lonnie correct? Show why or why not.
Answer:
No, Lonnie is not correct. The ratios 5:7 and 35:42 are not equivalent. They are not equivalent because 5 × 7 = 35, but 7 × 7 = 49, not 42.

Engage NY Eureka Math 6th Grade Module 1 Lesson 3 Answer Key

Eureka Math Grade 6 Module 1 Lesson 3 Exercise Answer Key

Exercise 1.
Write a one-sentence story problem about a ratio.
Answer:
Answers will vary. The ratio of the number of sunny days to the number of cloudy days in this town is 3: 1.

Write the ratio in two different forms.
Answer:
3: 1 and 3 to 1

Exercise 2.
Shanni and Mel are using ribbon to decorate a project in their art class. The ratio of the length of Shanni’s ribbon to the length of Mel’s ribbon is 7: 3.
Draw a tape diagram to represent this ratio.
Answer:

Exercise 3.
Mason and Laney ran laps to train for the long-distance running team. The ratio of the number of laps Mason ran to the number of laps Laney ran was 2 to 3.
a. If Mason ran 4 miles, how far did Laney run? Draw a tape diagram to demonstrate how you found the answer.
Answer:

b. If Laney ran 930 meters, how far did Mason run? Draw a tape diagram to determine how you found the answer.
Answer:

c. What ratios can we say are equivalent to 2: 3?
Answer:
4: 6 and 620: 930

Exercise 4.
Josie took a long multiple-choice, end-of-year vocabulary test. The ratio of the number of problems Josie got incorrect to the number of problems she got correct is 2: 9.
a. If Josie missed 8 questions, how many did she get correct? Draw a tape diagram to demonstrate how you found the answer.
Answer:

b. If Josie missed 20 questions, how many did she get correct? Draw a tape diagram to demonstrate how you found the answer.
Answer:

c. What ratios can we say are equivalent to 2: 9?
Answer:
8: 36 and 20: 90

d. Come up with another possible ratio of the number Josie got incorrect to the number she got correct.
Answer:

e. How did you find the numbers?
Answer:
Multiplied 5 × 2 and 5 × 9

f. Describe how to create equivalent ratios.
Answer:
Multiply both numbers of the ratio by the same number (any number you choose).

Eureka Math Grade 6 Module 1 Lesson 3 Problem Set Answer Key

Question 1.
Write two ratios that are equivalent to 1: 1.
Answer:
Answers will vary. 2:2, 50: 50, etc.

Question 2.
Write two ratios that are equivalent to 3: 11.
Answer:
Answers will vary. 6:22, 9:33, etc.

Question 3.
a. The ratio of the width of the rectangle to the height of the rectangle is _______ to _______.

Answer:
The ratio of the width of the rectangle to the height of the rectangle is   9     to   4    .

b. If each square in the grid has a side length of 8 mm, what is the width and height of the rectangle?
Answer:
72 mm wide and 32 mm high

Question 4.
For a project in their health class, Jasmine and Brenda recorded the amount of milk they drank every day. Jasmine drank 2 pints of milk each day, and Brenda drank 3 pints of milk each day.
a. Write a ratio of the number of pints of milk Jasmine drank to the number of pints of milk Brenda drank each day.
Answer:
2: 3

b. Represent this scenario with tape diagrams.
Answer:

c. If one pint of milk Is equivalent to 2 cups of milk, how many cups of milk did Jasmine and Brenda each drink? How do you know?
Answer:
Jasmine drank 4 cups of milk, and Brenda drank 6 cups of milk. Since each pint represents 2 cups, I multiplied
Jasmine’s 2 pints by 2 and multiplied Brenda’s 3 pints by 2.

d. Write a ratio of the number of cups of milk Jasmine drank to the number of cups of milk Brenda drank.
Answer:
4: 6

e. Are the two ratios you determined equivalent? Explain why or why not.
Answer:
2: 3 and 4: 6 are equivalent because they represent the same value. The diagrams never changed, only the value of each unit in the diagram.

Eureka Math Grade 6 Module 1 Lesson 3 Exit Ticket Answer Key

Pam and her brother both open savings accounts. Each begin with a balance of zero dollars. For every two dollars that Pam saves in her account, her brother saves five dollars in his account.

Question 1.
Determine a ratio to describe the money in Pam’s account to the money in her brother’s account.
Answer:
2: 5

Question 2.
If Pam has 40 dollars in her account, how much money does her brother have in his account? Use a tape diagram to support your answer.
Answer:

Question 3.
Record the equivalent ratio.
Answer:
40: 100

Question 4.
Create another possible ratio that describes the relationship between the amount of money in Pam’s account and the amount of money in her brother’s account.
Answer:
Answers will vary. 4: 10, 8: 20, etc.

Engage NY Eureka Math 6th Grade Module 1 Lesson 2 Answer Key

Eureka Math Grade 6 Module 1 Lesson 2 Exercise Answer Key

Exercise 1.
Come up with two examples of ratio relationships that are interesting to you.
Answer:
1. My brother watches twice as much television as I do. The ratio of number of hours he watches in a day to the number of hours I watch in a day is usually 2: 1.

2. For every 2 chores my mom gives my brother, she gives 3 to me. The ratio is 2:3.

Exploratory Challenge:
A T-shirt manufacturing company surveyed teenage girls on their favorite T-shirt color to guide the company’s decisions about how many of each color T-shirt they should design and manufacture. The results of the survey are shown here.

Exercises for Exploratory Challenge
Question 1.
Describe a ratio relationship, in the context of this survey, for which the ratio is 3: 5.
Answer:
The number of girls who answered orange to the number of girls who answered pink.

Question 2.
For each ratio relationship given, fill in the ratio it is describing.

Answer:

Question 3.
For each ratio given, fill in a description of the ratio relationship it could describe, using the context of the survey.

Answer:

Eureka Math Grade 6 Module 1 Lesson 2 Problem Set Answer Key

Question 1.
Using the floor tiles design shown below, create 4 different ratios related to the image. Describe the ratio
relationship, and write the ratio in the form A: B or the form A to B.

Answer:
For every 16 tiles, there are 4 white tiles.
The ratio of the number of black tiles to the number of white tiles is 2 to 4.
(Answers will vary.)

Question 2.
Billy wanted to write a ratio of the number of apples to the number of peppers in his refrigerator. He wrote 1: 3.
Did Billy write the ratio correctly? Explain your answer.

Answer:
Billy is incorrect. There are 3 apples and 1 pepper in the picture. The ratio of the number of apples to the number of peppers is 3: 1.

Eureka Math Grade 6 Module 1 Lesson 2 Exit Ticket Answer Key

Question 1.
Give two different ratios with a description of the ratio relationship using the following information:
There are 15 male teachers in the school. There are 35 female teachers in the school.
Answer:
Possible solutions:

• The ratio of the number of male teachers to the number of female teachers is 15: 35.
• The ratio of the number of female teachers to the number of male teachers is 35: 15.
• The ratio of the number of female teachers to the total number of teachers in the school is 35: 50.
• The ratio of the number of male teachers to the total number of teachers in the school is 15: 50.

Please note that some students may write other equivalent ratios as answers. For example, 3: 7 is equivalent to 15: 35.

Engage NY Eureka Math 6th Grade Module 1 Lesson 1 Answer Key

Eureka Math Grade 6 Module 1 Lesson 1 Example Answer Key

Example 1.
The coed soccer team has four times as many boys on it as it has girls. We say the ratio of the number of boys to the number of girls on the team is 4: 1. We read this as four to one.
Answer:
→ Let’s create a table to show how many boys and how many girls could be on the team.
Create a table like the one shown below to show possibilities of the number of boys and girls on the soccer team. Have students copy the table into their student materials.

→ So, we would have four boys and one girl on the team for a total of five players. Is this big enough for a team?
→ Adult teams require 11 players, but youth teams may have fewer. There is no right or wrong answer;
just encourage reflection on the question, thereby having students connect their math work back to the
context.
→ What are some other ratios that show four times as many boys as girls, or a ratio of boys to girls of 4 to 1?
→ Have students add each ratio to their table.

→ From the table, we can see that there are four boys for every one girl on the team.

Suppose the ratio of the number of boys to the number of girls on the team is 3: 2.
Answer:
Create a table like the one shown below to show possibilities of the number of boys and girls on the soccer team. Have students copy the table into their student materials.

→ What are some other team compositions where there are three boys for every two girls on the team?

→ I can’t say there are 3 times as many boys as girls. What would my multiplicative value have to be? There are ________ as many boys as girls.
Encourage students to articulate their thoughts, guiding them to say there are \(\frac{3}{2}\) as many boys as girls.
→ Can you visualize \(\frac{3}{2}\) as many boys as girls?
→ Can we make a tape diagram (or bar model) that shows that there \(\frac{3}{2}\) are as many boys as girls?
Boys
Girls
→ Which description makes the relationship easier to visualize: saying the ratio is 3 to 2 or saying there are 3
halves as many boys as girls?

Example 2.
Write the ratio of the number of boys to the number of girls in our class.
Answer:
Record a ratio for each of the examples the teacher provides.

1. Answers will vary. One example is 12: 10.
2. Answers will vary. One example is 10: 12.
3. Answers will vary. One example is 7: 15.
4. Answers will vary. One example is 15: 7.
5. Answers will vary. One example is 11: 11.
6. Answers will vary. One example is 11: 11.

Write the ratio of the number of girls to the number of boys in our class.
Answer:
Record a ratio for each of the examples the teacher provides.

1. Answers will vary. One example is 12: 10.
2. Answers will vary. One example is 10: 12.
3. Answers will vary. One example is 7: 15.
4. Answers will vary. One example is 15: 7.
5. Answers will vary. One example is 11: 11.
6. Answers will vary. One example is 11: 11.

Eureka Math Grade 6 Module 1 Lesson 1 Exercise Answer Key

Exercise 1.
My own ratio compares __________________ to __________________.
My ratio is __________________.
Answer:
My own ratio compares the number of students wearing jeans to the number of students not wearing jeans.
My ratio is 16: 6.

Exercise 2.
Using words, describe a ratio that represents each ratio below.
a. 1 to 12
Answer:
For every one year, there ore twelve months.

b. 12: 1
Answer:
For every twelve months, there is one year.

c. 2 to 5
Answer:
For every two non-school days in a week, there are five school days.

d. 5 to 2
Answer:
For every five female teachers I have, there are two male teachers.

e. 10: 2
Answer:
For every ten toes, there are two feet.

f. 2: 10
Answer:
For every two problems I can finish, there are ten minutes that pass.

Eureka Math Grade 6 Module 1 Lesson 1 Problem Set Answer Key

Question 1.
At the sixth grade school dance, there are 132 boys, 89 girls, and 14 adults.
a. Write the ratio of the number of boys to the number of girls.
Answer:
132: 89 or 132 to 89

b. Write the same ratio using another form (A: B vs. A to B).
Answer:
132 to 89 or 132: 89

c. Write the ratio of the number of boys to the number of adults.
Answer:
132: 14 or 132 to 14

d. Write the same ratio using another form.
Answer:
132 to 14 or 132: 14

Question 2.
In the cafeteria, loo milk cartons were put out for breakfast. At the end of breakfast, 27 remained.
a. What is the ratio of the number of milk cartons taken to the total number of milk cartons?
Answer:
73: 100 or 73 to 100

b. What is the ratio of the number of milk cartons remaining to the number of milk cartons taken
Answer:
27: 73 or 27 to 73

Question 3.
Choose a situation that could be described by the following ratios, and write a sentence to describe the ratio In the context of the situation you chose.
For example:
3: 2. When making pink paint, the art teacher uses the ratio 3: 2. For every 3 cups of white paint she uses in the
mixture, she needs to use 2 cups of red paint.
a. 1 to 2
Answer:
For every one nose, there are two eyes (answers will vary).

b. 29 to 30
Answer:
For every 29 girls in the cafeteria, there are 30 boys (answers will vary).

c. 52: 12
Answer:
For every 52 weeks in the year, there are 12 months (answers will vary).

Eureka Math Grade 6 Module 1 Lesson 1 Exit Ticket Answer Key

Question 1.
Write a ratio for the following description: Kaleel made three times as many baskets as John during basketball
Answer:
A ratio of 3: 1 or 3 to 1 can be used.

Question 2.
Describe a situation that could be modeled with the ratio 4: 1.
Answer:
Answers will vary but could include the following: For every four teaspoons of cream in a cup of tea, there is one teaspoon of honey.

Question 3.
Write a ratio for the following description: For every 6 cups of flour in a bread recipe, there are 2 cups of milk.
Answer:
A ratio of 6: 2 or 6 to 2 can be used, or students might recognize and suggest the equivalent ratio of 3: 1.

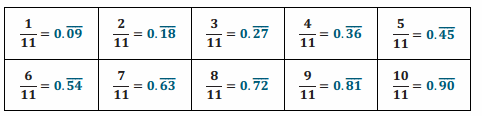
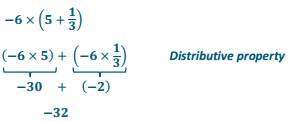
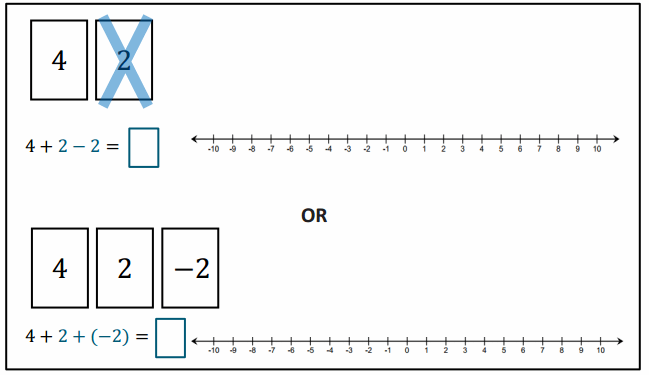
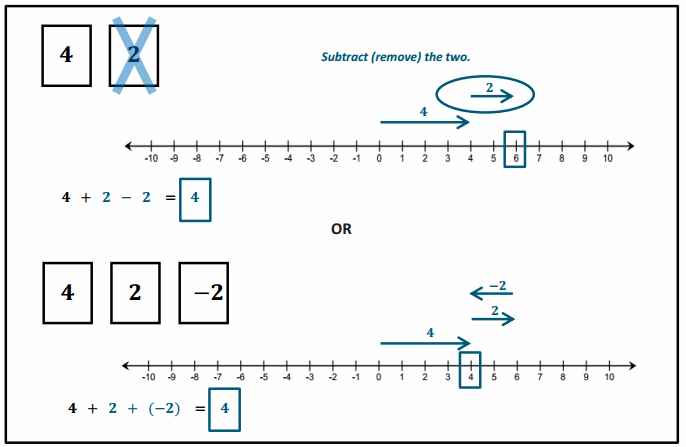
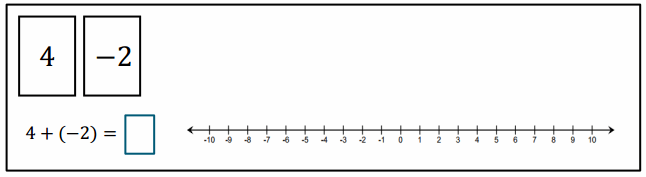
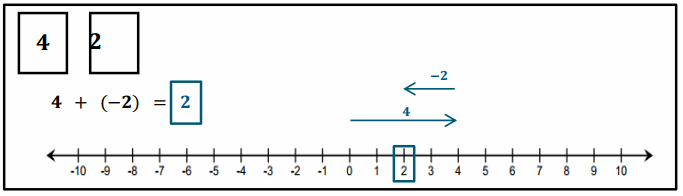
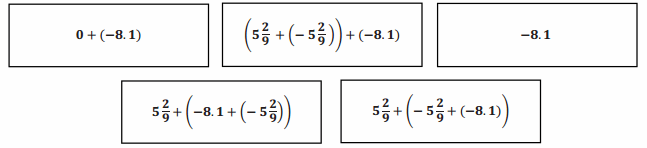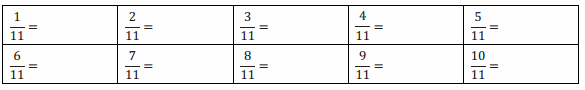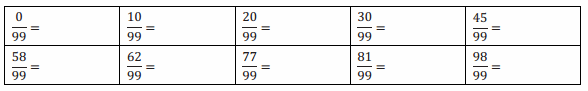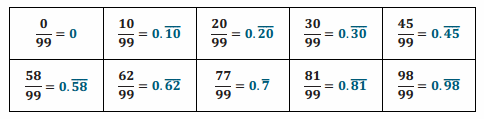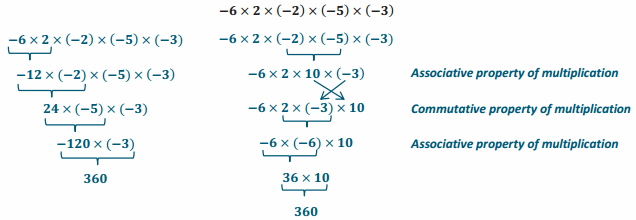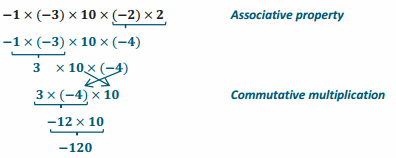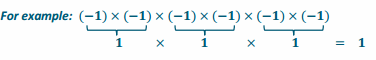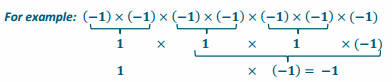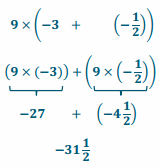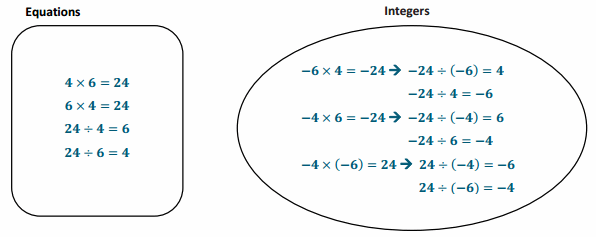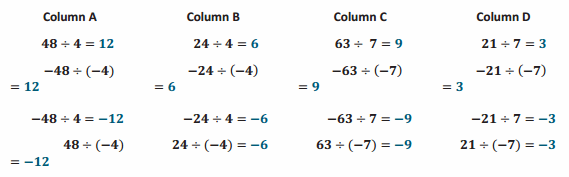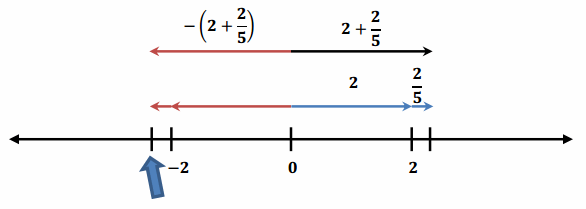Engage NY Eureka Math 7th Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 7 Module 2 Lesson 9 Example Answer Key

Represent each of the following expressions as one rational number. Show and explain your steps.

Example 1.
4\(\frac{4}{7}\) – (4\(\frac{4}{7}\) – 10)
= 4\(\frac{4}{7}\) – (4\(\frac{4}{7}\) + (- 10)) Subtracting a number is the same as adding its inverse.
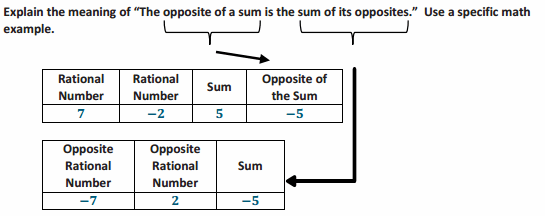
= 4\(\frac{4}{7}\) + (- 4\(\frac{4}{7}\) + 10) The opposite of a sum is the sum of its opposites.
= (4\(\frac{4}{7}\) + (- 4\(\frac{4}{7}\))) + 10 The associative property of addition
= 0 + 10 A number plus its opposite equals zero.
= 10

Example 2.
5 + (- 4\(\frac{4}{7}\))
= 5 + (- (4 +\(\frac{4}{7}\))) The mixed number 4\(\frac{4}{7}\) is equivalent to 4 +\(\frac{4}{7}\).
= 5 + (- 4 + (-\(\frac{4}{7}\))) The opposite of a sum is the sum of its opposites.
= (5 + (- 4)) + (-\(\frac{4}{7}\)) Associative property of addition
= 1 + (-\(\frac{4}{7}\)) 5 + (- 4) = 1
=\(\frac{7}{7}\) + (-\(\frac{4}{7}\))\(\frac{7}{7}\) =1
=\(\frac{3}{7}\)

Eureka Math Grade 7 Module 2 Lesson 9 Exercise Answer Key

Exercise 1
Unscramble the cards, and show the steps in the correct order to arrive at the solution to 5\(\frac{2}{9}\) – (8.1 + 5\(\frac{2}{9}\)) .

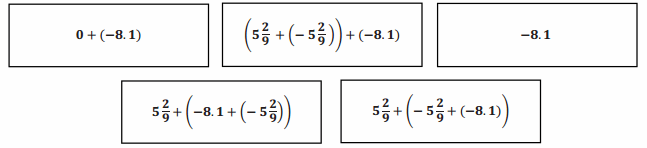
Answer:
5\(\frac{2}{9}\) + (- 8.1 + (- 5\(\frac{2}{9}\)) ) The opposite of a sum is the sum of its opposites.
5\(\frac{2}{9}\) + (- 5\(\frac{2}{9}\) + (- 8.1)) Apply the commutative property of addition.
(5\(\frac{2}{9}\) + (- 5\(\frac{2}{9}\)) ) + (- 8.1) Apply the associative property of addition.
0 + (- 8.1) A number plus its opposite equals zero.
– 8.1 Apply the additive identity property.

Exercise 2.
Team Work!
a. – 5.2 – (-3.1) + 5.2
Answer:
= – 5.2 + 3.1 + 5.2
= – 5.2 + 5.2 + 3.1
= 0 + 3.1
= 3.1

b. 32 + (- 12\(\frac{7}{8}\))
Answer:
= 32 + (- 12 + (-\(\frac{7}{8}\)) )
= (32 + (- 12)) + (-\(\frac{7}{8}\))
= 20 + (-\(\frac{7}{8}\))
= 19\(\frac{1}{8}\)

c. 3\(\frac{1}{6}\) + 20.3 – (- 5\(\frac{5}{6}\))
= 3\(\frac{1}{6}\) + 20.3 + 5\(\frac{5}{6}\)
= 3\(\frac{1}{6}\) + 5\(\frac{5}{6}\) + 20.3
= 8\(\frac{6}{6}\) + 20.3
= 9 + 20.3
= 29.3

d.\(\frac{16}{20}\) – (- 1.8) –\(\frac{4}{5}\)
=\(\frac{16}{20}\) + 1.8 –\(\frac{4}{5}\)
=\(\frac{16}{20}\) + 1.8 + (-\(\frac{4}{5}\))
=\(\frac{16}{20}\) + (-\(\frac{4}{5}\)) + 1.8
=\(\frac{16}{20}\) + (-\(\frac{16}{20}\)) + 1.8
= 0 + 1.8
= 1.8

Exercise 3.
Explain, step by step, how to arrive at a single rational number to represent the following expression. Show both a written explanation and the related math work for each step.
– 24 – (-\(\frac{1}{2}\)) – 12.5
Answer:
Subtracting (-\(\frac{1}{2}\)) is the same as adding its inverse\(\frac{1}{2}\): = – 24 +\(\frac{1}{2}\) + (- 12.5)
Next, I used the commutative property of addition to rewrite the expression: = – 24 + (- 12.5) +\(\frac{1}{2}\)
Next, I added both negative numbers: = – 36.5 +\(\frac{1}{2}\)
Next, I wrote\(\frac{1}{2}\) in its decimal form: = – 36.5 + 0.5
Lastly, I added – 36.5 + 0.5: = – 36

Eureka Math Grade 7 Module 2 Lesson 9 Problem Set Answer Key

Show all steps taken to rewrite each of the following as a single rational number.

Question 1.
80 + (- 22\(\frac{4}{15}\))
= 80 + (-22 + (-\(\frac{4}{15}\)))
= (80 + (-22)) + (-\(\frac{4}{15}\))
= 58 + (-\(\frac{4}{15}\))
= 57\(\frac{11}{15}\)

Question 2.
10 + (- 3\(\frac{3}{8}\))
Answer:
= 10 + (- 3 + (-\(\frac{3}{8}\)))
= (10 + (- 3)) + (-\(\frac{3}{8}\))
= 7 + (-\(\frac{3}{8}\))
= 6\(\frac{5}{8}\)

Question 3.
\(\frac{1}{5}\) + 20.3 – (-5\(\frac{3}{5}\))
= \(\frac{1}{5}\) + 20.3 + 5\(\frac{3}{5}\)
= \(\frac{1}{5}\) + 5\(\frac{3}{5}\) + 20.3
= 5\(\frac{4}{5}\) + 20.3
= 5\(\frac{4}{5}\) + 20\(\frac{3}{10}\)
= 5\(\frac{8}{10}\) + 20\(\frac{3}{10}\)
= 25\(\frac{11}{10}\)
= 26\(\frac{1}{10}\)

Question 4.
(\(\frac{11}{12}\)) – (- 10) – \(\frac{5}{6}\)
Answer:
= (\(\frac{11}{12}\)) + 10 + (-\(\frac{5}{6}\))
= (\(\frac{11}{12}\)) + (-\(\frac{5}{6}\)) + 10
= (\(\frac{11}{12}\)) + (- \(\frac{10}{12}\)) + 10
= (\(\frac{1}{12}\)) + 10
= 10 (\(\frac{1}{12}\))

Question 5.
Explain, step by step, how to arrive at a single rational number to represent the following expression. Show both a written explanation and the related math work for each step.
1 – \(\frac{3}{4}\) + (- 12\(\frac{1}{4}\))
Answer:
First, I rewrote the subtraction of \(\frac{3}{4}\) as the addition of its inverse – \(\frac{3}{4}\):
= 1 + (- \(\frac{3}{4}\)) + (- 12\(\frac{1}{4}\))
Next, I used the associative property of addition to regroup the addend:
= 1 + ((- \(\frac{3}{4}\)) + (- 12\(\frac{1}{4}\)))
Next, I separated – 12\(\frac{1}{4}\) into the sum of – 12 and –\(\frac{1}{4}\):
= 1 + ((-\(\frac{3}{4}\)) + (- 12) + (-\(\frac{1}{4}\)))
Next, I used the commutative property of addition:
= 1 + ((- \(\frac{3}{4}\)) + (-\(\frac{1}{4}\)) + (- 12))
Next, I found the sum of – \(\frac{3}{4}\) and –\(\frac{1}{4}\):
= 1 + ((- 1) + (- 12))
Next, I found the sum of – 1 and – 12:
= 1 + (- 13)
Lastly, since the absolute value of 13 is greater than the absolute value
of 1, and it is a negative 13, the answer will be a negative number.
The absolute value of 13 minus the absolute value of 1 equals 12,
so the answer is – 12.
= – 12

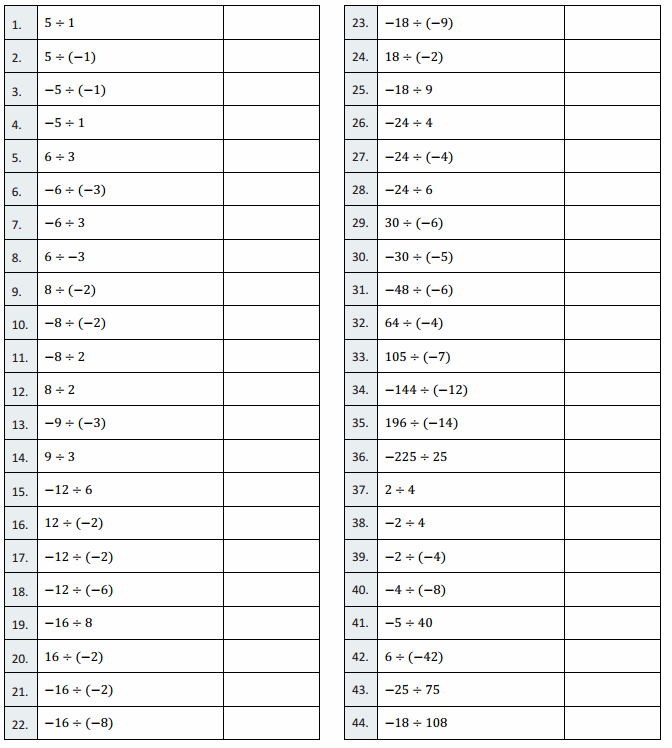
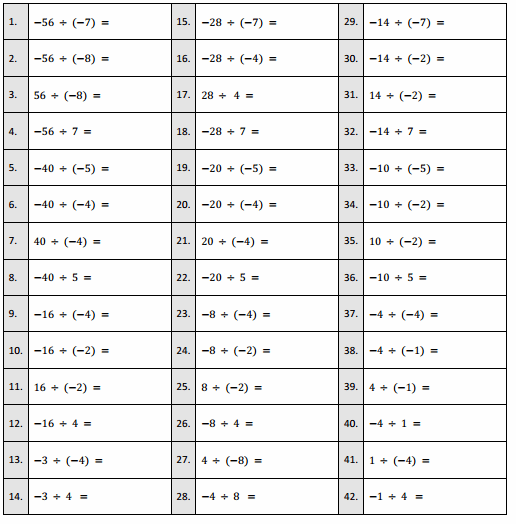
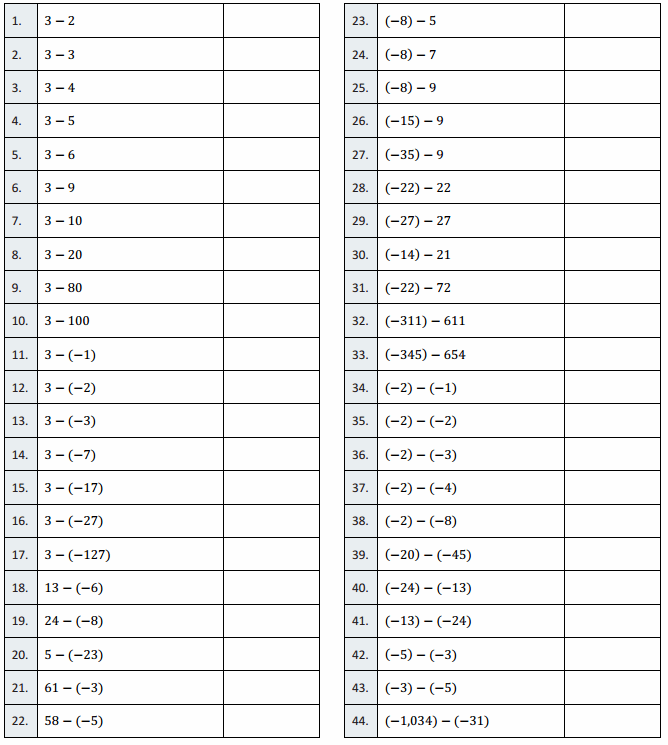
Eureka Math Grade 7 Module 2 Lesson 9 Integer Subtraction Round 1 Answer Key

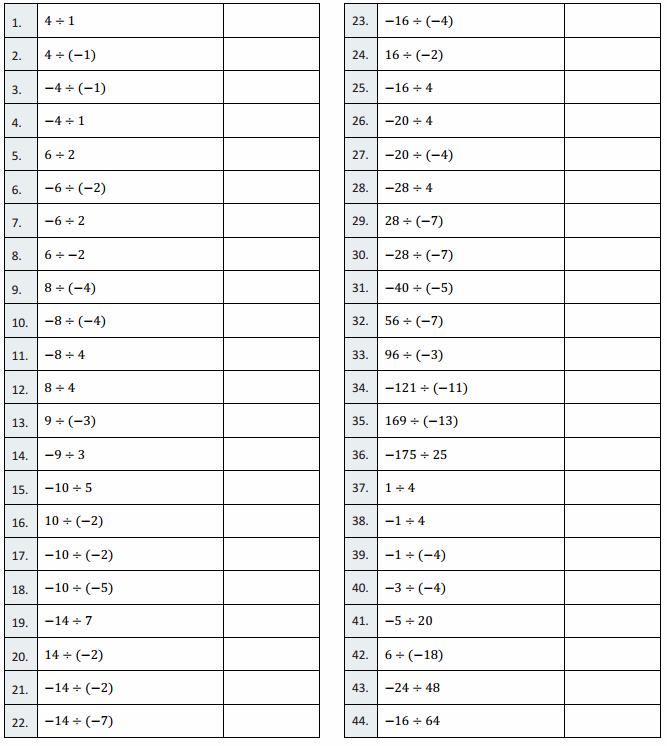
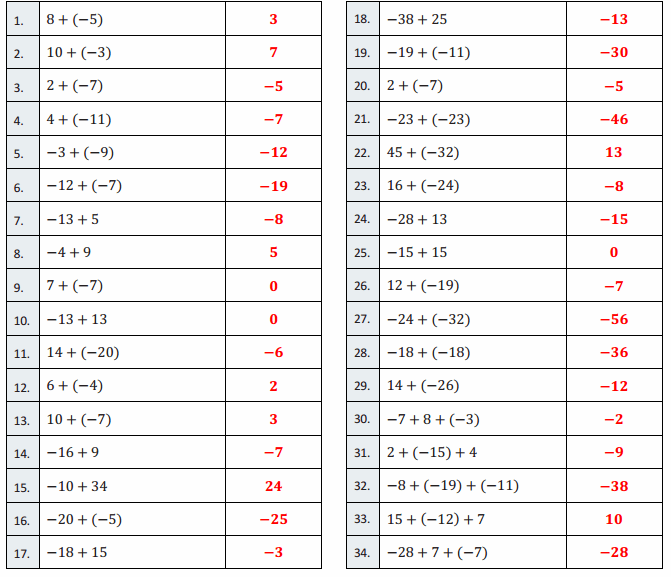
Directions: Determine the difference of the integers, and write it in the column to the right.

Answer:

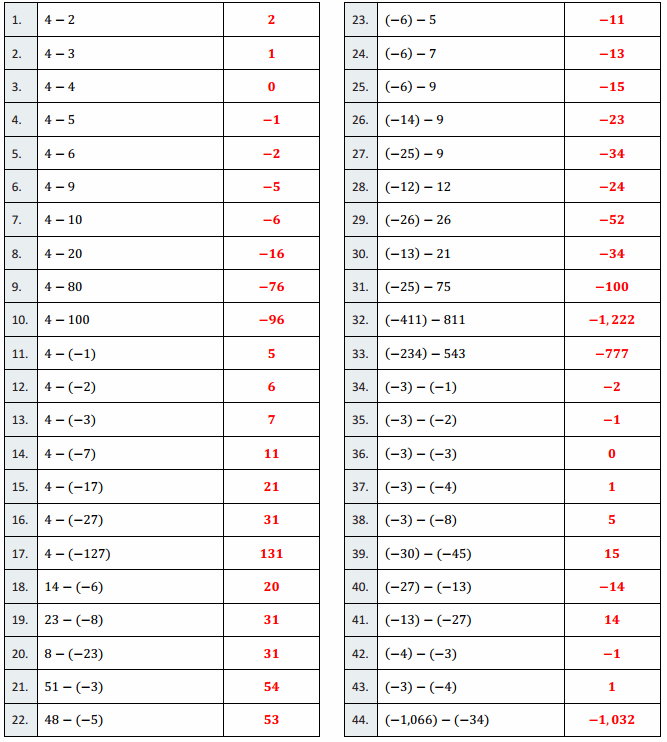
Question 1.
4 – 2
Answer:
2

Question 2.
4 – 3
Answer:
1

Question 3.
4 – 4
Answer:
0

Question 4.
4 – 5
– 1

Question 5.
4 – 6
Answer:
– 2

Question 6.
4 – 9
Answer:
– 5

Question 7.
4 – 10
Answer:
– 6

Question 8.
4 – 20
Answer:
– 16

Question 9.
4 – 80
Answer:
– 76

Question 10.
4 – 100
Answer:
– 96

Question 11.
4 – (- 1)
Answer:
5

Question 12.
4 – (- 2)
Answer:
6

Question 13.
4 – (- 3)
Answer:
7

Question 14.
4 – (- 7)
Answer:
11

Question 15.
4 – (- 17)
Answer:
21

Question 16.
4 – (- 27)
Answer:
31

Question 17.
4 – (- 127)
Answer:
131

Question 18.
14 – (- 6)
Answer:
20

Question 19.
23 – (- 8)
Answer:
31

Question 20.
8 – (- 23)
Answer:
31

Question 21.
51 – (- 3)
Answer:
54

Question 22.
48 – (- 5)
Answer:
53

Question 23.
(- 6) – 5
Answer:
– 11

Question 24.
(- 6) – 7
– 13

Question 25.
(- 6) – 9
Answer:
– 15

Question 26.
(- 14) – 9
Answer:
– 23

Question 27.
(- 25) – 9
Answer:
– 34

Question 28.
(- 12) – 12
Answer:
– 24

Question 29.
(- 26) – 26
Answer:
– 52

Question 30.
(- 13) – 21
Answer:
– 34

Question 31.
(- 25) – 75
Answer:
– 100

Question 32.
(- 411) – 811
Answer:
– 1,222

Question 33.
(- 234) – 543
Answer:
– 777

Question 34.
(- 3) – (- 1)
Answer:
– 2

Question 35.
(- 3) – (- 2)
Answer:
– 1

Question 36.
(- 3) – (- 3)
Answer:
0

Question 37.
(- 3) – (- 4)
Answer:
1

Question 38.
(- 3) – (- 8)
Answer:
5

Question 39.
(- 30) – (- 45)
Answer:
15

Question 40.
(- 27) – (- 13)
Answer:
– 14

Question 41.
(- 13) – (- 27)
Answer:
14

Question 42.
(- 4) – (- 3)
Answer:
– 1

Question 43.
(- 3) – (- 4)
Answer:
1

Question 44.
(- 1,066) – (- 34)
Answer:
– 1,032

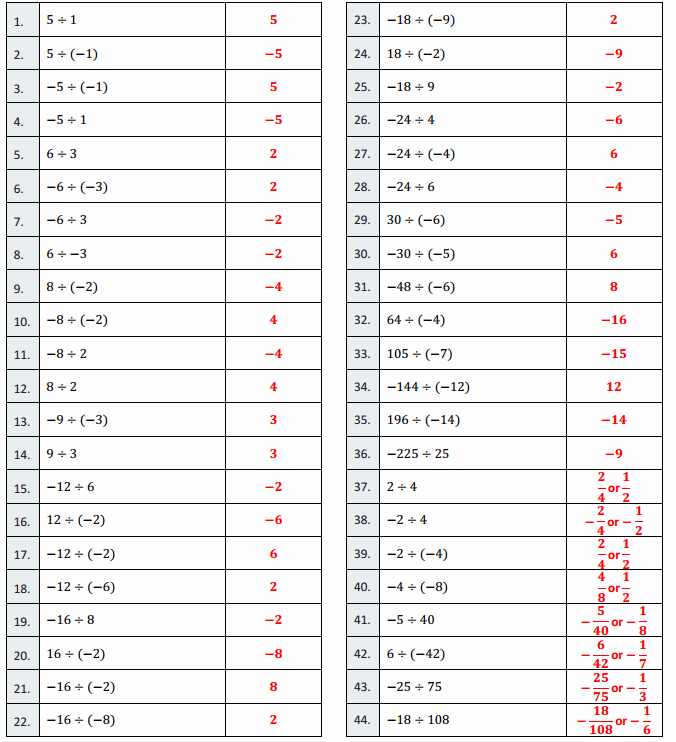
Eureka Math Grade 7 Module 2 Lesson 9 Integer Subtraction Round 2 Answer Key

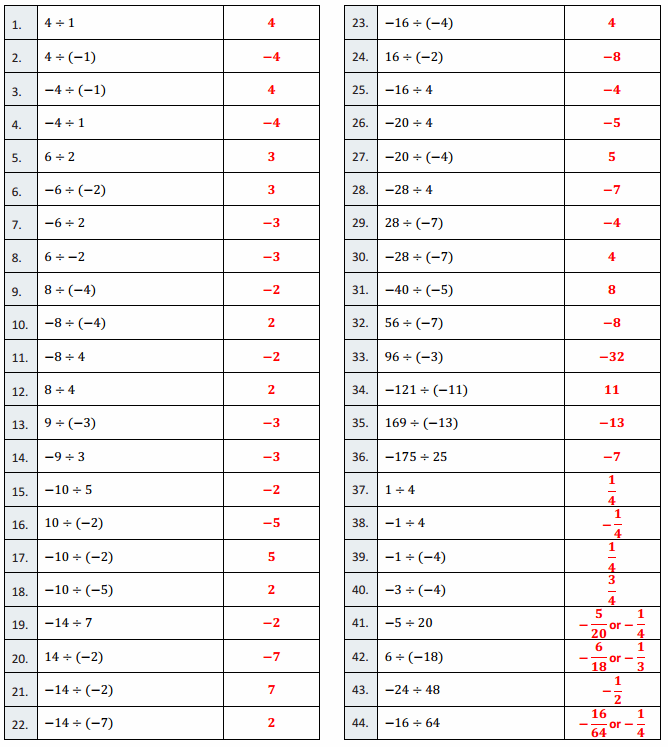
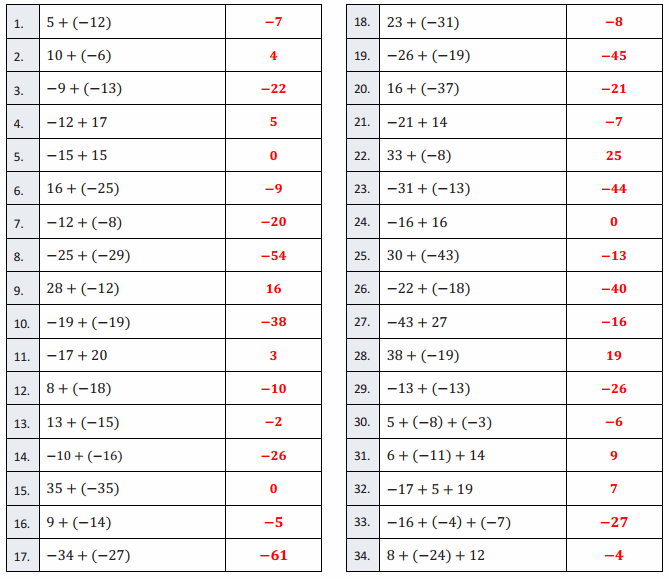
Directions: Determine the difference of the integers, and write it in the column to the right.

Answer:

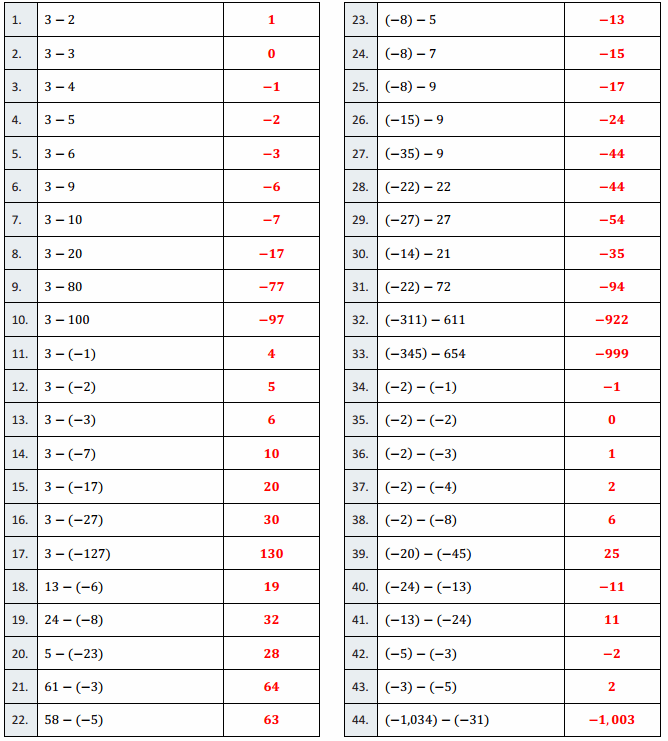
Question 1.
3 – 2
Answer:
1

Question 2.
3 – 3
Answer:
0

Question 3.
3 – 4
Answer:
– 1

Question 4.
3 – 5
Answer:
– 2

Question 5.
3 – 6
Answer:
– 3

Question 6.
3 – 9
Answer:
– 6

Question 7.
3 – 10
Answer:
– 7

Question 8.
3 – 20
Answer:
– 17

Question 9.
3 – 80
Answer:
– 77

Question 10.
3 – 100
Answer:
– 97

Question 11.
3 – (- 1)
Answer:
4

Question 12.
3 – (- 2)
Answer:
5

Question 13.
3 – (- 3)
Answer:
6

Question 14.
3 – (- 7)
Answer:
10

Question 15.
3 – (- 17)
Answer:
20

Question 16.
3 – (- 27)
Answer:
30

Question 17.
3 – (- 127)
Answer:
130

Question 18.
13 – (- 6)
Answer:
19

Question 19.
24 – (- 8)
Answer:
32

Question 20.
5 – (- 23)
Answer:
28

Question 31.
61 – (- 3)
Answer:
64

Question 32.
58 – (- 5)
Answer:
63

Question 33.
(- 8) – 5
Answer:
– 13

Question 34.
(- 8) – 7
Answer:
– 15

Question 35.
(- 8) – 9
Answer:
– 17

Question 36.
(- 15) – 9
Answer:
– 24

Question 37.
(- 35) – 9
Answer:
– 44

Question 38.
(- 22) – 22
Answer:
– 44

Question 39.
(- 27) – 27
Answer:
– 54

Question 40.
(- 14) – 21
Answer:
– 35

Question 41.
(- 22) – 72
Answer:
– 94

Question 42.
(- 311) – 611
Answer:
– 922

Question 43.
(- 345) – 654
Answer:
– 999

Question 44.
(- 2) – (- 1)
Answer:
– 1

Question 45.
(- 2) – (- 2)
Answer:
0

Question 46.
(- 2) – (- 3)
Answer:
1

Question 47.
(- 2) – (- 4)
Answer:
2

Question 48.
(- 2) – (- 8)
Answer:
6

Question 49.
(- 20) – (- 45)
Answer:
25

Question 41.
(- 24) – (- 13)
Answer:
– 11

Question 42.
(- 13) – (- 24)
Answer:
11

Question 43.
(- 5) – (- 3)
Answer:
– 2

Question 44.
(- 3) – (- 5)
Answer:
2

Question 45.
(- 1,034) – (- 31)
Answer:
– 1,003

Eureka Math Grade 7 Module 2 Lesson 9 Exit Ticket Answer Key

Question 1.
Jamie was working on his math homework with his friend, Kent. Jamie looked at the following problem.
-9.5 – (-8) – 6.5
He told Kent that he did not know how to subtract negative numbers. Kent said that he knew how to solve the problem using only addition. What did Kent mean by that? Explain. Then, show your work, and represent the answer as a single rational number.
Answer:
Kent meant that since any subtraction problem can be written as an addition problem by adding the opposite of the number you are subtracting, Jamie can solve the problem by using only addition.
Work Space:
-9.5 – (-8) – 6.5
= -9.5 + 8 + (-6.5)
= -9.5 + (-6.5) + 8
= -16 + 8
= -8
Answer:
-8

Question 2.
Use one rational number to represent the following expression. Show your work.
3 + (- 0.2) – 15\(\frac{1}{4}\)
Answer:
= 3 + (-0.2) + (-15 + (-\(\frac{1}{4}\)))
= 3 + (-0.2 + (-15) + (- 0.25))
= 3 + (-15.45)
= -12.45

Engage NY Eureka Math 7th Grade Module 2 Lesson 16 Answer Key

Eureka Math Grade 7 Module 2 Lesson 16 Example Answer Key

Example 1.
Using the Commutative and Associative Properties to Efficiently Multiply Rational Numbers
a. Evaluate the expression below.
-6 × 2 × (-2) × (-5) × (-3)
Answer:

b. What types of strategies were used to evaluate the expressions?
Answer:
The strategies used were order of operations, rearranging the terms using the commutative property, and multiplying the terms in various orders using the associative property.

c. Can you identify the benefits of choosing one strategy versus another?
Answer:
Multiplying the terms allowed me to combine factors in more manageable ways, such as multiplying
(-2) × (-5) to get 10. Multiplying other numbers by 10 is very easy.

d. What is the sign of the product, and how was the sign determined?
Answer:
The product is a positive value. When calculating the product of the first two factors, the answer will be negative because when the factors have opposite signs, the result is a negative product. Two negative values multiplied together yield a positive product. When a negative value is multiplied by a positive product, the sign of the product again changes to a negative value. When this negative product is multiplied by the last (fourth) negative value, the sign of the product again changes to a positive value.

Example 2.
Using the Distributive Property to Multiply Rational Numbers
Rewrite the mixed number as a sum; then, multiply using the distributive property.
-6 × (5 \(\frac{1}{3}\))
Answer:
-6 × (5+\(\frac{1}{3}\))

→ Did the distributive property make this problem easier to evaluate? How so?
→ Answers will vary, but most students will think that distributive property did make the problem easier to solve.

Example 3.
Using the Distributive Property to Multiply Rational Numbers
Evaluate using the distributive property.
16 × (-\(\frac{3}{8}\)) + 16 × \(\frac{1}{4}\)
16(-\(\frac{3}{8}\) + \(\frac{1}{4}\)) Distributive property
16(-\(\frac{3}{8}\) + \(\frac{2}{8}\)) Equivalent fractions
16(-\(\frac{1}{8}\))
-2

Example 4.
Using the Multiplicative Inverse to Rewrite Division as Multiplication
Rewrite the expression as only multiplication and evaluate.
1 ÷ \(\frac{2}{3}\) × (-8) × 3 ÷ (-\(\frac{1}{2}\))
Answer:
1 ÷ \(\frac{2}{3}\) × (-8) × 3 ÷ (-\(\frac{1}{2}\))

Eureka Math Grade 7 Module 2 Lesson 16 Exercise Answer Key

Exercise 1.
Find an efficient strategy to evaluate the expression and complete the necessary work.
-1 × (-3) × 10 × (-2) × 2
Answer:
Methods will vary.

Exercise 2.
Find an efficient strategy to evaluate the expression and complete the necessary work.
Methods will vary.
4 × \(\frac{1}{3}\) × (-8) × 9 × (-\(\frac{1}{2}\))
Answer:

Exercise 3.
What terms did you combine first and why?
Answer:
I multiplied the –\(\frac{1}{2}\) × -8 and \(\frac{1}{3}\) × 9 because their products are integers; this eliminated the fractions.

Exercise 4.
Refer to the example and exercises. Do you see an easy way to determine the sign of the product first?
Answer:
The product of two negative integers yields a positive product. If there is an even number of negative factors, then each negative value can be paired with another negative value yielding a positive product. This means that all factors become positive values and, therefore, have a positive product.

If there are an odd number of negative factors, then all except one can be paired with another negative. This leaves us with a product of a positive value and a negative value, which is negative.

Exercise 5.
Multiply the expression using the distributive property.
9 × (-3 \(\frac{1}{2}\))
Answer:

Exercise 6.
4.2 × (-\(\frac{1}{3}\))÷\(\frac{1}{6}\) × (-10)
Answer:
4.2 × (-\(\frac{1}{3}\))÷\(\frac{1}{6}\) × (-10)

Eureka Math Grade 7 Module 2 Lesson 16 Problem Set Answer Key

Question 1.
Evaluate the expression -2.2 × (-2)÷(-\(\frac{1}{4}\)) × 5
a. Using the order of operations only.
Answer:
4.4 ÷ (-\(\frac{1}{4}\)) × 5
-17.6 × 5
-88

b. Using the properties and methods used in Lesson 16.
Answer:
-2.2 × (-2) × (-4) × 5
-2.2 × (-2) × 5 × (-4)
-2.2 × (-10) × (-4)
22 × (-4)
-88

c. If you were asked to evaluate another expression, which method would you use, (a) or (b), and why?
Answer:
Answers will vary; however, most students should have found method (b) to be more efficient.

Question 2.
Evaluate the expressions using the distributive property.
a. (2 \(\frac{1}{4}\)) × (-8)
Answer:
2 × (-8)+\(\frac{1}{4}\) × (-8)
-16 + (-2)
-18

b. \(\frac{2}{3}\)(-7)+\(\frac{2}{3}\)(-5)
Answer:
\(\frac{2}{3}\) (-7+(-5))
\(\frac{2}{3}\) (-12)
-8

Question 3.
Mia evaluated the expression below but got an incorrect answer. Find Mia’s error(s), find the correct value of the expression, and explain how Mia could have avoided her error(s).
0.38 × 3÷(-\(\frac{1}{2}\)0) × 5÷(-8)
0.38 × 5 × (\(\frac{1}{2}\)0) × 3 × (-8)
0.38 × (\(\frac{1}{4}\)) × 3 × (-8)
0.38 × (\(\frac{1}{4}\)) × (-24)
0.38 × (-6)
-2.28
Answer:
Mia made two mistakes in the second line; first, she dropped the negative symbol from –\(\frac{1}{20}\) when she changed division to multiplication. The correct term should be (-20) because dividing a number is equivalent to multiplying its multiplicative inverse (or reciprocal). Mia’s second error occurred when she changed division to multiplication at the end of the expression; she changed only the operation, not the number. The term should be (-\(\frac{1}{8}\)). The correct value of the expressions is 14 \(\frac{1}{4}\), or 14.25.
Mia could have avoided part of her error if she had determined the sign of the product first. There are two negative values being multiplied, so her answer should have been a positive value.

Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 1 Answer Key

Directions: Determine the quotient of the integers, and write it in the column to the right.

Answer:

Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 2 Answer Key

Answer:

Eureka Math Grade 7 Module 2 Lesson 16 Exit Ticket Answer Key

Question 1.
Evaluate the expression below using the properties of operations.
18÷(-\(\frac{2}{3}\)) × 4÷(-7) × (-3)÷(\(\frac{1}{4}\))
Answer:
18 × (-\(\frac{3}{2}\)) × 4 × (-\(\frac{1}{7}\)) × (-3) × (\(\frac{4}{1}\))
-27 × 4 × (-\(\frac{1}{7}\)) × (-3) × (\(\frac{4}{1}\))
–\(\frac{1296}{7}\)
Answer: -185 \(\frac{1}{7}\) or –\(-185 . \overline{142857}\)

Question 2.
a. Given the expression below, what will the sign of the product be? Justify your answer.
-4 × (-\(\frac{8}{9}\)) × 2.78 × (1 \(\frac{1}{3}\)) × (-\(\frac{2}{5}\)) × (-6.2) × (-0.2873) × (3\(\frac{1}{11}\)) × A
Answer:
There are five negative values in the expression. Because the product of two numbers with the same sign yield a positive product, pairs of negative factors have positive products. Given an odd number of negative factors, all but one can be paired into positive products. The remaining negative factor causes the product of the terms without A to be a negative value. If the value of A is negative, then the pair of negative factors forms a positive product. If the value of A is positive, the product of the two factors with opposite signs yields a negative product.

b. Give a value for A that would result in a positive value for the expression.
Answer:
Answers will vary, but the answer must be negative. -2

c. Give a value for A that would result in a negative value for the expression.
Answer:
Answers will vary, but the answer must be positive. 3.6

Engage NY Eureka Math 7th Grade Module 2 Lesson 14 Answer Key

Eureka Math Grade 7 Module 2 Lesson 14 Example Answer Key

Example 1.
Can All Rational Numbers Be Written as Decimals?
a. Using the division button on your calculator, explore various quotients of integers 1 through 11. Record your fraction representations and their corresponding decimal representations in the space below.
Answer:
Fractions will vary. Examples:

b. What two types of decimals do you see?
Answer:
Some of the decimals stop, and some fill up the calculator screen (or keep going).

→ Did you find any quotients of integers that do not have decimal representations?
→ No. Dividing by zero is not allowed. All quotients have decimal representations, but some do not terminate (end).
→ All rational numbers can be represented in the form of a decimal. We have seen already that fractions with powers of ten in their denominators (and their equivalent fractions) can be represented as terminating decimals. Therefore, other fractions must be represented by decimals that do not terminate.

Example 2.
Decimal Representations of Rational Numbers
In the chart below, organize the fractions and their corresponding decimal representation listed in Example 1 according to their type of decimal.

Answer:

Example 3.
Converting Rational Numbers to Decimals Using Long Division
Use the long division algorithm to find the decimal value of –\(\frac{3}{4}\).
Answer:
The fraction is a negative value, so its decimal representation will be as well.
–\(\frac{3}{4}\) = -0.75

We know that -(-\(\frac{3}{4}\))= —\(\frac{3}{4}\) = \(\frac{3}{-4}\), so we use our rules for dividing integers. Dividing 3 by 4 gives us 0.75, but we know the value must be negative.
Answer: -0.75

Example 4.
Converting Rational Numbers to Decimals Using Long Division
Use long division to find the decimal representation of \(\frac{1}{3}\) .
Answer:
The remainders repeat, yielding the same dividend remainder in each step. This repeating remainder causes the numbers in the quotient to repeat as well. Because of this pattern, the decimal will go on forever, so we cannot write the exact quotient.

Example 5.
Fractions Represent Terminating or Repeating Decimals
How do we determine whether the decimal representation of a quotient of two integers, with the divisor not equal to zero, will terminate or repeat?
Answer:
In the division algorithm, if the remainder is zero, then the algorithm terminates, resulting in a terminating decimal.
If the value of the remainder is not zero, then it is limited to whole numbers 1, 2, 3, … , (d-1), where d is the divisor. This means that the value of the remainder must repeat within (d-1) steps. (For example, given a divisor of 9, the nonzero remainders are limited to whole numbers 1 through 8, so the remainder must repeat within 8 steps.) When the remainder repeats, the calculations that follow will also repeat in a cyclical pattern causing a repeating decimal.

Example 6.
Using Rational Number Conversions in Problem Solving
a. Eric and four of his friends are taking a trip across the New York State Thruway. They decide to split the cost of tolls equally. If the total cost of tolls is $8, how much will each person have to pay?
Answer:
There are five people taking the trip. The friends will each be responsible for $1.60 of the tolls due.

b. Just before leaving on the trip, two of Eric’s friends have a family emergency and cannot go. What is each person’s share of the $8 tolls now?
Answer:
There are now three people taking the trip. The resulting quotient is a repeating decimal because the remainders repeat
as 2s. The resulting quotient is \(\frac{8}{3}\) = 2.66666…= \(\text { 2. } \overline{6} \text { . }\) If each friend pays $2.66, they will be $0.02 shy of $8, so the amount must be rounded up to $2.67 per person.

Eureka Math Grade 7 Module 2 Lesson 14 Exercise Answer Key

Exercise 1.
Convert each rational number to its decimal form using long division.

a. –\(\frac{7}{8}\) =
Answer:

b. \(\frac{3}{16}\) =
Answer:
\(\frac{3}{16}\) = 0.1875

Students notice that since the remainders repeat, the quotient takes on a repeating pattern of 3s.
→ We cannot possibly write the exact value of the decimal because it has an infinite number of decimal places. Instead, we indicate that the decimal has a repeating pattern by placing a bar over the shortest sequence of repeating digits (called the repetend).
→ 0.333… = \(0 . \overline{3}\)
→ What part of your calculations causes the decimal to repeat?
→ When a remainder repeats, the calculations that follow must also repeat in a cyclical pattern, causing the digits in the quotient to also repeat in a cyclical pattern.
→ Circle the repeating remainders.
Refer to the graphic above.

Exercise 2.
Calculate the decimal values of the fraction below using long division. Express your answers using bars over the shortest sequence of repeating digits.
a. –\(\frac{4}{9}\)
Answer:
–\(\frac{4}{9}\) = -0.4444…= –\(0 . \overline{4}\)

b. –\(\frac{1}{11}\)
Answer:
–\(\frac{1}{11}\) = -0.090909…= –\(0 . \overline{09}\)

c. \(\frac{1}{7}\)
Answer:
\(\frac{1}{7}\) = 0.142857148…= \(0 . \overline{142857}\)

d. –\(\frac{5}{6}\)
Answer:
–\(\frac{5}{6}\) = -0.33333…= –\(0 . \overline{83}\)

Eureka Math Grade 7 Module 2 Lesson 14 Problem Set Answer Key

Question 1.
Convert each rational number into its decimal form.

Answer:

One of these decimal representations is not like the others. Why?
Answer:
\(\frac{3}{6}\) in its simplest form is \(\frac{1}{2}\) (the common factor of 3 divides out, leaving a denominator of 2, which in decimal form will terminate.

Enrichment:

Question 2.
Chandler tells Aubrey that the decimal value of –\(\frac{1}{17}\) is not a repeating decimal. Should Aubrey believe him? Explain.
No, Aubrey should not believe Chandler. The divisor 17 is a prime number containing no factors of 2 or 5, and therefore, cannot be written as a terminating decimal. By long division, –\(\frac{1}{17}\) = \(-0 . \overline{0588235294117647}\). The decimal appears as though it is not going to take on a repeating pattern because all 16 possible nonzero remainders appear before the remainder repeats. The seventeenth step produces a repeat remainder causing a cyclical decimal pattern.

Question 3.
Complete the quotients below without using a calculator, and answer the questions that follow.
a. Convert each rational number in the table to its decimal equivalent.

Answer:

Do you see a pattern? Explain.
Answer:
The two digits that repeat in each case have a sum of nine. As the numerator increases by one, the first of the two digits increases by one as the second of the digits decreases by one.

b. Convert each rational number in the table to its decimal equivalent.

Answer:

Do you see a pattern? Explain.
Answer:
The 2-digit numerator in each fraction is the repeating pattern in the decimal form.

c. Can you find other rational numbers that follow similar patterns?
Answer:
Answers will vary.

Eureka Math Grade 7 Module 2 Lesson 14 Exit Ticket Answer Key

Question 1.
What is the decimal value of \(\frac{4}{11}\) ?
Answer:
\(\frac{4}{11}\) = \(0 . \overline{36}\)

Question 2.
How do you know that \(\frac{4}{11}\) is a repeating decimal?
Answer:
The prime factor in the denominator is 11. Fractions that correspond with terminating decimals have only factors 2 and 5 in the denominator in simplest form.

Question 3.
What causes a repeating decimal in the long division algorithm?
Answer:
When a remainder repeats, the division algorithm takes on a cyclic pattern causing a repeating decimal.

Engage NY Eureka Math 7th Grade Module 2 Lesson 12 Answer Key

Eureka Math Grade 7 Module 2 Lesson 12 Example Answer Key

Example 1.
Transitioning from Integer Multiplication Rules to Integer Division Rules
Students make an integer multiplication facts bubble by expanding upon the four related math facts they wrote down.
Step 1: Students construct three similar integer multiplication problems, two problems using one negative number as a factor and one with both negative numbers as factors. Students may use the commutative property to extend their three equations to six.

Record your group’s number sentences in the space on the left below.

Answer:

Step 2: Students use the integer multiplication facts in their integer bubble to create six related integer division facts. Group members should discuss the inverse relationship and the resulting division fact that must be true based on each multiplication equation.

Step 3: Students use the equations in their integer bubble and the patterns they observed to answer the following questions.

a. List examples of division problems that produced a quotient that is a negative number.
Answer:
-24 ÷ 4 = -6 ; -24 ÷ 6 = -4 ; 24 ÷ (-4) = -6 ; 24 ÷ (-6) = -4

b. If the quotient is a negative number, what must be true about the signs of the dividend and divisor?
Answer:
The quotient is a negative number when the signs of the dividend and divisor are not the same; one is positive, and one is negative.

c. List your examples of division problems that produced a quotient that is a positive number.
Answer:
-24 ÷ (-4) = 6 ; -24 ÷ (-6) = 4 ; 24 ÷ 4 = 6 ; 24 ÷ 6 = 4

d. If the quotient is a positive number, what must be true about the signs of the dividend and divisor?
Answer:
The quotient is a positive number when the signs of the dividend and the divisor are the same in each case.

Step 4: Whole-group discussion. Students share answers from Step 3 with the class. The class comes to a consensus and realizes that since multiplication and division are related* (inverse operations), the integer rules for these operations are related. Students summarize the rules for division, which are stated in the Lesson Summary of the student materials. (*Reminder: The rules apply to all situations except dividing by zero.)

Rules for Dividing Two Integers:
→ A quotient is negative if the divisor and the dividend have __ signs.
Answer:
opposite

→ A quotient is positive if the divisor and the dividend have __ signs.
Answer:
the same

Eureka Math Grade 7 Module 2 Lesson 12 Exercise Answer Key

Exercise 2.
Is the Quotient of Two Integers Always an Integer?
Is the quotient of two integers always an integer? Use the work space below to create quotients of integers. Answer the question, and use examples or a counterexample to support your claim.

Work Space:

Answer:
-24 ÷ 6 = -4 Example of an integer quotient
6 ÷ (-24) = \(\frac{6}{-24}\) = \(\frac{1}{-4}\) = –\(\frac{1}{4}\) Counterexample: has a non-integer quotient
Answer:
No, quotients of integers are not always integers. In my first example above, -24 ÷ 6 yields an integer quotient -4. However, when I switched the divisor and dividend, that quotient divides a number with a smaller absolute value by a number with a greater absolute value, making the quotient a rational number between -1 and 1. In dividing 6 ÷ (-24), the quotient is \(\frac{6}{-24}\) = \(\frac{1}{-4}\). Of course, –\(\frac{1}{4}\) is not an integer but is the opposite value of the fraction \(\frac{1}{4}\). This counterexample shows that quotients of integers are not always integers.

Conclusion: Every quotient of two integers is always a rational number but not always an integer.
Once students have disproved the statement with a counterexample (where the quotient is a decimal or fraction), ask students to determine what must be true of two integers if their quotient is an integer. Students may need some time to study the examples where the quotient is an integer to determine that the quotient of two integers, \(\frac{A}{B}[/latex, B≠0, is an integer when either B = 1 or A = kB for any integer k.

Exercise 3.
Different Representation of the Same Quotient
Are the answers to the three quotients below the same or different? Why or why not?
a. -14 ÷ 7
Answer:
-14 ÷ 7 = -2

b. 14 ÷ (-7)
Answer:
14 ÷ (-7) = -2

c. -(14 ÷ 7)
Answer:
-(14 ÷ 7) = -(2) = -2

The answers to the problems are the same: -2. In part (c), the negative in front of the parentheses changes the value inside the parentheses to its opposite. The value in the parentheses is 2, and the opposite of 2 is -2.

Eureka Math Grade 7 Module 2 Lesson 12 Problem Set Answer Key

Question 1.
Find the missing values in each column.

Answer:

Question 2.
Describe the pattern you see in each column’s answers in Problem 1, relating it to the problems’ divisors and dividends. Why is this so?
Answer:
The pattern in the columns’ answers is the same two positive values followed by the same two negative values. This is so for the first two problems because the divisor and the dividend have the same signs and absolute values, which yields a positive quotient. This is so for the second two problems because the divisor and dividend have different signs but the same absolute values, which yields a negative quotient.

Question 3.
Describe the pattern you see between the answers for Columns A and B in Problem 1 (e.g., compare the first answer in Column A to the first answer in Column B; compare the second answer in Column A to the second answer in Column B). Why is this so?
Answer:
The answers in Column B are each one-half of the corresponding answers in Column A. That is because the dividend of 48 in Column A is divided by 4, and the dividend of 24 in Column B is divided by 4 (and so on with the same order and same absolute values but different signs). Since 24 is half of 48, the quotient (answer) in Column B will be one-half of the quotient in Column A.

Question 4.
Describe the pattern you see between the answers for Columns C and D in Problem 1. Why is this so?
Answer:
The answers in Column D are each one-third of the corresponding answers in Column C. That is because the dividend of 63 in Column C is divided by 7, and the dividend of 21 in Column D is divided by 7 (and so on with the same order and same absolute values but different signs). Since 21 is one-third of 63, the quotient (answer) in Column D will be one-third of the quotient in Column C.

Eureka Math Grade 7 Module 2 Lesson 12 Fluency Exercise: Integer Division Answer Key

Answer:

Question 1.
-56 ÷ (-7) =
Answer:
8

Question 2.
-56 ÷ (-8) =
Answer:
7

Question 3.
56 ÷ (-8) =
Answer:
-7

Question 4.
-56 ÷ 7 =
Answer:
-8

Question 5.
-40 ÷ (-5) =
Answer:
8

Question 6.
-40 ÷ (-4) =
Answer:
10

Question 7.
40 ÷ (-4) =
Answer:
-10

Question 8.
-40 ÷ 5 =
Answer:
-8

Question 9.
-16 ÷ (-4) =
Answer:
4

Question 11.
-16 ÷ (-2) =
Answer:
8

Question 12.
16 ÷ (-2) =
Answer:
-8

Question 13.
-16 ÷ 4 =
Answer:
-4

Question 14.
-3 ÷ (-4) =
Answer:
0.75

Question 15.
-3 ÷ 4 =
Answer:
-0.75

Question 16.
-28 ÷ (-7) =
Answer:
4

Question 17.
-28 ÷ (-4) =
Answer:
7

Question 18.
28 ÷ 4 =
Answer:
7

Question 19.
-28 ÷ 7 =
Answer:
-4

Question 20.
-20 ÷ (-5) =
Answer:
4

Question 21.
-20 ÷ (-4) =
Answer:
5

Question 22.
20 ÷ (-4) =
Answer:
-5

Question 23.
-20 ÷ 5 =
Answer:
-4

Question 34.
-8 ÷ (-4) =
Answer:
2

Question 35.
-8 ÷ (-2) =
Answer:
4

Question 36.
8 ÷ (-2) =
Answer:
-4

Question 37.
-8 ÷ 4 =
Answer:
-2

Question 38.
4 ÷ (-8)=
Answer:
-0.5

Question 39.
-4 ÷ 8 =
Answer:
-0.5

Question 40.
-14 ÷ (-7) =
Answer:
2

Question 41.
-14 ÷ (-2) =
Answer:
7

Question 42.
14 ÷ (-2)=
Answer:
-7

Question 43.
-14 ÷ 7 =
Answer:
-2

Question 44.
-10 ÷ (-5) =
Answer:
2

Question 45.
-10 ÷ (-2) =
Answer:
5

Question 46.
10 ÷ (-2)=
Answer:
-5

Question 47.
-10 ÷ 5 =
Answer:
-2

Question 48.
-4 ÷ (-4) =
Answer:
1

Question 49.
-4 ÷ (-1) =
Answer:
4

Question 50.
4 ÷ (-1) =
Answer:
-4

Question 51.
-4 ÷ 1 =
Answer:
-4

Question 52.
1 ÷ (-4)=
Answer:
-0.25

Question 53.
-1 ÷ 4 =
Answer:
-0.25

Eureka Math Grade 7 Module 2 Lesson 12 Exit Ticket Answer Key

Question 1.
Mrs. McIntire, a seventh-grade math teacher, is grading papers. Three students gave the following responses to the same math problem:
Student one: [latex]\frac{1}{-2}\)
Student two: -(\(\frac{1}{2}\))
Student three: –\(\frac{1}{2}\)
On Mrs. McIntire’s answer key for the assignment, the correct answer is -0.5. Which student answer(s) is (are) correct? Explain.
Answer:
All student answers are correct since they are all equivalent to -0.5.
For student one: \(\frac{1}{-2}\) means 1 divided by -2. When dividing a positive 1 by a negative 2, the answer will be negative five-tenths or -0.5.
For student two: -(\(\frac{1}{2}\)) means the opposite of \(\frac{1}{2}\). One-half is equivalent to five-tenths, and the opposite is negative five-tenths or -0.5.
For student three: –\(\frac{1}{2}\) means -1 divided by 2. When dividing a negative 1 by a positive 2, the answer will be negative five-tenths or -0.5.

Question 2.
Complete the table below. Provide an answer for each integer division problem, and write a related equation using integer multiplication.

Answer:

Engage NY Eureka Math 7th Grade Module 2 Lesson 8 Answer Key

Eureka Math Grade 7 Module 2 Lesson 8 Example Answer Key

Example 1.

Answer:

It means that if you have a sum and want to take the opposite, for instance, -(7 + (-2)), you can rewrite it as the sum of each addend’s opposite, -7 + 2.

Example 2.
A Mixed Number Is a Sum
Use the number line model shown below to explain and write the opposite of 2\(\frac{2}{5}\) as a sum of two rational numbers.

The opposite of a sum (top single arrow pointing left) and the sum of the opposites correspond to the same point on the number line.
Answer:
The opposite of 2\(\frac{2}{5}\) is -2 \(\frac{2}{5}\) .
-2 \(\frac{2}{5}\) written as the sum of two rational numbers is -2 + (-\(\frac{2}{5}\)).

Eureka Math Grade 7 Module 2 Lesson 8 Exercise Answer Key

Exercise 1.
Represent the following expression with a single rational number.
-2\(\frac{2}{5}\) + \(\frac{1}{4}\) – \(\frac{3}{5}\)
Answer:
Two Possible Methods:
-2\(\frac{8}{20}\) + 3\(\frac{5}{20}\) – \(\frac{12}{20}\)
–\(\frac{48}{20}\) + \(\frac{65}{20}\) – \(\frac{12}{20}\)
\(\frac{17}{20}\) – \(\frac{12}{20}\)
\(\frac{5}{20}\) or \(\frac{1}{4}\)

OR

-2\(\frac{2}{5}\) + 3\(\frac{1}{4}\) + (-\(\frac{3}{5}\))
-2\(\frac{2}{5}\) + (-\(\frac{3}{5}\)) + 3\(\frac{1}{4}\) commutative property
-2\(\frac{5}{5}\) + 3\(\frac{1}{4}\)
-3 + 3\(\frac{1}{4}\)
\(\frac{1}{4}\)

Exercise 2.
Rewrite each mixed number as the sum of two signed numbers.
a. -9\(\frac{5}{8}\)
Answer:
-9 + (-\(\frac{5}{8}\) )

b. -2\(\frac{1}{2}\)
Answer:
-2 + (-\(\frac{1}{2}\) )

c. 8\(\frac{11}{12}\)
8 + \(\frac{11}{12}\)

Exercise 3.
Represent each sum as a mixed number.
a. -1 + (-\(\frac{5}{12}\))
Answer:
-1 \(\frac{5}{12}\)

b. 30 + \(\frac{1}{8}\)
Answer:
30\(\frac{1}{8}\)

c. -17 + (-\(\frac{1}{9}\) )
-17 \(\frac{1}{9}\)

Note: Exercises 3 and 4 are designed to provide students with an opportunity to practice writing mixed numbers as sums so they can do so as the need arises in more complicated problems.

Exercise 4.
Mr. Mitchell lost 10 pounds over the summer by jogging each week. By winter, he had gained 5 \(\frac{1}{8}\) pounds. Represent this situation with an expression involving signed numbers. What is the overall change in Mr. Mitchell’s weight?
Answer:
-10 + 5 \(\frac{1}{8}\)
= -10 + 5 + \(\frac{1}{8}\)
=(-10 + 5) + \(\frac{1}{8}\)
=(-5) + \(\frac{1}{8}\)
= -4\(\frac{7}{8}\)
Mr. Mitchell’s weight dropped by 4 \(\frac{7}{8}\) pounds.

Exercise 5.
Jamal is completing a math problem and represents the expression -5\(\frac{5}{7}\) + 8 – 3\(\frac{2}{7}\) with a single rational number as shown in the steps below. Justify each of Jamal’s steps. Then, show another way to solve the problem.
= -5 \(\frac{5}{7}\) + 8 + (-3 \(\frac{2}{7}\) )
= -5 \(\frac{5}{7}\) + (-3 \(\frac{2}{7}\) ) + 8
= -5 + (-\(\frac{5}{7}\) ) + (-3) + (-\(\frac{2}{7}\) ) + 8
= -5 + (-\(\frac{5}{7}\) ) + (-\(\frac{2}{7}\) ) + (-3) + 8
= -5 + (-1) + (-3) + 8
= -6 + (-3) + 8
= (-9) + 8
= -1
Answer:
Step 1: Subtracting a number is the same as adding its inverse.
Step 2: Apply the commutative property of addition.
Step 3: The opposite of a sum is the sum of its opposites.
Step 4: Apply the commutative property of addition.
Step 5: Apply the associative property of addition.
(-\(\frac{5}{7}\)) + (-\(\frac{2}{7}\) ) = (-\(\frac{7}{7}\) )= -1
Step 6: -5 + (-1) = -6
Step 7: -6 + -3 = -9
Step 8: -9 + 8= -1
Answers will vary for other methods of reaching a single rational number. Students may choose to add -5 \(\frac{5}{7}\) and 8 together first, but a common mistake is to represent their sum as 3 \(\frac{5}{7}\) , rather than 2 \(\frac{2}{7}\) .

Eureka Math Grade 7 Module 2 Lesson 8 Problem Set Answer Key

Question 1.
Represent each sum as a single rational number.
a. -14 + (-\(\frac{8}{9}\) )
Answer:
-14 \(\frac{8}{9}\)

b. 7 + \(\frac{1}{9}\)
Answer:
7 \(\frac{1}{9}\)

c. -3 + (-\(\frac{1}{6}\) )
Answer:
-3 \(\frac{1}{6}\)

Rewrite each of the following to show that the opposite of a sum is the sum of the opposites. Problem 2 has been completed as an example.

Question 2.
-(9 + 8) = -9 + (-8)
-17 = -17
Answer:
Answer provided in student materials.

Question 3.
-(\(\frac{1}{4}\) + 6) = –\(\frac{1}{4}\) + (-6)
Answer:
-6 \(\frac{1}{4}\) = -6 \(\frac{1}{4}\)

Question 4.
-(10 + (-6)) = -10 + 6
Answer:
– 4 = -4

Question 5.
-((-55) + \(\frac{1}{2}\)) = 55 + (-\(\frac{1}{2}\) )
Answer:
54\(\frac{1}{2}\) = 54\(\frac{1}{2}\)

Use your knowledge of rational numbers to answer the following questions.

Question 6.
Meghan said the opposite of the sum of -12 and 4 is 8. Do you agree? Why or why not?
Answer:
Yes, I agree. The sum of -12 and 4 is -8, and the opposite of -8 is 8.

Question 7.
Jolene lost her wallet at the mall. It had $10 in it. When she got home, her brother felt sorry for her and gave her $5.75. Represent this situation with an expression involving rational numbers. What is the overall change in the amount of money Jolene has?
Answer:
-10 + 5.75 = -4.25. The overall change in the amount of money Jolene has is -4.25 dollars.

Question 8.
Isaiah is completing a math problem and is at the last step: 25 – 28\(\frac{1}{5}\). What is the answer? Show your work.
Answer:
25 – 28 \(\frac{1}{5}\) = 25 + (-28 + (-\(\frac{1}{5}\))) = (25 + -28) + (-\(\frac{1}{5}\)) = -3\(\frac{1}{5}\)

Question 9.
A number added to its opposite equals zero. What do you suppose is true about a sum added to its opposite? Use the following examples to reach a conclusion. Express the answer to each example as a single rational number.
Answer:
A sum added to its opposite is zero.
a. (3 + 4) + (-3 + -4)
Answer:
(3 + 4) + (-3 + -4) = 7 + (-7) = 0

b. (-8 + 1) + (8 + (- 1))
Answer:
(-8 + 1) + (8 + (- 1)) = (-7) + 7 = 0

c. (-\(\frac{1}{2}\) + (-\(\frac{1}{4}\) )) + (\(\frac{1}{2}\) + \(\frac{1}{4}\) )
Answer:
(-\(\frac{1}{2}\) + (-\(\frac{1}{4}\) )) + (\(\frac{1}{2}\) + \(\frac{1}{4}\) ) = (-\(\frac{3}{4}\) ) + \(\frac{3}{4}\) =0

Eureka Math Grade 7 Module 2 Lesson 8 Integer Addition—Round 1 Answer Key

Directions: Determine the sum of the integers, and write it in the column to the right.

Answer:

Question 1.
8 + (-5)
Answer:
3

Question 2.
10 + (-3)
Answer:
7

Question 3.
2 + (-7)
Answer:
-5

Question 4.
4 + (-11)
Answer:
-7

Question 5.
-3 + (-9)
Answer:
-12

Question 6.
-12 + (-7)
Answer:
-19

Question 7.
-13 + 5
Answer:
0

Question 8.
-4 + 9
Answer:
5

Question 9.
7 + (-7)
Answer:
0

Question 10.
-13 + 13
Answer:
0

Question 11.
14 + (-20)
Answer:
-6

Question 12.
6 + (-4)
Answer:
2

Question 13.
10 + (-7)
Answer:
3

Question 14.
-16 + 9
Answer:
-7

Question 15.
-10 + 34
Answer:
24

Question 16.
-20 + (-5)
Answer:
-25

Question 17.
-18 + 15
Answer:
-3

Question 18.
-38 + 25
Answer:
-13

Question 19.
-19 + (-11)
Answer:
-30

Question 20.
2 + (-7)
Answer:
-5

Question 21.
-23 + (-23)
Answer:
-46

Question 22.
45 + (-32)
Answer:
13

Question 23.
16 + (-24)
Answer:
-8

Question 24.
-28 + 13
Answer:
-15

Question 25.
-15 + 15
Answer:
0

Question 26.
12 + (-19)
Answer:
-7

Question 27.
-24 + (-32)
Answer:
-56

Question 28.
-18 + (-18)
Answer:
-36

Question 29.
14 + (-26)
Answer:
-12

Question 30.
-7 + 8 + (-3)
Answer:
-2

Question 31.
2 + (-15) + 4
Answer:
-9

Question 32.
-8 + (-19) + (-11)
Answer:
-38

Question 33.
15 + (-12) + 7
Answer:
10

Question 34.
-28 + 7 + (-7)
Answer:
-28

Eureka Math Grade 7 Module 2 Lesson 8 Integer Addition—Round 2 Answer Key

Answer:

Question 1.
5 + (-12)
Answer:
-7

Question 2.
10 + (-6)
Answer:
4

Question 3.
-9 + (-13)
Answer:
-22

Question 4.
-12 + 17
Answer:
5

Question 5.
-15 + 15
Answer:
0

Question 6.
16 + (-25)
Answer:
-9

Question 7.
-12 + (-8)
Answer:
-20

Question 8.
-25 + (-29)
Answer:
-54

Question 9.
28 + (-12)
Answer:
16

Question 10.
-19 + (-19)
Answer:
-38

Question 11.
-17 + 20
Answer:
3

Question 12.
8 + (-18)
Answer:
-10

Question 13.
13 + (-15)
Answer:
-2

Question 14.
-10 + (-16)
Answer:
-26

Question 15.
35 + (-35)
Answer:
0

Question 16.
9 + (-14)
Answer:
-5

Question 17.
-34 + (-27)
Answer:
-61

Question 18.
23 + (-31)
Answer:
-8

Question 19.
-26 + (-19)
Answer:
-45

Question 20.
16 + (-37)
Answer:
-21

Question 21.
-21 + 14
Answer:
-7

Question 22.
33 + (-8)
Answer:
25

Question 23.
-31 + (-13)
Answer:
-44

Question 24.
-16 + 16
Answer:
0

Question 25.
30 + (-43)
Answer:
-13

Question 26.
-22 + (-18)
Answer:
-40

Question 27.
-43 + 27
Answer:
-16

Question 28.
38 + (-19)
Answer:
19

Question 29.
-13 + (-13)
Answer:
-26

Question 30.
5 + (-8) + (-3)
Answer:
-6

Question 31.
6 + (-11) + 14
Answer:
9

Question 32.
-17 + 5 + 19
Answer:
7

Question 33.
-16 + (-4) + (-7)
Answer:
-27

Question 34.
8 + (-24) + 12
Answer:
-4

Eureka Math Grade 7 Module 2 Lesson 8 Exit Ticket Answer Key

Mariah and Shane both started to work on a math problem and were comparing their work in math class. Are both of their representations correct? Explain, and finish the math problem correctly to arrive at the correct answer.

Mariah started the problem as follows:
-5 – (-1\(\frac{3}{4}\) )
= -5 + 1 – \(\frac{3}{4}\)
Shane started the problem as follows:
-5 – (-1\(\frac{3}{4}\) )
= -5 + (1 \(\frac{3}{4}\))
= -5 + (1 + \(\frac{3}{4}\))
Answer:
Shane’s method is correct. In Mariah’s math work, she only dealt with part of the mixed number. The fractional part should have been positive too because the opposite of -1 \(\frac{3}{4}\) is 1 \(\frac{3}{4}\) , which contains both a positive 1 and a positive \(\frac{3}{4}\) .
The correct work would be
-5 – (-1\(\frac{3}{4}\)) = -5 + (1 \(\frac{3}{4}\)) = -5 + (1 + \(\frac{3}{4}\)) = (-5 + 1) + \(\frac{3}{4}\) = -4 + \(\frac{3}{4}\) = -3\(\frac{1}{4}\) .
The rational number would be -3 \(\frac{1}{4}\) , which means Jessica’s friend gave away 3 \(\frac{1}{4}\) dollars, or $3.25.

Engage NY Eureka Math 7th Grade Module 2 Lesson 7 Answer Key

Eureka Math Grade 7 Module 2 Lesson 7 Example Answer Key

Example 1.
Representing Sums of Rational Numbers on a Number Line
a. Place the tail of the arrow on 12.
b. The length of the arrow is the absolute value of -3\(\frac{1}{2}\) , |-3 \(\frac{1}{2}\) | = 3 \(\frac{1}{2}\) .
c. The direction of the arrow is to the left since you are adding a negative number to 12.
Draw the number line model in the space below.

Answer:

12 + ( -3\(\frac{1}{2}\) ) = 8\(\frac{1}{2}\) or 12 – 3\(\frac{1}{2}\) = 8\(\frac{1}{2}\)

Example 2.
Representing Differences of Rational Numbers on a Number Line
Find the following difference, and represent it on a number line: 1 – 2\(\frac{1}{4}\) .
a.
Answer:
Rewrite the difference 1 – 2\(\frac{1}{4}\) as a sum: 1 + (-2 \(\frac{1}{4}\)).
Now follow the steps to represent the sum:
b.
Answer:
Place the tail of the arrow on 1.

c.
Answer:
The length of the arrow is the absolute value of -2 \(\frac{1}{4}\) ; | -2 \(\frac{1}{4}\) |= 2\(\frac{1}{4}\) .

d.
Answer:
The direction of the arrow is to the left since you are adding a negative number to 1.

Draw the number line model in the space below.

Answer:

Eureka Math Grade 7 Module 2 Lesson 7 Exercise Answer Key

Exercise 1.
Real-World Connection to Adding and Subtracting Rational Numbers
Suppose a seventh grader’s birthday is today, and she is 12 years old. How old was she 3\(\frac{1}{2}\) years ago? Write an equation, and use a number line to model your answer.
Answer:
12 + ( -3\(\frac{1}{2}\)) = 8\(\frac{1}{2}\) or 12 – 3\(\frac{1}{2}\) = 8\(\frac{1}{2}\)

Exercise 2.
Find the following sum using a number line diagram: -2\(\frac{1}{2}\) + 5.
Answer:

(-2\(\frac{1}{2}\)) + 5 = 2\(\frac{1}{2}\)

Exercise 3.
Find the following difference, and represent it on a number line: -5\(\frac{1}{2}\) – (-8).

Answer:

(-5\(\frac{1}{2}\) ) + 8 = 2 \(\frac{1}{2}\)

Exercise 4.
Find the following sums and differences using a number line model.

a. -6 + 5\(\frac{1}{4}\)
Answer:

-6 + 5 \(\frac{1}{4}\) = –\(\frac{3}{4}\)

b. 7-(-0.9)
Answer:

7 + (0.9) = 7.9

c. 2.5 + (-\(\frac{1}{2}\) )
Answer:

2.5 + (-0.5) = 2

d. –\(\frac{1}{4}\) + 4
Answer:

–\(\frac{1}{4}\) + 4 = 3\(\frac{3}{4}\)

e. –\(\frac{1}{2}\) – (-3)
Answer:

\(\frac{1}{2}\) + 3 = 3 \(\frac{1}{2}\)

Exercise 5.
Create an equation and number line diagram to model each answer.
a. Samantha owes her father $7. She just got paid $5.50 for babysitting. If she gives that money to her dad, how much will she still owe him?
Answer:
-7 + 5.50 = -1.50. She still owes him $1.50.

b. At the start of a trip, a car’s gas tank contains 12 gallons of gasoline. During the trip, the car consumes 10\(\frac{1}{8}\) gallons of gasoline. How much gasoline is left in the tank?
Answer:
12 + (-10\(\frac{1}{8}\) ) = 1\(\frac{7}{8}\) or 12-10\(\frac{1}{8}\) =1 \(\frac{7}{8}\) ,There are 1\(\frac{7}{8}\) gallons of gas left in the tank.

c. A fish was swimming 3\(\frac{1}{2}\) feet below the water’s surface at 7:00 a.m. Four hours later, the fish was at a depth that is 5\(\frac{1}{4}\) feet below where it was at 7:00 a.m. What rational number represents the position of the fish with respect to the water’s surface at 11:00 a.m.?
Answer:
-3\(\frac{1}{2}\) +(-5\(\frac{1}{4}\) )= -8\(\frac{3}{4}\) . The fish is 8\(\frac{3}{4}\) feet below the water’s surface.

Eureka Math Grade 7 Module 2 Lesson 7 Problem Set Answer Key

Represent each of the following problems using both a number line diagram and an equation.

Question 1.
A bird that was perched atop a 15\(\frac{1}{2}\) -foot tree dives down six feet to a branch below. How far above the ground is the bird’s new location?
Answer:
15\(\frac{1}{2}\) + (-6) = 9\(\frac{1}{2}\)
The bird is 9\(\frac{1}{2}\) feet above the ground.

Question 2.
Mariah owed her grandfather $2.25 but was recently able to pay him back $1.50. How much does Mariah currently owe her grandfather?
Answer:
-2.25 + 1.50 = -0.75
Mariah owes her grandfather 75 cents.

Question 3.
Jake is hiking a trail that leads to the top of a canyon. The trail is 4.2 miles long, and Jake plans to stop for lunch after he completes 1.6 miles. How far from the top of the canyon will Jake be when he stops for lunch?
Answer:
4.2 – 1.6 = 2.6
Jake will be 2.6 miles from the top of the canyon.

Question 4.
Sonji and her friend Rachel are competing in a running race. When Sonji is 0.4 miles from the finish line, she notices that her friend Rachel has fallen. If Sonji runs one-tenth of a mile back to help her friend, how far will she be from the finish line?
Answer:
-0.4 + (-0.1) = -0.5 or -0.4 – 0.1 = -0.5
Sonji will be 0.5 miles from the finish line.

Question 5.
Mr. Henderson did not realize his checking account had a balance of $200 when he used his debit card for a $317.25 purchase. What is his checking account balance after the purchase?
Answer:
200 + (-317.25) = -117.25 or 200 – 317.25 = -117.25
Mr. Henderson’s checking account balance will be -$117.25.

Question 6.
If the temperature is -3°F at 10:00 p.m., and the temperature falls four degrees overnight, what is the resulting temperature?
Answer:
-3 – 4 = -3 + (-4) = -7
The resulting temperature is -7°F.

Eureka Math Grade 7 Module 2 Lesson 7 Exit Ticket Answer Key

At the beginning of the summer, the water level of a pond is 2 feet below its normal level. After an unusually dry summer, the water level of the pond dropped another 1\(\frac{1}{3}\) feet.

Question 1.
Use a number line diagram to model the pond’s current water level in relation to its normal water level.
Answer:
Move 1\(\frac{1}{3}\) units to the left of -2. -3\(\frac{1}{3}\)

Question 2.
Write an equation to show how far above or below the normal water level the pond is at the end of the summer.
Answer:
-2 – 1\(\frac{1}{3}\) = -3\(\frac{1}{3}\) or -2 + (-1\(\frac{1}{3}\)) = -3\(\frac{1}{3}\)

Engage NY Eureka Math 7th Grade Module 2 Lesson 5 Answer Key

Eureka Math Grade 7 Module 2 Lesson 5 Example Answer Key

Example 1.
Exploring Subtraction with the Integer Game
Play the Integer Game in your group. Start Round 1 by selecting four cards. Follow the steps for each round of play.
Write the value of your hand in the Total column.
Then, record what card values you select in the Action 1 column and discard from your hand in the Action 2 column.
After each action, calculate your new total, and record it under the appropriate Results column.
Based on the results, describe what happens to the value of your hand under the appropriate Descriptions column. For example, “Score increased by 3.”

Answer:
sample student work

Discussion: Making Connections to Integer Subtraction

Question 1.
How did selecting positive value cards change the value of your hand?
Answer:
It increased my score by the value of the card.

Question 2.
How did selecting negative value cards change the value of your hand?
Answer:
It decreased my score by the absolute value of the card.

Question 3.
How did discarding positive value cards change the value of your hand?
Answer:
It decreased my score by the value of the card.

Question 4.
How did discarding negative value cards change the value of your hand?
Answer:
It increased my score by the absolute value of the card.

Question 5.
What operation reflects selecting a card?
Answer:
Addition

Question 6.
What operation reflects discarding or removing a card?
Answer:
Subtraction

Question 7.
Based on the game, can you make a prediction about what happens to the result when

a. Subtracting a positive integer?
Answer:
The result of the hand will decrease by the value of the integer.

b. Subtracting a negative integer?
Answer:
The result of the hand will increase by the absolute value of the negative integer.

At the end of the lesson, the class reviews its predictions.

Example 2:
Subtracting a Positive Number
Follow along with your teacher to complete the diagrams below.

Answer:
If I had these two cards, the sum would be 6.

Show that discarding (subtracting) a positive card, which is the same as subtracting a positive number, decreases the value of the hand.

Answer:

If I discarded or removed the 2, my score would decrease by 2 because I would still have a 4 left in my hand.
4 + 2 – 2 = 4. Taking away, or subtracting, 2 causes my score to decrease by 2.

Removing ___ a positive card changes the score in the same way as ___ adding a card whose value is the ___ ___ (or opposite). In this case, adding the corresponding ____
Answer:
Removing (subtracting) a positive card changes the score in the same way as adding a card whose value is the
additive inverse (or opposite). In this case, adding the corresponding negative such that 4 – 2 = 4 + (-2).
Subtracting a positive q-value is represented on the number line as moving to the left on a number line.

Example 3.
Subtracting a Negative Number
Follow along with your teacher to complete the diagrams below.

How does removing a negative card change the score, or value, of the hand?
Answer:

If I discarded, or removed, the -2, my score would increase by 2 because I would still have a 4 left in my hand.
4 + (-2) – (-2) = 4. Taking away, or subtracting, -2 causes my score to increase by 2.

Answer:

Removing (___) a negative card changes the score in the same way as ___ a card whose value is the ___ (or opposite). In this case, adding the corresponding ____
Answer:
Removing (subtracting) a negative card changes the score in the same way as adding a card whose value is the
additive inverse (or opposite). In this case, adding the corresponding positive such that 4 – (-2) = 4 + 2.
Subtracting a negative q-value is represented on the number line as moving to the right on a number line because it is the opposite of subtracting a positive q-value (move to the left).

THE RULE OF SUBTRACTION: Subtracting a number is the same as adding its additive inverse (or opposite).

Eureka Math Grade 7 Module 2 Lesson 5 Exercise Answer Key

Question 1.
Using the rule of subtraction, rewrite the following subtraction sentences as addition sentences and solve. Use the number line below if needed.
a. 8 – 2
Answer:

b. 4 – 9
Answer:

c. -3 – 7
Answer:
-3 + (-7) = -10

d. – 9 – (-2)
Answer:

Exercise 2.
Find the differences.
a. -2 – (-5)
Answer:

b. 11 – (-8)
Answer:
11 + 8 = 19

c. -10 – (-4)
Answer:

Question 3.
Write two equivalent expressions that represent the situation. What is the difference in their elevations? An airplane flies at an altitude of 25,000 feet. A submarine dives to a depth of 600 feet below sea level.
Answer:
25,000 – (-600) and 25,000 + 600
The difference in their elevation is 25,600 feet.

Eureka Math Grade 7 Module 2 Lesson 5 Problem Set Answer Key

Question 1.
On a number line, find the difference of each number and 4. Complete the table to support your answers. The first example is provided.

Answer:

Question 2.
You and your partner were playing the Integer Game in class. Here are the cards in both hands.

a. Find the value of each hand. Who would win based on the current scores? (The score closest to 0 wins.)
Answer:
My hand: -8 + 6 + 1 + (-2) = -3
Partner’s hand: 9 + (-5) + 2 + (-7) = -1
My partner would win because -1 is closer to 0. It is 1 unit to the left of 0.

b. Find the value of each hand if you discarded the -2 and selected a 5, and your partner discarded the -5 and selected a 5. Show your work to support your answer.
Answer:
My hand: Discard the -2, -3 – (-2) = -1; Select a 5: -1 + 5 = 4.
Partner’s hand: Discard the -5, -1 – (-5) = 4; Select a 5: 4 + 5 = 9.

c. Use your score values from part (b) to determine who would win the game now.
Answer:
I would win now because 4 is closer to zero.

Question 3.
Write the following expressions as a single integer.
a. -2+16
Answer:
14

b. -2 – (-16)
Answer:
14

c. 18 – 26
Answer:
-8

d. -14 – 23
Answer:
-37

e. 30 – (-45)
Answer:
75

Question 4.
Explain what is meant by the following, and illustrate with an example:
“For any real numbers, p and q, p – q = p + (-q).”
Answer:
Subtracting a number is the same as adding its additive inverse. Examples will vary. A sample response is shown below.
p = 4, q = 6, 4 – 6 is the same as 4 + (-6) because -6 is the opposite of 6.
4 – 6 = -2
4 + (-6) = -2
So, 4 – 6 = 4 + (-6) because they both equal -2.

Question 5.
Choose an integer between -1 and -5 on the number line, and label it point P. Locate and label the following points on the number line. Show your work.
Answer:
Answers will vary. A sample response is shown below given that the student chose -3 for P.

a. Point A: P – 5
Answer:
Point A: -3 – 5 = -8

b. Point B: (P-4)+4
Answer:
Point B: (-3 – 4) + 4 = -3 (same as P)

c. Point C: -P-(-7)
Answer:
Point C: -(-3) – (-7) = 3 + 7 = 10

Eureka Math Grade 7 Module 2 Lesson 5 Exit Ticket Answer Key

Question 1.
If a player had the following cards, what is the value of his hand?
Answer:
The current value of the hand is -2. 1 + (-7) + 4 = -2.

a. Identify two different ways the player could get to a score of 5 by adding or removing only one card. Explain.
Answer:
He could remove the -7 or add 7. If he removes the -7, the value of the hand will be 5, which is 7 larger than -2. He could also get a sum of 5 by adding 7 to the hand. Therefore, removing the -7 gives him the same result as adding 7.

b. Write two equations for part (a), one for each of the methods you came up with for arriving at a score of 5.
Answer:
-2 – (-7) = 5 and -2 + 7 = 5

Question 2.
Using the rule of subtraction, rewrite the following subtraction expressions as addition expressions, and find the sums.
a. 5 – 9
Answer:
5 + (-9) = -4

b. -14 – (-2)
Answer:
-14 + 2 = -12

Eureka Math Grade 7 Module 2 Lesson 5 Challenge Problem Answer Key

Question 6.
Write two equivalent expressions that represent the situation. What is the difference in their elevations?
An airplane flies at an altitude of 26,000 feet. A submarine dives to a depth of 700 feet below sea level.
Answer:
Two equivalent expressions are 26,000 – (-700) and 26,000 + 700. The difference in their elevations is 26,700 feet.