A Linear indicates the straight line. We need to find out the linear relation between the two variables. Here, the two variables are x and y. We need to draw the graph for the linear relation between x and y. The basic expression for the linear relation with two variables in mathematics is ax + by + c = 0. Here, a, b, c are constants, and x and y are variables. The constants or real numbers are a and b. These real numbers are not equal to zero and that is called a linear equation with two variables. The below diagram is the basic diagram of the Graph of Standard Linear Relations between x and y.
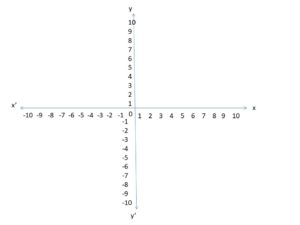
Quadrants of a Graph
Generally, the graph is divided into four quadrants. In the first quadrant both the variables, x and y are positive numbers. Where the x variable values are negative and the y variable values are positive, that is called the second quadrant of the graph. In the third quadrant, both the variables x and y are negative numbers. Finally, the fourth quadrant has the y variables as negative numbers and the x variables as positive numbers. That is
- The first quadrant – x and y variables are positive.
- The second quadrant – x variable is negative and the y variable is positive.
- The third quadrant – x and y variables are negative.
- The fourth quadrant – x variable is positive and y variable is negative.
Linear Relationship with Two Variables
In this section, we are elaborating on how we can find the variable values by using the linear equation.
| x value | x + 4 = y | y value | (x, y) |
|---|---|---|---|
| 2 | 2 + 4 = y | 6 | (2, 6) |
| 3 | 3 + 4 = y | 7 | (3, 7) |
| 0 | 0 + 4 = y | 4 | (0, 4) |
| -1 | -1 + 4 =y | 3 | (-1, 3) |
| -2 | -2 + 4 = y | 2 | (-2, 2) |
Plotting Points on a Graph with x and y Values.
(I) If x = 0 and y = 1, 2, -1, -2.
The given details are x = 0 and y = 1, 2, -1, -2.
The x and y variable values are mentioned on the below graph.
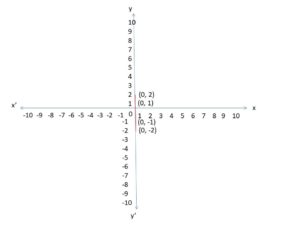
Here, x=0. So, all points are placed on the y- axis.
(ii) If y = 0 and x = 1, 2, -3, -6.
As per the given information y = 0 and x = 1, 2, -3, -6.
![]()
The x and y values are marked on the below graph.
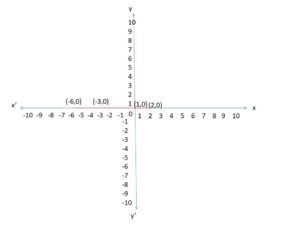
All the x and y related points are marked on the x-axis only.
(iii) If x = y

The x and y variables are marked on the below graph.
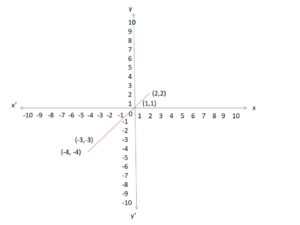
Solved Examples on Linear Relationship between x and y
1. If x = 1, 2, 0, -1, -2 and the linear equation is 2x + y +1 =0, then find the y values?
Solution:
As per the given information, x = 1, 2, 0, -1, -2.
The given linear equation is 2x + y + 1 = 0.
Substitute the ‘x’ values in the above linear equation, then we will get
If x = 1
Substitute x = 1 in the linear equation 2x + y + 1 = 0.
That is, 2(1) + y + 1 = 0.
3 + y = 0.
So, y = -3.
If x = 1 then y = -3.
If x = 2.
Substitute x = 2 in the linear equation 2x + y + 1 = 0.
That is, 2(2) + y + 1 = 0.
4 + y + 1 = 0.
5 + y = 0.
So, y = -5.
If x = 2 then y = -5.
If x = 0.
Substitute x = 0 in the linear equation 2x + y + 1 = 0.
That is, 2(0) + y + 1 = 0.
y + 1 = 0.
So, y = -1.
If x = 0 then y = -1.
If x = -1.
Substitute x = -1 in the linear equation 2x + y + 1 = 0.
That is, 2(-1) + y + 1 = 0.
– 2 + y + 1 = 0.
-1 + y = 0.
So, y = 1.
So, If x = -1 then y = 1.
If x = -2.
Substitute x = -2 in the linear equation 2x + y + 1 = 0.
That is, 2(-2) + y + 1 = 0.
-4 + y + 1 = 0.
-3 + y = 0.
So, y = 3.
So, If x = -2 then y = 3.
Finally, x and y variable values are
![]()
2. Find the two variable values by using the linear equation 2x + 3y = 10?
Solution:
From the given details, the linear equation is 2x + 3y = 10.
To find out the variable values, we need to substitute the x =0 and y = 0 in the linear equation.
Firstly, apply the x = 0 in the above linear equation. That is, 2x + 3y =10.
2(0) + 3y = 10.
3y = 10.
y = 10 / 3.
Now, apply y = 0 in the linear equation. Then we will get 2x + 3y = 10.
2x + 3(0) = 10.
2x = 10.
x = 10 / 2 = 5.
Therefore, the values of the variables are x = 5 and y = 10 / 3.
3. Find the variable values by using the linear equations 2x + 5y =10 and 3x + 6y = 6?
Solution:
The given linear equations are
2x + 5y = 10——–(1).
3x + 6y = 6———(2).
Multiply the equation (1) with 3 on both sides. That is,
3 * (2x + 5y) = 10 * 3.
6x + 15y = 30——–(3).
Multiply equation (2) with 2 on both sides. That is,
2 * (3x + 6y) = 6 *2.
6x + 12y = 12——–(4).
Subtract the equation (3) and equation (4). That is
6x + 15y = 30.
6x + 12y = 12.
(-) (-) (-)
3y = 18.
Y = 18 / 3 = 6.
Substitute the y = 6 in the equation (1). We will get
2x + 5y = 10.
2x + 5(6) = 10.
2x + 30 = 10.
2x = 10 – 30 = -20.
X = -20 / 2 = -10.
Therefore, the two variable values are x = -10 and y = 6.