Do you want to know one second is how many minutes? Then read this complete page. Here, you can learn about the seconds to minutes conversion with a detailed explanation. You will also learn the steps of converting seconds into minutes. Get to know more about what is a second, minute, and what are different units of time, and others. Refer to Seconds to Minutes Conversion Formula, Step by Step Procedure on how to convert seconds into minutes, solved examples, here.
Minutes and Seconds – Definitions
Minute, second are the different units of time. In general, hours is the highest unit, next minutes and then seconds. Minute is a period of time which is equal to sixty seconds or sixtieth of an hour. Actually, a second is the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom. And it is a small division of an hour.
Also, Check:
Seconds to Minutes Conversion Formula
The simple formula to convert minutes into seconds is as follows:
1 Minute = 60 Seconds
So, 1 Second = \(\frac { 1 }{ 60 } \) Minute
Number of minutes = \(\frac { 1 }{ 60 } \) x number of seconds
How to Convert Seconds to Minutes?
Check out the simple and detailed steps to convert the seconds into minutes. They are in the following fashion
- Let us take the number of seconds you want to convert into minutes.
- In general, 1 second = \(\frac { 1 }{ 60 } \) minute
- Multiply the given number of seconds by \(\frac { 1 }{ 60 } \).
- The result is called the minutes.
Also, Read
- Conversion of Hours into Seconds
- Conversion of Minutes into Hours
- Conversion of Hours into Minutes
- Conversion of Seconds into Hours
- Conversion of Minutes into Seconds
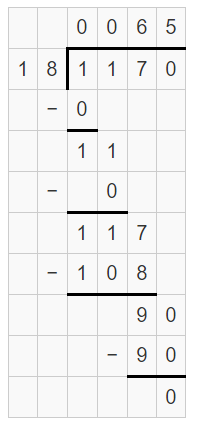
Seconds to Minutes Conversion Examples
Example 1:
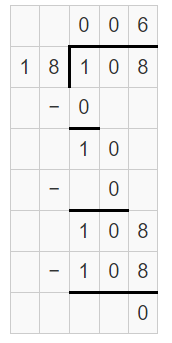
Convert 150 seconds into minutes?
Solution:
The given number of seconds = 150
Multiply 150 by (\(\frac { 1 }{ 60 } \))
So, 150 seconds = \(\frac { 150 }{ 60 } \)

Therefore, 150 seconds = 2.5 Minutes
Example 2:
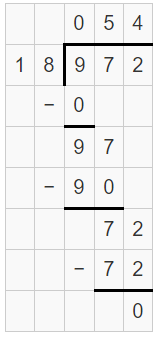
Convert 215 seconds into minutes.
Solution:
The given number of seconds = 215
Multiply 215 by \(\frac { 1 }{ 60 } \)
So, 215 seconds = \(\frac { 215 }{ 60 } \)

Therefore, 215 seconds = 3.583 minutes.
Example 3:
Convert 180 seconds into minutes.
Solution:
The given number of seconds = 180
Multiply 180 by \(\frac { 1 }{ 60 } \)
So, 180 seconds = \(\frac { 180 }{ 60 } \) minutes
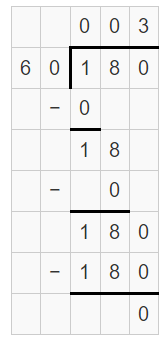
Therefore, 180 seconds = 3 minutes
Example 4:
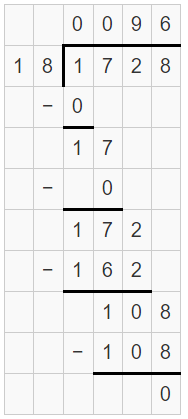
Convert 516 seconds into minutes.
Solution:
The given number of seconds = 516
Multiply 516 by \(\frac { 1 }{ 60 } \)
So, 516 seconds = \(\frac { 516 }{ 60 } \) minutes
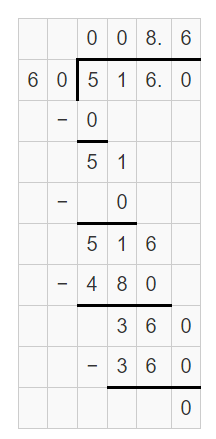
Therefore, 516 seconds = 8.6 minutes.
Example 5:
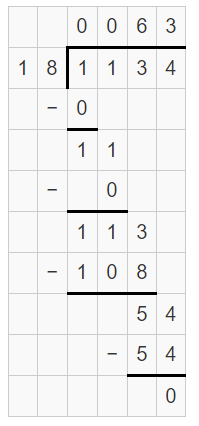
Convert 1020 seconds into minutes.
Solution:
The given number of seconds = 1020
Multiply 1020 by \(\frac { 1 }{ 60 } \)
So, 1020 seconds = \(\frac { 1020 }{ 60 } \) minutes

Therefore, 1020 seconds = 17 minutes.
Common Conversions Facts About Time
Below are a few easy & quick conversion facts about the unit of time.
1 Hour = 60 Minutes
1 Minute = 60 seconds
1 Second = \(\frac { 1 }{ 60 } \) Minute
1 Minute = \(\frac { 1 }{ 3600 } \) Hour
1 Hour = 3600 seconds
12 hours = 1 day
12 hours = 43,200 seconds
1 day = 24 hours = 1440 minutes
1 day = 24 hours = 86,400 seconds
Seconds to Minutes Conversion Table
Here is the conversion table of Seconds (sec) to Minutes (min):
| Seconds | Minutes |
|---|---|
| 1 Second | \(\frac { 1 }{ 60 } \) Minute |
| 2 Seconds | \(\frac { 2 }{ 60 } \) Minute |
| 10 Seconds | \(\frac { 1 }{ 6 } \) Minute |
| 25 Seconds | \(\frac { 25 }{ 60 } \) Minute |
| 50 Seconds | \(\frac { 5 }{ 6 } \) Minute |
| 60 Seconds | 1 Minute |
| 120 Seconds | 2 Minutes |
| 180 Seconds | 3 Minutes |
| 240 Seconds | 4 Minutes |
| 300 Seconds | 5 Minutes |
FAQ’s on Conversion of Seconds into Minutes
1. How do you convert seconds to minutes?
To convert seconds into minutes, multiply the number of seconds by \(\frac { 1 }{ 60 } \). The obtained product is the converted minutes.
2. How many minutes is 540 seconds?
540 seconds = \(\frac { 540 }{ 60 } \) = \(\frac { 54 }{ 6 } \)
540 seconds = 9 minutes.
3. How do you convert minutes into seconds?
Generally, we know that 1 minute = 60 seconds. To convert minutes into seconds, multiply the number of minutes by 60 to get the number of seconds.