Sruthi Reddy

A triangle is a polygon having 3 sides and three vertices. The sum of interior angles of a triangle is 180 degrees. Depending on the side length triangles are divided into three types they are equilateral triangle, isosceles triangle, and scalene triangle. And based on the angle measurement, triangles are again classified into three various types they are right, acute, oblique triangles. Both median, altitude is the lines in the triangle. Here, we will learn more about the Medians and Altitudes of a Triangle.

Also, Read

• Area and Perimeter of the Triangle
• The triangle on the Same Base and between Same Parallels Theorem
• Perimeter of a Triangle

Median of a Triangle – Definition

Median in a triangle is nothing but the straight line that joins one vertex and midpoint of the side that is opposite to the vertex. A triangle can have a maximum of three medians and the point of intersection of three medians is called the center of the triangle.

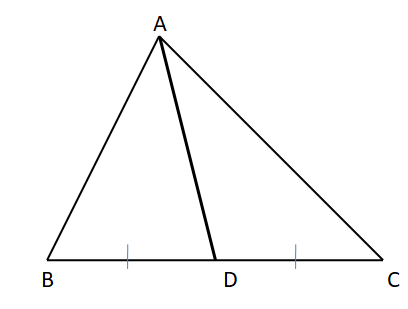
In △ ABC, AD is the median that divides a side BC into two equal parts. So, BD = CD.

Properties of a Triangle Median

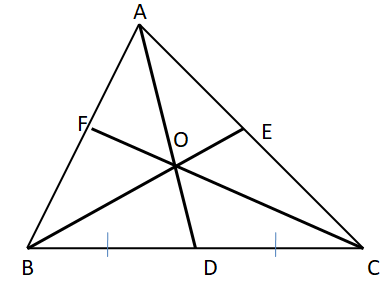
• All triangles have 3 medians, each one from the triangle vertex. Here AD, BE, CF are the 3 medians of the triangle ABC.
• The three medians meet at a single point.
• The point where 3 medians meet is called the centroid of the triangle. Here O is the centroid of △ ABC.
• Each median of a triangle divides the triangle into two smaller triangles having the same area.
• So, 3 medians divide a triangle into 6 smaller triangles of equal area.

Altitude of a Triangle – Definition

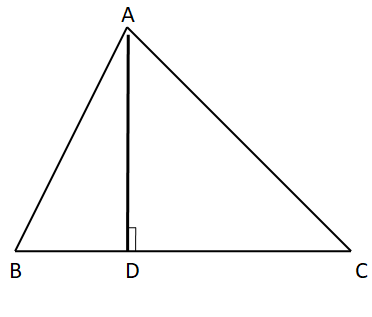
The altitude is a straight line that starts from the triangle vertex and stretches till the opposite side of the vertex making a right angle with the side of the triangle.

Properties of Altitude of a Triangle

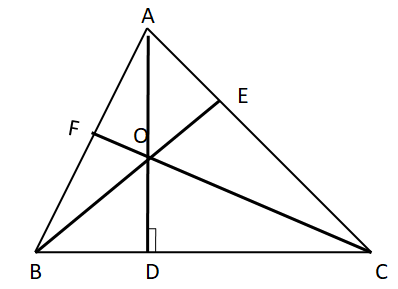
• Each triangle has 3 altitudes. Here AD, BE, CF are the altitudes of the triangle ABC.
• An altitude is also called the shortest distance from the vertex to the opposite side of a triangle.
• Three altitudes always meet at a single point.
• The point of intersection of three altitudes is called the ortho-center of the triangle. Here O is called the ortho-center of triangle ABC.
• The altitude of a triangle may lie inside or outside the triangle.

Median and Altitude of an Isosceles Triangle

Isosceles Triangle is a type of triangle that has two sides or angles of equal measurement. The median and altitude of an isosceles triangle have some particular features. They are along the lines.

• The Median, angle bisector is the same in an isosceles triangle when the altitude is drawn from the vertex to the base.
• Altitude, median, angle bisector interchange in case of an isosceles triangle.
• The Median, and altitude of the isosceles triangle are the same.

Medians and Altitudes of Triangles Examples

Example 1:

The given angles of a triangle ABC are in the ratio of 1 : 2 : 3. Evaluate all the angles of △ ABC.

Solution:

Let the first angle of triangle A is x.

So, ∠B = 2x, ∠C = 3x

We know that sum of all angles in a triangle is 180°

x + 2x + 3x = 180°

6x = 180

x = \(\frac { 180 }{ 6 } \)

x = 30°

So, ∠A = 30°

∠B = 2 x 30° = 60°

∠C = 3 x 30° = 90°

Therefore, the angles in a scalene triangle are different.

Example 2:

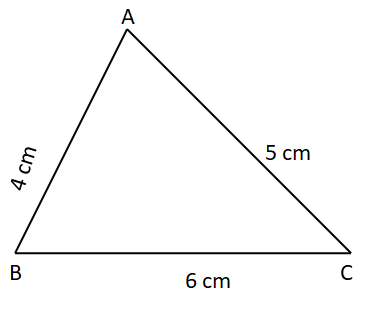
Construct ΔABC whose sides are AB = 4 cm, BC = 6 cm and AC = 5 cm and locate its orthocentre.

Solution:

Draw ΔABC using the given measurements.

Construct altitudes from any two vertices (A and C) to their opposite sides (BC and AB respectively).

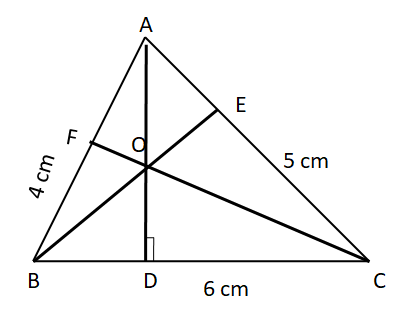
The point of intersection of the altitudes O is the orthocentre of the given ΔABC.

Example 3:

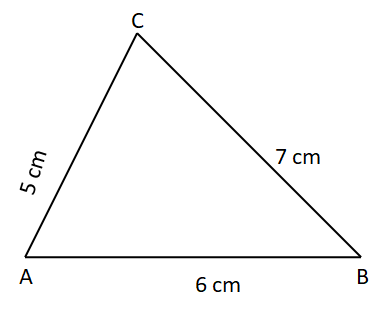
Construct the centroid of ΔABC whose sides are AB = 6 cm, BC = 7 cm, and AC = 5 cm.

Solution:

Draw ΔABC using the given measurements.

 

Construct the perpendicular bisectors of any two sides (AC and BC) to find the mid points D and E of AC and BC respectively.

Draw the medians AE and BD and let them meet at G.

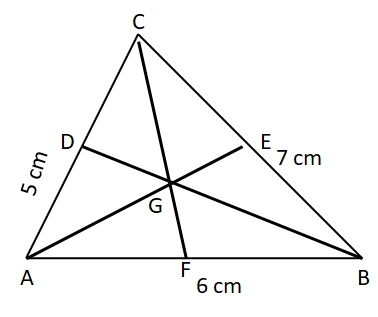
The point G is the centroid of the given ΔABC.

FAQs on Medians and Altitudes of a Triangle

1. How many medians can a triangle have?

Median is a line segment that connects a vertex to the mid point of the opposite side. Every triangle has exactly 3 medians each from one vertex.

2. What is the difference between the median and altitude of a triangle?

The altitude is a perpendicular bisector that falls on any side of the triangle and the median meets the side of a triangle at the midpoint. For an isosceles triangle, the altitude drawn to the base of a triangle is called the median, median drawn to the triangle base is called the altitude.

3. What is an ortho-center in a triangle?

The point where all three altitudes intersect is called the ortho-center of the triangle. The ortho-center may lie either inside or outside of a triangle.

The construction of angles is an important part of geometry as this knowledge is extended for the construction of other geometric figures. Constructing angles of unknown and unknown measures can be possible with geometric tools like compass, ruler, protractor. Here we will learn about the Construction of Angles by Using Compass in the following sections. You will find the Construction of Angles using Compass Examples with Solutions explained step by step.

Construction of Angles by Using Compass – Introduction

An angle is defined as the figure formed by two rays meeting at a common endpoint. The representation of angle is ∠. Construction of angles by using compass means you need to make an angle between two straight lines just with the compass. Take one straight line and draw an arc on the line with the compass with any radius from two ends of the line. Get the simple steps in the below-mentioned sections of this page.

Steps to Construct Angle of 60° with Compass

Check out the detailed steps to construct an angle of 60 degrees by using a compass.

• Draw a ray AB.
• By taking either A or B as a center and any suitable radius draw an arc above the ray and cutting at a point P.
• Now, with P as the center and having the same radius, draw another arc that meets the previous arc at C.
• Join AC or BC and produce it to D.
• Then ∠ADB = 60°.

More Related Articles

• Related Angles
• Pairs of Angles
• Types of Angles

Construction of Angles by Compass Examples

Example 1:

Construct an acute angle of 30° by using the compass?

Solution:

Take any ray OA

With O as a center and any radius draw an arc on OA at point P and draw another arc with P as the center, same radius.

The point of intersection of two arcs is Q.

∠AOR = 60°

• With center O and any convenient radius draw an arc cutting OA and OB at P and Q respectively.
• With centre P and radius more than \(\frac { 1 }{ 2 } \)(PQ), draw an arc in the interior of ∠AOB.
• With center Q and the same radius, as in step III, draw another arc intersecting the arc in step III at R.
• Join OR and product it to any point C.
• The angle ∠AOC is the angle of measure 30º.

Example 2:

Construct an obtuse angle of 120° by using the compass.

Solution:

• Draw a ray OA.
• By taking O as the center and any convenient radius, draw an arc cutting OA at P.
• By taking P as a center and same radius draw an arc, cutting the first arc at Q.
• With Q as the center and the same radius, draw an arc cutting the arc drawn in step II at R.
• Join OR and produce it to any point C.
• ∠AOC measures 120º.

Example 3:

Construct an angle of 90° by using the compass.

Solution:

• Draw a ray OA.
• With O as a center and any radius, draw an arc on OA at point P.
• By taking P as the center, the same radius, draw another arc cutting the first arc at point Q.
• With the point, Q as a center and the same radius draw an arc cutting the arc drawn in step II at R.
• By taking point Q as the center and same radius, draw an arc.
• With R as a center and the same radius, draw an arc, cutting the arc drawn in step V at B.
• Draw OB and extend it to C.
• ∠AOC measures an angle is 90º.

Example 4:

Construct an angle of 45° by using the compass.

Solution:

First of all, draw an angle of 90º.

Draw a bisector for 90º to measure 45º.

Skip counting means counting by a number that is not 1. Skip Counting by 4’s is an essential skill to learn when making the jump from counting to basic addition. The result of skip counting by 4s will be the multiples of 4. You can also get the result by using the addition operation. Get to know more about the concept in the following sections.

Skip Counting by 4 Chart

This skip counting by fours chart will help us to write the number to complete the series which involves skip counting by 4’s up to 25 times. Skip counting is a method of counting numbers by adding a number every time to the previous number. When we skip count natural numbers by 4 then we add 4 at each step. The highlighted numbers in the chart are skip counting by 4’s numbers. It helps in counting the number quickly and it has a huge application in the multiplication of tables.

Forward and Backward Skip Counting

Forward skip counting means we count the natural number in forward direction of a number. Here, we skip count for positive numbers. Skip counting has a huge application in the real life. if we have to count eggs that are in the 40s of a number, then we use the skip counting by fours method. Counting one egg will take more time.

Skip Counting by 4	Result
0 + 4	4
4 + 4	8
8 + 4	12
12 + 4	16
16 + 4	20
20 + 4	24
24 + 4	28
28 + 4	32
32 + 4	36
36 + 4	40
40 + 4	44

Backward skip counting means counting the numbers towards negative numbers. Here, you need to subtract 4 from the result.

Skip Counting by 4	Result
0 – 4	-4
-4 – 4	-8
-8 – 4	-12
-12 – 4	-16
-16 – 4	-20
-20 – 4	-24
-24 – 4	-28
-28 – 4	-32
-32 – 4	-36
-36 – 4	-40
-40 – 4	-44

Also, check out

• Skip Counting by 3S

Skip Counting by 4 Examples with Answers

Example 1:

Complete the fill in the blanks using the skip counting by fours chart.

(i) 4 x 19 = ______

(ii) 4 x 23 = ______

(iii) 4 x 12 = ______

Solution:

(i) 4 x 19 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 76

4 x 19 means add 4 19 times.

(ii) 4 x 23 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 92

4 x 23 means add 4 23 times.

(iii) 4 x 12 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 48

4 x 12 means add 4 12 times.

Example 2:

Complete the skip counting series by 4s:

(i) ____, ____, ____, ____, 36, ____, ____, 48.

(ii) 24, 28, ____, ____, ____, ____, ____, 52.

(iii) 8, 12, 16, ____, ____, ____, ____, ____.

Solution:

(i) Subtract and add 4 from the known numbers to know the before and after numbers.

So, 36 – 4 = 32

32 – 4 = 28

28 – 4 = 24

24 – 4 = 20

36 + 4 = 40

40 + 4 = 44

Therefore, the sequence is 20, 24, 28, 32, 36, 40, 44.

(ii) Add 4 from the known numbers to know the before and after numbers.

28 + 4 = 32

32 + 4 = 36

36 + 4 = 40

40 + 4 = 44

44 + 4 = 48

48 + 4 = 52

Therefore, the sequence is 24, 28, 32, 36, 40, 44, 48, 52.

(iii) Add 4 from the known numbers to know the before and after numbers.

8 + 4 = 12

12 + 4 = 16

16 + 4 = 20

20 + 4 = 24

24 + 4 = 28

28 + 4 = 32

32 + 4 = 36

Therefore, the sequence is 8, 12, 16, 20, 24, 28, 32, 36.

Example 3:

Complete the fill in the blanks using the skip counting by fours chart.

(i) 4 x 43 = _____

(ii) 4 x 25 = _____

(iii) 4 x 67 = _____

Solution:

(i) 4 x 43 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 172

4 x 43 means add 4 23 times.

(ii) 4 x 25 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 100

4 x 25 means add 4 25 times.

(iii) 4 x 67 = (4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4)

= 268

4 x 67 means add 4 67 times.

Example 4:

Complete the skip counting series by 4s:

(i) ____, ____, ____, ____, 88, 92, ____, 100.

(ii) ____, ____, 16, 20, ____, ____, ____, 36.

(iii) 72, 76, ____, ____, ____, ____, 96, ____.

Solution:

(i)

Subtract and add 4 from the known numbers to know the before and after numbers.

88 – 4 = 84

84 – 4 = 80

80 – 4 = 76

76 – 4 = 72

88 + 4 = 92

92 + 4 = 96

96 + 4 = 100

Therefore, the sequence is 72, 76, 80, 84, 88, 92, 96, 100.

(ii)

Subtract and add 4 from the known numbers to know the before and after numbers.

16 – 4 = 12

12 – 4 = 8

16 + 4 = 20

20 + 4 = 24

24 + 4 = 28

28 + 4 = 32

32 + 4 = 36

Therefore, the sequence is 8, 12, 16, 20, 24, 28, 32, 36.

(iii)

Subtract and add 4 from the known numbers to know the before and after numbers.

72 + 4 = 76

76 + 4 = 80

80 + 4 = 84

84 + 4 = 88

88 + 4 = 92

92 + 4 = 96

96 + 4 = 100

Therefore, the sequence is 72, 76, 80, 84, 88, 92, 96, 100.

FAQs on Skip Counting by 4S

1. What is skip counting?

Skip counting is a method of counting forward by any number apart from 1. If we skip count by 4 means we are adding 4 at each step to get another number.

2. How do we skip count?

Skip counting is a method of counting numbers by skipping them with a certain number.

3. How to skip count by 4?

The skip ccounting by 4’s means we have to skip 4 numbers in forward count and jump to next one. 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, . .

We have infinite points in the coordinate plane. A line passes through a point (x, y). The different forms of equations of straight lines are equations of horizontal and vertical lines, Point-slope form, two-point form, slope-intercept form, intercept form, and normal form. Get to know more about the Equation of a Line Parallel to the x-axis in the following sections of this page.

Also, Read:

• Types of Lines
• Angle Between Two Straight Lines
• Lines and Angles

Equation of a Line Parallel to X-Axis

A line can be defined as a straight one-dimensional geometric figure that doesn’t have the thickness and extends endlessly in both directions. A straight line on the coordinate plane can be described by an equation is called the equation of a line. If all the points the straight line having the same y-coordinate or ordinate values, then it is called the equation of a line parallel to the x-axis.

The general form of the equation of a line that is parallel to the x-ais is y = k. Here, k is the distance between the x-axis and the line. If a point P(x, y) lies on the line, then y = b. The equation of x-ais is y = 0 as the x-axis is parallel to itself at a distance of 0 from it.

Different Forms of the Equation of Line

The various forms of the equations of a straight line are long the lines.

Slope Intercept Form

The equation of a slope-intercept form of a straight line is y = mx + b.

Here, m is the slope,

b is the y-intercept.

Point Slope Form

The point-slope form of a line is y – y₁ = m(x – x₁)

Here, m is the slope of the line

(x₁, y₁) is a point on the line.

Two Point Form

The two points form of a line is \(\frac { y – y₁ }{ y₂ – y₁ } = \frac { x – x₁ }{ x₂ – x₁ }\)

Here, (x₁, y₁), (x₂, y₂) are the two points on the line

Slope of the line = \(\frac { y₂ – y₁ }{ x₂ – x₁ } \)

Intercept Form

Intercept form of a line is \(\frac { x }{ a } +\frac { y }{ b }\) = 1

Here, a is the x-intercept

b is the y-intercept

Equation of x-axis

The equation of x-axis is y = 0. Because the value of “ordinate” in all the points on the x-axis is zero.

Equation of y-axis

The equation of y-axis is x = 0. Why because the value of abscissa in all points on the y-axis is zero.

General Equation

The general equation of a straight line is ax + by + c = 0.

Equation of a Line Parallel to X-Axis Examples

Example 1:

Find the equation of a line parallel to the x-axis at a distance of 7 units above the x-axis?

Solution:

We know that the equation of a line parallel to the x-axis at a distance b from it is y = b.

Therefore, the equation of a straight line parallel to the x-axis at a distance 7 units above the x-axis is y = 7.

Example 2:

Find the equation of a line parallel to the x-axis at a distance of 5 units below the x-axis?

Solution:

We know that If a straight line is parallel and below to x-axis at a distance b, then its equation is y = -b.

Therefore, the equation of a line parallel to the x-axis at a distance of 5 units below the x-axis is y = -5.

Example 3:

Find the equation of a straight line parallel to the x-axis at a distance of 10 units above the x-axis?

Solution:

We know that the equation of a line parallel to the x-axis at a distance b from it is y = b.

Therefore, the equation of a straight line parallel to the x-axis at a distance 10 units above the x-axis is y = 10.

FAQs on Equation of Line Parallel to X-Axis

1. How do you find the equation of a line?

The general form of equation of a line is ax + by + c = 0. Any equation in this form is called the equation of a straight line.

2. What is the equation of the line parallel to the x-axis?

The equation of a straight line parallel to the x-axis is y = b as all the points on that line have y-coordinate values as zero’s. Here, b is the distance between the line and the x-axis.

3. How do you write an equation of a line parallel to a line?

The slope-intercept form of a line is y = mx + c. If two lines are parallel, then their slopes are equal and the y-intercept depends on the line points. So, if you know one line, then it is easy to find the equation of a line parallel to the given line and passes through one point.

Round off is a type of estimation. Estimation is used in subjects like mathematics and physics. Round off means making a number simpler by keeping its value intact closer to the next number. Round off to nearest 10 is nothing but making the unit digits of the number to zero and getting the estimated nearest 10 for that number. Check the rules, detailed steps, and solved examples on rounding the numbers to the nearest 10.

Round off to Nearest 10 – Definition

Round off is a process of making a number simpler to read and remember. It is done for the whole numbers, decimals for various places of tens, thousands, hundreds, etc. Round off to Nearest 10 means writing the nearest 10 of the given number. By using the Rounding Numbers to the Nearest 10, you can easily estimate the answer quickly and easily. It is also used to get the average score of people in the class.

Get More Related Articles

• Round off to Nearest 100
• Rounding Decimals to the Nearest Whole Number
• Correct to Two Decimal Places

Rules for Rounding Numbers to Nearest 10

We have two different rules for rounding numbers to the nearest 10. They are explained in the below modules

• Rule 1: When rounding the numbers to the nearest 10, if the digit in the unit’s place is less than 5 or between 0 and 4, then the unit’s place of the number is replaced by 0.
• Rule 2: If the digit in the unit’s place is greater than or equal to 5 or between 5 and 9, then the unit’s place is replaced by 0, and the tens place of the number is increased by 1.

How to Round Numbers to Nearest 10?

Follow the below-listed procedure to learn Round off to Nearest 10. They are along the lines

• Get a whole number for rounding.
• Identify the digit in the unit’s place.
• If the digit is between 0 and 4, then place zero in the unit’s place of the number.
• If the digit is or 6 or 7 or 8 or 9, then place zero in the unit place and add 1 to the tens place of the number.
• Now, write the new number as a rounded or estimated number.

Rounding to the Nearest Ten Examples

Example 1:

Round the following numbers to the nearest 10.

(i) 63

(ii) 578

(iii) 1052

Solution:

(i) The given number is 63

We see the digit in the unit place is 3 means that is less than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place.

Therefore, rounding off 63 to the nearest 10 is 60.

(ii) The given number is 578

We see the digit in the unit place is 8 means that is more than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, rounding off 578 to the nearest 10 is 580.

(iii) The given number is 1052

We see the digit in the unit place is 2 means that is less than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place.

Therefore, rounding off 1052 to the nearest 10 is 1050.

Example 2:

Round off the below-mentioned numbers to the nearest 10.

(i) 167

(ii) 55

(iii) 109

Solution:

(i) The given number is 167

We see the digit in the unit place is 7 means that is greater than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, the obtained number is 170.

(ii) The given number is 55

We see the digit in the unit place is 5 means that is equal to 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, rounding off 55 to the nearest 10 is 60.

(iii) The given number is 109

We see the digit in the unit place is 9 means that is more than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, round off 109 to the nearest 10 is 110.

Example 3:

Round off to Nearest 10.

(i) 221

(ii) 854

(iii) 57

Solution:

(i) The given number is 221

We see the digit in the unit place is 1 means that is lesser than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place.

Therefore, round off 221 to the nearest 10 is 220.

(ii) The given number is 854

We see the digit in the unit place is 4 means that is less than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place.

Therefore, round off 854 to the nearest 10 is 850.

(iii) The given number is 57

We see the digit in the unit place is 7 means that is more than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, round off 57 to the nearest 10 is 60.

Example 4:

Round the following numbers to the nearest tens.

(i) 5526

(ii) 328

Solution:

(i) The given number is 5526

We see the digit in the unit place is 6 means that is more than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, round off 5526 to the nearest 10 is 5530.

(ii) The given number is 328

We see the digit in the unit place is 8 means that is more than 5. So, we round to the nearest multiple of a ten which is less than the number. So place zero in the unit place and increase digit in tens place by 1.

Therefore, round off 328 to the nearest 10 is 330.

6 Times Multiplication Table is an important table in maths as most of the questions are based on it. Many of the students may feel that it is very difficult to learn and remember the 6 Times Table Multiplication Chart. But it is not, six table is nothing but multiplying the whole numbers with 6. Learning the Math Multiplication Table Charts from 0 to 25 is necessary at the time of primary schooling. Remembering the 6 Times Table enhances skills throughout your learning stages. Get the easy tricks to memorize the multiplication chart of 6, know how to read and write 6 table.

Six Times Table Multiplication Chart

Here, we will find the Multiplication Table of 6 in an image format to download and practice daily. This, 6 Times Table Multiplication Chart image is useful for future reference. So, download 6 Multiplication Table Image, paste a printed copy on your walls to refer regularly and solve more basic multiplication, division mathematical problems easily and quickly.

Writing 6 Times Table | Multiplication Table of 6 Up to 20

Get the 6 Times Table Multiplication Chart in the tabular format in the below sections and know how to write the 6 table. We have given the first 20 multiples of 6 here for your comfort. Use this handy and free Multiplication Table of 6 Chart to perform the arithmetic operations quickly. Have a deeper insight into the multiplication process by availing the 6 Multiplication Table present here.

6	x	0	=	0
6	x	1	=	6
6	x	2	=	12
6	x	3	=	18
6	x	4	=	24
6	x	5	=	30
6	x	6	=	36
6	x	7	=	42
6	x	8	=	48
6	x	9	=	54
6	x	10	=	60
6	x	11	=	66
6	x	12	=	72
6	x	13	=	78
6	x	14	=	84
6	x	15	=	90
6	x	16	=	96
6	x	17	=	102
6	x	18	=	108
6	x	19	=	114
6	x	20	=	120

Tips & Tricks to Memorize 6 Times Table

To memorize the 6 Times Table Multiplication Chart, have a look at the tricks mentioned here.

• Generally, multiples of 6 are multiples of both 2 and 3.
• If you multiply an even number with 6 the result will be the same even number in the unit digit i.e 6 x 2 = 12, 6 x 6 = 36, 6 x 8 = 48 and so on
• You can also learn the 6 Multiplication Table using the skip counting process.

How to Read Multiplication Table of 6 in Words?

One time six is 6.

Two times six is 12.

Three times six is 18.

Four times six is 24.

Five times six is 30.

Six times six is 36.

Seven times six is 42.

Eight times six is 48.

Nine times six is 54.

Ten times six is 60.

Why one Should Learn 6 Times Multiplication Table Chart

Learning the 6 Times Table Multiplication Chart is important and it has several advantages and they are listed along the lines.

• You can solve all the mathematical problems involving division, multiplication easily by learning the Multiplication Table of 6.
• This 6 Times Multiplication Table makes you perfect in performing the quick calculations.
• 6 Times Multiplication Chart is helpful to understand the patterns easily.
• It can be a great savior to do your mental math calculations right in your head.

Get More Math Table Multiplication Charts

0 Times Table Multiplication Chart	1 Times Table Multiplication Chart	2 Times Table Multiplication Chart
3 Times Table Multiplication Chart	4 Times Table Multiplication Chart	5 Times Table Multiplication Chart
7 Times Table Multiplication Chart	8 Times Table Multiplication Chart	9 Times Table Multiplication Chart
10 Times Table Multiplication Chart	11 Times Table Multiplication Chart	12 Times Table Multiplication Chart
13 Times Table Multiplication Chart	14 Times Table Multiplication Chart	15 Times Table Multiplication Chart
16 Times Table Multiplication Chart	17 Times Table Multiplication Chart	18 Times Table Multiplication Chart
19 Times Table Multiplication Chart	20 Times Table Multiplication Chart	21 Times Table Multiplication Chart
22 Times Table Multiplication Chart	23 Times Table Multiplication Chart	24 Times Table Multiplication Chart
25 Times Table Multiplication Chart

Solved Examples on 6 Times Table Multiplication Chart

Example 1:

What does 6 × 7 mean? What number is it equal to?

Solution:

6 x 7 means multiply 6 with 7 or 6 times 7

6 x 7 = 42

Therefore, 42 is equal to 6 times 7.

Example 2:

Eashwar eats 2 apples per day. How many apples will he eat in 6 days?

Solution:

Given that,

The number of apples Eashwar eats in a day = 2

The number of apples Eashwar eats in 6 days = 6 x 2

= 12

Therefore, Eashwar eats 12 apples in 6 days.

Example 3:

(i) How many sixes in 42?

(ii) How many sixes in 30?

(iii) How many sixes in 66?

Solution:

(i)

42 = 6 + 6 + 6 + 6 + 6 + 6 + 6

So, there are 7 sixes in 42.

(ii)

30 = 6 + 6 + 6 + 6 + 6

So, there are 5 sixes in 30.

(iii)

66 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6

So, there are 11 sixes in 66.

Example 4:

(i) What are 6 fives?

(ii) 12 times 6?

(iii) What is 4 multiplied by 6?

(iv) sixes 7?

Solution:

(i)

6 fives means 6 x 5 = 30

(ii)

12 times 6 means multiply 6 with 12

6 x 12 = 72

(iii)

4 multiplied by 6 means 6 times 4.

6 x 4 = 24.

(iv)

Sixes 7 means 6 times 7

6 x 7 = 42.

FAQs on 6 Multiplication Table

1. Is there a pattern in the 6 times table?

Multiples of 6 are multiples of 2 and 3. The pattern of 6 is 6, 2, 8, 4, 0 in the unit’s place. all the multiples of 6 are even numbers. When a multiple of 2 and 3 overlap, you will get 6 multiples.

2. How do you memorize the 6 Times Table Multiplication Chart?

The best trick to remember the 6 table is to add 1 to the multiples of 5 to get the multiples of 6. You can also perform 6 times 2 means add 6 twice to get the result.

3. What is the trick for multiplying by 6?

We don’t have any special tricks for the 6 multiplication table. You just have to read it and remember. When you multiply the even number the unit digit of the result remains the same.

A fraction shows the equal parts of a collection or whole. The number line is a straight line with numbers placed at equal intervals along its length. Representing Fractions on Number Line means pointing the fractions on the number line. It shows the interval between two numbers. Learn the process of how to represent fractional numbers on a number line from the below-provided segments of this page.

Representing Fractions on Number Line – Definition

First of all, representing whole numbers on a number line means pointing those numbers on the line. In the same way, we need to point to the fraction which is between two numbers on the number line. Here, we need to divide the space between two whole numbers on a number line into the number of parts. Make each part as a fraction and then point to the respective fraction.

Examples of Fractions are \(\frac { 2 }{ 5 } \), \(\frac { 1 }{ 2 } \), \(\frac { 5 }{ 6 } \).

How to Represent Fraction on Number Line?

Are you looking for any help on representing fractions on a number line then read the following points. Here you will get the detailed step-by-step procedure.

• Get the fraction and draw a number line.
• If the numerator of the fraction is more than the denominator, then convert the fraction into a mixed fraction.
• Divide the space between two consecutive whole numbers and the denominator number of parts.
• And consider each division as a fraction.
• Now, mark the points on the number line.

Also, Read More Related Articles

• Worksheet on Fractions
• Fractions

Representing Fractions on a Number Line Examples

Example 1:

Represent \(\frac { 52 }{ 5 } \) on the number line.

Solution:

First, convert \(\frac { 52 }{ 5 } \) into the mied fraction.

\(\frac { 52 }{ 5 } \) = 10\(\frac { 2 }{ 5 } \)

Now, we start from 10 and divide the section between 10 and 11 into 5 equal parts because the denominator is 5. The second point in the division is 2/5. Mark the point as 10\(\frac { 2 }{ 5 } \).

Example 2:

Draw a number line to represent the fractions –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \).

Solution:

Given fractions are –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \)

The denominator of all the factions is 4. So, divide each interval into 4 parts. Each part so obtained will represent the fraction 1/4 and the number line obtained will be in the form of as shown here.

To mark –\(\frac { 2 }{ 4 } \); move two parts on the left-side of zero.

To mark \(\frac { 3 }{ 4 } \); count three parts from the zero.

To mark \(\frac { 8 }{ 4 } \); count 8 parts from the zero.

To mark \(\frac { 14 }{ 4 } \); count 14 parts from the zero.

To mark \(\frac { 21 }{ 4 } \), count 21 parts from the zero.

The following diagram shows markings of fractions –\(\frac { 2 }{ 4 } \), \(\frac { 3 }{ 4 } \), \(\frac { 8 }{ 4 } \), \(\frac { 14 }{ 4 } \), and \(\frac { 21 }{ 4 } \) on a number line.

Example 3:

Represent the fractions \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \) on a number line.

Solution:

The given fractions are \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \)

The denominator of all the factions is 3. So, divide each interval into 3 parts. Each part so obtained will represent the fraction 1/3 and the number line obtained will be in the form of as shown here.

To mark \(\frac { 1 }{ 3 } \), move 1 point on the right side of zero.

To mark \(\frac { 12 }{ 3 } \), move 12 pionts on the right side of zero.

To mark \(\frac { 16 }{ 3 } \), move 16 points on the right side of zero.

To mark \(\frac { 8 }{ 3 } \), move 8 points on the right side of zero.

The following diagram shows markings of fractions \(\frac { 1 }{ 3 } \), \(\frac { 12 }{ 3 } \), \(\frac { 16 }{ 3 } \), \(\frac { 8 }{ 3 } \) on a number line.

 

 

Example 4:

Represent the fractions \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \) on a number line.

Solution:

The give fractions are \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \)

The denominator of all the factions is 4. So, divide each interval into 4 parts. Each part so obtained will represent the fraction 1/4 and the number line obtained will be in the form of as shown here.

To mark –\(\frac { 3 }{ 4 } \); move three parts on the left-side of zero.

To mark \(\frac { 1 }{ 4 } \); count one part from the zero.

To mark \(\frac { 15 }{ 4 } \); count 15 parts from the zero.

To mark \(\frac { 18 }{ 4 } \), count 18 parts from the zero.

The following diagram shows markings of fractions \(\frac { 15 }{ 4 } \), \(\frac { 1 }{ 4 } \), \(\frac { -3 }{ 4 } \), \(\frac { 18 }{ 4 } \) on a number line.

FAQ’s on Representing Fractions on Number Line

1. How do you represent a fraction on a number line?

To represent fractions on the number line, divide each line segment between 0 to 1 into the denominator number of parts. And count the numerator parts from zero and mark the fractions.

2. What is \(\frac { 3}{ 4 } \) on a number line?

The fraction \(\frac { 3}{ 4 } \) means 3 out of 4 equal parts. So, count 3 parts from 0 on the number line to get \(\frac { 3}{ 4 } \).

3. What does the denominator of a fraction represent on the number line?

A fraction has two parts numerator and denominator. The denominator means how many equal parts an item was divided into.

The division is a basic arithmetic operation and it is the inverse of multiplication. The terms of division are dividend, divisor, quotient, and remainder. The number which we divide is known as a dividend, the number by which we divide is called the divisor. The quotient means the number of times a division is completed fully, and the remainder is the quantity that doesn’t go fully into the divisor. Here, we will learn about how to estimate the quotient of two numbers easily with solved example questions.

What is Estimating the Quotient?

When we divide two numbers, the result we get is called the quotient. The formula to express the terms of division is divided ÷ divisor = quotient + remainder. It is important to know how to estimate the quotient. Estimating the quotient means, we not doing the division for the actual numbers. You need to round off the dividend and divisor to the nearest 10 and proceed for the division to get the estimated quotient value.

How to Estimate the Quotient?

Check out the step-by-step process to calculate the estimating quotient of two numbers.

• If the numbers have two or more digits, then round off the numbers to the nearest 10 or 100 or 1000.
• And divide those numbers to get the quotient.
• The obtained quotient is called the estimated quotient of the given numbers.

Also, Read More Articles:

• Division of a Decimal by a Whole Number
• Divisibility Rules from 1 to 13
• Dividend Divisor Quotient And Remainder

Example Questions on Estimating the Quotient

Example 1:

Find the estimated quotient and actual quotient when 78 divided by 36.

Solution:

Given that,

dividend = 78, divisor = 36

divided ÷ divisor = 78 ÷ 36

Actual quotient = 2

Round off the divided and divisor to the nearest 10

new divided = 80, new divisor = 40

80 ÷ 40 = 2

Estimated quotient = 2.

Example 2:

A school track is 9.76 meters wide. It is divided into 8 lanes of equal width. How wide is each lane?

Solution:

The width of each lane is nothing but the quotient when we divide 9.76 by 8.

Round off the school track to the nearest 10 i.e 9.76 is 10.

Divide 10 by 8

10 ÷ 8 = 1

Approximately, 1 meter wide each lane.

Example 3:

Aerobics classes cost $153.86 for 14 sessions. What is the estimated fee for one session?

Solution:

The fee for one session is nothing but the quotient when we divide 153.86 by 14.

Round off 153.86 to the nearest 10 i.e 150

Round off 14 to the nearest 10 i.e 10

Divide 150 by 10

150 ÷ 10 = 15

Therefore, the estimated fee for one session is $15.

Example 4:

Estimate quotient when 1058 divided by 50.

Solution:

Round off 1058 to the nearest 100 i.e 1100

Divide 1100 by 50

1100 ÷ 50 = 22

The estimated quotient is 22.

FAQs on Estimating the Quotient

1. How can you use estimation to check if a quotient is reasonable?

• Round off the divisor and dividend to the nearest 10 or 100 depending on the number of digits.
• Divide the rounded dividend by divisor to get the estimated quotient.
• Compare the estimated and exact answers to check whether the answer is reasonable or not.

2. How do you estimate the quotients?

To estimate the quotients, you need to round off each number to the nearest 10 or 100 or 100 and then divide. The result is called the estimated quotient.

3. What is a quotient?

Quotient means the answer a division problem. In the divisor parts, you divide the dividend to get the quotient.

A line is a one-dimensional geometric figure having length but no width. It is made up of points that are extended in opposite directions infinitely. The different types of lines are horizontal, vertical, parallel, perpendicular, curved, and slanting lines. The definitions of each type of line with an image are given below. Go through the entire article to learn in detail about the Types of Lines in Geometry and examples for each one of them.

What is a Line?

A line can be defined as the set of points that is extended in opposite directions. It has no width, no endpoints in opposite directions and it is a one-dimensional plane. The line has no thickness.

Types of Lines

There are different types of lines in geometry, the basic types of lines are listed below. Let us discuss in detail the figures, definitions, properties of each one of them. They are along the lines

• Vertical Lines
• Horizontal Lines
• Parallel Lines
• Skew Lines
• Perpendicular Lines
• Oblique or slanting lines
• Concurrent Lines
• Transversal line
• Coplanar Lines

Straight Lines:

Straight lines are the lines as shown below.

Horizontal Lines:

If the line moves from the left to the right side in a straight direction, it is called the horizontal line.

Vertical Lines:

If a line moves from the top to the bottom in a straight direction, then it is a vertical line.

Parallel Lines:

When two straight lines don’t intersect at any point, then they are parallel lines.

Perpendicular Lines:

When two straight lines meet at an angle of 90 degrees, then they are perpendicular lines.

Also, Read More Articles:

• Lines and Angles
• Parallel and Transversal Lines
• Transversal Lines
• Lines of Symmetry

Oblique or slanting lines:

If the lines are drawn in a slanting position, then they are called the oblique or slanting lines.

Skew Lines:

If two non-parallel lines are not intersecting in a space, then they are called the skew lines.

Concurrent Lines:

When two or more lines are passing through a common point, then those lines are called concurrent lines.

Transversal line:

A transversal line is a straight line that cuts 2 or more lines. The lines may or may not be parallel.

Coplanar lines:

Coplanar lines are lines that lie on the same plane.

Frequently Asked Questions on Types of Lines

1. What are the different types of lines?

The various types of lines are Horizontal Line, Vertical Line, Parallel Lines, Perpendicular Lines, Skew Lines, Oblique or slanting lines, Coplanar Lines, Concurrent Lines, and Transversal line.

2. Define a Line?

A straight line is a one-dimensional figure that has no thickness and extending infinitely from the extreme directions.

3. What is a line segment?

A line segment is a part of the line that has two fixed endpoints and it can’t be extended infinitely.

4. What are parallel and perpendicular lines?

When two straight lines extend in both directions and they don’t meet at any point is called parallel lines. Perpendicular lines intersect each other at right angles.

Class Boundaries are the data values that separate classes. These are not part of the classes or the data set. The class boundary is the middle point of the upper-class limit of one class and the lower class limit of the subsequent class. Each class has an upper and a lower class boundary. Find the definition of the class boundaries or actual class limits and example questions in the below-mentioned sections.

What is Class Boundary?

If we have different classes of data, then it has an upper-class limit and lower class limit which means the smaller and larger values. A class boundary is the midpoint of the upper-class limit of one class and the lower class limit of the subsequent class.

Lower class boundary = (lower class limit of the concerned class + upper-class limit of the previous class)/2

Upper class boundary = (upper-class limit of the concerned class + lower class limit of the subsequent class)/2

For the nonoverlapping class intervals,

The actual lower limit = lower limit – ½ x gap

The actual upper limit = upper limit + ½ x gap

Class Limit

The class limit can be defined as the minimum and maximum values contain in a class interval.

The minimum value is called the lower class limit and the maximum value is called the upper-class limit.

Solved Examples on True Class Limits

Example 1:

Class	Frequency
0 – 9	2
10 – 19	5
20 – 29	7

Find the lower, upper class boundaries?

Solution:

The class boundary of 0 – 9 is

Upper class boundary = (upper-class limit of the concerned class + lower class limit of the subsequent class)/2

= \(\frac { (9 + 10) }{ 2 } \)

= \(\frac { 19 }{ 2 } \)

Lower class boundary = (lower class limit of the concerned class + upper class limit of the previous class)/2

= \(\frac { (0 + 0) }{ 2 } \)

= 0

The class boundary of 10 – 19 is

Upper class boundary = \(\frac { (19 + 20) }{ 2 } \)

= \(\frac { 39 }{ 2 } \)

Lower Class boundary = \(\frac { (10 + 9) }{ 2 } \)

= \(\frac { 19 }{ 2 } \)

Example 2:

If the class marks of two consecutive overlapping intervals of equal size in distribution are 94 and 104 then find the corresponding intervals.

Solution:

The difference between 104 and 94 = 104 – 94 = 10

Therefore, the class intervals are (94 – \(\frac { 10 }{ 2 } \)) – (94 + \(\frac { 10 }{ 2 } \)) and (104 – \(\frac { 10 }{ 2 } \)) – (104 + \(\frac { 10 }{ 2 } \))

= (94 – 5) – (94 + 5) and (104 – 5) and (104 + 5)

= 89 – 99 and 99 – 109.

Example 3:

Weight in Kg (Class Interval)	Frequency
44-48	3
49-53	4
54-58	5
59-63	7
64-68	9
69-73	8

Find the upper, lower class boundaries?

Solution:

Lower Class Boundary of the first class interval = 44 – \(\frac { (49 – 48) }{ 2 } \)

= 44 – \(\frac { 1 }{ 2 } \)

= 44 – 0.5

= 43.5

Upper Class Boundary = 48 + \(\frac { (49 – 48) }{ 2 } \)

= 48 + \(\frac { 1 }{ 2 } \)

= 48 + 0.5

= 48.5.

FAQs on Class Boundaries

1. What is a Class Boundary?

A class boundary is the midpoint of the upper-class limit of one class and the lower class limit of the subsequent class.

2. What is the difference between class limits and class boundaries?

In the case of the class limit, the upper extreme value of the first class interval and the lower extreme value of the next class interval are not equal. However, in the class boundary, the upper extreme value of the first class interval and the lower extreme value of the next class interval are equal.

3. How to find Class Boundaries?

Follow the below-listed steps to calculate the Class Boundaries easily. They are along the lines

• Subtract the upper class limit for the first class from the lower class limit for the second class.
• Divide the result by two.
• Subtract the result from the lower class limit and add the result to the upper class limit for each class.

The angle is nothing but the figure formed by two rays. If two straight lines meet, then they form two sets of angles. The intersection forms a pair of acute angles and another pair of obtuse angles. The angle values will be based on the slopes of the intersecting lines. Check out the formula to calculate the angle between two straight lines, derivation, example questions with answers in the following sections of this page.

Angle between Two Lines – Definition

In a plane when two straight and non-parallel lines meet at a point, then it forms two opposite vertical angles. In the formed angles, one is lesser than 90 degrees and the other is greater than 90 degrees. We will find the angle between two straight and perpendicular lines is 90 degrees and parallel lines is zero degrees.

Angle between Two Straight Lines Formula and Derivation

Let us consider θ as the angle between two intersecting straight lines. And those straight lines be y = mx + c, Y = MX + C, then the angle θ is given by

tan θ = ± \(\frac { (M – m) }{ (1 + mM)} \)

Derivation

Two straight lines L₁, L₂ are intersecting each other to form acute and obtuse angles.

Let us take the slope measurement can be taken as

tan θ₁ = m₁ and tan θ₂ = m₂

From the figure, we can say that θ = θ₂ – θ₁

Now, tan θ = tan(θ₂ – θ₁)

tan θ = \(\frac { (tan θ₂ – tan θ₁) }{ (1 + tan θ₁ tan θ₂) } \)

Substitute tan θ₁ = m₁, tan θ₂ = m₂

tan θ = \(\frac { (m₂ – m₁) }{ (1 + m₁ m₂) } \)

How to find Angle Between Two Straight Lines?

If three points on a coordinate plane are given, then endpoints of a line are (x₁, y₁) and (x₂, y₂)

The equation of the slope is m = \(\frac { (y₂ – y₁) }{ (x₂ – x₁) } \)

m₁ and m₂ can be calculated by substituting in the formula, then the angle between two lines is given by

tan θ = ± \(\frac { m₂ – m₁) }{ (1 + m₁ m₂) } \)

Also Check:

• Pairs of Angles
• Angle of Elevation
• Angle of Depression

Angle between Two Straight Lines Examples

Example 1:

If A (-2, 1), B (2, 3), and C (-2, -4) are three points, find the angle between two straight lines AB, BC.

Solution:

Given that,

Three points are A (-2, 1), B (2, 3), and C (-2, -4)

The slope of line AB is m = \(\frac { (y₂ – y₁) }{ (x₂ – x₁) } \)

m = \(\frac { (3 – 1) }{ (2 – (-2)) } \)

= \(\frac { (2) }{ (2 + 2) } \)

= \(\frac { 2 }{ 4 } \)

= \(\frac { 1 }{ 2 } \)

Therefore, m₁ = \(\frac { 1 }{ 2 } \)

The slope of line BC is given by

m = \(\frac { (y₂ – y₁) }{ (x₂ – x₁) } \)

m = \(\frac { (-4 – 3) }{ (-2 – 2) } \)

= \(\frac { -7 }{ -4 } \)

= \(\frac { 7 }{ 4 } \)

Therefore, m₂ = \(\frac { 7 }{ 4 } \)

Substituting the values of m2 and m1 in the formula for the angle between two lines when we know the slopes of two sides, we have,

tan θ = ± \(\frac { (m₂ – m₁) }{ (1 + m₁ m₂) } \)

= ± \(\frac { (\frac { 7 }{ 4 } – \frac { 1 }{ 2 } ) }{ (1 + \frac { 1 }{ 2 }  * \frac { 7 }{ 4 }) } \)

= ± \(\frac { 2 }{ 3 } \)

Therefore,  θ = tan ^-1 (⅔)

So, the angle between the lines AB, BC is tan ^-1 (⅔).

Example 2:

Find the angle between the following lines 4x – 3y = 8, 2x + 5y = 4.

Solution:

Given two straight lines are 4x – 3y = 8, 2x + 5y = 4

Converting the given lines into slope intercept form

4x – 3y = 8

4x = 8 + 3y

3y = 4x – 8

y = \(\frac { 4x – 8 }{ 3 } \)

y = \(\frac { 4x }{ 3 } – \frac { 8 }{ 3 } \)

Therefore, the slope of line 4x – 3y = 8 is \(\frac { 4 }{ 3 } \)

2x + 5y = 4

5y = 4 – 2x

y = \(\frac { 4 – 2x }{ 5 } \)

y = \(\frac { -2x }{ 5 } + \frac { 4 }{ 5 } \)

Therefore, the slope of the line 2x + 5y = 4 is –\(\frac { 2 }{ 5 } \)

The angle between lines is tan θ = ± \(\frac { (m₂ – m₁) }{ (1 + m₁ m₂) } \)

= ± \(\frac { (\frac { -2 }{ 5 } – \frac { 4 }{ 3 } ) }{ (1 + \frac { 4 }{ 3 }  * \frac { (-2) }{ 5 }) } \)

= \(\frac { -26 }{ 7 } \)

θ = tan ^-1 (\(\frac { -26 }{ 7 } \))

Example 3:

Find the angle between two lines x + y = 4, x + 2y = 3.

Solution:

The given two lines are x + y = 4, x + 2y = 3.

The slope-intercept form of the first line is

x + y = 4

y = 4 – x

Therefore, slope of x + y = 4 is m₁ = -1

The slope-intercept form of the second line is

x + 2y = 3

2y = 3 – x

y = \(\frac { (3 – x) }{ 2 } \)

y = \(\frac { 3 }{ 2 } – \frac { x }{ 2 } \)

Therefore, slope of x + 2y = 3 is m₂ = \(\frac { -1 }{ 2 } \)

The angle between lines is tan θ = ± \(\frac { (m₂ – m₁) }{ (1 + m₁ m₂) } \)

= ± \(\frac { (\frac { -1 }{ 2 } – (-1) ) }{ (1 + \frac { -1 }{ 2 }  * (-1)) } \)

= \(\frac { 1 }{ 3 } \)

θ = tan^-1(\(\frac { 1 }{ 3 } \))

Example 4:

Find the angle between two straight lines x + 2y – 1 = 0 and 3x – 2y + 5 = 0

Solution:

The given lines are x + 2y – 1 = 0 and 3x – 2y + 5 = 0

The slope intercept form of first line is

x + 2y – 1 = 0

2y = 1 – x

y = \(\frac { 1 – x }{ 2 } \)

y = \(\frac { 1 }{ 2 } – \frac { x }{ 2 } \)

Therefore, the slope of line x + 2y – 1 = 0 is m₁ = \(\frac { -1 }{ 2 } \)

The slope-intercept form of the second line is

3x – 2y + 5 = 0

3x + 5 = 2y

y = \(\frac { 3x + 5 }{ 2 } \)

y = \(\frac { 3x }{ 2 } + \frac { 5 }{ 2 } \)

Therefore, the slope of line 3x – 2y + 5 = 0 is m₂ = \(\frac { 3 }{ 2 } \)

The angle between lines is tan θ = ± \(\frac { (m₂ – m₁) }{ (1 + m₁ m₂) } \)

= ± \(\frac { (\frac { 3 }{ 2 } – \frac { (-1 }{ 2 )} ) }{ (1 – \frac { 1 }{ 2 }  * \frac { (3) }{ 2 }) } \)

= 2

θ = tan^-1(2)

The angle of depression is created when the observer is higher than the object he is looking at. If a person looks at an object that is located at a distance lower than the person, the angle is formed below the horizontal line drawn with the level of the eye of the person and line joining object with the person’s eye. This angle is calculated by using the concept of trigonometry. Get the definition, formulas, and example questions with answers in the below sections.

Angle of Depression – Definition

The angle of depression is the angle formed between the horizontal line and the observation of the object from the horizontal line. This angle of depression is used to find the distance between the two objects when the angles, object’s distance from the ground are known parameters. It is also defined as the angle that is constructed with the horizontal line if the line of sight is downward from the horizontal line.

If the object observed by the observer is below the level of the observer, then the angle created between the horizontal line and the observer’s line of sight is called the angle of depression. In the above figure, θ is the angle of depression.

Angle of Depression Formulas

With the angle of elevation, if you know two sides of the right triangle are known, then the formula of the angle of depression is

tan θ = \(\frac { Opposite Side }{ Adjacent Side } \)

θ = tan^-1 (\(\frac { Opposite Side }{ Adjacent Side } \))

Also, check

• Angle of Elevation
• Angles
• Pairs of Angles

Angle of Elevation and Angle of Depression

The angle of elevation and angle of depression are opposite to each other. The elevation angle is formed when it is between the line of sight and the horizontal line. And if the line of sight is above the horizontal line, then the angle is called the angle of elevation. In the angle of depression, the line of sight is downwards to the horizontal line.

∠ABO = ∠O = θ

Angle of Depression Problems

Example 1:

The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find (i) The height of the lamp post. (ii) The difference between the height of the lamp post and the apartment. (iii) The distance between the lamp post and the apartment.

Solution:

Triangle AED forms a right triangle

So, tan 60° = \(\frac { ED }{ AD } \)

√3 = \(\frac { ED }{ AD } \)

AD = \(\frac { ED }{ √3 } \) —- (i)

In trinagle ABC,

tan 30° = \(\frac { AB }{ BC } \)

\(\frac { 1 }{ √3 } \) = \(\frac { 66 }{ BC }\)

BC = 66√3 —- (ii)

Equating both equations

\(\frac { ED }{ √3 } \) = 66√3

ED = 66√3 (√3 )

ED = 66(3)

ED = 198

(i) Height of lamp post = ED + DC

= 198 + 66

= 264 m

(ii) The difference between height of the lamp post and the apartment

= 364 – 66

= 198 m

(iii) The distance between the lamp post and the apartment

BC = 66√3

= 66(1.732)

= 114.31 m

Example 2:

An airplane is flying at a height of 2 miles above level ground. The angle of depression from the plane to the foot of the tree is 15°. What is the distance the plane must fly to be directly above the tree?

Solution:

To find the distance BA use the tangent function

tan 15° = \(\frac { 2 }{ BA } \)

0.26794919243 = \(\frac { 2 }{ BA } \)

BA = \(\frac { 2 }{ 0.26794919243 } \)

BA = 7.464

So, the plane must fly 7.464 ft horizontally to be directly over the tree.

Example 3:

A buoy in the ocean is observed from the top of a 40-meter-high oil rig. The angle of depression from the top of the tower to the buoy is 6°. How far is the buoy from the base of the oil rig?

Solution:

Given that,

The angle of depression from the top of the tower to the buoy = 6°

A buoy in the ocean is observed from the top of a 40-meter-high oil rig.

Tan 6° = \(\frac { 40 }{ h } \)

h = \(\frac { 40 }{ tan 6° } \)

h = \(\frac { 40 }{ 0.105104 } \)

h = 380.6

It is approximately 380.6 m from the buoy to the base of the oil rig.

Example 4:

A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is 30√3 feet from the entrance of the lift, find the speed of the lift which is descending.

Solution:

In the diagram above, in the right triangle ABC,

tan 30° = \(\frac { Opposite side }{ adjacent side } \)

\(\frac { 1 }{ √3 } \) = \(\frac { BC }{ 30√3 } \)

1 x 30√3 = √3 x BC

BC = 30

DC = DB – CB

DC = 90 – 30

DC = 60 feet

So, the left has descended 60 ft in 2 minutes.

Speed = \(\frac { Distance }{ Time } \)

Speed = \(\frac { 60 }{ 2 } \)

Speed = 30 ft/min

Speed = \(\frac { 30 ft }{ 60 sec } \)

Speed = 0.5 ft/sec

So, the speed of the lift which is descending is 0.5 ft/sec.

In geometry, line, line segment, and ray are one-dimensional figures that have no thickness. All these have a set of points connected. We draw different shapes triangle, square, rectangle using these lines, line segments, and rays. Let us discuss the definitions of each one of them and the differences between them in the below sections of this page.

What is Line?

A line can be defined as a straight set of points that extend in opposite directions. It is a one-dimensional figure and does not have a thickness, end in both directions.

The different types of lines are horizontal lines, vertical lines, parallel lines, and perpendicular lines. The images of these types are provided here for a better understanding of the concept.

If a line moves from left to right in a straight direction, it is a horizontal line.

If a line moves from top to bottom in a straight direction, then it is called the vertical line.

When two or more straight lines do not intersect each other at any point, then those are called parallel lines. The points A, B, C, D are called the points on the lines.

If two lines meet at a point at right angles, then they are perpendicular to each other.

Also, Read:

Lines and Angles

Line Segment – Definition

A line segment is a part of a line that has two endpoints. geometric shapes such as triangle, polygon, square, pentagon, and others are made up of a different number of line segments. The measurement of the line segment is called the length. As the line segment has two endpoints, it can not be extended and it is easy to measure its length. The below picture shows the line segment with points x, y.

What is Ray?

Ray is a combination of line and line segments that has an infinitely extending en and the other is terminating end. Its length can not be measured because one end is non-terminating. It is represented by \(\overrightarrow{AB}\).

Differences Between Line Segment, Ray and Line

From the below table you can get acquainted with the key differences between Line, Line Segment and Ray. They are as follows

Line Segment	Line	Ray
The line segment has two endpoints.	The line has no endpoints.	It has one starting point and another near the arrowhead.
The length of the line segment is definite. So, it can be measured.	As it has no endpoints, the length cannot be measured.	Its length can’t be measured as one point has no endpoint.
The symbol is ______.	The symbol is ↔.	The symbol of the ray is →.

Learning tables from 1 to 20 is the most important part of elementary education. Every student is supposed to study 13 table as mathematics have most of the problems depending on it. Become perfect with all math tables by going through our complete article. Some of the students may feel it is very difficult to remember the multiplication table of 13 as the values are hard to remember. Get the tricks and tips to memorize the 13 times table, know how to read and write Thirteen Times Table.

13 Times Table Chart

13 times multiplication tables in table format and image format is given here. So, it makes it easy for you to remember the values. Download 13 table charts for free and prepare well. The 13th table is helpful to perform the multiplication of numbers easily. You can save your time in competitive eams by learning these multiplication tables.

How to Read 13 Table?

Check the reading of the 13 multiplication table here.

One time thirteen is 13.

Two times thirteen is 26.

Three times thirteen is 39.

Four times thirteen is 52.

Five times thirteen is 65.

Six times thirteen is 78.

Seven times thirteen is 91.

Eight times thirteen is 104.

Nine times thirteen is 117.

Ten times thirteen is 130.

Importance of Multiplication Tables

Multiplication tables play an essential role in mathematics. It is the foundation of elementary maths. By learning the table chart, you will get self-confidence while doing multiplications. You can keep the information at your fingertips that help you to solve the questions quickly. Multiplication tables will enhance your memory power and improve the calculations speed.

Tables from 2 to 20 help in performing the simple arithmetic operations. So that you can save time and do calculations easily. Without learning the 13 times table, you can also calculate the multiplicative of 13 by performing the arithmetic multiplication operations.

Multiplication Table of 13 up to 20

Studying 13 Multiplication Table is an essential skill to solve the division and multiplication questions. Check out the below table to know how to write a 13 times table chart.

13	x	1	=	13
13	x	2	=	26
13	x	3	=	39
13	x	4	=	52
13	x	5	=	65
13	x	6	=	78
13	x	7	=	91
13	x	8	=	104
13	x	9	=	117
13	x	10	=	130
13	x	11	=	143
13	x	12	=	156
13	x	13	=	169
13	x	14	=	182
13	x	15	=	195
13	x	16	=	208
13	x	17	=	221
13	x	18	=	234
13	x	19	=	247
13	x	20	=	260

Tips and Tricks to Learn 13 Times Table

Here we are giving the easy tips that are helpful to remember the 13th table. Follow the below tricks and learn the multiplication tables quickly.

• To remember the 13 times table, first, we need to memorize the 3 times table. So, the multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, . . .
• For getting the multiples of 13, add natural numbers to the ten’s digit of the 3 multiples. Therefore, 13 times table is obtained as (1 + 0)3 = 13, (2 + 0)6 = 26 , (3 + 0)9 = 39, (4 + 1)2 = 52, (5 + 1)5 = 65, (6 + 1)8 = 78, (7 + 2)1 = 91, (8 + 2)4 = 104, (9 + 2)7 = 117, (10 + 3)0 = 130, . . .
• 13 does not have any rules that make the multiplication of 13 table easier to memorize, then there is a structure for every 10 multiples of 13. They are 13, 26, 39, 52, 65, 78, 91, 104, 117, 130. In all these multiples, the last digit i.e units place digit is repeating. So, one can remember this logic to memorize the table.

Get More Math Tables:

0 Times Table	1 Times Table	2 Times Table
3 Times Table	4 Times Table	5 Times Table
6 Times Table	7 Times Table	8 Times Table
9 Times Table	10 Times Table	11 Times Table
12 Times Table	14 Times Table	15 Times Table
16 Times Table	17 Times Table	18 Times Table
19 Times Table	20 Times Table	21 Times Table
22 Times Table	23 Times Table	24 Times Table
25 Times Table

Solved Examples on 13 Times Table Multiplication

Example 1:

Using the table of 13, calculate 13 times 13 plus 13?

Solution:

From the given data

We can express the given data in the form of Mathematical Expression

= (13 x 13) + 13

= 169 + 13

= 182

Therefore, 13 times 13 plus 13 is 182.

Example 2:

If David’s father has to pay the amount “12 less than 13 times 15” in dollars. Using the table of 13, find how much he needs to pay?

Solution:

From the given data,

The mathematical expression of 12 less than 13 times 15 = (13 x 15) – 12

= 195 – 12

= 183

therefore, David’s father is required to pay $183.

Example 3: 

Families in a colony are going on a picnic. If 13 people ride in each car and there are 5 cars, then how many people are going on a picnic?

Solution:

Given that,

The number of people going on picnic = 13

Number of cars = 5

Then, multiply the number of people on each car, total number of cars on the picnic to get the total number of persons going for the picnic.

The number of persons going on the picnic = 13 x 5

= 65

Therefore, 65 people going on a picnic.

Example 4:

Using the 13 times table, check whether 13 times 7 minus 1 plus 10 is 100?

Solution:

Firstly, let us express the given statement in the form of mathematical expression

13 times 7 minus 1 plus 10 = (13 x 7) – 1 + 10

= (91) + 9

= 100

Hence, 13 times 7 minus 1 plus 10 is 100.