Eureka Math

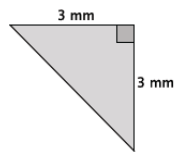
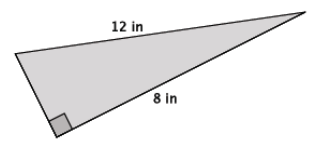
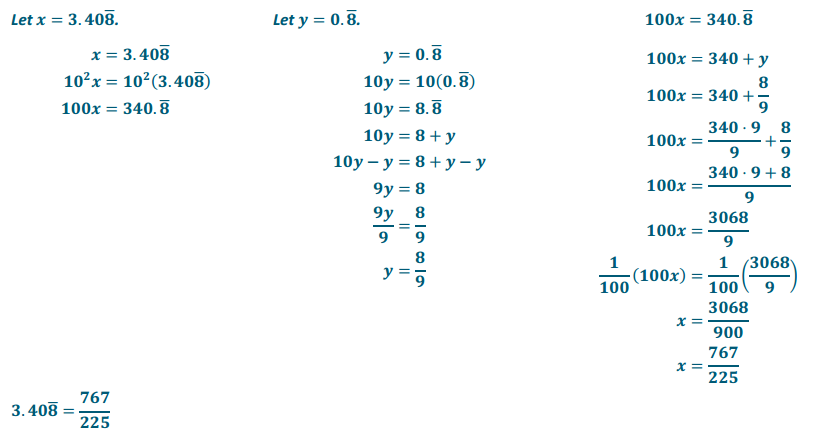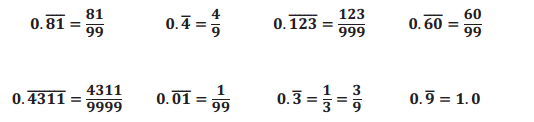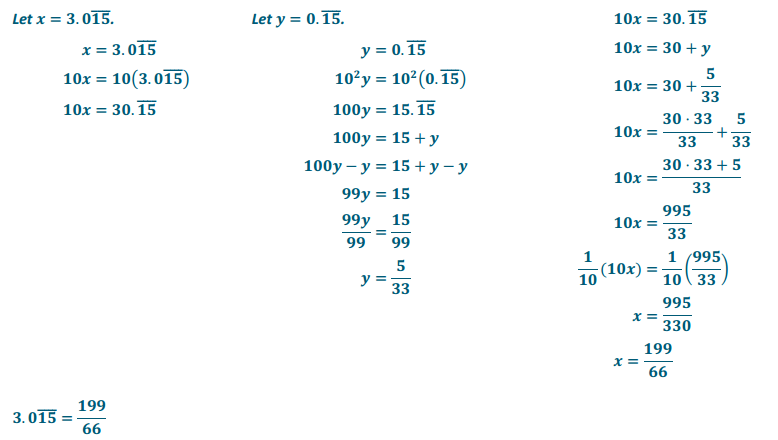Engage NY Eureka Math 8th Grade Module 7 Lesson 15 Answer Key

Eureka Math Grade 8 Module 7 Lesson 15 Classwork Answer Key

Classwork
Proof of the Pythagorean Theorem

Answer:
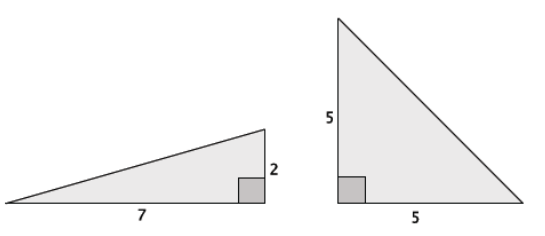
Using one right triangle, we created 3 right triangles. Name those triangles.
The three triangles are △ABC, △ACD, and △BCD.
We can use our basic rigid motions to reorient the triangles so they are easier to compare, as shown below.

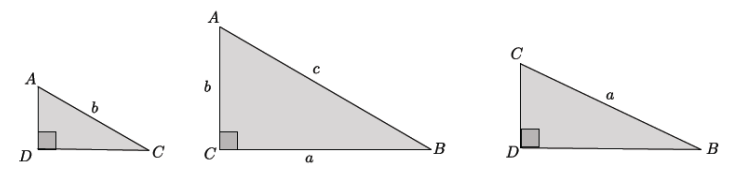
Answer:
→ The next step is to show that these triangles are similar. Begin by showing that
△ADC ~ △ACB. Discuss in your group.
△ADC and △ACB are similar because they each have a right angle, and they each share ∠A. Then, by the AA criterion for similarity, △ADC ~ △ACB.

→ Now, show that △ACB ~ △CDB. Discuss in your group.
△ACB ~ △CDB because they each have a right angle, and they each share ∠B. Then, by the AA criterion for similarity,
△ACB ~ △CDB.

→ Are △ADC and △CDB similar? Discuss in your group.
We know that similarity has the property of transitivity; therefore, since △ADC ~ △ACB, and
△ACB ~ △CDB, then △ADC ~ △CDB.

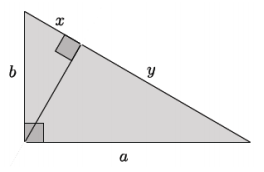
→ Let’s identify the segments that comprise side c as follows: |AD| = x and |BD| = y. (Ensure that students note x and y in their student materials.) Using this notation, we see that side c is equal to the sum of the lengths x and y (i.e., x + y = c).

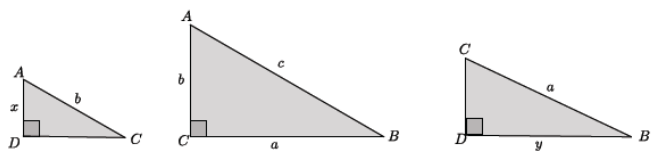
→ If we consider △ADC and △ACB, we can write a statement about corresponding sides being equal in a ratio that helps us reach our goal of showing a² + b² = c². Discuss in your group.
Using △ADC and △ACB, we can write
\(\frac{x}{b}\) = \(\frac{b}{c}\).
Now solve the equation for x.
x = \(\frac{b^{2}}{c}\)

→ Using △ACB and △CDB gives us another piece that we need. Discuss in your group.
Using △ACB and △CDB, we can write
\(\frac{a}{y}\) = \(\frac{c}{a}\).
Now solve the equation for y.
\(\frac{a^{2}}{c}\) = y

→ We know that x + y = c, and we just found expressions equal to x and y. Use this information to show that a² + b² = c². Discuss in your group.
By substituting \(\frac{b^{2}}{c}\) for x and \(\frac{a^{2}}{c}\) for y in c = x + y, we have
\(\frac{b^{2}}{c}\) + \(\frac{a^{2}}{c}\) = c.
Multiplying through by c we have
b² + a² = c².
By the commutative property of addition we can rewrite the left side as
a² + b² = c².

Discussion

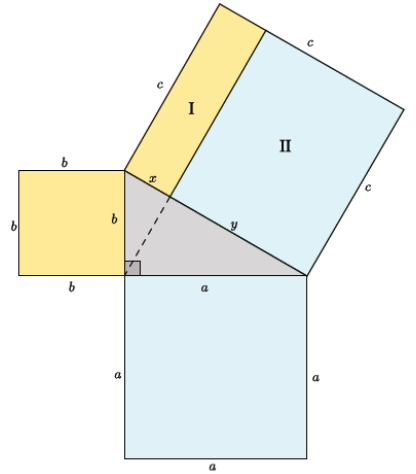
Let’s draw three squares on the right triangle. Notice that we can use the altitude to divide the large square, of area c², into two rectangles as shown. Call them rectangle I and rectangle II.

→ What would it mean, geometrically, for a² + b² to equal c²?
It means that the sum of the areas of a² and b² is equal to the area c².
There are two possible ways to continue; one way is by examining special cases on grid paper, as mentioned in the scaffolding box on the previous page, and showing the relationship between the squares physically. The other way is by using the algebraic proof of the general case that continues below.
→ What is the area of rectangle I?
The area of rectangle I is xc.
This is where the proof using similar triangles just completed is helpful. We said that x = \(\frac{b^{2}}{c}\). Therefore, the area of rectangle I is
xc = \(\frac{b^{2}}{c}\)⋅c = b².

→ Now use similar reasoning to determine the area of rectangle II.
The area of rectangle II is yc. When we substitute \(\frac{a^{2}}{c}\) for y we get yc = \(\frac{a^{2}}{c}\)⋅c = a².
→ Explain how the work thus far shows that the Pythagorean theorem is true.
The Pythagorean theorem states that given a right triangle with lengths a, b, c, then a² + b² = c². The diagram shows that the area of the rectangles drawn off of side c have a sum of a² + b². The square constructed off of side c clearly has an area of c². Thus, the diagram shows that the areas
a² + b² are equal to the area of c², which is exactly what the theorem states.

To solidify student understanding of the proof, consider showing students the six-minute video located at http://www.youtube.com/watch?v = QCyvxYLFSfU. If multiple computers or tablets are available, have small groups of students watch the video together so they can pause and replay parts of the proof as necessary.

Eureka Math Grade 8 Module 7 Lesson 15 Problem Set Answer Key

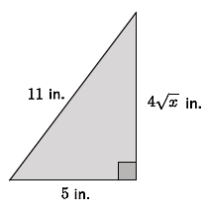
Question 1.
For the right triangle shown below, identify and use similar triangles to illustrate the Pythagorean theorem.

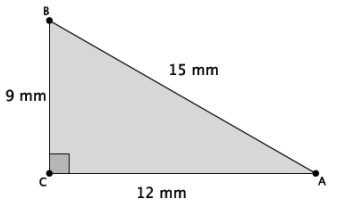
Answer:
First, I must draw a segment that is perpendicular to side AB that goes through point C. The point of intersection of that segment and side AB will be marked as point D.

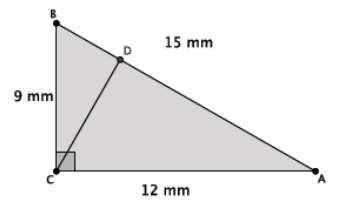
Then, I have three similar triangles, △ABC, △CBD, and △ACD, as shown below.

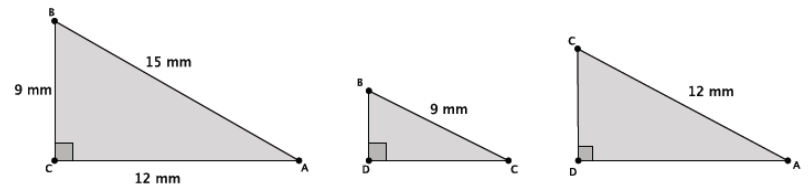
△ABC and △CBD are similar because each one has a right angle, and they both share ∠B. By AA criterion,
△ABC ~ △CBD. △ABC and △ACD are similar because each one has a right angle, and they both share ∠A.
By AA criterion, △ABC ~ △ACD. By the transitive property, we also know that △ACD ~ △CBD.
Since the triangles are similar, they have corresponding sides that are equal in ratio. For △ABC and △CBD,
\(\frac{9}{15}\) = \(\frac{|B D|}{9}\),
which is the same as 9² = 15(|BD|).
For △ABC and △ACD,
\(\frac{12}{15}\) = \(\frac{|A D|}{12}\),
which is the same as 12² = 15(|AD|).
Adding these two equations together I get
9² + 12² = 15(|BD|) + 15(|AD|).
By the distributive property,
9² + 12² = 15(|BD| + |AD|);
however, |BD| + |AD| = |AC| = 15. Therefore,
9² + 12² = 15(15)
9² + 12² = 15².

Question 2.
For the right triangle shown below, identify and use squares formed by the sides of the triangle to illustrate the Pythagorean theorem.

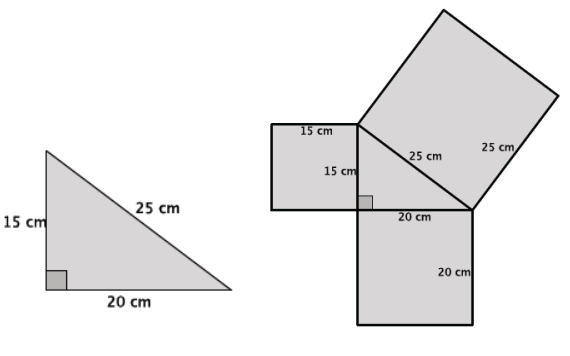
Answer:
The sum of the areas of the smallest squares is 15² cm² + 20² cm² = 625 cm². The area of the largest square is
25² cm² = 625 cm². The sum of the areas of the squares off of the legs is equal to the area of the square off of the hypotenuse; therefore, a² + b² = c².

Question 3.
Reese claimed that any figure can be drawn off the sides of a right triangle and that as long as they are similar figures, then the sum of the areas off of the legs will equal the area off of the hypotenuse. She drew the diagram by constructing rectangles off of each side of a known right triangle. Is Reese’s claim correct for this example? In order to prove or disprove Reese’s claim, you must first show that the rectangles are similar. If they are, then you can use computations to show that the sum of the areas of the figures off of the sides a and b equals the area of the figure off of side c.

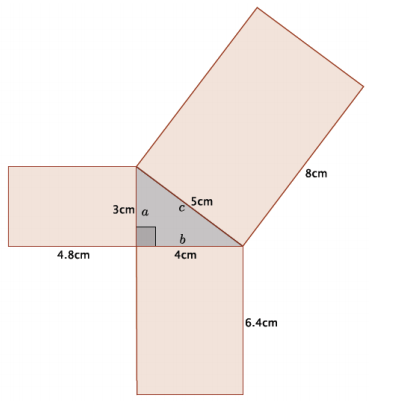
Answer:
The rectangles are similar because their corresponding side lengths are equal in scale factor. That is, if we compare the longest side of the rectangle to the side with the same length as the right triangle sides, we get the ratios
\(\frac{4.8}{3}\) = \(\frac{6.4}{4}\) = \(\frac{8}{5}\) = 1.6.
Since the corresponding sides were all equal to the same constant, then we know we have similar rectangles. The areas of the smaller rectangles are 14.4 cm² and 25.6 cm², and the area of the largest rectangle is 40 cm². The sum of the smaller areas is equal to the larger area:
14.4 + 25.6 = 40
40 = 40.
Therefore, we have shown that the sum of the areas of the two smaller rectangles is equal to the area of the larger rectangle, and Reese’s claim is correct.

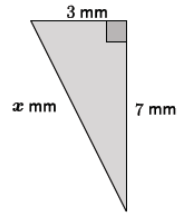
Question 4.
After learning the proof of the Pythagorean theorem using areas of squares, Joseph got really excited and tried explaining it to his younger brother. He realized during his explanation that he had done something wrong. Help Joseph find his error. Explain what he did wrong.

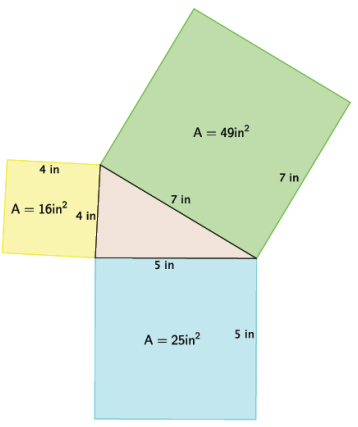
Answer:
Based on the proof shown in class, we would expect the sum of the two smaller areas to be equal to the sum of the larger area (i.e., 16 + 25 should equal 49). However, 16 + 25 = 41. Joseph correctly calculated the areas of each square, so that was not his mistake. His mistake was claiming that a triangle with side lengths of 4, 5, and 7 was a right triangle. We know that the Pythagorean theorem only works for right triangles. Considering the converse of the Pythagorean theorem, when we use the given side lengths, we do not get a true statement.
4² + 5² = 7²
16 + 25 = 49
41 ≠ 49
Therefore, the triangle Joseph began with is not a right triangle, so it makes sense that the areas of the squares were not adding up like we expected.

Question 5.
Draw a right triangle with squares constructed off of each side that Joseph can use the next time he wants to show his younger brother the proof of the Pythagorean theorem.
Answer:
Answers will vary. Verify that students begin, in fact, with a right triangle and do not make the same mistake that Joseph did. Consider having students share their drawings and explanations of the proof in future class meetings.

Question 6.
Explain the meaning of the Pythagorean theorem in your own words.
Answer:
If a triangle is a right triangle, then the sum of the squares of the legs will be equal to the square of the hypotenuse. Specifically, if the leg lengths are a and b, and the hypotenuse is length c, then for right triangles a² + b² = c².

Question 7.
Draw a diagram that shows an example illustrating the Pythagorean theorem.
Answer:
Diagrams will vary. Verify that students draw a right triangle with side lengths that satisfy the Pythagorean theorem.

Eureka Math Grade 8 Module 7 Lesson 15 Exit Ticket Answer Key

Question 1.
Explain a proof of the Pythagorean theorem in your own words. Use diagrams and concrete examples, as necessary, to support your explanation.
Answer:
Proofs will vary. The critical parts of the proof that demonstrate proficiency include an explanation of the similar triangles △ADC, △ACB, and △CDB, including a statement about the ratio of their corresponding sides being equal, leading to the conclusion of the proof.

Engage NY Eureka Math 8th Grade Module 7 Lesson 14 Answer Key

Eureka Math Grade 8 Module 7 Lesson 14 Exercise Answer Key

Opening Exercise
a. Write an equation for the area, A, of the circle shown.

Answer:
A < π(6.3) ²
< 39.69π
The area of the circle is 39.69π cm ² .

b. Write an equation for the circumference, C, of the circle shown.

Answer:
C < 2π(9.7)
< 19.4π
The circumference of the circle is 19.4π mm.

c. Each of the squares in the grid below has an area of 1 unit ² .

i. Estimate the area of the circle shown by counting squares.
Answer:
Estimates will vary. The approximate area of the circle is 78 units ² .

ii. Calculate the area of the circle using a radius of 5 units. Use 3.14 as an approximation for π.
Answer:
A≈3.14(5) ²
≈78.5
The area of the circle is approximately 78.5 units ² .

Exercises 1–4

Exercise 1.
Gerald and Sarah are building a wheel with a radius of 6.5 cm and are trying to determine the circumference. Gerald says, “Because 6.5 × 2 × 3.14 < 40.82, the circumference is 40.82 cm.” Sarah says, “Because
6.5 × 2 × 3.10 < 40.3 and 6.5 × 2 × 3.21 < 41.73, the circumference is somewhere between 40.3 and 41.73.” Explain the thinking of each student.
Answer:
Gerald is using a common approximation for the number π to determine the circumference of the wheel. That is why he used 3.14 in his calculation. Sarah is using an interval between which the value of π falls, based on the work we did in class. We know that 3.10 < π < 3.21; therefore, her calculations of the circumference uses numbers we know π to be between.

Exercise 2.
Estimate the value of the number (6.12486…) ² .
Answer:
6.12486 ² < (6.12486…) ² < 6.12487 ²
37.5139100196 < (6.12486…) ² < 37.5140325169
(6.12486…) ² < 37.51 is correct up to two decimal digits.

Exercise 3.
Estimate the value of the number (9.204107…) < sup>2 < /sup>.
Answer:
9.204107 ² < (9.204107… ) ² < 9.204108 ²
84.715585667449 < (9.204107…) ² < 84.715604075664
(9.20410…) ² < 84.715 is correct up to three decimal digits.

Exercise 4.
Estimate the value of the number (4.014325…) < sup>2 < /sup>.
Answer:
4.014325 ² < (4.014325…) ² < 4.014326 ²
16.114805205625 < (4.014325…) ² < 16.114813234276
(4.014325…) ² < 16.1148 is correct up to four decimal digits.

Eureka Math Grade 8 Module 7 Lesson 14 Problem Set Answer Key

Question 1.
Caitlin estimated π to be 3.10 < π < 3.21. If she uses this approximation of π to determine the area of a circle with a radius of 5 cm, what could the area be?
Answer:
The area of the circle with radius 5 cm will be between 77.5 cm² and 80.25 cm².

Question 2.
Myka estimated the circumference of a circle with a radius of 4.5 in. to be 28.44 in. What approximate value of π did she use? Is it an acceptable approximation of π? Explain.
Answer:
C < 2πr
28.44 < 2π(4.5)
28.44 < 9π
\(\frac{28.44}{9}\) < π
3.16 < π
Myka used 3.16 to approximate π. Student responses may vary with respect to whether or not 3.16 is an acceptable approximation for π. Accept any reasonable explanation.

Question 3.
A length of ribbon is being cut to decorate a cylindrical cookie jar. The ribbon must be cut to a length that stretches the length of the circumference of the jar. There is only enough ribbon to make one cut. When approximating π to calculate the circumference of the jar, which number in the interval 3.10 < π < 3.21 should be used? Explain.
Answer:
In order to make sure the ribbon is long enough, we should use an estimate of π that is closer to 3.21. We know that 3.10 is a fair estimate of π but less than the actual value of π. Similarly, we know that 3.21 is a fair estimate of π but greater than the actual value of π. Since we can only make one cut, we should cut the ribbon so that there is a little more than we need, not less than. For that reason, an approximation of π closer to 3.21 should be used.

Question 4.
Estimate the value of the number (1.86211…)².
Answer:
1.86211² < (1.86211…)² < 1.86212²
3.4674536521 < (1.86211…)² < 3.4674908944
(1.86211…)² < 3.4674 is correct up to four decimal digits.

Question 5.
Estimate the value of the number (5.9035687…)².
Answer:
5.9035687² < (5.9035687…)² < 5.9035688²
34.85212339561969 < (5.9035687…)² < 34.85212457633344
(5.9035687…)² < 34.85212 is correct up to five decimal digits.

Question 6.
Estimate the value of the number (12.30791…)².
Answer:
12.30791² < (12.30791…)² < 12.30792²
151.4846485681 < (12.30791…)² < 151.4848947264
(12.30791…)² < 151.484 is correct up to three decimal digits.

Question 7.
Estimate the value of the number (0.6289731…)².
Answer:
0.6289731² < (0.6289731…)² < 0.6289732²
0.39560716052361 < (0.6289731…)² < 0.39560728631824
(0.6289731…)² < 0.395607 is correct up to six decimal digits.

Question 8.
Estimate the value of the number (1.112223333…)².
Answer:
1.112223333² < (1.112223333…)² < 1.112223334²
1.2370407424696289 < (1.112223333…)² < 1.2370407446940756
(1.112223333…)² < 1.23704074 is correct up to eight decimal digits.

Question 9.
Which number is a better estimate for π, \(\frac{22}{7}\) or 3.14? Explain.
Answer:
Allow for both answers to be correct as long as the student provides a reasonable explanation.
A sample answer might be as follows.
I think that \(\frac{22}{7}\) is a better estimate because when I find the decimal expansion, \(\frac{22}{7}\)≈3.142857…; compared to the number 3.14, \(\frac{22}{7}\) is closer to the actual value of π.

Question 10.
To how many decimal digits can you correctly estimate the value of the number (4.56789012…)²?
Answer:
4.56789012² < (4.56789012…)² < 4.56789013²
20.8656201483936144 < (1.112223333…)² < 20.8656202397514169
(4.56789012…)² < 20.865620 is correct up to six decimal digits.

Eureka Math Grade 8 Module 7 Lesson 14 Exit Ticket Answer Key

Question 1.
Describe how we found a decimal approximation for π.
Answer:
To make our work easier, we looked at the number of unit squares in a quarter circle that comprised its area. We started by counting just the whole number of unit squares. Then, we continued to revise our estimate of the area by looking at parts of squares specifically to see if parts could be combined to make a whole unit square. We looked at the inside and outside boundaries and said that the value of π would be between these two numbers. The inside boundary is a conservative estimate of the value of π, and the outside boundary is an overestimate of the value of π. We could continue this process with smaller squares in order to refine our estimate for the decimal approximation of π.

Engage NY Eureka Math 8th Grade Module 7 Lesson 13 Answer Key

Eureka Math Grade 8 Module 7 Lesson 13 Exploratory Challenge/Exercise Answer Key

Exploratory Challenge/Exercises 1–11

Exercise 1.
Rodney thinks that \(\sqrt [ 3 ]{ 64 }\) is greater than \(\frac{17}{4}\). Sam thinks that \(\frac{17}{4}\) is greater. Who is right and why?
\(\sqrt [ 3 ]{ 64 }\) = \(\sqrt[3]{4^{3}}\) = 4
and
\(\frac{17}{4}\) = \(\frac{16}{4}\) + \(\frac{1}{4}\)
= 4 + \(\frac{1}{4}\)
= 4 \(\frac{1}{4}\)
We see that \(\sqrt [ 3 ]{ 64 }\) < \(\frac{17}{4}\). Sam is correct.

Exercise 2.
Which number is smaller, \(\sqrt [ 3 ]{ 27 }\) or 2.89? Explain.
Answer:
\(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{3^{3}}\) = 3
We see that 2.89 is smaller than \(\sqrt [ 3 ]{ 27 }\).

Exercise 3.
Which number is smaller, \(\sqrt{121}\) or \(\sqrt [ 3 ]{ 125 }\)? Explain.
Answer:
\(\sqrt{121}\) = \(\sqrt{11^{2}}\) = 11
\(\sqrt [ 3 ]{ 125 }\) = \(\sqrt[3]{5^{3}}\) = 5
We see that \(\sqrt [ 3 ]{ 125 }\) is smaller than \(\sqrt{121}\).

Exercise 4.
Which number is smaller, \(\sqrt{49}\) or \(\sqrt [ 3 ]{ 216 }\)? Explain.
Answer:
\(\sqrt{49}\) = \(\sqrt{7^{2}}\) = 7
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{6^{3}}\) = 6
We see that \(\sqrt [ 3 ]{ 216 }\) is smaller than \(\sqrt{49}\).

Exercise 5.
Which number is greater, \(\sqrt{50}\) or \(\frac{319}{45}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{319}{45}\) is equal to\(7.0 \overline{8}\).
The number \(\sqrt{50}\) is between 7 and 8 because 7² < 50 < 8². The number \(\sqrt{50}\) is between 7.0 and 7.1 because 7² < 50 < 7.1². The number \(\sqrt{50}\) is between 7.07 and 7.08 because 7.07² < 50 < 7.08². The approximate decimal value of \(\sqrt{50}\) is 7.07. Since 7.07 < \(7.0 \overline{8}\), then \(\sqrt{50}\) < \(\frac{319}{45}\); therefore, the fraction \(\frac{319}{45}\) is greater than \(\sqrt{50}\) .
Alternately: (\(\sqrt{50}\))² = 50 and (\(\frac{319}{45}\))² = 101761/2025>101250/2025 = 50. So, 319/45 must be larger.

Exercise 6.
Which number is greater, \(\frac{5}{11}\) or \(0. \overline{4}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{5}{11}\) is equal to \(0. \overline{45}\). Since 0.44444… < 0.454545…, then \(0. \overline{4}\) < \(\frac{5}{11}\); therefore, the fraction \(\frac{5}{11}\) is greater than 0.4 ̅.
Alternately: 0.444… = \(\frac{4}{9}\), and we can compare the fractions \(\frac{4}{9}\) and \(\frac{5}{11}\) using their equivalents, \(\frac{44}{99}\) and \(\frac{45}{99}\) to see that \(\frac{5}{11}\) is larger.

Exercise 7.
Which number is greater, \(\sqrt{38}\) or \(\frac{154}{25}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
\(\frac{154}{25}\) = \(\frac{154 \times 4}{25 \times 4} = \frac{616}{10^{2}}\) = 6.16
The number \(\sqrt{38}\) is between 6 and 7 because 6² < 38 < 7². The number \(\sqrt{38}\) is between 6.1 and 6.2 because
6.1² < 38 < 6.2². The number \(\sqrt{38}\) is between 6.16 and 6.17 because 6.16² < 38 < 6.17². Since \(\sqrt{38}\) is greater than 6.16, then \(\sqrt{38}\) is greater than 154/25.
Alternately: (\(\sqrt{38}\))² = 38 and (\(\frac{154}{25}\))² = \(\frac{23716}{625}\) < \(\frac{23750}{625}\) = 38. So, \(\sqrt{38}\) must be larger.

Exercise 8.
Which number is greater, \(\sqrt{2}\) or \(\frac{15}{9}\)? Explain.
Answer:
Students may use any method to determine the decimal expansion of the fraction.
The number \(\frac{15}{9}\) is equal to\(1 . \overline{6}\).

The number \(\sqrt{2}\) is between 1 and 2 because 1² < 2 < 2². The number \(\sqrt{2}\) is between 1.4 and 1.5 because
1.4² < 2 < 1.5². Therefore, \(\sqrt{2}\) < \(\frac{15}{9}\); the fraction \(\frac{15}{9}\) is greater.
Alternately: (\(\sqrt{2}\))² = 2 and (\(\frac{15}{9}\))² = (\(\frac{5}{3}\))² = \(\frac{28}{9}\)>2. So, \(\frac{15}{9}\) must be larger.

Exercise 9.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{25}\), \(\sqrt{28}\), \(\sqrt{30}\), \(\sqrt{32}\), \(\sqrt{35}\), and \(\sqrt{36}\).
Answer:
The solutions are shown in red:

The number \(\sqrt{25}\) = \(\sqrt{5^{2}}\) = 5.
The numbers \(\sqrt{28}\),\(\sqrt{30}\),\(\sqrt{32}\), and \(\sqrt{35}\) are between 5 and 6. The number \(\sqrt{28}\) is between 5.2 and 5.3 because 5.2² < 28 < 5.3². The number \(\sqrt{30}\) is between 5.4 and 5.5 because 5.4² < 30 < 5.5². The number \(\sqrt{32}\) is between 5.6 and 5.7 because 5.6² < 32 < 5.7². The number \(\sqrt{35}\) is between 5.9 and 6.0 because
5.9² < 35 < 6².
The number\(\sqrt{36}\) = \(\sqrt{6^{2}}\) = 6.

Exercise 10.
Challenge: Which number is larger, \(\sqrt{5}\) or \(\sqrt [ 3 ]{ 11 }\)?
Answer:
The number \(\sqrt{5}\) is between 2 and 3 because 2² < 5 < 3². The number \(\sqrt{5}\) is between 2.2 and 2.3 because
2.2² < 5 < 2.3². The number \(\sqrt{5}\) is between 2.23 and 2.24 because 2.23² < 5 < 2.24². The number \(\sqrt{5}\) is between 2.236 and 2.237 because 2.236² < 5 < 2.237². The decimal expansion of \(\sqrt{5}\) is approximately 2.236….
The number \(\sqrt [ 3 ]{ 11 }\) is between 2 and 3 because 2^3 < 11 < 3^3. The number \(\sqrt [ 3 ]{ 11 }\) is between 2.2 and 2.3 because 2.2^3 < 11 < 2.3^3. The number \(\sqrt [ 3 ]{ 11 }\) is between 2.22 and 2.23 because 2.22^3 < 11 < 2.23^3. The decimal expansion of \(\sqrt [ 3 ]{ 11 }\) is approximately 2.22…. Since 2.22″…” < 2.236″…” , then \(\sqrt [ 3 ]{ 11 }\) < \(\sqrt{5}\); therefore, \(\sqrt{5}\) is larger.

Alternately:
(\(\sqrt [ 3 ]{ 11 }\))^6 = 11² = 121
(\(\sqrt{5}\))^6 = 5^3 = 125
We see that \(\sqrt{5}\) must be larger.

Exercise 11.
A certain chessboard is being designed so that each square has an area of 3 in². What is the length of one edge of the board rounded to the tenths place? (A chessboard is composed of 64 squares as shown.)

Answer:
The area of one square is 3 in². So, if x is the length of one side of one square,
x² = 3
\(\sqrt{x^{2}}\) = \(\sqrt{3}\)
x = \(\sqrt{3}\).
There are 8 squares along one edge of the board, so the length of one edge is 8×\(\sqrt{3}\). The number \(\sqrt{3}\) is between 1 and 2 because
1² < 3 < 2². The number \(\sqrt{3}\) is between 1.7 and 1.8 because 1.7² < 3 < 1.8². The number \(\sqrt{3}\) is between 1.73 and 1.74 because 1.73² < 3 < 1.74². The number \(\sqrt{3}\) is approximately 1.73. So, the length of one edge of the chessboard is about
8×1.73 inches, which is approximately 13.8 in.
Note: Some students may determine the total area of the board, 64×3 = 192, and then determine the approximate value of \(\sqrt{192}\) as 13.8 to answer the question.

Eureka Math Grade 8 Module 7 Lesson 13 Problem Set Answer Key

Question 1.
Which number is smaller, \(\sqrt [ 3 ]{ 343 }\) or \(\sqrt{48}\) ? Explain.
Answer:
√(3&343) = \(\sqrt[3]{7^{3}}\) = 7
The number \(\sqrt{48}\) is between 6 and 7 but definitely less than 7. Therefore, \(\sqrt{48}\) < \(\sqrt [ 3 ]{ 343 }\), and √\(\sqrt{48}\) is smaller.

Question 2.
Which number is smaller, \(\sqrt{100}\) or \(\sqrt [ 3 ]{ 1000 }\)? Explain.
Answer:
\(\sqrt{100}\) = \(\sqrt{10^{2}}\) = 10
\(\sqrt [ 3 ]{ 1000 }\) = \(\sqrt[3]{10^{3}}\) = 10
The numbers \(\sqrt{100}\) and \(\sqrt [ 3 ]{ 1000 }\) are equal because both are equal to 10.

Question 3.
Which number is larger, \(\sqrt{87}\) or \(\frac{929}{99}\)? Explain.
Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\frac{929}{99}\) is equal to \(9 . \overline{38}\).

The number \(\sqrt{87}\) is between 9 and 10 because 9² < 87 < 10². The number \(\sqrt{87}\) is between 9.3 and 9.4 because 9.3² < 87 < 9.4². The number \(\sqrt{87}\) is between 9.32 and 9.33 because 9.32² < 87 < 9.33². Since \(\sqrt{87}\) < 9.3, then \(\sqrt{87}\) < \(\frac{929}{99}\). The fraction \(\frac{929}{99}\) is larger.

Question 4.
Which number is larger, \(\frac{9}{13}\) or \(0 . \overline{692}\)? Explain.
Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\frac{9}{13}\) is equal to \(0 . \overline{692307}\). Since 0.692307… < 0.692692…, then we see that 9/13 < \(0 . \overline{692}\).
The decimal \(0 . \overline{692}\) is larger.

Question 5.
Which number is larger, 9.1 or \(\sqrt{82}\)? Explain.
Answer:
The number \(\sqrt{82}\) is between 9 and 10 because 9² < 82 < 10². The number \(\sqrt{82}\) is between 9.0 and 9.1 because 9.0² < 82 < 9.1². Since \(\sqrt{82}\) < 9.1, then the number 9.1 is larger than the number \(\sqrt{82}\).

Question 6.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{144}\), \(\sqrt [ 3 ]{ 1000 }\), \(\sqrt{130}\), \(\sqrt{110}\), \(\sqrt{120}\), \(\sqrt{115}\), and \(\sqrt{133}\). Explain how you knew where to place the numbers.

Answer:
The solutions are shown in red:

The number \(\sqrt{144}\) = \(\sqrt{12^{2}}\) = 12.
The number \(\sqrt [ 3 ]{ 1000 }\) = \(\sqrt[3]{10^{3}}\) = 10.

The numbers \(\sqrt{110}\), \(\sqrt{115}\), and \(\sqrt{120}\) are all between 10 and 11 because when squared, their value falls between 10² and 11². The number \(\sqrt{110}\) is between 10.4 and 10.5 because 10.4² < 110 < 10.5². The number \(\sqrt{115}\) is between 10.7 and 10.8 because 10.7² < 115 < 10.8². The number \(\sqrt{120}\) is between 10.9 and 11 because 10.9² < 120 < 11².
The numbers √130 and \(\sqrt{133}\) are between 11 and 12 because when squared, their value falls between 11² and 12². The number √130 is between 11.4 and 11.5 because 11.4² < 130 < 11.5². The number \(\sqrt{133}\) is between 11.5 and 11.6 because 11.5² < 133 < 11.6².

Question 7.
Which of the two right triangles shown below, measured in units, has the longer hypotenuse? Approximately how much longer is it?

Answer:
Let x represent the length of the hypotenuse of the triangle on the left.
7² + 2² = x²
49 + 4 = x²
53 = x²
\(\sqrt{53}\) = x
The number \(\sqrt{53}\) is between 7 and 8 because 7² < 53 < 8². The number \(\sqrt{53}\) is between 7.2 and 7.3 because 7.2² < 53 < 7.3². The number \(\sqrt{53}\) is between 7.28 and 7.29 because 7.28² < 53 < 7.29². The approximate decimal value of \(\sqrt{53}\) is 7.28.
Let y represent the length of the hypotenuse of the triangle on the right.
5² + 5² = y²
25 + 25 = y²
50 = y²
\(\sqrt{50}\) = y
The number \(\sqrt{50}\) is between 7 and 8 because 7² < 50 < 8². The number \(\sqrt{50}\) is between 7.0 and 7.1 because 7.0² < 50 < 7.1². The number \(\sqrt{50}\) is between 7.07 and 7.08 because 7.07² < 50 < 7.08². The approximate decimal value of \(\sqrt{50}\) is 7.07.

The triangle on the left has the longer hypotenuse. It is approximately 0.21 units longer than the hypotenuse of the triangle on the right.
Note: Based on their experience, some students may reason that \(\sqrt{50}\) < \(\sqrt{53}\). To answer completely, students must determine the decimal expansion to approximate how much longer one hypotenuse is than the other.

Eureka Math Grade 8 Module 7 Lesson 13 Exit Ticket Answer Key

Question 1.
Place each of the following numbers at its approximate location on the number line: \(\sqrt{12}\), \(\sqrt{16}\), \(\frac{20}{6}\), \(3 . \overline{53}\), and \(\sqrt [ 3 ]{ 27 }\).

Answer:
Students may use any method to compute the first few decimal places of a fraction.
The number \(\sqrt{12}\) is between 3.4 and 3.5 since 3.4² < 12 < 3.5².
The number \(\sqrt{16}\) = \(\sqrt{4^{2}}\) = 4.
The number \(\frac{20}{6}\) is equal to \(3 . \overline{3}\).
The number \(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{3^{3}}\) = 3.
The solutions are shown in red:

Engage NY Eureka Math 8th Grade Module 7 Lesson 12 Answer Key

Eureka Math Grade 8 Module 7 Lesson 12 Example Answer Key

Example 1.
Find the decimal expansion of \(\frac{35}{11}\).
Answer:
For fun, let’s see if we can find the decimal expansion of \(\frac{35}{11}\) without using long division.
To start, can we say between which two integers this number lies?

The number \(\frac{35}{11}\) would lie between 3 and 4 on the number line because \(\frac{35}{11}\) = \(\frac{33}{11}\) + \(\frac{2}{11}\) = 3 + \(\frac{2}{11}\).
Could we say in which tenth between 3 and 4 the number 3 + \(\frac{2}{11}\) lies? Is this tricky?
We know that \(\frac{35}{11}\) has a decimal expansion beginning with 3 in the ones place because \(\frac{35}{11}\) = 3 + \(\frac{2}{11}\). Now we want to determine the tenths digit, the hundredths digit, and then the thousandths digit.

Ones Tenths Hundredths Thousandths
To figure out the tenths digit, we will use an inequality based on tenths. We are looking for the consecutive integers, m and m + 1, so that
3 + \(\frac{m}{10}\) < \(\frac{35}{11}\) < 3 + \(\frac{m + 1}{10}\) .

We can rewrite the middle term:
3 + \(\frac{m}{10}\) < 3 + \(\frac{2}{11}\) < 3 + \(\frac{m + 1}{10}\) .

This means we’re looking at
\(\frac{m}{10}\) < \(\frac{2}{11}\) < \(\frac{m + 1}{10}\).

Give students time to make sense of the inequalities 3 + \(\frac{m}{10}\) < \(\frac{35}{11}\) < 3 + \(\frac{m + 1}{10}\) and \(\frac{m}{10}\) < \(\frac{2}{11}\) < \(\frac{m + 1}{10}\).
Since the intervals of tenths are represented by \(\frac{m}{10}\) and \(\frac{m + 1}{10}\), consider using concrete numbers. The chart below may help students make sense of the intervals and the inequalities.

Eureka Math Grade 8 Module 7 Lesson 12 Exercise Answer Key

Exercises 1–3

Exercise 1.
Find the decimal expansion of \(\frac{5}{3}\) without using long division.
Answer:
\(\frac{5}{3}\) = \(\frac{3}{3}\) + \(\frac{2}{3}\)
= 1 + \(\frac{2}{3}\)
The decimal expansion begins with the integer 1.
Among the intervals of tenths, we are looking for integers m and m + 1 so that
1 + \(\frac{m}{10}\) < 1 + \(\frac{2}{3}\) < 1 + \(\frac{m + 1}{10}\),
which is the same as
\(\frac{m}{10}\) < \(\frac{2}{3}\) < \(\frac{m + 1}{10}\)
m < \(\frac{20}{3}\) < m + 1
and
\(\frac{20}{3}\) = \(\frac{18}{3}\) + \(\frac{2}{3}\)
= 6 + \(\frac{2}{3}\).
The tenths digit is 6.
Among the intervals of hundredths we are looking for integers m and m + 1 so that
1 + \(\frac{6}{10}\) + \(\frac{m}{100}\) < \(\frac{5}{3}\) < 1 + \(\frac{6}{10}\) + \(\frac{m + 1}{10}\) ,
which is equivalent to
\(\frac{m}{100}\) < \(\frac{2}{3}\) – \(\frac{6}{10}\) < \(\frac{m + 1}{10}\).
Now
\(\frac{2}{3}\) – \(\frac{6}{10}\) = \(\frac{2}{30}\) .
So we are looking for integers m and m + 1 where
\(\frac{m}{100}\) < \(\frac{2}{30}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{20}{3}\) < m + 1 .
But we already know that \(\frac{20}{3}\) = 6 + \(\frac{2}{3}\); therefore, the hundredths digit is 6. We feel like we are repeating our work, so we suspect \(\frac{5}{3}\) = 1.666″…” . To check: 0.6666″…” = 6/9 = \(\frac{2}{3}\) and 1.6666″…” = 1 + \(\frac{2}{3}\) = \(\frac{5}{3}\). We are correct.

Exercise 2.
Find the decimal expansion of \(\frac{5}{11}\) without using long division.
Answer:
Its decimal expansion begins with the integer 0.
In the intervals of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{5}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{50}{11}\) < m + 1
\(\frac{50}{11}\) = \(\frac{44}{11}\) + \(\frac{6}{11}\)
= 4 + \(\frac{6}{11}\)
The tenths digit is 4.
In the intervals of hundredths, we are looking for integers m and m + 1 so that

As
\(\frac{60}{11}\) = \(\frac{55}{11}\) + \(\frac{5}{11}\)
= 5 + \(\frac{5}{11}\)
we see that the hundredths digit is 5.
The fraction \(\frac{5}{11}\) has reappeared, which makes us suspect we are in a repeating pattern and we have
\(\frac{5}{11}\) = 0.454545″…” . To check: 0.454545″…” = \(\frac{45}{99}\) = \(\frac{5}{11}\). We are correct.

Exercise 3.
Find the decimal expansion of the number \(\frac{23}{99}\) first without using long division and then again using long division.
Answer:
The decimal expansion begins with the integer 0.
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{23}{99}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{230}{99}\) < m + 1.
Now
\(\frac{230}{99}\) = \(\frac{198}{99}\) + \(\frac{32}{99}\)
= 2 + \(\frac{32}{99}\)
showing that the tenths digit is 2.
In the interval of hundredths, we are looking for integers m and m + 1 so that

Now
\(\frac{320}{99}\) = \(\frac{297}{99}\) + \(\frac{23}{99}\)
= 3 + \(\frac{23}{99}\)
The hundredths digit is 3. The reappearance of 23/99 makes us suspect that we’re in a repeating pattern and \(\frac{23}{99}\) = 0.232323″…” . We check that 0.232323″…” does indeed equal \(\frac{23}{99}\) , and we are correct.

Eureka Math Grade 8 Module 7 Lesson 12 Problem Set Answer Key

Question 1.
Without using long division, explain why the tenths digit of \(\frac{3}{11}\) is a 2.
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{3}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{30}{11}\) < m + 1
\(\frac{30}{11}\) = \(\frac{22}{11}\) + \(\frac{8}{11}\)
= 2 + \(\frac{8}{11}\)
In looking at the interval of tenths, we see that the number \(\frac{3}{11}\) must be between \(\frac{2}{10}\) and \(\frac{3}{10}\)because \(\frac{2}{10}\) < \(\frac{3}{11}\) < \(\frac{3}{10}\). For this reason, the tenths digit of the decimal expansion of \(\frac{3}{11}\) must be 2.

Question 2.
Find the decimal expansion of \(\frac{25}{9}\) without using long division.
Answer:
\(\frac{25}{9}\) = \(\frac{18}{9}\) + \(\frac{7}{9}\)
= 2 + \(\frac{7}{9}\)
The ones digit is 2. In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{7}{9}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{70}{9}\) < m + 1
\(\frac{70}{9}\) = \(\frac{63}{9}\) + \(\frac{7}{9}\)
= 7 + \(\frac{7}{9}\)
The tenths digit is 7. The difference between \(\frac{7}{9}\) and \(\frac{7}{10}\) is
\(\frac{7}{9}\) – \(\frac{7}{10}\) = \(\frac{7}{90}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{7}{90}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{70}{9}\) < m + 1.
However, we already know that \(\frac{70}{9}\) = 7 + \(\frac{7}{9}\); therefore, the hundredths digit is 7. Because we keep getting \(\frac{7}{9}\), we can assume the digit of 7 will continue to repeat. Therefore, the decimal expansion of \(\frac{25}{9}\) is 2.777….

Question 3.
Find the decimal expansion of \(\frac{11}{41}\) to at least 5 digits without using long division.
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{11}{41}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{110}{41}\) < m + 1
\(\frac{110}{41}\) = \(\frac{82}{41}\) + \(\frac{28}{41}\) = 2 + \(\frac{28}{41}\).
The tenths digit is 2. The difference between \(\frac{11}{41}\) and \(\frac{2}{10}\) is
\(\frac{11}{41}\) – \(\frac{2}{10}\) = \(\frac{28}{410}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{28}{410}\) < \(\frac{m + 1}{100}\),
which is the same as

In the interval of ten – thousandths, we are looking for integers m and m + 1 so that

The hundred – thousandths digit is 9. We see again the fraction \(\frac{11}{41}\), so we can expect the decimal digits to repeat at this point. Therefore, the decimal approximation of \(\frac{11}{1}\) is 0.2682926829….

Question 4.
Which number is larger, \(\sqrt{10}\) or \(\frac{28}{9}\)? Answer this question without using long division.
Answer:
The number \(\sqrt{10}\) is between 3 and 4. In the sequence of tenths, \(\sqrt{10}\) is between 3.1 and 3.2 because
3.1² < (\(\sqrt{10}\))² < 3.2². In the sequence of hundredths, \(\sqrt{10}\) is between 3.16 and 3.17 because
3.16² < (\(\sqrt{10}\))² < 3.17². In the sequence of thousandths, \(\sqrt{10}\) is between 3.162 and 3.163 because
3.162² < (\(\sqrt{10}\))² < 3.163². The decimal expansion of \(\sqrt{10}\) is approximately 3.162….
\(\frac{28}{9}\) = \(\frac{27}{9}\) + \(\frac{1}{9}\)
= 3 + \(\frac{1}{9}\)
In the interval of tenths, we are looking for the integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{1}{9}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{10}{9}\) < m + 1
\(\frac{10}{9}\) = \(\frac{9}{9}\) + \(\frac{1}{9}\)
= 1 + \(\frac{1}{9}\)
The tenths digit is 1. Since the fraction \(\frac{1}{9}\) has reappeared, we can assume that the next digit is also 1, and the work will continue to repeat. Therefore, the decimal expansion of \(\frac{28}{9}\)9 is 3.1111….
Therefore, \(\frac{28}{9}\) < \(\sqrt{10}\).

Alternatively: (\(\sqrt{10}\))² = 10 and (\(\frac{28}{9}\))² = 784/81, which is less than \(\frac{810}{81}\) or 10. Thus, \(\frac{28}{9}\) is the smaller number.

Question 5.
Sam says that \(\frac{7}{11}\) = 0.63, and Jaylen says that \(\frac{7}{11}\) = 0.636. Who is correct? Why?
Answer:
In the interval of tenths, we are looking for integers m and m + 1 so that
\(\frac{m}{10}\) < \(\frac{7}{11}\) < \(\frac{m + 1}{10}\),
which is the same as
m < \(\frac{70}{11}\) < \(\frac{m + 1}{10}\)
\(\frac{70}{11}\) = \(\frac{66}{11}\) + \(\frac{4}{11}\)
= 6 + \(\frac{4}{11}\)
The tenths digit is 6. The difference between \(\frac{7}{11}\) and \(\frac{6}{10}\) is
\(\frac{7}{11}\) – \(\frac{6}{10}\) = \(\frac{4}{110}\).
In the interval of hundredths, we are looking for integers m and m + 1 so that
\(\frac{m}{100}\) < \(\frac{4}{110}\) < \(\frac{m + 1}{100}\),
which is the same as
m < \(\frac{40}{11}\) < m + 1
\(\frac{40}{11}\) = \(\frac{33}{11}\) + \(\frac{7}{11}\)
= 3 + \(\frac{7}{11}\)
The hundredths digit is 3. Again, we see the fraction \(\frac{7}{11}\), which means the next decimal digit will be 6, as it was in the tenths place. This means we will again see the fraction \(\frac{4}{11}\), meaning we will have another digit of 3. Therefore, the decimal expansion of \(\frac{7}{11}\) is 0.6363….

Technically, Sam and Jaylen are incorrect because the fraction \(\frac{7}{11}\) is an infinite decimal. However, Sam is correct to the first two decimal digits of the number, and Jaylen is correct to the first three decimal digits of the number.

Eureka Math Grade 8 Module 7 Lesson 12 Exit Ticket Answer Key

Question 1.
Find the decimal expansion of \(\frac{41}{6}\) without using long division.
Answer:
\(\frac{41}{6}\) = \(\frac{36}{6}\) + \(\frac{5}{6}\)
= 6 + \(\frac{5}{6}\)
The ones digit is 6.
To determine in which interval of tenths the fraction lies, we look for integers m and m + 1 so that

The tenths digit is 8.
To determine in which interval of hundredths the fraction lies, we look for integers m and m + 1 so that

We are a third over a whole number of tenths and a third over a whole number of hundredths. We suspect we are in a repeating pattern and that \(\frac{41}{6}\) = 6.83333….
To check:
x = 6.8333…
10x = 68.3333…
10x = 68 + 0.3333…
10x = 68 + \(\frac{1}{3}\)
10x = \(\frac{204}{3}\) + \(\frac{1}{3}\)
10x = \(\frac{205}{3}\)
x = \(\frac{205}{30}\)
x = \(\frac{41}{6}\)
We are correct.

Eureka Math Grade 8 Module 7 Lesson 12 Area and Volume I Answer Key

Question 1.
Find the area of the square shown below.

Answer:
A = (4 m)²
= 16 m²

Question 2.
Find the volume of the cube shown below.

Answer:
V = (4 m)³
= 64 m³

Question 3.
Find the area of the rectangle shown below.

Answer:
A = (8 cm)(4 cm)
= 32 cm²

Question 4.
Find the volume of the rectangular prism shown below.

Answer:
V = (32 cm²)(6 cm)
= 192 cm³

Question 5.
Find the area of the circle shown below.

Answer:
A = (7 m)² π
= 49π m²

Question 6.
Find the volume of the cylinder shown below.

Answer:
V = (49π m²)(12 m)
= 588π m³

Question 7.
Find the area of the circle shown below.

Answer:
A = (6 in.)² π
= 36π in²

Question 8.
Find the volume of the cone shown below.

Answer:
V = (\(\frac{1}{3}\))(36π in² )(10 in.)
= 120π in³

Question 9.
Find the area of the circle shown below.

Answer:
A = (8 mm)² π
= 64π mm²

Question 10.
Find the volume of the sphere shown below.

Answer:
V = (\(\frac{4}{3}\))π(64 mm² )(8 mm)
= \(\frac{2048}{2}\) π mm³

Engage NY Eureka Math 8th Grade Module 7 Lesson 11 Answer Key

Eureka Math Grade 8 Module 7 Lesson 11 Example Answer Key

Example 1.
Consider the decimal expansion of \(\sqrt{3}\).
Find the first two values of the decimal expansion using the following fact: If c² < 3 < d² for positive numbers c and d, then c < \(\sqrt{3}\) < d.
First approximation: Because 1 <3 < 4, we have 1 < \(\sqrt{3}\) < 2.
Answer:
We learned in Lesson 3 that if c and d are positive numbers, then c² < d² implies c² < d². It follows from this that if c² < N < d², then c<\(\sqrt{N}\) c < \(\sqrt{N}\) < d, then c² < N < d².)
Since 1 < 3 < 4, we get our first approximation: 1 < \(\sqrt{3}\) < 2.
To get more precise with our estimate of \(\sqrt{3}\), we can look at the tenths between the numbers 1 and 2.

Second approximation:

Answer:
→ Is \(\sqrt{3}\) between 1.2 and 1.3?
→ If 1.2 < \(\sqrt{3}\) < 1.3, then we should have 1.2² < 3 < 1.3². But we don’t: 1.2² = 1.44 and 1.3² = 1.69. These squares are too small.
→ Is \(\sqrt{3}\) between 1.8 and 1.9?
If 1.8 < \(\sqrt{3}\) < 1.9, then we should have 1.8²<3<1.9². But we don’t: 1.8² = 3.24 and 1.9² = 3.81. These squares are too large.

→ Can you find the right tenth interval in which \(\sqrt{3}\) belongs?
After some trial and error, students see that \(\sqrt{3}\) lies between 1.7 and 1.8 . We have 1.7² = 2.89 and 1.8² = 3.24, and so 2.89 < 3 < 3.24.
So the decimal expansion of \(\sqrt{3}\) begins 1.7…. How could we pin down its next decimal place?
Look for where \(\sqrt{3}\) lies in the interval between 1.7 and 1.8. Divide that interval into ten parts, too.
Let’s do that!

Third approximation:

Answer:

Have students use trial and error to eventually establish that \(\sqrt{3}\) lies between 1.73 and 1.74: we have 1.73² = 2.9929 and 1.74² = 3.0276 and 2.9926 < 3 < 3.0276.
→ So what are the first two places of the decimal expansion of \(\sqrt{3}\)?
We have \(\sqrt{3}\) = 1.73….
→ What do you think will need to be done to get an even more precise estimate of the number \(\sqrt{3}\)?
We will need to look at the interval between 1.73 and 1.74 more closely and repeat the process we did before.

→ Would you like to find the next decimal place for \(\sqrt{3}\) just for fun or leave it be for now?
Give students the option to find the next decimal place if they wish.
How accurate is our approximation \(\sqrt{3}\) = 1.73…? (If students computed
\(\sqrt{3}\) = 1.732…, adjust this question and the answer below appropriately.)
We know \(\sqrt{3}\) = 1.73abc… for some more digits a, b, c, and so on. Now 1.73 and 1.73abc… differ by 0.00abc…, which is less than 0.01. A decimal expansion computed to two decimal places gives an approximation that is accurate with an error that is at most 0.01.

Example 2.
Find the first few places of the decimal expansion of \(\sqrt{28}\).

First approximation:
Answer:
Between which two integers does \(\sqrt{28}\) lie?
Since 25 < 28 < 36, we see 5 < \(\sqrt{28}\) < 6 .
In which tenth between 5 and 6 does \(\sqrt{28}\) lie?

Second approximation:

Answer:
How do we determine which interval is correct?
What if we just square the numbers 5.0, 5.1, and 5.2 and see between which two squares 28 lies? After all, we are hoping to see that 5.3 < \(\sqrt{28}\) < 5.4, in which case we should have 5.3² < 28 <5 .4². (This interval is probably not correct, but we can check!)
Provide students time to determine in which interval the number \(\sqrt{28}\) lies. Ask students to share their findings, and then continue the discussion.
Now that we know that the number \(\sqrt{28}\) lies between 5.2 and 5.3, let’s look at hundredths.

Third approximation:

Answer:

Can we be efficient? Since 5.20² = 27.04 and 5.30² = 28.09, would an interval to the left, to the middle, or to the right likely contain \(\sqrt{28}\)?
We suspect that the interval between 5.29 and 5.30 might contain \(\sqrt{28}\) because 28 is close to 28.09.
Provide students time to determine which interval the number \(\sqrt{28}\) will lie between. Ask students to share their findings, and then continue the discussion.
Now we know that the number \(\sqrt{28}\) is between 5.29 and 5.30. Let’s go one step further and examine intervals of thousandths.

Fourth approximation:

Answer:

Since 5.290² = 27.9841 and 5.300² = 28.09, where should we begin our search?
We should begin with the intervals closer to 5.290 and 5.291 because 28 is closer to 27.9841 than to 28.09.
Provide students time to determine which interval the number \(\sqrt{28}\) will lie between. Ask students to share their findings, and then finish the discussion.
The number \(\sqrt{28}\) lies between 5.291 and 5.292 because 5.291² = 27.994681 and 5.292² = 28.005264. At this point, we have a fair approximation of the value of \(\sqrt{28}\). It is between 5.291 and 5.292 on the number line:

We could continue this process of rational approximation to see that \(\sqrt{28}\) = 5.291502622….
As before, use an online calculator to show the decimal expansion of \(\sqrt{28}\). Once displayed, ask students to examine the decimal expansion for any patterns, or lack thereof
Consider going back to the Opening Exercise to determine whose approximation was the closest.
Can we conduct this work to also pin down the location of \(\sqrt{121}\) on the number line?
No need! \(\sqrt{121}\) = 11, so we know where it sits!

Eureka Math Grade 8 Module 7 Lesson 11 Exercise Answer Key

Exercise 1.
In which interval of hundredths does \(\sqrt{14}\) lie? Show your work.
Answer:
The number \(\sqrt{14}\) is between integers 3 and 4 because 9<14<16. Then, \(\sqrt{14}\) must be checked for the interval of tenths between 3 and 4. Since \(\sqrt{14}\) is closer to 4, we will begin with the interval from 3.9 to 4.0. The number \(\sqrt{14}\) is between 3.7 and 3.8 because 3.7² = 13.69 and 3.8² = 14.44. Now, we must look at the interval of hundredths between 3.7 and 3.8. Since \(\sqrt{14}\) is closer to 3.7, we will begin with the interval 3.70 to 3.71. The number \(\sqrt{14}\) is between 3.74 and 3.75 because 3.74² = 13.9876 and 3.75² = 14.0625.

Eureka Math Grade 8 Module 7 Lesson 11 Problem Set Answer Key

Question 1.
In which hundredth interval of the number line does \(\sqrt{84}\) lie?
Answer:
The number \(\sqrt{84}\) is between 9 and 10 but closer to 9. Looking at the interval of tenths, beginning with 9.0 to 9.1, the number \(\sqrt{84}\) lies between 9.1 and 9.2 because 9.1² = 82.81 and 9.2² = 84.64 but is closer to 9.2. In the interval of hundredths, the number \(\sqrt{84}\) lies between 9.16 and 9.17 because 9.16² = 83.9056 and 9.17² = 84.0889.

Question 2.
Determine the three-decimal digit approximation of the number \(\sqrt{34}\).
Answer:
The number \(\sqrt{34}\) is between 5 and 6 but closer to 6. Looking at the interval of tenths, beginning with 5.9 to 6.0, the number \(\sqrt{34}\) lies between 5.8 and 5.9 because 5.8² = 33.64 and 5.9² = 34.81 and is closer to 5.8. In the interval of hundredths, the number \(\sqrt{34}\) lies between 5.83 and 5.84 because 5.83² = 33.9889 and 5.84² = 34.1056 and is closer to 5.83. In the interval of thousandths, the number \(\sqrt{34}\) lies between 5.830 and 5.831 because 5.830² = 33.9889 and 5.831² = 34.000   561 but is closer to 5.831. Since 34 is closer to 5.831² than 5.830², then the three-decimal digit approximation of the number is 5.831.

Question 3.
Write the decimal expansion of \(\sqrt{47}\) to at least two-decimal digits.
Answer:
The number \(\sqrt{47}\) is between 6 and 7 but closer to 7 because 6²<47<7². In the interval of tenths, the number \(\sqrt{47}\) is between 6.8 and 6.9 because 6.8² = 46.24 and 6.9² = 47.61. In the interval of hundredths, the number \(\sqrt{47}\) is between 6.85 and 6.86 because 6.85² = 46.9225 and 6.86² = 47.0596. Therefore, to two-decimal digits, the number \(\sqrt{47}\) is approximately 6.85

Question 4.
Write the decimal expansion of \(\sqrt{46}\) to at least two-decimal digits.
Answer:
The number \(\sqrt{46}\) is between integers 6 and 7 because 6²<46<7². Since \(\sqrt{46}\) is closer to 7, I will start checking the tenths intervals between 6.9 and 7. \(\sqrt{46}\) is between 6.7 and 6.8 since 6.7² = 44.89 and 6.8² = 46.24. Checking the hundredths interval, \(\sqrt{46}\) is between 6.78 and 6.79 since 6.78² = 45.9684 and 6.79² = 46.1041. The two-decimal approximation \(\sqrt{46}\) is 6.78.

Question 5.
Explain how to improve the accuracy of the decimal expansion of an irrational number.
Answer:
In order to improve the accuracy of the decimal expansion of an irrational number, you must examine increasingly smaller increments on the number line. Specifically, examine increments of decreasing powers of 10. The basic inequality allows us to determine which interval a number is between. We begin by determining which two integers the number lies between and then decreasing the power of 10 to look at the interval of tenths. Again using the basic inequality, we can narrow down the approximation to a specific interval of tenths. Then, we look at the interval of hundredths and use the basic inequality to determine which interval of hundredths the number would lie between. Then, we examine the interval of thousandths. Again, the basic inequality allows us to narrow down the approximation to thousandths. The more intervals we examine, the more accurate the decimal expansion of an irrational number will be.

Question 6.
Is the number \(\sqrt{144}\) rational or irrational? Explain.
Answer:
The number \(\sqrt{144}\) is 12, a rational number.

Question 7.
Is the number \(0 . \overline{64}\) = 0.646464646… rational or irrational? Explain.
Answer:
We have seen that every number that has a repeating decimal expansion is a fraction; that is, it is a rational number. In this case, 0.646   464   646… = \(\frac{64}{99}\), and is therefore a rational number.

Question 8.
Henri computed the first 100 decimal digits of the number \(\frac{652}{541}\) and got 0.650646950092421441774491682070240295748613678373382624768946
39556377079482439926062846580406654343807763401109057301294….
He saw no repeating pattern to the decimal and so concluded that the number is irrational. Do you agree with Henri’s conclusion? If not, what would you say to Henri?
Answer:
The fraction \(\frac{352}{541}\) is certainly a rational number, and so it will have a repeating decimal expansion. One probably has to go beyond 100 decimal places to see the digits repeat.
(This decimal actually repeats after the 540th decimal place.)

Question 9.
Use a calculator to determine the decimal expansion of \(\sqrt{35}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{35}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.

Question 10.
Use a calculator to determine the decimal expansion of \(\sqrt{101}\). Does the number appear to be rational or irrational? Explain.
Based on the decimal expansion, the number \(\sqrt{101}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.

Question 11.
Use a calculator to determine the decimal expansion of \(\sqrt{7}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{7}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.

Question 12.
Use a calculator to determine the decimal expansion of \(\sqrt{8720}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{8720}\) appears to be irrational. The decimal expansion is infinite and does not appear to have a repeating pattern.

Question 13.
Use a calculator to determine the decimal expansion of \(\sqrt{17956}\). Does the number appear to be rational or irrational? Explain.
Answer:
Based on the decimal expansion, the number \(\sqrt{17956}\) is rational because it is equivalent to 134.

Question 14.
Since the number \(\frac{3}{5}\) is rational, must the number (3/5)²be rational as well? Explain.
Answer:
Yes, since \(\frac{3}{5}\) is rational it makes sense that (\(\frac{3}{5}\))²would also be rational since (\(\frac{3}{5}\))² = \(\frac{9}{25}\) is a ratio of integers.

Question 15.
If a number x is rational, must the number x² be rational as well? Explain.
Answer:
If x is rational, then we can write x = \(\frac{a}{b}\) for some integers a and b. This means that x² = \(\frac{a^{2}}{b^{2}}\) and so is necessarily rational as well.

Question 16.
Challenge: Determine the two-decimal digit approximation of the number \(\sqrt [ 3 ]{ 9 }\).
Answer:
The number \(\sqrt [ 3 ]{ 9 }\) is between integers 2 and 3 because 2³<9<3³. Since \(\sqrt [ 3 ]{ 9 }\) is closer to 2, I will start checking the tenths intervals between 2 and 3. \(\sqrt [ 3 ]{ 9 }\) is between 2 and 2.1 since 2³ = 8 and 2.1³ = 9.261. Checking the hundredths interval, \(\sqrt [ 3 ]{ 9 }\) is between 2.08 and 2.09 since 2.08³ = 8.998912 and 2.09³ = 9.129329. The two-decimal digit approximation \(\sqrt [ 3 ]{ 9 }\) is 2.08.

Eureka Math Grade 8 Module 7 Lesson 11 Exit Ticket Answer Key

Question 1.
Determine the three-decimal digit approximation of the number \(\sqrt{17}\).
Answer:
The number \(\sqrt{17}\) is between integers 4 and 5 because 16<17<25. Since \(\sqrt{17}\) is closer to 4, I will start checking the tenths intervals closer to 4. \(\sqrt{17}\) is between 4.1 and 4.2 since 4.1² = 16.81 and 4.2² = 17.64. Checking the hundredths interval, \(\sqrt{17}\) is between 4.12 and 4.13 since 4.12² = 16.9744 and 4.13² = 17.0569. Checking the thousandths interval, \(\sqrt{17}\) is between 4.123 and 4.124 since 4.123² = 16.999129 and 4.124² = 17.007376.
The three-decimal digit approximation is 4.123.

Engage NY Eureka Math 8th Grade Module 7 Lesson 22 Answer Key

Eureka Math Grade 8 Module 7 Lesson 22 Exercise Answer Key

Exercise 1.
The height of a container in the shape of a circular cone is 7.5 ft., and the radius of its base is 3 ft., as shown. What is the total volume of the cone?

Answer:
= \(\frac{1}{3}\) π3² (7.5)
= 22.5π
The volume of the cone is 22.5π ft³.

Answer:

We know that the sand (or rice or water) being poured into the cone is poured at a constant rate, but is the level of the substance in the cone rising at a constant rate? Provide evidence to support your answer.

Provide students time to construct an argument based on the data collected to show that the substance in the cone is not rising at a constant rate. Have students share their reasoning with the class. Students should be able to show that the rate of change (slope) between any two data points is not the same using calculations like
\(\frac{2-1}{0.22-0.028}\) = \(\frac{1}{0.192}\) = 5.2 and \(\frac{7-6}{9.57-6.03}\) = \(\frac{1}{3.54}\) = 0.28, or by graphing the data and showing that it is not linear.

Answer:

Close the discussion by reminding students of the demonstration at the Opening of the lesson. Ask students if the math supported their conjectures about average rate of change of the water level of the cone.

Eureka Math Grade 8 Module 7 Lesson 22 Problem Set Answer Key

Question 1.
Complete the table below for more intervals of water levels of the cone discussed in class. Then, graph the data on a coordinate plane.


Answer:

Question 2.
Complete the table below, and graph the data on a coordinate plane. Compare the graphs from Problems 1 and 2. What do you notice? If you could write a rule to describe the function of the rate of change of the water level of the cone, what might the rule include?


Answer:


The graphs are similar in shape. The rule that describes the function for the rate of change likely includes a square root. Since the graphs of functions are the graphs of certain equations where their inputs and outputs are points on a coordinate plane, it makes sense that the rule producing such a curve would be a graph of some kind of square root.

Question 3.
Describe, intuitively, the rate of change of the water level if the container being filled were a cylinder. Would we get the same results as with the cone? Why or why not? Sketch a graph of what filling the cylinder might look like, and explain how the graph relates to your answer.

Answer:
If the container being filled were a cylinder, we would see a constant rate of change in the water level because there is no narrow or wide part like there is with a cone. Therefore, we would not see the same results as we did with the cone. The rate of change would be the same over any time interval for any given height of the cylinder. The following graph demonstrates this. If a cylinder were being filled at a constant rate, the graph would be linear as shown because the water that would flow into the cylinder would be filling up the same-sized solid throughout.

Question 4.
Describe, intuitively, the rate of change if the container being filled were a sphere. Would we get the same results as with the cone? Why or why not?
Answer:
The rate of change in the water level would not be constant if the container being filled were a sphere. The water level would rise quickly at first, then slow down, and then rise quickly again because of the narrower parts of the sphere at the top and the bottom and the wider parts of the sphere around the middle. We would not get the same results as we saw with the cone, but the results would be similar in that the rate of change is nonlinear.

Eureka Math Grade 8 Module 7 Lesson 22 Exit Ticket Answer Key

Question 1.
A container in the shape of a square base pyramid has a height of 5 ft. and a base length of 5 ft., as shown. Water flows into the container (in its inverted position) at a constant rate of 4 ft³ per minute. Calculate how many minutes it would take to fill the cone at 1 ft. intervals. Organize your data in the table below.

Answer:

a. How long will it take to fill up the container?
Answer:
It will take 10.42 min. to fill up the container.

b. Show that the water level is not rising at a constant rate. Explain.
Answer:
\(\frac{2-1}{0.67-0.08}\) = \(\frac{1}{0.59}\) ≈ 1.69

\(\frac{5-4}{10.42-5.33}\) = \(\frac{1}{5.09}\) ≈ 0.2
The rate at which the water is rising is not the same for the first foot as it is for the last foot. The rate at which the water is rising in the first foot is higher than the rate at which the water is rising in the last foot.

Engage NY Eureka Math 8th Grade Module 7 Lesson 21 Answer Key

Eureka Math Grade 8 Module 7 Lesson 21 Exercise Answer Key

Exercises 1–4

Exercise 1.
a. Write an expression that can be used to find the volume of the chest shown below. Explain what each part of your expression represents. (Assume the ends of the top portion of the chest are semicircular.)

Answer:
(4 × 15.3 × 6) + \(\frac{1}{2}\) (π(2)² (15.3))
The expression (4 × 15.3 × 6) represents the volume of the prism, and \(\frac{1}{2}\) (π(2)² (15.3)) is the volume of the half – cylinder on top of the chest. Adding the volumes together will give the total volume of the chest.

b. What is the approximate volume of the chest shown above? Use 3.14 for an approximation of π. Round your final answer to the tenths place.
Answer:
The rectangular prism at the bottom has the following volume:
V = 4 × 15.3 × 6
= 367.2.

The half – cylinder top has the following volume:
V = \(\frac{1}{2}\) (π(2)² (15.3))
= \(\frac{1}{2}\) (61.2π)
= 30.6π
≈ 96.084.
367.2 + 96.084 = 463.284 ≈ 463.3
The total volume of the chest shown is approximately 463.3 ft³.

Exercise 2.
a. Write an expression for finding the volume of the figure, an ice cream cone and scoop, shown below. Explain what each part of your expression represents. (Assume the sphere just touches the base of the cone.)

Answer:
\(\frac{4}{3}\) π(1)³ + \(\frac{1}{3}\) π(1)² (3)
The expression \(\frac{4}{3}\) π(1)³ represents the volume of the sphere, and \(\frac{1}{3}\) π(1)² (3) represents the volume of the cone. The sum of those two expressions gives the total volume of the figure.

b. Assuming every part of the cone can be filled with ice cream, what is the exact and approximate volume of the cone and scoop? (Recall that exact answers are left in terms of π, and approximate answers use 3.14 for π). Round your approximate answer to the hundredths place.
Answer:
The volume of the scoop is
V = \(\frac{4}{3}\) π(1)³
= \(\frac{4}{3}\) π
≈ 4.19.

The volume of the cone is
V = \(\frac{1}{3}\) π(1)² (3)
= π
≈ 3.14.
The total volume of the cone and scoop is approximately 4.19 in³ + 3.14 in³, which is 7.33 in³. The exact volume of the cone and scoop is \(\frac{4}{3}\) π in³ + π in³ = \(\frac{7}{3}\) π in³.

Exercise 3.
a. Write an expression for finding the volume of the figure shown below. Explain what each part of your expression represents.

Answer:
(5 × 5 × 2) + π(\(\frac{1}{2}\))² (6) + \(\frac{4}{3}\) π(2.5)³
The expression (5 × 5 × 2) represents the volume of the rectangular base, π(\(\frac{1}{2}\))² (6) represents the volume of the cylinder, and \(\frac{4}{3}\) π(2.5)³ is the volume of the sphere on top. The sum of the separate volumes gives the total volume of the figure.

b. Every part of the trophy shown is solid and made out of silver. How much silver is used to produce one trophy? Give an exact and approximate answer rounded to the hundredths place.
Answer:
The volume of the rectangular base is
V = 5 × 5 × 2
= 50.

The volume of the cylinder holding up the basketball is
V = π(\(\frac{1}{2}\))² (6)
= \(\frac{1}{4}\) π(6)
= \(\frac{3}{2}\) π
≈ 4.71.

The volume of the basketball is
V = \(\frac{4}{3}\) π(2.5)³
= \(\frac{4}{3}\) π(15.625)
= \(\frac{62.5}{3}\) π
≈ 65.42.
The approximate total volume of silver needed is 50 in³ + 4.71 in³ + 65.42 in³, which is 120.13 in³.
The exact volume of the trophy is calculated as follows:
V = 50 in³ + \(\frac{3}{2}\) π in³ + \(\frac{62.5}{2}\) π in³
= 50 in³ + (\(\frac{3}{2}\) + \(\frac{62.5}{2}\))π in³
= 50 in³ + \(\frac{134}{6}\) π in³
= 50 in³ + \(\frac{67}{3}\) π in³.

The exact volume of the trophy is 50 in³ + \(\frac{67}{3}\) π in³.

Exercise 4.
Use the diagram of scoops below to answer parts (a) and (b).
a. Order the scoops from least to greatest in terms of their volumes. Each scoop is measured in inches. (Assume the third scoop is hemi – spherical.).

Answer:
The volume of the cylindrical scoop is
V = π(\(\frac{1}{2}\))² (1)
= \(\frac{1}{4}\) π.

The volume of the spherical scoop is
V = \(\frac{1}{2}\) (\(\frac{4}{3}\) π(\(\frac{1}{2}\))³)
= \(\frac{1}{2}\) (\(\frac{4}{3}\) π(\(\frac{1}{8}\)))
= \(\frac{4}{48}\) π
= \(\frac{1}{12}\) π.

The volume of the truncated cone scoop is as follows.
Let x represent the height of the portion of the cone that was removed.
\(\frac{0.5}{0.375}\) = \(\frac{x + 1}{x}\)
0.5x = 0.375(x + 1)
0.5x = 0.375x + 0.375
0.125x = 0.375
x = 3
The volume of the small cone is
V = \(\frac{1}{3}\) π(0.375)² (3)
= \(\frac{9}{64}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(0.5)² (4)
= \(\frac{1}{3}\) π.

The volume of the truncated cone is
\(\frac{1}{3}\) π – \(\frac{9}{64}\) π = (\(\frac{1}{3}\) – \(\frac{9}{64}\))π
= \(\frac{64 – 27}{192}\) π
= \(\frac{37}{192}\)π.
The three scoops have volumes of \(\frac{1}{4}\) π in³, \(\frac{1}{12}\) π in³, and \(\frac{37}{192}\)π in³. In order from least to greatest, they are \(\frac{1}{12}\) π in³, \(\frac{37}{192}\) π in³, and \(\frac{1}{4}\) π in³. Therefore, the spherical scoop is the smallest, followed by the truncated cone scoop, and lastly the cylindrical scoop.

b. How many of each scoop would be needed to add a half – cup of sugar to a cupcake mixture? (One – half cup is approximately 7 in³.) Round your answer to a whole number of scoops.
Answer:
The cylindrical scoop is \(\frac{1}{4}\) π in³, which is approximately 0.785 in³. Let x be the number of scoops needed to fill one – half cup.
0.785x = 7
x = \(\frac{7}{0.785}\)
= 8.9171…
≈ 9
It would take about 9 scoops of the cylindrical cup to fill one – half cup.
The spherical scoop is \(\frac{1}{12}\) π in³, which is approximately 0.262 in³. Let x be the number of scoops needed to fill one – half cup.
0.262x = 7
x = \(\frac{7}{0.262}\)
= 26.71755…
≈ 27
It would take about 27 scoops of the cylindrical cup to fill one – half cup.
The truncated cone scoop is \(\frac{37}{192}\) π in³, which is approximately 0.605 in³. Let x be the number of scoops needed to fill one – half cup.
0.605x = 7
x = \(\frac{7}{0.605}\)
= 11.57024…
≈ 12
It would take about 12 scoops of the cylindrical cup to fill one – half cup.

Eureka Math Grade 8 Module 7 Lesson 21 Problem Set Answer Key

Question 1.
What volume of sand is required to completely fill up the hourglass shown below? Note: 12 m is the height of the truncated cone, not the lateral length of the cone.

Answer:
Let x m represent the height of the portion of the cone that has been removed.
\(\frac{4}{9}\) = \(\frac{x}{x + 12}\)
4(x + 12) = 9x
4x + 48 = 9x
48 = 5x
\(\frac{48}{5}\) = x
9.6 = x
The volume of the removed cone is
V = \(\frac{1}{3}\) π(4)² (9.6)
= \(\frac{153.6}{3}\) π.

The volume of the cone is
V = \(\frac{1}{3}\) π(9)² (21.6)
= \(\frac{1749.6}{2}\) π.

The volume of one truncated cone is
\(\frac{1749.6}{3}\) π – \(\frac{153.6}{3}\) π = (\(\frac{1749.6}{3}\) – \(\frac{153.6}{3}\))π
= \(\frac{1596}{3}\) π
= 532 π.
The volume of sand needed to fill the hourglass is 1064π m³.

Question 2.
a. Write an expression for finding the volume of the prism with the pyramid portion removed. Explain what each part of your expression represents.
(12)³ – 1/3 (12)³

Answer:
The expression (12)³ represents the volume of the cube, and \(\frac{1}{3}\) (12)³ represents the volume of the pyramid. Since the pyramid’s volume is being removed from the cube, we subtract the volume of the pyramid from the volume of the cube.

b. What is the volume of the prism shown above with the pyramid portion removed?
Answer:
The volume of the prism is
V = (12)³
= 1728.

The volume of the pyramid is
V = \(\frac{1}{3}\) (1728)
= 576.
The volume of the prism with the pyramid removed is 1,152 units³.

Question 3.
a. Write an expression for finding the volume of the funnel shown to the right. Explain what each part of your expression represents.

Answer:
π(4)² (14) + (\(\frac{1}{3}\) π(8)² (x + 16) – \(\frac{1}{3}\) π(4)² x)
The expression π(4)² (14) represents the volume of the cylinder. The expression (\(\frac{1}{3}\) π(8)² (x + 16) – \(\frac{1}{3}\) π(4)² x) represents the volume of the truncated cone.
The x represents the unknown height of the smaller cone that has been removed. When the volume of the cylinder is added to the volume of the truncated cone, then we will have the volume of the funnel shown.

b. Determine the exact volume of the funnel.
Answer:
The volume of the cylinder is
V = π(4)² (14)
= 224π.
Let x cm be the height of the cone that has been removed.
\(\frac{4}{8}\) = \(\frac{x}{x + 16}\)
4(x + 16) = 8x
4x + 64 = 8x
64 = 4x
16 = x
The volume of the small cone is
V = \(\frac{1}{3}\) π(4)² (16)
= \(\frac{256}{3}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(8)² (32)
= \(\frac{2048}{2}\) π.

The volume of the truncated cone is
\(\frac{2048}{3}\) π – \(\frac{256}{3}\) π = (\(\frac{2048}{3}\) – \(\frac{256}{3}\))π
= \(\frac{1792}{3}\) π.
The volume of the funnel is 224π cm³ + \(\frac{1792}{3}\) π cm³, which is 821 \(\frac{1}{3}\) π cm³.

Question 4.
What is the approximate volume of the rectangular prism with a cylindrical hole shown below? Use 3.14 for π. Round your answer to the tenths place.
The volume of the prism is

Answer:
V = (8.5)(6)(21.25)
= 1083.75.
The volume of the cylinder is
V = π(2.25)² (6)
= 30.375π
≈ 95.3775.
The volume of the prism with the cylindrical hole is approximately 988.4 in³, because 1083.75 in³ – 95.3775 in³ = 988.3725 in³.

Question 5.
A layered cake is being made to celebrate the end of the school year. What is the exact total volume of the cake shown below?

Answer:
The bottom layer’s volume is
V = (8)² π(4)
= 256π.

The middle layer’s volume is
V = (4)² π(4)
= 64π.

The top layer’s volume is
V = (2)² π(4)
= 16π.

The total volume of the cake is
256π in³ + 64π in³ + 16π in³ = (256 + 64 + 16)π in³ = 336π in³.

Eureka Math Grade 8 Module 7 Lesson 21 Exit Ticket Answer Key

Question 1.
Andrew bought a new pencil like the one shown below on the left. He used the pencil every day in his math class for a week, and now his pencil looks like the one shown below on the right. How much of the pencil, in terms of volume, did he use?
Note: Figures are not drawn to scale.

Answer:
V = π(0.375)² (8)
V = 1.125π
Volume of the pencil at the beginning of the week was 1.125π in³.
V = π(0.375)² (2.5)
V ≈ 0.3515π
The volume of the cylindrical part of the pencil is approximately 0.3515π in³.
V = \(\frac{1}{3}\) π(0.375)² (0.75)
V ≈ \(\frac{0.1054}{3}\) π
V ≈ 0.0351π
The volume of the cone part of the pencil is approximately 0.0351π in³.
0.3515π + 0.0351π = (0.3515 + 0.0351)π = 0.3866π
The total volume of the pencil after a week is approximately 0.3866π in³.
1.125π – 0.3866π = (1.125 – 0.3866)π = 0.7384π
In one week, Andrew used approximately 0.7384π in³ of the pencil’s total volume.

Elementary School Eureka Math Answers

• Engageny Eureka Math Pre K Answer Key
• Engageny Eureka Math Kindergarten Answer Key
• Engageny Eureka Math Grade 1 Answer Key
• Engageny Eureka Math Grade 2 Answer Key
• Engageny Eureka Math Grade 3 Answer Key
• Engageny Eureka Math Grade 4 Answer Key

Intermediate School Eureka Math Answers

• Engageny Eureka Math Grade 5 Answer Key
• Engageny Eureka Math Grade 6 Answer Key
• Engageny Eureka Math Grade 7 Answer Key
• Engageny Eureka Math Grade 8 Answer Key

High School/Commencement Level Eureka Math Answers

• Engageny Eureka Math Algebra 1 Answer Key
• Engageny Eureka Math Geometry Answer Key
• Engageny Eureka Math Algebra 2 Answer Key
• Engageny Precalculus and Advanced Topics Answer Key

Engage NY Eureka Math 8th Grade Module 7 Lesson 10 Answer Key

Eureka Math Grade 8 Module 7 Lesson 10 Example Answer Key

Example 1.
There is a fraction with an infinite decimal expansion of \(0 . \overline{81}\). Find the fraction.
Answer:
→ We want to find the fraction that is equal to the infinite decimal \(0 . \overline{81}\). Why might we want to write an infinite decimal as a fraction?
Maybe we want to use \(0 . \overline{81}\) in some calculation. It is unclear how to do arithmetic with infinitely long decimals. But if we recognize the decimal as a fraction, then we can do the arithmetic with
the fraction.

→ Let’s start by giving the decimal a name. Let x = \(0 . \overline{81}\) = 0.8181818181…. Any thoughts on what we might do to this number x? (Of course, our previous discussion was probably a hint!)

→ Allow students time to work in pairs or small groups to attempt to find the fraction equal to \(0 . \overline{81}\). Students should guess that multiplying x by some powers of 10 might yield something informative.
Let’s try multiplying x = \(0 . \overline{81}\) by some powers of 10.
x = 0.8181818181…
10x = 8.1818181…
100x = 81.81818181…
1000x = 818.1818181…
(Perhaps have students write x as \(\frac{8}{10} + \frac{1}{100} + \frac{8}{1000} + \frac{1}{10000} + \cdots\) to help with this process.)
Ask students to pause over the expression 100x. Can they observe anything interesting about it?

We see
100x = 81.81818181… = 81 + 0.818181… = 81 + x.
This now gives an equation for x students can solve.
100x = 81 + x
100x – x = 81 + x – x
(100 – 1)x = 81
99x = 81
\(\frac{99x}{99}\) = \(\frac{81}{99}\)
x = \(\frac{81}{99}\)
x = \(\frac{9}{11}\)
Therefore, the repeating decimal \(0 . \overline{81}\) = \(\frac{9}{11}\).
Have students use calculators to verify that this is correct.

Example 2.
Could it be that \(2.13 \overline{8}\) is also a fraction?
Answer:
→ We want to see if there is a fraction that is equal to the infinite decimal \(2.13 \overline{8}\). Notice that this time there is just one digit that repeats, but it is three places to the right of the decimal point.
→ Let’s multiply x = \(2.13 \overline{8}\) by various powers of 10 and see if any of the results seem helpful.
x = 2.138888…
10x = 21.38888…
100x = 213.8888…
1000x = 2138.888…
Do any of these seem helpful?
→ Students might not have any direct thoughts in response to this.
→ What if I asked as a separate question: Is 0.8888… the decimal expansion of a fraction? If knowing that 0.888… is a fraction, would any one of the equations we have then be of use to us?
If we know that 0.888… = \(\frac{a}{b}\), then we would see that 100x = 213 + 0.888… = 213 + \(\frac{a}{b}\). We could work out what x is from that.
Okay. As a side problem: Is 0.8888… the decimal expansion of some fraction?
Let y = \(0. \overline{8}\).
y = \(0. \overline{8}\)
10y = \(8. \overline{8}\)
10y = 8 + \(0. \overline{8}\)
10y = 8 + y
10y – y = 8 + y – y
9y = 8

\(\frac{9y}{9}\) = \(\frac{8}{9}\)
y = \(\frac{8}{9}\)
Now that we know that \(0. \overline{8}\) = \(\frac{8}{9}\), we will go back to our original problem.
100x = 213 + \(0. \overline{8}\)
100x = 213 + \(\frac{8}{9}\)
100x = \(\frac{213.9}{9}\) + \(\frac{8}{9}\)
100x = \(\frac{213.9 + 8}{9}\)
100x = \(\frac{1925}{9}\)
\(\frac{1}{100}\) (100x) = \(\frac{1}{100}\) (\(\frac{1925}{9}\))
x = \(\frac{1925}{900}\)
x = \(\frac{77}{36}\)
We can see that this technique applies to any infinite repeating decimal, even if there is a delay before the repeat begins, to show that every real number that has a repeating decimal expansion is, for sure, a rational number, that is, can be expressed as a fraction. And, conversely, we saw in Lesson 8 that every rational number has a repeating decimal expansion. So we have proven that the set of real numbers with repeating decimal expansions precisely matches the set of all rational numbers. Any number that has an infinitely long decimal expansion with no repeating pattern cannot be rational; that is, it must be an irrational number.

Eureka Math Grade 8 Module 7 Lesson 10 Exercise Answer Key

Exercises 1–2

Exercise 1.
There is a fraction with an infinite decimal expansion of \(0 . \overline{123}\). Let x = \(0 . \overline{123}\).
a. Explain why looking at 1000x helps us find the fractional representation of x.
Answer:
We have x = 0.123123123…, and we see that 1000x = 123.123123123…. This is the same as 123 + 0.123123123…, which is 123 + x. So we have the equation 1000x = 123 + x, which we can use to solve for x.

b. What is x as a fraction?
Answer:
1000x – x = 123 + x – x
999x = 123
\(\frac{999x}{999}\) = \(\frac{123}{999}\)
x = \(\frac{123}{999}\)
x = \(\frac{41}{333}\)

c. Is your answer reasonable? Check your answer using a calculator.
Answer:
Yes, my answer is reasonable and correct. It is reasonable because the denominator cannot be expressed as a product of 2’s and 5’s; therefore, I know that the fraction must represent an infinite decimal. It is also reasonable because the decimal value is closer to 0 than to 0.5, and the fraction \(\frac{41}{333}\) is also closer to 0 than to \(\frac{1}{2}\). It is correct because the division of \(\frac{41}{333}\) using a calculator is 0.123123….

Exercise 2.
There is a fraction with a decimal expansion of 0.4 ̅. Find the fraction, and check your answer using a calculator.
Answer:
Let x = \(0. \overline{4}\)
x = \(0 . \overline{4}\)
10x = (10)\(0 . \overline{4}\)
10x = \(4 . \overline{4}\)
10x = 4 + x
10x – x = 4 + x – x
9x = 4
\(\frac{9x}{9}\) = \(\frac{4}{9}\)
x = \(\frac{4}{9}\)

Exercises 3–4

Exercise 3.
Find the fraction equal to \(1.6 \overline{23}\). Check your answer using a calculator.
Answer:

Exercise 4.
Find the fraction equal to \(2.9 \overline{60}\). Check your answer using a calculator.
Answer:

Eureka Math Grade 8 Module 7 Lesson 10 Problem Set Answer Key

Question 1.
a. Let x = \(0 . \overline{631}\). Explain why multiplying both sides of this equation by 10³ will help us determine the fractional representation of x.
Answer:
When we multiply both sides of the equation by 10³, on the right side we will have 631.631631…. This is helpful because we will now see this as 631 + x.

b. What fraction is x?
Answer:
1000x = \(631 . \overline{631}\)
1000x = 631 + 0.631631…
1000x = 631 + x
1000x – x = 631 + x – x
999x = 631
\(\frac{999x}{999}\) = \(\frac{631}{999}\)
x = \(\frac{631}{999}\)

c. Is your answer reasonable? Check your answer using a calculator.
Answer:
Yes, my answer is reasonable and correct. It is reasonable because the denominator cannot be expressed as a product of 2’s and 5’s; therefore, I know that the fraction must represent an infinite decimal. Also, the number 0.631 is closer to 0.5 than 1, and the fraction is also closer to \(\frac{1}{2}\) than 1. It is correct because the division of \(\frac{631}{999}\) using the calculator is 0.631631….

Question 2.
Find the fraction equal to \(3.40 \overline{8}\). Check your answer using a calculator.
Answer:

Question 3.
Find the fraction equal to \(0 . \overline{5923}\). Check your answer using a calculator.
Answer:
Let x = \(0 . \overline{5923}\).
x = \(0 . \overline{5923}\)
10⁴ x = 10⁴ (\(0 . \overline{5923}\) )
10000x = \(5923 . \overline{5923}\)
10000x = 5923 + x
10000x – x = 5923 + x – x
9999x = 5923
\(\frac{9999x}{9999}\) = \(\frac{5923}{9999}\)
x = \(\frac{5923}{9999}\)

Question 4.
Find the fraction equal to \(2.3 \overline{82}\). Check your answer using a calculator.
Answer:

Question 5.
Find the fraction equal to \(0 . \overline{714285}\). Check your answer using a calculator.
Answer:
Let x = \(0 . \overline{714285}\).
x = \(0 . \overline{714285}\)
10⁶ x = 10⁶ (\(0 . \overline{714285}\))
1 000 000x = \(714825 . \overline{714285}\)
1 000 000x = 714 285 + x
1 000000x – x = 714 285 + x – x
999 999x = 714 285
\(\frac{999999x}{999999}\) = \(\frac{714285}{9999999}\)
x = \(\frac{714285}{9999999}\)
x = \(\frac{5}{7}\)

Question 6.
Explain why an infinite decimal that is not a repeating decimal cannot be rational.
Answer:
We proved in Lesson 8 that the decimal expansion of any rational number must fall into a repeating cycle. (This came from performing the long division algorithm.) So any number that has an infinitely long decimal expansion that does not repeat cannot be a rational number; that is, it must be irrational.

Question 7.
In a previous lesson, we were convinced that it is acceptable to write \(0 . \overline{9}\) = 1. Use what you learned today to show that it is true.
Answer:
Let x = \(0 . \overline{9}\)
x = \(0 . \overline{9}\)
10x = 10(\(0 . \overline{9}\))
10x = \(9 . \overline{9}\)
10x = 9 + x
10x – x = 9 + x – x
9x = 9
\(\frac{9x}{9}\) = \(\frac{9}{9}\)
x = \(\frac{9}{9}\)
x = 1

Question 8.
Examine the following repeating infinite decimals and their fraction equivalents. What do you notice? Why do you think what you observed is true?

Answer:
In each case, the fraction that represents the infinite decimal has a numerator that is exactly the repeating part of the decimal and a denominator comprised of 9’s. Specifically, the denominator has the same number of digits of 9’s as the number of digits that repeat. For example, \(0 . \overline{81}\)has two repeating decimal digits, and the denominator has two 9’s.
The pattern is even true for \(0 . \overline{9}\). According to the pattern, this decimal equals \(\frac{9}{9}\), which is 1.

Eureka Math Grade 8 Module 7 Lesson 10 Exit Ticket Answer Key

Question 1.
Find the fraction equal to \(0 . \overline{534}\).
Answer:
Let x = \(0 . \overline{534}\).
x = \(0 . \overline{534}\)
10³ x = 10³ (\(0 . \overline{534}\) )
1000x = \(534 . \overline{534}\)
1000x = 534 + x
1000x – x = 534 + x – x
999x = 534
\(\frac{999x}{999}\) = \(\frac{534}{999}\)
x = \(\frac{534}{999}\)
x = \(\frac{178}{333}\)
\(0 . \overline{534}\)̅ = \(\frac{178}{333}\)

Question 2.
Find the fraction equal to \(3 . 0\overline{15}\).
Answer:

Engage NY Eureka Math 8th Grade Module 7 Lesson 6 Answer Key

Eureka Math Grade 8 Module 7 Lesson 6 Example Answer Key

Example 1.
Consider the fraction \(\frac{5}{8}\). Write an equivalent form of this fraction with a denominator that is a power of 10, and write the decimal expansion of this fraction.
Answer:
Consider the fraction \(\frac{5}{8}\). Is it equivalent to one with a denominator that is a power of 10? How do you know?
Yes. The fraction 5/8 has denominator 8 and so has factors that are products of 2’s only.
Write \(\frac{5}{8}\)as an equivalent fraction with a denominator that is a power of 10.

We have \(\frac{5}{8}\) = \(\frac{5}{2 \times 2 \times 2} = \frac{5 \times 5 \times 5 \times 5}{2 \times 2 \times 2 \times 5 \times 5 \times 5} = \frac{625}{10 \times 10 \times 10} = \frac{625}{10^{3}}\)
What is \(\frac{5}{8}\) as a finite decimal?
\(\frac{5}{8}\) = \(\frac{625}{1000}\) = 0.625

Example 2.
Consider the fraction \(\frac{17}{125}\). Is it equal to a finite or an infinite decimal? How do you know?
Answer:
→ Let’s consider the fraction \(\frac{17}{125}\). We want the decimal value of this number. Will it be a finite or an infinite decimal? How do you know?
→ We know that the fraction \(\frac{17}{125}\) is equal to a finite decimal because the denominator 125 is a product of 5’s, specifically, 5³, and so we can write the fraction as one with a denominator that is a power of 10.

→ What will we need to multiply 5³ by to obtain a power of 10?
We will need to multiply by 2³. Then, 5³ × 2³ = (5 × 2)³ = 〖10〗³.
→ Write \(\frac{17}{125}\) or its equivalent 17/5³ as a finite decimal.
\(\frac{17}{125}\) = \(\frac{17}{5^{3}} = \frac{17 \times 2^{3}}{5^{3} \times 2^{3}} = \frac{17 \times 8}{(5 \times 2)^{3}} = \frac{136}{10^{3}}\) = 0.136
(If the above two points are too challenging for some students, have them write out:
\(\frac{17}{125}\) = \(\frac{17}{5 \times 5 \times 5} = \frac{17 \times 2 \times 2 \times 2}{5 \times 5 \times 5 \times 2 \times 2 \times 2}\) = \(\frac{136}{1000}\) = 0.136.)

Example 3.
Will the decimal expansion of \(\frac{7}{80}\) be finite or infinite? If it is finite, find it.
Answer:
→ Will \(\frac{7}{80}\) have a finite or infinite decimal expansion?
We know that the fraction \(\frac{7}{80}\) is equal to a finite decimal because the denominator 80 is a product of 2’s and 5’s. Specifically, 2⁴ × 5. This means the fraction is equivalent to one with a denominator that is a power of 10.

→ What will we need to multiply 2⁴ × 5 by so that it is equal to (2 × 5)ⁿ = 10ⁿ for some n?
We will need to multiply by 5³ so that 2⁴ × 5⁴ = (2 × 5)⁴ = 10⁴.

→ Begin with\(\frac{7}{80}\) or \(\frac{7}{2^{4} \times 5}\). Use what you know about equivalent fractions to rewrite \(\frac{7}{80}\) in the form \(\frac{k}{10^{n}}\) and then write the decimal form of the fraction.
\(\frac{7}{80}\) = \(\frac{7}{2^{4} \times 5} = \frac{7 \times 5^{3}}{2^{4} \times 5 \times 5^{3}} = \frac{7 \times 125}{(2 \times 5)^{4}} = \frac{875}{10^{4}}\) = 0.0875

Example 4.
Will the decimal expansion of \(\frac{3}{160}\) be finite or infinite? If it is finite, find it.
Answer:
→ Will \(\frac{3}{160}\) have a finite or infinite decimal expansion?
We know that the fraction \(\frac{3}{160}\) is equal to a finite decimal because the denominator 160 is a product of 2’s and 5’s. Specifically, 2⁵ × 5. This means the fraction is equivalent to one with a denominator that is a power of 10.

→ What will we need to multiply 2⁵ × 5 by so that it is equal to (2 × 5)ⁿ = 10ⁿ for some n?
We will need to multiply by 5⁴ so that 2⁵ × 5⁵ = (2 × 5)⁵ = 10⁵.
Begin with \(\frac{3}{160}\) or \(\frac{3}{2^{5} \times 5}\). Use what you know about equivalent fractions to rewrite \(\frac{3}{160}\) in the form \(\frac{k}{10^{n}}\) and then write the decimal form of the fraction.
\(\frac{3}{160}\) = \(\frac{3}{2^{5} \times 5}=\frac{3 \times 5^{4}}{2^{5} \times 5 \times 5^{4}}=\frac{3 \times 625}{(2 \times 5)^{5}}=\frac{1875}{10^{5}}\) = 0.01875

Eureka Math Grade 8 Module 7 Lesson 6 Exercise Answer Key

Opening Exercise
a. Use long division to determine the decimal expansion of \(\frac{54}{20}\).
Answer:
\(\frac{54}{20}\) = 2.7

b. Use long division to determine the decimal expansion of \(\frac{7}{8}\).
Answer:
\(\frac{7}{8}\) = 0.875

c. Use long division to determine the decimal expansion of \(\frac{8}{9}\).
Answer:
\(\frac{8}{9}\) = 0.8888 “…”

d. Use long division to determine the decimal expansion of \(\frac{22}{7}\).
Answer:
\(\frac{22}{7}\) = 3.142857 “…”

e. What do you notice about the decimal expansions of parts (a) and (b) compared to the decimal expansions of parts (c) and (d)?
Answer:
The decimal expansions of parts (a) and (b) ended. That is, when I did the long division, I was able to stop after a few steps. That was different from the work I had to do in parts (c) and (d). In part (c), I noticed that the same number kept coming up in the steps of the division, but it kept going on. In part (d), when I did the long division, it did not end. I stopped dividing after I found a few decimal digits of the decimal expansion.

Exercises 1–5
You may use a calculator, but show your steps for each problem.

Exercise 1.
Consider the fraction \(\frac{3}{8}\) .
a. Write the denominator as a product of 2’s and/or 5’s. Explain why this way of rewriting the denominator helps to find the decimal representation of \(\frac{3}{8}\) .
Answer:
The denominator is equal to 2³. It is helpful to know that 8 = 2³ because it shows how many factors of 5 will be needed to multiply the numerator and denominator by so that an equivalent fraction is produced with a denominator that is a multiple of 10. When the denominator is a multiple of 10, the fraction can easily be written as a decimal using what I know about place value.

b. Find the decimal representation of \(\frac{3}{8}\). Explain why your answer is reasonable.
Answer:
\(\frac{3}{8}\) = \(\frac{3}{2^{3}}=\frac{3 \times 5^{3}}{2^{3} \times 5^{3}}=\frac{375}{10^{3}}\) = 0.375
The answer is reasonable because the decimal value, 0.375, is less than \(\frac{1}{2}\), just like the fraction \(\frac{3}{8}\).

Exercise 2.
Find the first four places of the decimal expansion of the fraction \(\frac{43}{64}\).
Answer:
The denominator is equal to 2⁶.
\(\frac{43}{64}\) = \(\frac{43}{2^{6}}=\frac{43 \times 5^{6}}{2^{6} \times 5^{6}}=\frac{671875}{10^{6}}\) = 0.671875
The decimal expansion to the first four decimal places is 0.6718.

Exercise 3.
Find the first four places of the decimal expansion of the fraction \(\frac{29}{125}\).
Answer:
The denominator is equal to 5³.
\(\frac{29}{125}\) = \(\frac{29}{5^{3}} = \frac{29 \times 2^{3}}{5^{3} \times 2^{3}} = \frac{232}{10^{3}}\) = 0.232
The decimal expansion to the first four decimal places is 0.2320.

Exercise 4.
Find the first four decimal places of the decimal expansion of the fraction \(\frac{19}{34}\).
Answer:
Using long division, the decimal expansion to the first four places is 0.5588….

Exercise 5.
Identify the type of decimal expansion for each of the numbers in Exercises 1–4 as finite or infinite. Explain why their decimal expansion is such.
We know that the number \(\frac{7}{8}\) had a finite decimal expansion because the denominator 8 is a product of 2’s and so is equivalent to a fraction with a denominator that is a power of 10. We know that the number \(\frac{43}{64}\) had a finite decimal expansion because the denominator 64 is a product of 2’s and so is equivalent to a fraction with a denominator that is a power of 10. We know that the number \(\frac{29}{125}\) had a finite decimal expansion because the denominator 125 is a product of 5’s and so is equivalent to a fraction with a denominator that is a power of 10. We know that the number \(\frac{19}{34}\) had an infinite decimal expansion because the denominator was not a product of 2’s or 5’s; it had a factor of 17 and so is not equivalent to a fraction with a denominator that is a power of 10.

Exercises 6–8
You may use a calculator, but show your steps for each problem.

Exercise 6.
Convert the fraction \(\frac{37}{40}\) to a decimal.
a. Write the denominator as a product of 2’s and/or 5’s. Explain why this way of rewriting the denominator helps to find the decimal representation of \(\frac{37}{40}\).
Answer:
The denominator is equal to 2³ × 5. It is helpful to know that 40 is equal to 2³ × 5 because it shows by how many factors of 5 the numerator and denominator will need to be multiplied to produce an equivalent fraction with a denominator that is a power of 10. When the denominator is a power of 10, the fraction can easily be written as a decimal using what I know about place value.

b. Find the decimal representation of \(\frac{37}{40}\). Explain why your answer is reasonable.
Answer:
\(\frac{37}{40}\) = \(\frac{37}{2^{3} \times 5} = \frac{37 \times 5^{2}}{2^{3} \times 5 \times 5^{2}} = \frac{925}{10^{3}}\) = 0.925
The answer is reasonable because the decimal value, 0.925, is less than 1, just like the fraction 37/40. Also, it is reasonable and correct because the fraction \(\frac{925}{1000}\) = \(\frac{37}{40}\); therefore, it has the decimal expansion 0.925.

Exercise 7.
Convert the fraction \(\frac{3}{250}\) to a decimal.
Answer:
The denominator is equal to 2 × 5³.
\(\frac{3}{250}\) = \(\frac{3}{2 \times 5^{3}} = \frac{3 \times 2^{2}}{2 \times 2^{2} \times 5^{3}} = \frac{12}{10^{3}}\) = 0.012

Exercise 8.
Convert the fraction \(\frac{7}{1250}\) to a decimal.
Answer:
The denominator is equal to 2 × 5⁴.
\(\frac{7}{1250}\) = \(\frac{7}{2 \times 5^{4}} = \frac{7 \times 2^{3}}{2 \times 2^{3} \times 5^{4}} = \frac{56}{10^{4}}\) = 0.0056

Eureka Math Grade 8 Module 7 Lesson 6 Problem Set Answer Key

Convert each fraction given to a finite decimal, if possible. If the fraction cannot be written as a finite decimal, then state how you know. You may use a calculator, but show your steps for each problem.
Question 1.
\(\frac{2}{32}\)
The fraction \(\frac{2}{32}\) simplifies to \(\frac{1}{16}\).
The denominator is equal to 2⁴.
\(\frac{1}{16}\) = \(\frac{1}{2^{4}} = \frac{1 \times 5^{4}}{2^{4} \times 5^{4}} = \frac{625}{10^{4}}\) = 0.0625

Question 2.
\(\frac{99}{125}\)
Answer:
The denominator is equal to 5³.
\(\frac{99}{125}\) = \(\frac{99}{125}\) = 0.792

Question 3.
\(\frac{15}{128}\)
The denominator is equal to 2⁷.
\(\frac{15}{128}\) = \(\frac{15}{128}\) = 0.1171875

Question 4.
\(\frac{8}{15}\)
Answer:
The fraction \(\frac{8}{15}\) is not a finite decimal because the denominator is equal to 3 × 5. Since the denominator cannot be expressed as a product of 2’s and 5’s, then \(\frac{8}{15}\) is not a finite decimal.

Question 5.
\(\frac{3}{28}\)
Answer:
The fraction \(\frac{3}{28}\) is not a finite decimal because the denominator is equal to 2² × 7. Since the denominator cannot be expressed as a product of 2’s and 5’s, then \(\frac{3}{28}\) is not a finite decimal.

Question 6.
\(\frac{13}{400}\)
Answer:
The denominator is equal to 2⁴ × 5².
\(\frac{13}{400}\) = \(\frac{13}{2^{4} \times 5^{2}} = \frac{13 \times 5^{2}}{2^{4} \times 5^{2} \times 5^{2}} = \frac{325}{10^{4}}\) = 0.0325

Question 7.
\(\frac{5}{64}\)
Answer:
The denominator is equal to 2⁶.
\(\frac{5}{64}\) = \(\frac{5}{2^{6}} = \frac{5 \times 5^{6}}{2^{6} \times 5^{6}} = \frac{78125}{10^{6}}\) = 0.078125

Question 8.
\(\frac{15}{35}\)
Answer:
The fraction \(\frac{15}{35}\) reduces to \(\frac{3}{7}\). The denominator 7 cannot be expressed as a product of 2’s and 5’s. Therefore, \(\frac{3}{7}\) is not a finite decimal.

Question 9.
\(\frac{199}{250}\)
Answer:
The denominator is equal to 2 × 5³.
\(\frac{199}{250}\) = \(\frac{199}{2 \times 5^{3}} = \frac{199 \times 2^{2}}{2 \times 2^{2} \times 5^{3}} = \frac{796}{10^{3}}\) = 0.796

Question 10.
\(\frac{219}{625}\)
Answer:
The denominator is equal to 5⁴.
\(\frac{219}{625}\) = \(\frac{219}{5^{4}} = \frac{219 \times 2^{4}}{2^{4} \times 5^{4}} = \frac{3504}{10^{4}}\) = 0.3504

Eureka Math Grade 8 Module 7 Lesson 6 Exit Ticket Answer Key

Convert each fraction to a finite decimal if possible. If the fraction cannot be written as a finite decimal, then state how you know. You may use a calculator, but show your steps for each problem.
Question 1.
\(\frac{9}{16}\)
Answer:
The denominator is equal to 2⁴.
\(\frac{9}{16}\) = \(\frac{9}{2^{4}} = \frac{9 \times 5^{4}}{2^{4} \times 5^{4}} = \frac{9 \times 625}{10^{4}} = \frac{5625}{10^{4}}\) = 0.5625

Question 2.
\(\frac{8}{125}\)
Answer:
The denominator is equal to 5³.
\(\frac{8}{125}\) = \(\frac{8}{5^{3}} = \frac{8 \times 2^{3}}{5^{3} \times 2^{3}} = \frac{8 \times 8}{10^{3}} = \frac{64}{10^{3}}\) = 0.064

Question 3.
\(\frac{4}{15}\)
Answer:
The fraction \(\frac{4}{15}\) is not a finite decimal because the denominator is equal to 5 × 3. Since the denominator cannot be expressed as a product of 2’s and 5’s, then \(\frac{4}{15}\) is not a finite decimal.

Question 4.
\(\frac{1}{200}\)
Answer:
The denominator is equal to 2³ × 5².
\(\frac{1}{200}\) = \(\frac{1}{2^{3} \times 5^{2}} = \frac{1 \times 5}{2^{3} \times 5^{2} \times 5} = \frac{5}{2^{3} \times 5^{3}} = \frac{5}{10^{3}}\) = 0.005

Engage NY Eureka Math 8th Grade Module 7 Lesson 9 Answer Key

Eureka Math Grade 8 Module 7 Lesson 9 Exercise Answer Key

Opening Exercise
a. Compute the decimal expansions of \(\frac{5}{6}\) and \(\frac{7}{9}\).
Answer:
\(\frac{5}{6}\) = 0.8333… and \(\frac{7}{9}\) = 0.7777…

b. What is \(\frac{5}{6}\) + \(\frac{7}{9}\) as a fraction? What is the decimal expansion of this fraction?
Answer:
\(\frac{5}{6}\) + \(\frac{7}{9}\) = \(\frac{15 + 14}{18}\) = \(\frac{29}{18}\)
\(\frac{29}{18}\) = 1.61111″…”

c. What is \(\frac{5}{6}\) × \(\frac{7}{9}\) as a fraction? According to a calculator, what is the decimal expansion of the answer?
Answer:
\(\frac{5}{6}\) × \(\frac{7}{9}\) = \(\frac{35}{54}\) = 0.648 148 148 1″…”

d. If you were given just the decimal expansions of \(\frac{5}{6}\) and \(\frac{7}{9}\), without knowing which fractions produced them, do you think you could easily add the two decimals to find the decimal expansion of their sum? Could you easily multiply the two decimals to find the decimal expansion of their product?
Answer:
No. To add 0.8333… and 0.777…, we need to start by adding together their rightmost digits. But these decimals are infinitely long, and there are no rightmost digits. It is not clear how we can start the addition.
Thinking about how to multiply the two decimals, 0.8333… × 0.77777…, is even more confusing!

Exercise 1.
Two irrational numbers x and y have infinite decimal expansions that begin 0.67035267… for x and 0.84991341… for y.
a. Explain why 0.670 is an approximation for x with an error of less than one thousandth. Explain why 0.849 is an approximation for y with an error of less than one thousandth.
Answer:
The difference between 0.670 and 0.67035267… is 0.00035267…, which is less than 0.001, a thousandth.
The difference between 0.849 and 0.84991341… is 0.00091341…, which is less than 0.001, a thousandth.

b. Using the approximations given in part (a), what is an approximate value for x + y, for x × y, and for x² + 7y²?
Answer:
x + y is approximately 1.519 because 0.670 + 0.849 = 1.519.
x × y is approximately 0.56883 because 0.670 × 0.849 = 0.56883.
x² + 7y² is approximately 5.494507 because (0.670)² + 7(0.849)² = 5.494 507.

c. Repeat part (b), but use approximations for x and y that have errors less than \(\frac{1}{10^{5}}\).
Answer:
We want the error in the approximation to be less than 0.00001.
If we approximate x by truncating to five decimal places, that is, as 0.67035, then the error is 0.00000267…, which is indeed less than 0.00001.
Truncating y to five decimal places, that is, as 0.84991, gives an error of 0.00000341…, which is indeed less than 0.00001.
Now:
x + y is approximately 1.52026 because 0.67035 + 0.84991 = 1.52026.
x × y is approximately 0.5697371685 because 0.67035 × 0.84991 = 0.5697371685.
x² + 7y² is approximately 5.505798179 because (0.67035)² + 7(0.84991)² = 5.505798179.

Exercise 2.
Two real numbers have decimal expansions that begin with the following:
x = 0.1538461…
y = 0.3076923…
a. Using approximations for x and y that are accurate within a measure of \(\frac{1}{10^{3}}\), find approximate values for x + y and y-2x.
Answer:
Using x ≈ 0.153 and y ≈ 0.307, we obtain x + y ≈ 0.460 and y-2x ≈ 0.001.

b. Using approximations for x and y that are accurate within a measure of \(\frac{1}{10^{7}}\), find approximate values for x + y and y-2x.
Answer:
Using x ≈ 0.1538461 and y ≈ 0.3076923, we obtain x + y ≈ 0.4615384 and y-2x ≈ 0.0000001.

c. We now reveal that x = \(\frac{2}{13}\) and y = \(\frac{4}{13}\). How accurate is your approximate value to y-2x from part (a)? From part (b)?
Answer:
The error in part (a) is 0.001. The error in part (b) is 0.0000001.

d. Compute the first seven decimal places of \(\frac{6}{13}\). How accurate is your approximate value to x + y from part (a)? From part (b)?
Answer:
\(\frac{6}{13}\) = 0.4615384…
The error in part (a) is 0.4615384…-0.460 = 0.0015384…, which is less than 0.01.
Our approximate answer in part (b) and the exact answer match in the first seven decimal places. There is likely a mismatch from the eighth decimal place onward. This means that the error is no larger than 0.0000001, or \(\frac{1}{10^{7}}\).

Eureka Math Grade 8 Module 7 Lesson 9 Problem Set Answer Key

Question 1.
Two irrational numbers x and y have infinite decimal expansions that begin 0.3338117… for x and 0.9769112… for y.
a. Explain why 0.33 is an approximation for x with an error of less than one hundredth. Explain why 0.97 is an approximation for y with an error of less than one hundredth.
Answer:
The difference between 0.33 and 0.3338117… is 0.0038117…, which is less than 0.01, a hundredth.
The difference between 0.97 and 0.9769112… is 0.0069112…, which is less than 0.01, a hundredth.

b. Using the approximations given in part (a), what is an approximate value for 2x(y + 1)?
Answer:
2x(y + 1) is approximately 1.3002 because 2 × 0.33 × 1.97 = 1.3002.

c. Repeat part (b), but use approximations for x and y that have errors less than \(\frac{1}{10^{6}}\).
Answer:
We want the error in the approximation to be less than 0.000001.
If we approximate x by truncating to six decimal places, that is, as 0.333811, then the error is 0.0000007…, which is indeed less than 0.000001.
Truncating y to six decimal places, that is, as 0.976911, gives an error of 0.0000002…, which is indeed less than 0.000001.
Now:
2x(y + 1) is approximately 1.319829276, which is a rounding of 2 × 0.333811 × 1.976911.

Question 2.
Two real numbers have decimal expansions that begin with the following:
x = 0.70588…
y = 0.23529…
a. Using approximations for x and y that are accurate within a measure of \(\frac{1}{10^{2}}\), find approximate values for x + 1.25y and x/y.
Answer:
Using x ≈ 0.70 and y ≈ 0.23, we obtain x + 1.25y ≈ 0.9875 and x/y ≈ 3.0434….

b. Using approximations for x and y that are accurate within a measure of \(\frac{1}{10^{4}}\), find approximate values for x + 1.25y and \(\frac{x}{y}\).
Answer:
Using x ≈ 0.7058 and y ≈ 0.2352, we obtain x + 1.25y ≈ 0.9998 and \(\frac{x}{y}\) ≈ 3.000850….

c. We now reveal that x and y are rational numbers with the property that each of the values x + 1.25y and \(\frac{x}{y}\) is a whole number. Make a guess as to what whole numbers these values are, and use your guesses to find what fractions x and y might be.
Answer:
It looks like x + 1.25y = 1 and \(\frac{x}{y}\) = 3. Thus, we guess x = 3y and so 3y + 1.25y = 1, that is, 4.25y = 1, so y = \(\frac{1}{4.25}\) = \(\frac{100}{425}\) = \(\frac{4}{17}\) and x = 3y = \(\frac{12}{17}\).

Eureka Math Grade 8 Module 7 Lesson 9 Exit Ticket Answer Key

Question 1.
Suppose x = \(\frac{2}{3}\) = 0.6666… and y = \(\frac{5}{9}\) = 0.5555….
a. Using 0.666 as an approximation for x and 0.555 as an approximation for y, find an approximate value for x + y.
Answer:
x + y ≈ 0.666 + 0.555 = 1.221

b. What is the true value of x + y as an infinite decimal?
Answer:
x + y = \(\frac{2}{3}\) + \(\frac{5}{9}\) = \(\frac{11}{9}\) = 1 + \(\frac{2}{9}\) = 1.22222…

c. Use approximations for x and y, each accurate to within an error of \(\frac{1}{10^{5}}\), to estimate a value of the product x × y.
Answer:
x × y ≈ 0.66666 × 0.55555 = 0.3703629630

Engage NY Eureka Math 8th Grade Module 7 Lesson 8 Answer Key

Eureka Math Grade 8 Module 7 Lesson 8 Example Answer Key

Example 1.
Show that the decimal expansion of \(\frac{26}{4}\) is 6.5.
Answer:
Use the example with students so they have a model to complete Exercises 1–5.
→ Show that the decimal expansion of \(\frac{26}{4}\) is 6.5.
Students might use the long division algorithm, or they might simply observe \(\frac{26}{4}\) = \(\frac{13}{2}\) = 6.5.
→ Here is another way to see this: What is the greatest number of groups of 4 that are in 26?
There are 6 groups of 4 in 26.
→ Is there a remainder?
Yes, there are 2 left over.
→ This means we can write 26 as
26 = 6 × 4 + 2.
This means we could also compute \(\frac{26}{4}\) as follows:
\(\frac{26}{4}\) = \(\frac{6 \times 4 + 2}{4}\)
\(\frac{26}{4}\) = \(\frac{6 \times 4}{4}\) + \(\frac{2}{4}\)
\(\frac{26}{4}\) = 6 + \(\frac{2}{4}\)
\(\frac{26}{4}\) = 6\(\frac{2}{4}\) = 6 \(\frac{1}{2}\).
(Some students might note we are simply rewriting the fraction as a mixed number.)
The fraction \(\frac{26}{4}\) is equal to the finite decimal 6.5. When the fraction is not equal to a finite decimal, then we need to use the long division algorithm to determine the decimal expansion of the number.

Eureka Math Grade 8 Module 7 Lesson 8 Exploratory Challenge/Exercise Answer Key

Exploratory Challenge/Exercises 1–5

Exercise 1.
a. Use long division to determine the decimal expansion of \(\frac{142}{2}\).
Answer:

b. Fill in the blanks to show another way to determine the decimal expansion of \(\frac{142}{2}\).

Answer:

c. Does the number \(\frac{142}{2}\) have a finite or an infinite decimal expansion?
Answer:
The decimal expansion of \(\frac{142}{2}\) is 71.0 and is finite.

Exercise 2.
a. Use long division to determine the decimal expansion of \(\frac{142}{4}\).
Answer:

b. Fill in the blanks to show another way to determine the decimal expansion of \(\frac{142}{4}\).

Answer:

c. Does the number \(\frac{142}{4}\) have a finite or an infinite decimal expansion?
Answer:
The decimal expansion of \(\frac{142}{4}\) is 35.5 and is finite.

Exercise 3.
a. Use long division to determine the decimal expansion of \(\frac{142}{6}\).
Answer:

b. Fill in the blanks to show another way to determine the decimal expansion of \(\frac{142}{6}\).

Answer:

c. Does the number \(\frac{142}{6}\) have a finite or an infinite decimal expansion?
Answer:
The decimal expansion of \(\frac{142}{6}\) is 23.666… and is infinite.

Exercise 4.
a. Use long division to determine the decimal expansion of \(\frac{142}{11}\).
Answer:

b. Fill in the blanks to show another way to determine the decimal expansion of \(\frac{142}{11}\).

Answer:

c. Does the number \(\frac{142}{11}\) have a finite or an infinite decimal expansion?
Answer:
The decimal expansion of \(\frac{142}{11}\) is 12.90909… and is infinite.

Exercise 5.
In general, which fractions produce infinite decimal expansions?
Answer:
We discovered in Lesson 6 that fractions equivalent to ones with denominators that are a power of 10 are precisely the fractions with finite decimal expansions. These fractions, when written in simplified form, have denominators with factors composed of 2‘s and 5‘s. Thus any fraction, in simplified form, whose denominator contains a factor different from 2 or 5 must yield an infinite decimal expansion.

Exercises 6–10

Exercise 6.
Does the number \(\frac{65}{13}\) have a finite or an infinite decimal expansion? Does its decimal expansion have a repeating pattern?
Answer:
The number \(\frac{65}{13}\) is rational and so has a decimal expansion with a repeating pattern. Actually, \(\frac{65}{13}\) = \(\frac{5 \times 13}{13}\) = 5, so it is a finite decimal. Viewed as an infinite decimal, \(\frac{65}{13}\) is 5.0000… with a repeat block of 0.

Exercise 7.
Does the number \(\frac{17}{11}\) have a finite or an infinite decimal expansion? Does its decimal expansion have a repeating pattern?
Answer:
The rational \(\frac{17}{11}\) is in simplest form, and we see that it is not equivalent to a fraction with a denominator that is a power of 10. Thus, the rational has an infinite decimal expansion with a repeating pattern.

Exercise 8.
Is the number 0.212112111211112111112… rational? Explain. (Assume the pattern you see in the decimal expansion continues.)
Answer:
Although the decimal expansion of this number has a pattern, it is not a repeating pattern. The number cannot be rational. It is irrational.

Exercise 9.
Does the number \(\frac{860}{999}\) have a finite or an infinite decimal expansion? Does its decimal expansion have a
repeating pattern?
Answer:
The number is rational and so has a decimal expansion with a repeating pattern. Since the fraction is not equivalent to one with a denominator that is a power of 10, it is an infinite decimal expansion.

Exercise 10.
Is the number 0.1234567891011121314151617181920212223… rational? Explain. (Assume the pattern you see in the decimal expansion continues.)
Answer:
Although the decimal expansion of this number has a pattern, it is not a repeating pattern. The number cannot be rational. It is irrational.

Eureka Math Grade 8 Module 7 Lesson 8 Problem Set Answer Key

Question 1.
Write the decimal expansion of \(\frac{7000}{9}\) as an infinitely long repeating decimal.
Answer:
\(\frac{7000}{9}\) = \(\frac{777 \times 9}{9}\) + \(\frac{7}{9}\)
= \(\frac{7777}{9}\)

The decimal expansion of \(\frac{7000}{9}\) is \(777 . \overline{7}\)

Question 2.
Write the decimal expansion of \(\frac{6555555}{3}\) as an infinitely long repeating decimal.
Answer:
\(\frac{6555555}{3}\) = \(\frac{2185185 \times 3}{3}\) + \(\frac{0}{3}\)
= 2 185 185
The decimal expansion of \(\frac{6555555}{3}\) is \(2,185,185 . \overline{0}\).

Question 3.
Write the decimal expansion of \(\frac{350000}{11}\) as an infinitely long repeating decimal.
Answer:
\(\frac{350000}{11}\) = \(\frac{31818 \times 11}{11}\) + \(\frac{2}{11}\)
= 31818\(\frac{2}{11}\)

The decimal expansion of \(\frac{350000}{11}\) is \(31,818 . \overline{18}\).

Question 4.
Write the decimal expansion of \(\frac{12000000}{37}\) as an infinitely long repeating decimal.
Answer:
\(\frac{12000000}{37}\) = \(\frac{324324 \times 37}{37}\) + \(\frac{12}{37}\)
= 324324\(\frac{12}{37}\)

The decimal expansion of \(\frac{12000000}{37}\) is \(324,324 . \overline{324}\).

Question 5.
Someone notices that the long division of 2,222,222 by 6 has a quotient of 370,370 and a remainder of 2 and wonders why there is a repeating block of digits in the quotient, namely 370. Explain to the person why this happens.
Answer:
\(\frac{2222222}{6}\) = \(\frac{370370 \times 6}{6}\) + \(\frac{2}{6}\)
= 370370 \(\frac{2}{6}\)

The block of digits 370 keeps repeating because the long division algorithm leads us to perform the same division over and over again. In the algorithm shown above, we see that there are three groups of 6 in 22, leaving a remainder of 4. When we bring down the next 2, we see that there are exactly seven groups of 6 in 42. When we bring down the next 2, we see that there are zero groups of 6 in 2, leaving a remainder of 2. It is then that the process starts over because the next step is to bring down another 2, giving us 22, which is what we started with. Since the division repeats, then the digits in the quotient will repeat.

Question 6.
Is the answer to the division problem 10÷3.2 a rational number? Explain.
Answer:
Yes. This is equivalent to the division problem 100÷32, which can be written as \(\frac{100}{32}\), and so it is a rational number.

Question 7.
Is \(\frac{3 \pi}{77 \pi}\) a rational number? Explain.
Answer:
Yes. \(\frac{3 \pi}{77 \pi}\) is equal to \(\frac{3}{77}\) and so it is a rational number.

Question 8.
The decimal expansion of a real number x has every digit 0 except the first digit, the tenth digit, the hundredth digit, the thousandth digit, and so on, are each 1. Is x a rational number? Explain.
Answer:
No. Although there is a pattern to this decimal expansion, it is not a repeating pattern. Thus, x cannot be rational.

Eureka Math Grade 8 Module 7 Lesson 8 Exit Ticket Answer Key

Question 1.
Will the decimal expansion of \(\frac{125}{8}\) be finite or infinite? Explain. If we were to write the decimal expansion of this rational number as an infinitely long decimal, which block of numbers repeat?
Answer:
The decimal expansion of \(\frac{125}{8}\) will be finite because \(\frac{125}{8}\) is equivalent to a fraction with a denominator that is a power of 10. (Multiply the numerator and denominator each by 5 × 5 × 5.) If we were to write the decimal as an infinitely long decimal, then we’d have a repeating block consisting of 0.

Question 2.
Write the decimal expansion of \(\frac{13}{7}\) as an infinitely long repeating decimal.
Answer:
\(\frac{13}{7}\) = \(\frac{1 \times 7}{7}\) + \(\frac{6}{7}\)
= 1\(\frac{6}{7}\)

The decimal expansion of \(\frac{13}{7}\) is \(1 . \overline{857142}\).

Engage NY Eureka Math 8th Grade Module 7 Lesson 7 Answer Key

Eureka Math Grade 8 Module 7 Lesson 7 Example Answer Key

Example 1.
The number 0.253 is represented on the number line below.

Answer:
How can we locate the number 0.253 = \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) on the number line?
We can see that 0.253 is a tad larger than 0.2 and is smaller than 0.3. So if we divide the line segment from 0 to 1 into tenths, 0.253 lies somewhere in the segment between 0.2 and 0.3.

Now divide this segment into ten equal parts. (Those parts are hundredths of the original unit length.) We know that 0.253 is larger than 0.25 but smaller than 0.26, and so lies in the segment between these two values.

Now divide this small segment into tenths again. (We are now dealing with thousandths of the original unit length.) We can now see where exactly to pin 0.253 on the number line.

Writing 0.253 in its expanded decimal form of \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) illustrates this process:
The first decimal digit of 0.253 is 0.2, or \(\frac{2}{10}\), and this tells us within which tenth we are to place 0.253.
The first two decimal digits of 0.253 are 0.25 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) , or \(\frac{25}{10^{2}}\), and this tells us within which hundredth we are to place 0.253.

The first three decimal digits of 0.253 are 0.253 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) + \(\frac{3}{10^{3}}\), or \(\frac{253}{10^{3}}\), and this tells us within which thousandth we are to place 0.253. And since the decimal terminates here, we are done.
Have the students explain this process again in their own words, referring to the number line diagram as they do so.

How do you think this process would change if we tried to locate an infinite decimal on the number line?
The sequence for an infinite decimal would never end; it would go on infinitely.
We need to introduce some notation. If a decimal has a repeating pattern, as for 0.3333… or 7.45454545…, for instance, then a horizontal bar is used to indicate that a block of digits is being repeated. For example, 0.3333… is written as \(0 . \overline{3}\) and 7.45454545… as \(7 . \overline{45}\). It is conceivable that an infinite decimal could have no repeating pattern.

Example 2.
The number \(\frac{5}{6}\), which is equal to 0.833333…, or \(0 . \overline{83}\) is partially represented on the number line below.

Answer:
Now, consider the equality \(\frac{5}{6}\) = 0.833333″…” = \(0 . \overline{83}\). Notice that at the second step, the work feels as though it repeats, which coincides with the fact that the decimal digit of 3 repeats.

What is the expanded form of the decimal 0.833333…?
0.833333″…” = \(\frac{8}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\) + …………
We see again that at the second step the work begins to repeat.
Each step can be represented by increasing powers of 10 in the denominator: \(\frac{8}{10}, \frac{83}{10^{2}}, \frac{833}{10^{3}}, \frac{8333}{10^{4}}, \frac{83333}{10^{5}}, \frac{833333}{10^{6}}\), and so on. When will it end? Explain.
It will never end because the decimal is infinite.

As we step through this process we are pinning the exact location of 0.8333… into smaller and smaller intervals, intervals with sizes shrinking to zero: an interval of a tenth, and then a hundredth, then a thousandth, and, if we kept going, an interval of size \(\frac{1}{10^{20}}\), and later on to an interval of size \(\frac{1}{10^{100}}\), and so on, supposedly forever!
Okay. Let’s now think deeply about 0.9999…. Where do we find this number on the number line?

Draw on the board a sequence of number-line segments akin to those in Example 2, and have students give instructions on how to pin down the location of 0.9999…. In which tenth does it lie? In which hundredth? In which thousandth? And so on. Ask: At any stage of this process is 0.9999… right at the number 1 on the number line?
No. We are always just to the left of 1.
Right. And that makes sense as 0.9 is smaller than 1, and 0.99 is smaller than 1, as are 0.999 and 0.9999. At every stage of the process we are just shy of the number 1.

Eureka Math Grade 8 Module 7 Lesson 7 Exercise Answer Key

Opening Exercise
a. Write the expanded form of the decimal 0.3765 using powers of 10.
Answer:
0.3765 = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{6}{10^{3}} + \frac{5}{10^{4}}\)

b. Write the expanded form of the decimal 0.3333333… using powers of 10.
Answer:
0.333333″…” = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\)

c. Have you ever wondered about the value of 0.99999…? Some people say this infinite decimal has a value of 1. Some disagree. What do you think?
Answer:
Answers will vary. Have a brief discussion with students about this exercise. The answer will be revisited in the discussion below.

Exercises 1–5

Exercise 1.
a. Write the expanded form of the decimal 0.125 using powers of 10.
Answer:
0.125 = \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)

b. Show on the number line the placement of the decimal 0.125.

Answer:

Exercise 2.
a. Write the expanded form of the decimal 0.3875 using powers of 10.
Answer:
0.3875 = \(\frac{3}{10} + \frac{8}{10^{2}} + \frac{7}{10^{3}} + \frac{5}{10^{4}}\)

b. Show on the number line the placement of the decimal 0.3875.

Answer:

Exercise 3.
a. Write the expanded form of the decimal 0.777777… using powers of 10.
Answer:
0.777777… = \(\frac{7}{10} + \frac{7}{10^{2}} + \frac{7}{10^{3}} + \frac{7}{10^{4}} + \frac{7}{10^{5}} + \frac{7}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.777777… on the number line.

Answer:

Exercise 4.
a. Write the expanded form of the decimal \(0 . \overline{45}\) using powers of 10.
Answer:
\(0 . \overline{45}\) = \(\frac{4}{10} + \frac{5}{10^{2}} + \frac{4}{10^{3}} + \frac{5}{10^{4}} + \frac{4}{10^{5}} + \frac{5}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal \(0 . \overline{45}\) on the number line.

Answer:

Exercise 5.
a. Order the following numbers from least to greatest: 2.121212, 2.1, 2.2, and \(2 . \overline{12}\).
Answer:
2.1, 2.121212, \(2 . \overline{12}\), and 2.2

b. Explain how you knew which order to put the numbers in.
Answer:
Each number is the sum of the whole number 2 and a decimal. When you write each number in this manner, you get the following expansions.
2.121212 = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}}\)
2.1 = 2 + \(\frac{1}{10}\)
2.2 = 2 + \(\frac{2}{10}\)
\(2 . \overline{12}\) = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}} + \frac{1}{10^{7}} + \frac{2}{10^{8}} + \cdots\)
In this form, it is clear that 2.1 is the least of the four numbers, followed by the finite decimal 2.121212, then the infinite decimal \(2 . \overline{12}\), and finally 2.2.

Eureka Math Grade 8 Module 7 Lesson 7 Problem Set Answer Key

Question 1.
a. Write the expanded form of the decimal 0.625 using powers of 10.
Answer:
0.625 = \(\frac{6}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)

b. Place the decimal 0.625 on the number line.

Answer:

Question 2.
a. Write the expanded form of the decimal \(0 . \overline{370}\) using powers of 10.
Answer:
\(0 . \overline{370}\) = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{0}{10^{3}} + \frac{3}{10^{4}} + \frac{7}{10^{5}} + \frac{0}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.370370… on the number line.

Answer:

Question 3.
Which is a more accurate representation of the fraction \(\frac{2}{3}\): 0.6666 or \(0 . \overline{6}\)? Explain. Which would you prefer to compute with?
Answer:
The number \(\frac{2}{3}\) is more accurately represented by the decimal 0.6 ̅ compared to 0.6666. The long division algorithm with \(\frac{2}{3}\) shows that the digit 6 repeats. Then, the expanded form of the decimal \(0 . \overline{6}\) is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}} + \frac{6}{10^{5}} + \frac{6}{10^{6}} + \cdots\), and the expanded form of the decimal 0.6666 is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}}\). For this reason, \(0 . \overline{6}\) is precise, but 0.6666 is an approximation. For computations, I would prefer to use 0.6666. My answer would be less precise, but at least I would be able to compute with it. When attempting to compute with an infinite number, you would never finish writing it; thus, you could never compute with it.

Question 4.
Explain why we shorten infinite decimals to finite decimals to perform operations. Explain the effect of shortening an infinite decimal on our answers.
Answer:
We often shorten infinite decimals to finite decimals to perform operations because it would be impossible to represent an infinite decimal precisely since the sequence that describes infinite decimals has an infinite number of steps. Our answers are less precise; however, they are not that much less precise because with each additional digit we include in the sequence, we are adding a very small amount to the value of the number. The more decimals we include, the closer the value we add approaches zero. Therefore, it does not make that much of a difference with respect to our answer.

Question 5.
A classmate missed the discussion about why \(0 . \overline{9}\) = 1. Convince your classmate that this equality is true.
Answer:
Answers will vary. Accept any reasonable explanation. One is provided below.
Ask: Could there be any space between the locations of 0.9999… and 1 on the number line? We have that 0.9999… is larger than 0.9 and so is within one-tenth of 1 on the number line. We also have that 0.9999… is larger than 0.99 and so is within one-hundredth of 1 on the number line. And 0.9999… is larger than 0.999 and so is within one-thousandth of 1 on the number line, and so on. There can be no space between 0.9999… and 1 on the number line, as we can always argue that 0.9999… must be within any given distance from 1. Thus, 0.9999… and 1 must sit at the same location on the number line and so are the same number.

Question 6.
Explain why 0.3333 < 0.33333.
Answer:
0.3333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}}\), and 0.33333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}}\). That means that 0.33333 is exactly \(\frac{3}{10^{5}}\) larger than 0.3333. If we examined the numbers on the number line, 0.33333 is to the right of 0.3333, meaning that it is larger than 0.3333.

Eureka Math Grade 8 Module 7 Lesson 7 Exit Ticket Answer Key

Question 1.
a. Write the expanded form of the decimal 0.829 using powers of 10.
Answer:
0.829 = \(\frac{8}{10} + \frac{2}{10^{2}} + \frac{9}{10^{3}}\)

b. Show the placement of the decimal 0.829 on the number line.

Answer:

Question 2.
a. Write the expanded form of the decimal 0.55555… using powers of 10.
Answer:
0.55555″…” = \(\frac{5}{10} + \frac{5}{10^{2}} + \frac{5}{10^{3}} + \frac{5}{10^{4}} + \frac{5}{10^{5}} + \frac{5}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal 0.555555… on the number line.

Answer:

Question 3.
a. Write the expanded form of the decimal \(0 . \overline{573}\) using powers of 10.
Answer:
\(0 . \overline{573}\) = \(\frac{5}{10} + \frac{7}{10^{2}} + \frac{3}{10^{3}} + \frac{5}{10^{4}} + \frac{7}{10^{5}} + \frac{3}{10^{6}} + \cdots\)

b. Show the first few stages of placing the decimal \(0 . \overline{573}\) on the number line.

Answer:

Engage NY Eureka Math 8th Grade Module 7 Lesson 5 Answer Key

Eureka Math Grade 8 Module 7 Lesson 5 Example Answer Key

Example 1.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
Answer:
Now that we know about square roots and cube roots, we can combine that knowledge with our knowledge of the properties of equality to begin solving nonlinear equations like x³ + 9x = \(\frac{1}{2}\) (18x + 54). Transform the equation until you can determine the positive value of x that makes the equation true.
Challenge students to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
x³ + 9x = 9x + 27
x³ + 9x – 9x = 9x – 9x + 27
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = \(\sqrt[3]{3^{3}}\)
x = 3
Now, we verify our solution is correct.
3³ + 9(3) = \(\frac{1}{2}\) (18(3) + 54)
27 + 27 = \(\frac{1}{2}\) (54 + 54)
54 = \(\frac{1}{2}\) (108)
54 = 54
Since the left side is the same as the right side, our solution is correct.

Example 2.
x(x – 3) – 51 = – 3x + 13
Answer:
Let’s look at another nonlinear equation. Find the positive value of x that makes the equation true: x(x – 3) – 51 = – 3x + 13.
Provide students with time to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
Sample response:
x(x – 3) – 51 = – 3x + 13
x² – 3x – 51 = – 3x + 13
x² – 3x + 3x – 51 = – 3x + 3x + 13
x² – 51 = 13
x² – 51 + 51 = 13 + 51
x² = 64
\(\sqrt{x^{2}}\) = ±\(\sqrt{64}\)
x = ±\(\sqrt{64}\)
x = ±8
Now we verify our solution is correct.
Provide students time to check their work.
Let x = 8.
8(8 – 3) – 51 = – 3(8) + 13
8(5) – 51 = – 24 + 13
40 – 51 = – 11
– 11 = – 11

Let x = – 8.
– 8( – 8 – 3) – 51 = – 3( – 8) + 13
– 8( – 11) – 51 = 24 + 13
88 – 51 = 37
37 = 37
Now it is clear that the left side is exactly the same as the right side, and our solution is correct.

Eureka Math Grade 8 Module 7 Lesson 5 Exercise Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Exercise 1.
a. Solve x² – 14 = 5x + 67 – 5x.
Answer:
x² – 14 = 5x + 67 – 5x
x² – 14 = 67
x² – 14 + 14 = 67 + 14
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±\(\sqrt{81}\)
x = ±9

Check:
9² – 14 = 5(9) + 67 – 5(9)
81 – 14 = 45 + 67 – 45
67 = 67

( – 9)² – 14 = 5( – 9) + 67 – 5( – 9)
81 – 14 = – 45 + 67 + 45
67 = 67

b. Explain how you solved the equation.
Answer:
To solve the equation, I had to first use the properties of equality to transform the equation into the form of x² = 81. Then, I had to take the square root of both sides of the equation to determine that x = 9 since the number x is being squared.

Exercise 2.
Solve and simplify: x(x – 1) = 121 – x.
Answer:
x(x – 1) = 121 – x
x² – x = 121 – x
x² – x + x = 121 – x + x
x² = 121
\(\sqrt{x^{2}}\) = ±\(\sqrt{121}\)
x = ±\(\sqrt{121}\)
x = ±11

Check:
11(11 – 1) = 121 – 11
11(10) = 110
110 = 110

– 11( – 11 – 1) = 121 – ( – 11)
– 11( – 12) = 121 + 11
132 = 132

Exercise 3.
A square has a side length of 3x inches and an area of 324 in². What is the value of x?
Answer:
(3x)² = 324
3² x² = 324
9x² = 324
\(\frac{9 x^{2}}{9}\) = \(\frac{324}{9}\)
x² = 36
\(\sqrt{x^{2}}\) = \(\sqrt{36}\)
x = 6

Check:
(3(6)) ² = 324
18² = 324
324 = 324
A negative number would not make sense as a length, so x = 6.

Exercise 4.
– 3x³ + 14 = – 67
Answer:
– 3x³ + 14 = – 67
– 3x³ + 14 – 14 = – 67 – 14
– 3x³ = – 81
\(\frac{ – 3 x^{3}}{3}\) = \(\frac{ – 81}{ – 3}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
– 3(3)³ + 14 = – 67
– 3(27) + 14 = – 67
– 81 + 14 = – 67
– 67 = – 67

Exercise 5.
x(x + 4) – 3 = 4(x + 19.5)
Answer:
x(x + 4) – 3 = 4(x + 19.5)
x² + 4x – 3 = 4x + 78
x² + 4x – 4x – 3 = 4x – 4x + 78
x² – 3 = 78
x² – 3 + 3 = 78 + 3
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±9

Check:
9(9 + 4) – 3 = 4(9 + 19.5)
9(13) – 3 = 4(28.5)
117 – 3 = 114
114 = 114

– 9( – 9 + 4) – 3 = 4( – 9 + 19.5)
– 9( – 5) – 3 = 4(10.5)
45 – 3 = 42
42 = 42

Exercise 6.
216 + x = x(x² – 5) + 6x
Answer:
216 + x = x(x² – 5) + 6x
216 + x = x³ – 5x + 6x
216 + x = x³ + x
216 + x – x = x³ + x – x
216 = x³
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{x^{3}}\)
6 = x

Check:
216 + 6 = 6(6² – 5) + 6(6)
222 = 6(31) + 36
222 = 186 + 36
222 = 222

Exercise 7.
a. What are we trying to determine in the diagram below?

Answer:
We need to determine the value of x so that its square root, multiplied by 4, satisfies the equation
5² + (4\(\sqrt{x}\))² = 11².

b. Determine the value of x, and check your answer.
Answer:
5² + (4\(\sqrt{x}\))² = 11²
25 + 4² (\(\sqrt{x}\))² = 121
25 – 25 + 4² (\(\sqrt{x}\))² = 121 – 25
16x = 96
\(\frac{16x}{16}\) = \(\frac{96}{16}\)
x = 6
The value of x is 6.

Check:
5² + (4\(\sqrt{6}\))² = 11²
25 + 16(6) = 121
25 + 96 = 121
121 = 121

Eureka Math Grade 8 Module 7 Lesson 5 Problem Set Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Question 1.
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
Answer:
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
x³ + 7x² = 7x² + 8
x³ + 7x² – 7x² = 7x² – 7x² + 8
x³ = 8
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 8 }\)
x = 2

Check:
2² (2 + 7) = \(\frac{1}{2}\) (14(2² ) + 16)
4(9) = \(\frac{1}{2}\) (56 + 16)
36 = \(\frac{1}{2}\) (72)
36 = 36

Question 2.
x³ = 1331 ^{– 1}
Answer:
x³ = 1331 ^{– 1}
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{1331^{ – 1}}\)
x = \(\sqrt[3]{\frac{1}{1331}}\)
x = \(\sqrt[3]{\frac{1}{11^{3}}}\)
x = \(\frac{1}{11}\)

Check:
(\(\left(\frac{1}{11}\right)^{3}\))³ = 1331 ^{– 1}
\(\frac{1}{11^{3}}\) = 1331 ^{– 1}
\(\frac{1}{1331}\) = 1331 ^{– 1}
1331 ^{– 1} = 1331 ^{– 1}

Question 3.
Determine the positive value of x that makes the equation true, and then explain how you solved the equation.
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
Answer:
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
x² – 49 = 0
x² – 49 + 49 = 0 + 49
x² = 49
\(\sqrt{x^{2}}\) = \(\sqrt{49}\)
x = 7

Check:
7² – 49 = 0
49 – 49 = 0
0 = 0
To solve the equation, I first had to simplify the expression \(\frac{x^{9}}{x^{7}}\) to x². Next, I used the properties of equality to transform the equation into x² = 49. Finally, I had to take the square root of both sides of the equation to solve for x.

Question 4.
Determine the positive value of x that makes the equation true.
(8x)² = 1
Answer:
(8x)² = 1
64x² = 1
\(\sqrt{64^{2}}\) = \(\sqrt{1}\)
8x = 1
\(\frac{8x}{8}\) = \(\frac{1}{8}\)
x = \(\frac{1}{8}\)

Check:
(8(\(\frac{1}{8}\)))² = 1
1² = 1
1 = 1

Question 5.
(9\(\sqrt{x}\))² – 43x = 76
Answer:
(9\(\sqrt{x}\))² – 43x = 76
9² (√x)² – 43x = 76
81x – 43x = 76
38x = 76
\(\frac{38x}{38}\) = \(\frac{76}{38}\)
x = 2

Check:
(9(\(\sqrt{2}\)))² – 43(2) = 76
9² (\(\sqrt{2}\))² – 86 = 76
81(2) – 86 = 76
162 – 86 = 76
76 = 76

Question 6.
Determine the length of the hypotenuse of the right triangle below.

Answer:
3² + 7² = x²
9 + 49 = x²
58 = x²
\(\sqrt{58}\) = \(\sqrt{x^{2}}\)
\(\sqrt{58}\) = x

Check:
3² + 7² = (\(\sqrt{52}\))²
9 + 49 = 58
58 = 58
Since x = \(\sqrt{58}\), the length of the hypotenuse is \(\sqrt{58}\) mm.

Question 7.
Determine the length of the legs in the right triangle below.

Answer:
x² + x² = (14\(\sqrt{2}\))²
2x² = 14² (\(\sqrt{2}\))²
2x² = 196(2)
\(\frac{2 x^{2}}{2}\) = \(\frac{196(2)}{2}\)
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = \(\sqrt{14^{2}}\)
x = 14

Check:
14² + 14² = (14\(\sqrt{2}\))²
196 + 196 = 14² (\(\sqrt{2}\))²
392 = 196(2)
392 = 392
Since x = 14, the length of each of the legs of the right triangle is 14 cm.

Question 8.
An equilateral triangle has side lengths of 6 cm. What is the height of the triangle? What is the area of the triangle?

Answer:
Note: This problem has two solutions, one with a simplified root and one without. Choose the appropriate solution for your classes based on how much simplifying you have taught them.
Let h cm represent the height of the triangle.
3² + h² = 6²
9 + h² = 36
9 – 9 + h² = 36 – 9
h² = 27
\(\sqrt{h^{2}}\) = \(\sqrt{27}\)
h = \(\sqrt{27}\)
h = \(\sqrt{3^{3}}\)
h = \(\sqrt{3^{2}}\)×\(\sqrt{3}\)
h = 3\(\sqrt{3}\)

Let A represent the area of the triangle.
A = \(\frac{6(3 \sqrt{3})}{2}\))
A = 3(3\(\sqrt{3}\))
A = 9\(\sqrt{3}\)
Simplified: The height of the triangle is 3\(\sqrt{3}\) cm, and the area is 9\(\sqrt{3}\) cm².
Unsimplified: The height of the triangle is \(\sqrt{27}\) cm, and the area is 3\(\sqrt{27}\) cm²

Question 9.
Challenge: Find the positive value of x that makes the equation true.
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
Answer:
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
\(\frac{1}{4}\) x² – 3x = – 3x + 8
\(\frac{1}{4}\) x² – 3x + 3x = – 3x + 3x + 8
\(\frac{1}{4}\) x² = 8
4(\(\frac{1}{4}\)) x² = 8(4)
x² = 32
\(\sqrt{x^{2}}\) = \(\sqrt{32}\)
x = \(\sqrt{2^{5}}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2}\)
x = 4\(\sqrt{2}\)

Check:
(\(\frac{1}{2}\) (4\(\sqrt{2}\)))² – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) + 8 – 10(4\(\sqrt{2}\))
\(\frac{1}{4}\) (16)(2) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
\(\frac{32}{4}\) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = (7 – 10)(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8
8 – 8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8 – 8
– 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\))

Question 10.
Challenge: Find the positive value of x that makes the equation true.
11x + x(x – 4) = 7(x + 9)
Answer:
11x + x(x – 4) = 7(x + 9)
11x + x² – 4x = 7x + 63
7x + x² = 7x + 63
7x – 7x + x² = 7x – 7x + 63
x² = 63
\(\sqrt{x^{2}}\)) = \(\sqrt{63}\)
x = \(\sqrt{\left(3^{2}\right)(7)}\)
x = \(\sqrt{3^{2}}\) ⋅ \(\sqrt{7}\)
x = 3\(\sqrt{7}\)

Check:
11(3\(\sqrt{7}\)) + 3\(\sqrt{7}\) (3\(\sqrt{7}\) – 4) = 7(3\(\sqrt{7}\) + 9)
33\(\sqrt{7}\) + 3² (\(\sqrt{7}\))² – 4(3\(\sqrt{7}\)) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 4(3\(\sqrt{7}\)) + 9(7) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 12\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
(33 – 12) \(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 – 63 = 21\(\sqrt{7}\) + 63 – 63
21\(\sqrt{7}\) = 21\(\sqrt{7}\)

Eureka Math Grade 8 Module 7 Lesson 5 Exit Ticket Answer Key

Question 1.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
x² + 4x = 4(x + 16)
Answer:
x² + 4x = 4(x + 16)
x² + 4x = 4x + 64
x² + 4x – 4x = 4x – 4x + 64
x² = 64
\(\sqrt{x^{2}}\) = \(\sqrt{64}\)
x = 8

Check:
8² + 4(8) = 4(8 + 16)
64 + 32 = 4(24)
96 = 96

Question 2.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
(4x)³ = 1728
Answer:
(4x)³ = 1728
64x³ = 1728
\(\frac{1}{64}\)(64x³) = (1728)\(\frac{1}{64}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
(4(3))³ = 1728
12³ = 1728
1728 = 1728

Engage NY Eureka Math 8th Grade Module 7 Lesson 4 Answer Key

Eureka Math Grade 8 Module 7 Lesson 4 Example Answer Key

Example 1.
Simplify the square root as much as possible.
\(\sqrt{50}\) =
Answer:
→ Is the number 50 a perfect square? Explain.
The number 50 is not a perfect square because there is no integer squared that equals 50.

→ Since 50 is not a perfect square, when we need to simplify \(\sqrt{50}\), we write the factors of the number 50 looking specifically for those that are perfect squares. What are the factors of 50?
50 = 2 × 5²
Since 50 = 2 × 5², then \(\sqrt{50}\) = \(\sqrt{2 \times 5^{2}}\). We can rewrite \(\sqrt{50}\) as a product of its factors:
\(\sqrt{50}\) = \(\sqrt{2}\) × \(\sqrt{5^{2}}\).

→ Obviously, 5² is a perfect square. Therefore, \(\sqrt{5^{2}}\) = 5, so \(\sqrt{50}\) = 5 × \(\sqrt{2}\) = 5\(\sqrt{2}\). Since \(\sqrt{2}\) is not a perfect square, we leave it as it is. We have simplified this expression as much as possible because there are no other perfect square factors remaining in the square root.

→ The number \(\sqrt{50}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 5\(\sqrt{2}\) is the simplified form of \(\sqrt{50}\).
Now that we know \(\sqrt{50}\) can be expressed as a product of its factors, we also know that we can multiply expressions containing square roots. For example, if we are given \(\sqrt{2}\) × \(\sqrt{5^{2}}\), we can rewrite the expression as √(2 × 5² ) = \(\sqrt{50}\).

Example 2.
Simplify the square root as much as possible.
\(\sqrt{28}\) =
Answer:
→ Is the number 28 a perfect square? Explain.
The number 28 is not a perfect square because there is no integer squared that equals 28.

→ What are the factors of 28?
28 = 2² × 7
Since 28 = 2² × 7, then \(\sqrt{28}\) = \(\sqrt{2^{2} \times 7}\). We can rewrite \(\sqrt{28}\) as a product of its factors:
\(\sqrt{28}\) = \(\sqrt{2^{2}}\) × \(\sqrt{7}\).

→ Obviously, 2² is a perfect square. Therefore, \(\sqrt{2^{2}}\) = 2, and \(\sqrt{28}\) = 2 × \(\sqrt{7}\) = 2\(\sqrt{7}\). Since \(\sqrt{7}\) is not a perfect square, we leave it as it is.

→ The number \(\sqrt{28}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 2\(\sqrt{7}\) is the simplified form of \(\sqrt{28}\).

Example 3.
Simplify the square root as much as possible.
\(\sqrt{128}\) =
Answer:
→ In this example, students may or may not recognize 128 as 64 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{128}\) = \(\sqrt{64 \times 2}\) = \(\sqrt{64}\) × \(\sqrt{2}\) = 8 × \(\sqrt{2}\) = 8\(\sqrt{2}\).

→ Is the number 128 a perfect square? Explain.
The number 128 is not a perfect square because there is no integer squared that equals 128.

→ What are the factors of 128?
128 = 2⁷
→ Since 128 = 2⁷, then \(\sqrt{128}\) = √(2⁷ ). We know that we can simplify perfect squares, so we can rewrite 2⁷ as 2² × 2² × 2² × 2 because of what we know about the laws of exponents. Then,
\(\sqrt{128}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\).
Each 2² is a perfect square. Therefore, \(\sqrt{128}\) = 2 × 2 × 2 × \(\sqrt{2}\) = 8\(\sqrt{2}\).

Example 4.
Simplify the square root as much as possible.
\(\sqrt{288}\) =
Answer:
In this example, students may or may not recognize 288 as 144 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{288}\) = \(\sqrt{144 \times 2}\) = \(\sqrt{144}\) × \(\sqrt{2}\) = 12 × \(\sqrt{2}\) = 12\(\sqrt{2}\).

→ Is the number 288 a perfect square? Explain.
The number 288 is not a perfect square because there is no integer squared that equals 288.
→ What are the factors of 288?
288 = 2⁵ × 3²
Since 288 = 2⁵ × 3², then \(\sqrt{288}\) = √(2⁵ × 3² ). What do we do next?
Use the laws of exponents to rewrite 2⁵ as 2² × 2² × 2.

→ Then, \(\sqrt{288}\) is equivalent to
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\).

→ What does this simplify to?
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\)) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) ) × \(\sqrt{2}\) = 2 × 2 × 3 × \(\sqrt{2}\) = 12\(\sqrt{2}\)

Eureka Math Grade 8 Module 7 Lesson 4 Exercise Answer Key

Opening Exercise
a.
i. What does \(\sqrt{16}\) equal?
Answer:
4

ii. What does 4 × 4 equal?
Answer:
16

iii. Does \(\sqrt{16}\) = \(\sqrt{4 \times 4}\)?
Answer:
Yes

b.
i. What does \(\sqrt{36}\) equal?
Answer:
6

ii. What does 6 × 6 equal?
Answer:
36

iii. Does \(\sqrt{36}\) = \(\sqrt{6 \times 6}\)?
Answer:
Yes

c.
i. What does \(\sqrt{121}\) equal?
Answer:
11

ii. What does 11 × 11 equal?
Answer:
121

iii. Does \(\sqrt{121}\) = \(\sqrt{11 \times 11}\)?
Yes

d.
i. What does \(\sqrt{81}\) equal?
Answer:
9

ii. What does 9 × 9 equal?
Answer:
81

iii. Does \(\sqrt{81}\) = \(\sqrt{9 \times 9}\)?
Answer:
Yes

e. Rewrite \(\sqrt{20}\) using at least one perfect square factor.
Answer:
\(\sqrt{20}\) = \(\sqrt{4 \times 5}\)

f. Rewrite \(\sqrt{28}\) using at least one perfect square factor.
Answer:
\(\sqrt{28}\) = \(\sqrt{4 \times 7}\)

Exercises 1–4
Simplify the square roots as much as possible.

Exercise 1.
\(\sqrt{18}\)
Answer:
\(\sqrt{18}\) = \(\sqrt{2 \times 3^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{2}\)

Exercise 2.
\(\sqrt{44}\)
Answer:
\(\sqrt{44}\) = \(\sqrt{2^{2} \times 11}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11}\)
= 2\(\sqrt{11}\)

Exercise 3.
\(\sqrt{169}\)
Answer:
\(\sqrt{169}\) = \(\sqrt{13^{2}}\)
= 13

Exercise 4.
\(\sqrt{75}\)
Answer:
\(\sqrt{75}\) = \(\sqrt{3 \times 5^{2}}\)
= \(\sqrt{3}\) × \(\sqrt{5^{2}}\)
= 5\(\sqrt{3}\)

Exercises 5–8

Exercise 5.
Simplify \(\sqrt{108}\).
Answer:
\(\sqrt{108}\) = \(\sqrt{2^{2} \times 3^{3}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\)
= 2 × 3\(\sqrt{3}\)
= 6\(\sqrt{3}\)

Exercise 6.
Simplify \(\sqrt{250}\).
Answer:
\(\sqrt{250}\) = \(\sqrt{2 \times 5^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{5^{2}}\) × \(\sqrt{5}\)
= 5\(\sqrt{2}\) × \(\sqrt{5}\)
= 5\(\sqrt{10}\)

Exercise 7.
Simplify \(\sqrt{200}\).
Answer:
\(\sqrt{200}\) = \(\sqrt{2^{3} \times 5^{2}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{5^{2}}\)
= 2 × 5\(\sqrt{2}\)
= 10\(\sqrt{2}\)

Exercise 8.
Simplify \(\sqrt{504}\).
Answer:
\(\sqrt{504}\) = \(\sqrt{2^{3} \times 3^{2} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{7}\)
= 6\(\sqrt{14}\)

Eureka Math Grade 8 Module 7 Lesson 4 Problem Set Answer Key

Simplify each of the square roots in Problems 1–5 as much as possible.

Question 1.
\(\sqrt{98}\)
\(\sqrt{98}\) = \(\sqrt{2 \times 7^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{7^{2}}\)
= 7\(\sqrt{2}\)

Question 2.
\(\sqrt{54}\)
\(\sqrt{54}\) = \(\sqrt{2 \times 3^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{3}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{6}\)

Question 3.
\(\sqrt{144}\)
\(\sqrt{144}\) = \(\sqrt{12^{2}}\)
= 12

Question 4.
\(\sqrt{512}\)
\(\sqrt{512}\) = \(\sqrt{2^{9}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\)
= 2 × 2 × 2 × 2\(\sqrt{2}\)
= 16\(\sqrt{2}\)

Question 5.
\(\sqrt{756}\)
\(\sqrt{756}\) = \(\sqrt{2^{2} \times 3^{3} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{21}\)
= 6\(\sqrt{21}\)

Question 6.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c units represent the length of the hypotenuse.
(\(\sqrt{27}\))² + (\(\sqrt{48}\))² = c²
27 + 48 = c²
75 = c²
\(\sqrt{75}\) = \(\sqrt{c^{2}}\)
\(\sqrt{5^{2}}\) × \(\sqrt{3}\) = c
5\(\sqrt{3}\) = c
The length of the hypotenuse is 5\(\sqrt{3}\) units.

Question 7.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c cm represent the length of the hypotenuse.
3² + 8² = c²
9 + 64 = c²
73 = c²
\(\sqrt{73}\) = \(\sqrt{c^{2}}\)
\(\sqrt{73}\) = c
The length of the unknown side is \(\sqrt{73}\) cm.

Question 8.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let c mm represent the length of the hypotenuse.
3² + 3² = c²
9 + 9 = c²
18 = c²
\(\sqrt{18}\) = \(\sqrt{c^{2}}\)
\(\sqrt{18}\) = c
\(\sqrt{3^{2}}\) × \(\sqrt{2}\) = c
3\(\sqrt{2}\) = c
The length of the unknown side is 3\(\sqrt{2}\) mm.

Question 9.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.

Answer:
Let x in. represent the unknown length.
x² + 8² = 12²
x² + 64 = 144
x² + 64 – 64 = 144 – 64
x² = 80
\(\sqrt{x^{2}}\) = \(\sqrt{80}\)
x = \(\sqrt{80}\)
x = \(\sqrt{2^{4} \cdot 5}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{5}\)
x = 2 ⋅ 2\(\sqrt{5}\)
x = 4\(\sqrt{5}\)
The length of the unknown side is 4\(\sqrt{5}\) in.

Question 10.
Josue simplified \(\sqrt{450}\) as 15\(\sqrt{2}\) Is he correct? Explain why or why not.
Answer:
\(\sqrt{450}\) = \(\sqrt{2 \times 3^{2} \times 5^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5^{2}}\)
= 3 × 5 × \(\sqrt{1}\)
= 15\(\sqrt{1}\)
Yes, Josue is correct because the number 450 = 2 × 3² × 5². The factors that are perfect squares simplify to 15 leaving just the factor of 2 that cannot be simplified. Therefore, \(\sqrt{450}\) = 15\(\sqrt{2}\).

Question 11.
Tiah was absent from school the day that you learned how to simplify a square root. Using \(\sqrt{360}\), write Tiah an explanation for simplifying square roots.
Answer:
To simplify \(\sqrt{360}\), first write the factors of 360. The number 360 = 2³ × 3² × 5. Now, we can use the factors to write \(\sqrt{360}\) = \(\sqrt{2^{3} \times 3^{2} \times 5}\)), which can then be expressed as \(\sqrt{360}\) = \(\sqrt{2^{3}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5}\). Because we want to simplify square roots, we can rewrite the factor \(\sqrt{2^{3}}\) as \(\sqrt{2^{2}}\) × \(\sqrt{2}\) because of the laws of exponents. Now, we have
\(\sqrt{360}\) = \(\sqrt{2^{2}}\) × √2 × \(\sqrt{3^{2}}\) × \(\sqrt{5}\).
Each perfect square can be simplified as follows:
\(\sqrt{360}\) = 2 × \(\sqrt{2}\) × 3 × \(\sqrt{5}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{5}\)
= 6\(\sqrt{10}\).
The simplified version of \(\sqrt{360}\) = 6\(\sqrt{10}\).

Eureka Math Grade 8 Module 7 Lesson 4 Exit Ticket Answer Key

Simplify the square roots as much as possible.
Question 1.
\(\sqrt{24}\)
Answer:
\(\sqrt{24}\) = \(\sqrt{2^{2} \times 6}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{6}\)
= 2\(\sqrt{6}\)

Question 2.
\(\sqrt{338}\)
Answer:
\(\sqrt{338}\) = \(\sqrt{13^{2} \times 2}\)
= \(\sqrt{13^{2}}\) × \(\sqrt{24}\)
= 13\(\sqrt{2}\)

Question 3.
\(\sqrt{196}\)
Answer:
\(\sqrt{196}\) = \(\sqrt{14^{2}}\)
= 14

Question 4.
\(\sqrt{2420}\)
Answer:
\(\sqrt{2420}\) = \(\sqrt{2^{2} \times 11^{2} \times 5}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11^{2}}\) × \(\sqrt{5}\)
= 2 × 11 × \(\sqrt{5}\)
= 22\(\sqrt{5}\)