Eureka Math

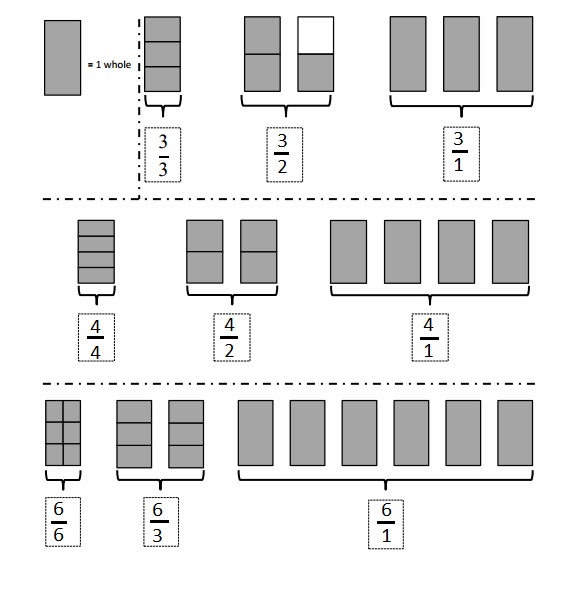
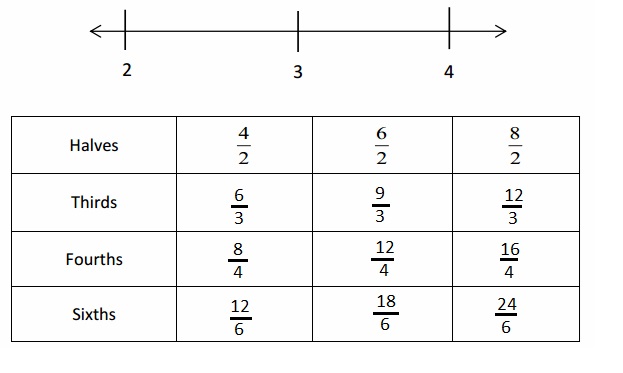
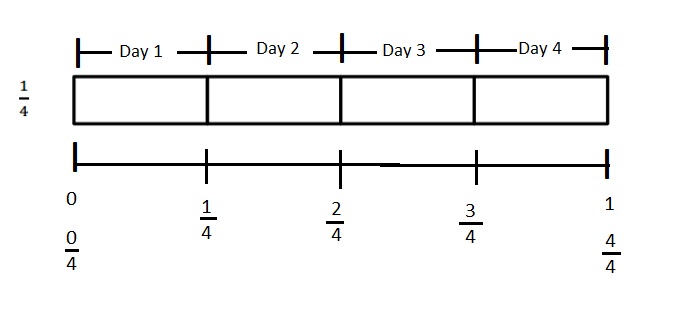
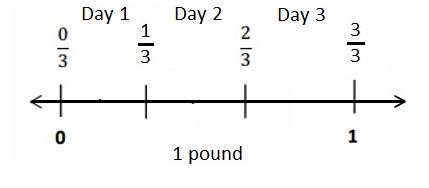
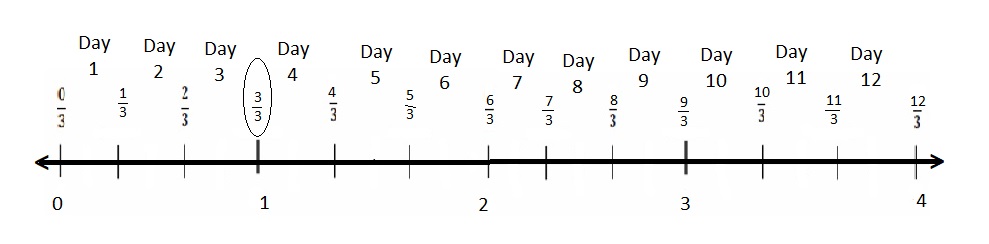
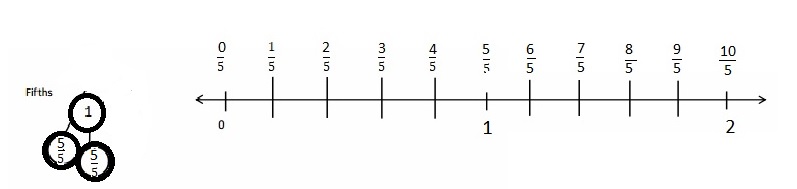
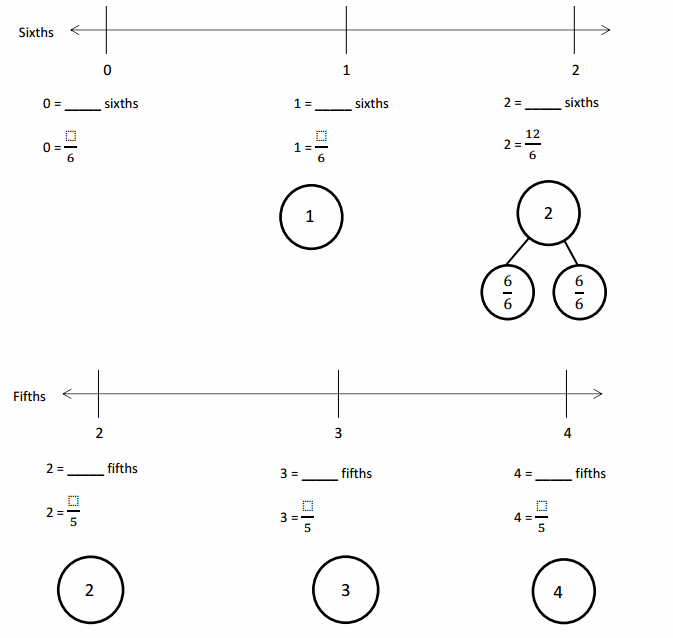
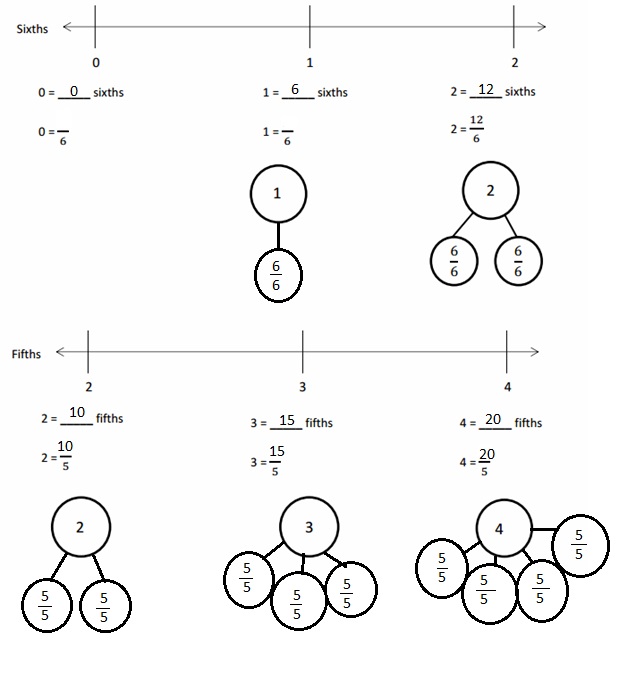
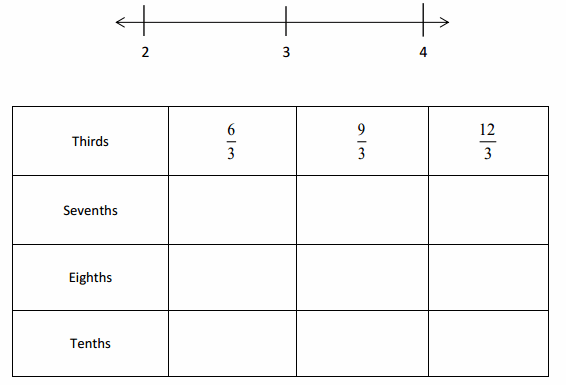
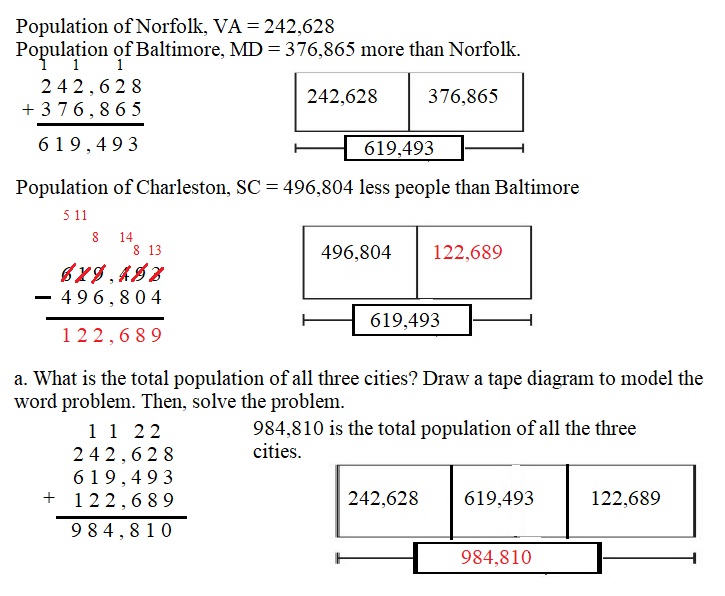
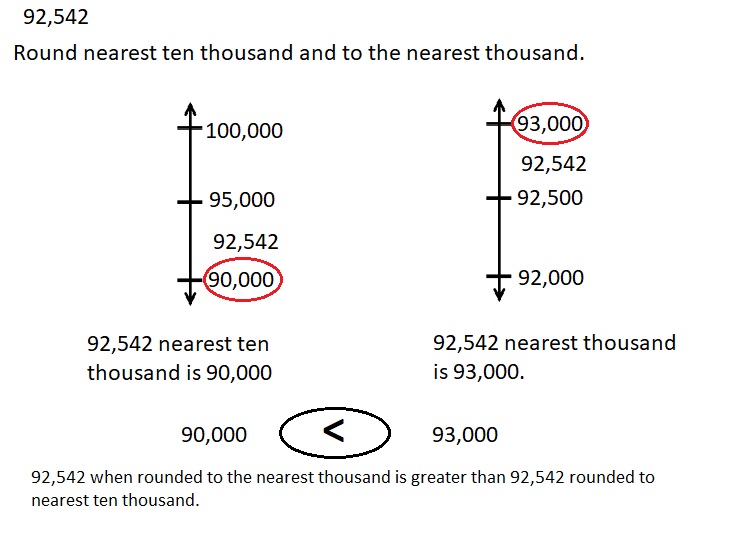
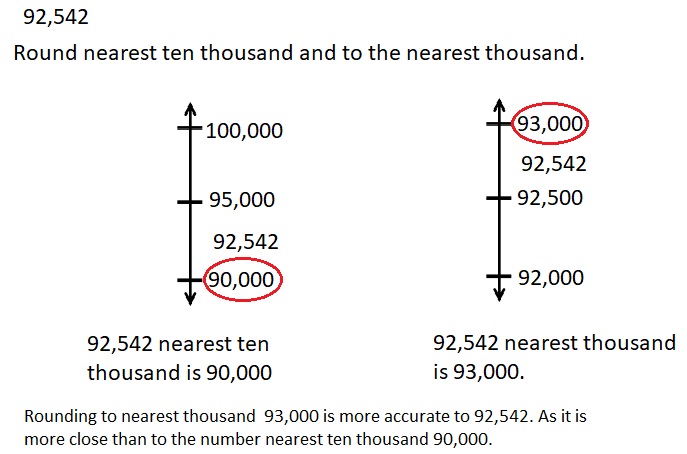
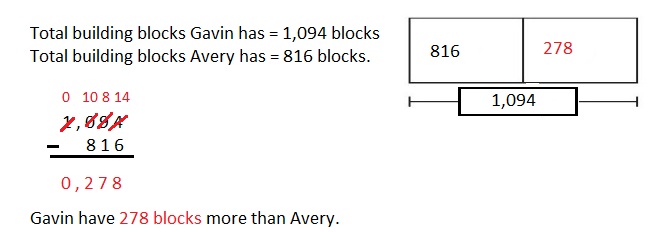
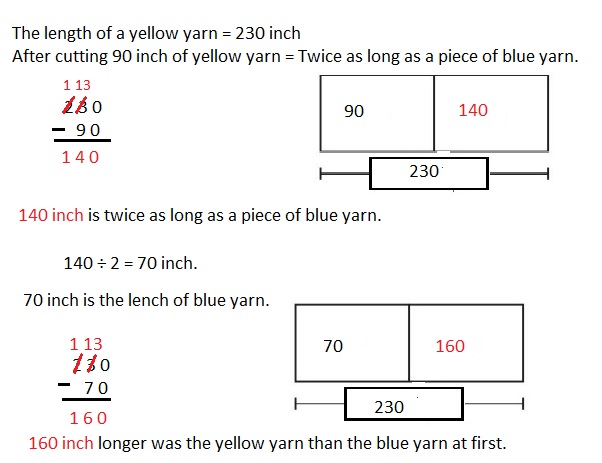
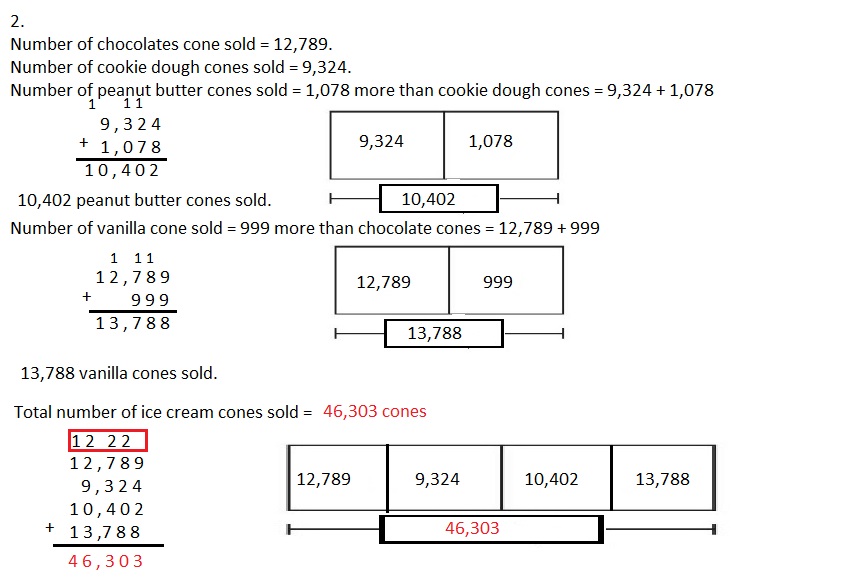
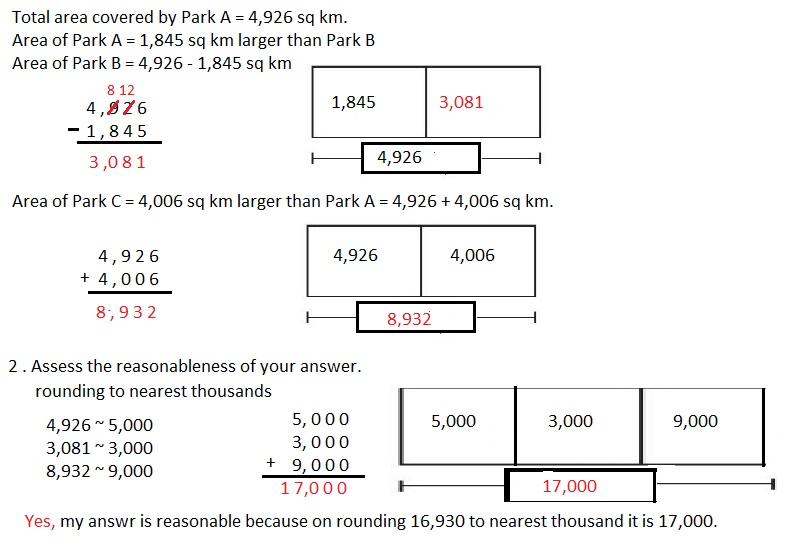
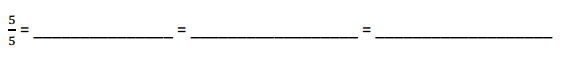Engage NY Eureka Math 4th Grade Module 3 Lesson 3 Answer Key

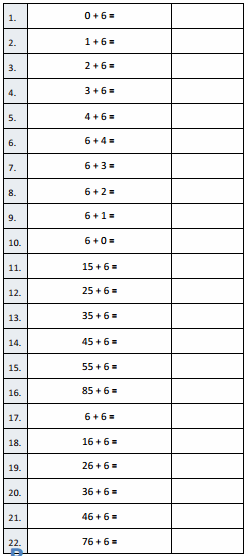
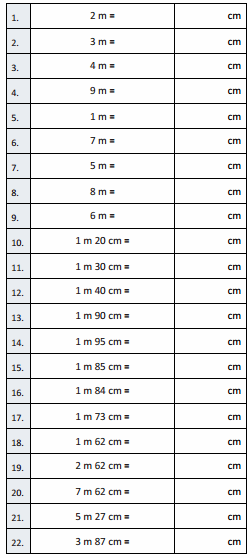
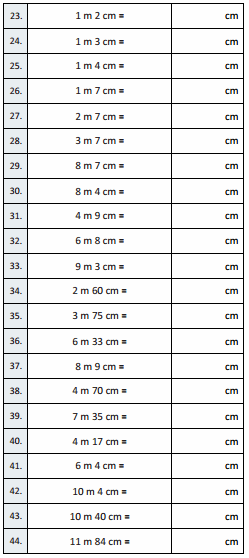
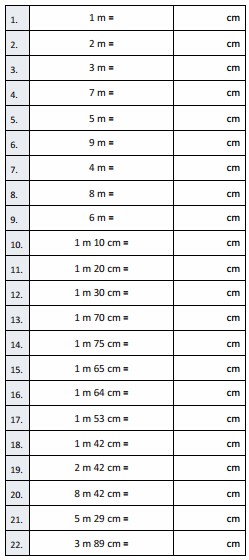
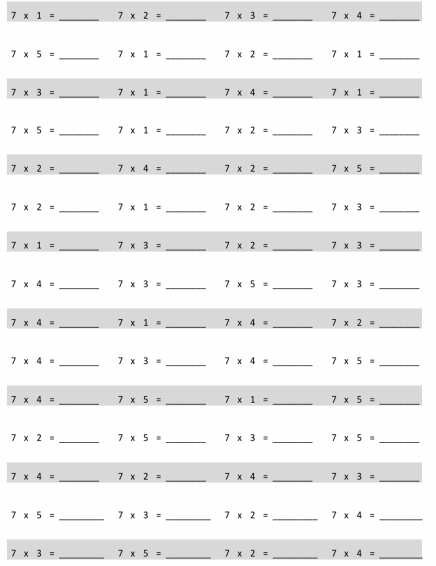
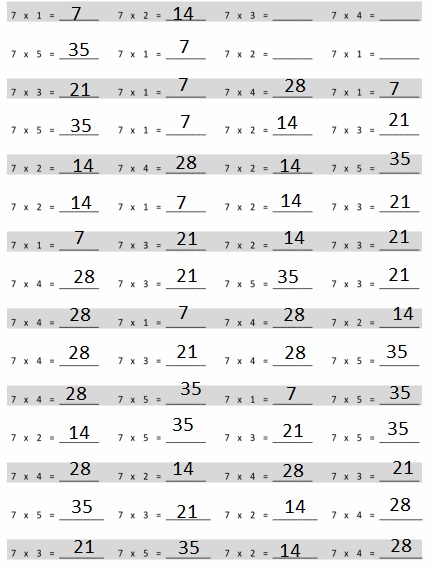
Eureka Math Grade 4 Module 3 Lesson 3 Sprint Answer Key

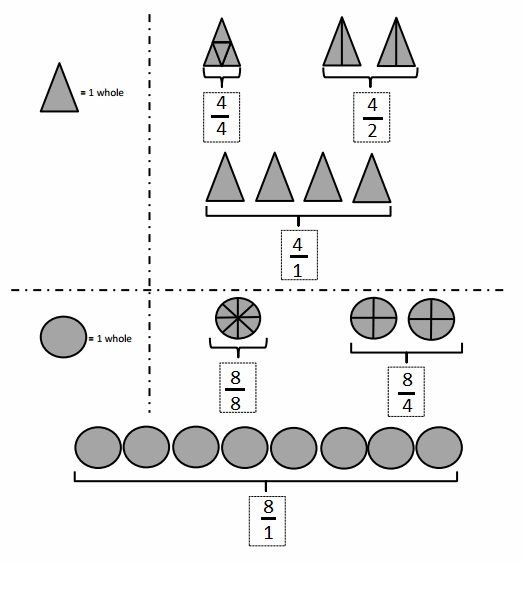
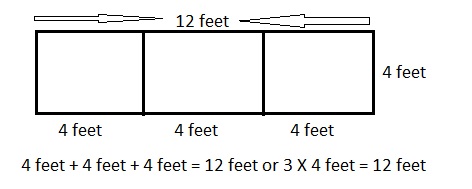
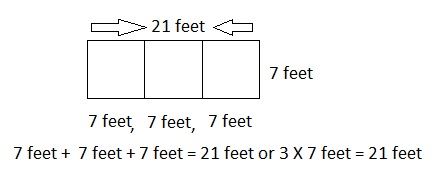
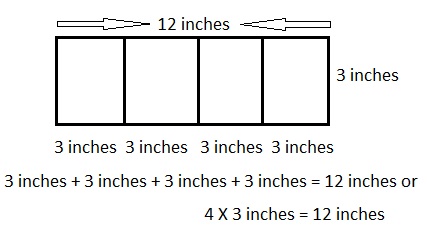
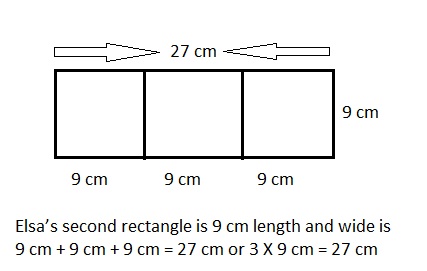
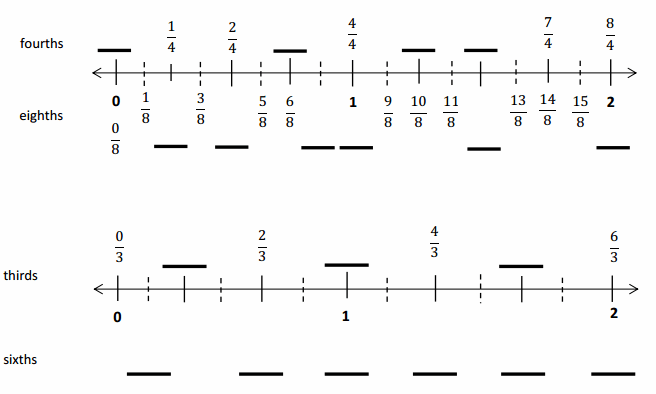
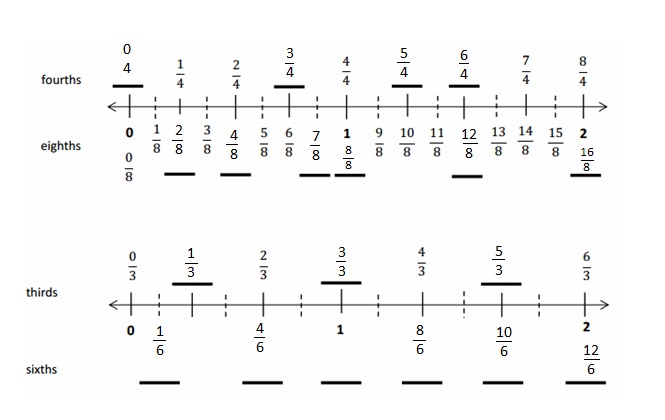
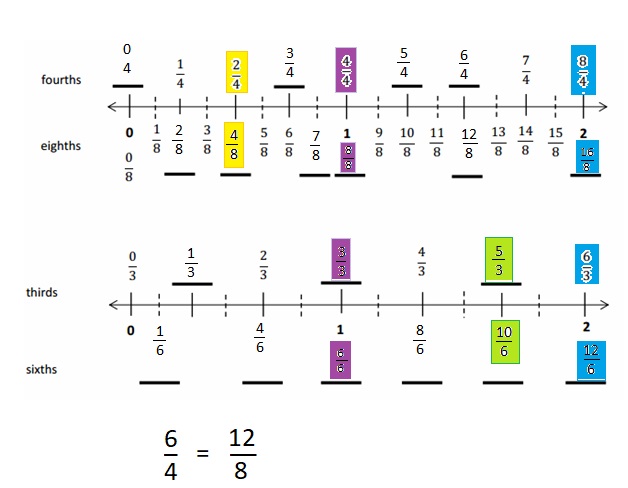
Squares and Unknown Factors

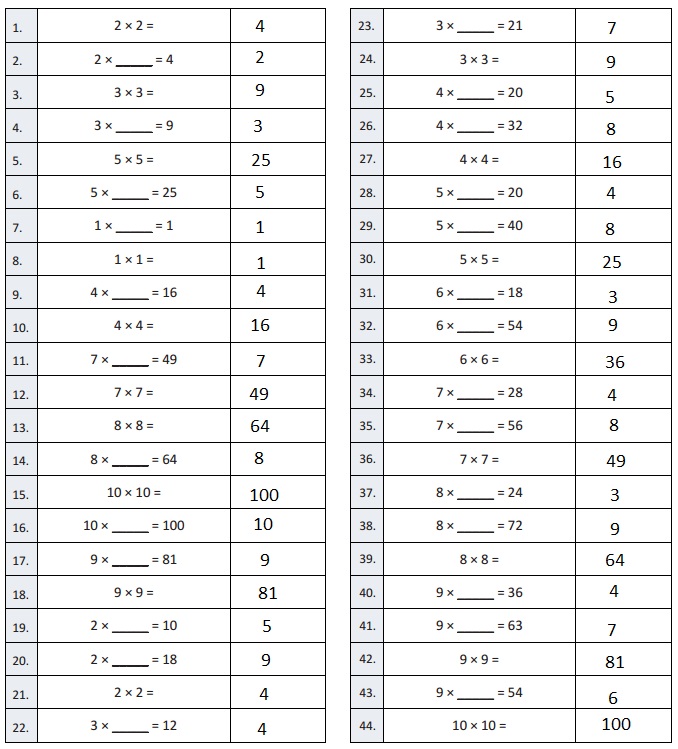
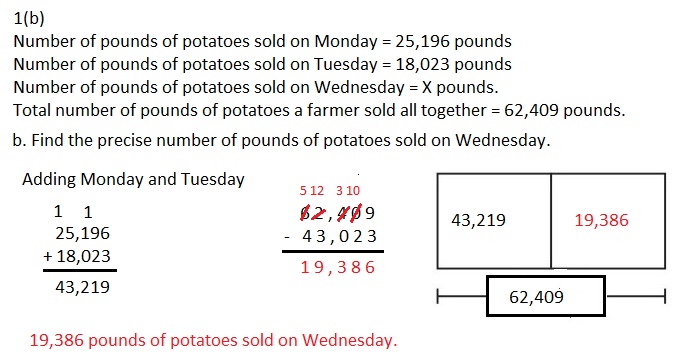
Question 1.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 2.
2 × _____ = 4
Answer:
2 X 2 = 4,

Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.

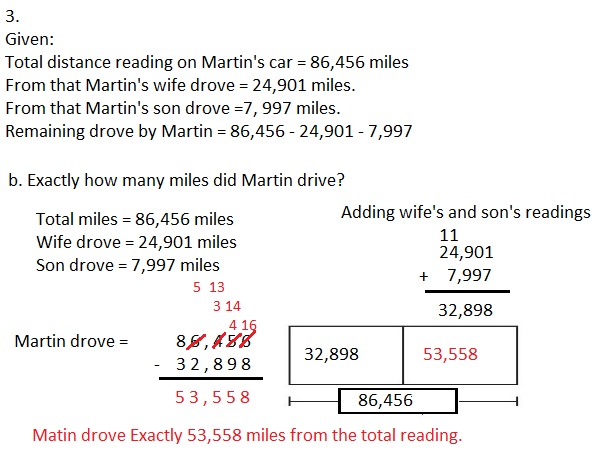
Question 3.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

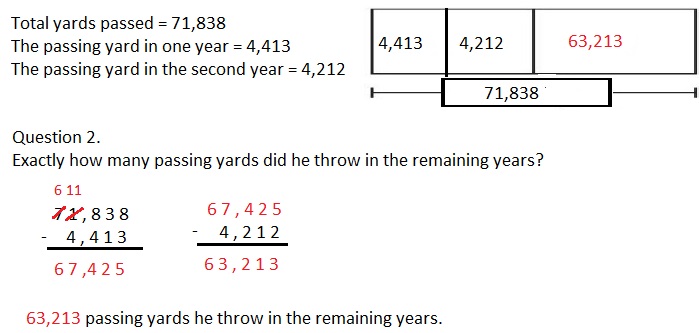
Question 4.
3 × _____ = 9
Answer:
3 X 3 = 9,

Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 2, So 3 X 3 = 9.

Question 5.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 6.
5 × _____ = 25
Answer:
5 X 5 = 25,

Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.

Question 7.
1 × _____ = 1
Answer:
1 x 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 8.
1 × 1 =
Answer:
1 X 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,

Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.

Question 10.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 11.
7 × _____ = 49
Answer:
7 X 7 = 49,

Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.

Question 12.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 13.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.

Question 14.
8 × _____ = 64
Answer:
8 X 8 = 64,

Explanation:
Given 8 × _____ = 64, the unknown factor is
64 ÷ 8 = 8, So 8 X 8 = 64.

Question 15.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,

Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.

Question 17.
9 × _____ = 81
Answer:
9 X 9 = 81,

Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.

Question 18.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.

Question 19.
2 × _____ = 10
Answer:
2 X 5 = 10,

Explanation:
Given 2 × _____ = 10, the unknown factor is
10 ÷ 2 = 5, So 2 X 5 = 10.

Question 20.
2 × _____ = 18
Answer:
2 X 9 = 18,

Explanation:
Given 2 × _____ = 18, the unknown factor is
18 ÷ 2 = 9, So 2 X 9 = 18.

Question 21.
2 × 2 =
Answer:
2 x 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 22.
3 × _____ = 12
Answer:
3 X 4 = 12,

Explanation:
Given 3 × _____ = 12, the unknown factor is
12 ÷ 3 = 4, So 3 X 4 = 12.

Question 23.
3 × _____ = 21
Answer:
3 X 7 = 21,

Explanation:
Given 3 × _____ = 21, the unknown factor is
21 ÷ 3 = 7, So 3 X 7 = 21.

Question 24.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

Question 25.
4 × _____ = 20
Answer:
4 X 5 = 20,

Explanation:
Given 4 × _____ = 20, the unknown factor is
20 ÷ 4 = 5, So 4 X 5 = 20.

Question 26.
4 × _____ = 32
Answer:
4 X 8 = 32,

Explanation:
Given 4 × _____ = 32, the unknown factor is
32 ÷ 4 = 8, So 4 X 8 = 32.

Question 27.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 28.
5 × _____ = 20
Answer:
5 X 4 = 20,

Explanation:
Given 5 × _____ = 20, the unknown factor is
20 ÷ 5 = 4, So 5 X 4 = 20.

Question 29.
5 × _____ = 40
Answer:
5 X 8 = 40,

Explanation:
Given 5 × _____ = 40, the unknown factor is
40 ÷ 5 = 8, So 5 X 8 = 40.

Question 30.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 31.
6 × _____ = 18
Answer:
6 X 3 = 18,

Explanation:
Given 6 × _____ = 18, the unknown factor is
18 ÷ 6 = 3, So 6 X 3 = 18.

Question 32.
6 × _____ = 54
Answer:
6 X 9 = 54,

Explanation:
Given 6 × _____ = 18, the unknown factor is
54 ÷ 6 = 9, So 6 X 9 = 54.

Question 33.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.

Question 34.
7 × _____ = 28
Answer:
7 X 4 = 28,

Explanation:
Given 7 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 7 X 4 = 28.

Question 35.
7 × _____ = 56
Answer:
7 X 8 = 56,

Explanation:
Given 7 × _____ = 56, the unknown factor is
56 ÷ 7 = 8, So 7 X 8 = 56.

Question 36.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = 49 the squares of 7 is 49 and
7 X 7 = 49.

Question 37.
8 × _____ = 24
Answer:
8 X 3 = 24,

Explanation:
Given 8 × _____ = 24, the unknown factor is
24 ÷ 8 = 3, So 8 X 3 = 24.

Question 38.
8 × _____ = 72
Answer:
8 X 9 = 72,

Explanation:
Given 8 × _____ = 72, the unknown factor is
72 ÷ 8 = 9, So 8 X 9 = 72.

Question 39.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8= 64 the squares of 8 is 64 and
8 X 8 = 64.

Question 40.
9 × _____ = 36
Answer:
9 X 4 = 36,

Explanation:
Given 9 × _____ = 36, the unknown factor is
36 ÷ 9 = 4, So 9 X 4 = 36.

Question 41.
9 × _____ = 63
Answer:
9 X 7 = 63,

Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.

Question 42.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9= 81 the squares of 9 is 81 and
9 X 9 = 81.

Question 43.
9 × _____ = 54
Answer:
9 X 6 = 54,

Explanation:
Given 9 × _____ = 54, the unknown factor is
54 ÷ 9 = 6, So 9 X 6 = 54.

Question 44.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10= 100 the squares of 10 is 100 and
10 X 10 = 100.

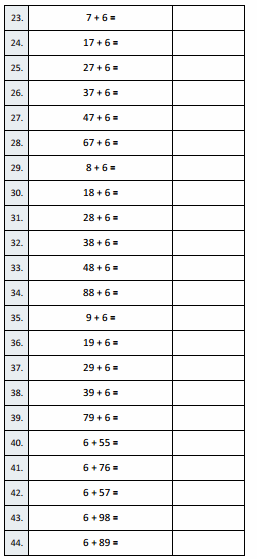
Squares and Unknown Factors

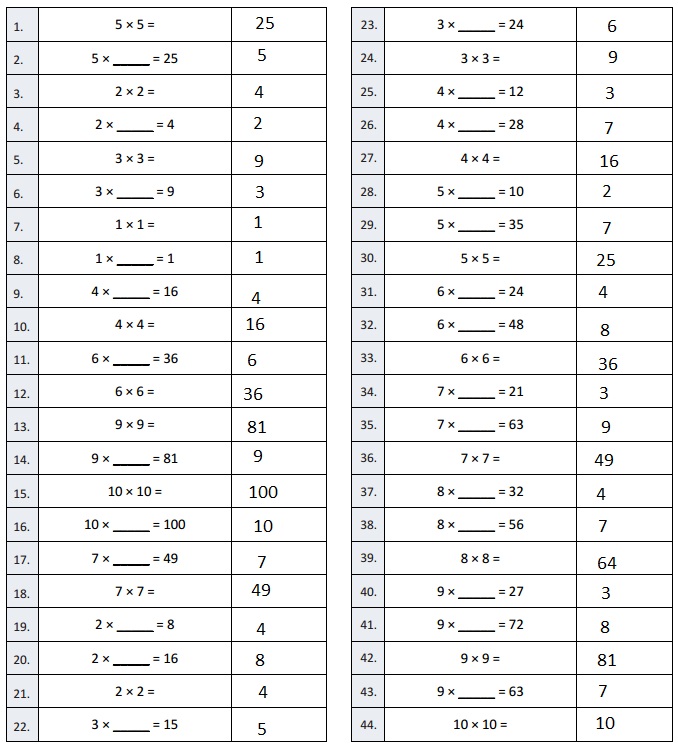
Question 1.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5= 25 the squares of 5 is 25 and
5 X 5 = 25.

Question 2.
5 × _____ = 25
Answer:
5 X 5 = 25,

Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.

Question 3.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2= 4 the squares of 2 is 4 and
2 X 2 = 4.

Question 4.
2 × _____ = 4
Answer:
2 X 2 = 4,

Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.

Question 5.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3= 9 the squares of 3 is 9 and
3 X 3 = 9.

Question 6.
3 × _____ = 9
Answer:
3 x 3 = 9,

Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 3, So 3 X 3 = 9.

Question 7.
1 × 1 =
Answer:
1 X 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 8.
1 × _____ = 1
Answer:
1 x 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,

Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.

Question 10.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 11.
6 × _____ = 36
Answer:
6 X 6 = 36,

Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.

Question 12.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.

Question 13.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.

Question 14.
9 × _____ = 81
Answer:
9 X 9 = 81,

Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.

Question 15.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,

Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.

Question 17.
7 × _____ = 49
Answer:
7 X 7 = 49,

Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.

Question 18.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 19.
2 × _____ = 8
Answer:
2 X 4 = 8,

Explanation:
Given 2 × _____ = 8, the unknown factor is
8 ÷ 2 = 4, So 2 X 4 = 8.

Question 20.
2 × _____ = 16
Answer:
2 X 8 = 16,

Explanation:
Given 2 × _____ = 16, the unknown factor is
16 ÷ 2 = 8, So 2 X 8 = 16.

Question 21.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 22.
3 × _____ = 15
Answer:
3 X 5 = 15,

Explanation:
Given 3 × _____ = 15, the unknown factor is
15 ÷ 3 = 5, So 3 X 5 = 15.

Question 23.
3 × _____ = 24
Answer:
3 X 8 = 24,

Explanation:
Given 3 × _____ = 24, the unknown factor is
24 ÷ 3 = 8, So 3 X 8 = 24.

Question 24.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

Question 25.
4 × _____ = 12
Answer:

Explanation:
Given 4 × _____ = 12, the unknown factor is
12 ÷ 4 = 3, So 4 X 3 = 12.

Question 26.
4 × _____ = 28
Answer:
4 X 7 = 28,

Explanation:
Given 4 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 4 X 7 = 28.

Question 27.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 28.
5 × _____ = 10,
Answer:
5 X 2 = 10,

Explanation:
Given 5 × _____ = 10, the unknown factor is
10 ÷ 5 = 2, So 5 X 2 = 10.

Question 29.
5 × _____ = 35,
Answer:
5 X 7 = 35,

Explanation:
Given 5 × _____ = 10, the unknown factor is
35 ÷ 5 = 7, So 5 X 7 = 35.

Question 30.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 31.
6 × _____ = 24
Answer:
6 X 4 = 24,

Explanation:
Given 6 × _____ = 24, the unknown factor is
24 ÷ 6 = 4, So 6 X 4 = 24.

Question 32.
6 × _____ = 48
Answer:
6 X 8 = 48,

Explanation:
Given 6 × _____ = 48, the unknown factor is
48 ÷ 6 = 8, So 6 X 8 = 48.

Question 33.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.

Question 34.
7 × _____ = 21
Answer:
7 X 3 = 21,

Explanation:
Given 7 × _____ = 21, the unknown factor is
21 ÷ 7 = 3, So 7 X 3 = 21.

Question 35.
7 × _____ = 63
Answer:
7 X 9 = 63,

Explanation:
Given 7 × _____ = 63, the unknown factor is
63 ÷ 7 = 9, So 7 X 9 = 63.

Question 36.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 37.
8 × _____ = 32
Answer:
8 X 4 = 32,

Explanation:
Given 8 × _____ = 32, the unknown factor is
32 ÷ 8 = 4, So 8 X 4 = 32.

Question 38.
8 × _____ = 56
Answer:
8 X 7 = 56,

Explanation:
Given 8 × _____ = 56, the unknown factor is
56 ÷ 8 = 7, So 8 X 7 = 56.

Question 39.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.

Question 40.
9 × _____ = 27
Answer:
9 X 3 = 27,

Explanation:
Given 9 × _____ = 27, the unknown factor is
27 ÷ 9 = 3, So 9 X 3 = 27.

Question 41.
9 × _____ = 72
Answer:
9 X 8 = 72,

Explanation:
Given 9 × _____ = 72, the unknown factor is
72 ÷ 9 = 8, So 9 X 8 = 72.

Question 42.
9 × 9 =
Answer:
9 X 9 = 81,

Explanation:
Given 9 X 9 = the squares of 8 is 64 and
9 X 9 = 81.

Question 43.
9 × _____ = 63
Answer:
9 X 7 = 63,

Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.

Question 44.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Eureka Math Grade 4 Module 3 Lesson 3 Problem Set Answer Key

Solve the following problems. Use pictures, numbers, or words to show your work.

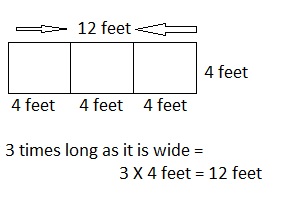
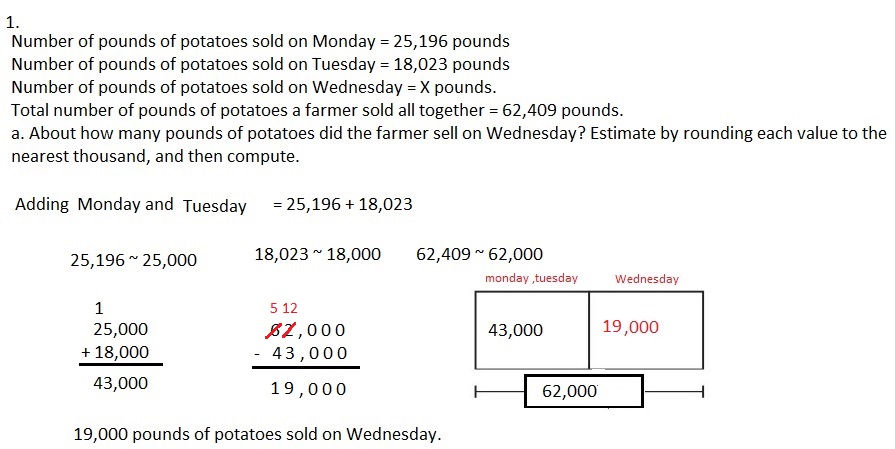
Question 1.
The rectangular projection screen in the school auditorium
is 5 times as long and 5 times as wide as the rectangular
screen in the library. The screen in the library is 4 feet long
with a perimeter of 14 feet. What is the perimeter of the
screen in the auditorium?
Answer:
The perimeter of the screen in the auditorium is 70 feet,

Explanation:
Given the rectangular projection screen in the school auditorium
is 5 times as long and 5 times as wide as the rectangular
screen in the library. The screen in the library is 4 feet long
with a perimeter of 14 feet. Let wide of of screen in library be w feet,
so 14 feet = 2 X (4 feet + w feet),
14 feet = 8 feet + 2 X w feet,
2 X w feet = 14 feet – 8 feet = 6 feet,
So wide = 6 feet ÷ 2 = 3 feet,
Now the rectangular projection screen in the school auditorium
is 5 X 4 feet = 20 feet long and wide is 5 X 3 feet = 15 feet wide,
So the perimeter of the screen in the auditorium is
2 X (20 feet + 15 feet) = 2 X 35 feet = 70 feet.

Question 2.
The width of David’s rectangular tent is 5 feet. The length is
twice the width. David’s rectangular air mattress measures
3 feet by 6 feet. If David puts the air mattress in the tent,
how many square feet of floor space will be available for
the rest of his things?
Answer:
32 square feet of floor space will be available for
the rest of his things,

Explanation:
Given the width of David’s rectangular tent is 5 feet. The length is
twice the width. David’s rectangular air mattress measures
3 feet by 6 feet. Area of the rectangular tent is
5 feet X ( 2 X 5 feet) = 5 feet X 10 feet = 50 square feet,
now David’s rectangular air mattress area is 3 feet x 6 feet =
18 square feet, If David puts the air mattress in the tent,
number of square feet of floor space will be available for
the rest of his things is 50 square feet – 18 square feet =
32 square feet.

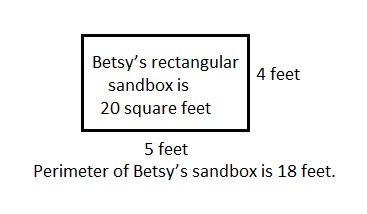
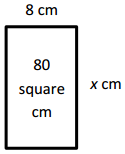
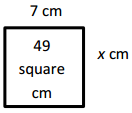
Question 3.
Jackson’s rectangular bedroom has an area of 90 square feet.
The area of his bedroom is 9 times that of his rectangular closet.
If the closet is 2 feet wide, what is its length?
Answer:
The closet length is 5 feet,

Explanation:
Given Jackson’s rectangular bedroom has an area of 90 square feet.
The area of his bedroom is 9 times that of his rectangular closet.
So closet area is 90 X feet X feet ÷ 9 = 10 square feet,
As given closet is 2 feet wide, the length will be
10 feet X feet = 2 feet X length of the closet,
length of the closet = 10 feet x feet ÷ 2 feet = 5 feet.
therefore the length of the closer is 5 feet.

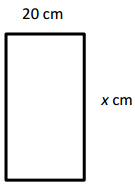
Question 4.
The length of a rectangular deck is 4 times its width.
If the deck’s perimeter is 30 feet, what is the deck’s area?
Answer:
The area of the deck is 36 square feet,

Explanation:
Given the length of a rectangular deck is 4 times its width.
If the deck’s perimeter is 30 feet, then
30 feet = 2 X (4 X width + width) ,
30 feet ÷ 2 = 5 X width,
15 feet = 5 width
therefore width = 15 feet ÷ 5 = 3 feet and
length = 4 X 3 feet = 12 feet,
Now the area of the deck is 12 feet X 3 feet = 36 square feet.

Eureka Math Grade 4 Module 3 Lesson 3 Exit Ticket Answer Key

Solve the following problem. Use pictures, numbers, or
words to show your work.

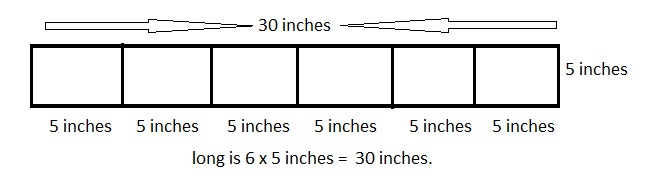
A rectangular poster is 3 times as long as it is wide.
A rectangular banner is 5 times as long as it is wide.
Both the banner and the poster have perimeters of 24 inches.
What are the lengths and widths of the poster and the banner?
Answer:
The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide,

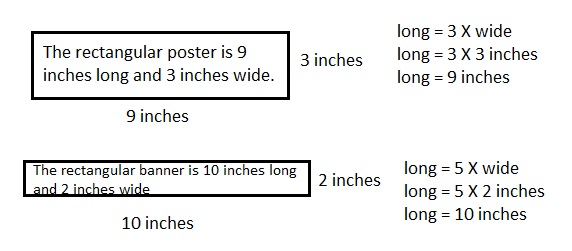
Explanation:
Given a rectangular poster is 3 times as long as it is wide.
A rectangular banner is 5 times as long as it is wide.
Both the banner and the poster have perimeters of 24 inches.
First rectangular poster, So 24 inches = 2 X (3 X wide + wide),
24 inches ÷ 2 = 4 wide,
12 inches = 4 wide
therefore wide = 12 inches ÷ 4 = 3 inches and
long =3 X 3 inches = 9 inches,
Now rectangular banner, 24 inches = 2 X (5 X wide + wide),
24 inches ÷ 2 = 6 wide,
12 inches = 6 wide,
wide = 12 inches ÷ 6 = 2 inches, and long = 5 X 2 inches = 10 inches,
Shown the work above in the picture,
Therefore, The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide.

Eureka Math Grade 4 Module 3 Lesson 3 Homework Answer Key

Solve the following problems. Use pictures, numbers, or words to show your work.

Question 1.
Katie cut out a rectangular piece of wrapping paper that was
2 times as long and 3 times as wide as the box that she
was wrapping. The box was 5 inches long and 4 inches wide.
What is the perimeter of the wrapping paper that Katie cut?
Answer:
The perimeter of the wrapping paper that Katie cut is 44 inches,

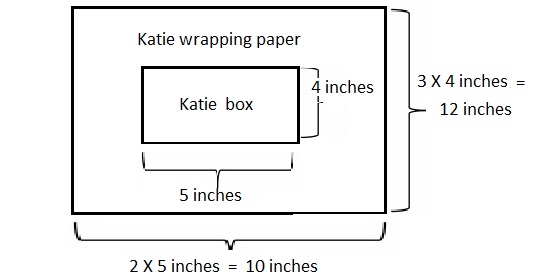
Explanation:
Given Katie cut out a rectangular piece of wrapping paper that was
2 times as long and 3 times as wide as the box that she
as wrapping. The box was 5 inches long and 4 inches wide.
So the wrapping paper length is 2 X 5 inches = 10 inches and
width is 3 X 4 inches = 12 inches, Now the perimeter of the
wrapping paper that Katie cut is 2 X (10 inches + 12 inches) =
2 X 22 inches = 44 inches. Shown the work above in the picture,
therefore, the perimeter of the wrapping paper that Katie cut is 44 inches.

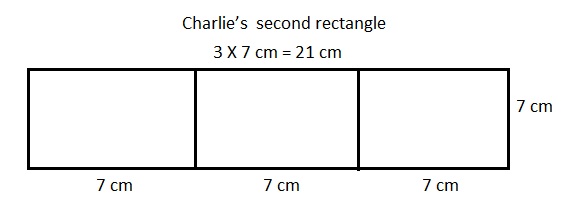
Question 2.
Alexis has a rectangular piece of red paper that is
4 centimeters wide. Its length is twice its width.
She glues a rectangular piece of blue paper on top
of the red piece measuring 3 centimeters by 7 centimeters.
How many square centimeters of red paper will be visible on top?
Answer:
11 square centimeters of red paper will be visible on top,

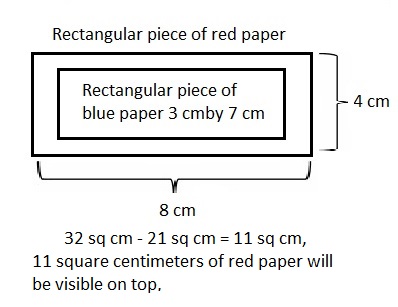
Explanation:
Given Alexis has a rectangular piece of red paper that is
4 centimeters wide. Its length is twice its width.
She glues a rectangular piece of blue paper on top
of the red piece measuring 3 centimeters by 7 centimeters.
Area of rectangular piece of red paper = 4 cm X ( 2 X 4 cm) =
4 cm X 8 cm = 32 square cm, Now area of rectangular piece
of blue paper on top of the red piece is 3 cm X 7 cm = 21 square cm,
So number of square centimeters of red paper will be visible on top
is 32 sq cm – 21 sq cm = 11 sq cm. Shown the work above in the picture,
Therefore, 11 square centimeters of red paper will be visible on top.

Question 3.
Brinn’s rectangular kitchen has an area of 81 square feet.
The kitchen is 9 times as many square feet as Brinn’s pantry.
If the rectangular pantry is 3 feet wide,
what is the length of the pantry?
Answer:
The length of the pantry is 3 feet,

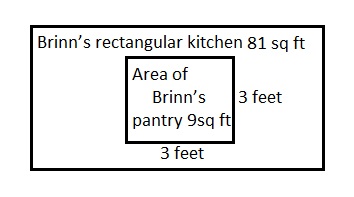
Explanation:
Given Brinn’s rectangular kitchen has an area of 81 square feet.
The kitchen is 9 times as many square feet as Brinn’s pantry.
So area of Brinn’s pantry is 81 sq feet ÷ 9 = 9 sq feet,
Given the rectangular pantry is 3 feet wide so
length of the pantry is 9 sq feet ÷ 3 feet = 3 feet,
Shown the work above in the picture, therefore
the length of the pantry is 3 feet.

Question 4.
The length of Marshall’s rectangular poster is 2 times its width.
If the perimeter is 24 inches, what is the area of the poster?
Answer:
The area of the Marshall’s poster is 32 square inches,

Explanation:
Given the length Marshall’s rectangular poster is 2 times its width
and the perimeter is 24 inches, so 24 inches = 2 X (2 X width + width),
24 inches ÷ 2 = 3 X width,
12 inches =  3 X width
So width = 12 inches ÷ 3 = 4 inches, length = 2 X 4 inches = 8 inches,
now area of the poster is 8 inches X 4 inches = 32 square inches,
Shown the work above in the picture, therefore
The area of the poster is 32 square inches.

Engage NY Eureka Math 4th Grade Module 3 Lesson 2 Answer Key

Eureka Math Grade 4 Module 3 Lesson 2 Problem Set Answer Key

Question 1.
A rectangular porch is 4 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the porch.

Answer:

Explanation:
Given a rectangular porch is 4 feet wide.
It is 3 times as long as it is wide.
Labeled the diagram with the dimensions of the porch as
shown above, width= 4 feet and long = 3 X 4 feet = 12 feet
or 4 feet + 4 feet + 4 feet = 12 feet respectively.

b. Find the perimeter of the porch.
Answer:
Perimeter of the porch is 32 feet,

Explanation:
Given width = 4 feet and long is 12 feet, so perimeter
of rectangular porch is 2 X ( 12 feet + 4 feet) =
2 X (16 feet) = 32 feet.

Question 2.
A narrow rectangular banner is 5 inches wide.
It is 6 times as long as it is wide.
a. Draw a diagram of the banner, and label its dimensions.
Answer:

Explanation:
Drawn a diagram of the banner, and labeled its dimensions
as shown above wide 5 inches and long is 6 x 5 inches =
30 inches.

b. Find the perimeter and area of the banner.
Answer:
Perimeter of the banner : 70 inches,
Area of the banner : 150 inches²,

Explanation:
Given a narrow rectangular banner is 5 inches wide.
It is 6 times as long as it is wide. So wide = 5 inches,
long = 6 X 5 inches = 30 inches,
Perimeter of the banner = 2 X (l + w) = 2 X (30 inches + 5 inches) =
2 X ( 35 inches) = 70 inches and area of the banner = l X w =
30 inches X 5 inches = 150 square inches.

Question 3.
The area of a rectangle is 42 square centimeters.
Its length is 7 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 6 centimeters,

Explanation:
Given The area of a rectangle is 42 square centimeters.
Its length is 7 centimeters. So let us take width as x cm,
so 42 sq cm = 7 cm X x cm, x cm = 42 sq cm X cm ÷ 7 cm = 6 cm,
therefore, the width of the rectangle is 6 centimeters.

b. Charlie wants to draw a second rectangle that is the
same length but is 3 times as wide. Draw and label
Charlie’s second rectangle.
Answer:

Explanation:
Given Charlie wants to draw a second rectangle that is the
same length but is 3 times as wide means length is 7 cm and
wide is 3 X 7 cm = 21 cm, Drawn and labeled Charlie’s
second rectangle as shown above.

c. What is the perimeter of Charlie’s second rectangle?
Answer:
Perimeter of Charlie’s second rectangle is 56 centimeters,

Explanation:
Given Charlie’s second rectangle has length 7 cm and
width as 21 cm so perimeter is 2 X ( 7 cm + 21 cm) =
2 X (28 cm) = 56 cm, therefore perimeter of Charlie’s
second rectangle is 56 centimeters.

Question 4.
The area of Betsy’s rectangular sandbox is 20 square feet.
The longer side measures 5 feet. The sandbox at the park is
twice as long and twice as wide as Betsy’s.
a. Draw and label a diagram of Betsy’s sandbox.
What is its perimeter?
Answer:
Perimeter of Betsy’s sandbox is 18 feet,

Explanation:
Given the area of Betsy’s rectangular sandbox is 20 square feet.
The longer side measures 5 feet. Drawn and labeled a diagram
of Betsy’s sandbox as shown above and the its perimeter is as
area = 20 square feet, lets take width as x feet so
x feet = 20 feet X feet ÷ 5 feet = 4 feet, now perimeter =
2 X ( 5 feet + 4 feet) = 2 X 9 feet = 18 feet,
therefore, Perimeter of Betsy’s sandbox is 18 feet.

b. Draw and label a diagram of the sandbox at the park.
What is its perimeter?
Answer:
The perimeter of the sand box at park is 36 feet,

Explanation:
Given the sandbox at the park is twice as long
and twice as wide as Betsy’s means long is
5 feet + 5 feet = 10 feet and wide is 4 feet + 4 feet = 8 feet,
Now draw and labeled a diagram of the sandbox at the park.
Perimeter of sandbox at park is 2 X (10 feet + 8 feet) =
2 X 18 feet = 36 feet.

c. What is the relationship between the two perimeters?
Answer:
Perimeter of sandbox at park is twice the perimeter of Betsy’s sandbox,

Explanation:
As both length and width of sandbox at park is twice of
Betsy’s sandbox, so their perimeter of sandbox at park is twice
the perimeter of Betsy’s sandbox.

d. Find the area of the park’s sandbox using the formula A = l × w.
Answer:
Area of the park’s sandbox is 80 square feet,

Explanation:
As sandbox at park has 10 feet long and 8 feet wide so
area of sandbox at park is 10 feet X 8 feet = 80 square feet.

e. The sandbox at the park has an area that is how many
times that of Betsy’s sandbox?
Answer:
The sandbox at the park has an area that is four
times that of Betsy’s sandbox,

Explanation:
Given area of Betsy’s rectangular sandbox is 20 square feet
and area of the park’s sandbox is 80 square feet,
so number of times more is 80 square feet ÷ 20 square feet = 4,
therefore the sandbox at the park has an area that is four
times that of Betsy’s sandbox.

f. Compare how the perimeter changed with how the area changed between the two sandboxes. Explain what you notice using words,
pictures, or numbers.
Answer:
Sand box at park has twice perimeter and area has became
four times that of Betsy’s sandbox,

Explanation:
As we know Perimeter of Betsy’s sandbox is 18 feet and
perimeter of the sand box at park is 36 feet,
Area of Betsy’s rectangular sandbox is 20 square feet and
area of the park’s sandbox is 80 square feet, Now on comparing
Sand box at park has twice perimeter and area has became
four times to that of Betsy’s sandbox.

Eureka Math Grade 4 Module 3 Lesson 2 Exit Ticket Answer Key

Question 1.
A table is 2 feet wide. It is 6 times as long as it is wide.
a. Label the diagram with the dimensions of the table.

Answer:

Explanation:
Labeled the diagram with the dimensions of the table as
shown above, wide= 2 feet and long is  6 X 2 feet = 12 feet.

b. Find the perimeter of the table.
Answer:
Perimeter of the table is 28 feet,

Explanation:
Given wide is 2 ffet and long is 12 feet,
So Perimeter of the table is 2 X ( 12 feet + 2 feet) =
2 X 14 feet = 28 feet.

Question 2.
A blanket is 4 feet wide. It is 3 times as long as it is wide.
a. Draw a diagram of the blanket, and label its dimensions.
Answer:

Explanation:
Labeled the diagram of the blanket with the dimensions as
shown above, wide= 4 feet and long is  3 X 4 feet = 12 feet.

b. Find the perimeter and area of the blanket.
Answer:
Perimeter is 32 feet and area of the blanket is 48 square feet,

Explanation:
Given wide as 4 feet and long is 12 feet, So perimeter of the
blanket is 2 X (12 feet + 4 feet) = 2 X (16 feet) = 32 feet and
area is 12 feet X 4 feet = 48 square feet.

Eureka Math Grade 4 Module 3 Lesson 2 Homework Answer Key

Question 1.
A rectangular pool is 7 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the pool.

Answer:

Explanation:
Labeled the diagram of the rectangular pool with
the dimensions as shown above, wide= 7 feet and
long is  3 X 7 feet = 21 feet.

b. Find the perimeter of the pool.
Answer:
Perimeter of the rectangular pool is 56 feet,

Explanation:
Given rectangular pool is 7 feet wide and 21 feet long,
So perimeter is 2 X (21 feet + 7 feet) = 2 X 28 feet = 56 feet.

Question 2.
A poster is 3 inches long. It is 4 times as wide as it is long.
a. Draw a diagram of the poster, and label its dimensions.
Answer:

Explanation:
Labeled the diagram of the poster with
the dimensions as shown above, long = 3 inches,
and wide is  4 X 3 inches = 12 inches.

b. Find the perimeter and area of the poster.
Answer:
Perimeter of the poster is 30 inches and
area of the poster is 36 square inches,

Explanation:
Given poster as 3 inches long and 4 X 3 inches = 12 inches wide,
So perimeter of the poster is 2 X ( 3 inches + 12 inches) =
2 X 15 inches = 30 inches and area of the poster is
3 inches X 12 inches = 36 square inches.

Question 3.
The area of a rectangle is 36 square centimeters, and
its length is 9 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 4 centimeters,

Explanation:
Given the area of a rectangle is 36 square centimeters
and its length is 9 centimeters so width of the rectangle is
36 sq cm = 9 cm X width , width = 36 cm X cm ÷ 9 cm = 4 cm,
therefore the width of the rectangle is 4 centimeters.

b. Elsa wants to draw a second rectangle that is the
same length but is 3 times as wide. Draw and label
Elsa’s second rectangle.
Answer:

Explanation:
Given Elsa wants to draw a second rectangle that is the
same length but is 3 times as wide. Drawn and labeled
Elsa’s second rectangle with length as 9 centimeters and
wide as 3 X 9 cm = 27 centimeters.

c. What is the perimeter of Elsa’s second rectangle?
Answer:
Perimeter of Elsa’s second rectangle is 72 centimeters,

Explanation:
Given Elsa’s second rectangle is with length 9 cm and
wide is 27 cm, So perimeter is 2 X (9 cm + 27 cm) =
2 X (36 cm) = 72 centimeters.
therefore, Perimeter of Elsa’s second rectangle is 72 centimeters.

Question 4.
The area of Nathan’s bedroom rug is 15 square feet.
The longer side measures 5 feet. His living room rug is
twice as long and twice as wide as the bedroom rug.
a. Draw and label a diagram of Nathan’s bedroom rug.
What is its perimeter?
Answer:

Perimeter of Nathan’s bedroom rug is 16 feet,

Explanation:
Given the area of Nathan’s bedroom rug is 15 square feet.
The longer side measures 5 feet so width is
15 feet X feet ÷ 5 feet = 3 feet, now preimeter of
Nathan’s bedroom rug is 2 X (5 feet + 3 feet) =
2 X 8 feet = 16 feet, Drawn and labeled a diagram of
Nathan’s bedroom rug as shown above.

b. Draw and label a diagram of Nathan’s living room rug.
What is its perimeter?
Answer:

Perimeter of Nathan’s living room rug is 32 feet,

Explanation:
Drawn and labeled a diagram of Nathan’s living room rug
as shown above with long as 2 X 5 feet = 10 feet and
width as 2 X 3 feet = 6 feet. Perimeter of Nathan’s
living room rug is2 X (10 feet + 6 feet) 2 X 16 feet = 32 feet.

c. What is the relationship between the two perimeters?
Answer:
The perimeter of Nathan’s living room rug is twice the
perimeter of Nathan’s bedroom rug,

Explanation:
As perimeter of Nathan’s bedroom rug is 16 feet and
perimeter of Nathan’s living room rug is 32 feet and
as both length and width of Nathan’s living room rug is
twice of Nathan’s bedroom rug.

d. Find the area of the living room rug using the formula A = l × w.
Answer:
The area of the living room rug is 60 square feet,

Explanation:
Given living room rug has long 10 feet and width 6 feet,
So area of the living room rug is 10 feet X 6 feet = 60 square feet.

e. The living room rug has an area that is how many
times that of the bedroom rug?
Answer:
The living room rug has an area that is four
times that of the bedroom rug,

Explanation:
The area of the living room rug is 60 square feet and
the area of Nathan’s bedroom rug is 15 square feet.
So number of times the area of the living room rug to
the area of Nathan’s bedroom rug is
60 sq feet ÷ 15 square feet = 4,
Therefore, the living room rug has an area that is four
times that of the bedroom rug.

f. Compare how the perimeter changed with how
the area changed between the two rugs.
Explain what you notice using words, pictures, or numbers.
Answer:
Nathan’s living room has twice perimeter and area has became
four times that of Nathan’s bedroom rug,

Explanation:
As we know Perimeter of  is Nathan’s bedroom rug 16 feet and
perimeter of Nathan’s living room is 32 feet,
Area of Nathan’s bedroom rug is 15 square feet and
area of Nathan’s living room is 60 square feet, Now on comparing
Nathan’s living room has twice perimeter and area has became
four times to that of Nathan’s bedroom rug.

Engage NY Eureka Math 4th Grade Module 3 Lesson 1 Answer Key

Eureka Math Grade 4 Module 3 Lesson 1 Problem Set Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

a. A = _____63 cm²__________     A = ______54 cm²_________

b. P = ______32 cm_________     P = ______30 cm_________
Answer:

a. A = 63 cm² , A = 54 cm²,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Area of rectangle is = l X b = 9 cm X 7 cm = 63 square cm,
and in figure B length = 6 cm , breadth = 9 cm,
Area of rectangle is = l X b = 6 cm X 9 cm = 54 square cm.

b. P = 32 cm,  P = 30 cm,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Perimeter of rectangle is =2 X (l + b) = 2(9 cm + 7 cm) =
2 X (16 cm) = 32 cm,
and in figure B length = 6 cm , breadth = 9 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (6 cm + 9 cm) =
2 X (15 cm) = 30 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

P = _____22 cm_______
A = _____30 cm²_______
Answer:
Perimeter = 22 cm,
Area = 30 cm²,

Explanation:
Given length = 5 cm and breadth = 6 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (5 cm + 6 cm) =
2 X (11 cm) = 22 cm,
Area of rectangle is = l X b = 5 cm X 6 cm = 30 square cm.

b.

P = ____22 cm_______
A = ____ 24 cm²________
Answer:
Perimeter = 22 cm,
Area = 24 cm²,

Explanation:
Given length = 8 cm and breadth = 3 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (8 cm + 3 cm) =
2 X (11 cm) = 22 cm,
Area of rectangle is = l X b = 8 cm X 3 cm = 24 square cm.

Question 3.
Determine the perimeter of each rectangle.
a.

P = ____530 m________
Answer:
Perimeter = 530 m,

Explanation:
Given length = 99 m and breadth = 166 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (99 m + 166 m) =
2 X ( 265 m) = 530 m.

b.

P = ____450 cm________
Answer:
Perimeter =  450 cm,

Explanation:
Given length = 75 cm and breadth = 1 m 50 cm,
we know 1 m = 100 cm ,
so breadth =  1 X 100 cm + 50 cm =150 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (75 cm + 150 cm) =
2 X (225 cm) = 450 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

x = ____10 cm________
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 8 cm and area as 80 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 80 sq cm = 8 cm X x cm,
So x cm = 80 sq cm ÷ 8 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

x = ____7 cm________
Answer:
Unknown side length = 7 cm,

Explanation:
Given width of rectangle as 7 cm and area as 49 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 49 sq cm = 7 cm X x cm,
So x cm = 49 sq cm ÷ 7 cm = 7 cm,
therefore unknown side length = 7 cm.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 120 cm

Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 20 cm and perimeter as 120 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 X (length + breadth),
So 120 cm = 2 X (x cm + 20 cm),
120 cm ÷ 2 = (x cm + 20 cm),
60 cm = (x cm + 20 cm),
So x cm = 60 cm – 20 cm = 40 cm,
therefore unknown side length = 40 cm.

b. p = 1000 m

Answer:
Unknown side width = 250 m,

Explanation:
Given length of rectangle as 250 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 X (length + breadth),
So 1000 m = 2 X (250 m + x m),
1000 m ÷ 2 = (250 m + x m ),
500 m = 250 m + x m ,
So x m = 500 m – 250 m = 250 m,
therefore unknown side length = 250 m.

Question 6.
Each of the following rectangles has whole number side lengths.
Given the area and perimeter, find the length and width.
a. P = 20 cm

Answer:
The whole number side lengths are
If length of rectangle is 4 cm then width is 6 cm or
length of rectangle is 6 cm then width is 4 cm,

Explanation:
Given area = 24 square cm and perimeter = 20 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 24 sq cm = l X w and
perimeter = 2 X (length + width) ,
20 cm = 2 X ( l + w), l + w = 20 cm ÷ 2 =10 cm,
so l = 10 cm – w, now 24 = (10 – w) X w,
we get w²– 10 w + 24 = 0,
So w²– 6 w – 4 w + 24 = 0,
w(w – 6) – 4(w – 6) = 0, therefore w = 6 cm or w = 4 cm,
So l = 10 cm – 6 cm = 4 cm or l = 10 cm  – 4 cm = 6 cm,
Therfore, If length of rectangle is 4 cm then width is 6 cm or
length of rectangle is 6 cm then width is 4 cm.

b. P = 28 m

Answer:
The whole number side lengths are
If length of rectangle is 2 m then width is 12 m or
length of rectangle is 12 m then width is 2 m.

Explanation:
Given area = 24 square m and perimeter = 28 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 24 sq m = l X w and
perimeter = 2 X (length + width) ,
28 m = 2 X ( l + w), l + w = 28 m ÷ 2 =14 m,
so l = 14 m – w, now 24 = (14 – w) X w,
we get w²– 14 w + 24 = 0,
So w²– 12 w – 2 w + 24 = 0,
w(w – 12) – 2(w – 12) = 0, therefore w = 12 m or w = 2 m,
So l = 14 m – 12 m = 2 m or l = 14 m – 2 m = 12 m,
Therfore, If length of rectangle is 2 m then width is 12 m or
length of rectangle is 12 m then width is 2 m.

Eureka Math Grade 4 Module 3 Lesson 1 Exit Ticket Answer Key

Question 1.
Determine the area and perimeter of the rectangle.

Answer:
Area = 16 cm²,
Perimeter = 20 cm,

Explanation:
Given length = 8 cm and breadth = 2 cm,
Area of rectangle is = l X b = 8 cm X 2 cm = 16 square cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (8 cm + 2 cm) =
2 X (10 cm) = 20 cm.

Question 2.
Determine the perimeter of the rectangle.

Answer:
Perimeter = 892 m,

Explanation:
Given length = 347 m and breadth = 99 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (347 m + 99 m) =
2 X (446 m) = 892 m.

Eureka Math Grade 4 Module 3 Lesson 1 Homework Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

a. A = _____40 cm²__________    A = ______35 cm²_________

b. P = ______26 cm_________    P = _______24 cm________
Answer:

a. A = 40 cm² , A = 35 cm²,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Area of rectangle is = l X b = 8 cm X 5 cm = 40 square cm,
and in figure B length = 5 cm , breadth = 7 cm,
Area of rectangle is = l X b = 5 cm X 7 cm = 35 square cm,

b. P = 26 cm,  P = 24 cm,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Perimeter of rectangle is =2 X (l + b) = 2(8 cm + 5 cm) =
2 X (13 cm) = 26 cm,
and in figure B length = 5 cm , breadth = 7 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (5 cm + 7 cm) =
2 X (12 cm) = 24 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

P = ____20 cm________
A = ___ 21 cm²____
Answer:
Perimeter = 20 cm,
Area = 21 cm²,

Explanation:
Given length = 7 cm and breadth = 3 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (7 cm + 3 cm) =
2 X (10 cm) = 20 cm,
Area of rectangle is = l X b = 7 cm X 3 cm = 21 square cm,

b.

P = ___26 cm_________
A = ______36 cm²______
Answer:
Perimeter = 26 cm,
Area = 36 cm²,

Explanation:
Given length = 9 cm and breadth = 4 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (9 cm + 4 cm) =
2 X (13 cm) = 26 cm,
Area of rectangle is = l X b = 9 cm X 4 cm = 36 square cm,

Question 3.
Determine the perimeter of each rectangle.
a.

P = _____850 m_______
Answer:
Perimeter = 850 m,

Explanation:
Given length = 76 m and breadth = 149 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (76 m + 149 cm) =
2 X ( 425 m) = 850 m.

b.

P = ____510 cm________
Answer:
Perimeter =  510 cm,

Explanation:
Given length = 45 cm and breadth = 2 m 10 cm,
we know 1 m = 100 cm ,
so breadth =  2 X 100 cm + 10 cm = 200 cm + 10 cm = 210 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (45 cm + 210 cm) =
2 X (255 cm) = 510 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

x = _____10 cm_______
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 6 cm and area as 60 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 60 sq cm = 6 cm X x cm,
So x cm = 60 sq cm ÷ 6 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

x = _____5 m_______
Answer:
Unknown side length = 5 m,

Explanation:
Given width of rectangle as 5 m and area as 25 square m,
and unknow side length is x m, we know area of rectangle is
length X breadth, So 25 sq m = 5 m X x m,
So x m = 25 sq m ÷ 5 m = 5 m,
therefore unknown side length = 5 m.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 180 cm

x = ____40 cm________
Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 40 cm and perimeter as 180 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 X (length + breadth),
So 180 cm = 2 X (x cm + 40 cm),
180 cm ÷ 2 = (x cm + 40 cm),
90 cm = (x cm + 40 cm),
So x cm = 90 cm – 40 cm = 50 cm,
therefore unknown side length = 50 cm.

b. P = 1,000 m

x = ____350 m________
Answer:
Unknown side width = 350 m,

Explanation:
Given length of rectangle as 150 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 X (length + breadth),
So 1000 m = 2 X (150 m + x m),
1000 m ÷ 2 = (150 m + x m ),
500 m = 150 m + x m ,
So x m = 500 m – 150 m = 350 m,
therefore unknown side length = 350 m.

Question 6.
Each of the following rectangles has whole number side lengths. Given the area and perimeter, find the length and width.
a. A = 32 square cm
P = 24 cm

Answer:
The whole number side lengths are
If length of recatangle is 4 cm then width is 8 cm or
length of rectangle is 8 cm then width is 4 cm,

Explanation:
Given area = 32 square cm and perimeter = 24 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 32 sq cm = l X w and
perimeter = 2 X (length + width) ,
24 cm = 2 X ( l + w), l + w = 24 cm ÷ 2 =12 cm,
so l = 12 cm – w, now 32 = (12 – w) X w,
we get w²– 12 w + 32 = 0,
So w²– 8 w – 4 w + 32 = 0,
w(w – 8) – 4(w – 8) = 0, therefore w = 8 cm or w = 4 cm,
So l = 12 cm – 8 cm = 4 cm or l = 12 cm  – 4 cm = 8 cm,
Therfore, If length of recatangle is 4 cm then width is 8 cm or
length of rectangle is 8 cm then width is 4 cm.

b. A = 36 square m
P = 30 m

Answer:
The whole number side lengths are
If length of rectangle is 3 m then width is 12 m or
length of rectangle is 12 m then width is 3 m.

Explanation:
Given area = 36 square m and perimeter = 30 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 36 sq m = l X w and
perimeter = 2 X (length + width) ,
30 m = 2 X ( l + w), l + w = 30 m ÷ 2 =15 m,
so l = 15 m – w, now 36 = (15 – w) X w,
we get w²– 15 w + 36 = 0,
So w²– 12 w – 3 w + 24 = 0,
w(w – 12) – 3(w – 12) = 0, therefore w = 12 m or w = 3 m,
So l = 15 m – 12 m = 3 m or l = 15 m – 3 m = 12 m,
Therfore, If length of rectangle is 3 m then width is 12 m or
length of rectangle is 12 m then width is 3 m.

Engage NY Eureka Math 4th Grade Module 1 End of Module Assessment Answer Key

Question 1.
Compare the values of each 7 in the number 771,548. Use a picture, numbers, or words to explain.
Answer:
In the given number 771,548 the two 7 represent 7 hundred thousand and 7 ten thousand.
7 hundred thousand > 7 ten thousand.
7 hundred thousand is ten times greater than 7 ten thousand.
Explanation:
expanded form of 771,548
700,000 + 70,000 + 1,000 + 500 + 40 + 8

Question 2.
Compare using >, <, or =. Write your answer inside the circle.
a. 234 thousands + 7 ten thousands  241,000
Answer:
234 thousands + 7 ten thousands  >  241,000
Explanation:

3 hundred thousands is greater than 2 hundred thousands.

b. 4 hundred thousands – 2 thousands 200,000
Answer:
4 hundred thousands – 2 thousands  > 200,000
Explanation:

c. 1 million 4 hundred thousands + 6 hundred thousands
Answer:
1 million = 4 hundred thousands + 6 hundred thousands
Explanation:

d. 709 thousands – 1 hundred thousand 708 thousands
Answer:
709 thousands – 1 hundred thousand < 708 thousands
Explanation:

Question 3.
Norfolk, VA, has a population of 242,628 people. Baltimore, MD, has 376,865 more people than Norfolk. Charleston, SC, has 496,804 less people than Baltimore.
Given:
Population of Norfolk, VA = 242,628
Population of Baltimore, MD = 376,865 more than Norfolk.
Population of Charleston, SC = 496,804 less people than Baltimore
a. What is the total population of all three cities? Draw a tape diagram to model the word problem. Then, solve the problem.
Answer:

b. Round to the nearest hundred thousand to check the reasonableness of your answer for the population of Charleston, SC.
Answer:

c. Record each city’s population in numbers, in words, and in expanded form.
Answer:

d. Compare the population of Norfolk and Charleston using >, <, or =.
Answer:

e. Eddie lives in Fredericksburg, VA, which has a population of 24,286. He says that Norfolk’s population is about 10 times as large as Fredericksburg’s population. Explain Eddie’s thinking.
Answer:
Population of Fredericksburg,VA, = 24,286
Population of Norfolk = 242,628
Norfolk population is almost 10 times as large as Fredericksburg’s population.
Highest place value of Fredericksburg is 2 ten thousand and Highest place value of Norfolk is 2 hundred thousand
2 ten thousand × 10 = 2 hundred thousand.
Eddie’s thinking is reasonable.

Engage NY Eureka Math 4th Grade Module 1 Mid Module Assessment Answer Key

Question 1.
a. Arrange the following numbers in order from least to greatest:

Answer:
4,450       44,500     504,054           505,045
Explanation:
The following numbers are arranged from least to greatest
place value chart

b. Use the words ten times to tell how you ordered the two smallest numbers using words, pictures, or numbers.
Answer:
4,450 and 44,500 are the smallest numbers
44,500 is ten times more than 4,450.
Explanation:
ten times more of thousand is ten thousand

Question 2.
Compare using >, <, or =. Write your answer inside the circle.
a. 1 hundred thousand  10,000
b. 200 thousands 4 hundreds  204,000
c. 7 hundreds + 4 thousands + 27 ones  6 thousands + 4 hundreds
d. 1,000,000  10 hundred thousands
Answer:

Explanation:
a . 1 hundred thousand is represented as 100,000. which is ten times more than 10,000. So, 100,000 > 10,000.
b. 200 thousands 4 hundreds = 200,400 . 204,00 is 200 thousands 4 thousand.
4 thousand is 10 times more than 4 hundred. So, 204,000 is greater than 200,400.
c. 7 hundreds + 4 thousands + 27 ones  6 thousands + 4 hundreds
                     700 + 4,000 + 27 = 4,727  <   6,000  + 400 = 6,400
So on comparing 6 thousand is more than 4 thousand.
d. 1,000,000 is represented as 1 million or 10 hundred thousands  and the other number is 10 hundred thousands. So,  both are same .

Question 3.
The football stadium at Louisiana State University (LSU) has a seating capacity of 92,542.
a. According to the 2010 census, the population of San Jose, CA, was approximately ten times the amount of people that LSU’s stadium can seat. What was the population of San Jose in 2010?
Answer:
The seating capacity of Louisiana state university = 92,542
The population of San Jose in 2010 = 925,420 population.
Explanation:
given :
seating capacity of LSU = 92,542. the highest place value of the value is ten thousand. ten times the highest place value is hundred thousand. Ten times 92,542 is 925,420.
b. Write the seating capacity of the LSU stadium in words and in expanded form.
Answer:
92,542 in words = ninety two thousand five hundred forty two.
expanded form = 90,000 + 2,000 + 500 + 40 + 2.
c. Draw two separate number lines to round the LSU stadium’s seating capacity to the nearest ten thousand and to the nearest thousand.
Answer:

d. Compare the stadium’s seating rounded to the nearest ten thousand and the seating rounded to the nearest thousand using >, <, or =.
Answer:

e. Which estimate (rounding to the nearest ten thousand or nearest thousand) is more accurate? Use words and numbers to explain.
Answer:

Engage NY Eureka Math 4th Grade Module 1 Lesson 17 Answer Key

Eureka Math Grade 4 Module 1 Lesson 17 Problem Set Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
Sean’s school raised $32,587. Leslie’s school raised $18,749. How much more money did Sean’s school raise?
Answer:
Sean’s school raised =$32,587
Leslie’s school raised = $18,749
The amount of more money raised by Sean’s school than Leslie’s school = 32,587 – 18,749

Question 2.
At a parade, 97,853 people sat in bleachers, and 388,547 people stood along the street. How many fewer people were in the bleachers than standing on the street?
Answer:
Number of people sat in bleachers = 97,853
Number of people stood along the street = 388,547
Number of fewer people in the bleachers than standing on the streets. = 388,547 – 97,853

Question 3.
A pair of hippos weighs 5,201 kilograms together. The female weighs 2,038 kilograms. How much more does the male weigh than the female?
Answer:
Weight of a pair hippos  together =5,201 kilograms.
Weight of a female hippo = 2,038 kilograms.
weight of the male hippo = 5,201 – 2,038

Question 4.
A copper wire was 240 meters long. After 60 meters was cut off, it was double the length of a steel wire. How much longer was the copper wire than the steel wire at first?
Answer:
Total length of a copper wire = 240 m
Number of meters used = 60 m.
After using 60 m the length of copper wire is double the steel wire =240 – 60 = 180 m = 180 ÷ 2 = 90 m
The length of the steel wire is 90 m.

Eureka Math Grade 4 Module 1 Lesson 17 Exit Ticket Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

A mixture of 2 chemicals measures 1,034 milliliters. It contains some of Chemical A and 755 milliliters of Chemical B. How much less of Chemical A than Chemical B is in the mixture?
Answer:
Mixture of 2 chemicals measures =1,034 milliliters.
Chemical B measures = 755 milliliters.
Chemical A measures = X milliliters.

Eureka Math Grade 4 Module 1 Lesson 17 Homework Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
Gavin has 1,094 toy building blocks. Avery only has 816 toy building blocks. How many more building blocks does Gavin have?
Answer:
Total building blocks Gavin has = 1,094 blocks
Total building blocks Avery has = 816 blocks.

Question 2.
Container B holds 2,391 liters of water. Together, Container A and Container B hold 11,875 liters of water. How many more liters of water does Container A hold than Container B?
Answer:
Total liters of water Container B holds = 2,391 liters
Together both Container A and Container B holds = 11,875 liters.

Question 3.
A piece of yellow yarn was 230 inches long. After 90 inches had been cut from it, the piece of yellow yarn was twice as long as a piece of blue yarn. At first, how much longer was the yellow yarn than the blue yarn?
Answer:
The length of a yellow yarn = 230 inch
After cutting 90 inch of yellow yarn = Twice as long as a piece of blue yarn.

Engage NY Eureka Math 4th Grade Module 1 Lesson 18 Answer Key

Eureka Math Grade 4 Module 1 Lesson 18 Problem Set Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
In one year, the factory used 11,650 meters of cotton, 4,950 fewer meters of silk than cotton, and 3,500 fewer meters of wool than silk. How many meters in all were used of the three fabrics?
Answer:
In one year, the factory
Total cotton used = 11,650 meters.
Total silk used = 4,950 m fewer than cotton = 11,650 – 4,950 m
Total wool used = 3,500 m fewer than silk = 11,650 – 4,950 – 3,500 m

Question 2.
The shop sold 12,789 chocolate and 9,324 cookie dough cones. It sold 1,078 more peanut butter cones than cookie dough cones and 999 more vanilla cones than chocolate cones. What was the total number of ice cream cones sold?
Answer:
Number of chocolates cone sold = 12,789.
Number of cookie dough cones sold = 9,324.
Number of peanut butter cones sold = 1,078 more than cookie dough cones = 9,324 + 1,078
Number of vanilla cone sold = 999 more than chocolate cones = 12,789 + 999

Question 3.
In the first week of June, a restaurant sold 10,345 omelets. In the second week, 1,096 fewer omelets were sold than in the first week. In the third week, 2 thousand more omelets were sold than in the first week. In the fourth week, 2 thousand fewer omelets were sold than in the first week. How many omelets were sold in all in June?
Answer:
Number of omelets sold In the first week = 10,345
Number of omelets sold In the second week = 1,096 fewer than first week = 10,345 – 1,096
Number of omelets sold In the third week = 2 thousand more omelets than first week = 2,000 + 10,345.
Number of omelets sold In the fourth week = 2 thousand fewer omelets than first week = 10,345 – 2,000

Eureka Math Grade 4 Module 1 Lesson 18 Exit Ticket Answer Key

Draw a tape diagram to represent the problem. Use numbers to solve, and write your answer as a statement.

Park A covers an area of 4,926 square kilometers. It is 1,845 square kilometers larger than Park B. Park C is 4,006 square kilometers larger than Park A.
Answer:
Total area covered by Park A = 4,926 sq km.
Area of Park A = 1,845 sq km larger than Park B = 4,926 – 1,845
Area of Park C = 4,006 sq km larger than Park A = 4,926 + 4,006 sq km.

Question 1.
What is the area of all three parks?
Answer:

Question 2.
Assess the reasonableness of your answer.
Answer:

Eureka Math Grade 4 Module 1 Lesson 18 Homework Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
There were 22,869 children, 49,563 men, and 2,872 more women than men at the fair. How many people were at the fair?
Answer:
Total children = 22,869
Total men = 49,563
Total women = 2,872 more than men = 2,872 + 49,563
Total number of people at the fair = children + men + women

Question 2.
Number A is 4,676. Number B is 10,043 greater than A. Number C is 2,610 less than B. What is the total value of numbers A, B, and C?
Answer:
Number A = 4,676
Number B = 10,043 greater than Number A.
Number C = 2,610 Less than Number B.
The total value of Numbers A, B, C =

Question 3.
A store sold a total of 21,650 balls. It sold 11,795 baseballs. It sold 4,150 fewer basketballs than baseballs. The rest of the balls sold were footballs. How many footballs did the store sell?
Answer:
Total balls sold = 21,650 balls
Number of baseball sold = 11,795
Number of basketball sold = 4,150 fewer than baseballs = 11,795 – 4,150
Rest  sold are footballs.
Number of footballs sold =

Engage NY Eureka Math 4th Grade Module 1 Lesson 16 Answer Key

Eureka Math Grade 4 Module 1 Lesson 16 Sprint Answer Key

A
Convert Meters and Centimeters to Centimeters


Explanation:
1 meter = 100 Centimeter
To convert from meters to centimeters, simply multiply the number of meters by 100 and change the units to cm.

Question 1.
2 m = cm
Answer:
2 m = 2× 100 cm = 200 cm.

Question 2.
3 m = cm
Answer:
3 m = 3× 100 cm = 300 cm.

Question 3.
4 m = cm
Answer:
4 m = 4 × 100 cm = 400 cm.

Question 4.
9 m = cm
Answer:
9 m = 9 × 100 = 900 cm.

Question 5.
1 m = cm
Answer:
1 m = 1×100 = 100 cm.

Question 6.
7 m = cm
Answer:
7 m = 7 × 100 = 700 cm.

Question 7.
5 m = cm
Answer:
5 m = 5×100 = 500 cm.

Question 8.
8 m = cm
Answer:
8 m = 8×100 = 800 cm.

Question 9.
6 m = cm
Answer:
6 m = 6×100 = 600 cm.

Question 10.
1 m 20 cm = cm
Answer:
1 m 20 cm = 1×100 cm 20 cm =100 cm 20 cm = 120 cm.

Question 11.
1 m 30 cm = cm
Answer:
1 m 30 cm = 1×100 cm 30 cm = 100 cm 30 cm = 130 cm.

Question 12.
1 m 40 cm = cm
Answer:
1 m 40 cm = 1×100 cm 40 cm = 100 cm 40 cm = 140 cm.

Question 13.
1 m 90 cm = cm
Answer:
1 m 90 cm = 1×100 cm 90 cm = 100 cm 90 cm = 190 cm.

Question 14.
1 m 95 cm = cm
Answer:
1 m 95 cm = 1×100 cm 95 cm = 195 cm.

Question 15.
1 m 85 cm = cm
Answer:
1 m 85 cm = 1×100 cm 85 cm =185 cm.

Question 16.
1 m 84 cm = cm
Answer:
1 m 84 cm = 1×100 cm 84 cm = 184 cm.

Question 17.
1 m 73 cm = cm
Answer:
1 m 73 cm = 1×100 cm 73 cm = 173 cm.

Question 18.
1 m 62 cm = cm
Answer:
1 m 62 cm = 1×100 cm 62 cm = 162 cm.

Question 19.
2 m 62 cm = cm
Answer:
2 m 62 cm = 2× 100 cm 62 cm = 262 cm.

Question 20.
7 m 62 cm = cm
Answer:
7 m 62 cm = 7×100 cm 62 cm = 762 cm.

Question 21.
5 m 27 cm = cm
Answer:
5 m 27 cm = 5× 100 cm 27 cm =527 cm.

Question 22.
3 m 87 cm = cm
Answer:
3 m 87 cm = 3×100 cm 87 cm = 387 cm.

Question 23.
1 m 2 cm = cm
Answer:
1 m 2 cm = 1×100 cm 2 cm = 102 cm.

Question 24.
1 m 3 cm = cm
Answer:
1 m 3 cm = 1×100 cm 3 cm = 103 cm.

Question 25.
1 m 4 cm = cm
Answer:
1 m 4 cm = 1× 100 cm 4 cm = 104 cm.

Question 26.
1 m 7 cm = cm
Answer:
1 m 7 cm = 1×100 cm 7 cm = 107 cm.

Question 27.
2 m 7 cm = cm
Answer:
2 m 7 cm = 2×100 cm 7 cm =207 cm.

Question 28.
3 m 7 cm = cm
Answer:
3 m 7 cm = 3×100 cm 7 cm = 307 cm.

Question 29.
8 m 7 cm = cm
Answer:
8 m 7 cm = 8×100 cm 7 cm =807 cm.

Question 30.
8 m 4 cm = cm
Answer:
8 m 4 cm = 8 ×100 cm 4 cm = 804 cm.

Question 31.
4 m 9 cm = cm
Answer:
4 m 9 cm = 4×100 cm 9 cm =409 cm.

Question 32.
6 m 8 cm = cm
Answer:
6 m 8 cm = 6×100 cm 8 cm =608 cm.

Question 33.
9 m 3 cm = cm
Answer:
9 m 3 cm = 9×100 cm 3 cm = 903 cm.

Question 34.
2 m 60 cm = cm
Answer:
2 m 60 cm =2 ×100 cm 60 cm =260 cm.

Question 35.
3 m 75 cm = cm
Answer:
3 m 75 cm = 3×100 cm 75 cm = 375 cm.

Question 36.
6 m 33 cm = cm
Answer:
6 m 33 cm = 6×100 cm 33 cm =633 cm.

Question 37.
8 m 9 cm = cm
Answer:
8 m 9 cm =8×100 cm 9 cm =809 cm.

Question 38.
4 m 70 cm = cm
Answer:
4 m 70 cm = 4×100 cm 70 cm = 470 cm.

Question 39.
7 m 35 cm = cm
Answer:
7 m 35 cm = 7×100 cm 35 cm =735 cm.

Question 40.
4 m 17 cm = cm
Answer:
4 m 17 cm = 4×100 cm 17 cm = 417 cm.

Question 41.
6 m 4 cm = cm
Answer:
6 m 4 cm = 6×100 cm 4 cm =604 cm.

Question 42.
10 m 4 cm = cm
Answer:
10 m 4 cm = 10 ×100 cm 4 cm =1004 cm.

Question 43.
10 m 40 cm = cm
Answer:
10 m 40 cm = 10 × 100 cm 40 cm =1000 cm 40 cm =1040 cm.

Question 44.
11 m 84 cm = cm
Answer:
11 m 84 cm =11×100 cm 84 cm =1100 cm 84 cm =1184 cm.

B
Convert Meters and Centimeters to Centimeters

Explanation:
1 meter = 100 Centimeter
To convert from meters to centimeters, simply multiply the number of meters by 100 and change the units to cm.

Question 1.
1 m = cm
Answer:
1 m = 1×100 cm = 100 cm.

Question 2.
2 m = cm
Answer:
2 m = 2×100 cm = 200 cm.

Question 3.
3 m = cm
Answer:
3 m = 3× 100 cm = 300 cm.

Question 4.
7 m = cm
Answer:
7 m = 7×100 cm = 700 cm.

Question 5.
5 m = cm
Answer:
5 m = 5 × 100 cm = 500 cm

Question 6.
9 m = cm
Answer:
9 m = 9 × 100 cm = 900 cm.

Question 7.
4 m = cm
Answer:
4 m = 4× 100 cm = 400 cm

Question 8.
8 m = cm
Answer:
8 m = 8 ×100 cm = 800 cm.

Question 9.
6 m = cm
Answer:
6 m = 6 × 100 cm = 600 cm.

Question 10.
1 m 10 cm = cm
Answer:
1 m 10 cm = 1× 100 cm 10 cm =100 cm 10 cm = 110 cm.

Question 11.
1 m 20 cm = cm
Answer:
1 m 20 cm = 1 × 100 cm 20 cm = 100 cm 20 cm = 120 cm.

Question 12.
1 m 30 cm = cm
Answer:
1 m 30 cm = 1×100 cm 30 cm = 100 cm 30 cm = 130 cm.

Question 13.
1 m 70 cm = cm
Answer:
1 m 70 cm = 1 × 100 cm 70 cm = 100 cm 70 cm = 170 cm.

Question 14.
1 m 75 cm = cm
Answer:
1 m 75 cm = 1×100 cm 75 cm = 100 cm 75 cm =175 cm.

Question 15.
1 m 65 cm = cm
Answer:
1 m 65 cm = 1×100 cm 65 cm =100 cm 65 cm =165 cm.

Question 16.
1 m 64 cm = cm
Answer:
1 m 64 cm = 1 × 100 cm 64 cm = 100 cm 64 cm = 164 cm.

Question 17.
1 m 53 cm = cm
Answer:
1 m 53 cm = 1 × 100 cm 53 cm = 100 cm 53 cm = 153 cm.

Question 18.
1 m 42 cm = cm
Answer:
1 m 42 cm = 1 × 100 cm 42 cm = 100 cm 42 cm = 142 cm.

Question 19.
2 m 42 cm = cm
Answer:
2 m 42 cm = 2 × 100 cm 42 cm = 200 cm 42 cm = 242 cm.

Question 20.
8 m 42 cm = cm
Answer:
8 m 42 cm = 8 × 100 cm 42 cm = 800 cm 42 cm = 842 cm.

Question 21.
5 m 29 cm = cm
Answer:
5 m 29 cm = 5 × 100 29 cm = 500 cm 29 cm = 529 cm.

Question 22.
3 m 89 cm = cm
Answer:
3 m 89 cm = 3 × 100 cm 89 cm = 300 cm 89 cm = 389 cm.

Question 23.
1 m 1 cm = cm
Answer:
1 m 1 cm = 1 × 100 cm 1 cm = 100 cm 1 cm = 101 cm.

Question 24.
1 m 2 cm = cm
Answer:
1 m 2 cm = 1 × 100 cm 2 cm = 100 cm 2 cm = 102 cm.

Question 25.
1 m 3 cm = cm
Answer:
1 m 3 cm = 1 × 100 cm 3 cm = 100 cm 3 cm = 103 cm.

Question 26.
1 m 9 cm = cm
Answer:
1 m 9 cm = 1 × 100 cm 9 cm = 100 cm 9 cm = 109 cm.

Question 27.
2 m 9 cm = cm
Answer:
2 m 9 cm = 2 × 100 cm 9 cm = 200 cm 9 cm = 209 cm.

Question 28.
3 m 9 cm = cm
Answer:
3 m 9 cm = 3 × 100 cm 9 cm = 300 cm 9 cm = 309 cm.

Question 29.
7 m 9 cm = cm
Answer:
7 m 9 cm = 7 × 100 cm 9 cm = 700 cm 9 cm = 709 cm.

Question 30.
7 m 4 cm = cm
Answer:
7 m 4 cm = 7 × 100 cm 4 cm = 700 cm 4 cm = 704 cm

Question 31.
4 m 8 cm = cm
Answer:
4 m 8 cm = 4 × 100 cm 8 cm = 400 cm 8 cm = 408 cm.

Question 32.
6 m 3 cm = cm
Answer:
6 m 3 cm = 6 × 100 cm 3 cm = 600 cm 3 cm = 603 cm.

Question 33.
9 m 5 cm = cm
Answer:
9 m 5 cm = 9 × 100 cm 5 cm = 900 cm 5 cm = 905 cm.

Question 34.
2 m 50 cm = cm
Answer:
2 m 50 cm = 2 × 100 cm 50 cm = 200 cm 50 cm = 250 cm

Question 35.
3 m 85 cm = cm
Answer:
3 m 85 cm = 3 × 100 cm 85 cm = 300 cm 85 cm = 385 cm.

Question 36.
6 m 31 cm = cm
Answer:
6 m 31 cm = 6 × 100 cm 31 cm = 600 cm 31 cm = 631 cm.

Question 37.
6 m 7 cm = cm
Answer:
6 m 7 cm = 6 × 100 cm 7 cm = 600 cm 7 cm = 607 cm.

Question 38.
4 m 60 cm = cm
Answer:
4 m = 4 × 100 = 400 cm 60 cm = 460 cm.

Question 39.
7 m 25 cm = cm
Answer:
7 m = 7 × 100 = 700 cm 25 cm = 725 cm

Question 40.
4 m 13 cm = cm
Answer:
4 m = 4 × 100 = 400 cm 13 cm = 413 cm

Question 41.
6 m 2 cm = cm
Answer:
6 m = 6 × 100 = 600 cm 2 cm = 602 cm

Question 42.
10 m 3 cm = cm
Answer:
10 m = 10 × 100 = 1000 cm 3 cm = 1003 cm

Question 43.
10 m 30 cm = cm
Answer:
10 m = 10 × 100 = 1000 cm 30 cm = 1030 cm

Question 44.
11 m 48 cm = cm
Answer:
11 m = 11 × 100 = 1100 cm
48 cm
1148 cm

Eureka Math Grade 4 Module 1 Lesson 16 Problem Set Answer Key

Estimate first, and then solve each problem. Model the problem with a tape diagram. Explain if your answer is reasonable.

Question 1.
On Monday, a farmer sold 25,196 pounds of potatoes. On Tuesday, he sold 18,023 pounds. On Wednesday, he sold some more potatoes. In all, he sold 62,409 pounds of potatoes.
Answer:
Number of pounds of potatoes sold on Monday = 25,196 pounds
Number of pounds of potatoes sold on Tuesday = 18,023 pounds
Number of pounds of potatoes sold on Wednesday = X pounds.
Total number of pounds of potatoes a farmer sold all together = 62,409 pounds.
a. About how many pounds of potatoes did the farmer sell on Wednesday? Estimate by rounding each value to the nearest thousand, and then compute.
Answer:

b. Find the precise number of pounds of potatoes sold on Wednesday.
Answer:

c. Is your precise answer reasonable? Compare your estimate from (a) to your answer from (b). Write a sentence to explain your reasoning.
Answer:
Yes, my precise answer is reasonable. On rounding to the nearest thousand answer is 19,000 and my precise value is 19,386 . Both the values are close enough.

Question 2.
A gas station had two pumps. Pump A dispensed 241,752 gallons. Pump B dispensed 113,916 more gallons than Pump A.
Answer:
Given:
Number of gallons of gas pumped by Pump A = 241,752 gallons
Number of gallons of gas pumped by Pump B = 113,916 more gallons than Pump A

a. About how many gallons did both pumps dispense? Estimate by rounding each value to the nearest hundred thousand and then compute.
Answer:

b. Exactly how many gallons did both pumps dispense?
Answer:

c. Assess the reasonableness of your answer in (b). Use your estimate from (a) to explain.
Answer:
The Exact and the Estimation Answers are so close to each other. The difference between them is
600,000 – 597,420 = 2,580 which is not a huge difference.

Question 3.
Martin’s car had 86,456 miles on it. Of that distance, Martin’s wife drove 24,901 miles, and his son drove 7,997 miles. Martin drove the rest.
Given:
Total distance reading on Martin’s car = 86,456 miles
From that Martin’s wife drove = 24,901 miles.
From that Martin’s son drove =7, 997 miles.
Remaining drove by Martin = 86,456 – 24,901 – 7,997
a. About how many miles did Martin drive? Round each value to estimate.
Answer:

b. Exactly how many miles did Martin drive?
Answer:

c. Assess the reasonableness of your answer in (b). Use your estimate from (a) to explain.
Answer:
Both the answer are relatively close. They both are reasonable answers.

Question 4.
A class read 3,452 pages the first week and 4,090 more pages in the second week than in the first week. How many pages had they read by the end of the second week? Is your answer reasonable? Explain how you know using estimation.
Answer:
Number of pages read by A class in the first week = 3,452 pages
Number of pages read by the class in the second week = 4,090 more than week 1 = 4,090 + 3,452

Question 5.
A cargo plane weighed 500,000 pounds. After the first load was taken off, the airplane weighed 437,981 pounds. Then 16,478 more pounds were taken off. What was the total number of pounds of cargo removed from the plane? Is your answer reasonable? Explain.
Answer:
Total weight of a cargo plane = 500,000 pounds
After the first load the weight of the plane = 437,981 pounds
Again a load of weight was taken off the plane = 16,478
The total number of pounds of cargo removed from the plane =

Eureka Math Grade 4 Module 1 Lesson 16 Exit Ticket Answer Key

Quarterback Brett Favre passed for 71,838 yards between the years 1991 and 2011. His all-time high was 4,413 passing yards in one year. In his second highest year, he threw 4,212 passing yards.
Answer:
Given:
Total yards passed = 71,838
The passing yard in one year = 4,413
The passing yard in the second year = 4,212

Question 1.
About how many passing yards did he throw in the remaining years? Estimate by rounding each value to the nearest thousand and then compute.
Answer:

Question 2.
Exactly how many passing yards did he throw in the remaining years?
Answer:

Question 3.
Assess the reasonableness of your answer in (b). Use your estimate from (a) to explain.
Answer:
The answer in (b) is 63,213 .and the estimated answer is 64,000. Both the answers are close and reasonable.

Eureka Math Grade 4 Module 1 Lesson 16 Homework Answer Key

Question 1.
Zachary’s final project for a college course took a semester to write and had 95,234 words. Zachary wrote 35,295 words the first month and 19,240 words the second month.
Given:
Total words written in the Zachary’s final project  in the complete semester = 95,234 words
Number of words Zachary’s wrote in the first month = 35,295 words
Number of words Zachary’s wrote in the second month = 19,240 words
a. Round each value to the nearest ten thousand to estimate how many words Zachary wrote during the remaining part of the semester.
Answer:

b. Find the exact number of words written during the remaining part of the semester.
Answer:

c. Use your answer from (a) to explain why your answer in (b) is reasonable.
Answer:
Yes, my answer is reasonable because 40,699 is estimated to 40,000 on rounding to nearest ten thousand.

Question 2.
During the first quarter of the year, 351,875 people downloaded an app for their smartphones. During the second quarter of the year, 101,949 fewer people downloaded the app than during the first quarter. How many downloads occurred during the two quarters of the year?
GIVEN:
Number of people downloaded an app during the first quarter of the year = 351,875
Number of people downloaded an app during the second quarter of the year = 351,875 -101,949
a. Round each number to the nearest hundred thousand to estimate how many downloads occurred during the first two quarters of the year.
Answer:

b. Determine exactly how many downloads occurred during the first two quarters of the year.
Answer:

c. Determine if your answer is reasonable. Explain.
Answer:
Yes, my answer is reasonable as 700,000 is the next highest hundred thousand number to 601,801.

Question 3.
A local store was having a two-week Back to School sale. They started the sale with 36,390 notebooks. During the first week of the sale, 7,424 notebooks were sold. During the second week of the sale, 8,967 notebooks were sold. How many notebooks were left at the end of the two weeks? Is your answer reasonable?
Answer:
The local store started the sale = 36,390 books
number of books sold during the first week =7,424 notebooks
Number of books sold during the second week = 8,967 notebooks.

Engage NY Eureka Math 3rd Grade Module 5 Lesson 21 Answer Key

Eureka Math Grade 3 Module 5 Lesson 21 Problem Set Answer Key

Question 1.
Use the fractional units on the left to count up on the number line. Label the missing fractions on the blanks.

Answer :

Explanation :
In the First figure the number line is divided into halves and fourths . The respective missing terms are written .
In the Second Figure The number line is divided into halves and Sixths .The respective Missing terms are written .

Question 2.
Use the number lines above to:

• Color fractions equal to 1 half blue.
• Color fractions equal to 1 yellow.
• Color fractions equal to 3 halves green.
• Color fractions equal to 2 red.

Answer :

Explanation :
Respective colors are marked to the respective Fractions .

Question 3.
Use the number lines above to make the number sentences true.

Answer :

Question 4.
Jack and Jill use rain gauges the same size and shape to measure rain on the top of a hill. Jack uses a rain gauge marked in fourths of an inch. Jill’s gauge measures rain in eighths of an inch. On Thursday, Jack’s gauge measured \(\frac{2}{4}\) inches of rain. They both had the same amount of water, so what was the reading on Jill’s gauge Thursday? Draw a number line to help explain your thinking.
Answer :

Explanation :
Jack Gauges is measured in Fourths and Jill’s Gauges is measured in Eighths.
Jack measures amount of rain = \(\frac{2}{4}\)
Both Gauges measures same . so amount of Rain in jill’s gauges = \(\frac{4}{8}\) .
It is shown in the figure .

Question 5.
Jack and Jill’s baby brother Rosco also had a gauge the same size and shape on the same hill. He told Jack and Jill that there had been \(\frac{1}{2}\) inch of rain on Thursday. Is he right? Why or why not? Use words and a number line to explain your answer.
Answer :
Yes, Rosco is correct .

Explanation :
Rosco is Correct Because his gauges is divided into halves . His amount of rain is equal to \(\frac{1}{2}\) .
It is clearly shown in the above figure .

Eureka Math Grade 3 Module 5 Lesson 21 Exit Ticket Answer Key

Question 1.
Claire went home after school and told her mother that 1 whole is the same as \(\frac{2}{2}\) and \(\frac{6}{6}\) . Her mother asked why, but Claire couldn’t explain. Use a number line and words to help Claire show and explain why
1 = \(\frac{2}{2}\) = \(\frac{6}{6}\).
Answer :

Explanation :
The number is marked for 1 whole . The 1 whole is divided into halves and sixths . we can \(\frac{2}{2}\) and \(\frac{6}{6}\) are marked at the same point. Both the fractions represents 1 so , they are equal .

Eureka Math Grade 3 Module 5 Lesson 21 Homework Answer Key

Question 1.
Use the fractional units on the left to count up on the number line. Label the missing fractions on the blanks.

Answer :

Explanation :
In the First figure the number line is divided into fourths and Eighths . The respective missing terms are written .
In the Second Figure The number line is divided into Thirds and Sixths .The respective Missing terms are written .

Question 2.
Use the number lines above to:

• Color fractions equal to 1 purple.
• Color fractions equal to 2 fourths yellow.
• Color fractions equal to 2 blue.
• Color fractions equal to 5 thirds green.
• Write a pair of fractions that are equivalent.

________________ = ________________
Answer :

Explanation :
Respective colors are marked for the respective fractions .

Question 3.
Use the number lines on the previous page to make the number sentences true.

Answer :

Question 4.
Mr. Fairfax ordered 3 large pizzas for a class party. Group A ate \(\frac{6}{6}\) of the first pizza, and Group B ate \(\frac{8}{6}\) of the remaining pizza. During the party, the class discussed which group ate more pizza.
a. Did Group A or B eat more pizza? Use words and pictures to explain your answer to the class.
b. Later, Group C ate all remaining slices of pizza. What fraction of the pizza did group C eat? Use words and pictures to explain your answer.
Answer :

a.
Each pizza is divided into 6 equal parts .
The Group A ate 1 complete pizza of 6 slices . 6 slices is equal to 1 pizza .
The Group B ate 1 complete pizza and 2 slices of third pizza that means total 8 slices of pizza .
Group B ate 2 slices more than Group A .
b.
Group B ate 2 slices of third pizza that means 4 slices are remaining . This remaining slices are eaten by Group C.
The Fraction of Group C ate is \(\frac{4}{6}\) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 20 Answer Key

Eureka Math Grade 3 Module 5 Lesson 20 Pattern Sheet Answer Key

Multiply.

Answer :

Explanation :
Here we see the seven table
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35

Eureka Math Grade 3 Module 5 Lesson 20 Problem Set Answer Key

Question 1.
Label what fraction of each shape is shaded. Then, circle the fractions that are equal.

Answer :

Explanation :
The Fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
fraction of each shape shaded are written and the fractions which are same are circled as shown in the above figure .

Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :

Explanation :
In figure a the Fraction of shaded = \(\frac{1}{4}\) the same fraction is represented with a circle divided into 4 equal parts and 1 part is shaded
In figure b the Fraction of shaded = \(\frac{1}{7}\) the same fraction is represented with a Rectangle which is divided into 7 equal parts and 1 part is shaded .

Question 3.
Ann has 6 small square pieces of paper. 2 squares are grey. Ann cuts the 2 grey squares in half with a diagonal line from one corner to the other.

a. What shapes does she have now?
b. How many of each shape does she have?
c. Use all the shapes with no overlaps. Draw at least 2 different ways Ann’s set of shapes might look. What fraction of the figure is grey?
Answer :

a. The shapes does she have now is Triangles and Squares.
b. 4 Triangles and 4 Squares .
c.
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
Fraction = \(\frac{2}{6}\) .

Question 4.
Laura has 2 different beakers that hold exactly 1 liter. She pours \(\frac{1}{2}\) liter of blue liquid into Beaker A. She pours \(\frac{1}{2}\) liter of orange liquid into Beaker B. Susan says the amounts are not equal. Cristina says they are. Explain who you think is correct and why.

Answer :
Cristine is Correct .
Explanation :
Here the Breaker A contains Blue Liquid of \(\frac{1}{2}\) liter
Breaker B contains Orange liquid of \(\frac{1}{2}\) liter .
Whatever may be the shapes of the breaker but both the Amount of Quantities are same .
Where as , Susan Comparing the breakers Shape and saying the quantities are different . But she is Wrong .

Eureka Math Grade 3 Module 5 Lesson 20 Exit Ticket Answer Key

Question 1.
Label what fraction of the figure is shaded. Then, circle the fractions that are equal.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .

Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The figure a has shaded fraction = \(\frac{5}{11}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 11 parts and 5 parts are shaded and another figure is Longer rectangular strip with 11 parts and 5 parts are shaded .
The figure b has shaded fraction = \(\frac{2}{10}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 10 parts and 2 parts are shaded and another figure is star shape with 10 parts of Triangles and 2 parts are shaded .

Eureka Math Grade 3 Module 5 Lesson 20 Homework Answer Key

Question 1.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The figure a has shaded fraction = \(\frac{3}{7}\)
The fraction is represented with 2 different shapes . The first is a Triangular strip with 7 parts and 3 parts are shaded and another figure is rectangular strip with 7 parts and 3 parts are shaded .

Question 2.
These two shapes both show \(\frac{4}{5}\).

a. Are the shapes equivalent? Why or why not?
b. Draw two different representations of \(\frac{4}{5}\) that are equivalent.
Answer :
a. No, The Shapes are not Equivalent , Both the shapes are \(\frac{4}{5}\) units but both the shapes are different .
b.

Explanation :
2 Different shapes of \(\frac{4}{5}\) units are represented in the above figure .

Question 3.
Diana ran a quarter mile straight down the street. Becky ran a quarter mile on a track. Who ran more? Explain your thinking.

Answer :
If the length of the down street and the track is same then
Diana and Becky both ran Quarter that means both ran same length .
Whereas if the length of the down street and the track is different , Then length of the Quarter will be different then both Ran different miles . The one who ran more can be known by if the length of the down street and track mile if given .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 22 Answer Key

Eureka Math Grade 3 Module 5 Lesson 22 Problem Set Answer Key

Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.

Answer :

Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .

Question 2.
Write the missing parts of the fractions.

Answer :

Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The Shaded fractions are written .

Question 3.
Why does it take 2 copies of \(\frac{1}{8}\) to show the same amount as 1 copy of \(\frac{1}{4}\)? Explain your answer in words and pictures.
Answer :

Explanation :
Because, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.
Since, by the Above diagram,

Thus, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.

Question 4.
How many sixths does it take to make the same amount as \(\frac{1}{3}\) ? Explain your answer in words and pictures.
Answer :

Explanation :
The Rectangular strip is divided into 3 parts and 6 parts . The first strip is marked \(\frac{1}{3}\) and the second is marked \(\frac{2}{6}\) which means \(\frac{1}{3}\) is equal to \(\frac{2}{6}\).
It takes two one-sixths to make a third.

Question 5.
Why does it take 10 copies of 1 sixth to make the same amount as 5 copies of 1 third? Explain your answer in words and pictures.
Answer :

Explanation :
The Sixths have as many as units as thirds .
So, \(\frac{10}{6}\) are as equal as \(\frac{5}{3}\) copies as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 22 Exit Ticket Answer Key

Question 1.
Draw and label two models that show equivalent fractions.
Answer :

Explanation :
From The above figure we notice
The First rectangular strip is divided into 2 equal parts and fraction shaded is \(\frac{1}{2}\) .
The Second rectangular strip is divided into 6 equal parts and the fraction shaded is \(\frac{3}{6}\) .
Both show the equivalent fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .

Question 2.
Draw a number line that proves your thinking about Problem 1.
Answer :

Explanation :
The number is represented for the above equivalent Fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .

Eureka Math Grade 3 Module 5 Lesson 22 Homework Answer Key

Question 1.
Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .

Question 2.
Complete the fractions to make true statements.
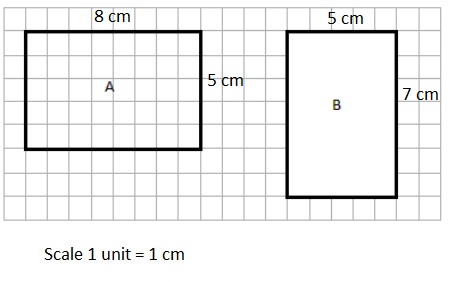
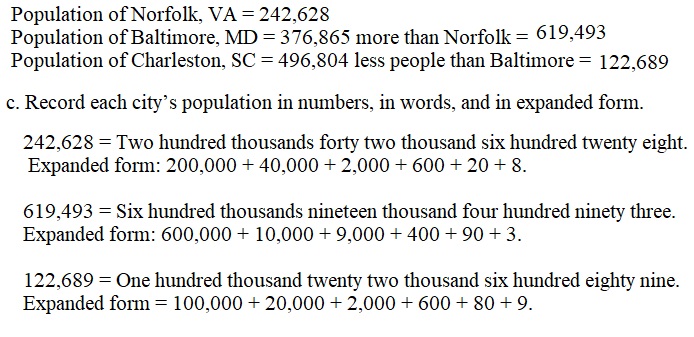
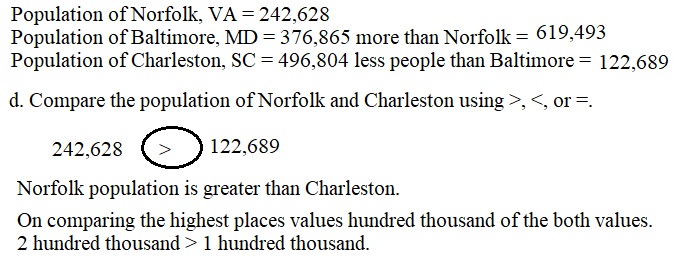
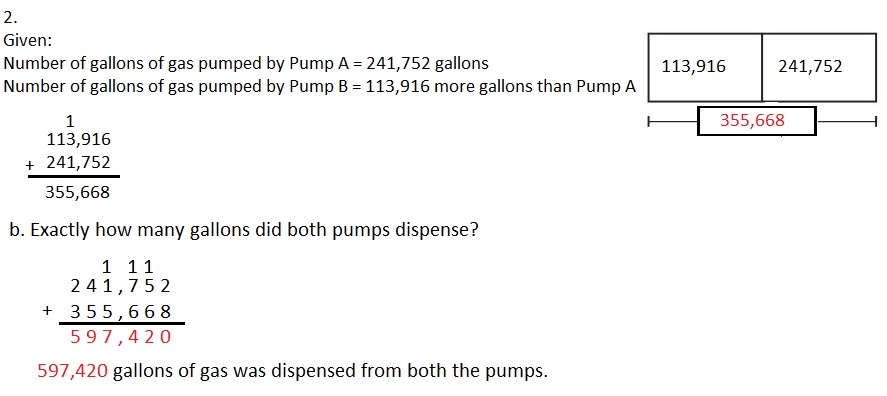
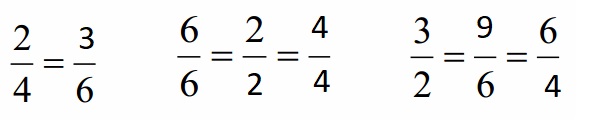
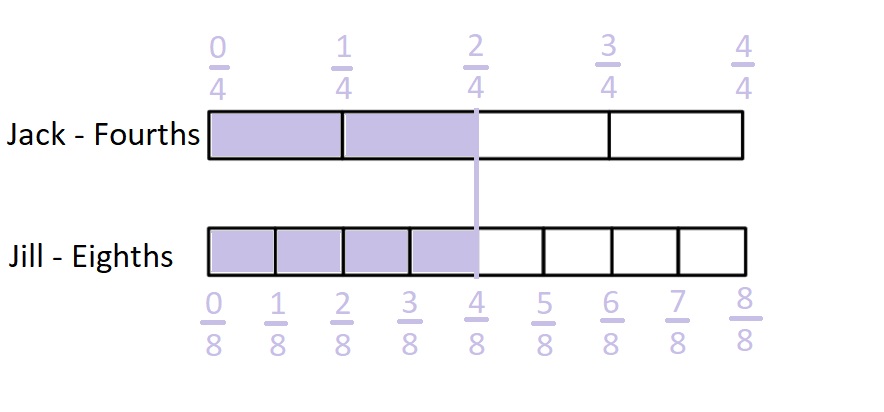
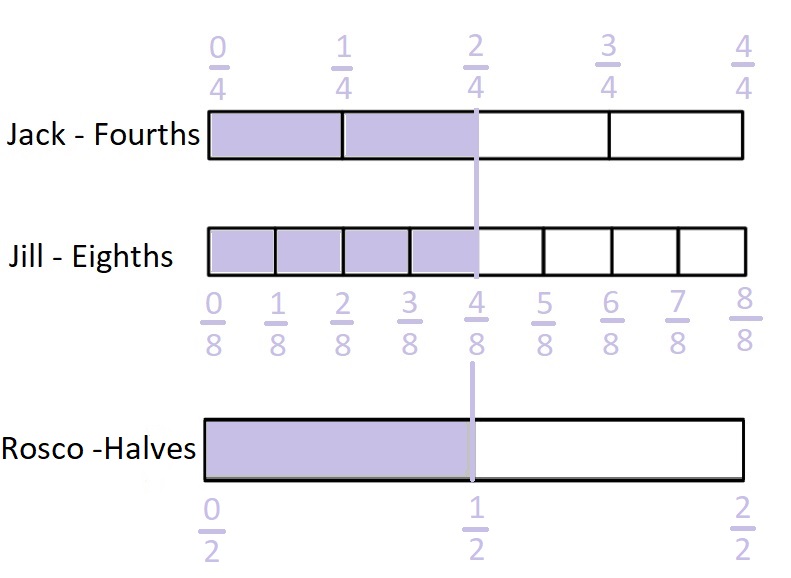
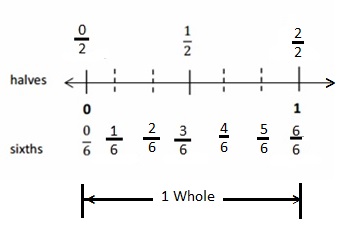
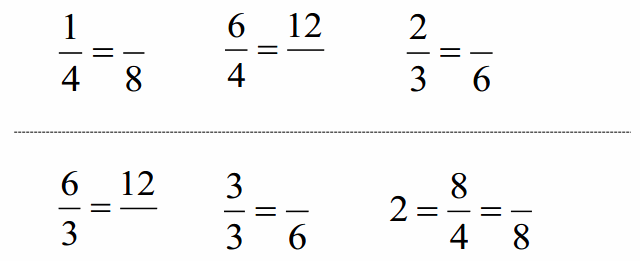
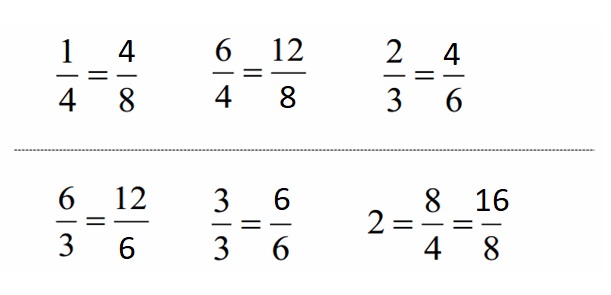
Answer :
Answer :

Explanation :
The Figures are divided into double and the shaded Fractions are compared .

Question 3.
Why does it take 3 copies of \(\frac{1}{6}\) to show the same amount as 1 copy of \(\frac{1}{2}\)? Explain your answer in words and pictures.
Answer :

Explanation :
The Two tape Diagram Shows 3 copies of \(\frac{3}{6}\) is the same length as 1 copy of \(\frac{1}{2}\) .

Question 4.
How many ninths does it take to make the same amount as \(\frac{1}{3}\)? Explain your answer in words and pictures.
Answer :

Explanation :
The Two tape Diagram Shows 3 ninths ( \(\frac{3}{9}\)) is the same length as 1Thirds (\(\frac{1}{3}\)) .

Question 5.
A pie was cut into 8 equal slices. If Ruben ate \(\frac{3}{4}\) of the pie, how many slices did he eat? Explain your answer using a number line and words.
Answer :

Explanation :
\(\frac{3}{4}\) is the same length as \(\frac{6}{8}\)
Ruben ate 6 slices which is \(\frac{6}{8}\) = \(\frac{3}{4}\).

Engage NY Eureka Math 3rd Grade Module 5 Lesson 23 Answer Key

Eureka Math Grade 3 Module 5 Lesson 23 Sprint Answer Key

A
Add by Six

Question 1.
0 + 6 =

Question 2.
1 + 6 =

Question 3.
2 + 6 =

Question 4.
3 + 6 =

Question 5.
4 + 6 =

Question 6.
6 + 4 =

Question 7.
6 + 3 =

Question 8.
6 + 2 =

Question 9.
6 + 1 =

Question 10.
6 + 0 =

Question 11.
15 + 6 =

Question 12.
25 + 6 =

Question 13.
35 + 6 =

Question 14.
45 + 6 =

Question 15.
55 + 6 =

Question 16.
85 + 6 =

Question 17.
6 + 6 =

Question 18.
16 + 6 =

Question 19.
26 + 6 =

Question 20.
36 + 6 =

Question 21.
46 + 6 =

Question 22.
76 + 6 =

Question 23.
7 + 6 =

Question 24.
17 + 6 =

Question 25.
27 + 6 =

Question 26.
37 + 6 =

Question 27.
47 + 6 =

Question 28.
77 + 6 =

Question 29.
8 + 6 =

Question 30.
18 + 6 =

Question 31.
28 + 6 =

Question 32.
38 + 6 =

Question 33.
48 + 6 =

Question 34.
78 + 6 =

Question 35.
9 + 6 =

Question 36.
19 + 6 =

Question 37.
29 + 6 =

Question 38.
39 + 6 =

Question 39.
89 + 6 =

Question 40.
6 + 75 =

Question 41.
6 + 56 =

Question 42.
6 + 77 =

Question 43.
6 + 88 =

Question 44.
6 + 99 =

B
Add by Six

Question 1.
6 + 0 =

Question 2.
6 + 1 =

Question 3.
6 + 2 =

Question 4.
6 + 3 =

Question 5.
6 + 4 =

Question 6.
4 + 6 =

Question 7.
3 + 6 =

Question 8.
2 + 6 =

Question 9.
1 + 6 =

Question 10.
0 + 6 =

Question 11.
5 + 6 =

Question 12.
15 + 6 =

Question 13.
25 + 6 =

Question 14.
35 + 6 =

Question 15.
45 + 6 =

Question 16.
75 + 6 =

Question 17.
6 + 6 =

Question 18.
16 + 6 =

Question 19.
26 + 6 =

Question 20.
36 + 6 =

Question 21.
46 + 6 =

Question 22.
86 + 6 =

Question 23.
7 + 6 =

Question 24.
17 + 6 =

Question 25.
27 + 6 =

Question 26.
37 + 6 =

Question 27.
47 + 6 =

Question 28.
67 + 6 =

Question 29.
8 + 6 =

Question 30.
18 + 6 =

Question 31.
28 + 6 =

Question 32.
38 + 6 =

Question 33.
48 + 6 =

Question 34.
88 + 6 =

Question 35.
9 + 6 =

Question 36.
19 + 6 =

Question 37.
29 + 6 =

Question 38.
39 + 6 =

Question 39.
79 + 6 =

Question 40.
6 + 55 =

Question 41.
6 + 76 =

Question 42.
6 + 57 =

Question 43.
6 + 98 =

Question 44.
6 + 89 =

Eureka Math Grade 3 Module 5 Lesson 23 Problem Set Answer Key

Question 1.
On the number line above, use a red colored pencil to divide each whole into fourths, and label each fraction above the line. Use a fraction strip to help you estimate, if necessary.
Answer :

Question 2.
On the number line above, use a blue colored pencil to divide each whole into eighths, and label each fraction below the line. Refold your fraction strip from Problem 1 to help you estimate.
Answer :

Question 3.
List the fractions that name the same place on the number line.
Answer :
The Fractions that have same place on the number line are
\(\frac{1}{4}\) = \(\frac{2}{8}\)
\(\frac{2}{4}\) = \(\frac{4}{8}\)
\(\frac{3}{4}\) = \(\frac{6}{8}\)
\(\frac{4}{4}\) = \(\frac{8}{8}\)
\(\frac{5}{4}\) = \(\frac{10}{8}\)
\(\frac{6}{4}\) = \(\frac{12}{8}\)
\(\frac{7}{4}\) = \(\frac{14}{8}\)
\(\frac{8}{4}\) = \(\frac{16}{8}\)
\(\frac{9}{4}\) = \(\frac{18}{8}\)
\(\frac{10}{4}\) = \(\frac{20}{8}\)
\(\frac{11}{4}\) = \(\frac{22}{8}\)
\(\frac{12}{4}\) = \(\frac{24}{8}\)

Question 4.
Using your number line to help, what red fraction and what blue fraction would be equal to \(\frac{7}{2}\)? Draw the part of the number line below that would include these fractions, and label it.
Answer :
\(\frac{7}{2}\) = \(\frac{14}{4}\) = \(\frac{28}{8}\).

Question 5.
Write two different fractions for the dot on the number line. You may use halves, thirds, fourths, fifths, sixths, or eighths. Use fraction strips to help you, if necessary.

_____________ = _____________

_____________ = _____________

_____________ = _____________
Answer :

Explanation :
The given 1 st number line is divided into 3 parts that means it can be partitioned into thirds and sixths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{6}\) = \(\frac{1}{3}\) .
The given 2nd number line is divided into 4 parts that means it can be partitioned intoFourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{4}\) = \(\frac{4}{8}\) .

Question 6.
Cameron and Terrance plan to run in the city race on Saturday. Cameron has decided that he will divide his race into 3 equal parts and will stop to rest after running 2 of them. Terrance divides his race into 6 equal parts and will stop and rest after running 2 of them. Will the boys rest at the same spot in the race? Why or why not? Draw a number line to explain your answer.
Answer :
No, they don’t spot in the same place .

Explanation :
The number line is divided into thirds and sixths .
The Cameron partitioned the race into 3 parts and fraction values are written below the number line .
The Cameron stop and rest after running 2 of them = \(\frac{2}{3}\) .
The Terrance partitioned the race into 6 parts and fraction values are written above the number line .
The Terrance stop and rest after running 2 of them = \(\frac{2}{6}\) .
That means they don’t spot the same place for rest .

Question 7.
Henry and Maddie were in a pie-eating contest. The pies were cut either into thirds or sixths. Henry picked up a pie cut into sixths and ate \(\frac{4}{6}\) of it in 1 minute. Maddie picked up a pie cut into thirds. What fraction of her pie does Maddie have to eat in 1 minute to tie with Henry? Draw a number line, and use words to explain your answer.
Answer :

Explanation :
Henry pie is cut in sixths.
Number of of pies ate by henry in 1 minute= \(\frac{4}{6}\)
Maddie pie cut in thirds.
Number of of pies ate by Maddie in 1 minute= ?
For tie Maddie should eat same quantity as Henry that means the point \(\frac{4}{6}\) is marked says number of pies Maddie should eat in thirds .
Number of of pies ate by Maddie in 1 minute=\(\frac{2}{3}\) .

Eureka Math Grade 3 Module 5 Lesson 23 Homework Answer Key

Question 1.
On the number line above, use a colored pencil to divide each whole into thirds and label each fraction above the line.
Answer :

Explanation :
Number line from 0 to 3 is partitioned into thirds . and all the fraction values are written above the number line .

Question 2.
On the number line above, use a different colored pencil to divide each whole into sixths and label each fraction below the line.
Answer :

Explanation :
Number line from 0 to 3 is partitioned into sixths . and all the fraction values are written below the number line .

Question 3.
Write the fractions that name the same place on the number line.
Answer :
The Fractions that have same place on the number line are
\(\frac{1}{3}\) = \(\frac{2}{6}\)
\(\frac{2}{3}\) = \(\frac{4}{6}\)
\(\frac{3}{3}\) = \(\frac{6}{6}\)
\(\frac{4}{3}\) = \(\frac{8}{6}\)
\(\frac{5}{3}\) = \(\frac{10}{6}\)
\(\frac{6}{3}\) = \(\frac{12}{6}\)
\(\frac{7}{3}\) = \(\frac{14}{6}\)
\(\frac{8}{3}\) = \(\frac{16}{6}\)
\(\frac{9}{3}\) = \(\frac{18}{6}\)

Question 4.
Using your number line to help, name the fraction equivalent to \(\frac{20}{6}\). Name the fraction equivalent to \(\frac{12}{3}\). Draw the part of the number line that would include these fractions below, and label it.

Answer :

Explanation :
Number line is partitioned from 3 to 4 into thirds and sixths and all the thirds fraction values are written above number line and  sixths fraction values are written below the number line .
We notice \(\frac{20}{6}\) = \(\frac{10}{3}\) and \(\frac{12}{3}\) = \(\frac{24}{6}\) .

Question 5.
Write two different fraction names for the dot on the number line. You may use halves, thirds, fourths, fifths, sixths, eighths, or tenths.

Answer :

Explanation :
The given 1 st number line is divided into 3 parts that means it can be partitioned into thirds and sixths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{4}{6}\) = \(\frac{2}{3}\) .
The given 2nd number line is divided into 4 parts that means it can be partitioned into Fourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{8}\) = \(\frac{1}{4}\) .
The given 3rd number line is divided into 4 parts that means it can be partitioned into Fourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{7}{4}\) = \(\frac{14}{8}\) .
The given 4th number line is divided into 5 parts that means it can be partitioned into fifths and tenths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{7}{5}\) = \(\frac{14}{10}\) .

Question 6.
Danielle and Mandy each ordered a large pizza for dinner. Danielle’s pizza was cut into sixths, and Mandy’s pizza was cut into twelfths. Danielle ate 2 sixths of her pizza. If Mandy wants to eat the same amount of pizza as Danielle, how many slices of pizza will she have to eat? Write the answer as a fraction. Draw a number line to explain your answer.
Answer :

Explanation :
Danielle pizza is cut in sixths.
Number of pizza pieces ate by Danielle = \(\frac{2}{6}\)
Mandy pizza cut in twelfths.
Number of pizza pieces ate by Mandy= ?
For same Quantity Mandy should eat same quantity as Danielle that means the point \(\frac{2}{6}\) is marked says number of pizza pieces Mandy should eat in twelfths .
Number of pizza pieces should eat by mandy =\(\frac{4}{12}\) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 24 Answer Key

Eureka Math Grade 3 Module 5 Lesson 24 Sprint Answer Key

A
Add by Seven

Question 1.
0 + 7 =
Answer :
0 + 7 = 7
Explanation :

Question 2.
1 + 7 =
Answer :
1 + 7 = 8
Explanation :

Question 3.
2 + 7 =
Answer :
2 + 7 = 9
Explanation :

Question 4.
3 + 7 =
Answer :
3 + 7 = 10
Explanation :

Question 5.
7 + 3 =
Answer :
7 + 3 = 10
Explanation :

Question 6.
7 + 2 =
Answer :
7 + 2 = 9
Explanation :

Question 7.
7 + 1 =
Answer :
7 + 1 = 8

Question 8.
7 + 0 =
Answer :
7 + 0 = 7

Question 9.
4 + 7 =
Answer :
4 + 7 = 11

Explanation :

Question 10.
14 + 7 =
Answer :
14 + 7 = 21

Explanation :

Question 11.
24 + 7 =
Answer :
24 + 7 = 31

Explanation :

Question 12.
34 + 7 =
Answer :
34 + 7 = 41

Explanation :

Question 13.
44 + 7 =
Answer :
44 + 7 = 51

Explanation :

Question 14.
84 + 7 =
Answer :
84 + 7 = 91

Explanation :

Question 15.
64 + 7 =
Answer :
64 + 7 = 71

Explanation :

Question 16.
5 + 7 =
Answer :
5 + 7 = 12

Explanation :

Question 17.
15 + 7 =
Answer :
15 + 7 = 22

Explanation :

Question 18.
25 + 7 =
Answer :
25 + 7 = 32

Explanation :

Question 19.
35 + 7 =
Answer :
35 + 7 = 42

Explanation :

Question 20.
45 + 7 =
Answer :
45 + 7 = 52

Explanation :

Question 21.
75 + 7 =
Answer :
75 + 7 = 82

Explanation :

Question 22.
55 + 7 =
Answer :
55 + 7 = 62

Explanation :

Question23.
6 + 7 =

Question 24.
16 + 7 =
Answer :
16 + 7 = 23

Explanation :

Question 25.
26 + 7 =
Answer :
26 + 7 = 33

Explanation :

Question 26.
36 + 7 =
Answer :
36 + 7 = 43

Explanation :

Question 27.
46 + 7 =
Answer :
46 + 7 = 53

Explanation :

Question 28.
66 + 7 =
Answer :
66 + 7 = 73

Explanation :

Question 29.
7 + 7 =
Answer :
7 + 7 = 14

Question 30.
17 + 7 =
Answer :
17 + 7 = 24

Explanation :

Question 31.
27 + 7 =
Answer :
27 + 7 = 34

Explanation :

Question 32.
37 + 7 =
Answer :
37 + 7 = 44

Explanation :

Question 33.
87 + 7 =
Answer :
87 + 7 = 94

Explanation :

Question 34.
8 + 7 =
Answer :
8 + 7 = 15

Question 35.
18 + 7 =
Answer :
18 + 7 = 25
Explanation :

Question 36.
28 + 7 =
Answer :
28 + 7 = 35

Explanation :

Question 37.
38 + 7 =
Answer :
38 + 7 = 45
Explanation :

Question 38.
78 + 7 =
Answer :
78 + 7 = 85

Explanation :

Question 39.
9 + 7 =
Answer :
9 + 7 =
Answer :
9 + 7 =  16

Question 40.
19 + 7 =
Answer :
19 + 7 = 26
Explanation :

Question 41.
29 + 7 =
Answer :
29 + 7 = 36

Explanation :

Question 42.
39 + 7 =
Answer :
39 + 7 = 46

Explanation :

Question 43.
49 + 7 =
Answer :
49 + 7 = 56
Explanation :

Question 44.
79 + 7 =
Answer :
79 + 7 = 86

Explanation :

B
Add by Seven

Question 1.
7 + 0 =
Answer :
7 + 0 = 7

Question 2.
7 + 1 =
Answer :
7 + 1 = 8

Question 3.
7 + 2 =
Answer :
7 + 2 = 9

Question 4.
7 + 3 =
Answer :
7 + 3 = 10

Question 5.
3 + 7 =
Answer :
3 + 7 = 10

Question 6.
2 + 7 =
Answer :
2 + 7 = 9

Question 7.
1 + 7 =
Answer :
1 + 7 = 8

Question 8.
0 + 7 =
Answer :
0 + 7 = 7

Question 9.
4 + 7 =
Answer :
4 + 7 = 11

Question 10.
14 + 7 =
Answer :
14 + 7 = 21

Question 11.
24 + 7 =
Answer :
24 + 7 = 31

Question 12.
34 + 7 =
Answer :
34 + 7 = 41

Question 13.
44 + 7 =
Answer :
44 + 7 = 51

Question 14.
74 + 7 =
Answer :
74 + 7 = 81

Question 15.
54 + 7 =
Answer :
54 + 7 = 61

Question 16.
5 + 7 =
Answer :
5 + 7 = 12

Question 17.
15 + 7 =
Answer :
15 + 7 = 22

Question 18.
25 + 7 =
Answer :
25 + 7 = 32

Question 19.
35 + 7 =
Answer :
35 + 7 = 42

Question 20.
45 + 7 =
Answer :
45 + 7 = 52

Question 21.
85 + 7 =
Answer :
85 + 7 = 92

Question 22.
65 + 7 =
Answer :
65 + 7 = 72

Question 23.
6 + 7 =
Answer :
6 + 7 = 13

Question 24.
16 + 7 =
Answer :
16 + 7 = 23

Question 25.
26 + 7 =
Answer :
26 + 7 = 33

Question 26.
36 + 7 =
Answer :
36 + 7 = 43

Question 27.
46 + 7 =
Answer :
46 + 7 = 53

Question 28.
76 + 7 =
Answer :
76 + 7 = 83

Question 29.
7 + 7 =
Answer :
7 + 7 = 14

Question 30.
17 + 7 =
Answer :
17 + 7 = 24

Question 31.
27 + 7 =
Answer :
27 + 7 = 34

Question 32.
37 + 7 =
Answer :
37 + 7 = 44

Question 33.
67 + 7 =
Answer :
67 + 7 = 74

Question 34.
8 + 7 =
Answer :
8 + 7 = 15

Question 35.
18 + 7 =
Answer :
18 + 7 = 25

Question 36.
28 + 7 =
Answer :
28 + 7 = 35

Question 37.
38 + 7 =
Answer :
38 + 7 = 45

Question 38.
88 + 7 =
Answer :
88 + 7 = 95

Question 39.
9 + 7 =
Answer :
9 + 7 = 16

Question 40.
19 + 7 =
Answer :
19 + 7 = 26

Question 41.
29 + 7 =
Answer :
29 + 7 = 36

Question 42.
39 + 7 =
Answer :
39 + 7 = 46

Question 43.
49 + 7 =
Answer :
49 + 7 = 56

Question 44.
89 + 7 =
Answer :
89 + 7 = 96

Eureka Math Grade 3 Module 5 Lesson 24 Problem Set Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit. The first one is done for you.

Answer :

Explanation :
The number line is divided into halves , thirds , Fourths and fifths and respective number bond is represented in the above figure .
Thirds: Number bond showing 3 units of \(\frac{1}{3}\) ; number line partitioned and labeled from 0 to 1
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ;number line partitioned and labeled from 0 to 1
Fifths: Number bond showing 5 units of \(\frac{1}{5}\) ; number line partitioned and labeled from 0 to 1

Question 2.
Circle all the fractions in Problem 1 that are equal to 1. Write them in a number sentence below.

Answer :

Question 3.
What pattern do you notice in the fractions that are equivalent to 1?
Answer :
The fractions that are equivalent to 1 have The Numerator and the Denominator same .

Question 4.
Taylor took his little brother to get pizza. Each boy ordered a small pizza. Taylor’s pizza was cut in fourths, and his brother’s was cut in thirds. After they had both eaten all of their pizza, Taylor’s little brother said, “Hey that was no fair! You got more than me! You got 4 pieces, and I only got 3.”
Should Taylor’s little brother be mad? What could you say to explain the situation to him? Use words, pictures, or a number line.
Answer :

Explanation :
The Taylor’s pizza and His brother pizza ordered small size pizza. Both the pizza’s are of same length.
The Taylor’s pizza is divided into fourths that means into 4 parts.
His Brother’s pizza is divided into thirds that means into 3 parts.
The slice of Taylor’s pizza is smaller than compared to his brother’s pizza .
The size doesn’t depends on the number of slices .

Eureka Math Grade 3 Module 5 Lesson 24 Exit Ticket Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit.

Answer :

Explanation :
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ; number line partitioned and labeled from 0 to 1

Question 2.
How many copies of \(\frac{1}{4}\) does it take to make 1 whole? What’s the fraction for 1 whole in this case? Use the number line or the number bond in Problem 1 to help you explain.
Answer :
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ; number line partitioned and labeled from 0 to 1 in the above figure .
For 1 whole we notice \(\frac{4}{4}\) Fraction in the figure that means we require 4 \(\frac{1}{4}\) copies to make 1 Whole .

Eureka Math Grade 3 Module 5 Lesson 24 Homework Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit.

Answer :

Explanation :
The number line is divided into fifths, Sixths, Sevenths and Eighths and respective number bond is represented in the above figure .
Fifths: Number bond showing 5 units of \(\frac{1}{5}\) ; number line partitioned and labeled from 0 to 1
Sixths: Number bond showing 6 units of \(\frac{1}{6}\) ; number line partitioned and labeled from 0 to 1
Seventhss: Number bond showing 7 units of \(\frac{1}{7}\) ;number line partitioned and labeled from 0 to 1
Eigths: Number bond showing 8 units of \(\frac{1}{8}\) ; number line partitioned and labeled from 0 to 1

Question 2.
Circle all the fractions in Problem 1 that are equal to 1. Write them in a number sentence below.

Answer :
\(\frac{5}{5}\) = \(\frac{6}{6}\) = \(\frac{7}{7}\) = \(\frac{8}{8}\) .

Question 3.
What pattern do you notice in the fractions that are equivalent to 1? Following this pattern, how would you represent ninths as 1 whole?
Answer :
The Fractions that are equivalent to 1 follow the pattern have Numerator and Denominator Equal .
To represent Ninths are 1 whole = \(\frac{9}{9}\) .

Question 4.
In Art class, Mr. Joselyn gave everyone a 1-foot stick to measure and cut. Vivian measured and cut her stick into 5 equal pieces. Scott measured and cut his into 7 equal pieces. Scott said to Vivian, “The total length of my stick is longer than yours because I have 7 pieces, and you only have 5.” Is Scott correct? Use words, pictures, or a number line to help you explain.
Answer :

Explanation :
Scott is wrong , Even though he has more pieces than Vivian Both the Lengths of Sticks = 1 foot .
Scott pieces are smaller because his stick is broken into more pieces .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 25 Answer Key

Eureka Math Grade 3 Module 5 Lesson 25 Problem Set Answer Key

A
Subtract by Six

Question 1.
16 – 6 =

Question 2.
6 – 6 =

Question 3.
26 – 6 =

Question 4.
7 – 6 =

Question 5.
17 – 6 =

Question 6.
37 – 6 =

Question 7.
8 – 6 =

Question 8.
18 – 6 =

Question 9.
48 – 6 =

Question 10.
9 – 6 =

Question 11.
19 – 6 =

Question 12.
59 – 6 =

Question 13.
10 – 6 =

Question 14.
20 – 6 =

Question 15.
70 – 6 =

Question 16.
11 – 6 =

Question 17.
21 – 6 =

Question 18.
81 – 6 =

Question 19.
12 – 6 =

Question 20.
22 – 6 =

Question 21.
82 – 6 =

Question 22.
13 – 6 =

Question 23.
23 – 6 =

Question 24.
33 – 6 =

Question 25.
63 – 6 =

Question 26.
83 – 6 =

Question 27.
14 – 6 =

Question 28.
24 – 6 =

Question 29.
34 – 6 =

Question 30.
74 – 6 =

Question 31.
54 – 6 =

Question 32.
15 – 6 =

Question 33.
25 – 6 =

Question 34.
35 – 6 =

Question 35.
85 – 6 =

Question 36.
65 – 6 =

Question 37.
90 – 6 =

Question 38.
53 – 6 =

Question 39.
42 – 6 =

Question 40.
71 – 6 =

Question 41.
74 – 6 =

Question 42.
95 – 6 =

Question 43.
51 – 6 =

Question 44.
92 – 6 =

B
Subtract by Six

Question 1.
6 – 6 =

Question 2.
16 – 6 =

Question 3.
26 – 6 =

Question 4.
7 – 6 =

Question 5.
17 – 6 =

Question 6.
67 – 6 =

Question 7.
8 – 6 =

Question 8.
18 – 6 =

Question 9.
78 – 6 =

Question 10.
9 – 6 =

Question 11.
19 – 6 =

Question 12.
89 – 6 =

Question 13.
10 – 6 =

Question 14.
20 – 6 =

Question 15.
90 – 6 =

Question 16.
11 – 6 =

Question 17.
21 – 6 =

Question 18.
41 – 6 =

Question 19.
12 – 6 =

Question 20.
22 – 6 =

Question 21.
42 – 6 =

Question 22.
13 – 6 =

Question 23.
23 – 6 =

Question 24.
33 – 6 =

Question 25.
53 – 6 =

Question 26.
73 – 6 =

Question 27.
14 – 6 =

Question 28.
24 – 6 =

Question 29.
34 – 6 =

Question 30.
64 – 6 =

Question 31.
44 – 6 =

Question 32.
15 – 6 =

Question 33.
25 – 6 =

Question 34.
35 – 6 =

Question 35.
75 – 6 =

Question 36.
55 – 6 =

Question 37.
70 – 6 =

Question 38.
63 – 6 =

Question 39.
52 – 6 =

Question 40.
81 – 6 =

Question 41.
64 – 6 =

Question 42.
85 – 6 =

Question 43.
91 – 6 =

Question 44.
52 – 6 =

Eureka Math Grade 3 Module 5 Lesson 25 Problem Set Answer Key

Question 1.
Label the following models as a fraction inside the dotted box. The first one has been done for you.

Answer :

Explanation :
\(\frac{4}{1}\) means it is 4 whole . ( you have 4 copies of 1 whole ).
\(\frac{4}{4}\) means you have 1 whole . ( you have 4 copies of \(\frac{1}{4}\) ) .
\(\frac{4}{2}\) means you have 2 whole .( you have 4 copies of \(\frac{1}{2}\) ) .
and similar for others .

Question 2.
Fill in the missing whole numbers in the boxes below the number line. Rename the whole numbers as fractions in the boxes above the number line.

Answer :

Question 3.
Explain the difference between these two fractions with words and pictures.

Answer :

Explanation :
\(\frac{2}{1}\) means it is 2 whole . ( you have 2 copies of 1 whole ).
\(\frac{2}{2}\) means you have 1 whole . ( you have 2 copies of \(\frac{1}{2}\) ) .

Eureka Math Grade 3 Module 5 Lesson 25 Exit Ticket Answer Key

Question 1.
Label the model as a fraction inside the box.

Answer :

Question 2.
Partition the wholes into thirds. Rename the fraction for 3 wholes. Use the number line and words to explain your answer.

Answer :

Explanation :
Number line partitioned into thirds; fraction for 3 wholes renamed as \(\frac{9}{3}\)

Eureka Math Grade 3 Module 5 Lesson 25 Homework Answer Key

Question 1.
Label the following models as fractions inside the boxes.

Answer :

Explanation :
\(\frac{4}{1}\) means it is 4 whole . ( you have 4 copies of 1 whole ).
\(\frac{4}{4}\) means you have 1 whole . ( you have 4 copies of \(\frac{1}{4}\) ) .
\(\frac{4}{2}\) means you have 2 whole .( you have 4 copies of \(\frac{1}{2}\) ) .

\(\frac{8}{1}\) means it is 8 whole . ( you have 8 copies of 1 whole ).
\(\frac{8}{8}\) means you have 1 whole . ( you have 8 copies of \(\frac{1}{8}\) ) .
\(\frac{8}{2}\) means you have 2 whole .( you have 8 copies of \(\frac{1}{4}\) ) .

Fill in the missing whole numbers in the boxes below the number line. Rename the wholes as fractions in the boxes above the number line.

Answer :

Answer :
Number is represented from 0 to 12 and from 15 to 21 .the whole numbers are renamed in fraction form. All the missing whole numbers and fraction numbers are written .

Question 3.
Explain the difference between these fractions with words and pictures.

Answer :

Explanation :
\(\frac{5}{1}\) means it is 5 whole . ( you have 5 copies of 1 whole ).
\(\frac{5}{5}\) means you have 1 whole . ( you have 5 copies of \(\frac{1}{5}\) ) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 26 Answer Key

Eureka Math Grade 3 Module 5 Lesson 26 Sprint Answer Key

A
Add by Eight

Question 1.
0 + 8 =

Question 2.
1 + 8 =

Question 3.
2 + 8 =

Question 4.
8 + 2 =

Question 5.
1 + 8 =

Question 6.
0 + 8 =

Question 7.
3 + 8 =

Question 8.
13 + 8 =

Question 9.
23 + 8 =

Question 10.
33 + 8 =

Question 11.
43 + 8 =

Question 12.
83 + 8 =

Question 13.
4 + 8 =

Question 14.
14 + 8 =

Question 15.
24 + 8 =

Question 16.
34 + 8 =

Question 17.
44 + 8 =

Question 18.
74 + 8 =

Question 19.
5 + 8 =

Question 20.
15 + 8 =

Question 21.
25 + 8 =

Question 22.
35 + 8 =

Question 23.
65 + 8 =

Question 24.
6 + 8 =

Question 25.
16 + 8 =

Question 26.
26 + 8 =

Question 27.
36 + 8 =

Question 28.
86 + 8 =

Question 29.
46 + 8 =

Question 30.
7 + 8 =

Question 31.
17 + 8 =

Question 32.
27 + 8 =

Question 33.
37 + 8 =

Question 34.
77 + 8 =

Question 35.
8 + 8 =

Question 36.
18 + 8 =

Question 37.
28 + 8 =

Question 38.
38 + 8 =

Question 39.
68 + 8 =

Question 40.
9 + 8 =

Question 41.
19 + 8 =

Question 42.
29 + 8 =

Question 43.
39 + 8 =

Question 44.
89 + 8 =

B
Add by Eight

Question 1.
8 + 0 =

Question 2.
8 + 1 =

Question 3.
8 + 2 =

Question 4.
2 + 8 =

Question 5.
1 + 8 =

Question 6.
0 + 8 =

Question 7.
3 + 8 =

Question 8.
13 + 8 =

Question 9.
23 + 8 =

Question 10.
33 + 8 =

Question 11.
43 + 8 =

Question 12.
73 + 8 =

Question 13.
4 + 8 =

Question 14.
14 + 8 =

Question 15.
24 + 8 =

Question 16.
34 + 8 =

Question 17.
44 + 8 =

Question 18.
84 + 8 =

Question 19.
5 + 8 =

Question 20.
15 + 8 =

Question 21.
25 + 8 =

Question 22.
35 + 8 =

Question 23.
55 + 8 =

Question 24.
6 + 8 =

Question 25.
16 + 8 =

Question 26.
26 + 8 =

Question 27.
36 + 8 =

Question 28.
66 + 8 =

Question 29.
56 + 8 =

Question 30.
7 + 8 =

Question 31.
17 + 8 =

Question 32.
27 + 8 =

Question 33.
37 + 8 =

Question 34.
67 + 8 =

Question 35.
8 + 8 =

Question 36.
18 + 8 =

Question 37.
28 + 8 =

Question 38.
38 + 8 =

Question 39.
78 + 8 =

Question 40.
9 + 8 =

Question 41.
19 + 8 =

Question 42.
29 + 8 =

Question 43.
39 + 8 =

Question 44.
89 + 8 =

Eureka Math Grade 3 Module 5 Lesson 26 Problem Set Answer Key

Question 1.
Partition the number line to show the fractional units. Then, draw number bonds using copies of 1 whole for the circled whole numbers.

Answer :

Explanation :
The number line is divided into halves from 0 to 2 and whole numbers are represented in fraction form and number bond is completed .
The number line is divided into thirds from 2 to 4  and whole numbers are represented in fraction form and number bond is completed .

Question 2.
Write the fractions that name the whole numbers for each fractional unit. The first one has been done.

Answer :

Question 3.
Sammy uses \(\frac{1}{4}\) meter of wire each day to make things.
a. Draw a number line to represent 1 meter of wire. Partition the number line to represent how much Sammy uses each day. How many days does the wire last?
b. How many days will 3 meters of wire last?
Answer :
a.

Explanation :
Number line is partitioned into Fourths . Each day he does \(\frac{1}{4}\) . In four days he completes the 1 meter work .
b.
Each day he works \(\frac{1}{4}\).
In 4 days he completes 1 meter work .
For 3 meter work it takes 4 × 3 = 12 days .

Question 4.
Cindy feeds her dog \(\frac{1}{3}\) pound of food each day.
a. Draw a number line to represent 1 pound of food. Partition the number line to represent how much food she uses each day.
b. Draw another number line to represent 4 pounds of food. After 3 days, how many pounds of food has she given her dog?
c. After 6 days, how many pounds of food has she given her dog?
Answer :
a.

Explanation :
A number of 1 pound food is partitioned into thirds . Each day Cindy feeds her dog \(\frac{1}{3}\) pound of food . She can feed for 3 days of 1 pound food .
b.

Explanation
The Number Line is partitioned in thirds for 4 pounds of food .Each day Cindy feeds her dog \(\frac{1}{3}\) pound of food .After 3 days she feeds 1 pound of food to her dog  .
c.
After 6 days she feeds 2 pound of food to her dog .
For Every 3 days she completes 1 pound of food .

Eureka Math Grade 3 Module 5 Lesson 26 Exit Ticket Answer Key

Irene has 2 yards of fabric.
a. Draw a number line to represent the total length of Irene’s fabric.
b. Irene cuts her fabric into pieces of \(\frac{1}{5}\) yard in length. Partition the number line to show her cuts.
c. How many \(\frac{1}{5}\)-yard pieces does she cut altogether? Use number bonds with copies of wholes to help you explain.
Answer :

Explanation :
a. Number line drawn to represent 2 yards of fabric
b. Number line partitioned and labeled to show fifths
c. 10peices are cut al together ; number bond completed

Eureka Math Grade 3 Module 5 Lesson 26 Homework Answer Key

Question 1.
Partition the number line to show the fractional units. Then, draw number bonds with copies of 1 whole for the circled whole numbers.

Answer :

Explanation :
The number line is divided into sixths from 0 to 2 and whole numbers are represented in fraction form and number bond is completed .
The number line is divided into Fifths from 2 to 4  and whole numbers are represented in fraction form and number bond is completed .

Question 2.
Write the fractions that name the whole numbers for each fractional unit. The first one has been done for you.

Answer :

Question 3.
Rider dribbles the ball down \(\frac{1}{3}\) of the basketball court on the first day of practice. Each day after that, he dribbles \(\frac{1}{3}\) of the way more than he did the day before. Draw a number line to represent the court. Partition the number line to represent how far Rider dribbles on Day 1, Day 2, and Day 3 of practice. What fraction of the way does he dribble on Day 3?
Answer :

Explanation :
Number line drawn to represent the basketball court, partitioned into thirds, and labeled correctly;
Day 1: \(\frac{1}{3}\)
Day 2: \(\frac{2}{3}\)
Day 3: \(\frac{3}{3}\)
The Fraction that dribble on Day 3 is \(\frac{3}{3}\) . He dribbles the complete way .