Engage NY Eureka Math 3rd Grade Module 5 Lesson 22 Answer Key
Eureka Math Grade 3 Module 5 Lesson 22 Problem Set Answer Key
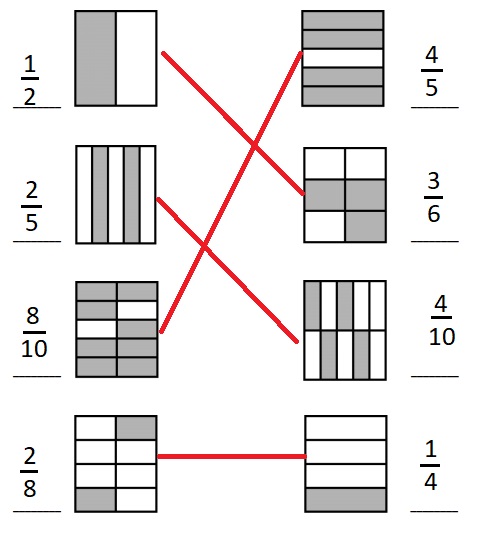
Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.
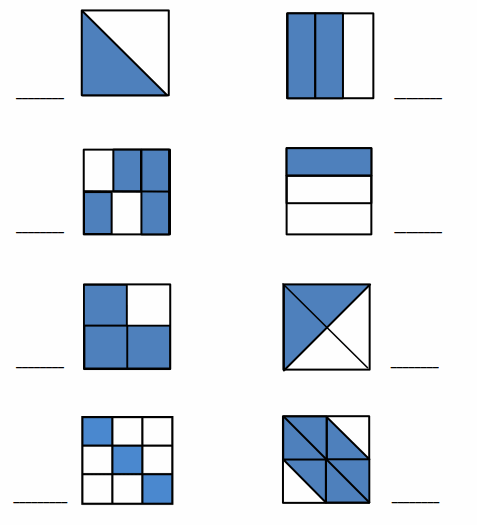
Answer :
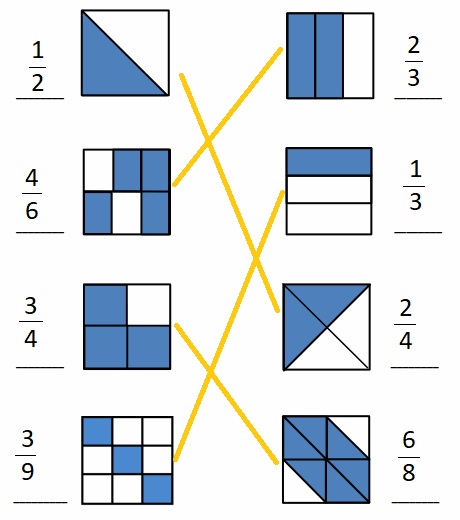
Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .
Question 2.
Write the missing parts of the fractions.
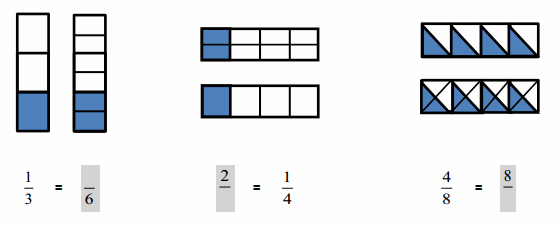
Answer :
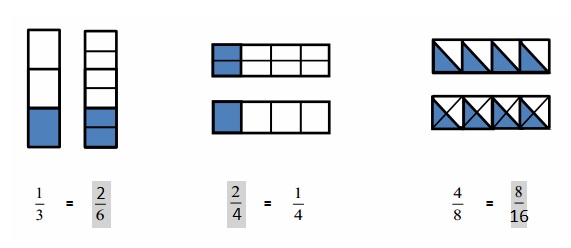
Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The Shaded fractions are written .
Question 3.
Why does it take 2 copies of \(\frac{1}{8}\) to show the same amount as 1 copy of \(\frac{1}{4}\)? Explain your answer in words and pictures.
Answer :
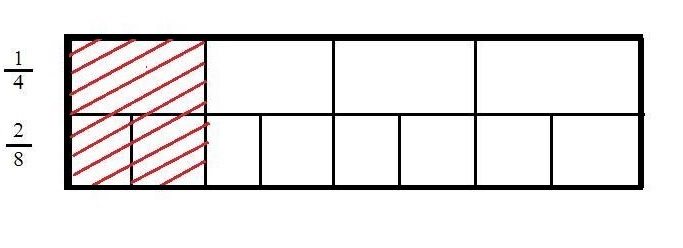
Explanation :
Because, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.
Since, by the Above diagram,
Thus, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.
Question 4.
How many sixths does it take to make the same amount as \(\frac{1}{3}\) ? Explain your answer in words and pictures.
Answer :
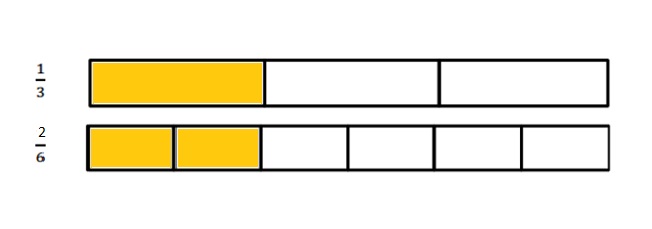
Explanation :
The Rectangular strip is divided into 3 parts and 6 parts . The first strip is marked \(\frac{1}{3}\) and the second is marked \(\frac{2}{6}\) which means \(\frac{1}{3}\) is equal to \(\frac{2}{6}\).
It takes two one-sixths to make a third.
Question 5.
Why does it take 10 copies of 1 sixth to make the same amount as 5 copies of 1 third? Explain your answer in words and pictures.
Answer :
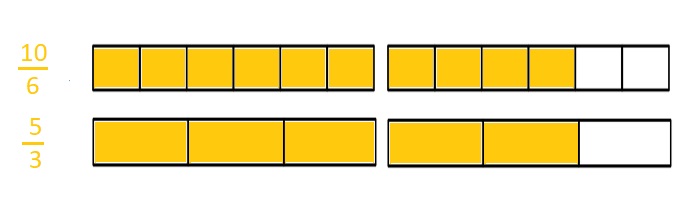
Explanation :
The Sixths have as many as units as thirds .
So, \(\frac{10}{6}\) are as equal as \(\frac{5}{3}\) copies as shown in above figure .
Eureka Math Grade 3 Module 5 Lesson 22 Exit Ticket Answer Key
Question 1.
Draw and label two models that show equivalent fractions.
Answer :
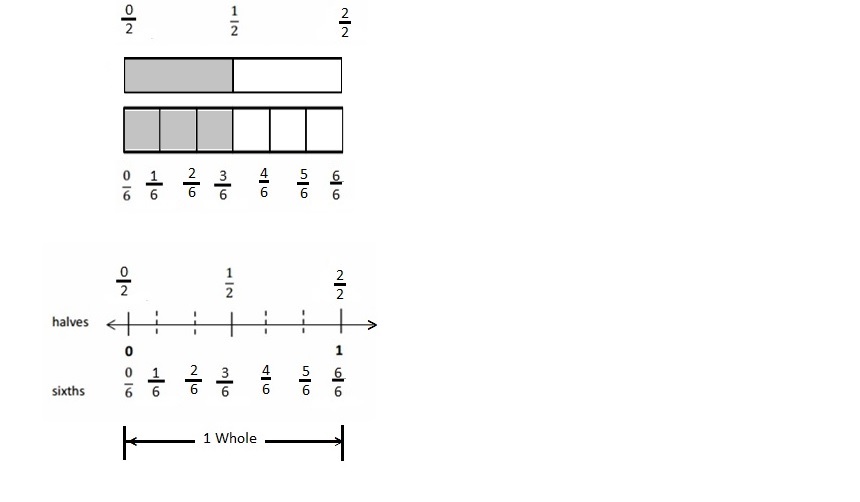
Explanation :
From The above figure we notice
The First rectangular strip is divided into 2 equal parts and fraction shaded is \(\frac{1}{2}\) .
The Second rectangular strip is divided into 6 equal parts and the fraction shaded is \(\frac{3}{6}\) .
Both show the equivalent fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .
Question 2.
Draw a number line that proves your thinking about Problem 1.
Answer :
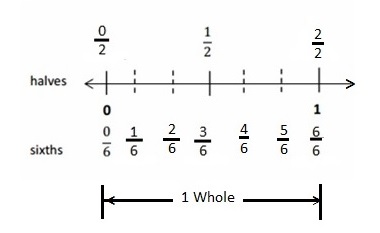
Explanation :
The number is represented for the above equivalent Fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .
Eureka Math Grade 3 Module 5 Lesson 22 Homework Answer Key
Question 1.
Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.
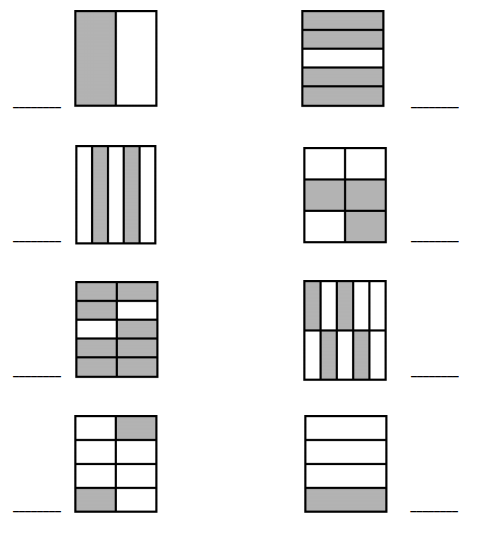
Answer :
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .
Question 2.
Complete the fractions to make true statements.
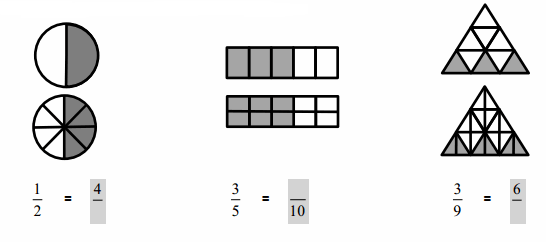 Answer :
Answer :
Answer :
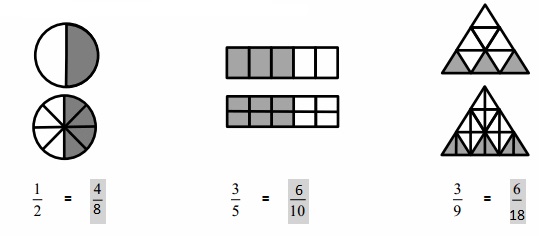
Explanation :
The Figures are divided into double and the shaded Fractions are compared .
Question 3.
Why does it take 3 copies of \(\frac{1}{6}\) to show the same amount as 1 copy of \(\frac{1}{2}\)? Explain your answer in words and pictures.
Answer :
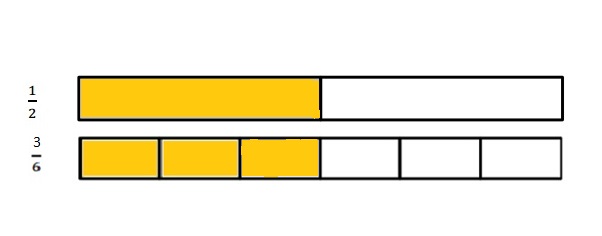
Explanation :
The Two tape Diagram Shows 3 copies of \(\frac{3}{6}\) is the same length as 1 copy of \(\frac{1}{2}\) .
Question 4.
How many ninths does it take to make the same amount as \(\frac{1}{3}\)? Explain your answer in words and pictures.
Answer :
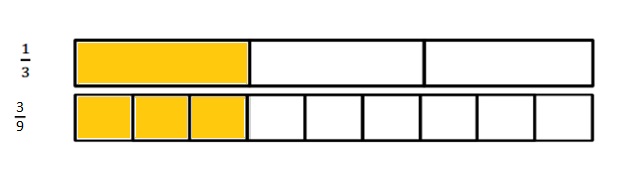
Explanation :
The Two tape Diagram Shows 3 ninths ( \(\frac{3}{9}\)) is the same length as 1Thirds (\(\frac{1}{3}\)) .
Question 5.
A pie was cut into 8 equal slices. If Ruben ate \(\frac{3}{4}\) of the pie, how many slices did he eat? Explain your answer using a number line and words.
Answer :
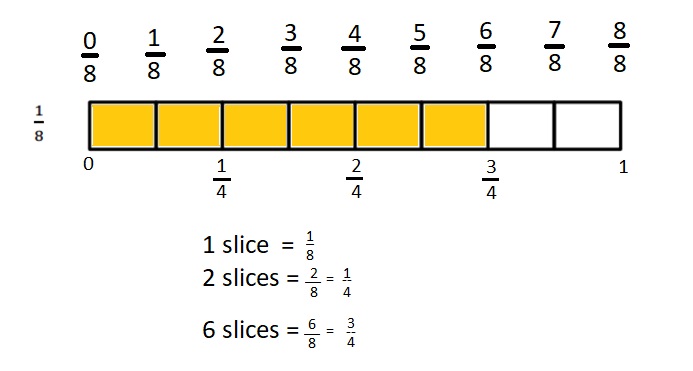
Explanation :
\(\frac{3}{4}\) is the same length as \(\frac{6}{8}\)
Ruben ate 6 slices which is \(\frac{6}{8}\) = \(\frac{3}{4}\).