Engage NY Eureka Math 3rd Grade Module 5 Lesson 20 Answer Key
Eureka Math Grade 3 Module 5 Lesson 20 Pattern Sheet Answer Key
Multiply.
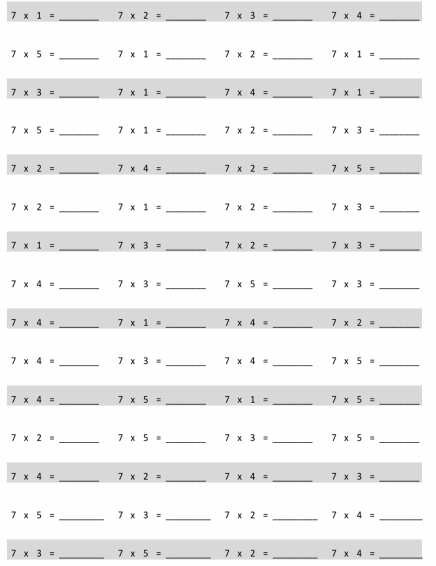
Answer :
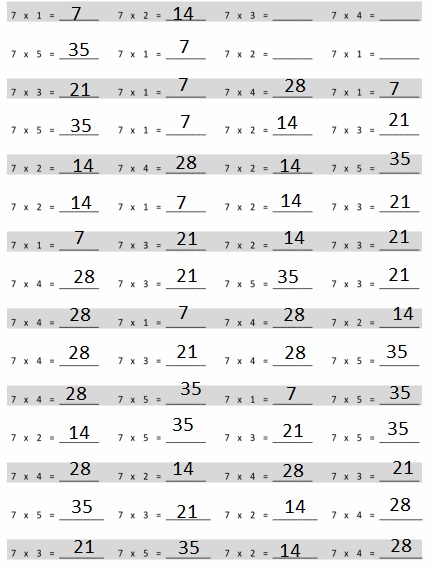
Explanation :
Here we see the seven table
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
Eureka Math Grade 3 Module 5 Lesson 20 Problem Set Answer Key
Question 1.
Label what fraction of each shape is shaded. Then, circle the fractions that are equal.
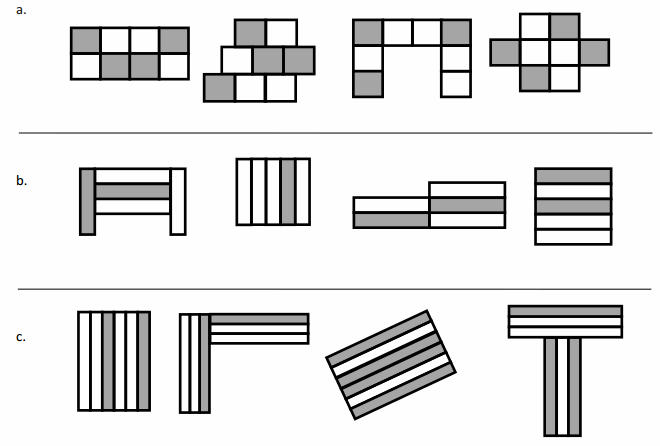
Answer :
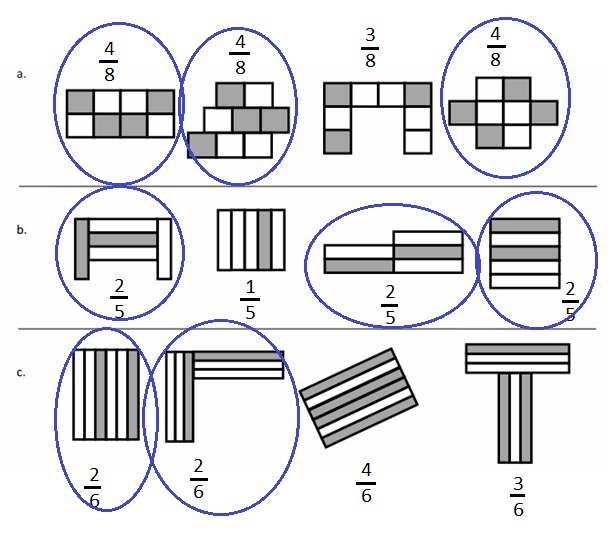
Explanation :
The Fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
fraction of each shape shaded are written and the fractions which are same are circled as shown in the above figure .
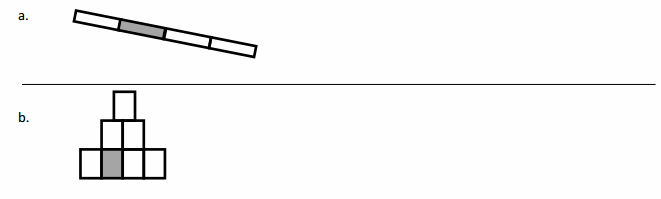
Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.
Answer :
Explanation :
In figure a the Fraction of shaded = \(\frac{1}{4}\) the same fraction is represented with a circle divided into 4 equal parts and 1 part is shaded
In figure b the Fraction of shaded = \(\frac{1}{7}\) the same fraction is represented with a Rectangle which is divided into 7 equal parts and 1 part is shaded .
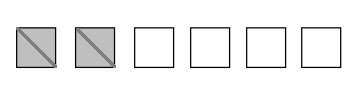
Question 3.
Ann has 6 small square pieces of paper. 2 squares are grey. Ann cuts the 2 grey squares in half with a diagonal line from one corner to the other.
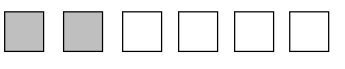
a. What shapes does she have now?
b. How many of each shape does she have?
c. Use all the shapes with no overlaps. Draw at least 2 different ways Ann’s set of shapes might look. What fraction of the figure is grey?
Answer :
a. The shapes does she have now is Triangles and Squares.
b. 4 Triangles and 4 Squares .
c. 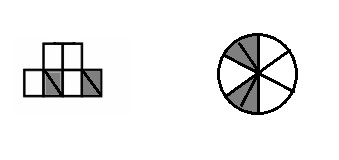
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
Fraction = \(\frac{2}{6}\) .
Question 4.
Laura has 2 different beakers that hold exactly 1 liter. She pours \(\frac{1}{2}\) liter of blue liquid into Beaker A. She pours \(\frac{1}{2}\) liter of orange liquid into Beaker B. Susan says the amounts are not equal. Cristina says they are. Explain who you think is correct and why.
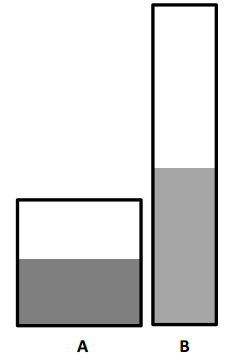
Answer :
Cristine is Correct .
Explanation :
Here the Breaker A contains Blue Liquid of \(\frac{1}{2}\) liter
Breaker B contains Orange liquid of \(\frac{1}{2}\) liter .
Whatever may be the shapes of the breaker but both the Amount of Quantities are same .
Where as , Susan Comparing the breakers Shape and saying the quantities are different . But she is Wrong .
Eureka Math Grade 3 Module 5 Lesson 20 Exit Ticket Answer Key
Question 1.
Label what fraction of the figure is shaded. Then, circle the fractions that are equal.
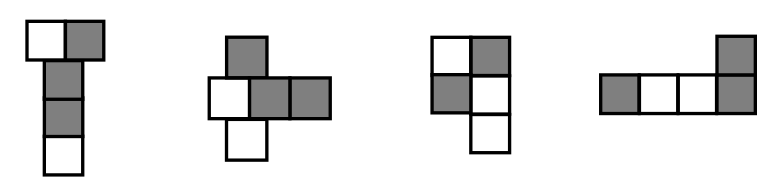
Answer :
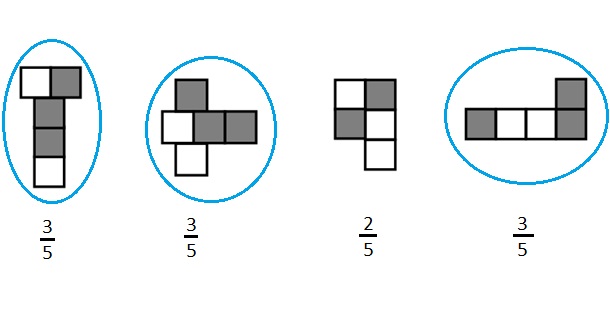
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
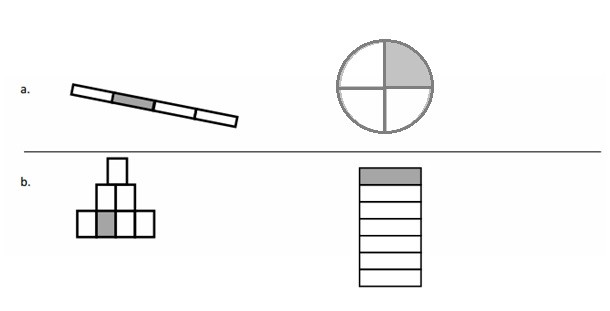
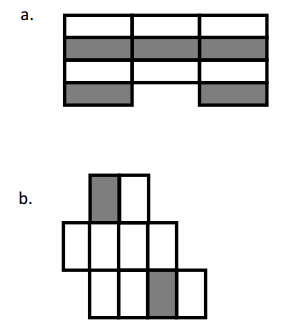
Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.
Answer : 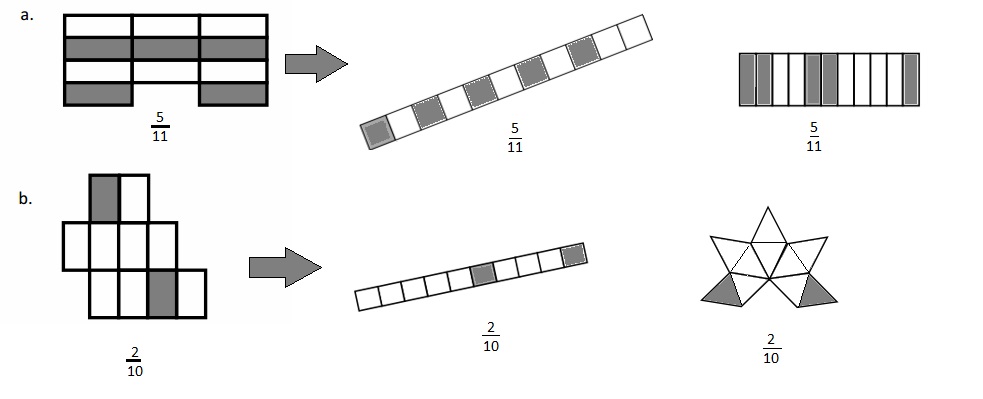
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The figure a has shaded fraction = \(\frac{5}{11}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 11 parts and 5 parts are shaded and another figure is Longer rectangular strip with 11 parts and 5 parts are shaded .
The figure b has shaded fraction = \(\frac{2}{10}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 10 parts and 2 parts are shaded and another figure is star shape with 10 parts of Triangles and 2 parts are shaded .
Eureka Math Grade 3 Module 5 Lesson 20 Homework Answer Key
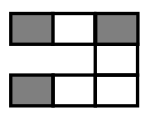
Question 1.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.
Answer :
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
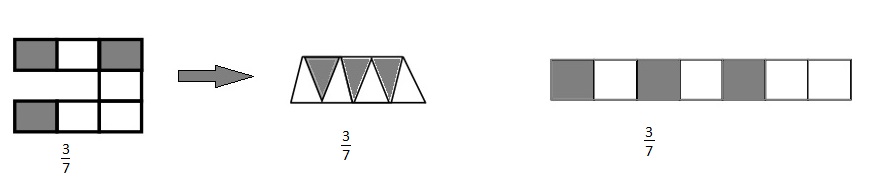
The figure a has shaded fraction = \(\frac{3}{7}\)
The fraction is represented with 2 different shapes . The first is a Triangular strip with 7 parts and 3 parts are shaded and another figure is rectangular strip with 7 parts and 3 parts are shaded .
Question 2.
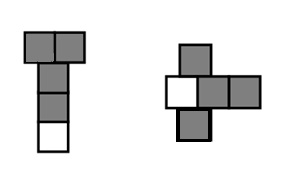
These two shapes both show \(\frac{4}{5}\).

a. Are the shapes equivalent? Why or why not?
b. Draw two different representations of \(\frac{4}{5}\) that are equivalent.
Answer :
a. No, The Shapes are not Equivalent , Both the shapes are \(\frac{4}{5}\) units but both the shapes are different .
b.
Explanation :
2 Different shapes of \(\frac{4}{5}\) units are represented in the above figure .
Question 3.
Diana ran a quarter mile straight down the street. Becky ran a quarter mile on a track. Who ran more? Explain your thinking.
Answer :
If the length of the down street and the track is same then
Diana and Becky both ran Quarter that means both ran same length .
Whereas if the length of the down street and the track is different , Then length of the Quarter will be different then both Ran different miles . The one who ran more can be known by if the length of the down street and track mile if given .