Eureka Math

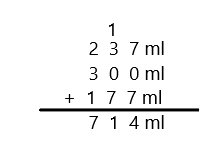
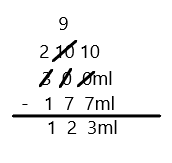
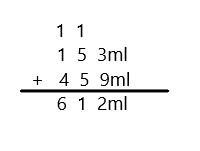
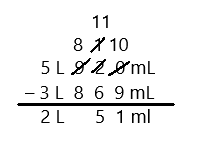
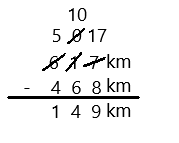
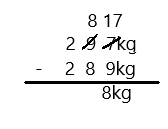
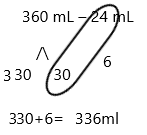
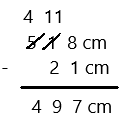
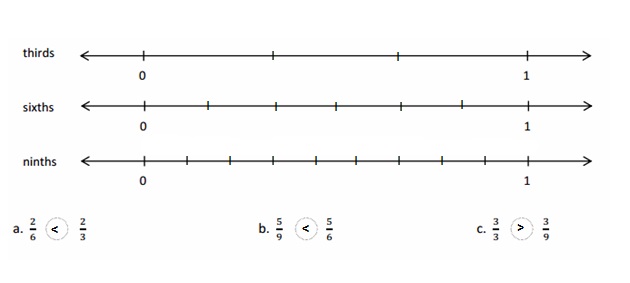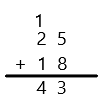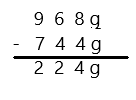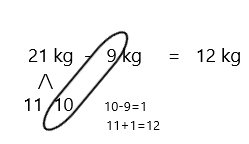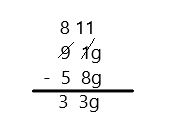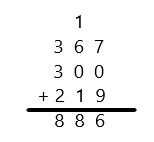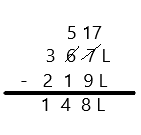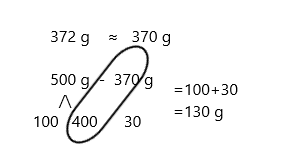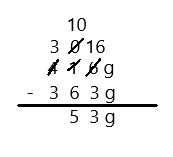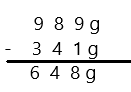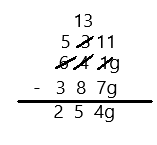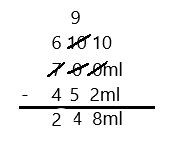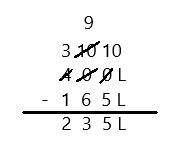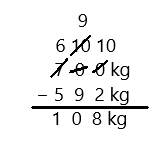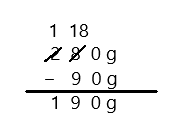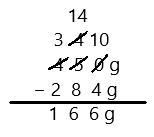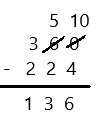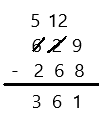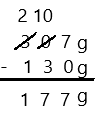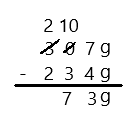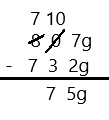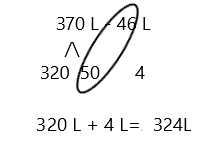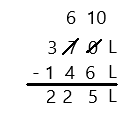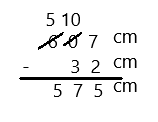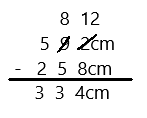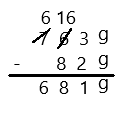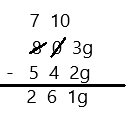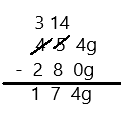Engage NY Eureka Math 3rd Grade Module 5 Lesson 27 Answer Key

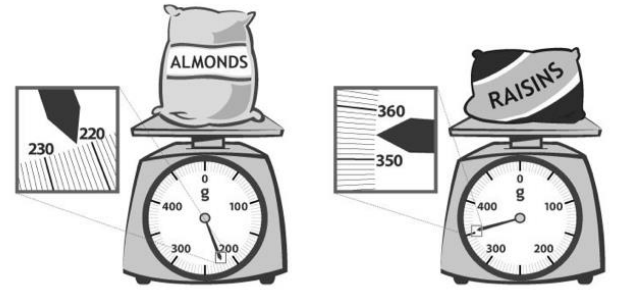
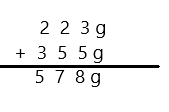
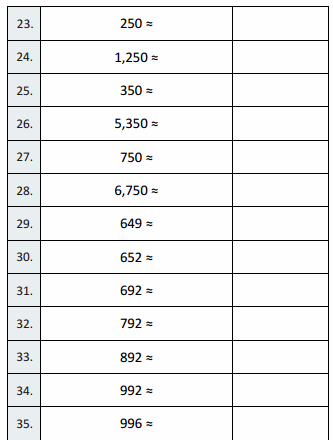
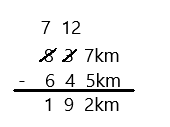
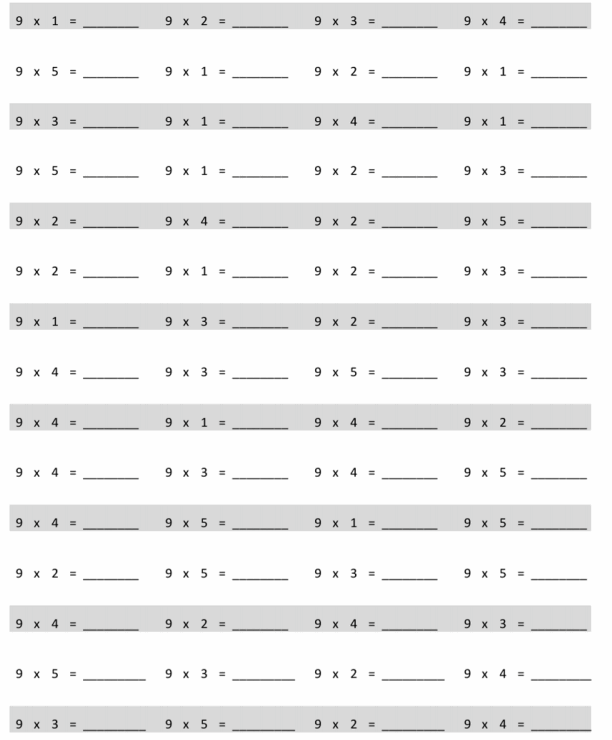
Eureka Math Grade 3 Module 5 Lesson 27 Sprint Answer Key

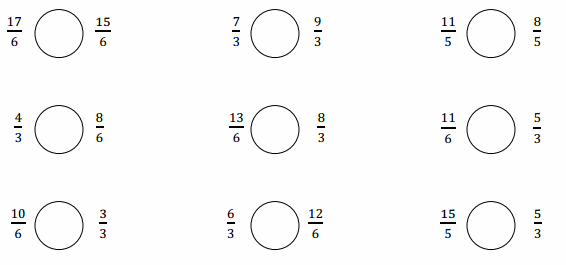
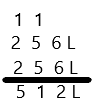
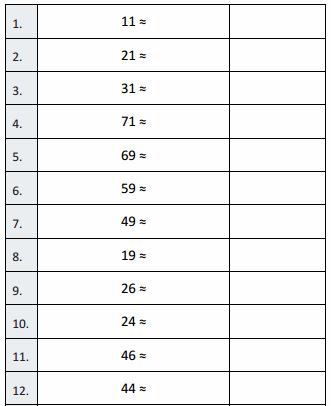
A
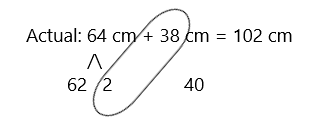
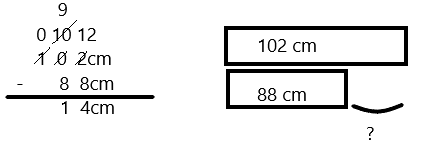
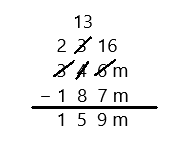
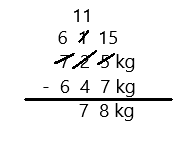
Subtract by Seven

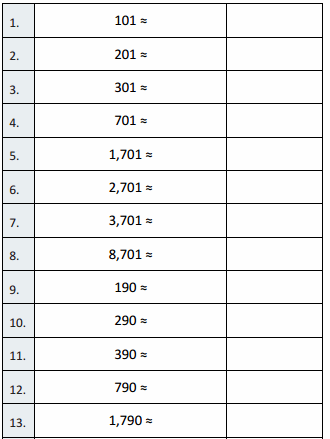
Question 1.
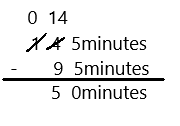
17 – 7 =

Question 2.
7 – 7 =

Question 3.
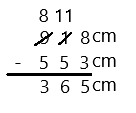
27 – 7 =

Question 4.
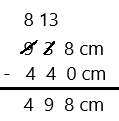
8 – 7 =

Question 5.
18 – 7 =

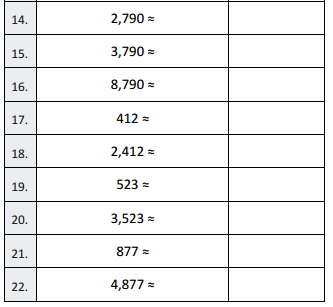
Question 6.
38 – 7 =

Question 7.
9 – 7 =

Question 8.
19 – 7 =

Question 9.
49 – 7 =

Question 10.
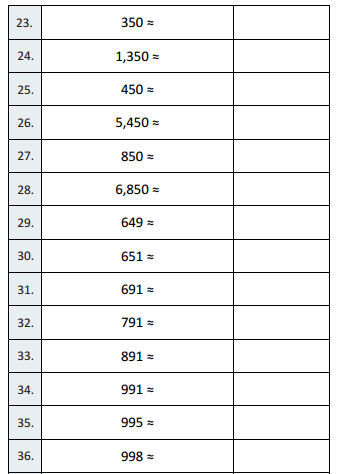
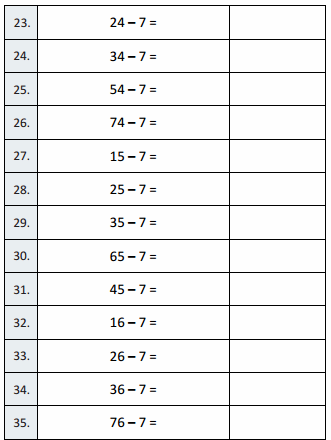
10 – 7 =

Question 11.
20 – 7 =

Question 12.
60 – 7 =

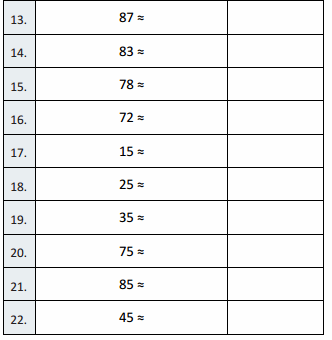
Question 13.
11 – 7 =

Question 14.
21 – 7 =

Question 15.
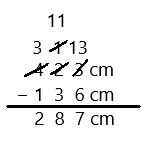
71 – 7 =

Question 16.
12 – 7 =

Question 17.
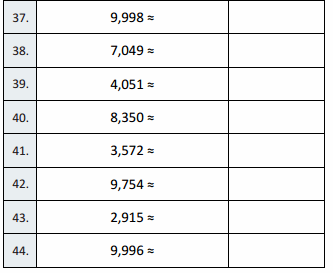
22 – 7 =

Question 18.
82 – 7 =

Question 19.
13 – 7 =

Question 20.
23 – 7 =

Question 21.
83 – 7 =

Question 22.
14 – 7 =

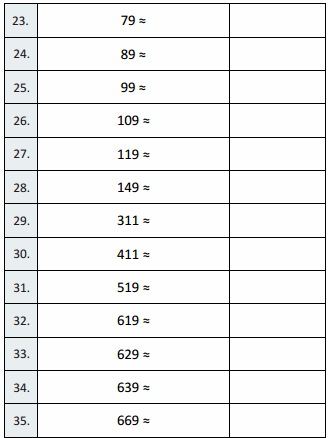
Question 23.
24 – 7 =

Question 24.
34 – 7 =

Question 25.
64 – 7 =

Question 26.
84 – 7 =

Question 27.
15 – 7 =

Question 28.
25 – 7 =

Question 29.
35 – 7 =

Question 30.
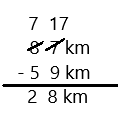
75 – 7 =

Question 31.
55 – 7 =

Question 32.
16 – 7 =

Question 33.
26 – 7 =

Question 34.
36 – 7 =

Question 35.
86 – 7 =

Question 36.
66 – 7 =

Question 37.
90 – 7 =

Question 38.
53 – 7 =

Question 39.
42 – 7 =

Question 40.
71 – 7 =

Question 41.
74 – 7 =

Question 42.
56 – 7 =

Question 43.
95 – 7 =

Question 44.
92 – 7 =

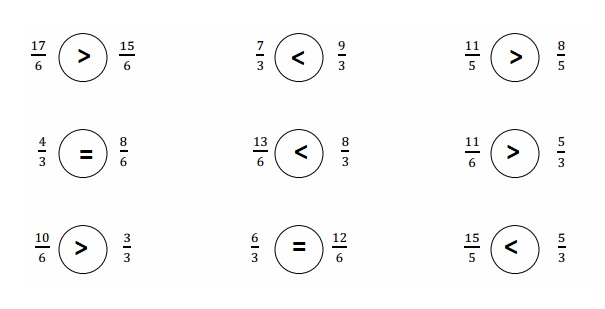
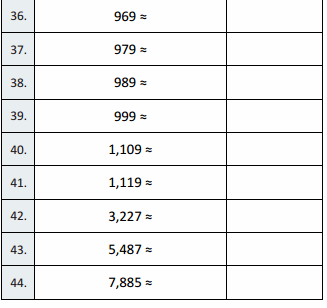
B
Subtract by Seven

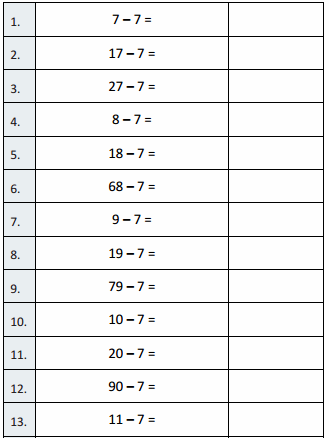
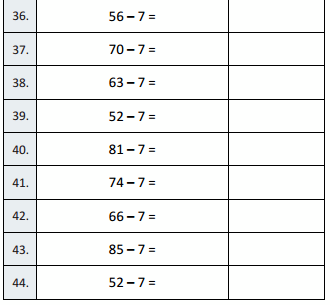
Question 1.
7 – 7 =

Question 2.
17 – 7 =

Question 3.
27 – 7 =

Question 4.
8 – 7 =

Question 5.
18 – 7 =

Question 6.
68 – 7 =

Question 7.
9 – 7 =

Question 8.
19 – 7 =

Question 9.
79 – 7 =

Question 10.
10 – 7 =

Question 11.
20 – 7 =

Question 12.
90 – 7 =

Question 13.
11 – 7 =

Question 14.
21 – 7 =

Question 15.
91 – 7 =

Question 16.
12 – 7 =

Question 17.
22 – 7 =

Question 18.
42 – 7 =

Question 19.
13 – 7 =

Question 20.
23 – 7 =

Question 21.
43 – 7 =

Question 22.
14 – 7 =

Question 23.
24 – 7 =

Question 24.
34 – 7 =

Question 25.
54 – 7 =

Question 26.
74 – 7 =

Question 27.
15 – 7 =

Question 28.
25 – 7 =

Question 29.
35 – 7 =

Question 30.
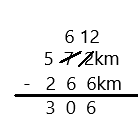
65 – 7 =

Question 31.
45 – 7 =

Question 32.
16 – 7 =

Question 33.
26 – 7 =

Question 34.
36 – 7 =

Question 35.
76 – 7 =

Question 36.
56 – 7 =

Question 37.
70 – 7 =

Question 38.
63 – 7 =

Question 39.
52 – 7 =

Question 40.
81 – 7 =

Question 41.
74 – 7 =

Question 42.
66 – 7 =

Question 43.
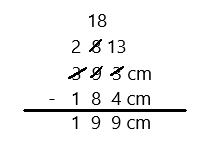
85 – 7 =

Question 44.
52 – 7 =

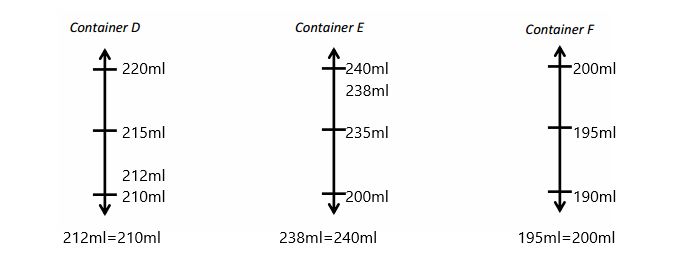
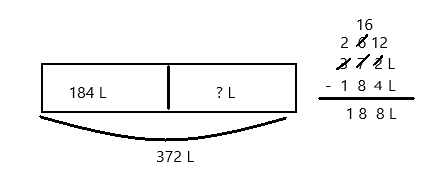
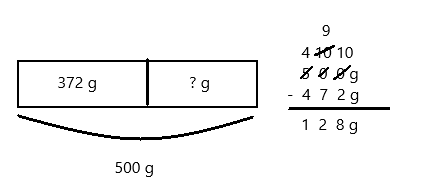
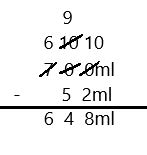
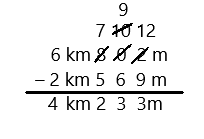
Eureka Math Grade 3 Module 5 Lesson 27 Problem Set Answer Key

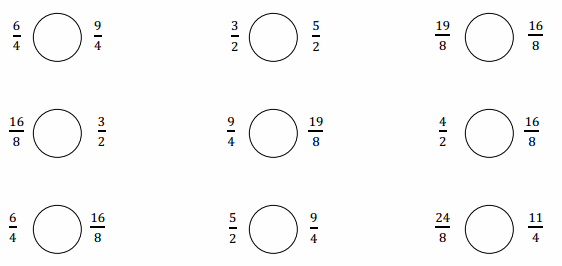
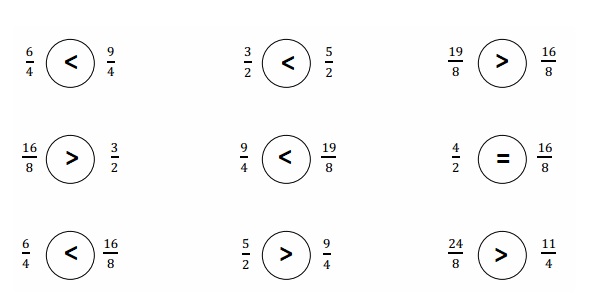
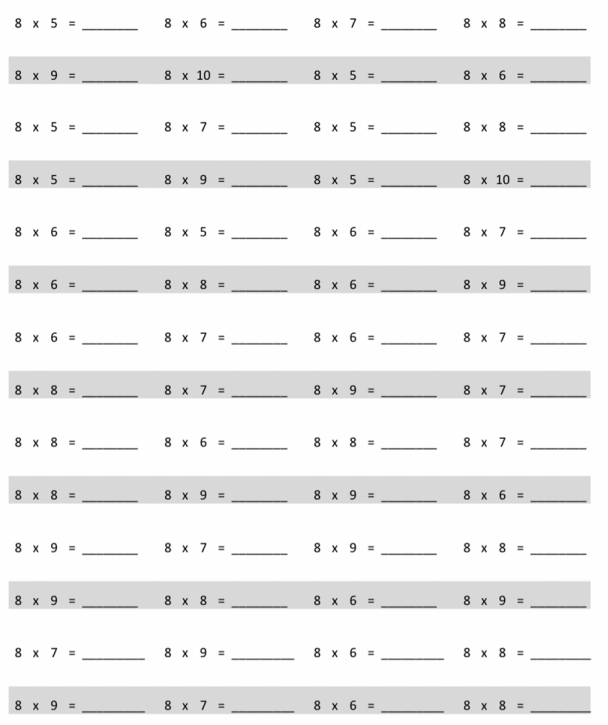
Question 1.
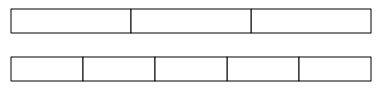
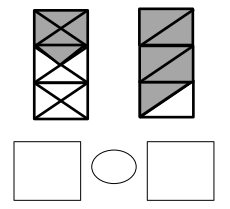
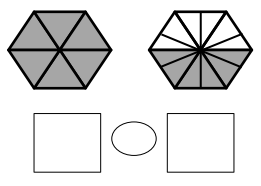
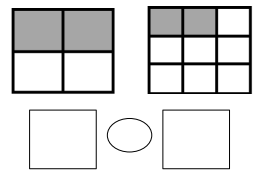
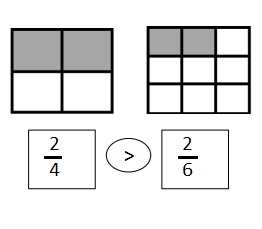
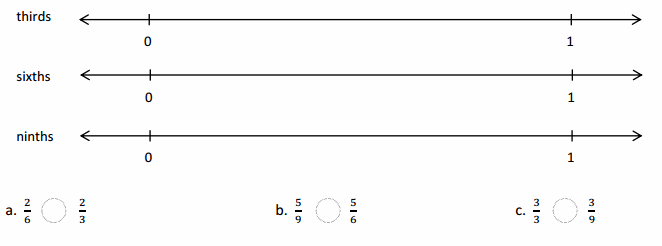
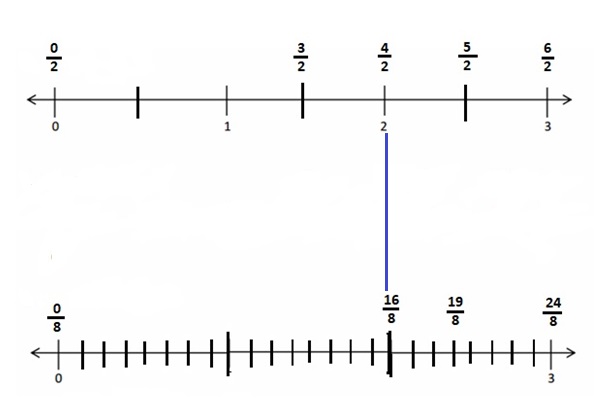
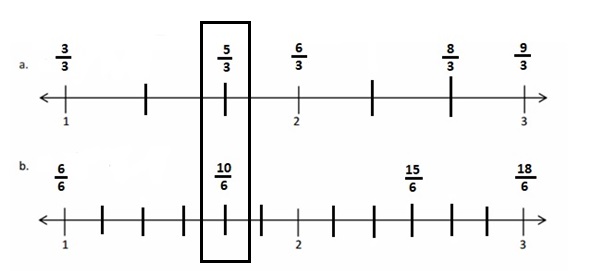
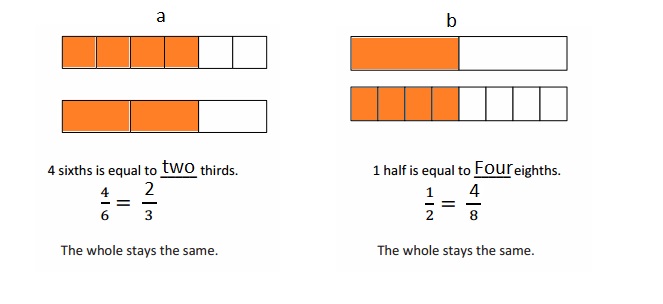
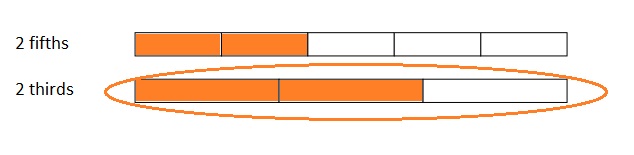
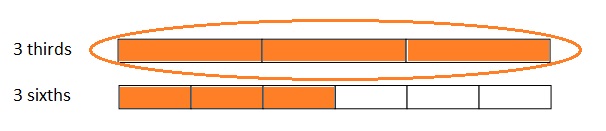
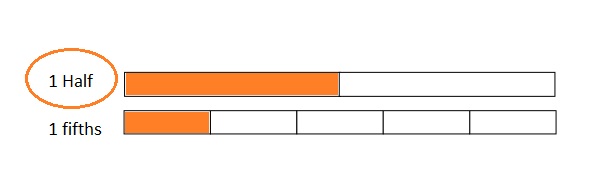
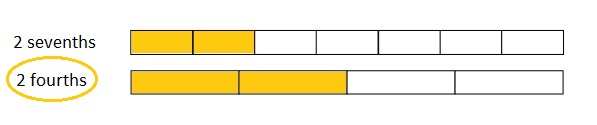
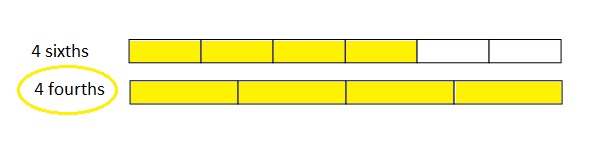
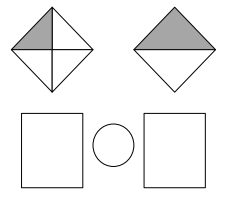
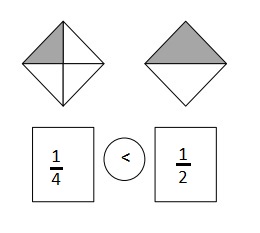
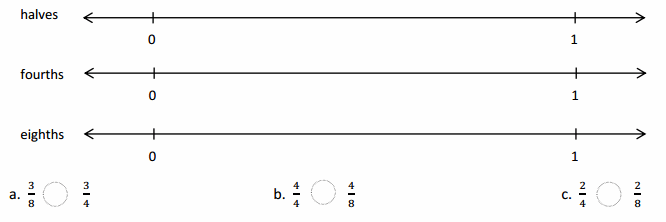
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.

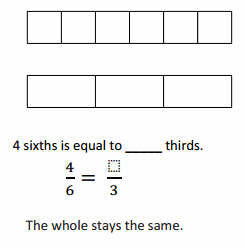
What happened to the size of the equal parts when there were fewer equal parts?
What happened to the number of equal parts when the equal parts became larger?

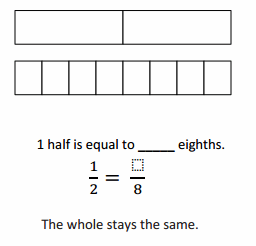
What happened to the size of the equal parts when there were more equal parts?
What happened to the number of equal parts when the equal parts became smaller?
Answer :

Explanation :
In figure a
When there are fewer parts the size of the equal parts are bigger .
When the equal parts became larger The number of equal parts will become fewer .
In figure b
when there were more equal parts the size of the equal parts are smaller .
when the equal parts became smaller the number of equal parts will become more .

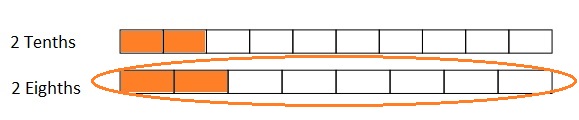
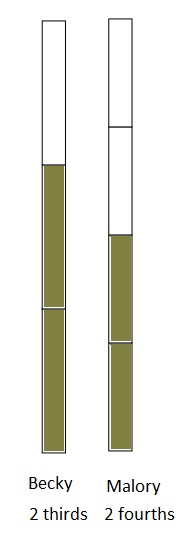
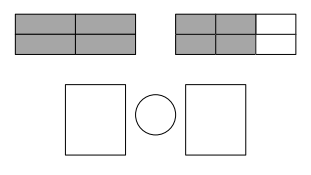
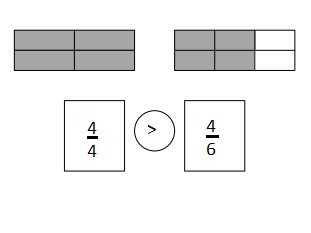
Question 2.
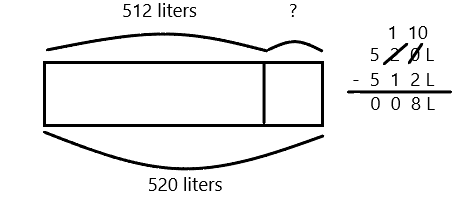
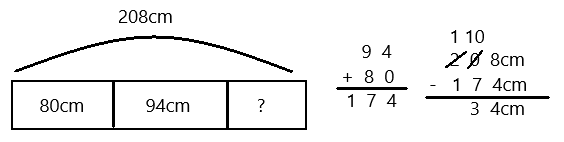
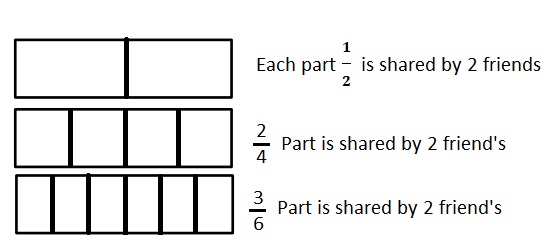
6 friends want to share 3 chocolate bars that are all the same size, which are represented by the 3 rectangles below. When the bars are unwrapped, the friends notice that the first chocolate bar is cut into 2 equal parts, the second is cut into 4 equal parts, and the third is cut into 6 equal parts. How can the 6 friends share the chocolate bars equally without breaking any of the pieces?

Answer :

Explanation :
The First Chocolate is shared by 2 friend’s with \(\frac{1}{2}\) part each .
The Second chocolate is shared by 2 friend’s with\(\frac{2}{4}\) part each .
The Third chocolate is shared by 2 friend’s with\(\frac{3}{6}\) part each .
That means each friend will get \(\frac{1}{2}\) of one chocolate .

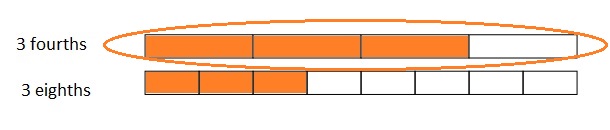
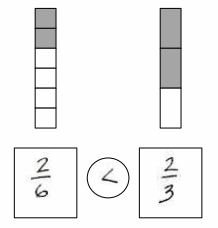
Question 3.
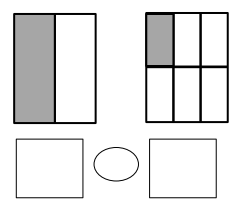
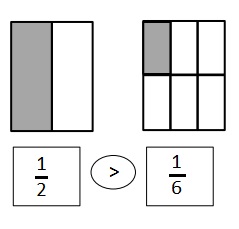
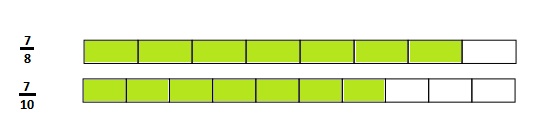
When the whole is the same, why does it take 6 copies of 1 eighth to equal 3 copies of 1 fourth? Draw a model to support your answer.
Answer :

Explanation :
It takes Six one-Eighths to make Three one Fourths.
\(\frac{3}{4}\) is equivalent to \(\frac{6}{8}\) .

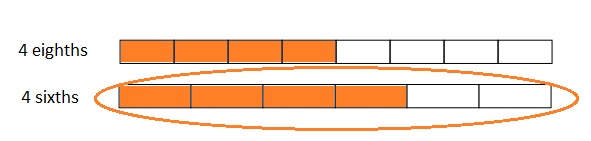
Question 4.
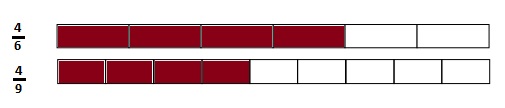
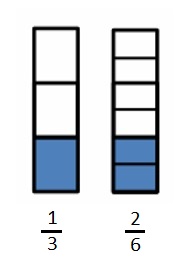
When the whole is the same, how many sixths does it take to equal 1 third? Draw a model to support your answer.
Answer :

Explanation :
It takes two one-sixths to make a third. and we can see that there are \(\frac{1}{6}\) = 6 sixths in a whole.

Question 5.
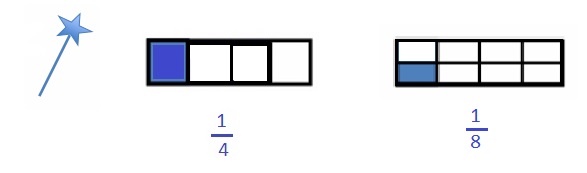
You have a magic wand that doubles the number of equal parts but keeps the whole the same size. Use your magic wand. In the space below, draw to show what happens to a rectangle that is partitioned in fourths after you tap it with your wand. Use words and numbers to explain what happened.

Answer :

Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in Fourths. after magic the Rectangular strip is partitioned into eigths with same length by dividing the rectangular strip in middle  as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 27 Exit Ticket Answer Key

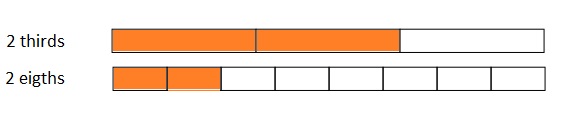
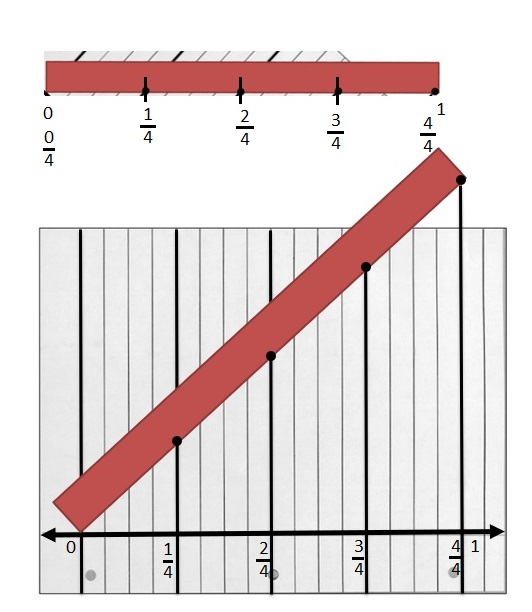
Question 1.
Solve.
2 thirds is equal to __ twelfths

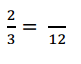
Answer :
2 thirds is equal to 8 twelfths

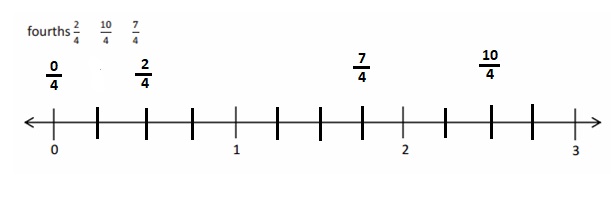
Question 2.
Draw and label two models that show fractions equivalent to those in Problem 1.
Answer :

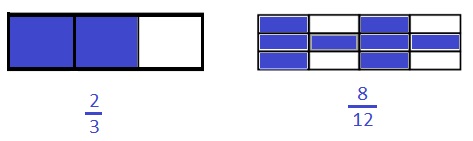
Explanation :
2 thirds is equal to 8 twelfths

Question 3.
Use words to explain why the two fractions in Problem 1 are equal.
Answer :
Both the wholes have same length .
The Rectangular strip is partitioned in Thirds. The Same Rectangular strip is partitioned into twelfths with same length by dividing the rectangular strip in middle into by 2 strips as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 27 Homework Answer Key

Question 1.
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.

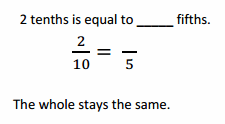
What happened to the size of the equal parts when there were fewer equal parts?

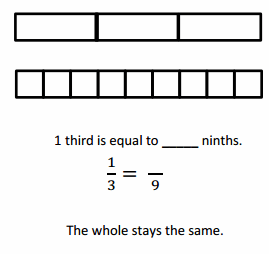
What happened to the size of the equal parts when there were more equal parts?
Answer :

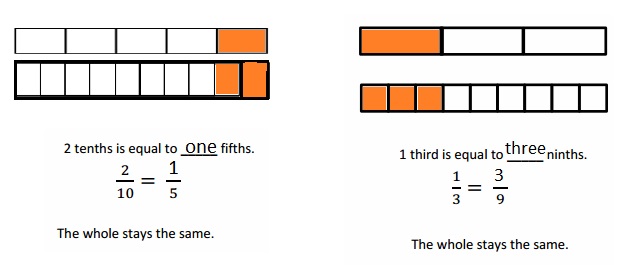
Explanation :
when there were fewer equal parts the number of parts are bigger .
when there were more equal parts the number of parts are smaller .

Question 2.
8 students share 2 pizzas that are the same size, which are represented by the 2 circles below. They notice that the first pizza is cut into 4 equal slices, and the second is cut into 8 equal slices. How can the 8 students share the pizzas equally without cutting any of the pieces?

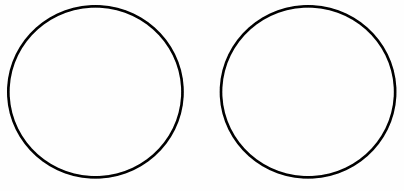
Answer :

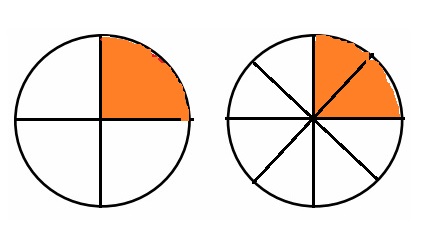
Explanation :
Each student gets \(\frac{1}{4}\) or \(\frac{2}{8}\) of the pizza . From 1 st pizza 4 students get \(\frac{1}{4}\) of the pizza and from 2nd pizza 4 students get \(\frac{2}{8}\) of the pizza .

Question 3.
When the whole is the same, why does it take 4 copies of 1 tenth to equal 2 copies of 1 fifth? Draw a model to support your answer.
Answer :

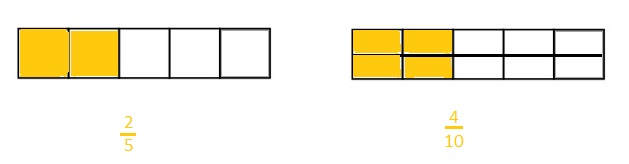
Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fifths. The Another Rectangular strip is partitioned into tenths with same length by dividing the rectangular strip in middle as shown in above figure .
two one fifths is equal to four one tenths .

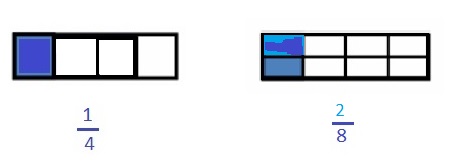
Question 4.
When the whole is the same, how many eighths does it take to equal 1 fourth? Draw a model to support your Answer.

Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fourths. The Another Rectangular strip is partitioned into Eigths with same length by dividing the rectangular strip in middle as shown in above figure .
one fourths is equal to four two Eighths .

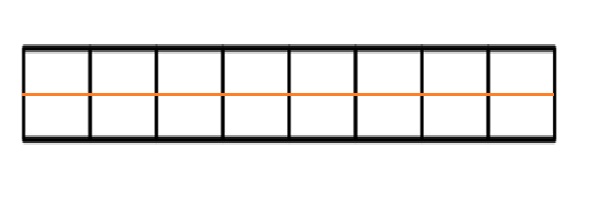
Question 5.
Mr. Pham cuts a cake into 8 equal slices. Then, he cuts every slice in half. How many of the smaller slices does he have? Use words and numbers to explain your answer.
Answer :

Explanation :
The figure shows a cake of 8 slices .the middle orange line shows the cake is sliced in half , creating 16 small slices .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 28 Answer Key

Eureka Math Grade 3 Module 5 Lesson 28 Sprint Answer Key

A
Subtract by Eight

Question 1.
18 – 8 =

Question 2.
8 – 8 =

Question 3.
28 – 8 =

Question 4.
9 – 8 =

Question 5.
19 – 8 =

Question 6.
39 – 8 =

Question 7.
10 – 8 =

Question 8.
20 – 8 =

Question 9.
50 – 8 =

Question 10.
11 – 8 =

Question 11.
21 – 8 =

Question 12.
71 – 8 =

Question 13.
12 – 8 =

Question 14.
22 – 8 =

Question 15.
82 – 8 =

Question 16.
13 – 8 =

Question 17.
23 – 8 =

Question 18.
83 – 8 =

Question 19.
14 – 8 =

Question 20.
24 – 8 =

Question 21.
34 – 8 =

Question 22.
54 – 8 =

Question 23.
74 – 8 =

Question 24.
15 – 8 =

Question 25.
25 – 8 =

Question 26.
35 – 8 =

Question 27.
85 – 8 =

Question 28.
65 – 8 =

Question 29.
16 – 8 =

Question 30.
26 – 8 =

Question 31.
36 – 8 =

Question 32.
96 – 8 =

Question 33.
76 – 8 =

Question 34.
17 – 8 =

Question 35.
27 – 8 =

Question 36.
37 – 8 =

Question 37.
87 – 8 =

Question 38.
67 – 8 =

Question 39.
70 – 8 =

Question 40.
62 – 8 =

Question 41.
84 – 8 =

Question 42.
66 – 8 =

Question 43.
91 – 8 =

Question 44.
75 – 8 =

B
Subtract by Eight

Question 1.
8 – 8 =

Question 2.
18 – 8 =

Question 3.
28 – 8 =

Question 4.
9 – 8 =

Question 5.
19 – 8 =

Question 6.
69 – 8 =

Question 7.
10 – 8 =

Question 8.
20 – 8 =

Question 9.
60 – 8 =

Question 10.
11 – 8 =

Question 11.
21 – 8 =

Question 12.
81 – 8 =

Question 13.
12 – 8 =

Question 14.
22 – 8 =

Question 15.
52 – 8 =

Question 16.
13 – 8 =

Question 17.
23 – 8 =

Question 18.
93 – 8 =

Question 19.
14 – 8 =

Question 20.
24 – 8 =

Question 21.
34 – 8 =

Question 22.
74 – 8 =

Question 23.
94 – 8 =

Question 24.
15 – 8 =

Question 25.
25 – 8 =

Question 26.
35 – 8 =

Question 27.
95 – 8 =

Question 28.
75 – 8 =

Question 29.
16 – 8 =

Question 30.
26 – 8 =

Question 31.
36 – 8 =

Question 32.
66 – 8 =

Question 33.
46 – 8 =

Question 34.
17 – 8 =

Question 35.
27 – 8 =

Question 36.
37 – 8 =

Question 37.
97 – 8 =

Question 38.
77 – 8 =

Question 39.
80 – 8 =

Question 40.
71 – 8 =

Question 41.
53 – 8 =

Question 42.
45 – 8 =

Question 43.
87 – 8 =

Question 44.
54 – 8 =

Eureka Math Grade 3 Module 5 Lesson 28 Problem Set Answer Key

Shade the models to compare the fractions. Circle the larger fraction for each problem.

Question 1.
2 fifths
2 thirds
Answer :

Explanation :
The Length of 2 thirds is greater than the length of the 2 fifths that means \(\frac{2}{3}\) is greater than \(\frac{2}{5}\) .

Question 2.
2 tenths
2 eighths
Answer :

Explanation :
The Length of 2 Eighths is longer than the length of the 2 Tenths that means \(\frac{2}{8}\) is greater than \(\frac{2}{10}\) .

Question 3.
3 fourths
3 eighths
Answer :

Explanation :
The Length of 3 Fourths is longer than the length of the 3 eighths that means \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) .

Question 4.
4 eighths
4 sixths
Answer :

Explanation :
The Length of 4 sixths is longer than the length of the 4 eighths that means \(\frac{4}{6}\) is greater than \(\frac{4}{8}\) .

Question 5.
3 thirds
3 sixths
Answer :

Explanation :
The Length of 3 thirds is longer than the length of the 3 sixths that means \(\frac{3}{3}\) is 1 whole is greater than \(\frac{3}{6}\) .

Question 6.
After softball, Leslie and Kelly each buy a half-liter bottle of water. Leslie drinks 3 fourths of her water. Kelly drinks 3 fifths of her water. Who drinks the least amount of water? Draw a picture to support your answer.
Answer :
Kelly drinks least amount of water .

Explanation :
Leslie drinks \(\frac{3}{4}\) amount of half litre water .
Kelly drinks \(\frac{3}{5}\) amount of half litre water .
The Length of 3 fourths s is longer than the length of the 3 fifths
that means \(\frac{3}{5}\) is smaller than \(\frac{3}{4}\) .
So, Kelly drinks least amount of water .

Question 7.
Becky and Malory get matching piggy banks. Becky fills \(\frac{2}{3}\) of her piggy bank with pennies. Malory fills \(\frac{2}{4}\) of her piggy bank with pennies. Whose piggy bank has more pennies? Draw a picture to support your answer.
Answer :

Explanation :
Length of becky piggy bank filled = \(\frac{2}{3}\)
Length of Malory piggy bank filled = \(\frac{2}{4}\)
The length of becky bank is more than length of malory bank  that means more the length more number of pennies .
So, becky piggy bank has more pennies .

Question 8.
Heidi lines up her dolls in order from shortest to tallest. Doll A is \(\frac{2}{4}\) foot tall, Doll B is \(\frac{2}{6}\) foot tall, and Doll C is \(\frac{2}{3}\) foot tall. Compare the heights of the dolls to show how Heidi puts them in order. Draw a picture to support your answer.
Answer :

Explanation :
The Height of Doll A is \(\frac{2}{4}\)
The Height of Doll B is \(\frac{2}{6}\)
The height of Doll C is \(\frac{2}{3}\)
Longer the Length of Doll more than fraction value .
Therefore , \(\frac{2}{3}\) > \(\frac{2}{4}\)

Eureka Math Grade 3 Module 5 Lesson 28 Exit Ticket Answer Key

Question 1.
Shade the models to compare the fractions.
2 thirds
2 eighths
Which is larger, 2 thirds or 2 eighths? Why? Use words to explain.
Answer :

Explanation :
The Length of 2 thirds is longer than the length of the 2 eigths that means \(\frac{2}{3}\) is greater than \(\frac{2}{8}\) .

Question 2.
Draw a model for each fraction. Circle the smaller fraction.
3 sevenths

3 fourths
Answer :

Explanation :
The Length of 3 fourths is longer than the length of the 3 sevenths that means \(\frac{3}{4}\) is greater than \(\frac{3}{7}\) .

Eureka Math Grade 3 Module 5 Lesson 28 Homework Answer Key

Shade the models to compare the fractions. Circle the larger fraction for each problem.

Question 1.
1 half
1 fifth
Answer :

Explanation :
The Length of 1 Halfs is longer than the length of the 1 fifths that means \(\frac{1}{2}\) is greater than \(\frac{1}{5}\) .

Question 2.
2 sevenths
2 fourths
Answer :

Explanation :
The Length of 2 sevenths is longer than the length of the 2 fourths that means \(\frac{2}{7}\) is greater than \(\frac{2}{4}\) .

Question 3.
4 fifths
4 ninths

Answer:

Explanation :
The Length of 4 fifths is longer than the length of the 4 ninths that means \(\frac{4}{5}\) is greater than \(\frac{4}{9}\) .

Question 4.
5 sevenths
5 tenths

Answer :

Explanation :
The Length of 5 sevenths is longer than the length of the 5 tenths that means \(\frac{5}{7}\) is greater than \(\frac{5}{10}\) .

Question 5.
4 sixths
4 fourths

Answer :

Explanation :
The Length of 4 sixths is smaller than the length of the 4 fourths that means \(\frac{4}{4}\) is greater than \(\frac{4}{6}\) .

Question 6.
Saleem and Edwin use inch rulers to measure the lengths of their caterpillars. Saleem’s caterpillar measures 3 fourths of an inch. Edwin’s caterpillar measures 3 eighths of an inch. Whose caterpillar is longer? Draw a picture to support your answer.
Answer :

Explanation :
Length of Saleem’s caterpillar = 3 fourths
Length of Edwin’s caterpillar = 3 eighths
Length of Saleem’s caterpillar is longer than Edwin’s caterpillar
So, \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) .

Question 7.
Lily and Jasmine each bake the same-sized chocolate cake. Lily puts \(\frac{5}{10}\) of a cup of sugar into her cake. Jasmine puts \(\frac{5}{6}\) of a cup of sugar into her cake. Who uses less sugar? Draw a picture to support your answer.
Answer :

Explanation :
Amount of sugar used by lily = \(\frac{5}{10}\)
Amount of sugar used by Jasmine = \(\frac{5}{6}\)
\(\frac{5}{10}\)  is less than \(\frac{5}{6}\) .
So, lily used less sugar than jasmine .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 30 Answer Key

Eureka Math Grade 3 Module 5 Lesson 30 Pattern Sheet Answer Key

Multiply.

multiply by 9 (1–5)
Answer :

Explanation :
multiply by 9 (1–5)
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45

Eureka Math Grade 3 Module 5 Lesson 30 Homework Answer Key

Describe step by step the experience you had of partitioning a length into equal units by simply using a piece of notebook paper and a straight edge. Illustrate the process.

Answer :

Explanation :
Turn the page into vertical lines .
Mark 0 at one point and make equal differences in the above figure i am leaving 4 vertical lines and marking the next point  as \(\frac{1}{4}\), and next leave another 4 vertical lines and mark the next point as \(\frac{2}{4}\) mark all the points in the same way till 1 that means \(\frac{4}{4}\).
Mark all the points and draw the vertical lines from these points .
Next take a rectangular strip point one the end on point 0 and put another end on the vertical line of point 1.
Mark the points where the rectangular strip are touching these points .
Then take the same strip and place it horizontal then the strip is divided into 4 equal parts .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 29 Answer Key

Eureka Math Grade 3 Module 5 Lesson 29 Pattern Sheet Answer Key

Multiply.

multiply by 8 (5–9)
Answer :

Explanation :
MULTIPLICATION of 8 (5 – 9 ) are given here .
8 × 5 = 40
8 × 6 = 48
8 × 7 = 56
8 × 8 = 64
8 × 9 = 72

Eureka Math Grade 3 Module 5 Lesson 29 Problem Set Answer Key

Label each shaded fraction. Use >, <, or = to compare. The first one has been done for you.

Question 1.

Question 2.

Answer :

Question 3.

Answer :

Question 4.

Answer :

Question 5.
Partition each number line into the units labeled on the left. Then, use the number lines to compare the fractions.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .

Draw your own model to compare the following fractions.

Question 6.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .
The length of \(\frac{3}{10}\) is shorter than the length of \(\frac{3}{5}\) .
That means \(\frac{3}{5}\) is greater than \(\frac{3}{10}\) .

Question 7.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .
The length of \(\frac{3}{10}\) is shorter than the length of \(\frac{3}{5}\) .
That means \(\frac{3}{5}\) is greater than \(\frac{3}{10}\) .

Question 8.
John ran 2 thirds of a kilometer after school. Nicholas ran 2 fifths of a kilometer after school. Who ran the shorter distance? Use the model below to support your answer. Be sure to label 1 whole as 1 kilometer.

Answer :

Explanation :
Distance ran by John = \(\frac{2}{3}\)
Distance ran by Nicholas = \(\frac{2}{5}\)
The distance traveled by John is more than Nicholas .
Therefore, \(\frac{2}{3}\) > \(\frac{2}{5}\) .

Question 9.
Erica ate 2 ninths of a licorice stick. Robbie ate 2 fifths of an identical licorice stick. Who ate more?
Use the model below to support your answer.

Answer :

Explanation :
Licorice stick ate by Erica = \(\frac{2}{9}\)
Licorice stick ate by Robbie = \(\frac{2}{5}\)
From the above image we notice that Robbie ate more than Erica which means more length of orange strip is marked by Robbie .
Therefore, \(\frac{2}{9}\) < \(\frac{2}{5}\) .

Eureka Math Grade 3 Module 5 Lesson 29 Exit Ticket Answer Key

Question 1.
Complete the number sentence by writing >, <, or =.

Answer :
\(\frac{3}{5}\) > \(\frac{3}{9}\)

Question 2.
Draw 2 number lines with endpoints 0 and 1 to show each fraction in Problem 1. Use the number lines to explain how you know your comparison in Problem 1 is correct.
Answer :

Explanation :
The length of strip marked for \(\frac{3}{5}\) in the above number line is longer than the length of strip marked for \(\frac{3}{9}\).
More the length of strip marked on the number line means greater is the number .
Therefore \(\frac{3}{5}\) > \(\frac{3}{9}\)

Eureka Math Grade 3 Module 5 Lesson 29 Homework Answer Key

Label each shaded fraction. Use >, <, or = to compare.

Question 1.

Answer :

Question 2.

Answer :

Question 3.

Answer :

Question 4.

Answer :

Question 5.
Partition each number line into the units labeled on the left. Then, use the number lines to compare the fractions.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .

Draw your own models to compare the following fractions.
Question 6.

Answer :

Explanation :
The length of strip marked for \(\frac{7}{8}\) in the above figure is longer than the length of strip marked for \(\frac{7}{10}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{7}{8}\) > \(\frac{7}{10}\)

Question 7.

Answer :

Explanation :
The length of strip marked for \(\frac{4}{6}\) in the above figure is longer than the length of strip marked for \(\frac{4}{9}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{4}{6}\) > \(\frac{4}{9}\)

Question 8.
For an art project, Michello used \(\frac{3}{4}\) of a glue stick. Yamin used \(\frac{3}{6}\) of an identical glue stick. Who used more of the glue stick? Use the model below to support your answer. Be sure to label 1 whole as 1 glue stick.

Answer :

Explanation :
Glue stick Used by Michello = \(\frac{3}{4}\)
Glue stick used by Yamin = \(\frac{3}{6}\)
The length of strip marked for \(\frac{3}{4}\) in the above figure is longer than the length of strip marked for \(\frac{3}{6}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{3}{4}\) > \(\frac{3}{6}\)

Question 9.
After gym class, Jahsir drank 2 eighths of a bottle of water. Jade drank 2 fifths of an identical bottle of water. Who drank less water? Use the model below to support your answer.

Answer :

Explanation :
Quantity of Water drank by Jahsir = \(\frac{2}{8}\)
Quantity of water drank by Jade = \(\frac{2}{5}\)
The length of strip marked for \(\frac{2}{5}\) in the above figure is longer than the length of strip marked for \(\frac{2}{8}\).
Less the length of strip marked on the rectangular strip means lesser is the number .
Therefore \(\frac{2}{8}\) < \(\frac{2}{5}\) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 19 Answer Key

Eureka Math Grade 3 Module 5 Lesson 19 Sprint Answer Key

A
Express Fractions as Whole Numbers

Question 1.
\(\frac { 2 }{ 1 }\) =
Answer :
\(\frac { 2 }{ 1 }\) = 2

Question 2.
\(\frac { 2 }{ 2 }\) =
Answer :
\(\frac { 2 }{ 2 }\) = 1

Question 3.
\(\frac { 4 }{ 2 }\) =
Answer :
\(\frac { 4 }{ 2 }\) = 2
Explanation :
2 x 2 = 4

Question 4.
\(\frac { 6 }{ 2 }\) =
Answer :
\(\frac { 6 }{ 2 }\) = 3
Explanation :
2 x 3 = 6

Question 5.
\(\frac { 10 }{ 2 }\) =
Answer :
\(\frac { 10 }{ 2 }\) = 5
Explanation :
2  ×  5  = 10

Question 6.
\(\frac { 8 }{ 2 }\) =
Answer :
\(\frac { 8 }{ 2 }\) = 4
Explanation :
2  × 4  = 8

Question 7.
\(\frac { 5 }{ 1 }\) =
Answer :
\(\frac { 5 }{ 1 }\) = 5
Explanation :
1  × 5 = 5

Question 8.
\(\frac { 5 }{ 5 }\) =
Answer :
\(\frac { 5 }{ 5 }\) = 1
Explanation :
1  × 5 = 5

Question 9.
\(\frac { 10 }{ 5 }\) =
Answer :
\(\frac { 10 }{ 5 }\) = 2
Explanation :
2  × 5 = 10

Question 10.
\(\frac { 15 }{ 5 }\) =
Answer :
\(\frac { 15 }{ 5 }\) = 3
Explanation :
3  × 5 = 15

Question 11.
\(\frac { 25 }{ 5 }\) =
Answer :
\(\frac { 25 }{ 5 }\) = 5
Explanation :
5  × 5 = 25

Question 12.
\(\frac { 20 }{ 5 }\) =
Answer :
\(\frac { 20 }{ 5 }\) = 4
Explanation :
4  × 5 = 20

Question 13.
\(\frac { 10 }{ 10 }\) =
Answer :
\(\frac { 10 }{ 10 }\) = 1
Explanation :
1  × 10 = 10

Question 14.
\(\frac { 50 }{ 10 }\) =
Answer :
\(\frac { 50 }{ 10 }\) = 5
Explanation :
10  × 5 = 50

Question 15.
\(\frac { 30 }{ 10 }\) =
Answer :
\(\frac { 30 }{ 10 }\) = 3
Explanation :
10  × 3 = 30

Question 16.
\(\frac { 10 }{ 1 }\) =
Answer :
\(\frac { 10 }{ 1 }\) = 10
Explanation :
10  × 1 = 10

Question 17.
\(\frac { 20 }{ 10 }\) =
Answer :
\(\frac { 20 }{ 10 }\) = 2
Explanation :
10  × 2 = 20

Question 18.
\(\frac { 40 }{ 10 }\) =
Answer :
\(\frac { 40 }{ 10 }\) = 4
Explanation :
10  × 4 = 40

Question 19.
\(\frac { 8 }{ 4 }\) =
Answer :
\(\frac { 8 }{ 4 }\) = 2
Explanation :
2  × 4 = 8

Question 20.
\(\frac { 4 }{ 4 }\) =
Answer :
\(\frac { 4 }{ 4 }\) = 1
Explanation :
1  × 4 = 4

Question 21.
\(\frac { 4 }{ 1 }\) =
Answer :
\(\frac { 4 }{ 1 }\) = 4
Explanation :
1  × 4 = 4

Question 22.
\(\frac { 12 }{ 4 }\) =
Answer :
\(\frac { 12 }{ 4 }\) = 3
Explanation :
3  × 4 = 12

Question 23.
\(\frac { 6 }{ 3 }\) =
Answer :
\(\frac { 6 }{ 3 }\) = 2
Explanation :
3  × 2 = 6

Question 24.
\(\frac { 3 }{ 3 }\) =
Answer :
\(\frac { 3 }{ 3 }\) = 1
Explanation :
1  × 3 = 3

Question 25.
\(\frac { 3 }{ 1 }\) =
Answer :
\(\frac { 3 }{ 1 }\) = 3
Explanation :
1  × 3 = 3

Question 26.
\(\frac { 9 }{ 3 }\) =
Answer :
\(\frac { 9 }{ 3 }\) = 3
Explanation :
3  × 3 = 9

Question 27.
\(\frac { 16 }{ 4 }\) =
Answer :
\(\frac { 16 }{ 4 }\) = 4
Explanation :
4  × 4 = 16

Question 28.
\(\frac { 20 }{ 4 }\) =
Answer :
\(\frac { 20 }{ 4 }\) = 5
Explanation :
4  × 5 = 20

Question 29.
\(\frac { 12 }{ 3 }\) =
Answer :
\(\frac { 12 }{ 3 }\) = 4
Explanation :
4  × 3 = 12

Question 30.
\(\frac { 15 }{ 3 }\) =
Answer :
\(\frac { 15 }{ 3 }\) = 5
Explanation :
3  × 5 = 15

Question 31.
\(\frac { 70 }{ 10 }\) =
Answer :
\(\frac { 70 }{ 10 }\) = 7
Explanation :
10  × 7 = 70

Question 32.
\(\frac { 12 }{ 2 }\) =
Answer :
\(\frac { 12 }{ 2 }\) = 6
Explanation :
2  × 6 = 12

Question 33.
\(\frac { 14 }{ 2 }\) =
Answer :
\(\frac { 14 }{ 2 }\) = 7
Explanation :
2  × 7 = 14

Question 34.
\(\frac { 90 }{ 10 }\) =
Answer :
\(\frac { 90 }{ 10 }\) = 9
Explanation :
10  × 9 = 90

Question 35.
\(\frac { 30 }{ 5 }\) =
Answer :
\(\frac { 30 }{ 5 }\) = 6
Explanation :
5  × 6 = 30

Question 36.
\(\frac { 35 }{ 5 }\) =
Answer :
\(\frac { 35 }{ 5 }\) = 7
Explanation :
5  × 7 = 35

Question 37.
\(\frac { 60 }{ 10 }\) =
Answer :
\(\frac { 60 }{ 10 }\) = 6
Explanation :
10  × 6 = 60

Question 38.
\(\frac { 18 }{ 2 }\) =
Answer :
\(\frac { 18 }{ 2 }\) = 9
Explanation :
2 × 9 = 18

Question 39.
\(\frac { 40 }{ 5 }\) =
Answer :
\(\frac { 40 }{ 5 }\) = 8
Explanation :
5  × 8 = 40

Question 40.
\(\frac { 80 }{ 10 }\) =
Answer :
\(\frac { 80 }{ 10 }\) = 8
Explanation :
10  × 8 = 80

Question 41.
\(\frac { 16 }{ 2 }\) =
Answer :
\(\frac { 16 }{ 2 }\) = 8
Explanation :
2  × 8 = 16

Question 42.
\(\frac { 45 }{ 5 }\) =
Answer :
\(\frac { 45 }{ 5 }\) = 9
Explanation :
5  × 9 = 45

Question 43.
\(\frac { 27 }{ 3 }\) =
Answer :
\(\frac { 27 }{ 3 }\) = 9
Explanation :
3 × 9 = 27

Question 44.
\(\frac { 32 }{ 4 }\) =
Answer :
\(\frac { 32 }{ 4 }\) = 8
Explanation :
3  × 8 = 32

B
Express Fractions as Whole Numbers

Question 1.
\(\frac { 5 }{ 1 }\) =
Answer :
\(\frac { 5 }{ 1 }\) = 5
Explanation :
5  × 1 = 5

Question 2.
\(\frac { 5 }{ 5 }\) =
Answer :
\(\frac { 5 }{ 5 }\) = 1
Explanation :
5  × 1 = 5

Question 3.
\(\frac { 10 }{ 5 }\) =
Answer :
\(\frac { 10 }{ 5 }\) = 2
Explanation :
5  × 2 = 10

Question 4.
\(\frac { 15 }{ 5 }\) =
Answer :
\(\frac { 15 }{ 5 }\) = 3
Explanation :
5  × 3 = 1

Question 5.
\(\frac { 25 }{ 5 }\) =
Answer :
\(\frac { 25 }{ 5 }\) = 5
Explanation :
5  × 5 = 25

Question 6.
\(\frac { 20 }{ 5 }\) =
Answer :
\(\frac { 20 }{ 5 }\) = 4
Explanation :
5  × 4 = 20

Question 7.
\(\frac { 2 }{ 1 }\) =
Answer :
\(\frac { 2 }{ 1 }\) = 2
Explanation :
1  × 2 = 2

Question 8.
\(\frac { 2 }{ 2 }\) =
Answer :
\(\frac { 2 }{ 2 }\) = 1
Explanation :
1  × 2 = 2

Question 9.
\(\frac { 4 }{ 2 }\) =
Answer :
\(\frac { 4 }{ 2 }\) = 2
Explanation :
2 × 2 = 4

Question 10.
\(\frac { 6 }{ 2 }\) =
Answer :
\(\frac { 6 }{ 2 }\) = 3
Explanation :
2 × 3 = 6

Question 11.
\(\frac { 10 }{ 2 }\) =
Answer :
\(\frac { 10 }{ 2 }\) = 5
Explanation :
2 × 5 = 10

Question 12.
\(\frac { 8 }{ 2 }\) =
Answer :
\(\frac { 8 }{ 2 }\) = 4
Explanation :
2 × 4 = 8

Question 13.
\(\frac { 10 }{ 1 }\) =
Answer :
\(\frac { 10 }{ 1 }\) = 10
Explanation :
1 × 10 = 10

Question 14.
\(\frac { 10 }{ 10 }\) =
Answer :
\(\frac { 10 }{ 10 }\) = 1
Explanation :
1 × 10 = 10

Question 15.
\(\frac { 50 }{ 10 }\) =
Answer :
\(\frac { 50 }{ 10 }\) = 5
Explanation :
10 × 5 = 50

Question 16.
\(\frac { 30 }{ 10 }\) =
Answer :
\(\frac { 30 }{ 10 }\) = 3
Explanation :
10 × 3 = 30

Question 17.
\(\frac { 20 }{ 10 }\) =
Answer :
\(\frac { 20 }{ 10 }\) = 2
Explanation :
10 × 2 = 20

Question 18.
\(\frac { 40 }{ 10 }\) =
Answer :
\(\frac { 40 }{ 10 }\) = 4
Explanation :
10 × 4 = 40

Question 19.
\(\frac { 6 }{ 3 }\) =
Answer :
\(\frac { 6 }{ 3 }\) = 2
Explanation :
2 × 3 = 6

Question 20.
\(\frac { 3 }{ 3 }\) =
Answer :
\(\frac { 3 }{ 3 }\) = 1
Explanation :
1 × 3 = 3

Question 21.
\(\frac { 3 }{ 1 }\) =
Answer :
\(\frac { 3 }{ 1 }\) = 3
Explanation :
1 × 3 = 3

Question 22.
\(\frac { 9 }{ 3 }\) =
Answer :
\(\frac { 9 }{ 3 }\) =3
Explanation :
3 × 3 = 9

Question 23.
\(\frac { 8 }{ 4 }\) =
Answer :
\(\frac { 8 }{ 4 }\) = 2
Explanation :
2 × 4 = 8

Question 24.
\(\frac { 4 }{ 4 }\) =
Answer :
\(\frac { 4 }{ 4 }\) = 1
Explanation :
1 × 4 = 4

Question 25.
\(\frac { 4 }{ 1 }\) =
Answer :
\(\frac { 4 }{ 1 }\) = 4
Explanation :
1 × 4 = 4

Question 26.
\(\frac { 12 }{ 4 }\) =
Answer :
\(\frac { 12 }{ 4 }\) = 3
Explanation :
3 × 4 = 12

Question 27.
\(\frac { 12 }{ 3 }\) =
Answer :
\(\frac { 12 }{ 3 }\) = 4
Explanation :
3 × 4 = 12

Question 28.
\(\frac { 15 }{ 3 }\) =
Answer :
\(\frac { 15 }{ 3 }\) = 5
Explanation :
5 × 3 = 15

Question 29.
\(\frac { 16 }{ 4 }\) =
Answer :
\(\frac { 16 }{ 4 }\) = 4
Explanation :
4 × 4 = 16

Question 30.
\(\frac { 20 }{ 4 }\) =
Answer :
\(\frac { 20 }{ 4 }\) = 5
Explanation :
5 × 4 = 20

Question 31.
\(\frac { 90 }{ 10 }\) =
Answer :
\(\frac { 90 }{ 10 }\) = 9
Explanation :
10 × 9 = 90

Question 32.
\(\frac { 30 }{ 5 }\) =
Answer :
\(\frac { 30 }{ 5 }\) = 6
Explanation :
5 × 6 = 30

Question 33.
\(\frac { 35 }{ 5 }\) =
Answer :
\(\frac { 35 }{ 5 }\) = 7
Explanation :
5 × 7 = 35

Question 34.
\(\frac { 70 }{ 10 }\) =
Answer :
\(\frac { 70 }{ 10 }\) = 7
Explanation :
10 × 7 = 70

Question 35.
\(\frac { 12 }{ 2 }\) =
Answer :
\(\frac { 12 }{ 2 }\) = 6
Explanation :
2 × 6 = 12

Question 36.
\(\frac { 14 }{ 2 }\) =
Answer :
\(\frac { 14 }{ 2 }\) = 7
Explanation :
2 × 7 = 14

Question 37.
\(\frac { 80 }{ 10 }\) =
Answer :
\(\frac { 80 }{ 10 }\) = 8
Explanation :
10 × 9 = 90

Question 38.
\(\frac { 45 }{ 5 }\) =
Answer :
\(\frac { 45 }{ 5 }\) = 9
Explanation :
5 × 9 = 45

Question 39.
\(\frac { 16 }{ 2 }\) =
Answer :
\(\frac { 16 }{ 2 }\) = 8
Explanation :
2 × 8 = 16

Question 40.
\(\frac { 60 }{ 10 }\) =
Answer :
\(\frac { 60 }{ 10 }\) = 6
Explanation :
10 × 6 = 60

Question 41.
\(\frac { 18 }{ 2 }\) =
Answer :
\(\frac { 18 }{ 2 }\) = 9
Explanation :
2 × 9 = 18

Question 42.
\(\frac { 40 }{ 5 }\) =
Answer :
\(\frac { 40 }{ 5 }\) =8
Explanation :
5 × 8 = 40

Question 43.
\(\frac { 36 }{ 4 }\) =
Answer :
\(\frac { 36 }{ 4 }\) = 9
Explanation :
4 × 9 = 36

Question 44.
\(\frac { 24 }{ 3 }\) =
Answer :
\(\frac { 24 }{ 3 }\) = 8
Explanation :
4 × 8 = 32

Eureka Math Grade 3 Module 5 Lesson 19 Problem Set Answer Key

Question 1.
Divide each number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

Answer :

Explanation :
Number lines are represented and the given fractions are located and labeled .

Question 2.
Use the number lines above to compare the following fractions using >, <, or =.

Answer :

Explanation :
From the above figure the comparisons are done .

Question 3.
Choose a greater than comparison you made in Problem 2. Use pictures, numbers, and words to explain how you made that comparison.
Answer :

\(\frac {5 }{ 2 }\) is greater than \(\frac { 3 }{ 2 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {5 }{ 2 }\) is right on the number of \(\frac {3 }{ 2 }\)
So, \(\frac {5 }{ 2 }\) is greater than \(\frac { 3 }{ 2 }\)

Question 4.
Choose a less than comparison you made in Problem 2. Use pictures, numbers, and words to explain a different way of thinking about the comparison than what you wrote in Problem 3.
Answer :

\(\frac {6 }{ 4 }\) is lesser than \(\frac {11 }{ 4 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {6 }{ 4 }\) is left of the number of \(\frac {11 }{ 4 }\)
So, \(\frac {6 }{ 4 }\) is lesser than \(\frac {11 }{ 4 }\)

Question 5.
Choose an equal to comparison you made in Problem 2. Use pictures, numbers, and words to explain two ways that you can prove your comparison is true.
Answer :

Explanation :
\(\frac { 4 }{ 2 }\) = \(\frac { 16 }{ 8 }\) both the points intersect as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 19 Exit Ticket Answer Key

Question 1.
Divide the number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

Answer :

Question 2.
Use the number line above to compare the following fractions using >, <, or =.

Answer :

Question 3.
Use the number line from Problem 1. Which is larger: 2 wholes or \(\frac{9}{4}\)? Use words, pictures, and numbers to explain your answer.
Answer :

Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {9 }{ 4 }\) is right of the number of 2 wholes
So, \(\frac {9 }{ 4 }\) > 2 wholes .

Eureka Math Grade 3 Module 5 Lesson 19 Homework Answer Key

Question 1.
Divide each number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

Answer :

Question 2.
Use the number lines above to compare the following fractions using >, <, or =.

Answer :

Question 3.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is greater than ____________.
Answer :
\(\frac { 18 }{ 6 }\) is greater than \(\frac { 15 }{ 6 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac { 18 }{ 6 }\) is right of the number of \(\frac { 15 }{ 6 }\)
So, \(\frac { 18 }{ 6 }\) > \(\frac { 15 }{ 6 }\)

Question 4.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is less than ____________.
Answer :
\(\frac { 5 }{ 3 }\) is lesser than \(\frac { 6 }{ 3 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac { 5 }{ 3 }\) is right of the number of \(\frac { 6 }{ 3 }\)
So, \(\frac { 5 }{ 3 }\) < \(\frac { 6 }{ 3 }\)

Question 5.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is equal to ____________.

Answer :
\(\frac { 5 }{ 3 }\) is Equal to \(\frac { 10 }{ 6 }\)

Explanation :
\(\frac { 5 }{ 3 }\) = \(\frac { 10 }{ 6 }\)
Both the numbers are of equal distance and lies at the point as shown in the above figure .

Engage NY Eureka Math 3rd Grade Module 7 Lesson 28 Answer Key

Eureka Math Grade 3 Module 7 Lesson 28 Pattern Sheet Answer Key

Multiply.

multiply by 8 (6–10)
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Problem Set Answer Key

Question 1.
Gia measures her rectangular garden and finds the width is 9 yards and the length is 7 yards.
a. Estimate to draw Gia’s garden, and label the side lengths.
b. What is the area of Gia’s garden?
c. What is the perimeter of Gia’s garden?
Answer:

Question 2.
Elijah draws a square that has side lengths of 8 centimeters.
a. Estimate to draw Elijah’s square, and label the side lengths.
b. What is the area of Elijah’s square?
c. What is the perimeter of Elijah’s square?
d. Elijah connects three of these squares to make one long rectangle. What is the perimeter of this rectangle?
Answer:

Question 3.
The area of Mason’s rectangular painting is 72 square inches. The width of the painting is 8 inches.
a. Estimate to draw Mason’s painting, and label the side lengths.
b. What is the length of the painting?
c. What is the perimeter of Mason’s painting?
d. Mason’s mom hangs the painting on a wall that already has two of Mason’s other paintings. The areas of the other paintings are 64 square inches and 81 square inches. What is the total area of the wall that is covered with Mason’s paintings?
Answer:

Question 4.
The perimeter of Jillian’s rectangular bedroom is 34 feet. The length of her bedroom is 9 feet.
a. Estimate to draw Jillian’s bedroom, and label the side lengths.
b. What is the width of Jillian’s bedroom?
c. What is the area of Jillian’s bedroom?
d. Jillian has a 4-foot by 6-foot rug in her room. What is the area of the floor that is not covered by the rug?
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Exit Ticket Answer Key

Jennifer measures her rectangular sandbox and finds the width is 8 feet and the length is 6 feet.
a. Estimate to draw Jennifer’s sandbox, and label the side lengths.
b. What is the area of Jennifer’s sandbox?
c. What is the perimeter of Jennifer’s sandbox?
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Homework Answer Key

Question 1.
Carl draws a square that has side lengths of 7 centimeters.
a. Estimate to draw Carl’s square, and label the side lengths.
b. What is the area of Carl’s square?
c. What is the perimeter of Carl’s square?
d. Carl draws two of these squares to make one long rectangle. What is the perimeter of this rectangle?
Answer:

Question 2.
Mr. Briggs puts food for the class party on a rectangular table. The table has a perimeter of 18 feet and a width of 3 feet.
a. Estimate to draw the table, and label the side lengths.
b. What is the length of the table?
c. What is the area of the table?
d. Mr. Briggs puts three of these tables together side by side to make 1 long table. What is the area of the long table?
Answer:

Engage NY Eureka Math 3rd Grade Module 2 End of Module Assessment Answer Key

Eureka Math Grade 3 Module 2 End of Module Assessment Task Answer Key

Question 1.
Paul is moving to Australia. The total weight of his 4 suitcases is shown on the scale to the right. On a number line, round the total weight to the nearest 100 kilograms.

Answer:

Explanation:
Paul is moving to Australia. The total weight of his 4 suitcases is 127 kg.
Rounded to the nearest 100 kg, his suit cases weighs 100kg.

Question 2.
Paul buys snacks for his flight. He compares cashews to yogurt raisins. The cashews weigh 205 grams, and the yogurt raisins weigh 186 grams. What is the difference between the weight of the cashews and yogurt raisins?

Answer:

Explanation:
Paul buys snacks for his flight, The cashews weigh 205 grams, and the yogurt raisins weigh 186 grams.
The difference between the weight of the cashews and yogurt raisins is 205-186=19 grams.

Question 3.
The clock to the right shows what time it is now.
a. Estimate the time to the nearest 10 minutes.

Answer:

Explanation:
10:19
The time is 10:20 rounded to the nearest 10 minutes.

b. The clock to the right show Paul’s departure time. Estimate the time to the nearest 10 minutes.

Answer:

Explanation:
10:53
Paul’s departure time is 10:50 rounded to the nearest 10 minutes.

c. Use your answers from Parts (a) and (b) to estimate how long Paul has before his flight leaves.

Answer:
The time is 10:20, Paul’s departure time is 10:50.
To find how long Paul has before his flight leaves subtract 20 from 50
50 min – 20 min = 30 min
Therefore, Paul has about 30 minutes before his flight leaves.

Question 4.
A large airplane uses about 256 liters of fuel every minute.
a. Round to the nearest ten liters to estimate how many liters of fuel get used every minute.

Answer:

Explanation:
A large airplane uses about 256 liters of fuel every minute, rounding to nearest tens.
About 260 L of fuel is used every minute.

b. Use your estimate to find about how many liters of fuel are used every 2 minutes.

Answer:

Explanation:
To find the fuel  used every 2 minutes add the fuel used in 1 minute with it again.
260+260=520L
About 520 L of fuel is used for every 2 minutes.

c. Calculate precisely how many liters of fuel are used every 2 minutes.

Answer:

Explanation:
The actual fuel used in a minute is 256.
To find the actual fuel used add 256+256=512 L
Therefore 512 liters of fuel are used every 2 minutes.

d. Draw a tape diagram to find the difference between your estimate and the precise calculation.

Answer:

Explanation:

The difference between the calculation and the estimate is 8 liters.

Question 5.
Baggage handlers lift heavy luggage into the plane. The weight of one bag is shown on the scale to the right.
a. One baggage handler lifts 3 bags of the same weight. Round to estimate the total weight he lifts. Then, calculate exactly.

Answer:

Explanation:
65 kg is about 70 kg
Baggage handler lifts about 210 kgs in total
Baggage handle lifts exactly 195 kg.

b. Another baggage handler lifts luggage that weighs a total of 200 kilograms. Write and solve an equation to show how much more weight he lifts than the first handler in Part (a).

Answer:

Explanation:
If another baggage handler lifts luggage that weighs a total of 200 kilograms then             200kg-195kg=5 kg
Therefore, another baggage handler lifts 5kg moe than the first handler.

c. The baggage handlers load luggage for 18 minutes. If they start at 10:25 p.m., what time do they finish?

Answer:

Explanation:
The baggage handlers load luggage for 18 minutes
If they start at 10:25 p.m., they will finish at 18+25=43
Therefore, they finish at 10:43pm.

d. One baggage handler drinks the amount of water shown below every day at work. How many liters of water does he drink during all 7 days of the week?

Answer:
One baggage handler drinks 4 L of water every day at work,
To find the number of liters of water he drinks in 7 days of the week is
7 x 4L = 28 L
Therefore, One baggage handler drinks 28 Liters of water in 7 days of the week.

Question 6.
Complete as many problems as you can in 100 seconds. The teacher will time you and tell you when to stop.

Answer:

Engage NY Eureka Math 3rd Grade Module 2 Mid Module Assessment Answer Key

Eureka Math Grade 3 Module 2 Mid Module Assessment Task Answer Key

Question 1.
Fatima runs errands.
a. The clock to the right shows what time she leaves home. What time does she leave?

Answer:
Famita leaves at 2:07 pm.

Explanation:
In the above clock the hours hand on 2 and the minutes hand is on 7.So, the time is 2:07pm.

b. It takes Fatima 17 minutes to go from her home to the market. Use the number line below to show what time she gets to the market.

Answer:

Explanation:
Famita leaves at 2:07 pm
It takes Fatima 17 minutes to go from her home to the market,
Add 7 and 17
7+17=24
She gets to the market at 2:24pm.
c. The clock to the right shows what time Fatima leaves the market. What time does she leave the market?

Answer:
Fatima leaves the market at 2:53pm

Explanation:
In the above clock the hours hand is on 2 and the minutes hand is on 53.So, the time is 2:53pm.

d. How long does Fatima spend at the market?

Answer:

Explanation:
Fatima leaves the market at 2:53pm, She gets to the market at 2:24pm.
Subtract 24 from 53 to find the number of minutes fatima spends in the store.
Fatima is at the store for 29 minutes.

Question 2.
At the market, Fatima uses a scale to weigh a bag of almonds and a bag of raisins, shown below. What is the total weight of the almonds and raisins?

Answer:
We know from the above picture,
The weight of Almonds is 223 grams,
The weight of Raisins is 355 grams.

The total weight of the almonds and the raisins is 578 grams.

Question 3.
The amount of juice in 1 bottle is shown to the right. Fatima needs 18 liters for a party. Draw and label a tape diagram to find how many bottles of juice she should buy.

Answer:

Explanation:
The amount of juice in 1 bottle is shown to the right. Fatima needs 18 liters for a party
To find the bottles of juice she should buy divide
18/2=9
Fatima needs to buy 9 bottles of juice for the party.

Question 4.
Altogether, Fatima’s lettuce, broccoli, and peas weigh 968 grams. The total weight of her lettuce and broccoli is shown to the right. Write and solve a number sentence to find how much the peas weigh.

Answer:
Fatima’s lettuce, broccoli, and peas weigh 968 grams.
The total weight of her lettuce and broccoli is 744 grams.
To find the weight of peas subtract 744 from 968

Fatima’s Peas weighs 244 grams.

Question 5.
Fatima weighs a watermelon, shown to the right.
a. How much does the watermelon weigh?

Answer:
From the above picture we know that the weight of watermelon is 3 kg.

b. Leaving the store Fatima thinks, “Each bag of groceries seems as heavy as a watermelon!” Use Fatima’s idea about the weight of the watermelon to estimate the total weight of 7 bags.

Answer:
Each bag of groceries seems as heavy as a watermelon
Fatima’s idea about the weight of the watermelon to estimate the total weight of 7 bags
7 x 3 = 21 kg
Fatima estimates the bags weigh about 21 kg altogether.

c. The grocer helps carry about 9 kilograms. Fatima carries the rest. Estimate how many kilograms of groceries Fatima carries.

Answer:
The grocer helps carry about 9 kilograms,Fatima’s bags weigh about 21 kg altogether.
Fatima carries the rest
To find the weight Fatima carries subtract 9 from 21.

Fatima carries about 12 kg of groceries.

d. It takes Fatima 12 minutes to drive to the bank after she leaves the store and then 34 more minutes to drive home. How many minutes does Fatima drive after she leaves the store?

Answer:
It takes Fatima 12 minutes to drive to the bank, 34 more minutes to drive home.
To find the number of minutes famita drives after she leaves the store then
Add 12 and 34
12 minutes + 34 minutes= 46 minutes.
Fatima drives for 46 minutes after she leaves the store.

Engage NY Eureka Math 3rd Grade Module 2 Lesson 21 Answer Key

Question 1.
Weigh the bags of beans and rice on the scale. Then, write the weight on the scales below.

a. Estimate, and then find the total weight of the beans and rice.
Estimate:________ + ________ ≈ ________ + ________ = _________
Actual: ________ + ________ = _________

Answer:
Estimate: 91g+58g ≈ 90g+60g=150g
Actual:91g+58g=149g

b. Estimate, and then find the difference between the weight of the beans and rice.
Estimate: ________ – ________ ≈ ________ – ________ = _________
Actual: ________ – ________ = _________

Answer:
Estimate:91g-58g ≈ 90g-60g=30g
Actual:91g-58g=33g

c. Are your answers reasonable? Explain why.

Answer:
My answers are reasonable because 150g is only 1 more than 149g and 30g is only 3 less than 33g.

Question 2.
Measure the lengths of the three pieces of yarn.
a. Estimate the total length of Yarn A and Yarn C. Then, find the actual total length.

Estimate:60cm+40cm=100cm

The estimated total is 100cm and the actual total is 102cm.

b. Subtract to estimate the difference between the total length of Yarns A and C, and the length of Yarn B. Then, find the actual difference. Model the problem with a tape diagram.

Answer:
Estimate:
100cm-90cm=10cm
Actual:102cm-88cm=14cm
Yarn A+Yarn C=102cm, Yarn B=88cm

Difference between the total length of Yarns A and C, and the length of Yarn B is 102-88=14cm.

Question 3.
Plot the amount of liquid in the three containers on the number lines below. Then, round to the nearest 10 milliliters.

Answer:

a. Estimate the total amount of liquid in three containers. Then, find the actual amount.

Answer:
Estimate:210+240+200=650ml

The estimated total 650ml and the actual total is 645ml.

b. Estimate to find the difference between the amount of water in Containers D and E. Then, find the actual difference. Model the problem with a tape diagram.

Answer:

The estimated difference is 30ml and the actual difference is 26ml.

Question 4.
Shane watches a movie in the theater that is 115 minutes long, including the trailers. The chart to the right shows the length in minutes of each trailer.
a. Find the total number of minutes for all 5 trailers.

Answer:
The total is 5+4+3+5+4=21 minutes

b. Estimate to find the length of the movie without trailers. Then, find the actual length of the movie by calculating the difference between 115 minutes and the total minutes of trailers.

Answer:
115min – 21 min    120-20=100min
115min-21min=94min
The estimated length is 100 minutes and the actual length is 94minutes.

c. Is your answer reasonable? Explain why.

Answer:
Yes, it is reasonable because 94minutes is close to 100minutes.

Eureka Math Grade 3 Module 2 Lesson 21 Exit Ticket Answer Key

Rogelio drinks water at every meal. At breakfast, he drinks 237 milliliters. At lunch, he drinks 300 milliliters. At dinner, he drinks 177 milliliters.
a. Estimate the total amount of water Rogelio drinks. Then, find the actual amount of water he drinks at all three meals.

Answer:
Estimate:
237 ml  ≈ 200 ml
300 ml ≈ 300 ml
177 ml ≈ 177 ml
200+300+177=677ml
About 677ml amount of water Rogelio drinks

Actual:
237+300+177ml=714 ml

Therefore, the actual amount of water he drinks at all three meals is 714.

b. Estimate how much more water Rogelio drinks at lunch than at dinner. Then, find how much more water Rogelio actually drinks at lunch than at dinner.

Answer:
Estimate:
300 ml ≈ 300 ml
177 ml ≈ 200 ml
300-200=100 ml
About 100ml more water Rogelio drinks at lunch than at dinner

Actual:
300 ml- 177 ml=123ml.

123 ml of water Rogelio actually drinks at lunch than at dinner

Eureka Math Grade 3 Module 2 Lesson 21 Homework Answer Key

Question 1.
There are 153 milliliters of juice in 1 carton. A three-pack of juice boxes contains a total of 459 milliliters. Estimate, and then find the actual total amount of juice in 1 carton and in a three-pack of juice boxes.
153 mL + 459 mL ≈ ______ + ______ =______
153 mL + 459 mL = ______

Answer:
153 ml + 459 ml ≈ 200 ml + 500 ml=700ml
153 ml + 459 ml =612 ml

b. Estimate, and then find the actual difference between the amount in 1 carton and in a three-pack of juice boxes.
459 mL − 153 mL ≈ ______ − ______ = ______
459 mL − 153 mL = ______

Answer:
459 ml – 153 ml ≈ 500 ml – 200 ml=300ml
459 ml – 153 ml = 306 ml

c. Are your answers reasonable? Why?
Answer:
No, my answer in addition is not reasonable as it is not close to the actual answer.
Yes, my answers in subtraction is reasonable as it is close to the actual answer.

Question 2.
Mr. Williams owns a gas station. He sells 367 liters of gas in the morning, 300 liters of gas in the afternoon, and 219 liters of gas in the evening.
a. Estimate, and then find the actual total amount of gas he sells in one day.

Answer:
Estimate:
367 L + 300 L + 219 L ≈ 400 L + 300 L + 200 L = 900 L
The estimated total amount of gas Mr.Williams sells in one day is 900L.

Actual:
367 L + 300 L + 219 L =886 L

The actual total amount of gas Mr.Williams sells in one day is 886 L.

b. Estimate, and then find the actual difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening.

Answer:
367 L – 219 L ≈ 400 L – 200 L = 200 L
The estimated difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening

Actual:
367 L – 219 L = 148 L

The actual difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening

Question 3.
The Blue Team runs a relay. The chart shows the time, in minutes, that each team member spends running.
a. How many minutes does it take the Blue Team to run the relay?

Answer:
The Blue Team took 28 minutes to run the relay.

b. It takes the Red Team 37 minutes to run the relay. Estimate, and then find the actual difference in time between the two teams.

Answer:
Estimate:
37 min ≈ 40 min
26 min ≈ 30min
40-30=10min
The estimated difference in time between the two teams is 10 minutes

Actual:
37 min – 26 min=11 min

The actual difference in time between the two teams is 11 minutes.

Question 4.
The lengths of three banners are shown to the right.
a. Estimate, and then find the actual total length of Banner A and Banner C.

Answer:
Estimate:
437 cm + 332 cm ≈ 400 L + 300 L =700 L
The estimate total length of Banner A and Banner C = 700 cm.

Actual:
437 cm + 332 cm = 769 cm

The actual total length of Banner A and Banner C = 769 cm.

b. Estimate, and then find the actual difference in length between Banner B and the combined length of Banner A and Banner C. Model the problem with a tape diagram.

Answer:
Estimate:
(437 cm+332 cm) – 457 L ≈ (400+300cm) – 400 L = 700 cm – 400 L =300 L
The estimated difference in length between Banner B and the combined length of Banner A and Banner C is 300 cm

Actual:
(437 cm+332 cm) – 457 L = 769 cm – 457 cm = 312 cm.

The actual difference in length between Banner B and the combined length of Banner A and Banner C is 312 cm

Engage NY Eureka Math 3rd Grade Module 2 Lesson 20 Answer Key

Eureka Math Grade 3 Module 2 Lesson 20 Sprint Answer Key

A
Round to the Nearest Hundred

Question 1.
201 ≈

Answer:
201 ≈ 200

Question 2.
301 ≈

Answer:
301 ≈ 300

Question 3.
401 ≈

Answer:
401 ≈ 400

Question 4.
801 ≈

Answer:
801 ≈ 800

Question 5.
1,801 ≈

Answer:
1801 ≈ 1800

Question 6.
2,801 ≈

Answer:
2801 ≈ 2800

Question 7.
3,801 ≈

Answer:
3801 ≈ 3800

Question 8.
7,801 ≈

Answer:
7801 ≈ 7800

Question 9.
290 ≈

Answer:
290 ≈ 300

Question 10.
390 ≈

Answer:
390 ≈ 400

Question 11.
490 ≈

Answer:
490 ≈ 500

Question 12.
890 ≈

Answer:
890 ≈ 900

Question 13.
1,890 ≈

Answer:
1890 ≈ 1900

Question 14.
2,890 ≈

Answer:
2890 ≈ 2900

Question 15.
3,890 ≈

Answer:
3890 ≈ 3900

Question 16.
7,890 ≈

Answer:
7890 ≈ 7900

Question 17.
512 ≈

Answer:
512 ≈ 500

Question 18.
2,512 ≈

Answer:
2512 ≈ 2500

Question 19.
423 ≈

Answer:
423 ≈ 400

Question 20.
3,423 ≈

Answer:
3423 ≈ 3400

Question 21.
677 ≈

Answer:
677 ≈ 700

Question 22.
4,677 ≈

Answer:
4677 ≈ 4700

Question 23.
350 ≈

Answer:
350 ≈ 400

Question 24.
1,350 ≈

Answer:
1350 ≈ 1400

Question 25.
450 ≈

Answer:
450 ≈ 500

Question 26.
5,450 ≈

Answer:
5540 ≈ 5500

Question 27.
850 ≈

Answer:
850 ≈ 900

Question 28.
6,850 ≈

Answer:
6850 ≈ 6900

Question 29.
649 ≈

Answer:
649 ≈ 600

Question 30.
651 ≈

Answer:
651 ≈ 700

Question 31.
691 ≈

Answer:
691 ≈ 700

Question 32.
791 ≈

Answer:
791 ≈ 800

Question 33.
891 ≈

Answer:
891 ≈ 900

Question 34.
991 ≈

Answer:
991 ≈ 1000

Question 35.
995 ≈

Answer:
995 ≈ 1000

Question 36.
998 ≈

Answer:
998 ≈ 1000

Question 37.
9,998 ≈

Answer:
9998 ≈ 10000

Question 38.
7,049 ≈

Answer:
7049 ≈ 7000

Question 39.
4,051 ≈

Answer:
4051 ≈ 4100

Question 40.
8,350 ≈

Answer:
8350 ≈ 8400

Question 41.
3,572 ≈

Answer:
3572 ≈ 3600

Question 42.
9,754 ≈

Answer:
9754 ≈ 9800

Question 43.
2,915 ≈

Answer:
2915 ≈ 2900

Question 44.
9,996 ≈

Answer:
9996 ≈ 10000

B
Round to the Nearest Hundred

Question 1.
101 ≈

Answer:
101 ≈ 100

Question 2.
201 ≈

Answer:
201 ≈ 200

Question 3.
301 ≈

Answer:
301 ≈ 300

Question 4.
701 ≈

Answer:
701 ≈ 700

Question 5.
1,701 ≈

Answer:
1701 ≈ 1700

Question 6.
2,701 ≈

Answer:
2701 ≈ 2700

Question 7.
3,701 ≈

Answer:
3701 ≈ 3700

Question 8.
8,701 ≈

Answer:
8701 ≈ 8700

Question 9.
190 ≈

Answer:
190 ≈ 200

Question 10.
290 ≈

Answer:
290 ≈ 300

Question 11.
390 ≈

Answer:
390 ≈ 400

Question 12.
790 ≈

Answer:
790 ≈ 800

Question 13.
1,790 ≈

Answer:
1790 ≈ 1800

Question 14.
2,790 ≈

Answer:
2790 ≈ 2800

Question 15.
3,790 ≈

Answer:
3790 ≈ 3800

Question 16.
8,790 ≈

Answer:
8790 ≈ 8800

Question 17.
412 ≈

Answer:
412 ≈ 400

Question 18.
2,412 ≈

Answer:
2412 ≈ 2400

Question 19.
523 ≈

Answer:
523 ≈ 500

Question 20.
3,523 ≈

Answer:
3523 ≈ 3500

Question 21.
877 ≈

Answer:
877 ≈ 900

Question 22.
4,877 ≈

Answer:
4877 ≈ 4900

Question 23.
250 ≈

Answer:
250 ≈ 300

Question 24.
1,250 ≈

Answer:
1250 ≈ 1300

Question 25.
350 ≈

Answer:
350 ≈ 400

Question 26.
5,350 ≈

Answer:
5350 ≈ 5400

Question 27.
750 ≈

Answer:
750 ≈ 800

Question 28.
6,750 ≈

Answer:
6750 ≈ 6800

Question 29.
649 ≈

Answer:
649 ≈ 600

Question 30.
652 ≈

Answer:
652 ≈ 700

Question 31.
692 ≈

Answer:
692 ≈ 700

Question 32.
792 ≈

Answer:
792 ≈ 800

Question 33.
892 ≈

Answer:
892 ≈ 900

Question 34.
992 ≈

Answer:
992 ≈ 1000

Question 35.
996 ≈

Answer:
996 ≈ 1000

Question 36.
999 ≈

Answer:
999 ≈ 1000

Question 37.
9,999 ≈

Answer:
9999 ≈ 10000

Question 38.
4,049 ≈

Answer:
4049 ≈ 4000

Question 39.
2,051 ≈

Answer:
2051 ≈ 2100

Question 40.
7,350 ≈

Answer:
7350 ≈ 7400

Question 41.
4,572 ≈

Answer:
4572 ≈ 4600

Question 42.
8,754 ≈

Answer:
8754 ≈ 8800

Question 43.
3,915 ≈

Answer:
3915 ≈ 3900

Question 44.
9,997 ≈

Answer:
9997 ≈ 10000

Eureka Math Grade 3 Module 2 Lesson 20 Problem Set Answer Key

Question 1.
a. Find the actual differences either on paper or using mental math. Round each total and part to the nearest hundred and find the estimated differences.

Answer:

b. Look at the differences that gave the most precise estimates. Explain below what they have in common. You might use a number line to support your explanation.

Answer:

Explanation:
In the differences that gave the most precise estimates both numbers either rounded down or both numbers rounded up.So, its different for subtractions than for additions.
When the numbers round the same way the distance is staying about the same.When we round in opposite directions the distance gets either much longer or shorter!

Question 2.
Camden uses a total of 372 liters of gas in two months. He uses 184 liters of gas in the first month. How many liters of gas does he use in the second month?
a. Estimate the amount of gas Camden uses in the second month by rounding each number as you think best.

Answer:
372 L ≈ 400 L
184 L ≈ 200 L
400L-200L=200L
Camden uses about 200 liters of gas in the second month.

b. How many liters of gas does Camden actually use in the second month? Model the problem with a tape diagram.

Answer:

Explanation:
Camden actually uses 188 L of gas in the second month.

Eureka Math Grade 3 Module 2 Lesson 20 Exit Ticket Answer Key

Question 3.
The weight of a pear, apple, and peach are shown to the right. The pear and apple together weigh 372 grams. How much does the peach weigh?
a. Estimate the weight of the peach by rounding each number as you think best. Explain your choice.

Answer:

Explanation:
The peach weighs about 130g.I decided to round 372g to the nearest 10g and do mental math.500g is already rounded to the nearest 10g.

b. How much does the peach actually weigh? Model the problem with a tape diagram.

Answer:

Explanation:
The peach weighs 128grams.

Question:4
Kathy buys a total of 416 grams of frozen yogurt for herself and a friend. She buys 1 large cup and 1 small cup.

a. Estimate how many grams are in the small cup of yogurt by rounding.

Answer:
416 g ≈ 400 g
363 g ≈ 400 g
400-400=0 g
Therefore the estimated weight of small cup of yogurt by rounding to nearest hundreds is 0

b. Estimate how many grams are in the small cup of yogurt by rounding in a different way.

Answer:
416 g ≈ 420 g
363 g ≈ 360 g
420-360=60 g
Therefore the estimated weight of small cup of yogurt by rounding to nearest tens is 60 g.

c. How many grams are actually in the small cup of yogurt?

Answer:

d. Is your answer reasonable? Which estimate was closer to the exact weight? Explain why.

Answer:
Yes my answer was reasonable.The estimate where we rounded the numbers to the nearest tens is close to the exact weight as the difference between the estimated and the exact weight is just 7 g.

Eureka Math Grade 3 Module 2 Lesson 20 Homework Answer Key

Question 1.
Melissa and her mom go on a road trip. They drive 87 kilometers before lunch. They drive 59 kilometers after lunch.
a. Estimate how many more kilometers they drive before lunch than after lunch by rounding to the nearest 10 kilometers.

Answer:
87 km ≈  90 km
59 km ≈  60 km
90-60=30km
Melissa and her mom drove 30 km before lunch than after lunch.

b. Precisely how much farther do they drive before lunch than after lunch?

Answer:
87-59=28 km

c. Compare your estimate from (a) to your answer from (b). Is your answer reasonable? Write a sentence to explain your thinking.

Answer:
30 km is near to 28 km.
Yes my answer is reasonable as their is only 2 km difference ib between the estimated and the actual answer.

Question 2.
Amy measures ribbon. She measures a total of 393 centimeters of ribbon and cuts it into two pieces. The first piece is 184 centimeters long. How long is the second piece of ribbon?
a. Estimate the length of the second piece of ribbon by rounding in two different ways.

Answer:
Round of to nearest hundreds
393 cm ≈ 400 cm

184 cm ≈ 200 cm
400-200cm=200cm
The second piece of ribbon is about 200cm.

Rund of to nearest tens.
393 cm ≈ 390 cm
184 cm ≈ 180 cm
390-180=210 cm
The second piece of ribbon is about 210cm.

b. Precisely how long is the second piece of ribbon? Explain why one estimate was closer.

Answer:

The actual length of the second piece of ribbon is 199cm.
My first estimate when rounded to nearest hundreds is very close to the actual answer just by 1cm difference.

Question 3.
The weight of a chicken leg, steak, and ham are shown to the right. The chicken leg and the steak together weigh 341 grams. How much does the ham weigh?
a. Estimate the weight of the ham by rounding.

Answer:
989 g ≈ 1000 g
341 g ≈ 300 g
1000-300=600 g
The estimated weight of the ham by rounding is 600 g.

b. How much does the ham actually weigh?
989-341=648 g

Question 4.
Kate uses 506 liters of water each week to water plants. She uses 252 liters to water the plants in the greenhouse. How much water does she use for the other plants?
a. Estimate how much water Kate uses for the other plants by rounding.

Answer:
Round of to nearest hundreds
506 L ≈ 500 L
252 L ≈ 300 L
500-300=200 L
Kate uses 200 L of water for the other plants by rounding.

b. Estimate how much water Kate uses for the other plants by rounding a different way.

Answer:
Round of to nearest tens.
506 L ≈ 500 L
252 L ≈  250 L
500-250=250 L
Kate uses 250 L of water for the other plants by rounding.

c. How much water does Kate actually use for the other plants? Which estimate was closer? Explain why.

Answer:
506 L-252 L=254 L

My estimate where i rounded the numbers to the nearest tens is closer as the difference between the estimated and the actual answer is 4 L only.

Engage NY Eureka Math 3rd Grade Module 2 Lesson 19 Answer Key

Eureka Math Grade 3 Module 2 Lesson 19 Problem Set Answer Key

Question 1.
Solve the subtraction problems below.
a. 340 cm – 60 cm

Answer:
340 cm – 60 cm=380cm

b. 340 cm – 260 cm

Answer:
340 cm – 260 cm=80cm

c. 513 g – 148 g

Answer:
513 g – 148 g=365g

d. 641 g – 387 g

Answer:
641 g – 387 g=254g

e. 700 mL – 52 mL

Answer:
700 mL – 52 mL=648ml

f. 700 mL – 452 mL

Answer:
700 mL – 452 mL=248ml

g. 6 km 802 m – 2 km 569 m

Answer:
6 km 802 m – 2 km 569 m=4 km 233m

h. 5 L 920 mL – 3 L 869 mL

Answer:
5 L 920 mL – 3 L 869 mL=2 L 51mL

Question 2.
David is driving from Los Angeles to San Francisco. The total distance is 617 kilometers. He has 468 kilometers left to drive. How many kilometers has he driven so far?

Answer:

Explanation:
David is driving from Los Angeles to San Francisco. The total distance is 617 kilometers. He has 468 kilometers left to drive
Subtract 468 from 617
617-468=149 km
David has driven 149 kilometers so far.

Question 3.
The piano weighs 289 kilograms more than the piano bench. How much does the bench weigh?

Answer:

Explanation:
The piano weighs 289 kilograms more than the piano bench, the piano weighs 290kg
To find the weight of the bench subtract 289 from 297kg
297-289kg=8kg
Therefore, the weight of the bench is 8kg.

Question 4.
Tank A holds 165 fewer liters of water than Tank B. Tank B holds 400 liters of water. How much water does Tank A hold?

Answer:

Explanation:
Tank A holds 165 fewer liters of water than Tank B. Tank B holds 400 liters of water
Subtract 165 from 400
400-165=235L
Therefore, Tank A holds 235L.

Eureka Math Grade 3 Module 2 Lesson 19 Exit Ticket Answer Key

Question 1.
Solve the subtraction problems below.
a. 346 m − 187 m

Answer:
346 m − 187 m=159m

b. 700 kg − 592 kg

Answer:
700 kg − 592 kg=108kg

Question 2.
The farmer’s sheep weighs 647 kilograms less than the farmer’s cow. The cow weighs 725 kilograms. How much does the sheep weigh?

Answer:

Explanation:
The farmer’s sheep weighs 647 kilograms less than the farmer’s cow. The cow weighs 725 kilograms
To find the weight of sheep subtract 647 from 725kg
725-647=78kg
Therefore, the sheep weighs 78kg.

Eureka Math Grade 3 Module 2 Lesson 19 Homework Answer Key

Question 1.
Solve the subtraction problems below.
a. 280 g − 90 g

Answer:
280 g − 90 g=190g

b. 450 g − 284 g

Answer:

450 g – 284 g=166g

c. 423 cm − 136 cm

Answer:
423 cm – 136 cm=287 cm

d. 567 cm − 246 cm

Answer:
567 cm – 246 cm = 321 cm

e. 900 g − 58 g

Answer:
900 g – 58 g = 842 g

f. 900 g − 358 g

Answer:
900 g – 358 g = 542 g

g. 4 L 710 mL − 2 L 690 mL

Answer:
4 L 710 ml – 2 L 690 ml = 2 L  20ml

h. 8 L 830 mL − 4 L 378 mL

Answer:
8 L 830 ml – 4 L 378 ml =4 L 452 ml

Question 2.
The total weight of a giraffe and her calf is 904 kilograms. How much does the calf weigh? Use a tape diagram to model your thinking.

Answer:

Explanation:
The total weight of a giraffe and her calf is 904 kilograms, the weight of giraffe is 829 kg.
To find the weight of calf subtract 829 from 904
904-829=75kg
Therefore, the calf weighs 75kg.

Question 3.
The Erie Canal runs 584 kilometers from Albany to Buffalo. Salvador travels on the canal from Albany. He must travel 396 kilometers more before he reaches Buffalo. How many kilometers has he traveled so far?

Answer:

Explanation:
The Erie Canal runs 584 kilometers from Albany to Buffalo. Salvador travels on the canal from Albany. He must travel 396 kilometers more before he reaches Buffalo.
To find the number of kilometers he traveled so far subtarct 396km from 584km
584-396=188km
Therefore, Salvador traveled 188km so far.

Question 4.
Mr. Nguyen fills two inflatable pools. The kiddie pool holds 185 liters of water. The larger pool holds 600 liters of water. How much more water does the larger pool hold than the kiddie pool?

Answer:

Explanation:
Mr. Nguyen fills two inflatable pools. The kiddie pool holds 185 liters of water. The larger pool holds 600 liters of water
To find the number of liters the larger pool hold than the kiddie pool subtract 185l from 60l
600-185=415L
Therefore, the larger pool holds 415L of water more than the kiddie pool.

Engage NY Eureka Math 3rd Grade Module 2 Lesson 18 Answer Key

Eureka Math Grade 3 Module 2 Lesson 18 Problem Set Answer Key

Question 1.
Solve the subtraction problems below.
a. 60 mL – 24 mL

Answer:
60 mL – 24 mL=36ml

b. 360 mL – 24 mL

Answer:
360 mL – 24 mL=336ml

c. 360 mL – 224 mL

Answer:
360 mL – 224 mL=136ml

d. 518 cm – 21 cm

Answer:
518 cm – 21 cm=497ml

e. 629 cm – 268 cm

Answer:
629cm-268cm=361cm

f. 938 cm – 440 cm

Answer:
938cm-440cm=498cm

g. 307 g – 130 g

Answer:
307g-130g=177g

h. 307 g – 234 g

Answer:
307g-234g=73g

i. 807 g – 732 g

Answer:
807g-732g=75g

j. 2 km 770 m – 1 km 455 m

Answer:
2 km 770 m – 1 km 455 m=1km 315m

k. 3 kg 924 g – 1 kg 893 g

Answer:
3 kg 924 g – 1 kg 893 g=2kg 31g

Question 2.
The total weight of 3 books is shown to the right. If 2 books weigh 233 grams, how much does the third book weigh? Use a tape diagram to model the problem.

Answer:

Explanation:
The total weight of 3 books is 405g, If 2 books weigh 233 grams the the weight of 3rd book is 405g-233g.
Therefore, the third book weigh is 172g.

Question 3.
The chart to the right shows the lengths of three movies.
a. The movie Champions is 22 minutes shorter than The Lost Ship. How long is Champions?

Answer:

Explanation:
The movie Champions is 22 minutes shorter than The Lost Ship, The Lost Ship is 117minutes long.
117-22min=95min
Therefore, the movie Champions is 95 minutes long.

b. How much longer is Magical Forests than Champions?

Answer:

Explanation:
The movie Champions is 95 minutes long, Magical Forests is 145min long.
145-95=50min
Therefore, Magical Forests is 50min longer than Champions.

Question 4.
The total length of a rope is 208 centimeters. Scott cuts it into 3 pieces. The first piece is 80 centimeters long. The second piece is 94 centimeters long. How long is the third piece of rope?

Answer:

Explanation:
The total length of a rope is 208 centimeters, The first piece is 80 centimeters long. The second piece is 94 centimeters long.
Length of 2 pieces is 94+80=174cm
The third piece is 208-174=34cm.

Eureka Math Grade 3 Module 2 Lesson 18 Exit Ticket Answer Key

Question 1.
Solve the subtraction problems below.
a. 381 mL − 146 =235mlmL

Answer:
381 mL − 146 mL

b. 730 m − 426 m

Answer:
730 m − 426 m=304m

c. 509 kg − 384 kg

Answer:
509 kg − 384 kg=125kg

Question 2.
The total length of a banner is 408 centimeters. Carly paints it in 3 sections. The first 2 sections she paints are 187 centimeters long altogether. How long is the third section?

Answer:

Explanation:
The total length of a banner is 408 centimeters, Carly paints it in 3 sections. The first 2 sections she paints are 187 centimeters long altogether
The length of the third section is 408-187cm=221cm.

Eureka Math Grade 3 Module 2 Lesson 18 Homework Answer Key

Question 1.
Solve the subtraction problems below.
a. 70 L − 46 L

Answer:
70 L − 46 L=24L

b. 370 L – 46 L

Answer:

370 L – 46 L=324L

c. 370 L – 146 L

Answer:
370 L – 146 L=225L

d. 607 cm − 32 cm

Answer:
607 cm − 32 cm=575cm

e. 592 cm − 258 cm

Answer:
592 cm − 258 cm=334cm

f. 918 cm − 553 cm

Answer:

918 cm − 553 cm=365cm

g. 763 g − 82 g

Answer:
763 g − 82 g=681g

h. 803 g − 542 g

Answer:
803 g − 542 g=261g

i. 572 km − 266 km

Answer:

572 km − 266 km=306km

j. 837 km − 645 km

Answer:
837 km − 645 km=192km

Question 2.
The magazine weighs 280 grams less than the newspaper. The weight of the newspaper is shown below. How much does the magazine weigh? Use a tape diagram to model your thinking.

Answer:

Explanation:
The weight of the newspaper is 454g, the magazine weighs 280 grams less than the newspaper.
454-280=174g
Therefore, the magazine weighs 174g.

Question 3.
The chart to the right shows how long it takes to play 3 games.
a. Francesca’s basketball game is 22 minutes shorter than Lucas’s baseball game. How long is Francesca’s basketball game?

b. How much longer is Francesca’s basketball game than Joey’s football game?

Engage NY Eureka Math 3rd Grade Module 2 Lesson 17 Answer Key

Eureka Math Grade 3 Module 2 Lesson 17 Sprint Answer Key

A
Round to the Nearest Ten

Question 1.
21 ≈

Answer:
21 ≈ 20

Question 2.
31 ≈

Answer:
31≈30

Question 3.
41 ≈

Answer:
41≈40

Question 4.
81 ≈

Answer:
81≈80

Question 5.
59 ≈

Answer:
59≈60

Question 6.
49 ≈

Answer:
49≈50

Question 7.
39 ≈

Answer:
39≈40

Question 8.
19 ≈

Answer:
19≈20

Question 9.
36 ≈

Answer:
36≈40

Question 10.
34 ≈

Answer:
34≈30

Question 11.
56 ≈

Answer:
56≈60

Question 12.
54 ≈

Answer:
54≈50

Question 13.
77 ≈

Answer:
77≈80

Question 14.
73 ≈

Answer:
73≈70

Question 15.
68 ≈

Answer:
68≈70

Question 16.
62 ≈

Answer:
62≈60

Question 17.
25 ≈

Answer:
25≈30

Question 18.
35 ≈

Answer:
35≈40

Question 19.
45 ≈

Answer:
45≈50

Question 20.
75 ≈

Answer:
75≈80

Question 21.
85 ≈

Answer:
85≈90

Question 22.
15 ≈

Answer:
15≈20

Question 23.
79 ≈

Answer:
79≈80

Question 24.
89 ≈

Answer:
89≈90

Question 25.
99 ≈

Answer:
99≈100

Question 26.
109 ≈

Answer:
109≈110

Question 27.
119 ≈

Answer:
119≈120

Question 28.
149 ≈

Answer:
149≈150

Question 29.
311 ≈

Answer:
311≈310

Question 30.
411 ≈

Answer:
411≈410

Question 31.
519 ≈

Answer:
519≈520

Question 32.
619 ≈

Answer:
619≈620

Question 33.
629 ≈

Answer:
629≈630

Question 34.
639 ≈

Answer:
639≈640

Question 35.
669 ≈

Answer:
669≈670

Question 36.
969 ≈

Answer:
969≈970

Question 37.
979 ≈

Answer:
979≈980

Question 38.
989 ≈

Answer:
989≈990

Question 39.
999 ≈

Answer:
999≈1000

Question 40.
1,109 ≈

Answer:
1109≈1110

Question 41.
1,119 ≈

Answer:
1119≈1120

Question 42.
3,227 ≈

Answer:
3227≈3230

Question 43.
5,487 ≈

Answer:
5487≈5490

Question 44.
7,885 ≈

Answer:
7885≈7890

B
Round to the Nearest Ten

Question 1.
11 ≈

Answer:
11≈10

Question 2.
21 ≈

Answer:
21≈20

Question 3.
31 ≈

Answer:
31≈30

Question 4.
71 ≈

Answer:
71≈70

Question 5.
69 ≈

Answer:
69≈70

Question 6.
59 ≈

Answer:
59≈60

Question 7.
49 ≈

Answer:
49≈50

Question 8.
19 ≈

Answer:
19≈20

Question 9.
26 ≈

Answer:
26≈30

Question 10.
24 ≈

Answer:
24≈20

Question 11.
46 ≈

Answer:
46≈50

Question 12.
44 ≈

Answer:
44≈40

Question 13.
87 ≈

Answer:
87≈90

Question 14.
83 ≈

Answer:
83≈80

Question 15.
78 ≈

Answer:
78≈80

Question 16.
72 ≈

Answer:
72≈70

Question 17.
15 ≈

Answer:
15≈20

Question 18.
25 ≈

Answer:
25≈30

Question 19.
35 ≈

Answer:
35≈40

Question 20.
75 ≈

Answer:
75≈80

Question 21.
85 ≈

Answer:
85≈90

Question 22.
45 ≈

Answer:
45≈50

Question 23.
79 ≈

Answer:
79≈80

Question 24.
89 ≈

Answer:
89≈90

Question 25.
99 ≈

Answer:
99≈100

Question 26.
109 ≈

Answer:
109≈110

Question 27.
119 ≈

Answer:
119≈120

Question 28.
159 ≈

Answer:
159≈160

Question 29.
211 ≈

Answer:
211≈210

Question 30.
311 ≈

Answer:
311≈310

Question 31.
418 ≈

Answer:
418≈420

Question 32.
518 ≈

Answer:
518≈520

Question 33.
528 ≈

Answer:
528≈530

Question 34.
538 ≈

Answer:540
538≈

Question 35.
568 ≈

Answer:
568≈570

Question 36.
968 ≈

Answer:
968≈970

Question 37.
978 ≈

Answer:
978≈980

Question 38.
988 ≈

Answer:
988≈990

Question 39.
998 ≈

Answer:
998≈1000

Question 40.
1,108 ≈

Answer:
1108≈1110

Question 41.
1,118 ≈

Answer:
1118≈1120

Question 42.
2,337 ≈

Answer:
2337≈2340

Question 43.
4,578 ≈

Answer:
4578≈4580

Question 44.
8,785 ≈

Answer:
8785≈8790

Eureka Math Grade 3 Module 2 Lesson 17 Problem Set Answer Key

Question 1.
a. Find the actual sum either on paper or using mental math. Round each addend to the nearest hundred, and find the estimated sums.

Answer:

b. Look at the sums that gave the most precise estimates. Explain below what they have in common. You might use a number line to support your explanation.

Answer:
All of the numbers that i added were really close to the halfway point.In the sums that gave the most precise estimates, one number always rounded up and one number always rounded down.So, they balanced eachother out and gave the most precise estimate.
Part:A     451+249=700
451   500                                    249    200

500+200=700   It gave the same answer.

Question 2.
Janet watched a movie that is 94 minutes long on Friday night. She watched a movie that is 151 minutes long on Saturday night.
a. Decide how to round the minutes. Then, estimate the total minutes Janet watched movies on Friday and Saturday.

Answer:
The total minutes Janet watched movies on Friday and Saturday is about 240minutes.

Explanation:
94 ≈ 90
151 ≈ 150
150+90=240minutes
I decided to round the numbers to the nearest ten minutes and estimated that
the total minutes Janet watched movies on Friday and Saturday is 240minutes.

b. How much time did Janet actually spend watching movies?

Answer:
The time Janet actually spend watching movies is 245 minutes.

Explanation:
The time Janet actually spend watching movies is 94 minutes on friday and 151 minutes on saturday.
Add to find the total
94+151=245
The time Janet actually spend watching movies is 245 minutes.

c. Explain whether or not your estimated sum is close to the actual sum. Round in a different way, and see which estimate is closer.

Answer:
Yes, the estimated sum is close to the real sum when we rounded of he numbers to the nearest tens.Actual sum is 240 and the real sum is 245.
If we round of the numbers to nearest hundred the sum is not very close to the actual sum.
94 ≈ 100, 151 ≈ 200.

Question 3.
Sadie, a bear at the zoo, weighs 182 kilograms. Her cub weighs 74 kilograms.
a. Estimate the total weight of Sadie and her cub using whatever method you think best.

Answer:
250kilograms is the estimated total weight of Sadie and her cub

Explanation:
Using rounding to nearest tens
182 ≈ 180
74 ≈ 70
180+70=250
250kilograms is the estimated total weight of Sadie and her cub

b. What is the actual weight of Sadie and her cub? Model the problem with a tape diagram.

Answer:
256kilograms is the actual weight of Sadie and her cub.

Eureka Math Grade 3 Module 2 Lesson 17 Exit Ticket Answer Key

Jesse practices the trumpet for a total of 165 minutes during the first week of school. He practices for 245 minutes during the second week.
a. Estimate the total amount of time Jesse practices by rounding to the nearest 10 minutes.

Answer:
420 minutes is the total amount of time Jesse practices by rounding to the nearest 10 minutes.

Explanation:
165 ≈ 170
245 ≈ 250
170+250=420minutes
The total amount of time Jesse practices by rounding to the nearest 10 minutes is 420minutes.

b. Estimate the total amount of time Jesse practices by rounding to the nearest 100 minutes.

Answer:
400minutes is the total amount of time Jesse practices by rounding to the nearest 100 minutes.

Explanation:
165 ≈ 200
245 ≈ 200
200+200=400minutes
The total amount of time Jesse practices by rounding to the nearest 100 minutes is 240minutes.

c. Explain why the estimates are so close to each other.

Answer:
When we rounded of the numbers to the nearest hundreds one number is rounded up to the next hundred and one is rounded down to the previous hundred which made it balanced.So , both the estimates are close to each other.

Eureka Math Grade 3 Module 2 Lesson 17 Homework Answer Key

Question 1.
Cathy collects the following information about her dogs, Stella and Oliver.

Use the information in the charts to answer the questions below.
a. Estimate the total weight of Stella and Oliver.

Answer:
Weight of Stella and oliver are 32 and 7 kgs.
32  ≈   30
7  ≈   10
30+10=40kgs
Estimated total weight of Stella and Oliver is 40kg

b. What is the actual total weight of Stella and Oliver?

Answer:
Weight of Stella and oliver are 32 and 7 kgs
32+7=39kg
39kg is the actual total weight of Stella and Oliver.

c. Estimate the total amount of time Cathy spends giving her dogs a bath.

Answer:
Bath time of Stella and Oliver are 36minutes and 25minutes.
36 ≈ 40
25 ≈ 30
40+30=70minutes
The estimated total amount of time Cathy spends giving her dogs a bath is 70minutes.

d. What is the actual total time Cathy spends giving her dogs a bath?

Answer:
Bath time of Stella and Oliver are 36minutes and 25minutes
36+25=61minutes
The actual total time Cathy spends giving her dogs a bath is 61 minutes.

Answer:
e. Explain how estimating helps you check the reasonableness of your answers.

Answer:
We can use estimation to check for reasonableness with all numbers. When we use estimation, it won’t tell us whether we actually have the correct answer, but it will tell us if we’re close and our answer is probably right

Question 2.
Dena reads for 361 minutes during Week 1 of her school’s two-week long Read-A-Thon. She reads for 212 minutes during Week 2 of the Read-A-Thon.
a. Estimate the total amount of time Dena reads during the Read-A-Thon by rounding.

Answer:
Dena reads for 361 minutes during Week 1,for 212 minutes during Week 2
Round of to tens.
361 ≈  360
212 ≈ 210
360+210=570minutes
The estimated total amount of time Dena reads during the Read-A-Thon by rounding is 570minutes.

b. Estimate the total amount of time Dena reads during the Read-A-Thon by rounding in a different way.

Answer:
Dena reads for 361 minutes during Week 1,for 212 minutes during Week 2
Round of to hundreds.
361 ≈ 400
212  ≈ 200
400+200=600minutes
The estimated total amount of time Dena reads during the Read-A-Thon by rounding is 600 minutes.

c. Calculate the actual number of minutes that Dena reads during the Read-A-Thon. Which method of rounding was more precise? Why?

Answer:
Dena reads for 361 minutes during Week 1,for 212 minutes during Week 2
361+212=573

The actual number of minutes that Dena reads during the Read-A-Thon is 573 minutes.
Rounding to the nearest tens was more precise as it is just 3 minutes more than the actual answer.

Engage NY Eureka Math 3rd Grade Module 2 Lesson 16 Answer Key

Read more

Engage NY Eureka Math 3rd Grade Module 2 Lesson 1 Answer Key

Eureka Math Grade 3 Module 2 Lesson 1 Problem Set Answer Key

Question 1.
Use a stopwatch. How long does it take you to snap your fingers 10 times?
It takes ___________ to snap 10 times.

Answer:
It takes 4 seconds  to snap 10 times

Question 2.
Use a stopwatch. How long does it take to write every whole number from 0 to 25?

It takes ___________________ to write every whole number from 0 to 25.

Answer:

It takes 30 seconds to write every whole number from 0 to 25

Question 3.
Use a stopwatch. How long does it take you to name 10 animals? Record them below.

It takes ___________________________ to name 10 animals.

Answer:

It takes 35 seconds to name 10 animals.

Question 4.
Use a stopwatch. How long does it take you to write 7 × 8 = 56 fifteen times? Record the time below.

It takes _______________________ to write 7 × 8 = 56 fifteen times.

Answer:

It takes 50 seconds to write 7 × 8 = 56 fifteen times

Question 5.
Work with your group. Use a stopwatch to measure the time for each of the following activities.

Answer:

Question 6.
100 meter relay: Use a stopwatch to measure and record your team’s times.

The table to the right shows how much time it takes each of the 5 students to do 15 jumping jacks.
a. Who finished 15 jumping jacks the fastest?

Answer:
Jake finished 15 jumping jacks the fastest in 14 seconds.

b. Who finished their jumping jacks in the exact same amount of time?

Answer:
Riley and Nicholas finished their jumping jacks in the same amount of time that is 15 seconds.

c. How many seconds faster did Jake finish than Adeline?

Answer:
Andeline finished in 17 seconds and Jake in 15 seconds.So, Jake finished 2 seconds faster than Adeline.

Eureka Math Grade 3 Module 2 Lesson 1 Homework Answer Key

Question 1.
The table to the right shows how much time it takes each of the 5 students to run 100 meters.
a. Who is the fastest runner?

Answer:
Dominique is the fastest runner(18 seconds of time).

b. Who is the slowest runner?

Answer:
Chester is the slowest runner(26 seconds of time).

c. How many seconds faster did Samantha run than Louie?

Answer:
Samantha ran in 19 seconds and Louie ran in 24 seconds.So, 24-19=5
Therefore, Samantha ran 5 seconds faster than Louie.

Question 2.
List activities at home that take about the following amounts of time to complete. If you do not have a stopwatch, you can use the strategy of counting by 1 Mississippi, 2 Mississippi, 3 Mississippi, ….
Time Activities at home

Question 3.
Match the analog clock with the correct digital clock.

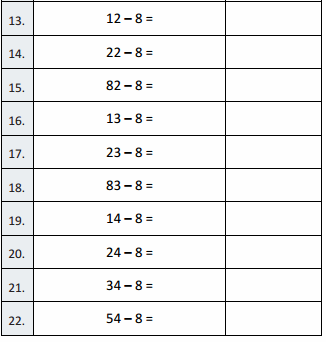
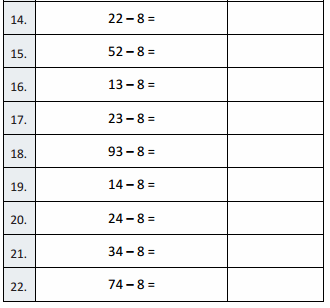
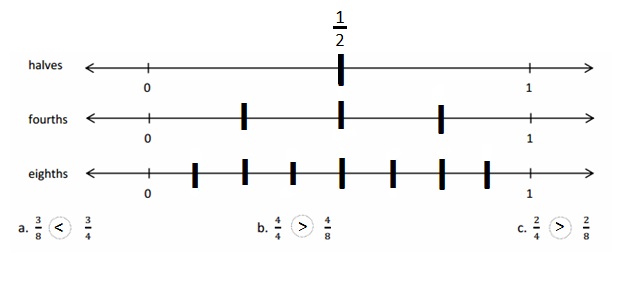
Answer: