Eureka Math

Engage NY Eureka Math Grade 6 Module 6 Lesson 10 Answer Key

Eureka Math Grade 6 Module 6 Lesson 10 Example Answer Key

Example 1: Describing Distributions

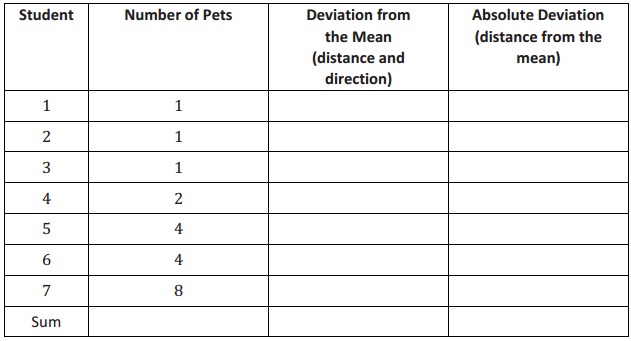
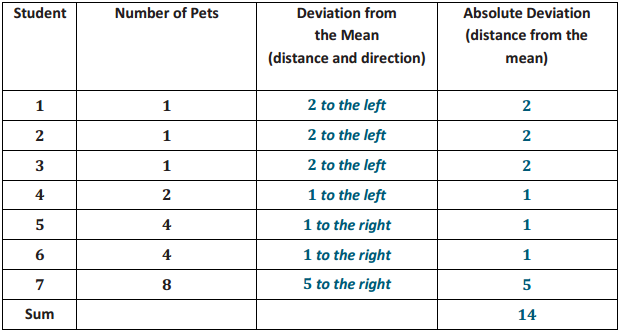
In Lesson 9, Sabina developed the mean absolute deviation (MAD) as a number that measures variability in a data distribution. Using the mean and MAD along with a dot plot allows you to describe the center, spread, and shape of a data distribution. For example, suppose that data on the number of pets for ten students are shown in the dot plot below.

There are several ways to describe the data distribution. The mean number of pets for these students is 3, which is a measure of center. There is variability in the number of pets the students have, and data values differ from the mean by about 2.2 pets on average (the MAD). The shape of the distribution is heavy on the left, and then it this out to the right.

Exercises 1 – 4:

Exercise 1.
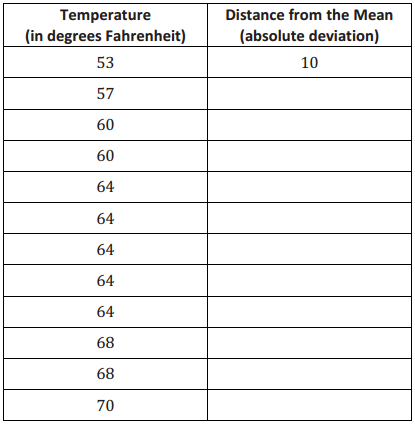
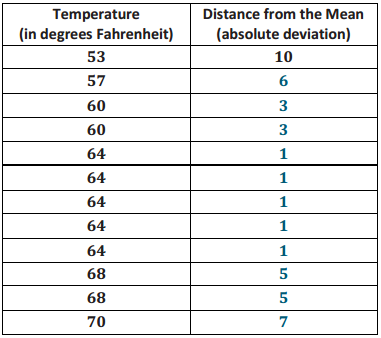
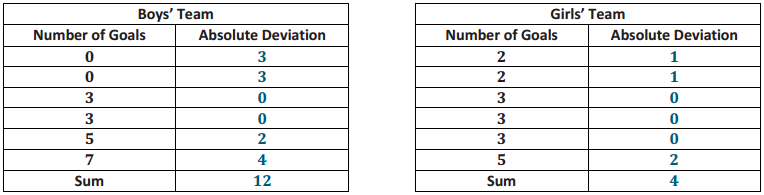
sSuppose that the weights of seven middle school students’ backpacks are given below.

a. Fill in the following table.

Answer:

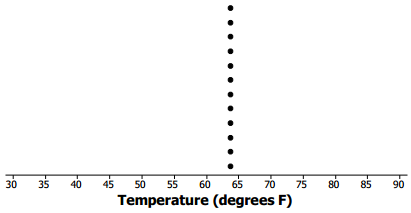
b. Draw a dot plot for these data, and calculate the mean and MAD.
Answer:

The mean is 18 pounds.
The MAD is 0 pounds.

c. Describe this distribution of weights of backpacks by discussing the center, spread, and shape.
Answer:
The mean is 18 pounds. There is no variability.
All of the data values are equal.

Exercise 2.
Suppose that the weight of Elisha’s backpack is 17 pounds rather than 18 pounds.

a. Draw a dot plot for the new distribution.
Answer:

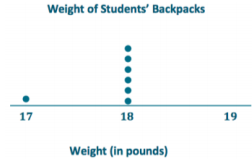
b. Without doing any calculations, how is the mean affected by the lighter weight? Would the new mean be the same, smaller, or larger?
Answer:
The mean will be smaller because the new weight is smaller than the other weights.

c. Without doing any calculations, how is the MAD affected by the lighter weight? Would the new MAD be the same, smaller, or larger?
Answer:
The MAD would be larger because now there is variability, so the MAD is greater than zero.

Exercise 3.
Suppose that in addition to Elisha’s backpack weight having changed from 18 to 17 pounds, Fred’s backpack weight is changed from 18 to 19 pounds.

a. Draw a dot plot for the new distribution.
Answer:

b. Without doing any calculations, how would the new mean compare to the original mean?
Answer:
The new mean is 18 1b., which was also the original mean.

c. Without doing any calculations, would the MAD for the new distribution be the same as, smaller than, or larger than the original MAD?
Answer:
Since there is more variability, the MAD is larger than the original MAD.

d. Without doing any calculations, how would the MAD for the new distribution compare to the one in Exercise 2?
Answer:
There is more variability, so the MAD is greater than the MAD in Exercise 2.

Exercise 4.
Suppose that seven-second graders’ backpack weights were as follows:

a. How is the distribution of backpack weights for the second graders similar to the original distribution for the middle school students given in Exercise 1?
Answer:
Both have no variability, so the MAD is 0 pounds in both cases. The shapes of the distributions on the dot plots are the same.

b. How are the distributions different?
Answer:
The means are different. One mean is 18 pounds, and the other is 5 pounds.

Example 2: Using the MAD

Using data to make decisions often involves comparing distributions. Recall that Robert is trying to decide whether to move to New York City or to San Francisco based on temperature. Comparing the center, spread, and shape for the two temperature distributions could help him decide.

Dot Plot of Temperature for New York City

Dot Plot of Temperature for San Francisco

From the dot plots, Robert saw that monthly temperatures in New York City were spread fairly evenly from around 40 degrees to around 85 degrees, but in San Francisco, the monthly temperatures did not vary as much. He was surprised that the mean temperature was about the same for both cities. The MAD of 14 degrees for New York City told him that, on average, a month’s temperature was 14 degrees away from the mean of 63 degrees.

That is a lot of variability, which is consistent with the dot plot. On the other hand, the MAD for San Francisco told him that San Francisco’s monthly temperatures differ, on average, only 3.5 degrees from the mean of 64 degrees. So, the mean doesn’t help Robert very much in making a decision, but the MAD and dot plot are helpful.

Which city should he choose if he loves warm weather and really dislikes cold weather?
Answer:
He should choose San Francisco because there is little variability, and it does not get as cold as New York City.

Exercises 5 – 7:

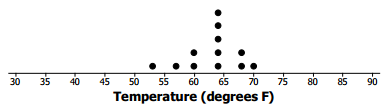
Exercise 5.
Robert wants to compare temperatures for Cities B and C.

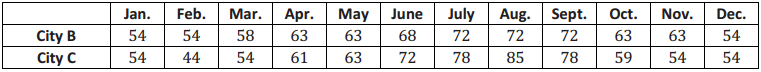
a. Draw a dot plot of the monthly temperatures for each of the cities.
Answer:
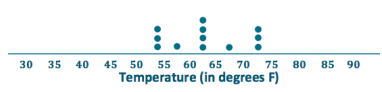
City B

City C

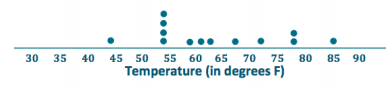
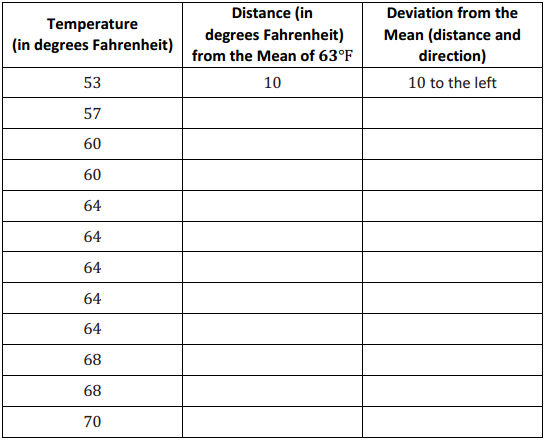
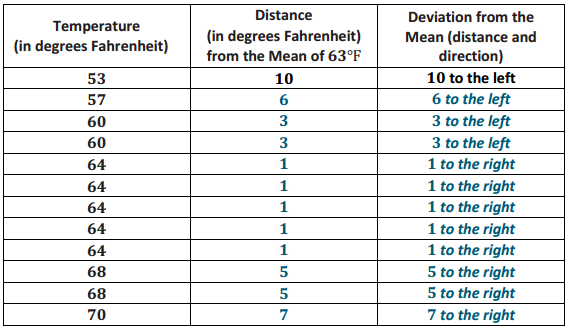
b. Verify that the mean monthly temperature for each distribution is 63 degrees.
Answer:
The data are nearly symmetrical around 63 degrees for City B. The sum of the distances to the left of the mean is equal to the sum of the distances to the right of the mean. Each of these sums is equal to 32 degrees.
For City C, the sum of the distances to the left of the mean is equal to the sum of the distances to the right of the mean. Each sum is equal to 61.

c. Find the MAD for each of the cities. Interpret the two MADs in words, and compare their values. Round your answers to the nearest tenth of a degree.
Answer:
1. The MAD is 5.3 degrees for City B, which means that, on average, the monthly temperatures differ by 5.3 degrees from the mean of 63 degrees.
2. The MAD is 10.2 degrees for City C, which means that, on average, the monthly temperatures differ by 10.2 degrees from the mean of 63 degrees.

Exercise 6.
How would you describe the differences in the shapes of the monthly temperature distributions of the two cities?
Answer:
The temperatures are nearly symmetric around the mean in City B. The temperatures are compact to the left of the mean for City C and then spread out to the right (skewed right).

Exercise 7.
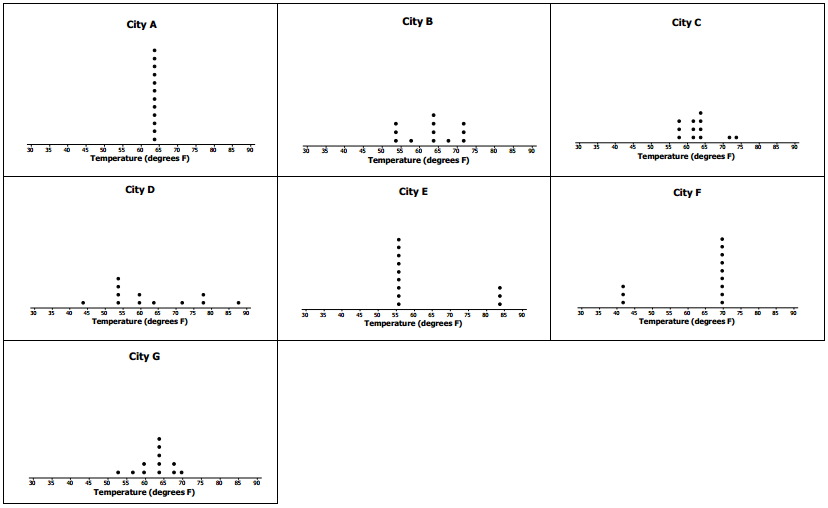
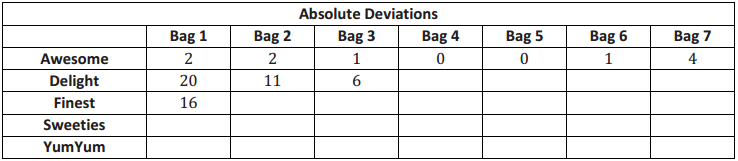
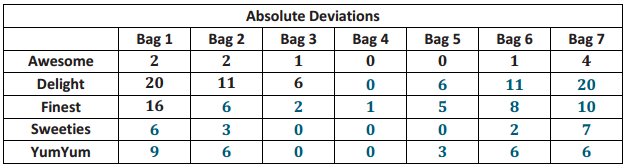
Suppose that Robert had to decide between Cities D, E, and F.

a. Draw a dot plot for each distribution.
Answer:

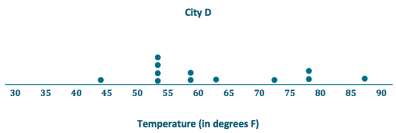
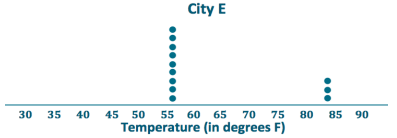
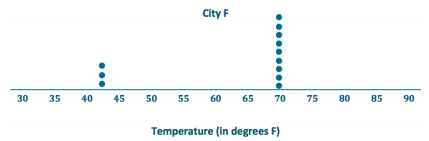
b. Interpret the MAD for the distributions. What does this mean about variability?
Answer:
The MADs are, all the same, so the monthly temperatures differ, on average, 10.5 degrees from the mean of 63 degrees. This means that all of the distributions have the same amount of variability.

c. How will Robert decide to which city he should move to? List possible reasons Robert might have for choosing each city.
Answer:
Robert needs to look more at the shapes of the distributions to help him make a decision.
City D – Appears to have four seasons with widespread temperatures.
City E – Has mainly cold weather and ¡s only hot for 3 months.
City F – Has mainly moderate weather and only a few cold months.

Eureka Math Grade 6 Module 6 Lesson 10 Problem Set Answer Key

Question 1.
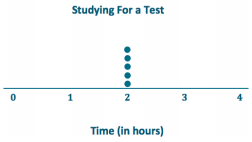
Draw a dot plot of the times that five students studied for a test if the meantime they studied was 2 hours and the MAD was 0 hours.
Answer:
Since the MAD is 0 hours, all data values are all the same, and they would be equal to the mean value.

Question 2.
Suppose the times that five students studied for a test are as follows:

Michelle said that the MAD for this data set is 0 hours because the dot plot is balanced around 2. Without doing any calculations, do you agree with Michelle? Why or why not?
Answer:
No. Michelle is wrong. There is variability within the data set, so the MAD is greater than 0 hours.
Note:
If students agree with Michelle, then they have not yet mastered an understanding that the MAD is measuring variability. They need to understand that if data values differ in a distribution, whether the distribution is symmetric or not, then there is variability. Therefore, the MAD cannot be 0 hours.

Question 3.
Suppose that the number of text messages eight students receive on a typical day is as follows:

a. Draw a dot plot for the number of text messages received on a typical day for these eight students.
Answer:

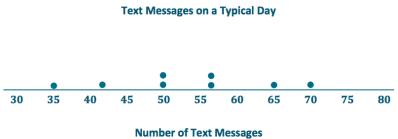
b. Find the mean number of text messages these eight students receive on a typical day.
Answer:
Since the distribution appears to be somewhat symmetrical around a value in the 50’s, students could guess a value for the mean, such as 52 or 53, and then check the sum of the distances on either side of their predictions. Using the formula, the mean is 53 text messages because \(\frac{424}{8}\) = 53.

c. Find the MAD for the number of text messages, and explain its meaning using the words of this problem.
Answer:
The sum of the absolute deviations is 70. So, \(\frac{70}{8}\) yields a MAD of 8. 75 text messages.
This means that, on average, the number of text messages these eight students receive on a typical day differs by 8.75 text messages from the group mean of 53 text messages.

d. Describe the shape of this data distribution.
Answer:
The shape of this distribution is fairly symmetrical (balanced) around the mean of 53 messages.

e. Suppose that in the original data set, Student 3 receives an additional five text messages per day and Student 4 receives five fewer text messages per day.

i. Without doing any calculations, does the mean for the new data set stay the same, increase, or decrease as compared to the original mean? Explain your reasoning.
Answer:
The mean would remain at 53 messages because one data value moved the same number of units to the right as another data value moved to the left. So, the balance point of the distribution does not change.

ii. Without doing any calculations, does the MAD for the new data set stay the same, increase, or decrease as compared to the original MAD? Explain your reasoning.
Answer:
Since the lowest data point moved closer to the mean and the highest dota point moved closer to the mean, the resulting distribution would be more compact than the original distribution. Therefore, the MAD would decrease.

Eureka Math Grade 6 Module 6 Lesson 10 Exit Ticket Answer Key

Question 1.
A dot plot of times that five students studied for a test is displayed below.

a. Calculate the mean number of hours that these five students studied. Then, use the mean to calculate the absolute deviations, and complete the table.
Answer:
The mean is 2 hours since the sums of the distances on either side of 2 hours are equal.

b. Find and interpret the MAD for this data set.
Answer:
\(\frac{5}{5}\) = 1
The MAD is 1 hour. This means that, on average, the study times differed by 1 hour from the group mean of 2 hours.

Question 2.
The same five students are preparing to take a second test. Suppose that the numbers of study hours were the same except that Ben studied 2.5 hours for the second test (1. 5 hours more), and Emma studied only 3 hours for the second test (1. 5 hours less).

a. Without doing any calculations, is the mean for the second test the same as, greater than, or less than the mean for the first test? Explain your reasoning.
Answer:
The mean would be the same since the distance that one data value moved to the right was matched by the distance another data value moved to the left. The distribution is still balanced at the same place.

b. Without doing any calculations, is the MAD for the second test the same as, greater than, or less than the MAD for the first test? Explain your reasoning.
Answer:
The MAD would be smaller since the data values are clustered closer to the mean.

Engage NY Eureka Math Grade 6 Module 6 Lesson 9 Answer Key

Eureka Math Grade 6 Module 6 Lesson 9 Example Answer Key

Example 1: Variability

In Lesson 8, Robert wanted to decide where he would rather move (New York City or San Francisco). He planned to make his decision by comparing the average monthly temperatures for the two cities. Since the mean of the average monthly temperatures for New York City and the mean for San Francisco turned out to be about the same, he decided instead to compare the cities based on the variability in their monthly average temperatures.

He looked at the two distributions and decided that the New York City temperatures were more spread out from their mean than were the San Francisco temperatures from their mean.

Exercises 1 – 3:

The following temperature distributions for seven other cities all have a mean monthly temperature of approximately 63 degrees Fahrenheit. They do not have the same variability.

Exercise 1.
Which distribution has the smallest variability? Explain your answer.
Answer:
City A has the smallest variability because all the data points are the same.

Exercise 2.
Which distribution or distributions seem to have the most variability? Explain your answer.
Answer:
One or more of the following is acceptable: Cities D, E, and F. They appear to have data points that are the most
spread out.

Exercise 3.
Order the seven distributions from least variability to most variability. Explain why you listed the distributions in
the order that you chose.
Answer:
Several orderings are reasonable. Focus on student’s explanations for choosing the order, making sure that the ordering is consistent with an understanding of spread. There are some that will be hard for students to order, and if students have trouble, use this opportunity to point out that it would be useful to have a more formal way to measure variability in a data set. Such a measure is developed in Example 2.

Example 2: Measuring Variability

Based on just looking at the distributions, there are different orderings of variability that seem to make some sense. Sabina is interested in developing a formula that will produce a number that measures the variability in a data distribution. She would then use the formula to measure the variability in each data set and use these values to order the distributions from smallest variability to largest variability. She proposes beginning by looking at how far the values in a data set are from the mean of the data set.

Exercises 4 – 5:

The dot plot for the monthly temperatures in City G is shown below. Use the dot plot and the mean monthly temperature of 63 degrees Fahrenheit to answer the following questions.

City G

Exercise 4.
Fill in the following table for City G’s temperature deviations.

Answer:

Exercise 5.
What is the sum of the distances to the left of the mean? What is the sum of the distances to the right of the mean?
Answer:
The sum of the distances to the left of the mean is 10 + 6 + 3 + 3 = 22. The sum of the distances to the right of the mean is 1 + 1 + 1 + 1 + 1 + 5 + 5 + 7 = 22.

Example 3: Finding the Mean Absolute Deviation (MAD)

Sabina notices that when there is not much variability in a data set, the distances from the mean are small and that when there is a lot of variability in a data set, the data values are spread out and at least some of the distances from the mean are large. She wonders how she can use the distances from the mean to help her develop a formula to measure variability.

Exercises 6 – 7:

Exercise 6.
Use the data on monthly temperatures for City G given in Exercise 4 to answer the following questions.

a. Fill in the following table.

Answer:

b. The absolute deviation for a data value is its distance from the mean of the data set. For example, for the first temperature value for City G (53 degrees), the absolute deviation is 10. What !s the sum of the absolute deviations?
Answer:
The sum of the absolute deviations is 10 + 6 + 3 + 3 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 7 = 44.

c. Sabina suggests that the mean of the absolute deviations (the mean of the distances) could be a measure of the variability in a data set. Its value is the average distance of the data values from the mean of the monthly temperatures. It is called the mean absolute deviation and is denoted by the letters MAD. Find the MAD for this data set of City G’s temperatures. Round to the nearest tenth.
Answer:
The MAD (mean absolute deviation) is \(\frac{44}{12^{\prime}}\) or 3.7 degrees to the nearest tenth of a degree.

d. Find the MAD values in degrees Fahrenheit for each of the seven city temperature distributions and use the values to order the distributions from least variability to most variability. Recall that the mean for each data set is 63 degrees Fahrenheit. Looking only at the distributions, does the list that you made in Exercise 2 match the list made by ordering MAD values?

Answer:
If time is a factor in completing this lesson, assign cities to individual students. After each student has calculated the mean deviation, organize the results for the whole class. Direct students to calculate the MAD to the nearest tenth of a degree.

MAD values (in °F):
City A = 0
City B = 5.3
City C = 3.2
City D = 10.5
City E = 10.5
City F = 10.5
City G = 3.7
The order from least to greatest is A, C, G, B, and D, E, and F(all tied).

e. Which of the following is a correct interpretation of the MAD?
i. The monthly temperatures in City G are all within 3. 7 degrees from the approximate mean of 63 degrees.
ii. The monthly temperatures in City G are, on average, 3. 7 degrees from the approximate mean temperature of 63 degrees.
iii. All of the monthly temperatures in City G differ from the approximate mean temperature of 63 degrees by 3. 7 degrees.
Answer:
The answer is (ii). Remind students that the MAD is an average of the distances from the mean, so some distances may be smaller and some larger than the value of the MAD. Point out that the distances from the mean for City G were not all equal to 3.7 and that some were smaller (for example, the distances of 1 and 3) and that some were larger (for example, the distances of 5 and 10).

Exercise 7.
The dot plot for City A’s temperatures follows.
City A

a. How much variability is there in City A’s temperatures? Why?
Answer:
There is no variability in City A’s temperatures. The absolute deviations (distances from the mean) are all 0.

b. Does the MAD agree with your answer In part (a)?
Answer:
The MAD does agree with my answer from part (a). The value of the MAD is 0.

Eureka Math Grade 6 Module 6 Lesson 9 Problem Set Answer Key

Question 1.
Suppose the dot plot on the left shows the number of goals a boys’ soccer team has scored in six games so far this
season, and the dot plot on the right shows the number of goals a girls’ soccer team has scored in six games so far
this season. The mean for both of these teams is 3.

a. Before doing any calculations, which dot plot has the larger MAD? Explain how you know.
Answer:
The graph of the boys’ team has a larger MAD because the data are more spread out and have the larger distances from the mean.

b. Use the following tables to find the MAD for each distribution. Round your calculations to the nearest hundredth.

Answer:

The MAD for the boy’s team is 2 goals because \(\frac{12}{6}\) = 2. The MAD for the girls’ team is 0.67 goal because \(\frac{4}{6}\) ≈ 0.67

c. Based on the computed MAD values, for which distribution is the mean a better indication of a typical value? Explain your answer.
Answer:
The mean is a better indicator of a typical value for the girl’s team because the measure of variability given by the MAD is lower (0.67 goal) than the boys’ MAD (2 goals).

Question 2.
Recall Robert’s problem of deciding whether to move to New York City or to San Francisco. A table of temperatures (in degrees Fahrenheit) and absolute deviations for New York City follows:

a. The absolute deviations for the monthly temperatures are shown in the above table. Use this information to calculate the MAD. Explain what the MAD means in words.
Answer:
The sum of the absolute deviations is 168. The MAD is the average of the absolute deviations. The MAD is 14 degrees because \(\frac{168}{12}\) = 14. On average, the monthly temperatures in New York City differ from the mean of 63 degrees Fahrenheit by 14 degrees.

b. Complete the following table, and then use the values to calculate the MAD for the San Francisco data distribution.

Answer:
The sum of the absolute deviations is 42. The MAD is the mean of the absolute deviations. The MAD is 3.5 degrees because \(\frac{42}{12}\) = 3. 5.

c. Comparing the MAD values for New York City and San Francisco, which city would Robert choose to move to if he is interested in having a lot of variability in monthly temperatures? Explain using the MAD.
Answer:
New York City has a MAD of 14 degrees, as compared to 3.5 degrees in San Francisco. Robert should choose
New York City if he wants to have more variability in monthly temperatures.

Question 3.
Consider the following data of the number of green jelly beans in seven bags sampled from each of five different candy manufacturers (Awesome, Delight, Finest, Sweeties, YumYum). Note that the mean of each distribution is 42 green jelly beans.

a. Complete the following table of the absolute deviations for the seven bags for each candy manufacturer.

Answer:

b. Based on what you learned about MAD, which manufacturer do you think will have the lowest MAD? Calculate the MAD for the manufacturer you selected.

Answer:
Use the MAD for each manufacturer to evaluate student’s responses.

Eureka Math Grade 6 Module 6 Lesson 9 Exit Ticket Answer Key

Question 1.
The mean absolute deviation (MAD) is a measure of variability for a data set. What does a data distribution look like if its MAD equals zero? Explain.
Answer:
If the MAD is zero, then all of the absolute deviations are zero. The MAD measures the average distance from the mean, and the distance is never negative. The only way the MAD could average to zero is if all the absolute deviations are zero. For example, City A had a dot plot where all of the temperatures were the same. Because all of the temperatures were the same, all of the absolute deviations were zero, which indicates that there was no variability in the temperatures.

Question 2.
Is it possible to have a negative value for the MAD of a data set?
Answer:
Because a MAD is the average of distances, which can never be negative, the MAD is always zero or a positive number.

Question 3.
Suppose that seven students have the following numbers of pets: 1, 1, 1, 2, 4, 4, 8.

a. The mean number of pets for these seven students is 3 pets. Use the following table to find the MAD for this distribution of number of pets.

Answer:
\(\frac{14}{7}\)
The MAD number of pets is 2.

b. Explain in words what the MAD means for this data set.
Answer:
On average, the number of pets for these students differs by 2 from the mean of 3 pets.