The construction of angles is an important part of geometry as this knowledge is extended for the construction of other geometric figures. Constructing angles of unknown and unknown measures can be possible with geometric tools like compass, ruler, protractor. Here we will learn about the Construction of Angles by Using Compass in the following sections. You will find the Construction of Angles using Compass Examples with Solutions explained step by step.
Construction of Angles by Using Compass – Introduction
An angle is defined as the figure formed by two rays meeting at a common endpoint. The representation of angle is ∠. Construction of angles by using compass means you need to make an angle between two straight lines just with the compass. Take one straight line and draw an arc on the line with the compass with any radius from two ends of the line. Get the simple steps in the below-mentioned sections of this page.
Steps to Construct Angle of 60° with Compass
Check out the detailed steps to construct an angle of 60 degrees by using a compass.
- Draw a ray AB.
- By taking either A or B as a center and any suitable radius draw an arc above the ray and cutting at a point P.
- Now, with P as the center and having the same radius, draw another arc that meets the previous arc at C.
- Join AC or BC and produce it to D.
- Then ∠ADB = 60°.
More Related Articles
Construction of Angles by Compass Examples
Example 1:
Construct an acute angle of 30° by using the compass?
Solution:
Take any ray OA

With O as a center and any radius draw an arc on OA at point P and draw another arc with P as the center, same radius.
The point of intersection of two arcs is Q.
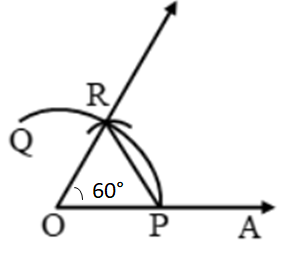
∠AOR = 60°
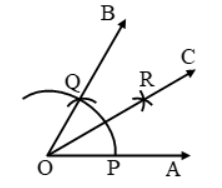
- With center O and any convenient radius draw an arc cutting OA and OB at P and Q respectively.
- With centre P and radius more than \(\frac { 1 }{ 2 } \)(PQ), draw an arc in the interior of ∠AOB.
- With center Q and the same radius, as in step III, draw another arc intersecting the arc in step III at R.
- Join OR and product it to any point C.
- The angle ∠AOC is the angle of measure 30º.
Example 2:
Construct an obtuse angle of 120° by using the compass.
Solution:
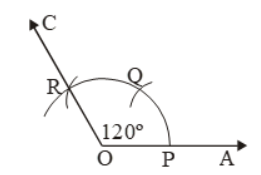
- Draw a ray OA.
- By taking O as the center and any convenient radius, draw an arc cutting OA at P.
- By taking P as a center and same radius draw an arc, cutting the first arc at Q.
- With Q as the center and the same radius, draw an arc cutting the arc drawn in step II at R.
- Join OR and produce it to any point C.
- ∠AOC measures 120º.
Example 3:
Construct an angle of 90° by using the compass.
Solution:
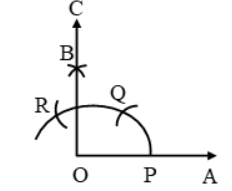
- Draw a ray OA.
- With O as a center and any radius, draw an arc on OA at point P.
- By taking P as the center, the same radius, draw another arc cutting the first arc at point Q.
- With the point, Q as a center and the same radius draw an arc cutting the arc drawn in step II at R.
- By taking point Q as the center and same radius, draw an arc.
- With R as a center and the same radius, draw an arc, cutting the arc drawn in step V at B.
- Draw OB and extend it to C.
- ∠AOC measures an angle is 90º.
Example 4:
Construct an angle of 45° by using the compass.
Solution:
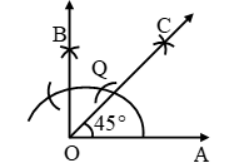
First of all, draw an angle of 90º.
Draw a bisector for 90º to measure 45º.
